1. Introduction
Let
S be a finite probability space. Without loss of generality, suppose that
. Let
be a probability measure on
S. Suppose that a random sample
is drawn from
S according to
. The
missing mass is the random variable
, defined by:
In words, is the total probability mass of the set of those elements of S not observed at all in the sample. According to the definition of , it is easy to verify that . When we wish to make the dependence on the measure explicit, we will write instead of .
One of the earliest mentions of the
missing mass is in Good–Turing frequency estimation [
1]. The latter is a statistical technique for estimating the probability of encountering an object of a hitherto unseen species, given a set of past observations of objects from different species. This estimator has been used extensively in many machine learning tasks. For example, in the field of natural language modeling, for any sample of words, there is a set of words not occurring in that sample. The total probability mass of the words not in the sample is the so-called
missing mass [
2]. Another example of using Good–Turing
missing mass estimation is in [
3], where the total summed probability of all patterns not observed in the training data is estimated. In [
4], Berend and Kontorovich showed that the expectation of the
missing mass is bounded above as follows:
(Additionally, deviation bounds were provided in [
5].)
Moreover, they have shown that:
For an infinitely countable set
S, one cannot generally provide a non-trivial upper bound on
in terms of
t only. Indeed, for each
n, consider the probability measure on
supported on
, giving equal probabilities to these
n atoms. Clearly,
in this case, and the right-hand side becomes arbitrarily close to 1 as
n grows. In [
4] it was shown that
where
roughly measures the size of sets of atoms of comparable mass and
c is a universal constant (for an exact definition, we refer to [
4]). The bound given in (
1) is non-trivial only if the sequence
decreases “sufficiently fast”. Such results may be useful, as shown in [
6,
7,
8,
9]. Another possible restriction that makes the problem interesting is that the entropy of
is bounded above by some given value. A similar restriction can be found in [
10] in the context of discrete distribution estimation under
loss. In this work, we study the possibility of providing tight bounds on
under the restriction of some bound on the entropy. Thus, we can formulate our problem as follows:
subject to
where
is the maximal allowed entropy.
In the case of distributions over countably infinite spaces we set
; otherwise,
, or in short,
. Note that we are looking for the supremum, since in the case
it is not a priori clear that the maximum exists (in fact, it turns out that the maximum does exist—see Theorem 2). Additionally, we will show that the maximum is obtained for a measure with finite support, which leads us to study the problem for the case of distributions over finite spaces. We also study the structure of local and global maxima and obtain some results analogous to [
4].
2. Main Results
Our first result is that in the case of
, an optimal solution exploits all the available entropy. Denote the entropy of a probability measure
by
:
Proposition 1. Let , and let be a probability measure on S. If , then there exists a probability measure on S for which and .
Corollary 1. In the problem given by (2)–(4), we may replace (4) by In Theorem 1, we refer to the case and show that an optimal solution of (2)–(4) cannot assume more than four distinct non-zero values.
Theorem 1. Let , and be any locally optimal solution. Then, the ’s assume at most four non-zero values; i.e., if the ’s are sorted, then for some indices and m, we have .
We do not know whether in some cases there are indeed atoms of four distinct sizes in the optimal solution.
In the case , it is easy to see that is continuous with respect to , and thus attains its maximum. On the other hand, when , it is not a priori clear. Our next result shows that attains its maximum in this case as well.
Theorem 2. Let .
- (i)
For each , the function attains its maximum.
- (ii)
If is a global maximum point of , then has a finite support.
Denote . Recall that for each t.
Theorem 3. For all , we have .
In particular, .
In Theorem 4 we show that given a fixed h, we cannot significantly improve the upper bound from Theorem 3.
Theorem 4. For fixed h and every , if t is large enough then there exists a distribution with , for which .
As mentioned earlier, the parameter t represents the size of the sample. It appears that the optimization problem cannot be solved analytically for any fixed arbitrary t. The following results relate to the case . Obviously, this case is not typical, as one would hardly try to learn much from a sample of size 1. Yet, it may be instructive, as in this case we obtain almost the best possible results.
Proposition 2.
Next, we describe the structure of an optimal solution for the case with .
Proposition 3. Let , and let be an optimal solution of the problemsubject towhere . Then (after sorting), is of the form That is, the non-zero atoms of consist of one “light” atom and “heavy” ones.
Denote the mass of the light atom in the proposition by p and that of the heavy ones by q. In view of Proposition 3, it suffices to consider the case , namely . For , the following proposition gives a tight upper bound on :
Proposition 4. .
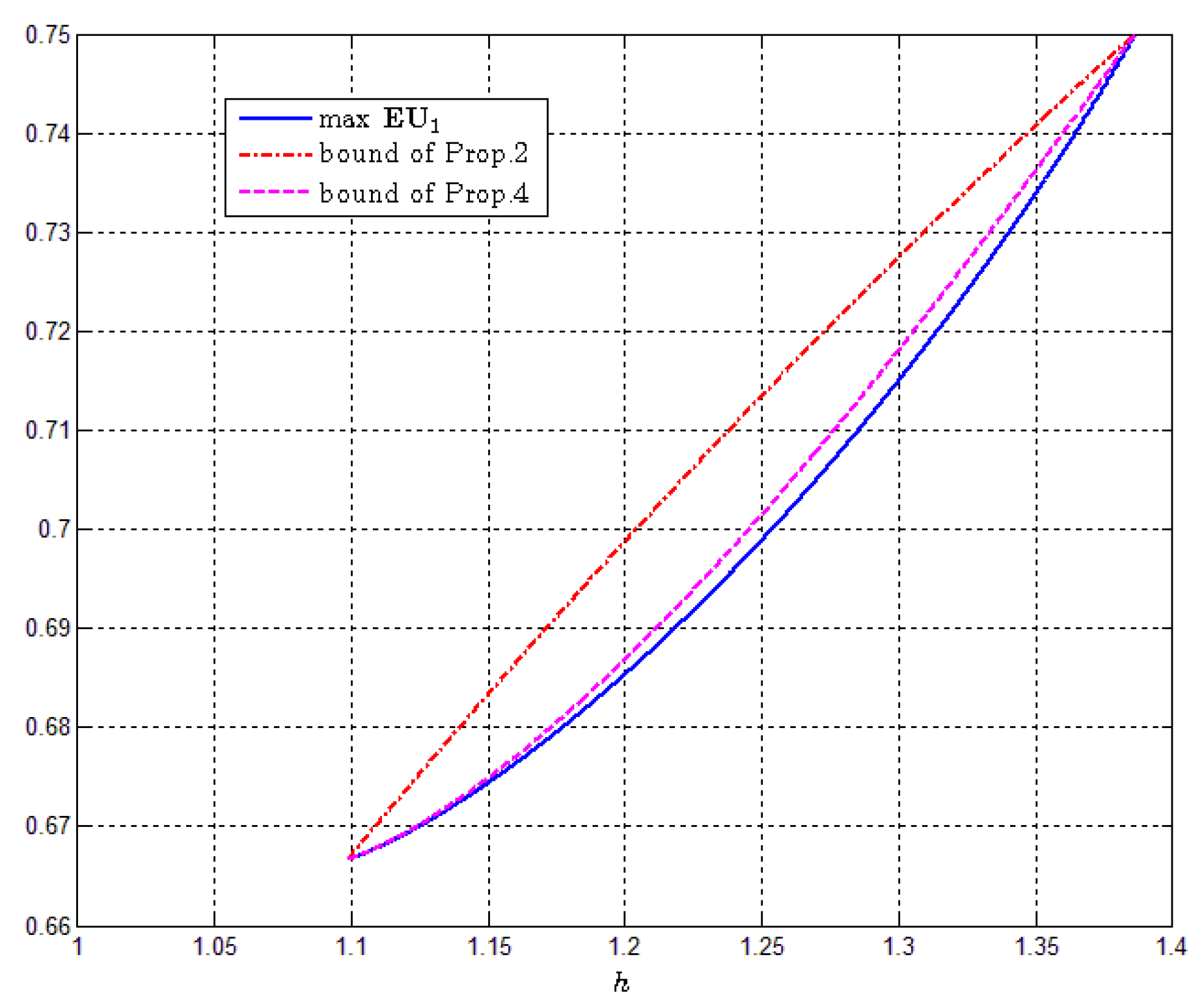
Remark 1. When (or ), there is an equality without the last term (see the proof of Proposition 3). At these points, the last term indeed vanishes. Inside the interval , Proposition 4 provides an improvement over Proposition 2. In Figure 1, we plot the exact value of max (calculated numerically using MATLAB) against the bounds of Propositions 2 and 4 for . It appears that the additional term in Proposition 4 captures most of the error in Proposition 2. 3. Proofs
Proof of Proposition 1. Change the measure
by splitting some atom
i into two atoms of sizes
and
where
and
. Let
be the new measure. The entropy of
is smaller than that of
since
Now
which implies that
. Similarly, splitting any number of atoms, we increase both the entropy and
.
Now, take the first atom, for example, and split it into
k sub-atoms, the first
of which are of size
p each and the
k-th of size
, where
and
, and
k is still to be determined. The entropy of the new measure is
For sufficiently large k and , this entropy becomes arbitrarily large, and in particular exceeds h. Take such a k, and consider the entropy of the obtained measure as p grows continuously from 0 to . For , we have basically the original measure (and thus an entropy less than h), while for the entropy is larger than h. Hence for an appropriate intermediate value of p, the entropy is exactly h. The measure obtained for this p proves our claim. ☐
Proof of Theorem 1. Write down the Lagrangian:
The first-order conditions yield:
We claim that
vanishes at most three times in
. Indeed,
when
Denote the left-hand side of (8) by
. Then:
For every two points for which (8) holds, there is an intermediate point such that . Now, clearly vanishes at no more than two points, so that (8) holds for at most three values of x. It follows that each assumes one of up to (the same) four values. ☐
Before we prove Theorem 2 we need two auxiliary lemmas. For , let be the subset of consisting of all non-increasing sequences satisfying the following properties:
Lemma 1. is compact under the metric.
Proof of Lemma 1. Let be a sequence in , say for . We want to show that it has a convergent subsequence in . Employing the diagonal method, we may assume that converges component-wise. Let be the limit. It is clear that has non-negative and non-increasing entries, so we only need to show that , that , and that in .
Assume first that
. Then, there exists an index
such that
. Hence for sufficiently large
n, we have
, which is a contradiction. Hence
. Now assume that
. Put
. Let
be an integer, to be determined later. We have
for all sufficiently large
n. Note that for every
we have
. Now we can bound from below the tail entropy of
:
Taking large enough, we can make the right-hand side larger than h, which is impossible. Hence .
We now show similarly that . Assume that . Then there exists an such that . Then, however, for sufficiently large n, which yields a contradiction.
To prove convergence in
, we estimate
. Let
. Since
, we can find an
such that
. Due to the component-wise convergence, for sufficiently large
n we have
. For such
n we also have
since
Hence we have convergence in . This proves the lemma. ☐
Example 1. Note that the subset of consisting of all those vectors whose entropy is exactly h is not compact. Let us demonstrate this fact, say, for . We choose , where will be defined momentarily. For arbitrary fixed , put: We claim that there exists a unique solution to the equation . Indeed, this follows readily from the fact that is concave and . Denoting , we have Henceso thatand in particular . Thus, while and , which completes the example. For arbitrary fixed t, the quantity assigns to each point in a real number. We will denote this function by .
Lemma 2. The mapping : is Lipschitz with constant 1 with respect to the metric.
Proof of Lemma 2. Consider the function
given by
. Let
M be the Lipschitz constant for
. According to Lemma 7 from [
4], the candidates for assuming the maximum of
are the points
and
. Now
and
. Hence the Lipschitz constant for
is 1. It follows that if
, then:
☐
Proof of Theorem 2. - (i)
Follows from Lemma 1 and Lemma 2.
- (ii)
Suppose that
does not have a finite support. Then, we can find an
such that the first
entries
of
assume more than four different values. Put
and let
and
. Consider the optimization problem
subject to
Theorem 1 is still applicable to (9)–(11) with a minor variation. In the beginning of the proof, replace the Lagrangian by
and proceed as previously. Since
maximizes
, the vector
is a global optimum of this finite-dimensional problem. By Theorem 1,
cannot assume more than four distinct values.
☐
Proof of Theorem 3. For each term on the right-hand side of (12) and for
, we have
Proof of Theorem 4. Let
be an integer and
. Define
by:
Proof of Proposition 2. Let
P be the random variable assigning to each atom
its probability:
Denote
. Then:
The function
is concave, so by Jensen’s inequality:
☐
Remark 2. If for some positive integer k, then the bound is attained for the uniform distribution on a space of k points.
Proof of Proposition 3. First, in the case where we have a unique optimal solution, which is . It is straightforward to check that is feasible and attains the upper bound in Proposition 2, and is optimal. Moreover, is unique because any feasible non-uniform choice of leads to a strict inequality in Jensen’s inequality that was used in Proposition 2.
Thus, we deal with the case of strict inequalities,
. We start by showing that any optimal solution
assumes at most two non-zero distinct values. Write down the Lagrangian:
The first-order conditions yield, at any optimal point,
for every
i with
. Define the function
f by
. The function vanishes at most twice in
because its derivative
vanishes at most once. Thus, the non-zero
s assume at most two distinct values. In fact, if all were equal, we would have
, where
k is the number of non-zero
s, so that we would have exactly two distinct values for the
s. Disposing of the points of mass 0, we may assume that all
n points of
S have positive mass. Denote the number of “light” atoms by
ℓ. We will show that
decreases as we increase
ℓ. Denote the mass of a “light” atom by
p and write down the entropy constraint with
ℓ “light” atoms and
“heavy” ones:
Now, define the function
by:
Note that we treat
ℓ as a continuous variable. The equation
implicitly defines the function
. Using the implicit function theorem, we can write an analytic expression for
:
Now write down
as a function of
ℓ and take the derivative with respect to
ℓ:
Notice that the term
is actually the mass of the “heavy” atom, so to simplify notation we put
. Substituting the expression for
, we obtain:
To show that
decreases as we increase
ℓ, it is enough to check that
. It suffices to work out the second term in the product of (14). Using the change of variables
, we may write:
It is straightforward to check that
:
Notice that
, and hence it is enough to check that the numerator is negative. Indeed,
and
Now and . Thus, .
It follows that ℓ should be as small as possible, which means (since there is at least one light atom) that . Finally, as there is one light atom and heavy ones, the entropy h lies in the interval . Reverting to the original notations, we have . ☐
Proof of Proposition 4. We use the following refinement of Jensen’s inequality [
11]: For any random variable
X and concave function
,
where
denotes the right-hand derivative of
. For
and
, the left-hand side of (15) is
The right-hand side of (15) gives:
☐