A Novel Geometric Dictionary Construction Approach for Sparse Representation Based Image Fusion
Abstract
:1. Introduction
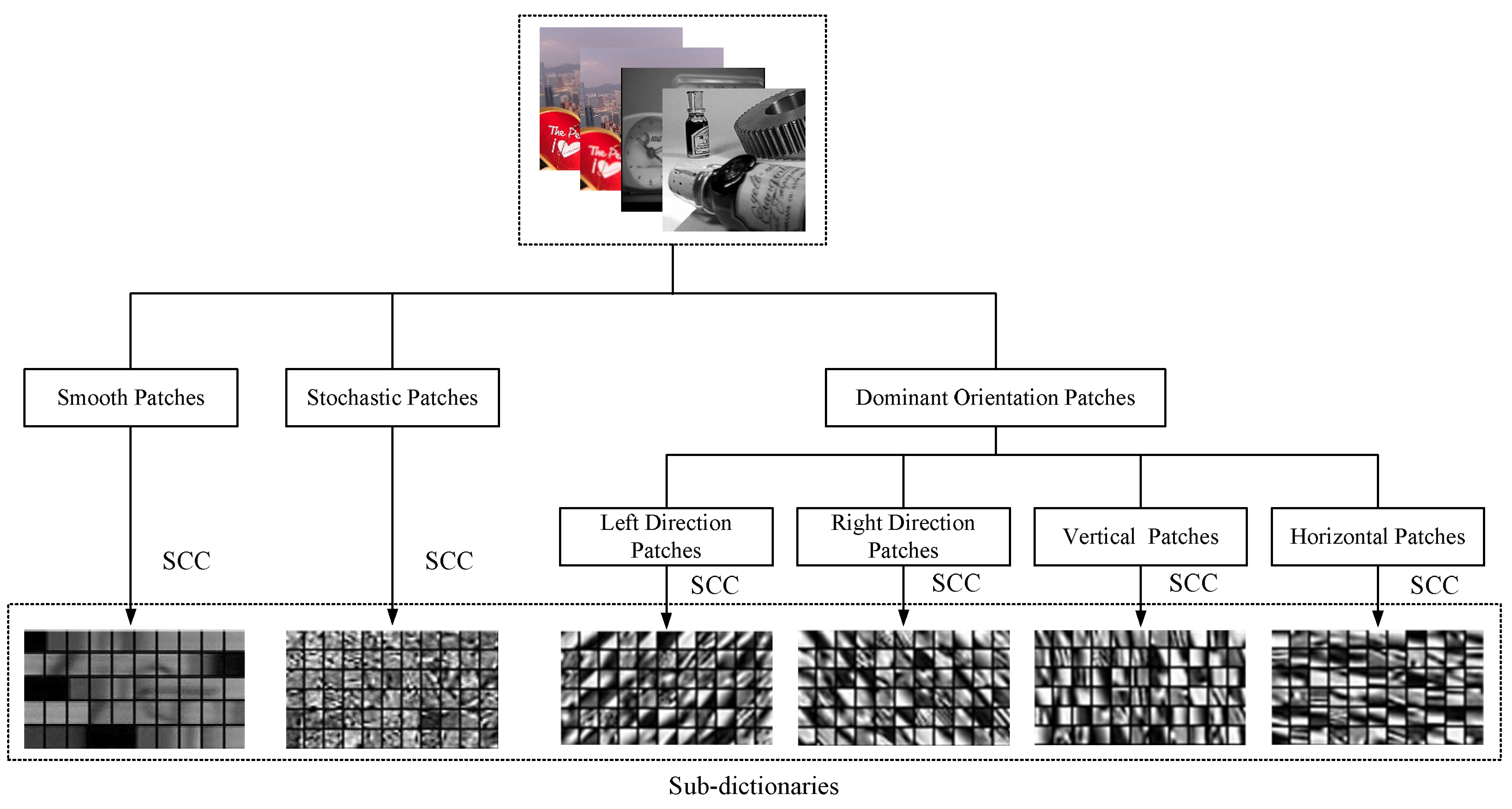
- A geometric-information based classification method is proposed and applied to a sub-dictionary learning of image patches. The proposed classification method can accurately split source image patches into different groups for sub-dictionary learning based on the corresponding geometry features. Sub-dictionary bases extracted from each image-patch group contain the key geometry features of source images. These extracted sub-dictionary bases are trained to form informative and compact sub-dictionaries for image fusion.
- A dictionary combination method is developed to construct an informative and compact sub-dictionary. Each image patch of a fused image is composed of corresponding source image patches using a constructed-sub-dictionary (CSD). According to the classification of geometry features, each source image patch is trained and categorized into a group of sub-dictionaries. Corresponding image patches, that appear at the same place of the two source images, at most have two groups of sub-dictionary. Redundant geometric information of source image patches is eliminated.
2. Geometry-Based Image Fusion Framework
2.1. Dictionary Learning
| Algorithm 1 SCC Algorithm. |
| Input: Image patches of Wth cluster Output: Sub-dictionary , and for Initialize , , and for for to ∂ do for to n do Get image patch Update via one or a few steps of coordinate descent: Update the Hessian matrix and the learning rate: Update the support of the dictionary via SGD (Stochastic Gradient Descent): if then Set end if end for end for |
| Algorithm 2 SOMP Algorithm. |
| Input: Dictionary D, image patches , , threshold , an empty matrix Output: Sparse coefficients Initialize the residuals , for , set iteration counter . Select the index which indicates the next best coefficient atom to simultaneously provide good reconstruction for all signals by solving: . Update sets . Compute new coefficients (sparse representations), approximations, and residuals as: , for , , for , , for . Increase the iteration counter , if , go back to step 2. |
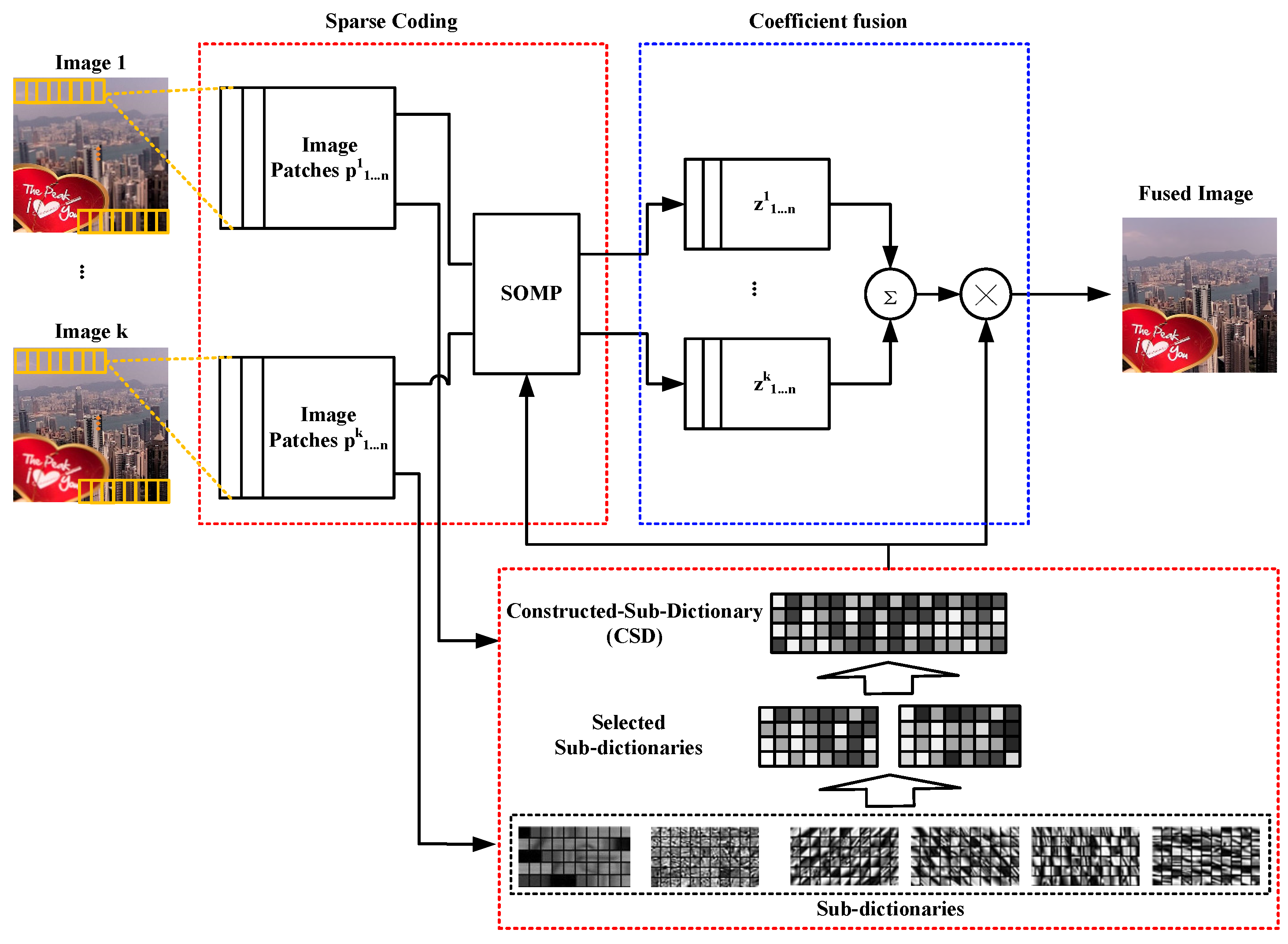
2.2. Image Sparse Coding and Fusion
- Step 1: Use the sliding window technique to divide each source image , from left-top to right-bottom, into patches of size , i.e., the size of the atom in the dictionary. These image patches are vectorized to image pixel vectors in the linewise direction. The obtained image pixel vectors only have one dimension.
- Step 2: For the ith image patch of one source image , it can be sparse coded using the trained dictionary D.
- Step 3: When all of the image patches are sparse coded, the corresponding image patches of each image use Equation (5) to do fusion:where is a sparse coefficient corresponding to the i-th image patch in j-th image .
- Step 4: Fused coefficients are inversely transformed to fused image pixel vectors, using Equation (6), and transform these vectors back to the fused image patches. Then, it reconstructs the fused image by using fused image patches. The dictionary D in Equation (6) is the same as dictionary D in Algorithm 3:
| Algorithm 3 CSD Construction Algorithm. |
| Input: Sub-dictionaries , image patches for fusion and Output: CSD D Figure out sub-dictionaries , , that correspond to image patch groups of and . ifthen Set else Set end if |
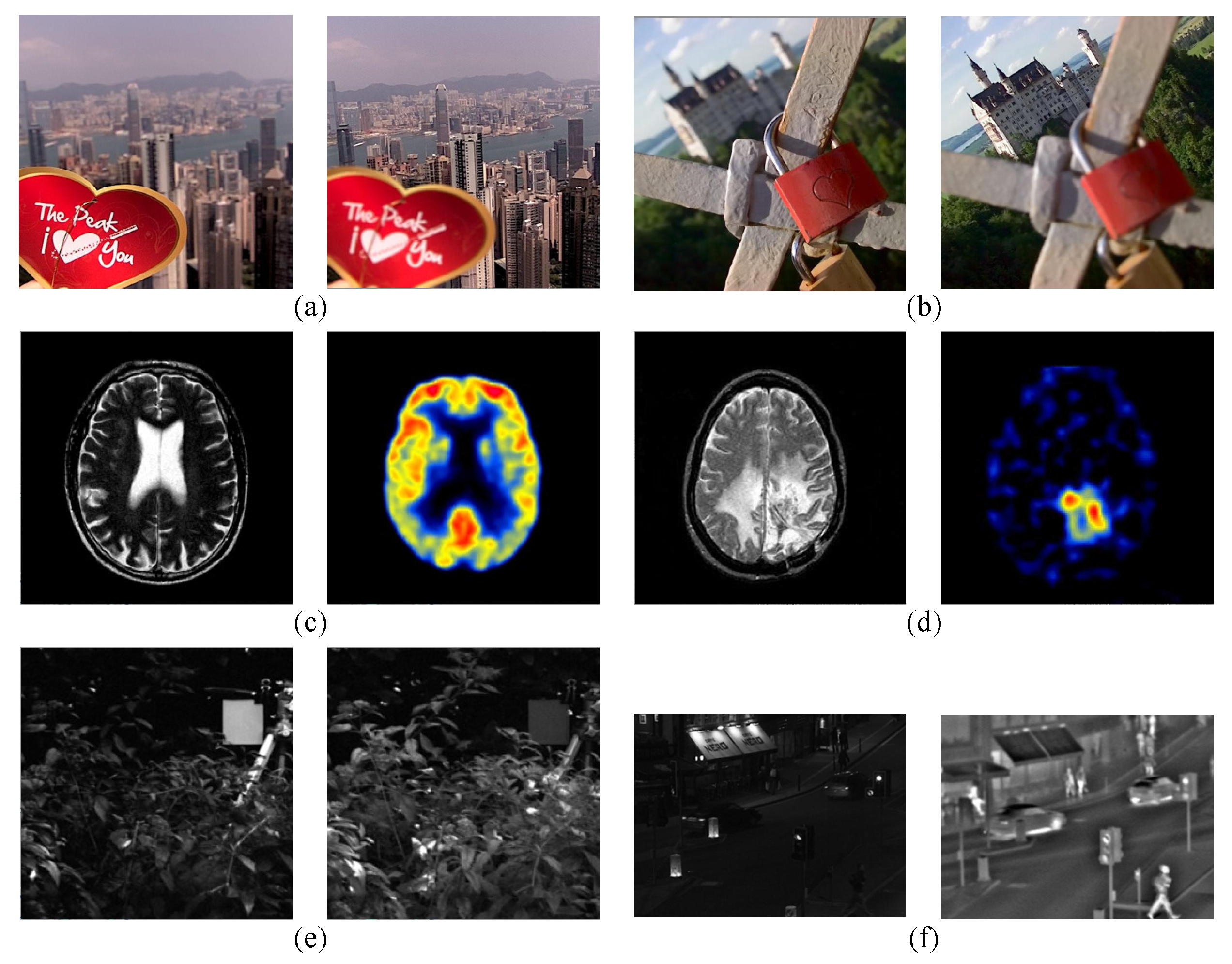
3. Experiments and Analyses
- Twenty pairs of size multi-focus images are obtained from the Lytro-multi-focus data-set http://mansournejati.ece.iut.ac.ir.
- Thirty pairs of medical images are from www.med.harvard.edu/aanlib/home.html. All of them are size.
- Ten pairs of visible-infrared images are obtained from from www.quxiaobo.org consisting of four and six image pairs.
3.1. Objective Evaluation Methods
3.1.1. Mutual Information
3.1.2.
3.1.3. Visual Information Fidelity
3.1.4.
3.1.5.
3.2. Image Quality
3.2.1. Multi-Focus Comparison
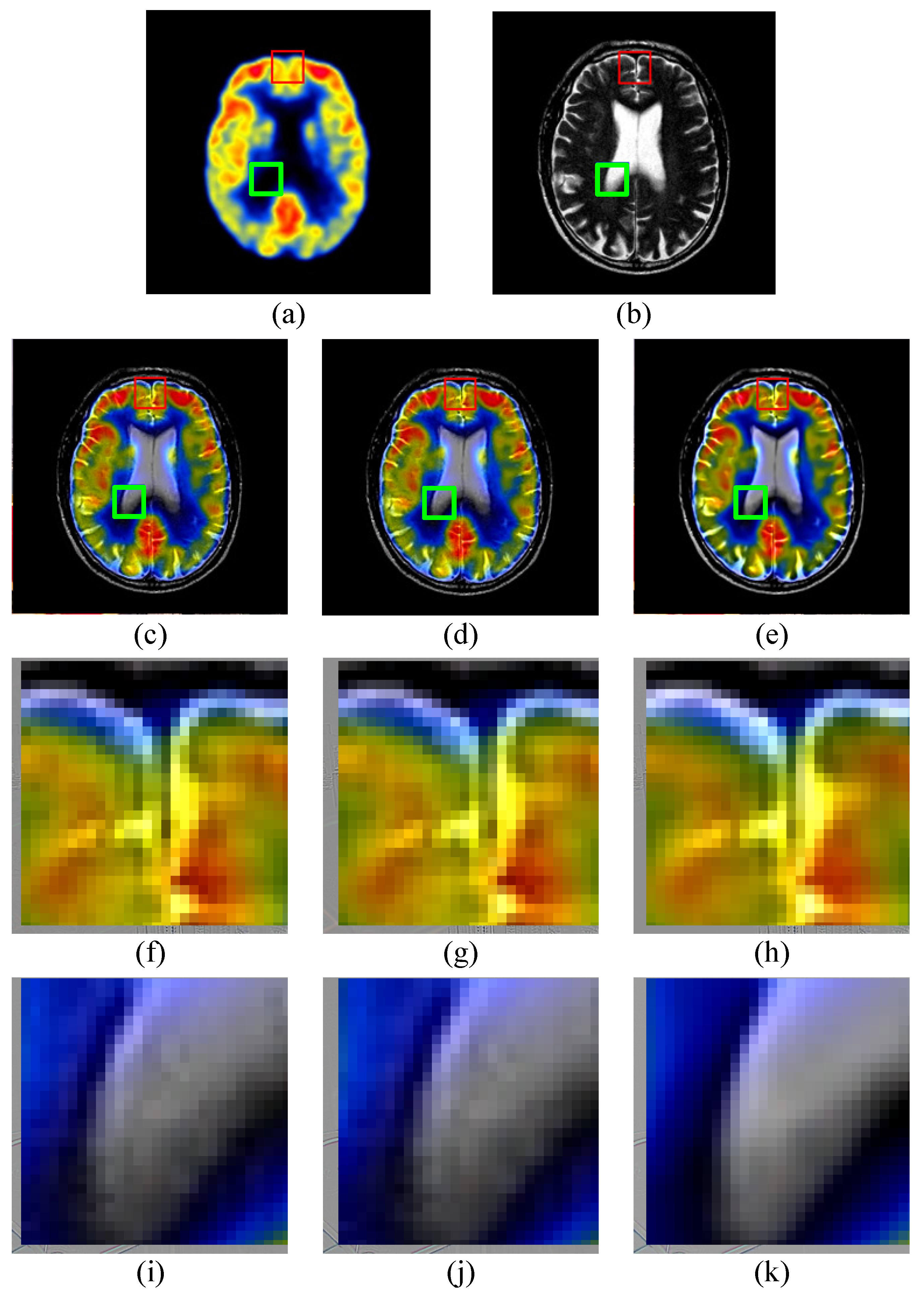
3.2.2. Medical Comparison
3.2.3. Visible-Infrared Comparison
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, S.; Kang, X.; Hu, J.; Yang, B. Image matting for fusion of multi-focus images in dynamic scenes. Inf. Fusion 2013, 14, 147–162. [Google Scholar] [CrossRef]
- Zhu, Z.; Qi, G.; Chai, Y.; Li, P. A Geometric Dictionary Learning Based Approach for Fluorescence Spectroscopy Image Fusion. Appl. Sci. 2017, 7, 161. [Google Scholar] [CrossRef]
- Li, H.; Chai, Y.; Li, Z. A new fusion scheme for multifocus images based on focused pixels detection. Mach. Vis. Appl. 2013, 24, 1167–1181. [Google Scholar] [CrossRef]
- Nejati, M.; Samavi, S.; Shirani, S. Multi-focus image fusion using dictionary-based sparse representation. Inf. Fusion 2015, 25, 72–84. [Google Scholar] [CrossRef]
- Li, H.; Liu, X.; Yu, Z.; Zhang, Y. Performance improvement scheme of multifocus image fusion derived by difference images. Signal Process. 2016, 128, 474–493. [Google Scholar] [CrossRef]
- Li, S.; Yang, B. Multifocus image fusion using region segmentation and spatial frequency. Image Vis. Comput. 2008, 26, 971–979. [Google Scholar] [CrossRef]
- Keerqinhu; Qi, G.; Tsai, W.; Hong, Y.; Wang, W.; Hou, G.; Zhu, Z. Fault-Diagnosis for Reciprocating Compressors Using Big Data. In Proceedings of the Second IEEE International Conference on Big Data Computing Service and Applications, Big Data Service 2016, Oxford, UK, 29 March–1 April 2016; pp. 72–81. [Google Scholar]
- Li, H.; Yu, Z.; Mao, C. Fractional differential and variational method for image fusion and super-resolution. Neurocomputing 2016, 171, 138–148. [Google Scholar] [CrossRef]
- Wang, K.; Chai, Y.; Su, C. Sparsely corrupted stimulated scattering signals recovery by iterative reweighted continuous basis pursuit. Rev. Sci. Instrum. 2014, 84, 83–103. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Qiu, H.; Yu, Z.; Zhang, Y. Infrared and visible image fusion scheme based on NSCT and low-level visual features. Infrared Phys. Technol. 2016, 76, 174–184. [Google Scholar] [CrossRef]
- Tsai, W.; Qi, G.; Zhu, Z. Scalable SaaS Indexing Algorithms with Automated Redundancy and Recovery Management. Int. J. Softw. Inform. 2013, 7, 63–84. [Google Scholar]
- Li, S.; Yang, B.; Hu, J. Performance comparison of different multi-resolution transforms for image fusion. Inf. Fusion 2011, 12, 74–84. [Google Scholar] [CrossRef]
- Li, H.; Qiu, H.; Yu, Z.; Li, B. Multifocus image fusion via fixed window technique of multiscale images and non-local means filtering. Signal Process. 2017, 138, 71–85. [Google Scholar] [CrossRef]
- Vijayarajan, R.; Muttan, S. Discrete wavelet transform based principal component averaging fusion for medical images. AEU Int. J. Electron. Commun. 2015, 69, 896–902. [Google Scholar] [CrossRef]
- Pajares, G.; de la Cruz, J.M. A wavelet-based image fusion tutorial. Pattern Recognit. 2004, 37, 1855–1872. [Google Scholar] [CrossRef]
- Makbol, N.M.; Khoo, B.E. Robust blind image watermarking scheme based on Redundant Discrete Wavelet Transform and Singular Value Decomposition. AEU Int. J. Electron. Commun. 2013, 67, 102–112. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, Z.; Wu, X. A novel algorithm of remote sensing image fusion based on shift-invariant Shearlet transform and regional selection. AEU Int. J. Electron. Commun. 2016, 70, 186–197. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Y.; Wang, J. Image fusion based on shearlet transform and regional features. AEU Int. J. Electron. Commun. 2014, 68, 471–477. [Google Scholar] [CrossRef]
- Sulochana, S.; Vidhya, R.; Manonmani, R. Optical image fusion using support value transform (SVT) and curvelets. Opt. Int. J. Light Electron Opt. 2015, 126, 1672–1675. [Google Scholar] [CrossRef]
- Yu, B.; Jia, B.; Ding, L.; Cai, Z.; Wu, Q.; Law, R.; Huang, J.; Song, L.; Fu, S. Hybrid dual-tree complex wavelet transform and support vector machine for digital multi-focus image fusion. Neurocomputing 2016, 182, 1–9. [Google Scholar] [CrossRef]
- Seal, A.; Bhattacharjee, D.; Nasipuri, M. Human face recognition using random forest based fusion of à-trous wavelet transform coefficients from thermal and visible images. AEU Int. J. Electron. Commun. 2016, 70, 1041–1049. [Google Scholar] [CrossRef]
- Qu, X.B.; Yan, J.W.; Xiao, H.Z.; Zhu, Z.Q. Image Fusion Algorithm Based on Spatial Frequency-Motivated Pulse Coupled Neural Networks in Nonsubsampled Contourlet Transform Domain. Acta Autom. Sin. 2008, 34, 1508–1514. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image Denoising Via Learned Dictionaries and Sparse representation. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2006), New York, NY, USA, 17–22 June 2006; pp. 895–900. [Google Scholar]
- Dar, Y.; Bruckstein, A.M.; Elad, M.; Giryes, R. Postprocessing of Compressed Images via Sequential Denoising. IEEE Trans. Image Process. 2016, 25, 3044–3058. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Hirakawa, K. Blind Deblurring and Denoising of Images Corrupted by Unidirectional Object Motion Blur and Sensor Noise. IEEE Trans. Image Process. 2016, 25, 4129–4144. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Yu, Y.; Sun, F.; Gu, J. Visual-Tactile Fusion for Object Recognition. IEEE Trans. Autom. Sci. Eng. 2016, 14, 1–13. [Google Scholar] [CrossRef]
- Tsai, W.T.; Qi, G.; Hu, K. Autonomous Decentralized Combinatorial Testing. In Proceedings of the 2015 IEEE Twelfth International Symposium on Autonomous Decentralized Systems, Taichung, Taiwan, 25–27 March 2015; pp. 40–47. [Google Scholar]
- Zhang, Y.; Liu, J.; Yang, W.; Guo, Z. Image Super-Resolution Based on Structure-Modulated Sparse Representation. IEEE Trans. Image Process. 2015, 24, 2797–2810. [Google Scholar] [CrossRef] [PubMed]
- Tsai, W.T.; Qi, G. Integrated Adaptive Reasoning Testing Framework with Automated Fault Detection. In Proceedings of the 2015 IEEE Symposium on Service-Oriented System Engineering, San Francisco Bay, CA, USA, 30 March–3 April 2015; pp. 169–178. [Google Scholar]
- Yang, B.; Li, S. Multifocus Image Fusion and Restoration With Sparse Representation. IEEE Trans. Instrum. Meas. 2010, 59, 884–892. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Z. A general framework for image fusion based on multi-scale transform and sparse representation. Inf. Fusion 2015, 24, 147–164. [Google Scholar] [CrossRef]
- Yin, M.; Duan, P.; Liu, W.; Liang, X. A novel infrared and visible image fusion algorithm based on shift-invariant dual-tree complex shearlet transform and sparse representation. Neurocomputing 2017, 226, 182–191. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Yin, H.; Li, Y.; Chai, Y.; Liu, Z.; Zhu, Z. A novel sparse-representation-based multi-focus image fusion approach. Neurocomputing 2016, 216, 216–229. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; He, N. Exposure fusion based on sparse representation using approximate K-SVD. Neurocomputing 2014, 135, 145–154. [Google Scholar] [CrossRef]
- Kim, M.; Han, D.K.; Ko, H. Joint patch clustering-based dictionary learning for multimodal image fusion. Inf. Fusion 2016, 27, 198–214. [Google Scholar] [CrossRef]
- Zhu, Z.; Chai, Y.; Yin, H.; Li, Y.; Liu, Z. A novel dictionary learning approach for multi-modality medical image fusion. Neurocomputing 2016, 214, 471–482. [Google Scholar] [CrossRef]
- Zhu, Z.; Qi, G.; Chai, Y.; Chen, Y. A Novel Multi-Focus Image Fusion Method Based on Stochastic Coordinate Coding and Local Density Peaks Clustering. Future Int. 2016, 8, 53. [Google Scholar] [CrossRef]
- Yang, S.; Wang, M.; Chen, Y.; Sun, Y. Single-Image Super-Resolution Reconstruction via Learned Geometric Dictionaries and Clustered Sparse Coding. IEEE Trans. Image Process. 2012, 21, 4016–4028. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Qi, G.; Chai, Y.; Yin, H.; Sun, J. A Novel Visible-infrared Image Fusion Framework for Smart City. Int. J. Simul. Process Model. 2016, in press. [Google Scholar]
- Yang, M.; Zhang, L.; Feng, X.; Zhang, D. Sparse Representation Based Fisher Discrimination Dictionary Learning for Image Classification. Int. J. Comput. Vis. 2014, 109, 209–232. [Google Scholar] [CrossRef]
- Tsai, W.T.; Qi, G. Integrated fault detection and test algebra for combinatorial testing in TaaS (Testing-as-a-Service). Simul. Model. Pract. Theory 2016, 68, 108–124. [Google Scholar] [CrossRef]
- Edelman, A. Eigenvalues and Condition Numbers of Random Matrices. SIAM J. Matrix Anal. Appl. 1988, 9, 543–560. [Google Scholar] [CrossRef]
- Lin, B.; Li, Q.; Sun, Q.; Lai, M.J.; Davidson, I.; Fan, W.; Ye, J. Stochastic Coordinate Coding and Its Application for Drosophila Gene Expression Pattern Annotation. arXiv, 2014; arXiv:1407.8147. [Google Scholar]
- Yang, B.; Li, S. Pixel-level image fusion with simultaneous orthogonal matching pursuit. Inf. Fusion 2012, 13, 10–19. [Google Scholar] [CrossRef]
- Wu, W.; Tsai, W.T.; Jin, C.; Qi, G.; Luo, J. Test-Algebra Execution in a Cloud Environment. In Proceedings of the 2014 IEEE 8th International Symposium on Service Oriented System Engineering, Oxford, UK, 7–11 April 2014; pp. 59–69. [Google Scholar]
- Petrovic, V.S. Subjective tests for image fusion evaluation and objective metric validation. Inf. Fusion 2007, 8, 208–216. [Google Scholar] [CrossRef]
- Wang, Q.; Shen, Y.; Zhang, Y.; Zhang, J.Q. Fast quantitative correlation analysis and information deviation analysis for evaluating the performances of image fusion techniques. IEEE Trans. Instrum. Meas. 2004, 53, 1441–1447. [Google Scholar] [CrossRef]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhang, J.Q.; Wang, X.R.; Liu, X. A novel similarity based quality metric for image fusion. Inf. Fusion 2008, 9, 156–160. [Google Scholar] [CrossRef]
- Liu, Z.; Blasch, E.; Xue, Z.; Zhao, J.; Laganiere, R.; Wu, W. Objective Assessment of Multiresolution Image Fusion Algorithms for Context Enhancement in Night Vision: A Comparative Study. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 94–109. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Blum, R.S. A new automated quality assessment algorithm for image fusion. Image Vis. Comput. 2009, 27, 1421–1432. [Google Scholar] [CrossRef]
- Tsai, W.T.; Luo, J.; Qi, G.; Wu, W. Concurrent Test Algebra Execution with Combinatorial Testing. In Proceedings of the 2014 IEEE 8th International Symposium on Service Oriented System Engineering, Oxford, UK, 7–11 April 2014; pp. 35–46. [Google Scholar]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A Critical Comparison Among Pansharpening Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Tsai, W.T.; Qi, G.; Chen, Y. A Cost-Effective Intelligent Configuration Model in Cloud Computing. In Proceedings of the 2012 32nd International Conference on Distributed Computing Systems Workshops, Macau, China, 18–21 June 2012; pp. 400–408. [Google Scholar]
- Tsai, W.T.; Qi, G. DICB: Dynamic Intelligent Customizable Benign Pricing Strategy for Cloud Computing. In Proceedings of the 2012 IEEE Fifth International Conference on Cloud Computing, Honolulu, HI, USA, 24–29 June 2012; pp. 654–661. [Google Scholar]


| K-SVD | 0.4753 | 4.5992 | 0.7705 | 0.6897 | 0.6408 |
| JCPD | 0.5331 | 4.5586 | 0.7571 | 0.7403 | 0.6317 |
| Proposed | 0.5374 | 4.9561 | 0.7778 | 0.7420 | 0.6613 |
| K-SVD | 0.2886 | 1.8554 | 0.2831 | 0.3294 | 0.6700 |
| JCPD | 0.2880 | 1.8575 | 0.2829 | 0.3290 | 0.6680 |
| Proposed | 0.3088 | 1.8869 | 0.2878 | 0.3591 | 0.6854 |
| K-SVD | 0.4784 | 1.7713 | 0.3585 | 0.5670 | 0.5370 |
| JCPD | 0.5648 | 1.4563 | 0.3173 | 0.6562 | 0.4653 |
| Proposed | 0.6449 | 1.8398 | 0.3597 | 0.7647 | 0.5437 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Qi, G.; Zhu, Z.; Chai, Y. A Novel Geometric Dictionary Construction Approach for Sparse Representation Based Image Fusion. Entropy 2017, 19, 306. https://doi.org/10.3390/e19070306
Wang K, Qi G, Zhu Z, Chai Y. A Novel Geometric Dictionary Construction Approach for Sparse Representation Based Image Fusion. Entropy. 2017; 19(7):306. https://doi.org/10.3390/e19070306
Chicago/Turabian StyleWang, Kunpeng, Guanqiu Qi, Zhiqin Zhu, and Yi Chai. 2017. "A Novel Geometric Dictionary Construction Approach for Sparse Representation Based Image Fusion" Entropy 19, no. 7: 306. https://doi.org/10.3390/e19070306
APA StyleWang, K., Qi, G., Zhu, Z., & Chai, Y. (2017). A Novel Geometric Dictionary Construction Approach for Sparse Representation Based Image Fusion. Entropy, 19(7), 306. https://doi.org/10.3390/e19070306







