Node Importance Ranking of Complex Networks with Entropy Variation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methods
2.1.1. Entropy Variation as a Metric of Node Importance
2.1.2. Rank the Top-k Most Important Nodes
| Algorithm 1. Rank the Top-k Most Important Nodes. | |
| Input: | Graph with |
| Output: | Top-k most important nodes with their corresponding importance series |
| 1: | Calculate , the entropy of graph as in Equation (5) |
| 2: | For each do |
| 3: | Generate by removing from as in Equation (11) |
| 4: | Calculate , the entropy of as in Equation (5) |
| 5: | Set the importance of as in Equation (10) |
| 6: | End for |
| 7: | Get the importance sequence: |
| 8: | Get the descending importance series: |
| 9: | Return , the first elements of |
2.1.3. Performance Evaluation
2.2. Materials
2.2.1. Snake Idioms Network
2.2.2. Other Well-Known Networks to Be Investigated
3. Results
3.1. On the Snake Idioms Network
3.2. On Other Well-Known Networks
4. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
References
- Ye, C.; Wilson, R.C.; Comin, C.H.; Costa, L.D.; Hancock, E.R. Approximate von Neumann entropy for directed graphs. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 5, 052804. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.K.; Zhang, S.S.; Dang, W.D.; Li, S.; Cai, Q. Multilayer network from multivariate time series for characterizing nonlinear flow behavior. Int. J. Bifurc. Chaos 2017, 27, 1750059. [Google Scholar] [CrossRef]
- Gao, Z.K.; Cai, Q.; Yang, Y.X.; Dong, N.; Zhang, S.S. Visibility graph from adaptive optimal kernel time-frequency representation for classification of epileptiform EEG. Int. J. Neural Syst. 2017, 27, 1750005. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.K.; Dang, W.D.; Yang, Y.X.; Cai, Q. Multiplex multivariate recurrence network from multi-channel signals for revealing oil-water spatial flow behavior. Chaos 2017, 27, 035809. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.K.; Small, M.; Kurths, J. Complex network analysis of time series. EPL 2016, 116, 50001. [Google Scholar] [CrossRef]
- Lü, L.; Chen, D.; Ren, X.L.; Zhang, Q.M.; Zhang, Y.C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Chen, D.; Lü, L.; Shang, M.S.; Zhang, Y.C.; Zhou, T. Identifying influential nodes in complex networks. Phys. A Stat. Mech. Appl. 2012, 4, 1777–1787. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Zhang, H.; Guan, Z.H.; Li, T.; Zhang, X.H.; Zhang, D.X. A stochastic sir epidemic on scale-free network with community structure. Phys. A Stat. Mech. Appl. 2013, 392, 974–981. [Google Scholar] [CrossRef]
- Richardson, M.; Domingos, P. Mining knowledge-sharing sites for viral marketing. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’02), New York, NY, USA, 23–25 July 2002; pp. 61–70. [Google Scholar]
- Radicchi, F.; Fortunato, S.; Markines, B.; Vespignani, A. Diffusion of scientific credits and the ranking of scientists. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 80, 056103. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Xie, H.; Maslov, S.; Redner, S. Finding scientific gems with Google’s PageRank algorithm. J. Informetr. 2008, 1, 8–15. [Google Scholar] [CrossRef]
- Csermely, P.; Korcsmáros, T.; Kiss, H.J.M.; London, G.; Nussinov, R. Structure and dynamics of molecular networks: A novel paradigm of drug discovery. Pharmacol. Ther. 2013, 3, 333–408. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Albert, I.; Nakarado, G.L. Structural vulnerability of the North American power grid. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 69, 025103. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Hatano, N. A vibrational approach to node centrality and vulnerability in complex networks. Phys. A Stat. Mech. Appl. 2009, 17, 3648–3660. [Google Scholar] [CrossRef]
- Chen, G.R.; Wang, X.F.; Li, X. Introduction to Complex Networks: Models, Structures and Dynamics; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1979, 3, 215–239. [Google Scholar] [CrossRef]
- Hage, P.; Harary, F. Eccentricity and centrality in networks. Soc. Netw. 1995, 1, 57–63. [Google Scholar] [CrossRef]
- Korn, A.; Schubert, A.; Telcs, A. Lobby index in networks. Phys. A Stat. Mech. Appl. 2008, 11, 2221–2226. [Google Scholar] [CrossRef]
- Hébertdufresne, L.; Allard, A.; Young, J.G.; Dubé, L.J. Global efficiency of local immunization on complex networks. Sci. Rep. 2012, 8, 2171. [Google Scholar]
- Brin, S.; Page, L. Reprint of: The anatomy of a large-scale hypertextual web search engine. Comput. Netw. 2012, 18, 3825–3833. [Google Scholar] [CrossRef]
- Kleinberg, J.M. Authoritative Sources in a Hyperlinked Environment. J. ACM 1999, 5, 604–632. [Google Scholar] [CrossRef]
- Estrada, E.; Rodríguez-Velázquez, J.A. Subgraph centrality in complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 2, 056103. [Google Scholar] [CrossRef] [PubMed]
- Stephenson, K.; Zelen, M. Rethinking centrality: Methods and examples. Soc. Netw. 1989, 1, 1–37. [Google Scholar] [CrossRef]
- Bonacich, P.; Paulette, L. Eigenvector-like measures of centrality for asymmetric relations. Soc. Netw. 2001, 23, 191–201. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 1, 35–41. [Google Scholar] [CrossRef]
- Brandes, U. On Variants of Shortest-Path Betweenness Centrality and their Generic Computation. Soc. Netw. 2008, 30, 136–145. [Google Scholar] [CrossRef]
- Shimbel, A. Structural Parameters of Communication Networks. Bull. Math. Biophys. 1953, 15, 501–507. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Everett, M.G. A graph-theoretic perspective on centrality. Soc. Netw. 2006, 4, 466–484. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 7291, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Anand, K.; Krioukov, D.; Bianconi, G. Entropy distribution and condensation in random networks with a given degree distribution. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 6, 062807. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Tan, Q.; Zhang, Y. Network connectivity entropy and its application on network connectivity reliability. Phys. A Stat. Mech. Appl. 2013, 21, 5536–5541. [Google Scholar] [CrossRef]
- Sorkhoh, I.; Mahdi, K.; Safar, M. Cyclic Entropy of Complex Networks. In Proceedings of the IEEE/AXM International Conference on Advances in Social Networks Analysis and Mining, Istanbul, Turkey, 26–29 August 2012; pp. 1050–1055. [Google Scholar]
- Nie, T.; Guo, Z.; Zhao, K.; Lu, Z.M. Using mapping entropy to identify node centrality in complex networks. Phys. A Stat. Mech. Appl. 2016, 453, 290–297. [Google Scholar] [CrossRef]
- Yuan, P.; Ma, H.; Fu, H. Hotspot-entropy based data forwarding in opportunistic social networks. Pervasive Mob. Comput. 2015, 16, 136–154. [Google Scholar] [CrossRef]
- Franzosi, R.; Felice, D.; Mancini, S.; Pettini, M. Riemannian-geometric entropy for measuring network complexity. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2016, 93, 062317. [Google Scholar] [CrossRef] [PubMed]
- Chehreghani, M.H.; Abdessalem, T. Upper and lower bounds for the q -entropy of network models with application to network model selection. Inf. Process. Lett. 2017, 119, 1–8. [Google Scholar] [CrossRef]
- Chen, B.; Wang, Z.X.; Chen, L. Integrated evaluation approach for node importance of complex networks based on relative entropy. J. Syst. Eng. Electron. 2016, 6, 1219–1226. [Google Scholar] [CrossRef]
- Lawyer, G. Understanding the influence of all nodes in a network. Sci. Rep. 2015, 5, 8665. [Google Scholar] [CrossRef] [PubMed]
- Cao, S.; Dehmer, M.; Shi, Y. Extremality of degree-based graph entropies. Inf. Sci. 2014, 10, 22–33. [Google Scholar] [CrossRef]
- Lu, L.; Tan, Q.M. Maximum entropy distribution algorithm and its application. Syst. Eng. Electron. 2007, 29, 820–822. [Google Scholar]
- Schürmann, T. A note on entropy estimation. Neural Comput. 2015, 27, 2097. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.Q.; Ren, F.X.; Shen, H.W.; Zhang, Z.K.; Zhou, T. Bridgeness: A Local Index on Edge Significance in Maintaining Global Connectivity. J. Stat. Mech. Theory Exp. 2010, 10, 595–685. [Google Scholar] [CrossRef]
- Schneider, C.M.; Moreira, A.A.; José, A.J., Jr.; Havlin, S.; Herrmann, H.J. Mitigation of malicious attacks on networks. Proc. Natl. Acad. Sci. USA 2011, 10, 3838–3841. [Google Scholar] [CrossRef] [PubMed]
- Trajanovski, S.; Martínhernández, J.; Winterbach, W.; van Mieghem, P. Robustness envelopes of networks. J. Complex Netw. 2013, 1, 44–62. [Google Scholar] [CrossRef]
- Fan, W.L.; Liu, Z.G.; Hu, P. Identifying node importance based on information entropy in complex networks. Phys. Scr. 2013, 6, 5201. [Google Scholar]
- Wang, L.; Yu, S.; Wang, Z.; Qu, W.; Wang, H. A Study on Metaphors in Idioms Based on Chinese Idiom Knowledge Base. Lect. Notes Comput. Sci. 2014, 8922, 434–440. [Google Scholar]
- An, Y.; Wang, S. Narrative Idioms for Elementary-Level Chinese as a Second Language Learners. Lect. Notes Comput. Sci. 2015, 9332, 457–464. [Google Scholar]
- Liang, W.; Shi, Y.; Chi, K.T.; Liu, J.; Wang, Y.; Cui, X. Comparison of co-occurrence networks of the Chinese and English languages. Phys. A Stat. Mech. Appl. 2009, 23, 4901–4909. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tanio, K.; Sassano, M. Effects of game on user engagement with spoken dialogue system. In Proceedings of the 16th Annual Meeting of the Special Interest Group on Discourse and Dialogue, Prague, Czech Republic, 2–4 September 2015; pp. 422–426. [Google Scholar]
- Dictionary Research Center. Chinese Idiom Dictionary, 6th ed.; Commercial Press: Beijing, China, 2016. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org/ (accessed on 12 May 2017).
- Almende, B.V.; Benoit, T. visNetwork: Network Visualization Using ‘vis.js’ Library. R Package Version 1.0.3. 2016. Available online: https://CRAN.R-project.org/package=visNetwork (accessed on 12 May 2017).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer-Verlag: New York, NY, USA, 2009. [Google Scholar]
- Pons, P.; Latapy, M. Computing Communities in Large Networks Using Random Walks. Lect. Notes Comput. Sci. 2005, 3733, 284–293. [Google Scholar]
- Federal Aviation Administration. Air Traffic Control System Command Center. Available online: http://www.fly.faa.gov/ (accessed on 12 May 2017).
- Adamic, L.A.; Glance, N. The political blogosphere and the 2004 U.S. election: Divided they blog. In Proceedings of the 3rd International Workshop on Link Discovery, Chicago, IL, USA, 21–25 August 2005; Volume 62, pp. 36–43. [Google Scholar]
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. Data 2007, 1, 2. [Google Scholar] [CrossRef]
- Guhl, A.M. Social behavior of the domestic fowl. Trans. Kansas Acad. Sci. 1968, 71, 379. [Google Scholar] [CrossRef] [PubMed]
- Coleman, J.S. Introduction to Mathematical Sociology; London Free Press: Glencoe, UK, 1964. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of “small-world” networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Coleman, J.; Katz, E.; Menzel, H. The diffusion of an innovation among physicians. Soc. Netw. 1977, 20, 107–124. [Google Scholar]
- Stanford Large Network Dataset Collection. Available online: http://snap.stanford.edu/data/index.html (accessed on 10 June 2017).
- Koblenz Network Collection. Available online: http://konect.uni-koblenz.de/ (accessed on 10 June 2017).
- Csardi, G.; Nepusz, T. The Igraph Software Package for Complex Network Research, InterJournal, Complex Systems 1695. 2006. Available online: http://igraph.org (accessed on 12 May 2017).
- Carter, T.B. sna: Tools for Social Network Analysis. R Package Version 2.4. 2016. Available online: https://CRAN.R-project.org/package=sna (accessed on 12 May 2017).
- Ai, X. Node Entropy Variation. 2017. Available online: https://github.com/byaxb/NodeEntropyVariation (accessed on 26 June 2017).
- Revolution, Analytics; Steve, Weston. doParallel: Foreach Parallel Adaptor for the ‘Parallel’ Package. R Package Version 1.0.10. 2015. Available online: https://CRAN.R-project.org/package=doParallel (accessed on 12 May 2017).
- Revolution, Analytics; Steve, Weston. foreach: Provides Foreach Looping Construct for R. R Package Version 1.4.3. 2015. Available online: https://CRAN.R-project.org/package=foreach (accessed on 12 May 2017).
- Jahanpour, E.; Chen, X. Analysis of complex network performance and heuristic node removal strategies. Commun. Nonlinear Sci. Numer. Simul. 2013, 12, 3458–3468. [Google Scholar] [CrossRef]
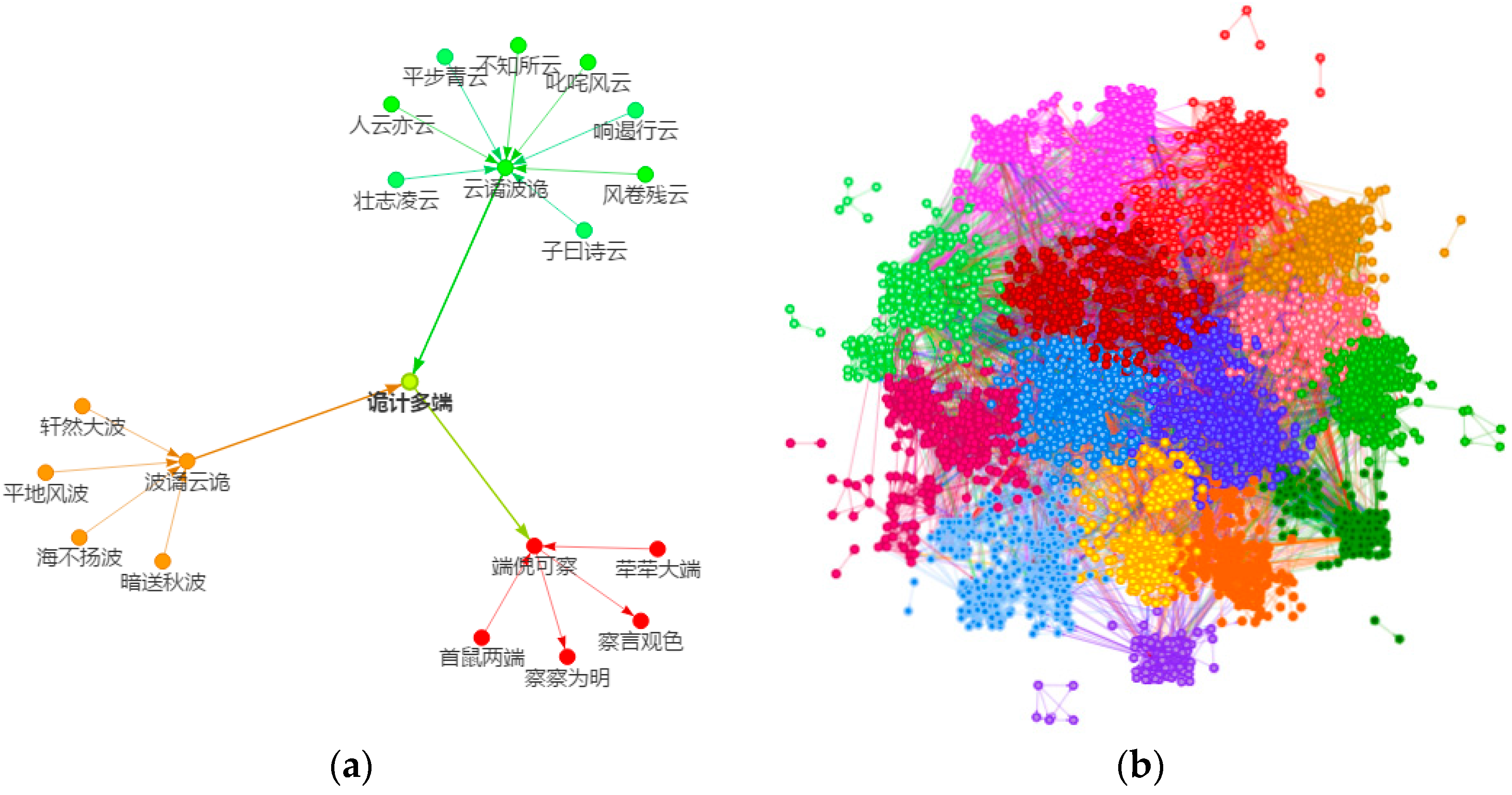
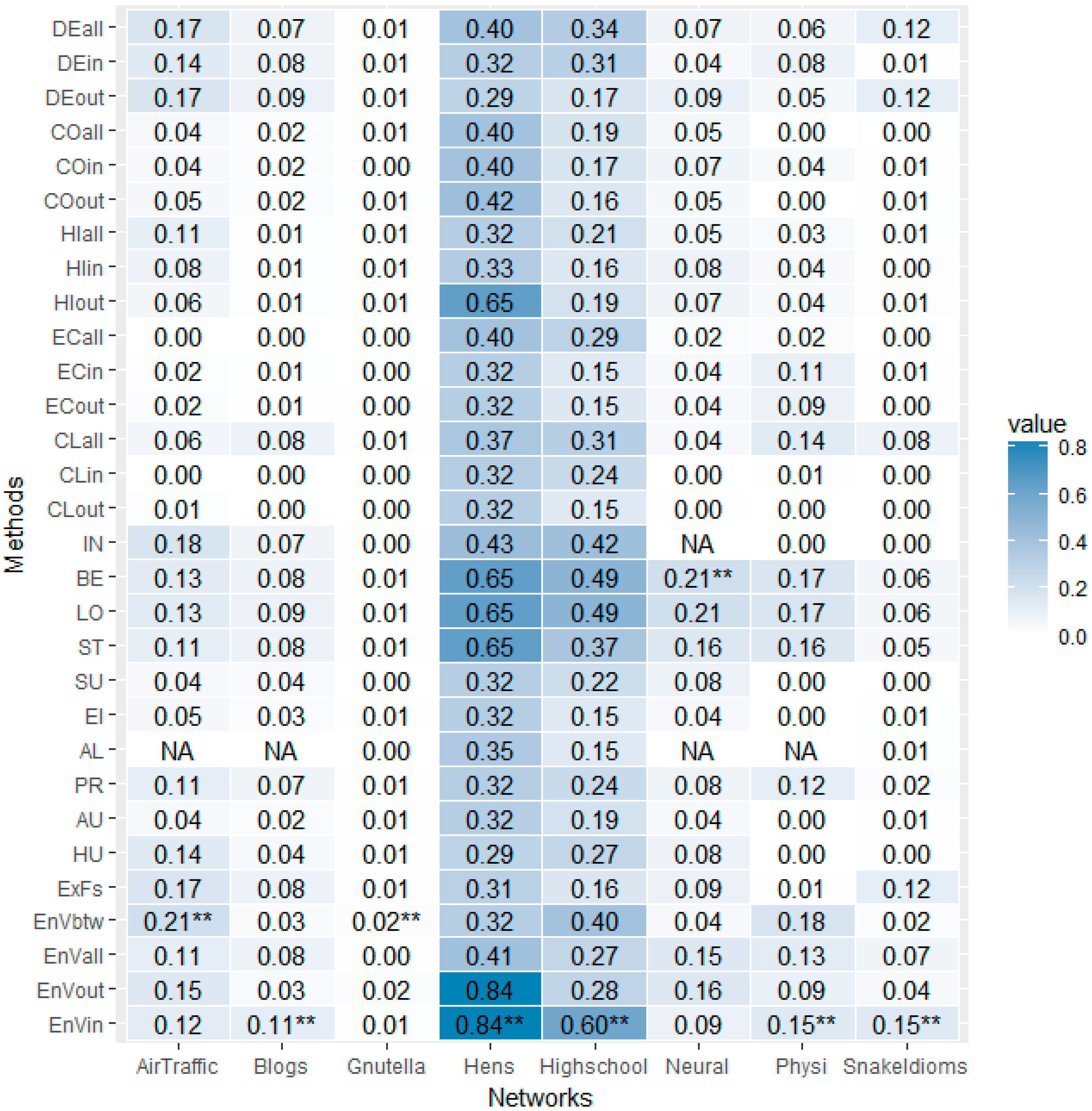
| Network | Number of Nodes | Number of Edges | Density | Diameter | Average Path Length | SCC Size |
|---|---|---|---|---|---|---|
| Air traffic control | 1226 | 2615 | 0.00174 | 25 | 7.96 | 792 |
| Blogs | 1224 | 19,025 | 0.01271 | 9 | 3.39 | 793 |
| Gnutella | 6301 | 20,777 | 0.00052 | 20 | 6.63 | 2068 |
| Hens | 32 | 496 | 0.50000 | 6 | 1.96 | 31 |
| High School | 70 | 366 | 0.07578 | 12 | 3.97 | 67 |
| Neural | 297 | 2359 | 0.02683 | 14 | 3.99 | 239 |
| Physicians | 241 | 1098 | 0.01898 | 9 | 3.31 | 95 |
| Snake Idioms | 4234 | 21,067 | 0.00118 | 16 | 6.14 | 1907 |
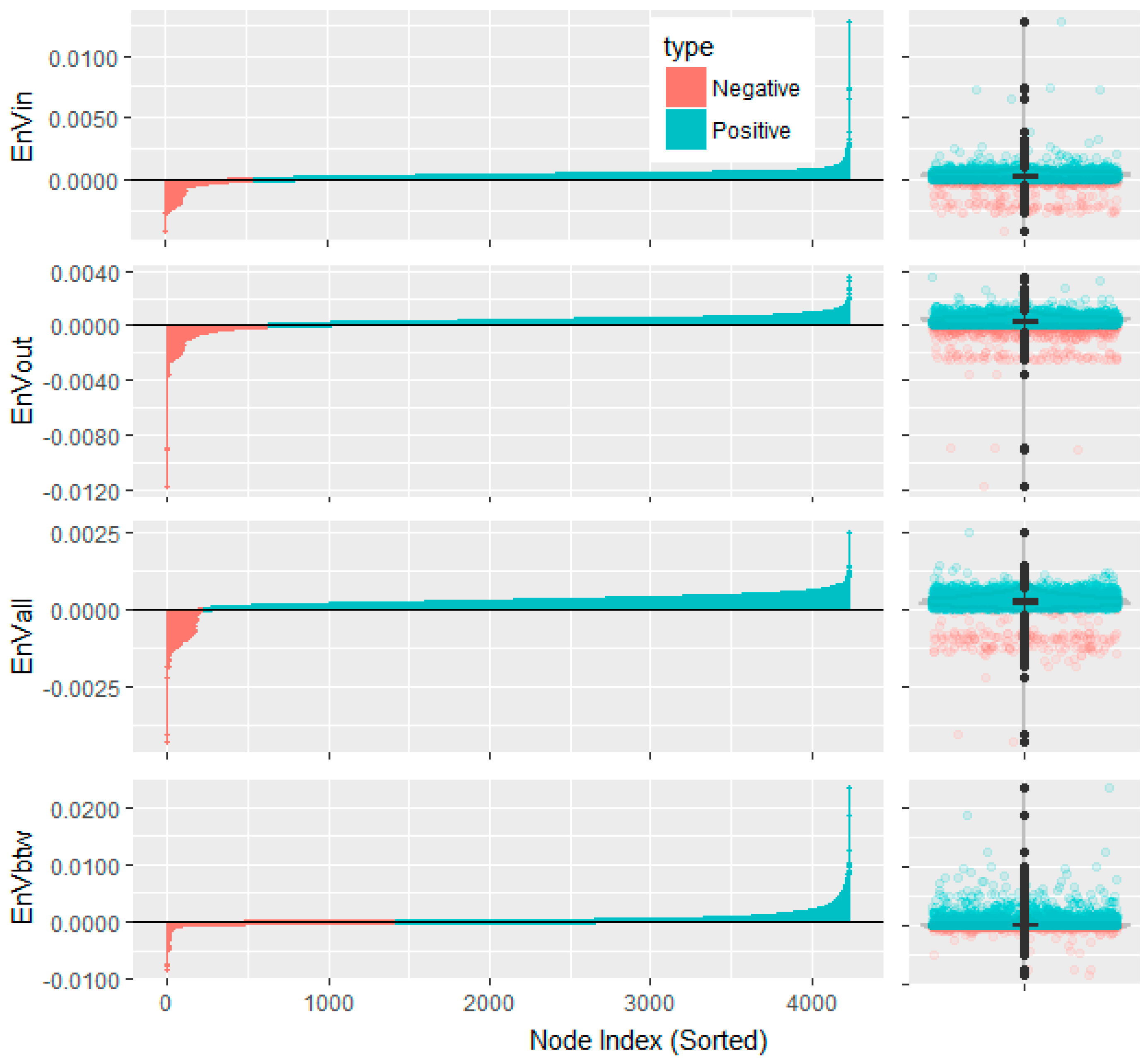
| Information Function | Minimum | 1st Quartile | Median | 3rd Quartile | Maximum |
|---|---|---|---|---|---|
| in-degree | −0.00414 | 0.000126 | 0.00032 | 0.000475 | 0.012829 |
| out-degree | −0.0117 | 0.000143 | 0.00033 | 0.000507 | 0.00357 |
| all-degree | −0.00431 | 0.00017 | 0.000279 | 0.000396 | 0.002523 |
| betweenness | −0.00844 | −0.000043 | 0.0000776 | 0.000382 | 0.023602 |
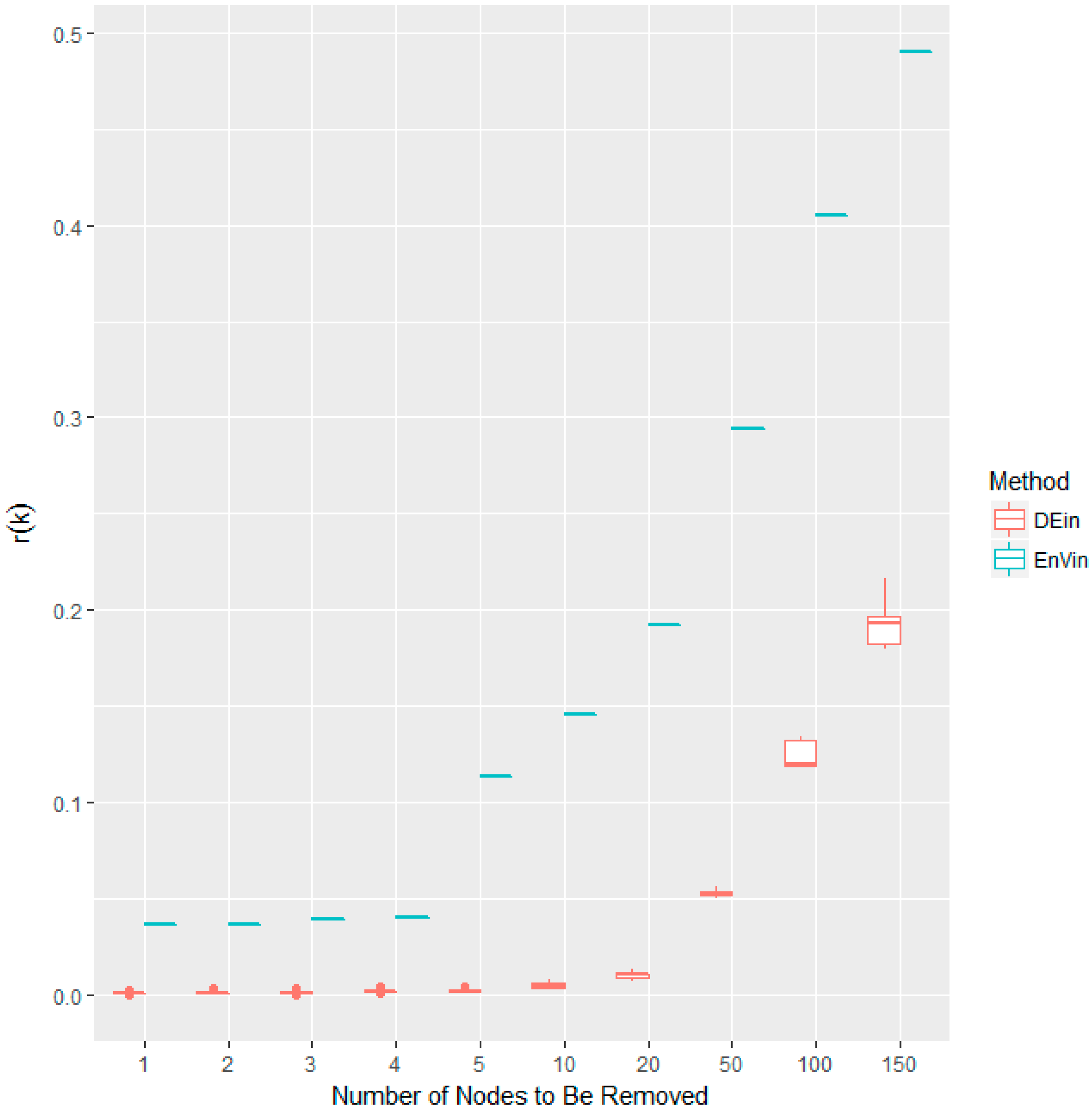
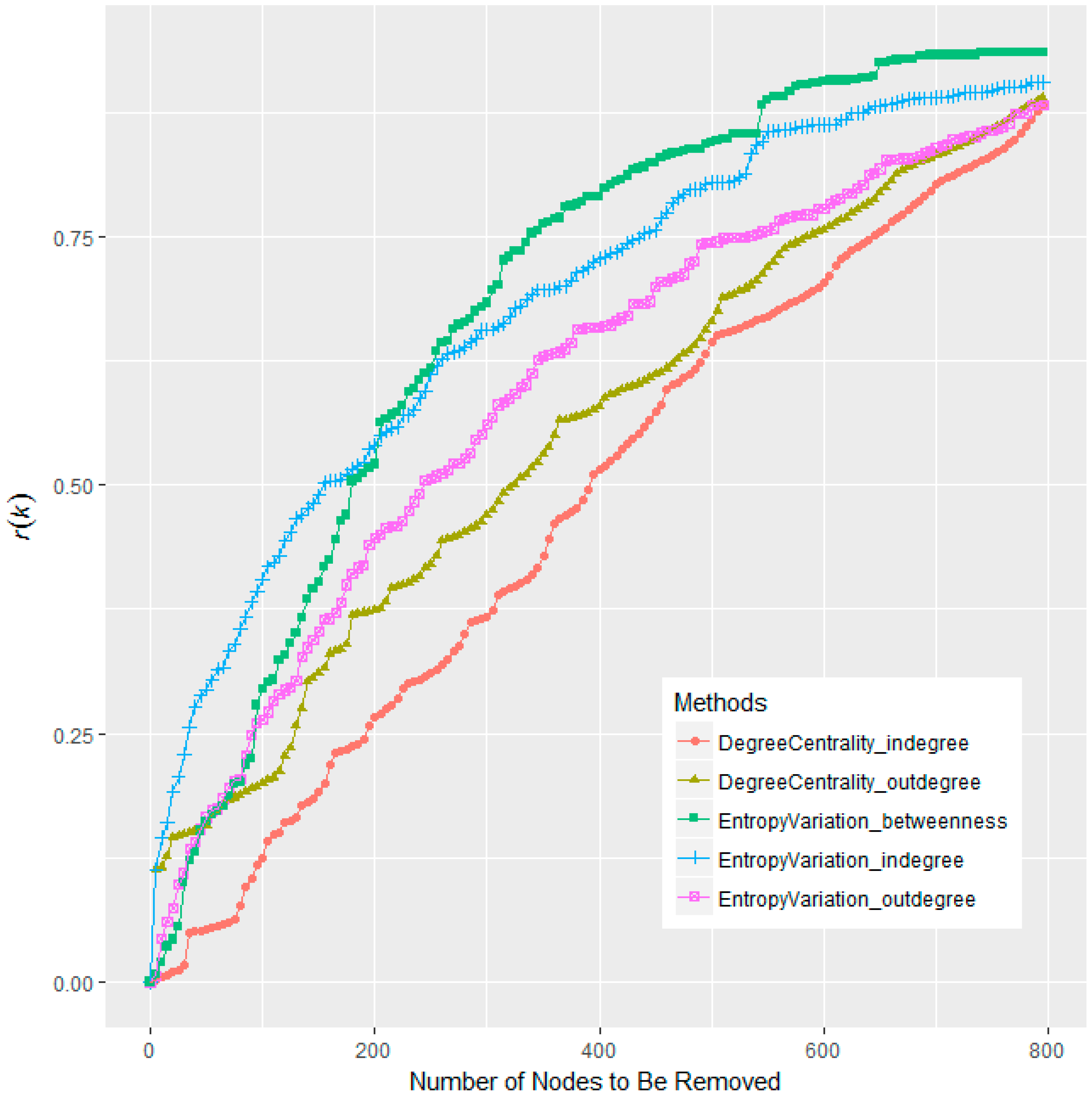
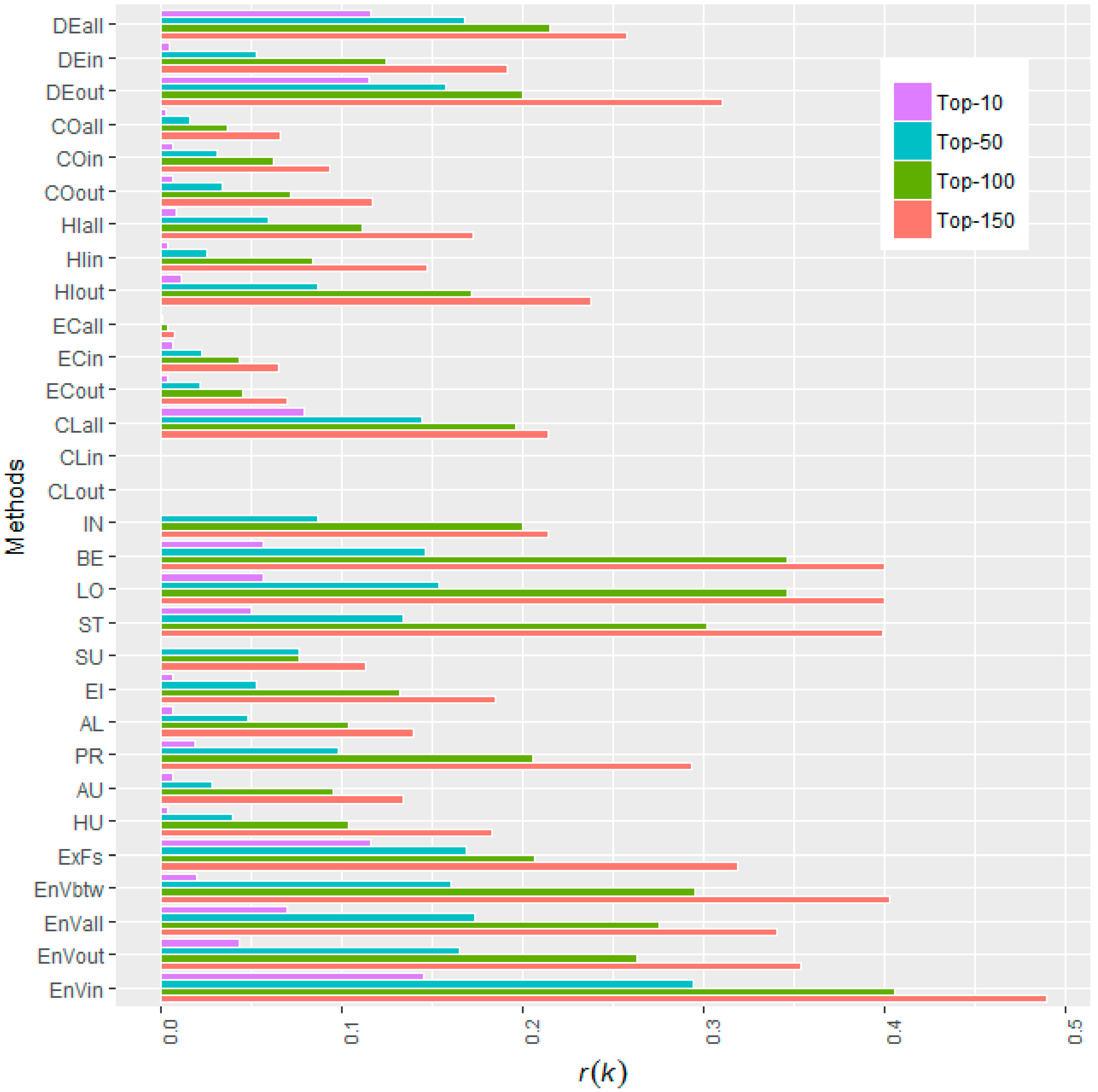
| Methods | r(k) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k = 10 | k = 50 | k = 100 | k = 150 | |||||||
| Degree (all) | 0.12 | #2 | 0.17 | #4 | 0.22 | #8 | 0.26 | #11 | 29.07 | #8 |
| Degree (in) | 0.01 | #21 | 0.05 | #18 | 0.12 | #16 | 0.19 | #15 | 13.32 | #16 |
| Degree (out) | 0.12 | #4 | 0.16 | #7 | 0.20 | #11 | 0.31 | #9 | 28.26 | #10 |
| Coreness (all) | 0.00 | #25 | 0.02 | #27 | 0.04 | #27 | 0.07 | #26 | 4.32 | #27 |
| Coreness (in) | 0.01 | #20 | 0.03 | #22 | 0.06 | #24 | 0.09 | #24 | 7.07 | #24 |
| Coreness (out) | 0.01 | #17 | 0.03 | #21 | 0.07 | #23 | 0.12 | #22 | 8.34 | #23 |
| H-index(all) | 0.01 | #14 | 0.06 | #16 | 0.11 | #17 | 0.17 | #18 | 12.63 | #17 |
| H-index (in) | 0.00 | #22 | 0.03 | #24 | 0.08 | #21 | 0.15 | #19 | 9.20 | #21 |
| H-index (out) | 0.01 | #13 | 0.09 | #13 | 0.17 | #14 | 0.24 | #12 | 19.74 | #13 |
| Eccentricity (all) | 0.00 | #26 | 0.00 | #28 | 0.00 | #28 | 0.01 | #28 | 0.48 | #28 |
| Eccentricity (in) | 0.01 | #18 | 0.02 | #25 | 0.04 | #26 | 0.07 | #27 | 4.96 | #26 |
| Eccentricity (out) | 0.00 | #24 | 0.02 | #26 | 0.05 | #25 | 0.07 | #25 | 5.20 | #25 |
| Closeness (all) | 0.08 | #5 | 0.14 | #10 | 0.20 | #13 | 0.21 | #14 | 23.25 | #12 |
| Closeness (in) | 0.00 | #27 | 0.00 | #29 | 0.00 | #29 | 0.00 | #29 | 0.00 | #29 |
| Closeness (out) | 0.00 | #28 | 0.00 | #30 | 0.00 | #30 | 0.00 | #30 | 0.00 | #30 |
| Information index | 0.00 | #29 | 0.09 | #14 | 0.20 | #12 | 0.21 | #13 | 19.32 | #14 |
| Betweenness centrality | 0.06 | #7 | 0.15 | #9 | 0.35 | #2 | 0.40 | #3 | 35.07 | #3 |
| Load centrality | 0.06 | #8 | 0.15 | #8 | 0.35 | #3 | 0.40 | #4 | 36.13 | #2 |
| Stress centrality | 0.05 | #9 | 0.13 | #11 | 0.30 | #4 | 0.40 | #5 | 32.42 | #4 |
| Subgraph centrality | 0.00 | #30 | 0.08 | #15 | 0.08 | #22 | 0.11 | #23 | 11.09 | #20 |
| Eigenvector centrality | 0.01 | #15 | 0.05 | #17 | 0.13 | #15 | 0.19 | #16 | 13.35 | #15 |
| Alpha centrality | 0.01 | #16 | 0.05 | #19 | 0.10 | #19 | 0.14 | #20 | 11.29 | #19 |
| Page Rank | 0.02 | #12 | 0.10 | #12 | 0.21 | #10 | 0.29 | #10 | 23.61 | #11 |
| HITs (Authority) | 0.01 | #19 | 0.03 | #23 | 0.10 | #20 | 0.13 | #21 | 8.91 | #22 |
| HITs (Hub) | 0.00 | #23 | 0.04 | #20 | 0.10 | #18 | 0.18 | #17 | 12.60 | #18 |
| Expected Force (ExF) | 0.12 | #3 | 0.17 | #3 | 0.21 | #9 | 0.32 | #8 | 29.04 | #9 |
| Entropy Variation (btw) | 0.02 | #11 | 0.16 | #6 | 0.30 | #5 | 0.40 | #2 | 31.45 | #6 |
| Entropy Variation (all) | 0.07 | #6 | 0.17 | #2 | 0.28 | #6 | 0.34 | #7 | 32.21 | #5 |
| Entropy Variation(out) | 0.04 | #10 | 0.17 | #5 | 0.26 | #7 | 0.35 | #6 | 30.35 | #7 |
| Entropy Variation(in) | 0.15 | #1 | 0.29 | #1 | 0.41 | #1 | 0.49 | #1 | 50.13 | #1 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, X. Node Importance Ranking of Complex Networks with Entropy Variation. Entropy 2017, 19, 303. https://doi.org/10.3390/e19070303
Ai X. Node Importance Ranking of Complex Networks with Entropy Variation. Entropy. 2017; 19(7):303. https://doi.org/10.3390/e19070303
Chicago/Turabian StyleAi, Xinbo. 2017. "Node Importance Ranking of Complex Networks with Entropy Variation" Entropy 19, no. 7: 303. https://doi.org/10.3390/e19070303
APA StyleAi, X. (2017). Node Importance Ranking of Complex Networks with Entropy Variation. Entropy, 19(7), 303. https://doi.org/10.3390/e19070303




