An Information-Spectrum Approach to the Capacity Region of the Interference Channel †
Abstract
:1. Introduction
2. Basic Definitions and Problem Statement
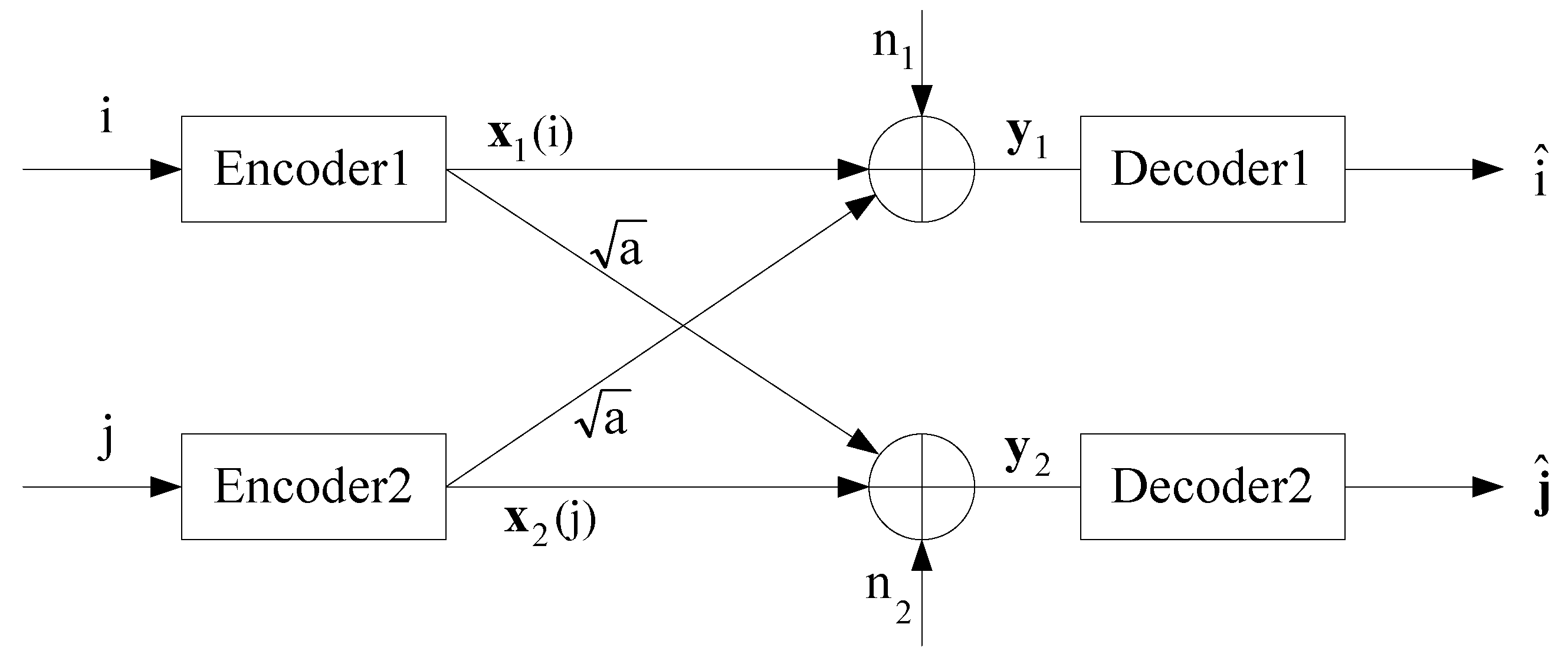
2.1. General IC
- (a)
- message sets:
- (b)
- sets of codewords:For Sender 1 to transmit message i, Encoder 1 outputs the codeword . Similarly, for Sender 2 to transmit message j, Encoder 2 outputs the codeword .
- (c)
- collections of decoding sets:where for and for . That is, and are the disjoint partitions of and determined in advance, respectively. After receiving , Decoder 1 outputs whenever . Similarly, after receiving , Decoder 2 outputs whenever .
- (d)
- probabilities of decoding errors:where "" denotes the complement of a set. Here we have assumed that each message of and is produced independently with uniform distribution.
2.2. Preliminaries of Information-Spectrum Approach
3. The Capacity Region of General IC
3.1. The Main Theorem
3.2. The Algorithm to Compute Achievable Rate Pairs
- (1)
- the channel is stationary and memoryless, that is, the transition probability of the channel can be written as
- (2)
- sources are restricted to be stationary and ergodic discrete Markov processes.
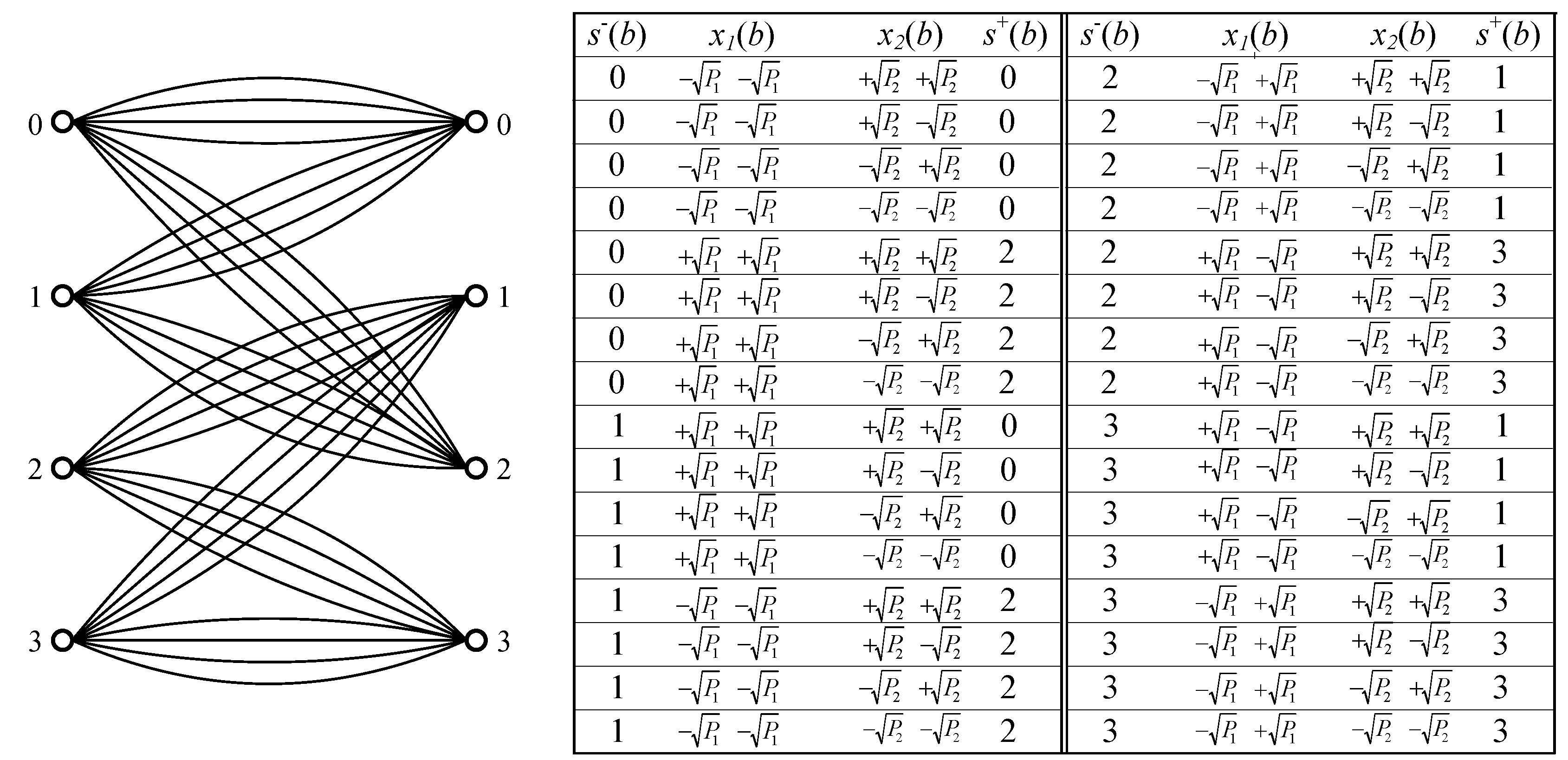
- Both the left and right states are selected from the set ;
- Each branch is represented by a three-tuple , where is the left state, is the right state, and the symbol is the associated label. We also assume that a branch b is uniquely determined by and ;
- At time , the source starts from state . If at time , the source is in the state , then at time , the source generates a symbol according to the conditional probability and goes into a state such that is a branch. Obviously, when the source runs from time to , a sequence is generated. The Markov property says thatSo the probability of a given sequence with the initial state can be factored as
- The product trellis has the state set , where “×” denotes Cartesian product.
- Each branch is represented by a four-tuple , where is the left state, is the right state. Then and are the associated labels in branch b such that and are branches in and , respectively.
- At time , the sources start from state . If at time , the sources are in the state , then at time , the sources generate symbols according to the conditional probability and go into a state such that is a branch.
- Branch metrics: To each branch , we assign a metricIn the computation of , the metric is replaced by .
- State transition probabilities: The transition probability from to is defined as
- Forward recursion variables: We define the a posteriori probabilitiesThenwhere the values of can be computed recursively by
- 1.
- Initializations: Choose a sufficiently large number n. Set the initial state of the trellis to be . The forward recursion variables are initialized as if and otherwise .
- 2.
- Simulations for Sender 1: Generate a Markov sequence according to the trellis of source .
- 3.
- Simulations for Sender 2: Generate a Markov sequence according to the trellis of source .
- 4.
- Simulations for Receiver 1: Generate the received sequence according to the transition probability .
- 5.
- Computations:
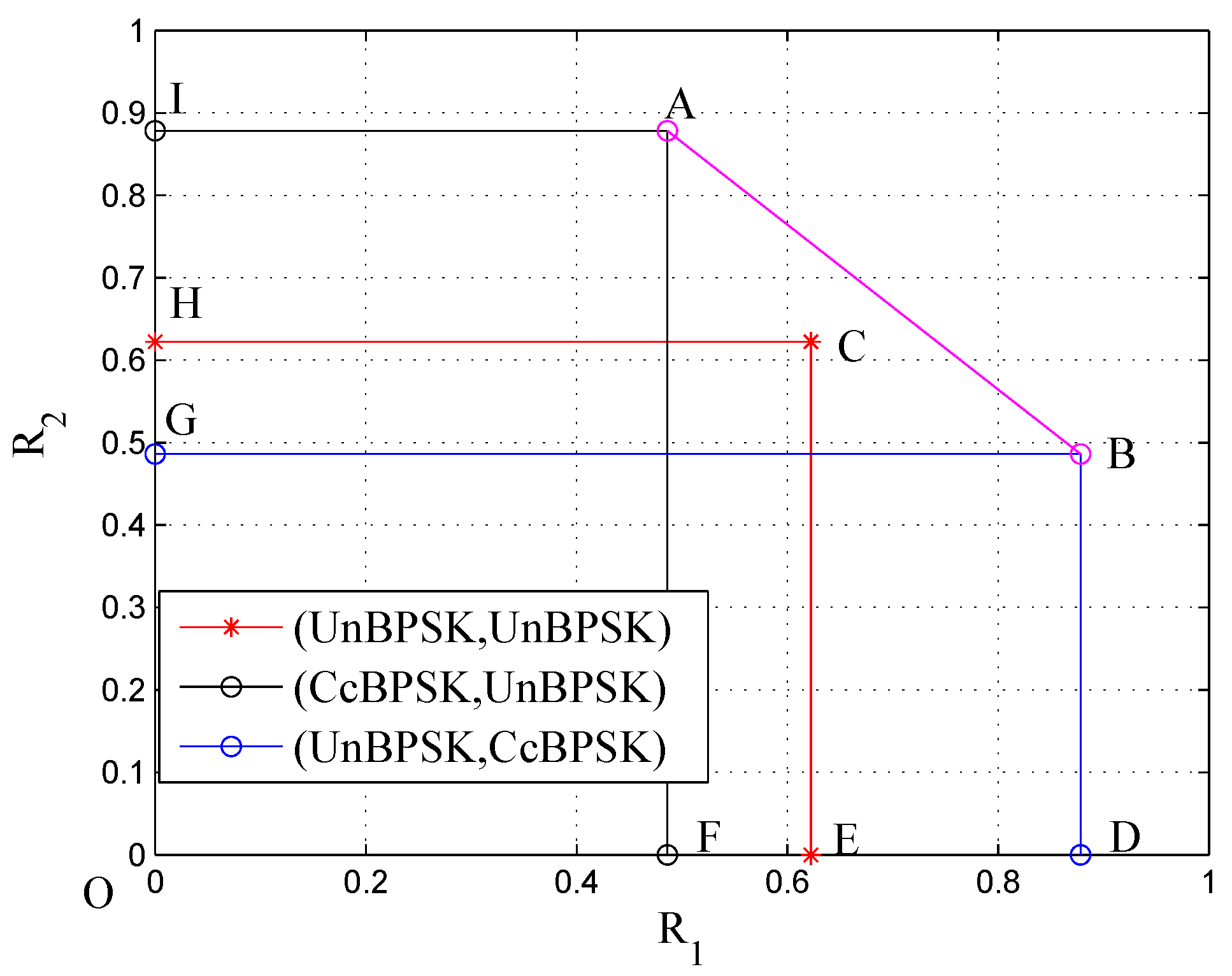
3.3. Numerical Results
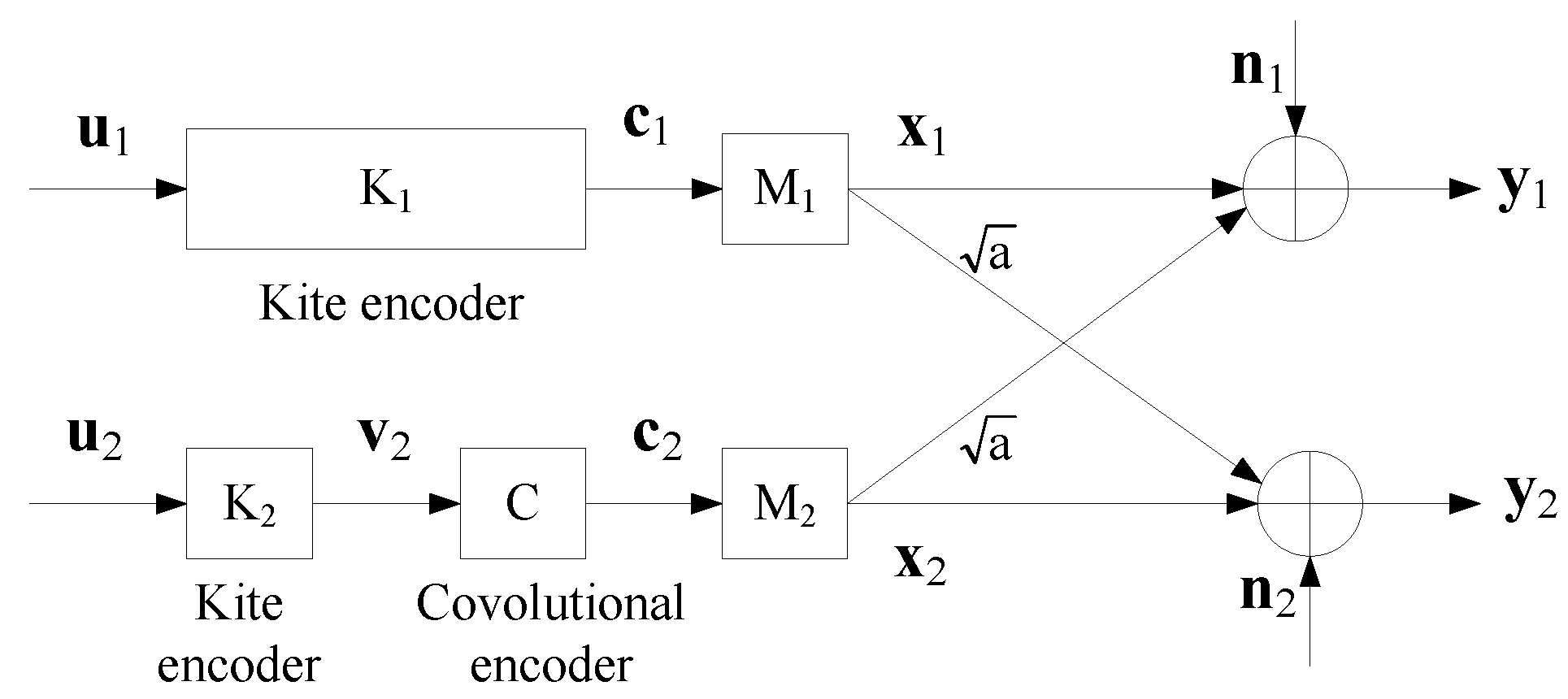
4. Decoding Algorithms for Channels with Structured Interference
4.1. A Coding Scheme
4.2. Decoding Algorithms
4.2.1. Message Processing/Passing Algorithms over Normal Graphs
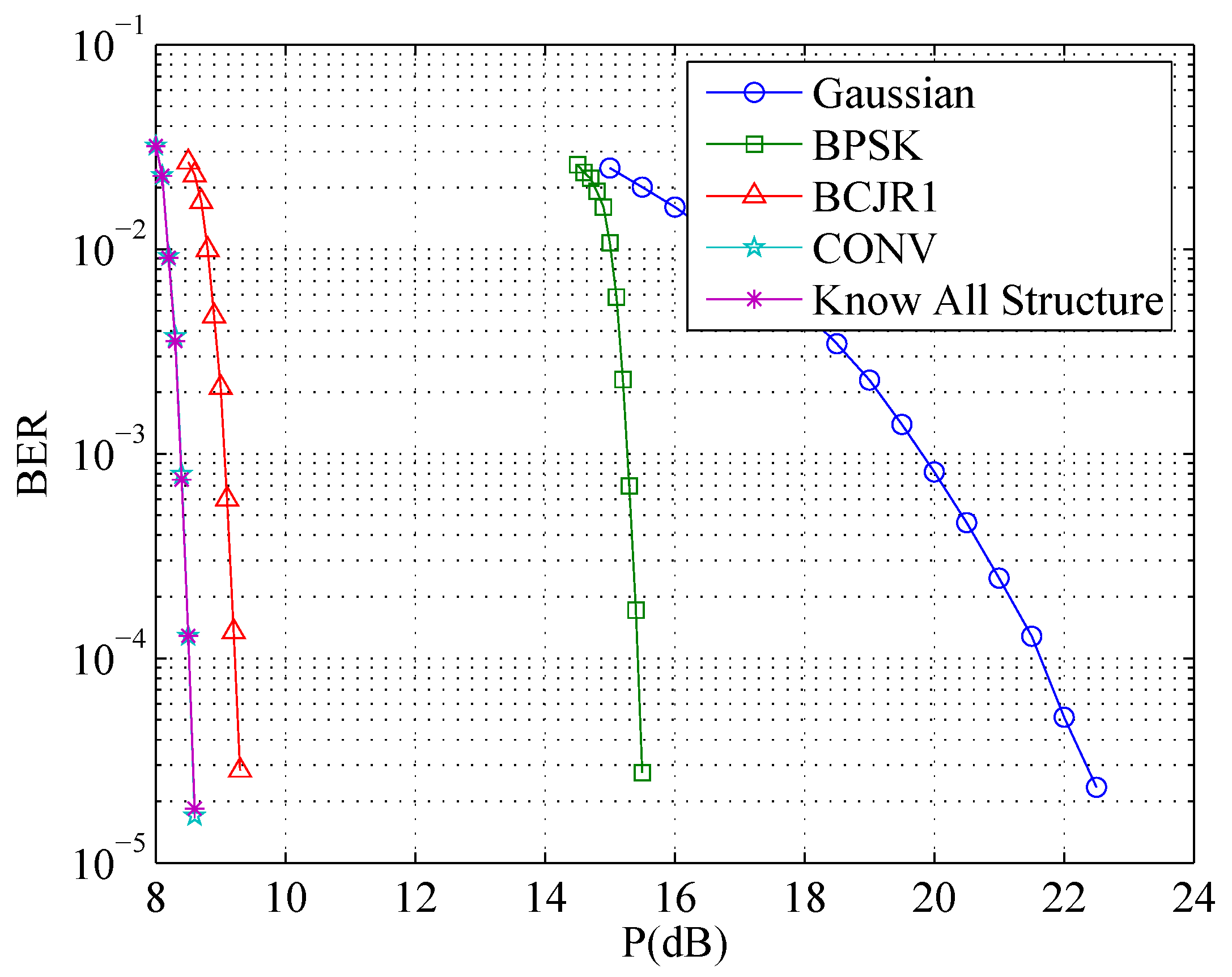
4.2.2. Knowing Only the Power of the Interference
- Initialization:
- 1.
- Initialize for and .
- 2.
- Compute for and according to (24).
- 3.
- Set a maximum iteration number J and iteration variable .
- Repeat while :
- End decoding.
4.2.3. Knowing the Signaling of the Interference
- Initialization:
- 1.
- Initialize for and .
- 2.
- Compute for and according to (27).
- 3.
- Set a maximum iteration number J and iteration variable .
- Repeat while :
- End decoding.
4.2.4. Knowing the CC
- Initialization:
- 1.
- Initialize pmf and for and for .
- 2.
- Compute extrinsic messages for , using BCJR algorithm over the parallel branch trellis .
- 3.
- Set a maximum iteration number J and iteration variable .
- Repeat while :
- End Decoding
- Initialization:
- 1.
- Initialize pmf and for and for .
- 2.
- Set a maximum iteration number J and iteration variable .
- Repeat while :
- End Decoding
4.2.5. Knowing the Whole Structure
- Initialization:
- 1.
- Initialize pmf and for and for .
- 2.
- Set a maximum iteration number J and iteration variable .
- Repeat while :
- 1.
- Compute extrinsic messages for , and for , using BCJR algorithm over the parallel branch trellis .
- 2.
- Compute extrinsic messages and for and using SPA.
- 3.
- Compute extrinsic messages for using SPA.
- 4.
- 5.
- Compute the syndrome . If , output and and exit the iteration.
- 6.
- Set . If and , report a decoding failure.
- End Decoding
4.3. Numerical Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Carleial, A.B. Interference channels. IEEE Trans. Inf. Theory 1978, 24, 60–70. [Google Scholar] [CrossRef]
- Shannon, C.E. Two-way communication channels. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkely, CA, USA, 20 June–30 July 1960; Neyman, J., Ed.; University of California Press: Berkely, CA, USA, 1961; Volume 1, pp. 611–644. [Google Scholar]
- Ahlswede, R. The capacity region of a channel with two senders and two receivers. Ann. Probab. 1974, 2, 805–814. [Google Scholar] [CrossRef]
- Carleial, A.B. A case where interference does not reduce capacity. IEEE Trans. Inf. Theory 1975, 21, 569–570. [Google Scholar] [CrossRef]
- Han, T.S.; Kobayashi, K. A new achievable rate region for the interference channel. IEEE Trans. Inf. Theory 1981, 27, 49–60. [Google Scholar] [CrossRef]
- El Gamal, A.A.; Costa, M.H.M. The capacity region of a class of deterministic interference channels. IEEE Trans. Inf. Theory 1982, 28, 343–346. [Google Scholar] [CrossRef]
- Costa, M.H.M.; El Gamal, A.A. The capacity region of the discrete memoryless interference channel with strong interference. IEEE Trans. Inf. Theory 1987, 33, 710–711. [Google Scholar] [CrossRef]
- Kramer, G. Outer bounds on the capacity of Gaussian interference channels. IEEE Trans. Inf. Theory 2004, 50, 581–586. [Google Scholar] [CrossRef]
- Sato, H. Two-user communication channels. IEEE Trans. Inf. Theory 1977, 23, 295–304. [Google Scholar] [CrossRef]
- Carleial, A.B. Outer bounds on the capacity of interference channels. IEEE Trans. Inf. Theory 1983, 29, 602–606. [Google Scholar] [CrossRef]
- Sato, H. On degraded Gaussian two-user channels. IEEE Trans. Inf. Theory 1978, 24, 637–640. [Google Scholar] [CrossRef]
- Costa, M.H.M. On the Gaussian interference channel. IEEE Trans. Inf. Theory 1985, 31, 607–615. [Google Scholar] [CrossRef]
- Kramer, G. Review of rate regions for interference channels. In Proceedings of the 2006 IEEE International Zurich Seminar on Communications (IZS), Zurich, Switzerland, 22–24 February 2006; pp. 162–165. [Google Scholar]
- Chong, H.F.; Motani, M.; Garg, H.K.; Gamal, H.E. On the Han-Kobayashi region for the interference channel. IEEE Trans. Inf. Theory 2008, 54, 3188–3195. [Google Scholar] [CrossRef]
- Etkin, R.H.; Tse, D.N.C.; Wang, H. Gaussian interference channel capacity to within one bit. IEEE Trans. Inf. Theory 2008, 54, 5534–5562. [Google Scholar] [CrossRef]
- Huang, X.; Ma, X.; Lin, L.; Bai, B. Accessible Capacity of Secondary Users over the Gaussian Interference Channel. In Proceedings of the IEEE International Symposium on Information Theory, St. Petersburg, Russia, 31 July–5 August 2011; pp. 811–815. [Google Scholar]
- Huang, X.; Ma, X.; Lin, L.; Bai, B. Accessible Capacity of Secondary Users. IEEE Trans. Inf. Theory 2014, 60, 4722–4738. [Google Scholar] [CrossRef]
- Baccelli, F.; El Gamal, A.A.; Tse, D. Interference Networks with Point-to-Point Codes. IEEE Trans. Inf. Theory 2011, 57, 2582–2596. [Google Scholar] [CrossRef]
- Moshksar, K.; Ghasemi, A.; Khandani, A.K. An Alternative To Decoding Interference or Treating Interference As Gaussian Noise. In Proceedings of the IEEE International Symposium on Information Theory, St. Petersburg, Russia, 31 July–5 August 2011; pp. 1176–1180. [Google Scholar]
- Han, T.S.; Verdú, S. Approximation theory of output statistics. IEEE Trans. Inf. Theory 1993, 39, 752–772. [Google Scholar] [CrossRef]
- Han, T.S. Information-Spectrum Methods in Information Theory; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Verdú, S.; Han, T.S. A general formula for channel capacity. IEEE Trans. Inf. Theory 1994, 40, 1147–1157. [Google Scholar] [CrossRef]
- Han, T.S. An information-spectrum approach to capacity theorems for the general multiple-access channel. IEEE Trans. Inf. Theory 1998, 44, 2773–2795. [Google Scholar]
- Lin, L.; Ma, X.; Huang, X.; Bai, B. An information spectrum approach to the capacity region of general interference channel. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012; pp. 2261–2265. [Google Scholar]
- Etkin, R.H.; Merhav, N.; Ordentlich, E. Error Exponents of Optimum Decoding for the Interference Channel. IEEE Trans. Inf. Theory 2010, 56, 40–56. [Google Scholar] [CrossRef]
- Kavčić, A. On the capacity of Markov sources over noisy channels. In Proceedings of the IEEE 2001 Global Telecommunications Conference, San Antonio, TX, USA, 25–29 November 2001; Volume 5, pp. 2997–3001. [Google Scholar]
- Arnold, D.M.; Loeliger, H.A. On the information rate of binary-input channels with memory. In Proceedings of the IEEE International Conference on Communications, Helsinki, Finland, 11–14 June 2001; Volume 9, pp. 2692–2695. [Google Scholar]
- Pfister, H.D.; Soriaga, J.B.; Siegel, P.H. On the achievable information rates of finite state ISI channels. In Proceedings of the IEEE Global Telecommunications Conference, San Antonio, TX, USA, 25–29 November 2001; Volume 5, pp. 2992–2996. [Google Scholar]
- Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J. Optimal decoding of linear codes for minimizing symbol error rate. IEEE Trans. Inf. Theory 1974, 20, 284–287. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Ma, X.; Zhao, S.; Zhang, K.; Bai, B. Kite codes over Groups. In Proceedings of the IEEE Information Theory Workshop, Paraty, Brazil, 16–20 October 2011; pp. 481–485. [Google Scholar]
- Zhang, K.; Ma, X.; Zhao, S.; Bai, B.; Zhang, X. A New Ensemble of Rate-Compatible LDPC Codes. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012. [Google Scholar]
- Wiberg, N.; Loeliger, H.A.; Kötter, R. Codes and iterative decoding on general graphs. Eur. Trans. Commun. 1995, 6, 513–526. [Google Scholar]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Forney, G.D., Jr. Codes on graphs: Normal realizations. IEEE Trans. Inf. Theory 2001, 47, 520–548. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, K.; Chen, H.; Bai, B. Low Complexity X-EMS Algorithms for Nonbinary LDPC Codes. IEEE Trans. Commun. 2012, 60, 9–13. [Google Scholar] [CrossRef]
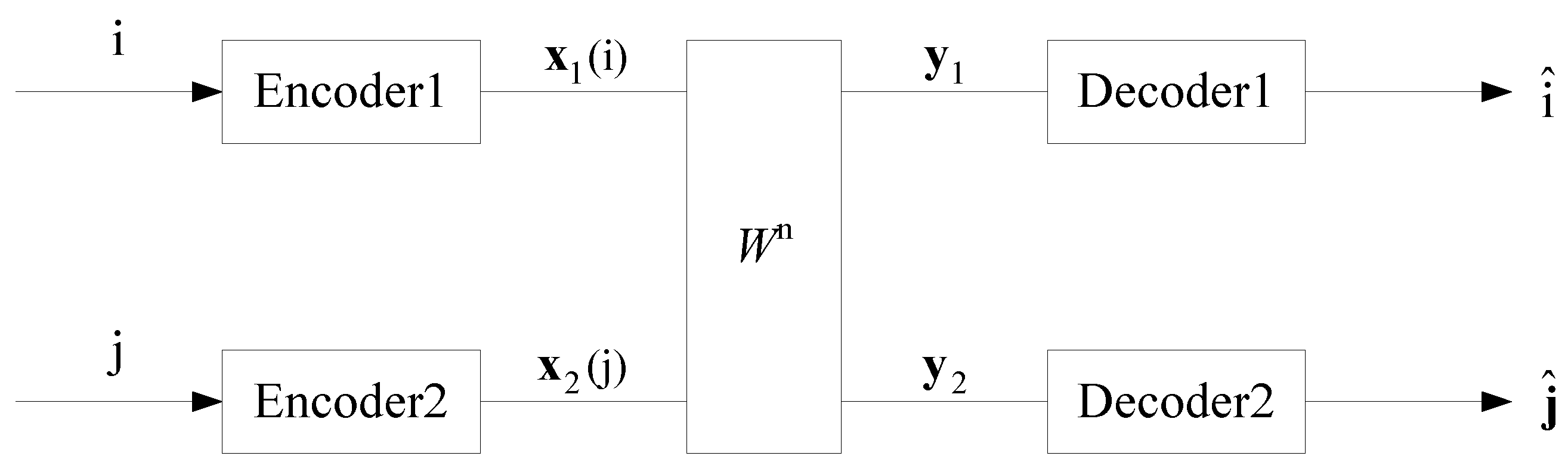
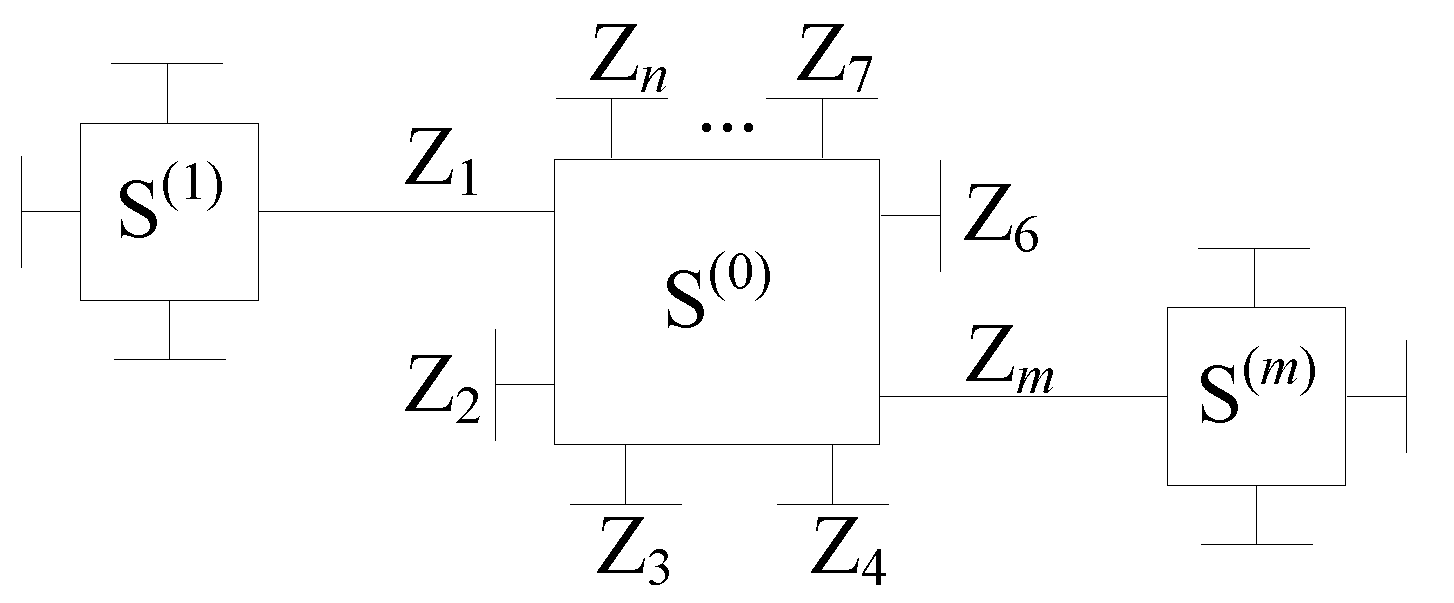
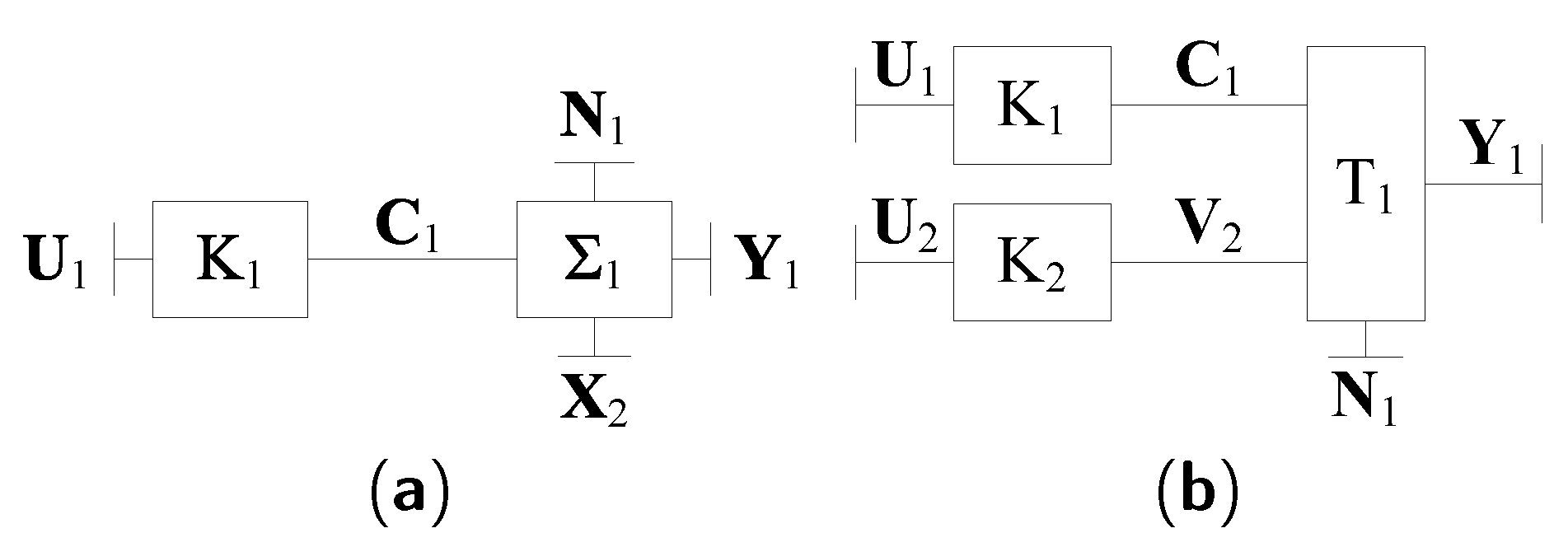
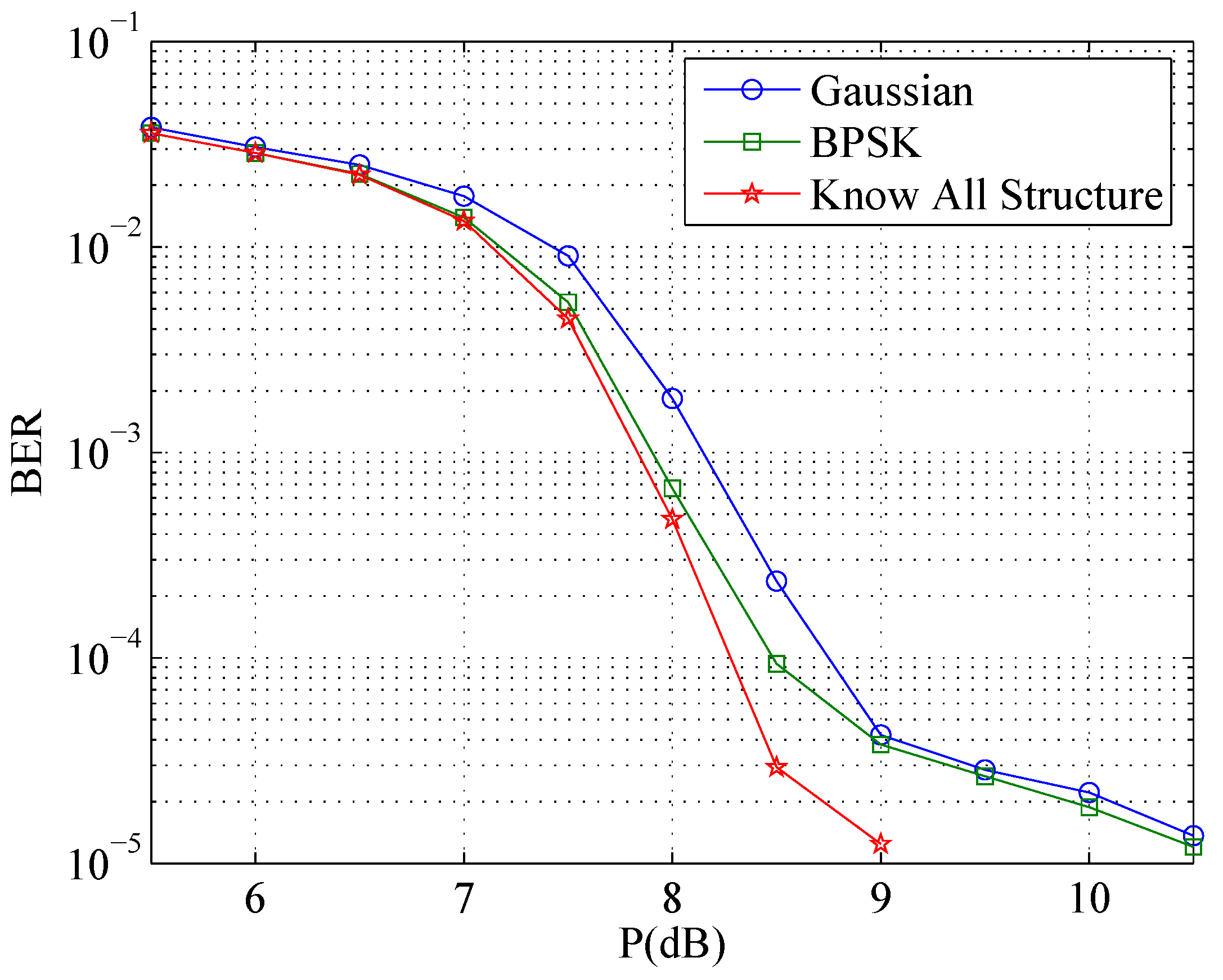
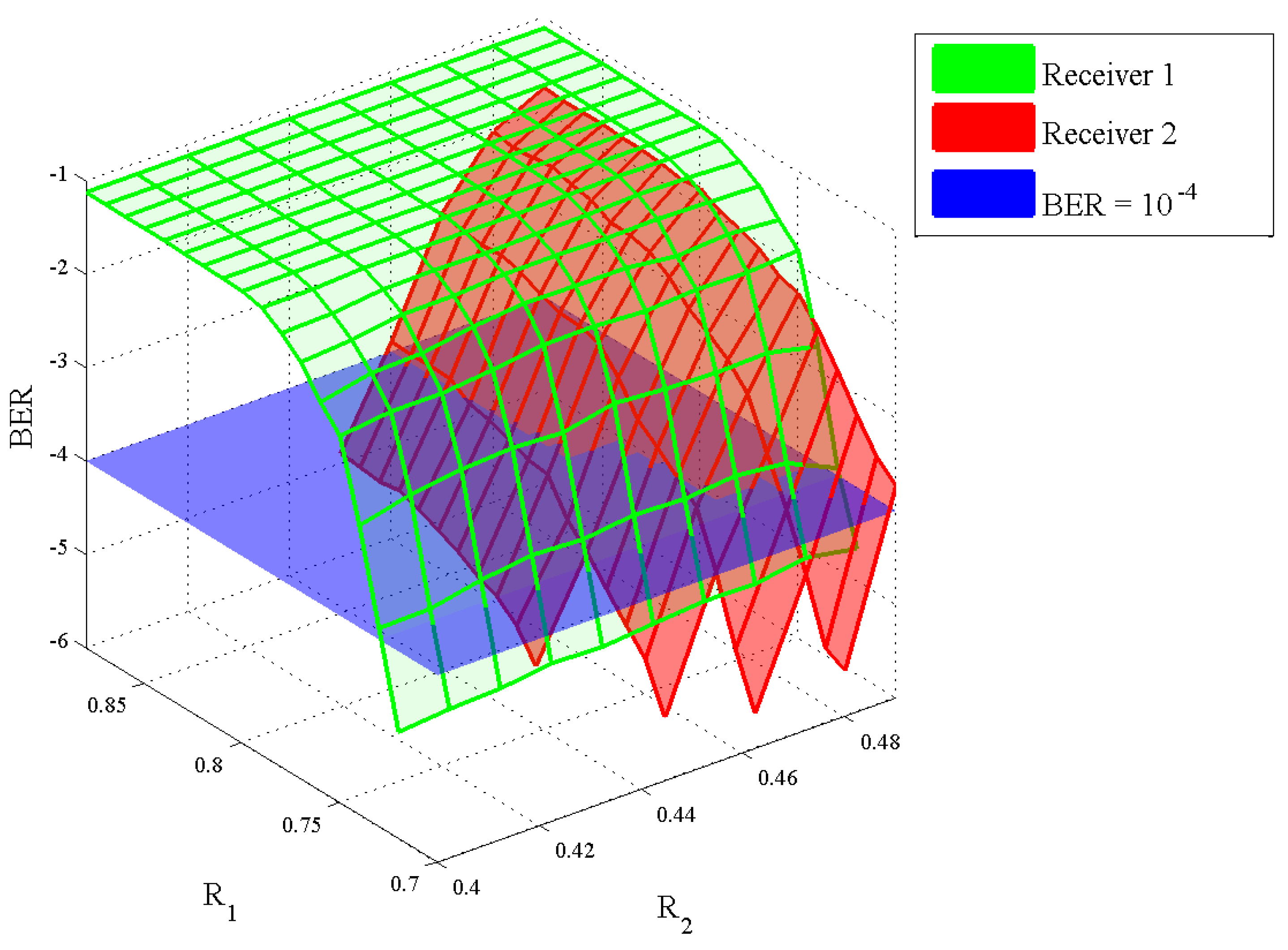
| Parameters | Values |
|---|---|
| Square of interference coefficient a | 0.5 |
| Maximum iteration number J | 200 |
| Kite Code of Sender 1 | |
| Kite Code of Sender 2 | |
| Generator matrix | |
| Code rate pair |
| Parameters | Values |
|---|---|
| Square of interference coefficient a | |
| Maximum iteration number J | 200 |
| Code length N of Kite Code of Sender 1 | 10000 |
| Code length of Kite Code of Sender 2 | 5000 |
| Generator matrix | |
| Step length | 100 |
| Range of message length | |
| Range of message length |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.; Ma, X.; Liang, C.; Huang, X.; Bai, B. An Information-Spectrum Approach to the Capacity Region of the Interference Channel. Entropy 2017, 19, 270. https://doi.org/10.3390/e19060270
Lin L, Ma X, Liang C, Huang X, Bai B. An Information-Spectrum Approach to the Capacity Region of the Interference Channel. Entropy. 2017; 19(6):270. https://doi.org/10.3390/e19060270
Chicago/Turabian StyleLin, Lei, Xiao Ma, Chulong Liang, Xiujie Huang, and Baoming Bai. 2017. "An Information-Spectrum Approach to the Capacity Region of the Interference Channel" Entropy 19, no. 6: 270. https://doi.org/10.3390/e19060270
APA StyleLin, L., Ma, X., Liang, C., Huang, X., & Bai, B. (2017). An Information-Spectrum Approach to the Capacity Region of the Interference Channel. Entropy, 19(6), 270. https://doi.org/10.3390/e19060270







