Abstract
The Internet of Things (IoT) is placing new demands on existing communication systems. The limited orthogonal resources do not meet the demands of massive connectivity of future IoT systems that require efficient multiple access. Interleave-division multiple access (IDMA) is a promising method of improving spectral efficiency and supporting massive connectivity for IoT networks. In a given time, not all sensors signal information to an aggregation node, but each node transmits a short frame on occasion, e.g., time-controlled or event-driven. The sporadic nature of the uplink transmission, low data rates, and massive connectivity in IoT scenarios necessitates minimal control overhead communication schemes. Therefore, sensor activity and data detection should be implemented on the receiver side. However, the current chip-by-chip (CBC) iterative multi-user detection (MUD) assumes that sensor activity is precisely known at the receiver. In this paper, we propose three schemes to solve the MUD problem in a sporadic IDMA uplink transmission system. Firstly, inspired by the observation of sensor sparsity, we incorporate compressed sensing (CS) to MUD in order to jointly perform activity and data detection. Secondly, as CS detection could provide reliable activity detection, we combine CS and CBC and propose a CS-CBC detector. In addition, a CBC-based MUD named CBC-AD is proposed to provide a comparable baseline scheme.
1. Introduction
In modern wireless communication scenarios, the Internet of Things (IoT) is seen as a major innovative technology and provides competitive advantages over current solutions in a number of fields, such as health care [1], environmental monitoring [2], and so on. The total communication traffic between accessing devices and aggregation point can be enormous due to the increased demand of connected things. As a consequence, one more efficient physical layer technology should be applied to achieve highly reliable massive connectivity. Multiple access schemes present themselves as the key revolutionary technologies to distinguish different transmission efficiencies in wireless communication systems with multiple users. Specifically, interleave-division multiple access (IDMA) is attractive for simultaneous massive device access [3].
IDMA is a relatively novel multiple access method, which is considered as a special case of code division multiple access (CDMA) due to the use of low-rate code in spreading and separating users from specific interleavers [4]. Such a multiple access techinique inherits many distinguished features of the well-studied CDMA, and has further improvement in terms of performance and spectrum efficiency [5]. Furthermore, it allows a low-cost chip-by-chip (CBC) iterative multi-user detection strategy [4]. Several advanced technologies, such as orthogonal frequency-division multiplexing (OFDM), combine with IDMA based on chip-by-chip detection to enable reliable performance for a large number of devices accessing simultaneously [6,7].
For a more practical uplink communication in an IoT scenario, not all devices simultaneously transmit data in a given time but only a fraction of users’ signals arrive at the aggregation node at a low data rate. This means that IoT devices are only sporadically active. Conventionally, a reservation multiple access protocol is adopted in order to position the active users and then data can be recovered through a multi-user detection scheme. However, a significant amount of additional transmission will be produced due to the large number of connected devices in an IoT scenario. To reduce the transmission overhead, direct random access can be applied in order to avoid signaling user activity and, thus, reliable multi-user detection (MUD) [8] should be performed on the receiver side by jointly detecting all users’ activity and active users’ transmitting data. It is noteworthy that the chip-by-chip iterative detector in the IDMA system is usually realized based on the assumption that active users are exactly known at the receiver, which is challenging in practice. Therefore, accurate detection of user activity and data is required to enable large-scale connectivity in sporadic IDMA transmission, and this vital issue is rarely investigated in the literature.
As a novel theory guaranteeing the perfect reconstruction of a sparse signal even in an under-determined system, compressed sensing (CS) [9,10] is a popular application in many research fields, such as signal processing [11], radar [12], and so on. In order to perform a reliable MUD in the case of different sparsity, the authors of [13] adopted a switching MUD scheme between linear minimum mean square error (LMMSE) and orthogonal matching pursuit (OMP), which is the most famous CS reconstruction algorithm. The innovative attempt, bringing CS to MUD, prompted many researchers to develop MUD schemes based on CS. In a sporadic wireless communication scenario, CS could also provide reliable activity and data detection [14,15]. To date, investigations of CS-based MUD have primarily focused on CDMA, which is not a feasible choice for massive connectivity in sporadic IoT scenarios.
In this paper, we will provide a detailed description of CS-based multi-user activity and data detection for sporadic IDMA uplink transmission, in which CS theory is brought into IoT communications. Firstly, on the basis of an IDMA chip-rate multi-user model, we will apply CS detection to achieve joint activity and data recovery and explain the main difference between IDMA and CDMA systems in terms of the measurement matrix of CS. Secondly, for incorporating CBC’s good capability of data recovery into CS, we propose a CS-CBC detector to realize both user activity and data detection in a sporadic IDMA transmission system. Specifically, CS-CBC employs CS to achieve reliable positioning of non-zero values in sparse signals (i.e., accurate active sensor detection), and CBC to obtain data recovery. Furthermore, as users generally signal their information on a frame basis, where each frame is usually composed of several continuous symbols, and we exploit the block-sparsity to improve the signal detection performance under the CS framework. In addition, inspired by the observation that a posterior probability produced by decoders contains activity information, we propose a CBC-based MUD, named CBC-AD, to provide a comparable baseline scheme.
The remainder of this paper is organized as follows: the sporadic IDMA multi-user transmission system model and the conventional CBC algorithm for multi-user detection are summarized in Section 2. In Section 3, we introduce CS detection in detail, validate the CS algorithm’s feasibility in joint activity and data detection, and further describe the CS-CBC algorithm. Then, simulation results are discussed in Section 4, and finally, conclusions are drawn in Section 5.
Throughout this paper, the following notation is employed: lower case bold characters d denote vectors, whereas upper case bold characters A denote matrices. Moreover, scalar values are given by regular letters, such as m; denotes the f-th chip of user k; dk(i) denotes the i-th symbol of user k.
2. Sporadic IDMA Transmission System Model and Chip-by-Chip Multi-User Detection
2.1. Sporadic IDMA Transmission System Model
Consider a sporadic wireless uplink IDMA transmission system in an IoT scenario, where K sensor nodes communicate with a single aggregation point, as depicted in Figure 1. Generally speaking, all sensors transmit collected information with low cost and low-energy consumption, whereas the aggregation point can support more complex computational consumption, such as advanced signal processing. Since not all sensors are signaling in a given time, that is, only a few sensors are active on occasion, we call this sporadic transmission. Each sensor changes their active state on a frame basis whenever it transmits data, such that the transmission is organized in time frames. We model the sporadic nature of transmission with respect that all sensors transmit with a relatively small active identical probability pa in a frame time, i.e., a simple Bernoulli traffic model. In a practical IoT, the average the number of active users Kact is small due to a large number of sensors connecting with the aggregation point.
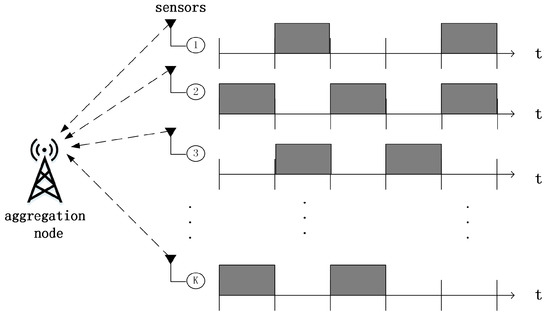
Figure 1.
IoT uplink scenario with K sensors sporadically transmitting frames to an aggregation node.
Additionally, all sensors are equipped with IDMA transmitters and the transmitter structure with K sensors is shown in Figure 2. The common core parts of an IDMA transmitter are a spreader (repetition encoder) and chip interleaver. Herein, the symbols are repeated and then processed with a flip-mask in the spreader. Compared to CDMA, the spreader is the same for all users and specific interleavers are used to separate users in IDMA. The bit stream of user k is encoded and modulated to a symbol vector . Then the transmitted symbols are spread to a chip vector by a Ns-length spreading sequence, where F is the length of the chip vector and . Finally, a chip interleaver specific to each user is applied and the chip vector is permutated to an interleaved chip vector . To detect both node activity and data, the IDMA system model contains all possible frames from K sensors. Further, we model that the transmitted symbols for active nodes are taken from the discrete finite modulation alphabet , while all zeros symbols for inactive users. Thus, the signal which be detected is from the augmented modulation alphabet .
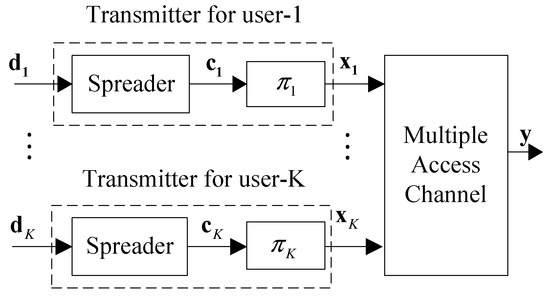
Figure 2.
Transmitter structure of an IDMA scheme with K sensors, including a multiple access channel.
After that, all transmitted symbols are superimposed in the receiver, and the receiver signal matrix y is modeled as:
For the k-th user, is the previous defined vector including transmitted symbols. Each column of contains the spreading sequence , describes the matrix form of user specific interleaver , and is a channel matrix for the node-specific block-fading channel hk. The total influence of transmission can be represented as one matrix , which is the concatenation of . Vector is the stacked vector of all dk, where . Further, the noise vector is i.i.d. zero-mean Gaussian distributed, i.e., . Herein, the symbols of d are taken from the discrete augmented alphabet .
Synchronous reception and perfect channel state information are assumed in Equation (1). The precondition of these two assumes are appropriate delay and channel estimation. As previous research has shown, in addition to detecting activity and data, it is feasible for CS in detecting delays and channel coefficients [16,17].
2.2. Chip-by-Chip Iterative Multi-Users Detection
At the receiver of IDMA systems, a typical iterative sub-optimal receiver, CBC-MUD with acceptable complexity, has been proposed to achieve reliable multi-user data recovery by taking the advantage of interference cancellation among multiple users. Specifically, CBC MUD can be illustrated in Figure 3, in which all transmitted symbols from K sensors are taken from the modulation alphabet , i.e., assuming all sensors are active in a whole frame.
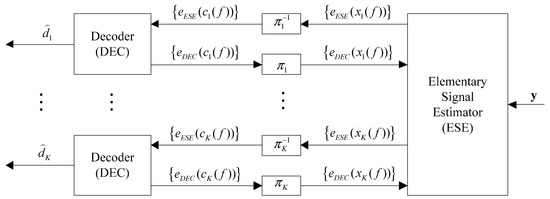
Figure 3.
Chip-by-chip iterative multi-user detection.
The CBC-MUD scheme contains mainly two parts: an elementary signal estimator (ESE) and K single-user a posteriori probability (APP) decoders (DECs). In the whole turbo iterative process, the ESE and the DECs generate logarithmic likelihood ratios (LLRs) of as extrinsic information, which is defined in Equation (2), for interchange:
2.2.1. The Basic ESE Function
Due to the specific interleaver of each sensor, the adjacent chips are approximately uncorrelated, so that the ESE carries out operation in a chip-by-chip manner. The received chip y(f) can be written as:
where the distortion (including interference and noise) of sensor k is:
where hk is the a priori channel coefficient at the receiver side, and nf is the sample of additive white Gaussian noise (AWGN) with variance .
The function of elementary signal estimator (ESE) is mainly divided into two steps:
Step i. Estimation of interference mean and variance:
Step ii. LLR generation:
2.2.2. The DEC Function
The function of DEC is mainly divided into two parts. One is calculating extrinsic information LLRs based on the output of ESE. Then, ESE generates the following statistics to update the interference mean and variance:
The other is implementing APP decoding with the a posteriori LLRs LAPP(dk(i)) of each sensor after several iterations. The DEC calculates LAPP(dk(i)) as following:
As discussed above, the CBC-MUD has a low complexity compared to the maximum a posteriori (MAP) MUD. Specifically, compared with CDMA, the extra cost of CBC-MUD is concentrated in ESE, which is very modest due to seven multiplications and five additions per coded bit per user. Therefore, the overall complexity of CBC-MUD is roughly comparable to that of a single-user one.
Although CBC-MUD can provide a considerably good performance in terms of complexity and multi-user data detection, it assumes that sensor activity information is exactly known at the receiver side. In a sporadic IDMA uplink transmission system, in order to facilitate an efficient transmission, sensors can randomly transmit signals without scheduling. Therefore, both sensor activity and data detection should be performed at the receiver side.
3. Activity and Data Detection Based on Compressed Sensing
3.1. CS Detection
3.1.1. Compressed Sensing
To clarify the connection of CS detection and sporadic IDMA system model, we will firstly introduce CS theory [9,10]. Rather than the classical Nyquist-Shannon sampling theorem, the core part of CS is that a compressible signal can be represented or sampled with fewer samples from a set of non-adaptive linear measurements. In the context of CS, a high-dimensional compressible signal can be sampled via a measurement matrix to a low-dimensional measurement vector , where compressible denotes that the signal z can be expressed by S-sparse vector in an appropriate basis , e.g., a Fourier transformation. Specifically, S-sparse means that the vector x contains S non-zero elements, i.e., . Therefore, the measurement vector y can be written as:
where combines the overall influence of and . Generally, A is considered to be a fat matrix, that is, M is smaller than N.
In CS, considering a reliable recovery of the original signal z from the measurement vector y, CS mainly focuses on the recovery of the sparse signal x, instead of z. For a noise model setting, we conclude the model of measurement vector y from Equation (9):
where is uncorrelated noise. As long as has a low sparsity, CS can provide reliable recovery performance even for under-determined systems, i.e., [18,19]. More specifically, CS can detect the signal x easily, that is to say, the position and the values of non-zero items can be jointly recovered.
3.1.2. Application to Multi-User Detection
Due to the fact that CS provides a generic solution to the sparse signal recovery, a wide range of potential applications has been researched. As to the IDMA sporadic wireless communication, the connected nodes transmit signals continuously in a frame basis by a low probability. Since sensors are active or inactive for a whole frame, the non-zero symbols of the sparse vector d appear in groups or blocks forming a fixed length. This feature is also known as block sparsity or group sparsity [20]. For the sake of uniform expression in this paper, we choose block sparsity in the following. The MUD problem can be treated as a block-sparse signal recovery, inherently, which naturally incorporates the powerful tool CS into the joint user activity and data detection problem.
In terms of CDMA model in sporadic communication, the application of CS detection to multi-user signal recovery has been proved to have considerably advantages than conventional MUD schemes [14,15]. As a special case of CDMA, IDMA has similar system model summarized in Equation (10), which is in conformity with the common CS detection form. Therefore, CS detection can be applied to the sporadic IDMA transmission system. It should be noted that, compared to CDMA model, IDMA adopts interleaving process to separate users after spreading. The apparent difference reflected in the structure of matrix A is that CDMA blocks the non-zero elements together, whereas IDMA distributes them randomly. That is to say, in IDMA, the individual symbols are interconnected with many more symbols than in CDMA. This randomness feature in IDMA conforms to the matrix selection of CS, which results in better performance of multi-user signal detection [21], which will be proved by simulations in Section 4.
In the context of IDMA sporadic communications, adopting CS detection to MUD will bring two main benefits. On one hand, even in under-determined system, CS detection solution provides reliable recovery of block sparse signal d. From the perspective of bandwidth constrained wireless communication, this leads to a high resource efficiency, since the number of measurements of y is strikingly smaller than the number of transmitted symbols. On the other hand, in order to recover the sparse signal, CS provides various detectors in the case of different structures of the sparse signal d.
To date, several CS algorithms have been proposed which can be mainly divided into two categories: greedy algorithms or convex optimization. Considering the complexity, greedy algorithms are utilized for more practical applications. Orthogonal matching pursuit (OMP) [22] is one of the famous sub-optimal and greedy algorithms to solve the CS problem. Here, we focus on efficient CS algorithms that exploit block information for further processing. Therefore, the greedy group orthogonal matching pursuit (GOMP) [23] detector will be described in the following paragraphs.
3.1.3. GOMP
The GOMP algorithm exploits the block-sparsity in order to improve the detection performance, as listed in Algorithm 1 below. It is derived from OMP, which is one of the legendary greedy and sub-optimal algorithms to solve CS detection problem. The difference between OMP and GOMP is mainly concentrated in the active support selection methods. While selecting the non-zero elements, the OMP iteratively builds the support of d by simply selecting the indices of those columns of matrix A. This method has the maximum usefulness, but neglects the additional information that the user activity symbols of one user are the same. In order to utilize the additional information, during each iteration, the GOMP algorithm, builds support by adding indices of groups to a group index set G, instead of a single index in OMP.
| Algorithm 1: Group orthogonal matching pursuit. |
| Input: y, A, Output: 1: initialize |
| 2: repeat |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: 8: until 9: |
For the algorithms, we use the following notations: is a set of group-indices and is the complementary set. and specify the vector-indices counterpart to any group in G or group l, respectively. specifies the sub-matrix that contains those columns with indices in . Similarly, specifies the corresponding elements of d. Additionally, the superscript t always denotes the t-th iteration, e.g., dt, At, and Gt. Further, is the Moore-Penrose pseudo-inverse of matrix A, and AH denotes the Hermitian matrix of A.
Specifically, the main procedure of the GOMP algorithm at the t-th iteration with the initial group support can be summarized as follows [23]:
- (1)
- (Step 4 in Algorithm 1) Group support selection: To be specific, the GOMP chooses the group , which has the highest correlation to the previous residual as the active support.
- (2)
- (Step 5 in Algorithm 1) Update the group-indices set G: The set of the newly-selected group index obtained in the previous step is added to the set
- (3)
- (Steps 6 and 7 in Algorithm 1) LS estimation is executed by using the sub-matrix of all columns in to determine the values of nonzero elements in and renew the current residual.
It is noted that the activity detection of GOMP is affected by the errors in data estimation owing to the fact that subsequent iteration depends on the previous residual rl − 1. An ideal stopping criterion is adopted to terminating the algorithm after a number of iterations, e.g., l = Kact.
3.2. CBC-AD
The core part of MUD based on CBC is mainly the implementing of interference cancellation. From the view of one user, interference cancellation is achieved by subtracting all uninterested data from the incoming data signal. This method will reduce/cancel the interference from other users. In general, the bits of other users are unknown and only estimates are obtained from the decoder’s soft outputs. Utilizing the a posteriori LLRs generated in DEC for each user after several iterations, hard decisions can be reached to realize data detection. It should be noted that, in order to realize the data detection, the a posteriori LLRs LAPP(bk(i)) is only treated as the input information of the hard decision, whereas the LAPP(bk(i)) contains the activity information, but not been utilized [24]. In order to exploit the activity information, we adopt the activity detection strategy on the basis of CBC that summing up a frame of the absolute value of a posteriori LLRs produced in DEC for each user to determine active users. User-k activity information can be computed by:
where LAPP(bk(i)) denotes the a posteriori LLRs of the i-th symbol in the k-th user. Principally, LAPP(bk(i)) contains activity information of user-k. Therefore, active users are identified on the basis of a threshold given by the assumed noise model. However, to provide a fair comparison with CS detection and avoid threshold dependencies, we assume that the activity detector has perfect knowledge of the instantaneous number of active users Kact. Thus, the nodes with the highest Kact values are collected in the set of active nodes G. Subsequently, hard decisions on active set G can be applied to estimate the transmitted symbols of active users.
3.3. CS-CBC
In sporadic communication, the well-known sensor activity information is the premise of CBC-based data detection at the receiver. As discussed before, CS detection provides various detectors to implement reliable activity detection. In order to enhance the robustness of uplink sporadic IDMA transmission, as shown in Figure 4, we propose a CS-CBC multi-user detector that can accurately detect the sensor activity and efficiently implement data detection. It should be noted that, since classical CS can jointly recover the activity and data detection, CS-CBC employs CS detection to accurately detect positions of non-zero elements in the sparse signal d, rather than the values of non-zero elements.
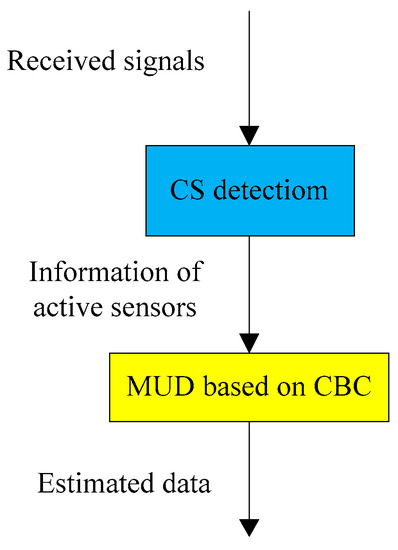
Figure 4.
Diagram representation of the proposed CS-CBC multi-user detection.
After the user activity information is obtained above, the received signal y, which composes of the symbols transmitted by active sensors and modulated by interleaved spreading sequences, can be expressed as:
where dactive contains the transmitted symbols of active sensors, A2 has the same form as A in Equation (1) except that it only includes interleaved spreading sequences and channel influence for active sensors. Then, CBC algorithm can be implemented to realize active data detection.
The proposed CS-CBC detector combines the advantages of CBC and CS detection to achieve both sensor activity and data detection at the same time. Observing that the sparse signal d has the structure of block sparse, we take GOMP algorithm as the choice of CS detection part. The GOMP algorithm can provide good performance in detecting the support of sparse signal even in a high-noise environment. Compared to CS detection, CS-CBC only increases the complexity of MUD based on CBC, which is upper bounded by O(Kact).
4. Simulation Results and Discussions
In this section, we analyze the symbol error rate (SER) performance of the MUD approaches described in Section 3.
We consider an overloaded IDMA system, which result in under-determined equation system for CS detection. The main simulation parameters are set as follows: the total number of users is K = 100, the frame length M is set to 50, and random interleavers [4] are adopted. All users use the same spreading sequence, which is generated based on repetition coding and multiplied by a mask sequence with alternant signs, i.e., +1, −1, +1, −1,..., The spreading length Ns is 64. Therefore, the overloading factor is 156%. Binary phase shift keying (BPSK) signaling is always considered. In many sporadic communication scenarios, such as machine-to-machine communication and sensor networks, only low data rates are required and, thus, small bandwidth is used. For a small requirement of bandwidth, a non-frequency selective channel is more practical most of the time, which means multi-path propagation has little influence on the frame transmission. Thus, we consider a single-tap channel, in which the real part coefficients are generally correspondent to Gaussian distribution. The estimation of received power and the phase are assumed to be well prepared for each node before detection. Therefore, we adopt the AWGN channel as a simplified channel model, such that the channel matrix Hk for each user is an identity matrix.
4.1. The SER Performance Comparison between IDMA and CDMA System
As discussed in Section 3.1.2, the properties of system matrix A will vary for different multiple access technologies, and further distinguish the symbol error rate (SER) performance of multi-user detection based on CS. For fair comparison, we adopt the GOMP algorithm to implement MUD for both multiple access system. Figure 5 shows the SER performance comparison between IDMA and CDMA system, with two active probabilities setting, i.e., pa = 0.1 and pa = 0.3.
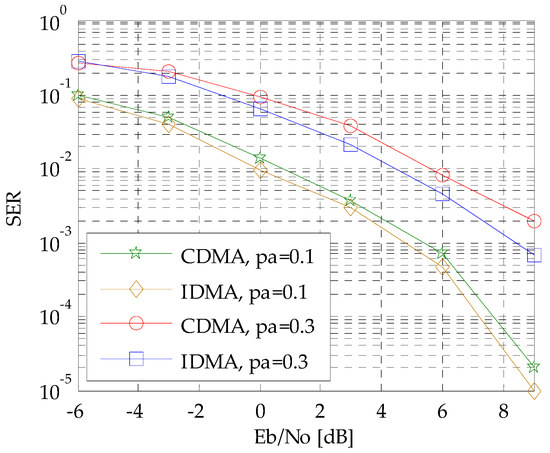
Figure 5.
The SER performance comparison between IDMA and CDMA systems.
It is apparent from Figure 5 that the IDMA system outperform CDMA system. The result conforms that the transmitting structure of IDMA leads to deeper randomness in the system matrix, which is more beneficial for the data reconstruction in CS theory. The SER performance gap is more pronounced with increasing active probability, which might be attributed to the larger matrix structure difference due to an increasing amount of interleaved non-zeros elements.
4.2. SER Performance with Different Eb/N0
In this subsection, we consider SER performance with different in a given active probability pa. Active probability pa reflects the frequency of sensors’ activity in the whole wireless sensor networks. The larger the active probability pa is, the more data sensors will be transmitted. Assuming the active probabilities are pa = 0.1, pa = 0.2, pa = 0.3 and pa = 0.4, respectively, the simulation results are illustrated in Figure 6.
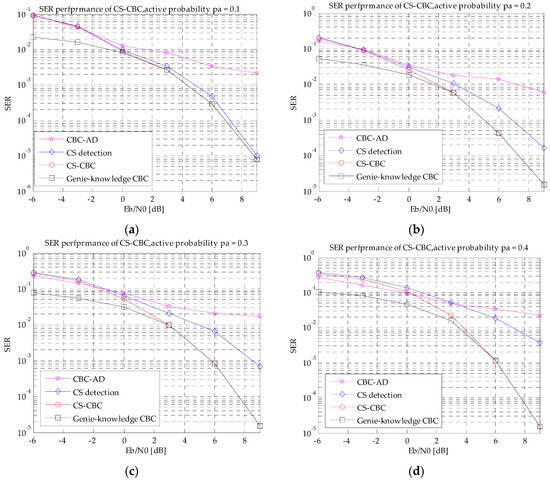
Figure 6.
SER performance with different Eb/N0. (a) pa = 0.1; (b) pa = 0.2; (c) pa = 0.3; and (d) pa = 0.4.
Figure 6 compares the SER performance of the following four detectors: CBC-AD, CS detection, the proposed CS-CBC, and Genie-knowledge CBC. Herein, the Genie-knowledge CBC algorithm plays a lower bound. Figure 6 demonstrates that CBC-AD is superior to CS detection and CS-CBC algorithm under low Eb/N0 and the SER performance gap is more pronounced with increasing active probability. The CBC-AD takes the advantage of full frame activity knowledge, which results in a good performance in a high noise levels due the averaging. Two obvious characteristics should be noted when Eb/N0 increases: on one hand, due to the high correlation of the interleaves in overloaded system, the performance of the CBC-AD quickly hits an error floor; on the other hand, CS-CBC is superior to CS detection and CBC-AD and their gaps become larger with higher Eb/N0. Furthermore, it is close to the performance of Genie-knowledge CBC under high Eb/N0. Thanks to the reliable performance of CS detection, CS-CBC has perfect knowledge of active sensors to position non-zero items, and makes data recovery better than CS detection.
4.3. SER Performance with Different Active Probability pa
In this subsection, we consider the SER performance with different pa and a given . Simulation results are illustrated in Figure 7.
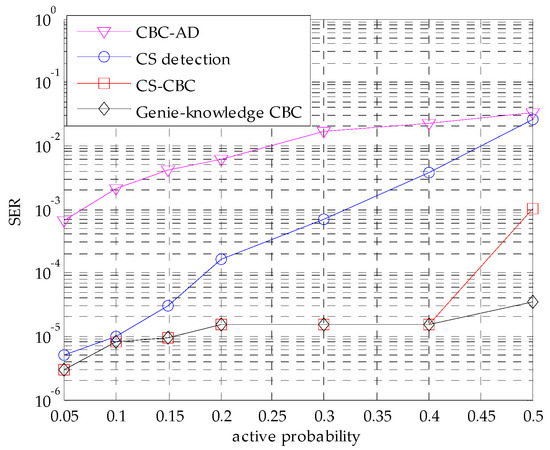
Figure 7.
The SER performance comparison with different active probabilities.
Figure 7 demonstrates the effect of different active probabilities pa, where the Eb/N0 is 9 dB. As can be seen, CBC-AD and CS detection deteriorate with increasing pa and the difference between them becomes smaller. This is because the number of active sensors becomes larger, and the number of errors caused by highly correlated sensors become larger. The CS-CBC is superior than CS detection and CBC-AD and the difference between them becomes larger with increasing pa. It should be noted that CS-CBC can maintain the same SER performance with Genie-knowledge CBC before pa reaches 0.4. When pa is greater than 0.4, CS-CBC deteriorates more quickly than Genie-knowledge CBC. This means that there exists incorrect detections in active sensors when pa is too high, which results in the decay of CS-CBC.
5. Conclusions
In this paper, we investigated the MUD problem based on CS theory in a sporadic IDMA uplink transmission in order to provide reliable massive connectivity in IoT scenarios. We formulated a sporadic IDMA system model and described the main differences compared to a CDMA system. Then the influence of multiple access schemes on the measurement matrix are analyzed from the CS perspective. Simulation results confirmed that the randomness produced in the chip-interleaved process of the IDMA transmitter structure leads to better detection performance. Moreover, we combined the benefits of CS detection and the conventional CBC MUD to propose a CS-CBC detector. The method is simple, but can efficiently improve the SER performance. Compared to existing MUD methods, CS-CBC is superior to the conventional CS detector with increasing active probability, and gains an SER performance very close to a Genie-knowledge CBC detector even in a high activity situation. In this way, the sporadic IDMA uplink transmission becomes feasible and robust. The method can significantly reduce the signaling control overhead and time latency for massive connectivity in IoT scenarios.
Acknowledgments
This work is partly supported by National Natural Science Foundation of China (Nos. 61401118, 61371100, and 61671184), Natural Science Foundation of Shandong Province (No. ZR2014FP016), the Fundamental Research Funds for the Central Universities (Nos. HIT.NSRIF.2016100 and 201720), and the Scientific Research Foundation of Harbin Institute of Technology at Weihai (Nos. HIT(WH)201409 and HIT(WH)201410).
Author Contributions
Bo Li and Wenjing Kang conceived and designed the experiments; Rui Du performed the experiments under the guidance of Bo Li; Gongliang Liu contributed the simulation tools; and Bo Li and Rui Du wrote the paper and make the revisions. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Islam, S.M.R.; Kwak, D.; Kabir, M.H.; Hossain, M. The Internet of things for health care: A comprehensive survey. IEEE Access 2015, 3, 678–708. [Google Scholar] [CrossRef]
- Fang, S.; Xu, L.D.; Zhu, Y.; Ahati, J. An integrated system for regional environmental monitoring and management based on internet of things. IEEE Trans. Ind. Inf. 2014, 10, 1596–1605. [Google Scholar] [CrossRef]
- Chen, Y.; Schaich, F.; Wild, T. Multiple Access and Waveforms for 5G: IDMA and Universal Filtered Multi-Carrier. In Proceedings of the 2014 IEEE 79th Vehicular Technology Conference, Seoul, Korea, 18–21 May 2014. [Google Scholar]
- Ping, L.; Liu, L.; Wu, K.; Leung, W.K. Interleave division multiple-access. IEEE Trans. Wirel. Commun. 2006, 5, 938–947. [Google Scholar] [CrossRef]
- Kusume, K.; Bauch, G.; Utschick, W. Idma vs. cdma: Analysis and comparison of two multiple access schemes. IEEE Trans. Wirel. Commun. 2012, 11, 78–87. [Google Scholar] [CrossRef]
- Ping, L.; Guo, Q.; Tong, J. The OFDM-IDMA approach to wireless communication systems. IEEE Wirel. Commun. Mag. 2007, 14, 18–24. [Google Scholar] [CrossRef]
- Peng, T.; Xiao, Y.; He, X.; Li, S. Improved detection of uplink OFDM-IDMA signals with carrier frequency offsets. IEEE Commun. Lett. 2012, 16, 646–649. [Google Scholar] [CrossRef]
- Verdu, S. Multiuser Detection; Cambridge University Press: Cambridge, UK, 1998; pp. 3–18. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2004, 52, 489–509. [Google Scholar] [CrossRef]
- Xu, W.; Lin, J.; Niu, K.; He, Z. A joint recovery algorithm for distributed compressed sensing. Trans. Emerg. Telecommun. Technol. 2012, 23, 550–559. [Google Scholar] [CrossRef]
- Baraniuk, R.; Steeghs, P. Compressive Radar Imaging. In Proceedings of the 2007 IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007. [Google Scholar]
- Shim, B.; Song, B. Multiuser detection via compressive sensing. IEEE Commun. Lett. 2012, 16, 972–974. [Google Scholar] [CrossRef]
- Bockelmann, C.; Schepker, H.F.; Dekorsy, A. Compressive sensing based multi-user detection for machine-to-machine communication. Trans. Emerg. Telecommun. Technol. 2013, 24, 389–400. [Google Scholar] [CrossRef]
- Monsees, F.; Woltering, M.; Bockelmann, C.; Dekorsy, A. Compressive Sensing Multi-User Detection for Multicarrier Systems in Sporadic Machine Type Communication. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference, Glasgow, UK, 11–14 May 2015. [Google Scholar]
- Schepker, H.F.; Bockelmann, C.; Dekorsy, A. Coping with CDMA Asynchronicity in Compressive Sensing Multi-User Detection. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference, Dresden, Germany, 2–5 June 2013. [Google Scholar]
- Schepker, H.F.; Bockelmann, C.; Dekorsy, A. Exploiting Sparsity in Channel and Data Estimation for Sporadic Multi-User Communication. In Proceedings of the Tenth International Symposium on Wireless Communication Systems, Ilmenau, Germany, 27–30 August 2013. [Google Scholar]
- Donoho, D.L.; Tanner, J. Precise undersampling theorems. Proc. IEEE 2013, 98, 913–924. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kuppinger, P.; Lcskei, H. Block-sparse signals: Uncertainty relations and efficient recovery. IEEE Trans. Signal Process. 2010, 58, 3042–3054. [Google Scholar] [CrossRef]
- Baraniuk, R.; Davenport, M.; Devore, R.; Wakin, M. A simple proof of the restricted isometry property for random matrices. Constr. Approx. 2008, 28, 253–263. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. Signals Syst. Comput. 1993, 1, 40–44. [Google Scholar]
- Majumdar, A.; Ward, R.K. Fast group sparse classification. Can. J. Electr. Comput. Eng. 2009, 34, 136–144. [Google Scholar] [CrossRef]
- Bockelmann, C. Iterative Soft Interference Cancellation for Sparse BPSK Signals. IEEE Commun. Lett. 2015, 19, 855–858. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).