Time-Shift Multiscale Entropy Analysis of Physiological Signals
Abstract
:1. Introduction
2. Time-Shift Multiscale Entropy
3. Results and Discussion
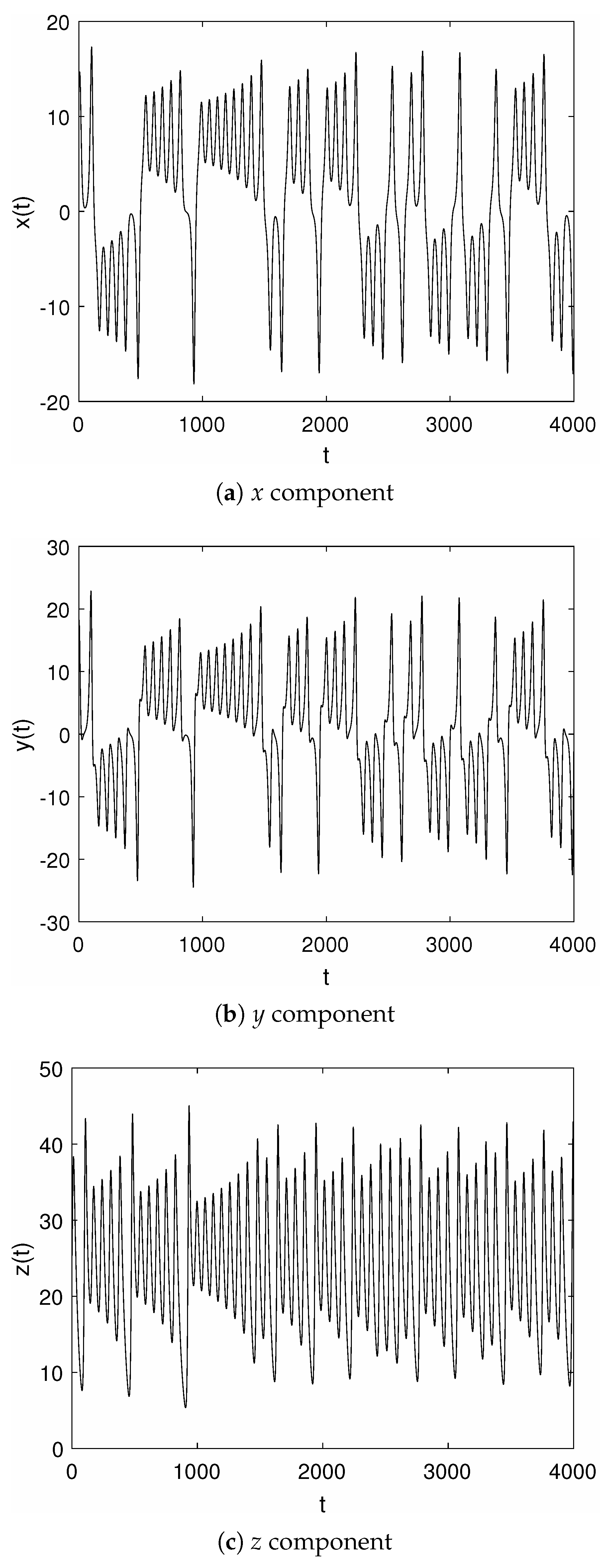
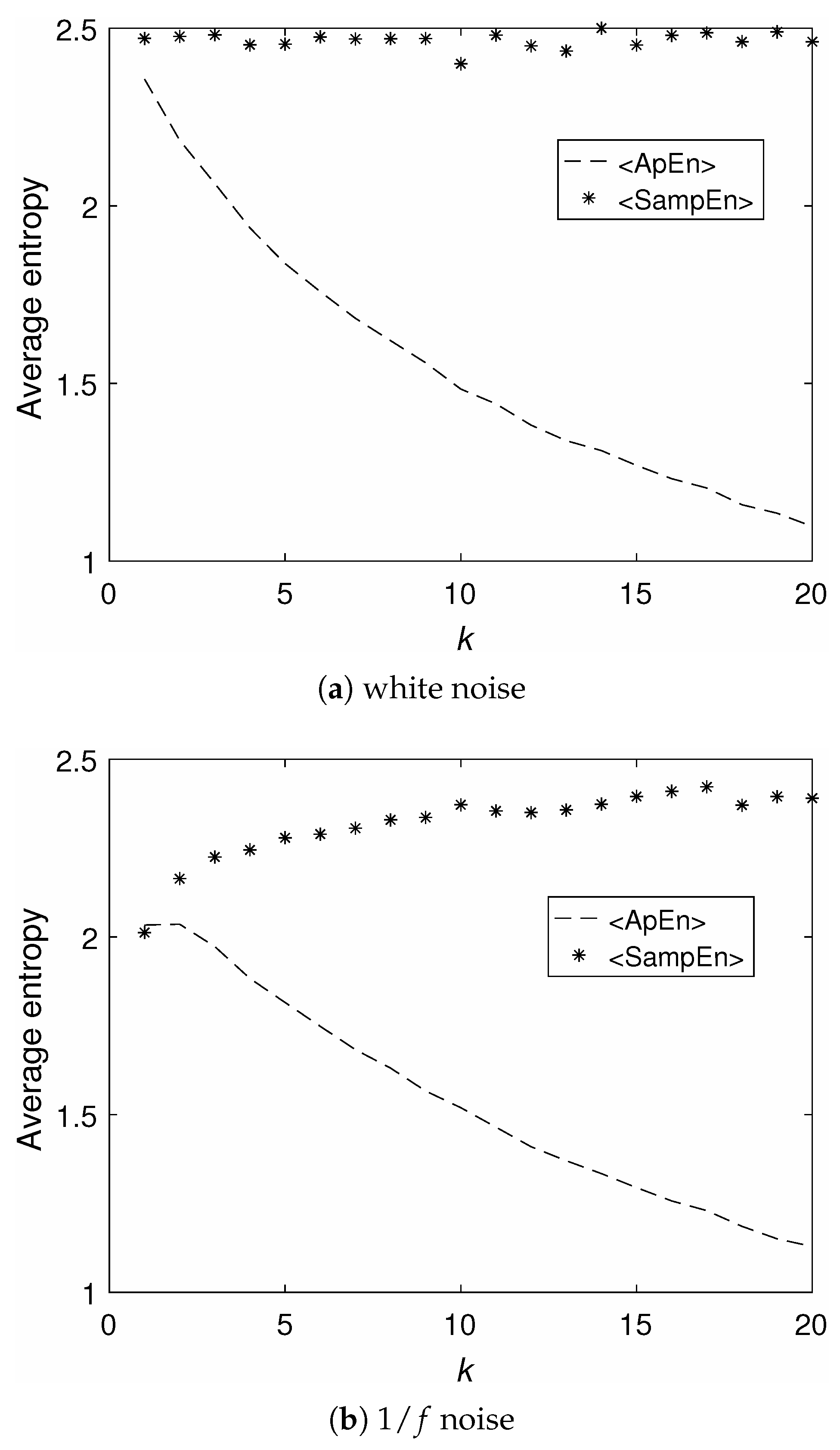
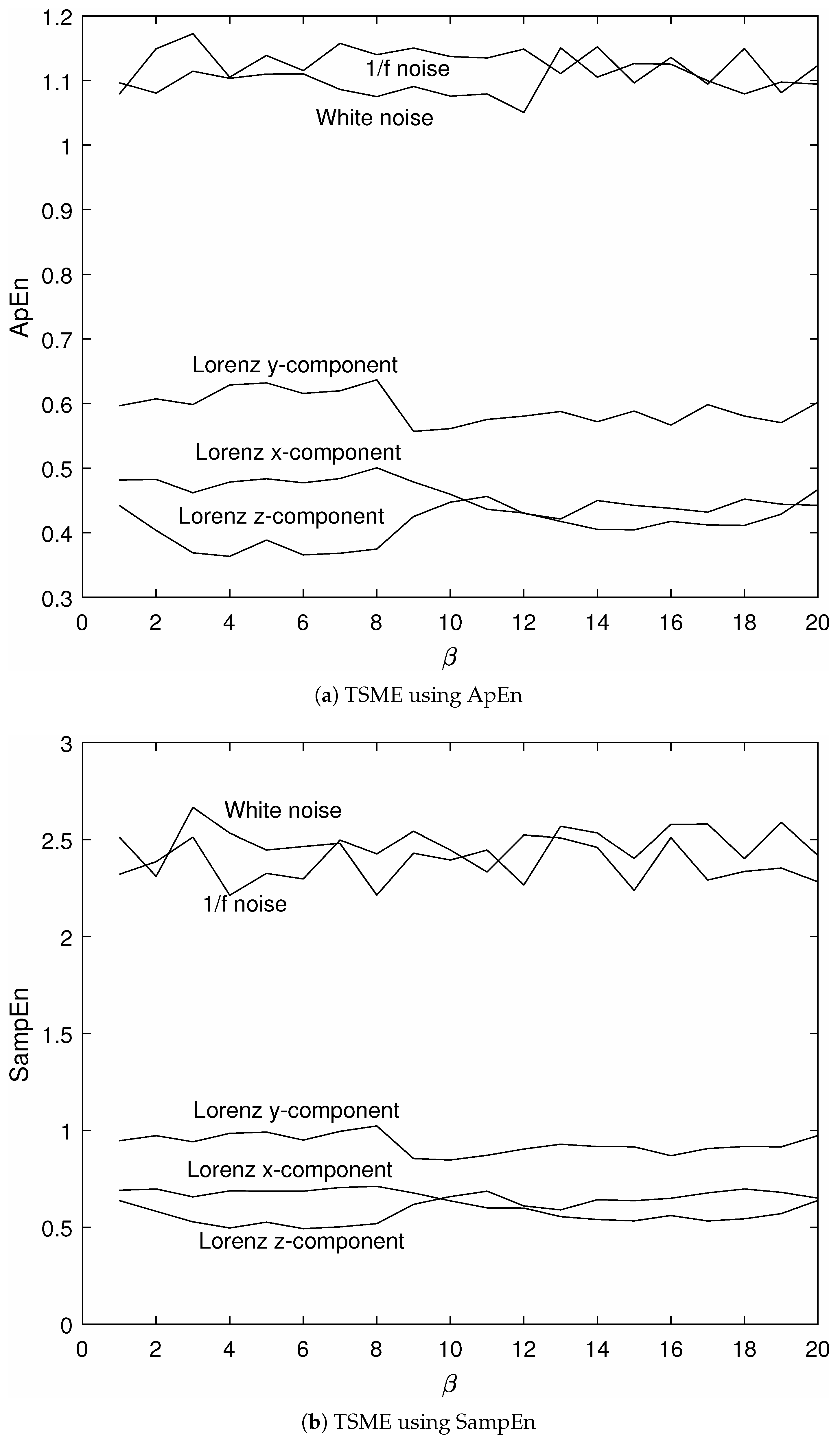
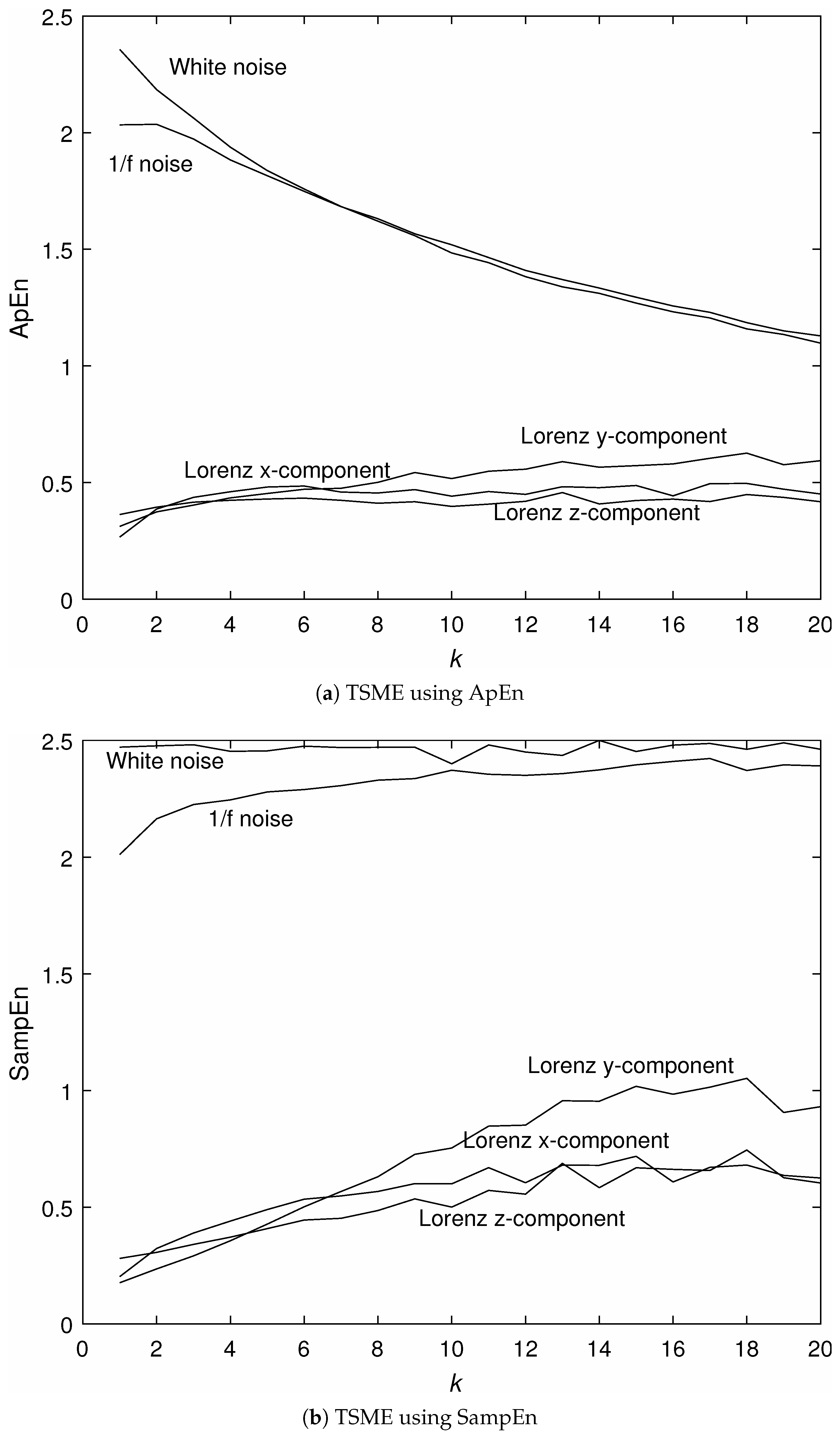
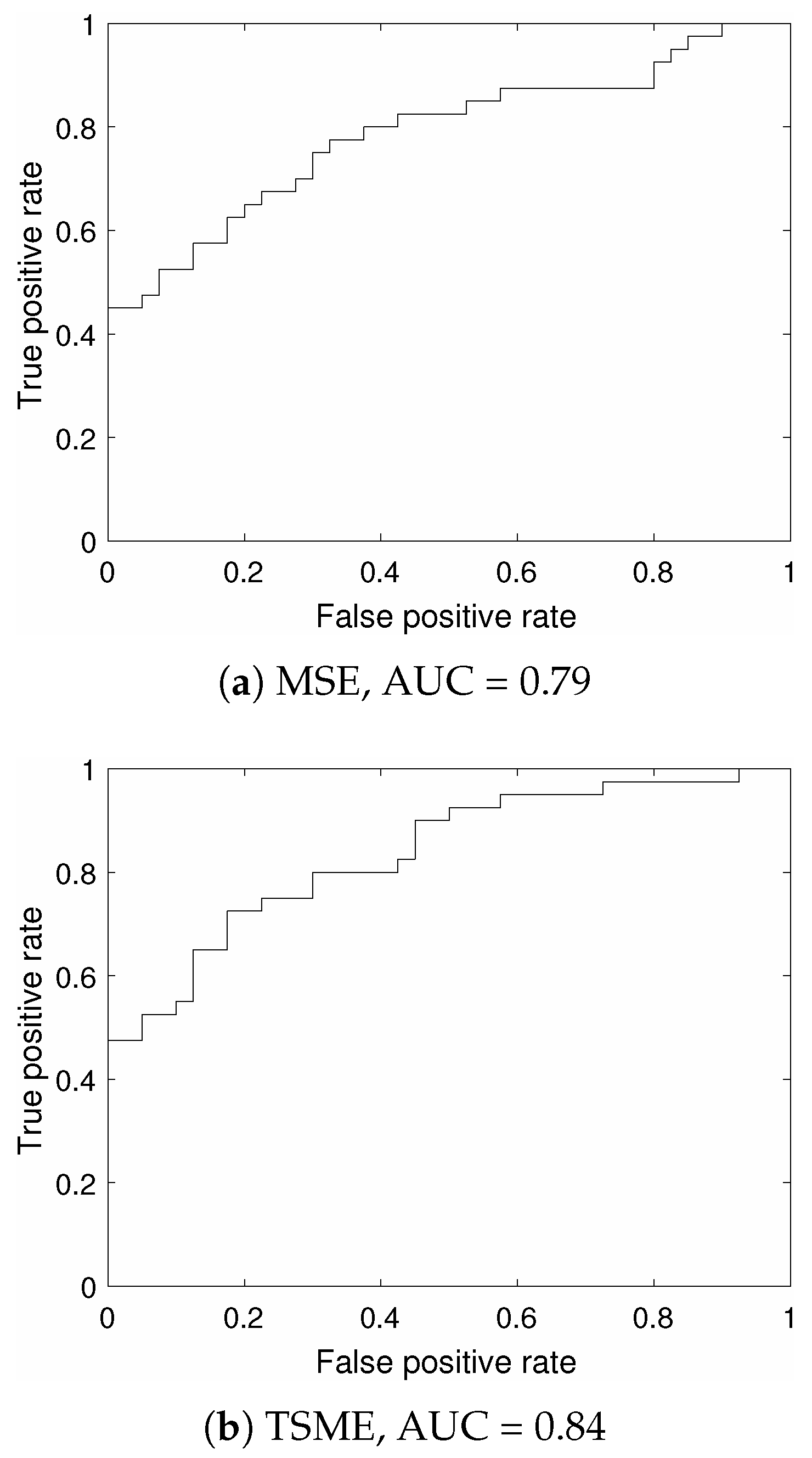
3.1. Analysis of Signals with Known Properties
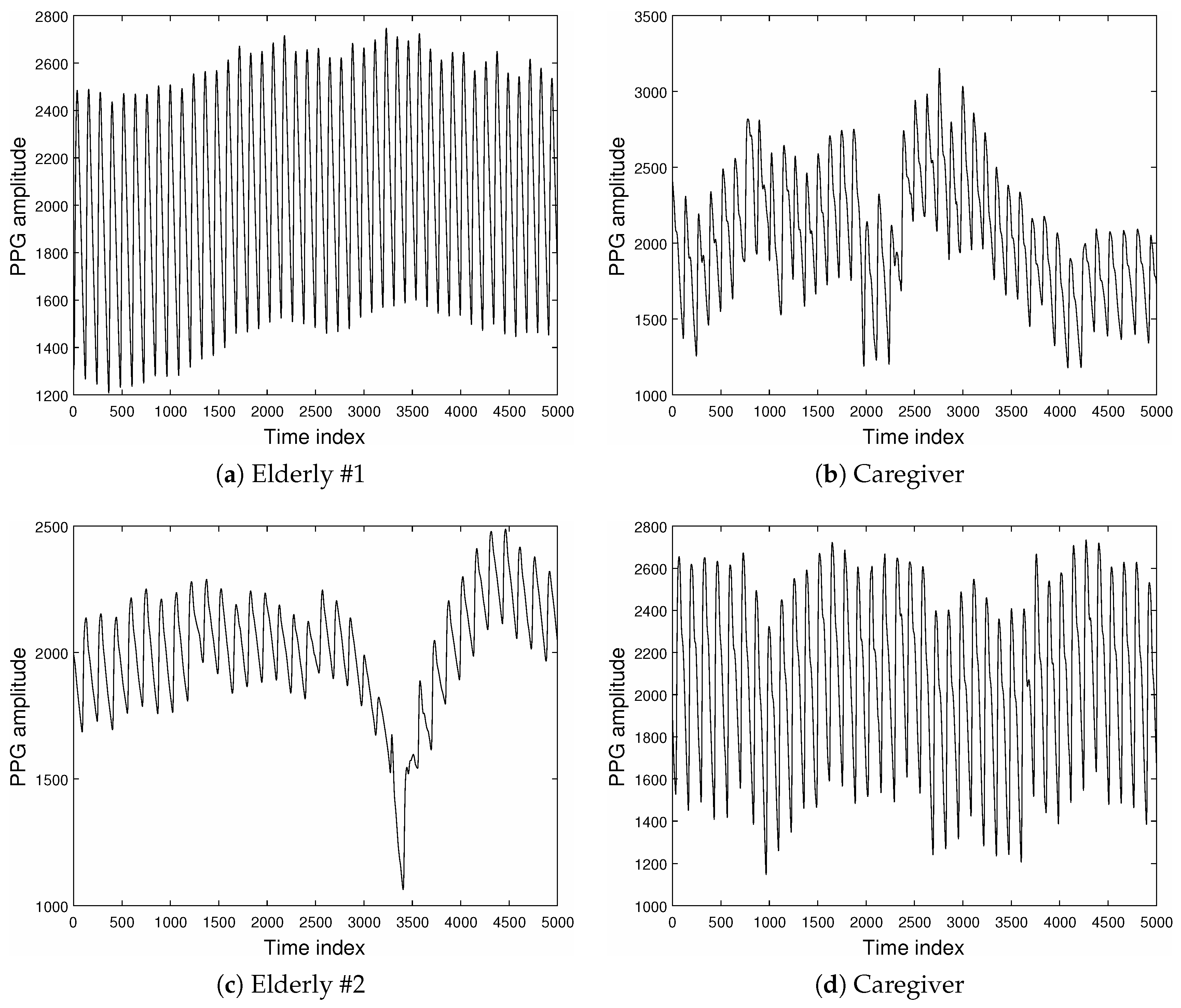
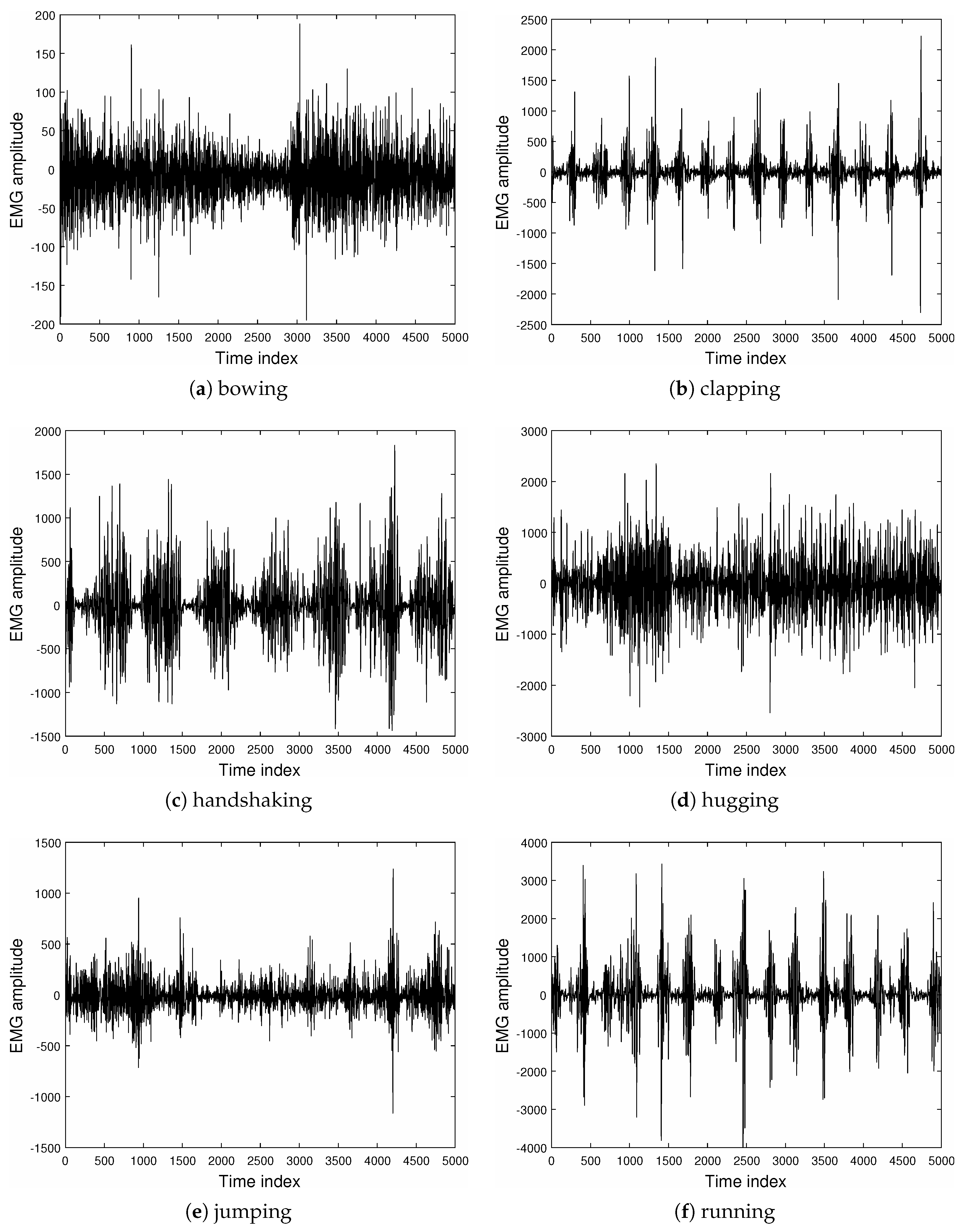
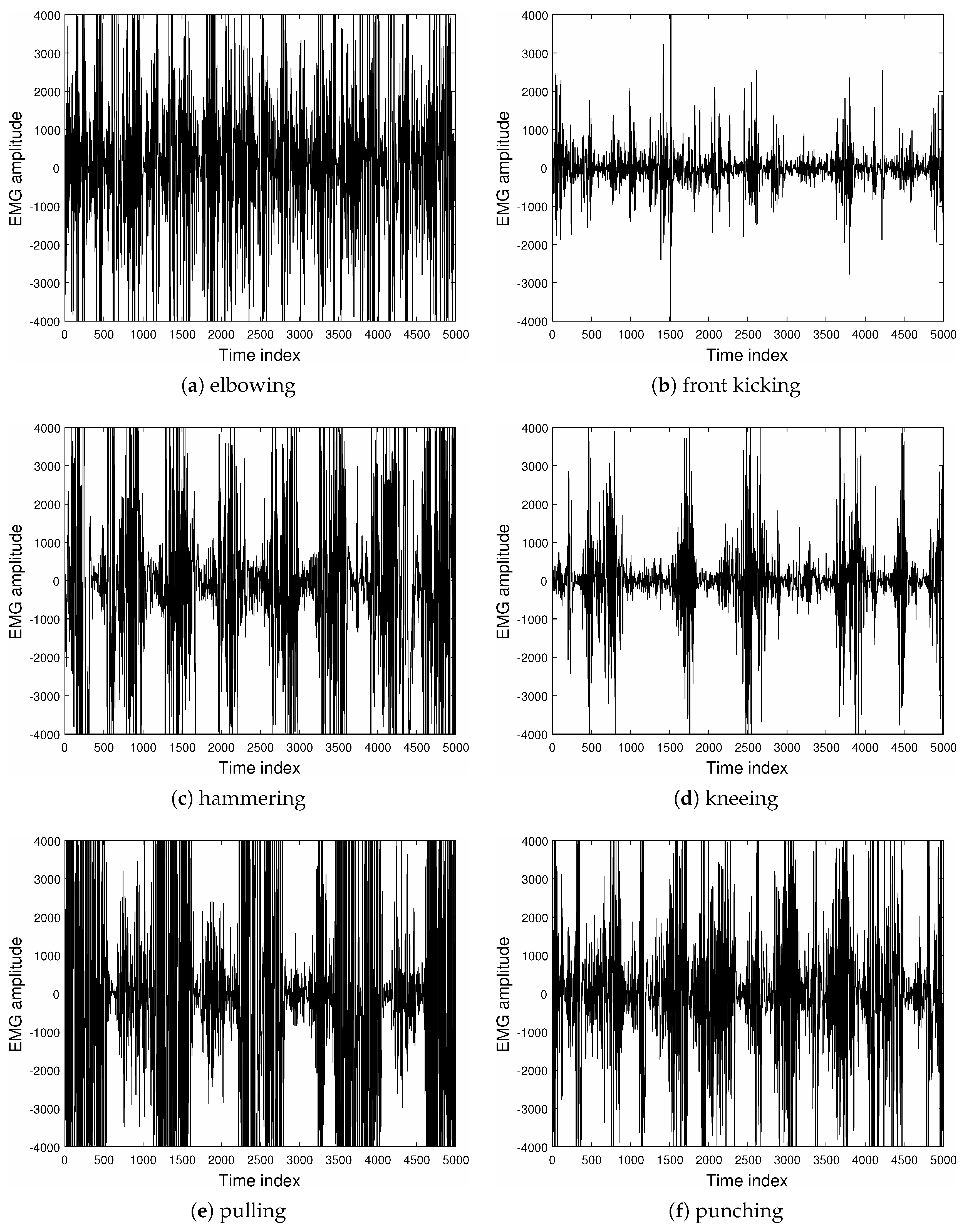
3.2. Analysis of PPG and EMG Signals
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Al-Angari, H.M.; Sahakian, A.V. Use of sample entropy approach to study heart rate variability in obstructive sleep apnea syndrome. IEEE Trans. Biomed. Eng. 2007, 54, 1900–1904. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz, R.; Rieta, J.J. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms. Biomed. Signal Process. Control 2010, 5, 1–14. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time-series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Pincus, S.M.; Gladstone, I.M.; Ehrenkranz, R.A. A regularity statistic for medical data analysis. J. Clin. Monit. 1991, 7, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Grandy, T.H.; Garrett, D.D.; Schmiedek, F.; Werkle-Bergner, M. On the estimation of brain signal entropy from sparse neuroimaging data. Sci. Rep. 2016, 6, 23073. [Google Scholar] [CrossRef] [PubMed]
- Busa, M.A.; van Emmerik, R.E.A. Multiscale entropy: A tool for understanding the complexity of postural control. J. Sport Health Sci. 2016, 57, 44–51. [Google Scholar] [CrossRef]
- Stosic, D.; Stosic, D.; Ludermir, T.; Stosic, T. Correlations of multiscale entropy in the FX market. Phys. A Stat. Mech. Appl. 2016, 457, 52–61. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Higuchi, T. Relationship between the fractal dimension and the power law index for a time series: A numerical investigation. Phys. D 1990, 46, 254–264. [Google Scholar] [CrossRef]
- Spasic, S.; Culic, M.; Grbic, G.; Martac, L.; Sekulic, S.; Mutavdzic, D. Spectral and fractal analysis of cerebellar activity after single and repeated brain injury. Bull. Math. Biol. 2008, 70, 1235–1249. [Google Scholar] [CrossRef] [PubMed]
- Spasic, S.; Kesic, S.; Kalauzi, A.; Aponjic, J. Different anaesthesia in rat induces distinct inter-structure brain dynamic detected by Higuchi fractal dimension. Fractals 2011, 19, 113–123. [Google Scholar] [CrossRef]
- Klonowski, W. Everything you wanted to ask about EEG but were afraid to get the right answer. Nonlinear Biomed. Phys. 2009, 3. [Google Scholar] [CrossRef] [PubMed]
- Kesic, S.; Spasic, S.Z. Application of Higuchi’s fractal dimension from basic to clinical neurophysiology: A review. Comput. Methods Progr. Biomed. 2016, 133, 55–70. [Google Scholar] [CrossRef] [PubMed]
- Steeb, W.H. The Nonlinear Workbook; World Scientific: Singapore, 2015. [Google Scholar]
- Carter, B. Op Amps for Everyone, 4th ed.; Elsevier: Waltham, MA, USA, 2013. [Google Scholar]
- Ward, L.M.; Greenwood, P.E. 1/f noise. Scholarpedia 2007, 2, 1537. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Pham, T.D.; Oyama-Higa, M.; Truong, C.T.; Okamoto, K.; Futaba, T.; Kanemoto, S.; Sugiyama, M.; Lampe, L. Computerized assessment of communication for cognitive stimulation for people with cognitive decline using spectral-distortion measures and phylogenetic inference. PLoS ONE 2015, 10, e0118739. [Google Scholar] [CrossRef] [PubMed]
- Lichman, M. UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 8 September 2016).
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- McLachlan, G.J. Discriminant Analysis and Statistical Pattern Recognition; Wiley-Interscience: New York, NY, USA, 2004. [Google Scholar]
- Metz, C.E. Basic principles of ROC analysis. Semin. Nucl. Med. 1978, 8, 283–298. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. Multivariate generalized multiscale entropy analysis. Entropy 2016, 18, 411. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Chanwimalueang, T.; Thayyil, S.; Mandic, D.P. A multivariate multiscale fuzzy entropy algorithm with application to uterine EMG complexity analysis. Entropy 2017, 19, 2. [Google Scholar] [CrossRef]
- Darmon, D. Specific differential entropy rate estimation for continuous-valued time series. Entropy 2016, 18, 190. [Google Scholar] [CrossRef]
- Lake, D.E. Renyi entropy measures of heart rate Gaussianity. IEEE Trans. Biomed. Eng. 2006, 53, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Lake, D.E.; Moorman, J.R. Accurate estimation of entropy in very short physiological time series: The problem of atrial fibrillation detection in implanted ventricular devices. Am. J. Physiol. Heart Circ. Physiol. 2011, 300, H319–H325. [Google Scholar] [CrossRef] [PubMed]
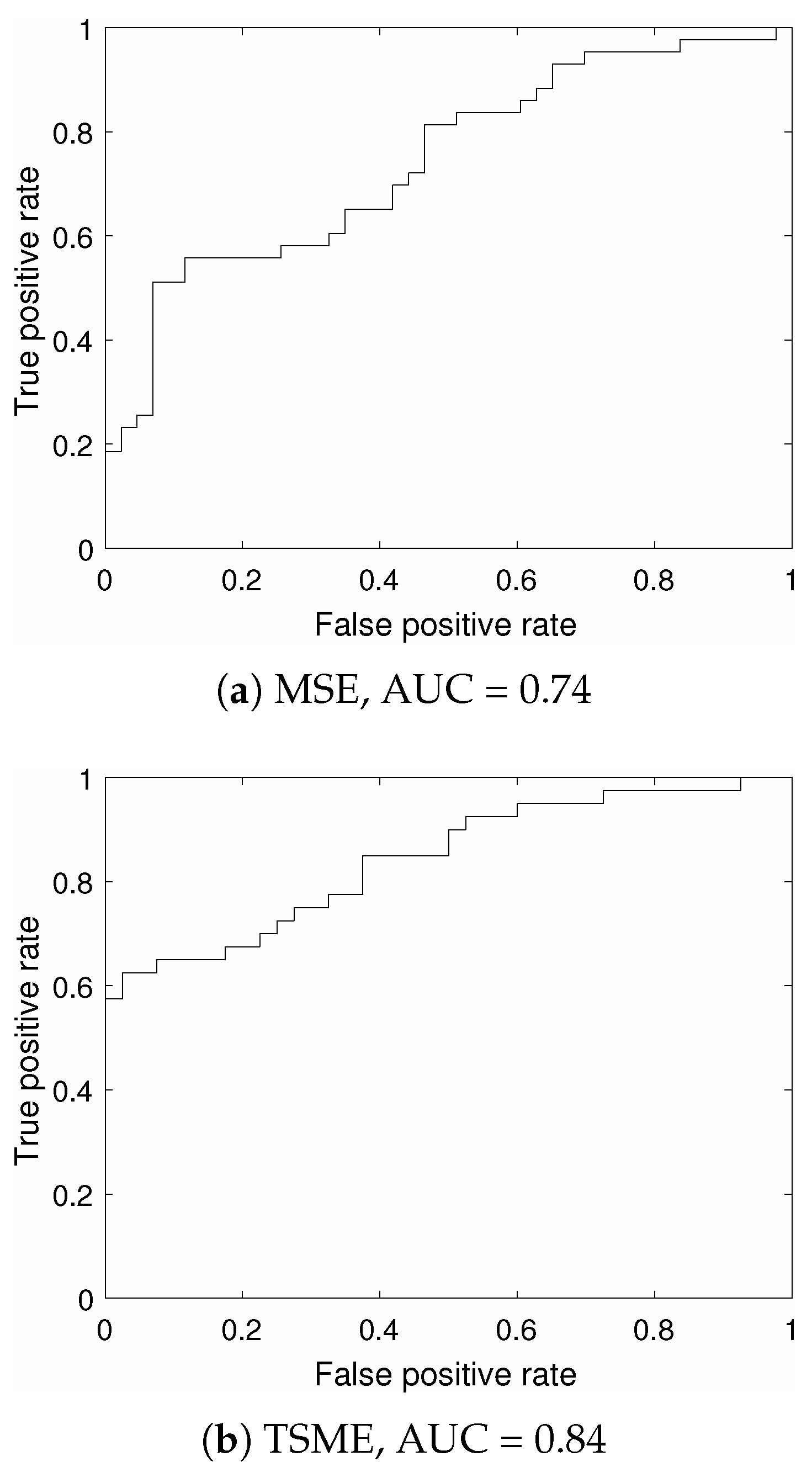
| Feature | SEN (%) | SPE (%) | LOO (%) |
|---|---|---|---|
| MSE | 51.16 | 93.02 | 44.19 |
| TSME | 62.50 | 97.50 | 62.50 |
| Feature | SEN (%) | SPE (%) | LOO (%) |
|---|---|---|---|
| MSE | 67.50 | 77.50 | 50.00 |
| TSME | 82.50 | 72.50 | 61.25 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.D. Time-Shift Multiscale Entropy Analysis of Physiological Signals. Entropy 2017, 19, 257. https://doi.org/10.3390/e19060257
Pham TD. Time-Shift Multiscale Entropy Analysis of Physiological Signals. Entropy. 2017; 19(6):257. https://doi.org/10.3390/e19060257
Chicago/Turabian StylePham, Tuan D. 2017. "Time-Shift Multiscale Entropy Analysis of Physiological Signals" Entropy 19, no. 6: 257. https://doi.org/10.3390/e19060257
APA StylePham, T. D. (2017). Time-Shift Multiscale Entropy Analysis of Physiological Signals. Entropy, 19(6), 257. https://doi.org/10.3390/e19060257





