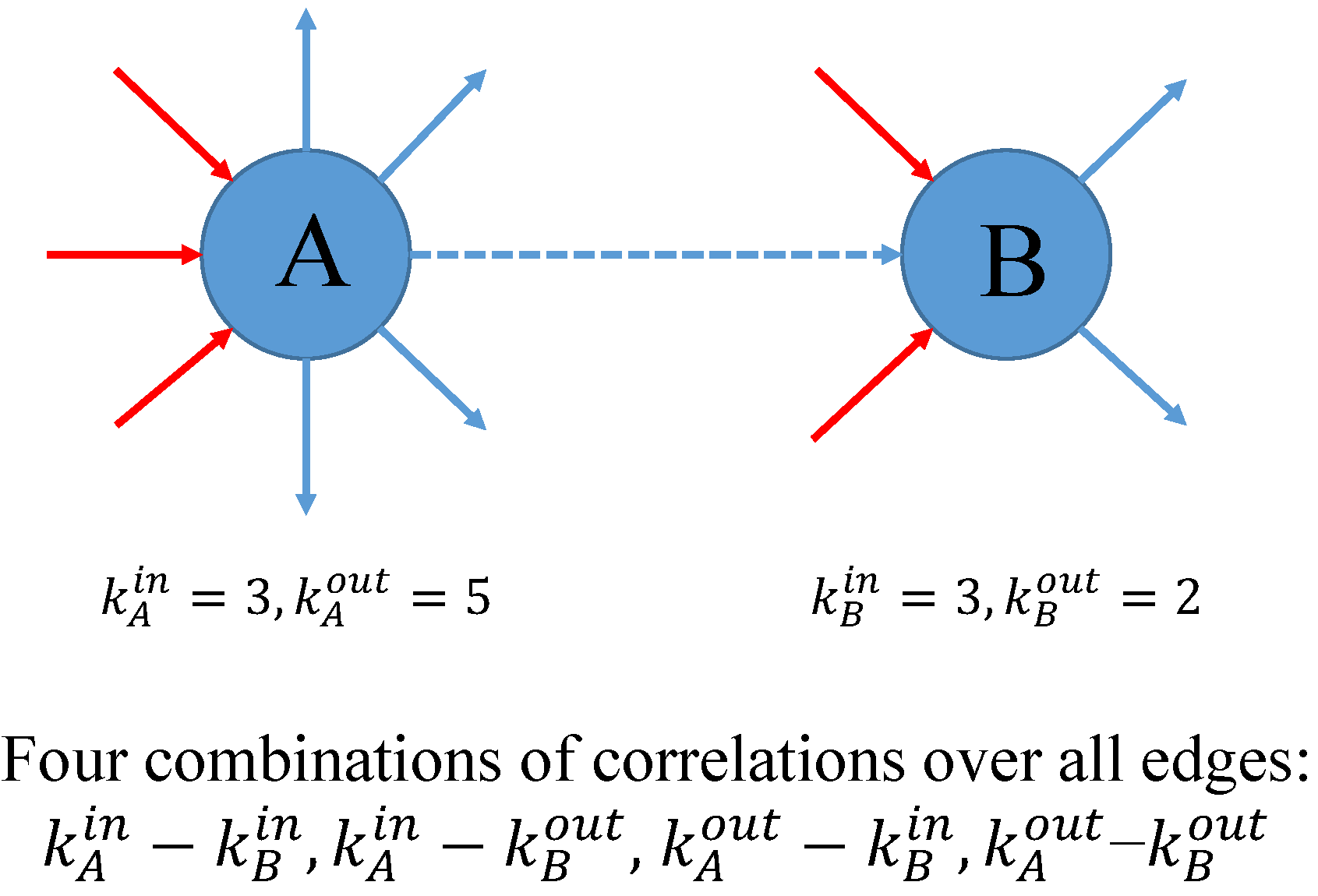
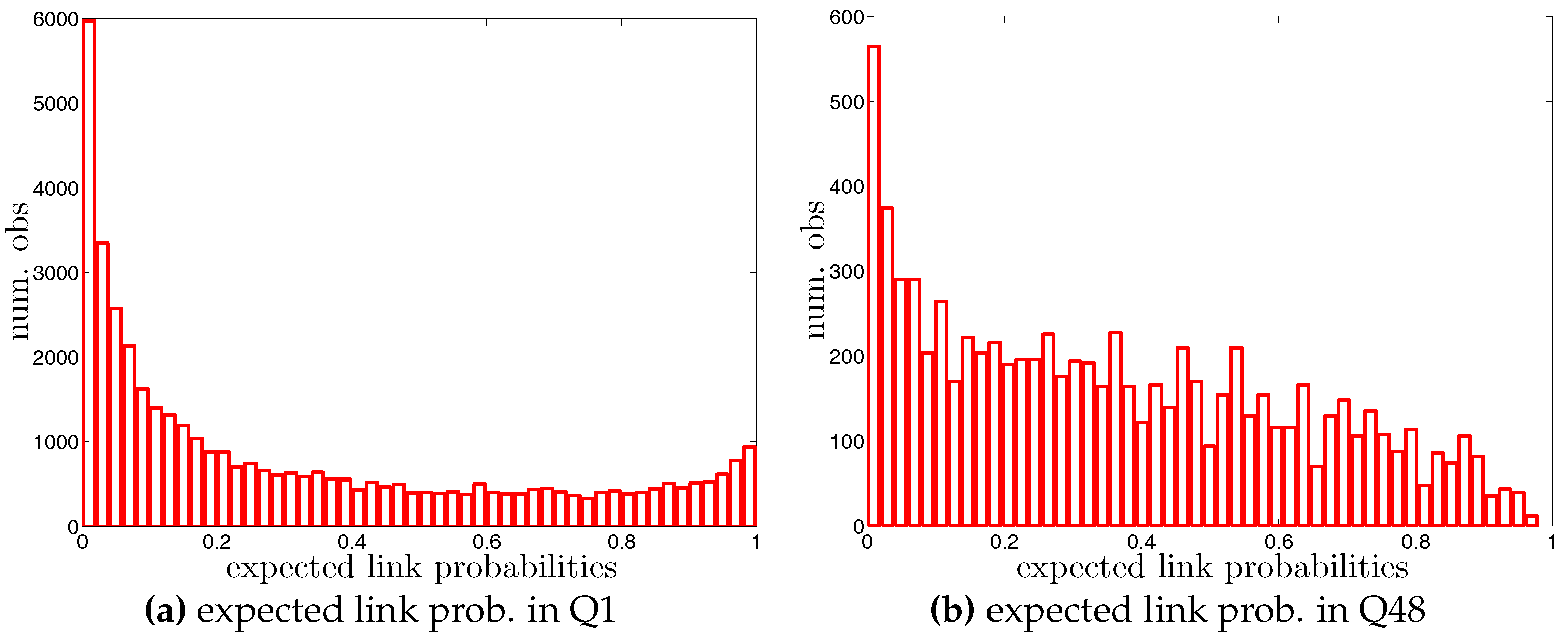
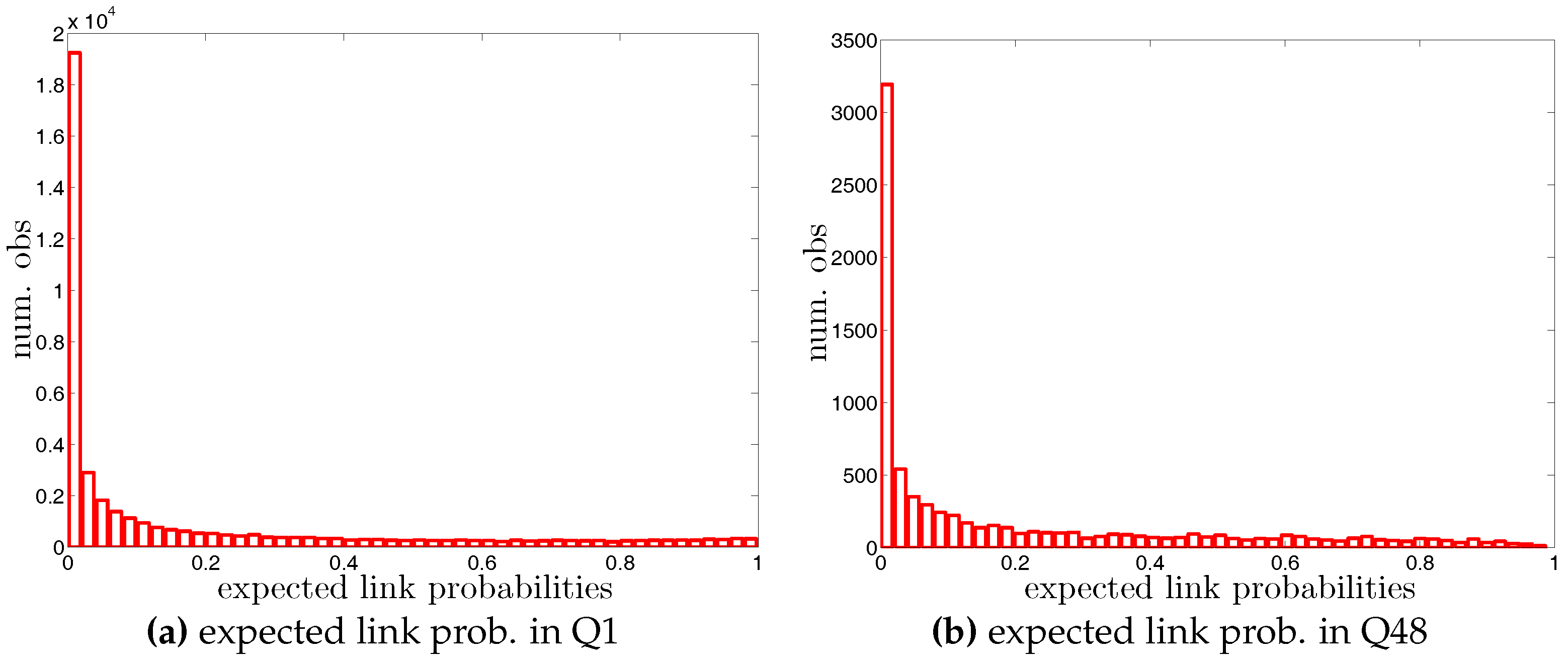
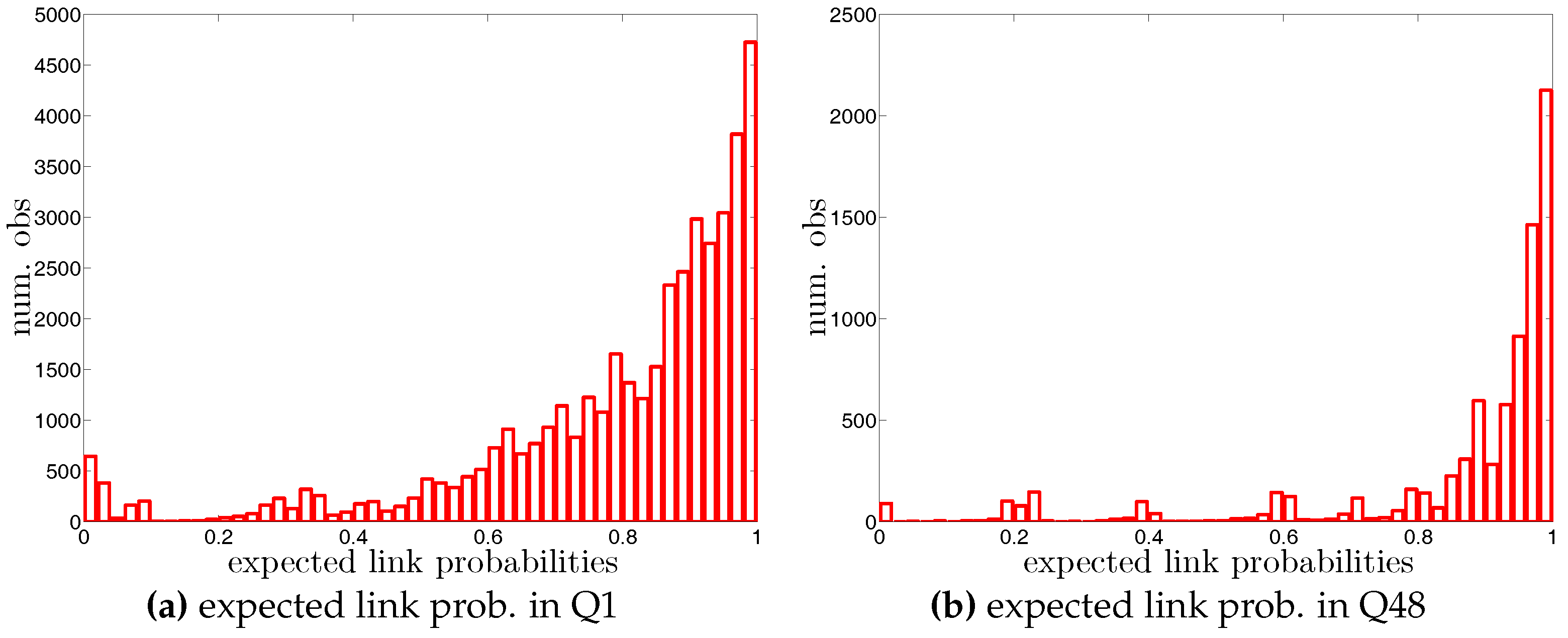
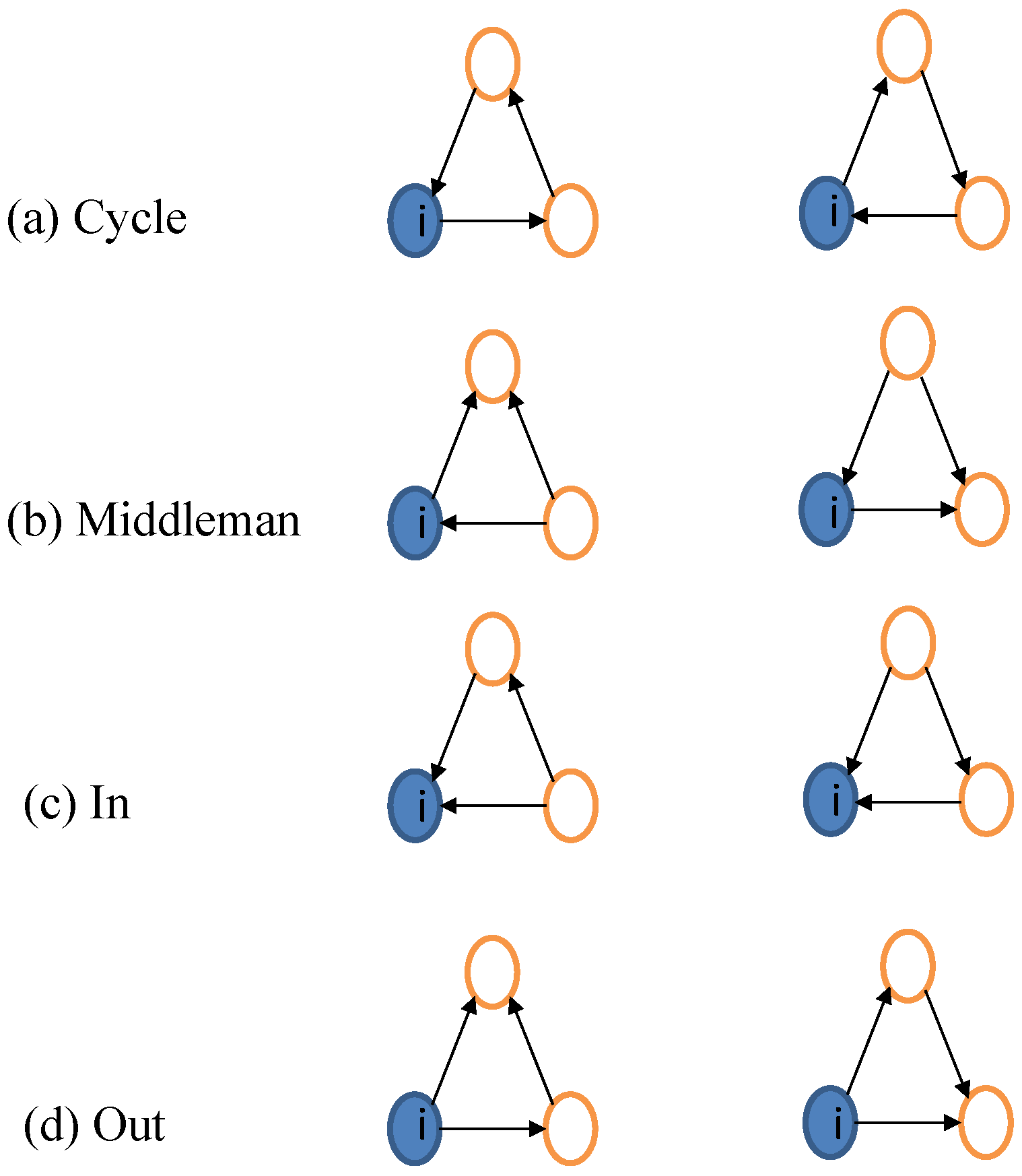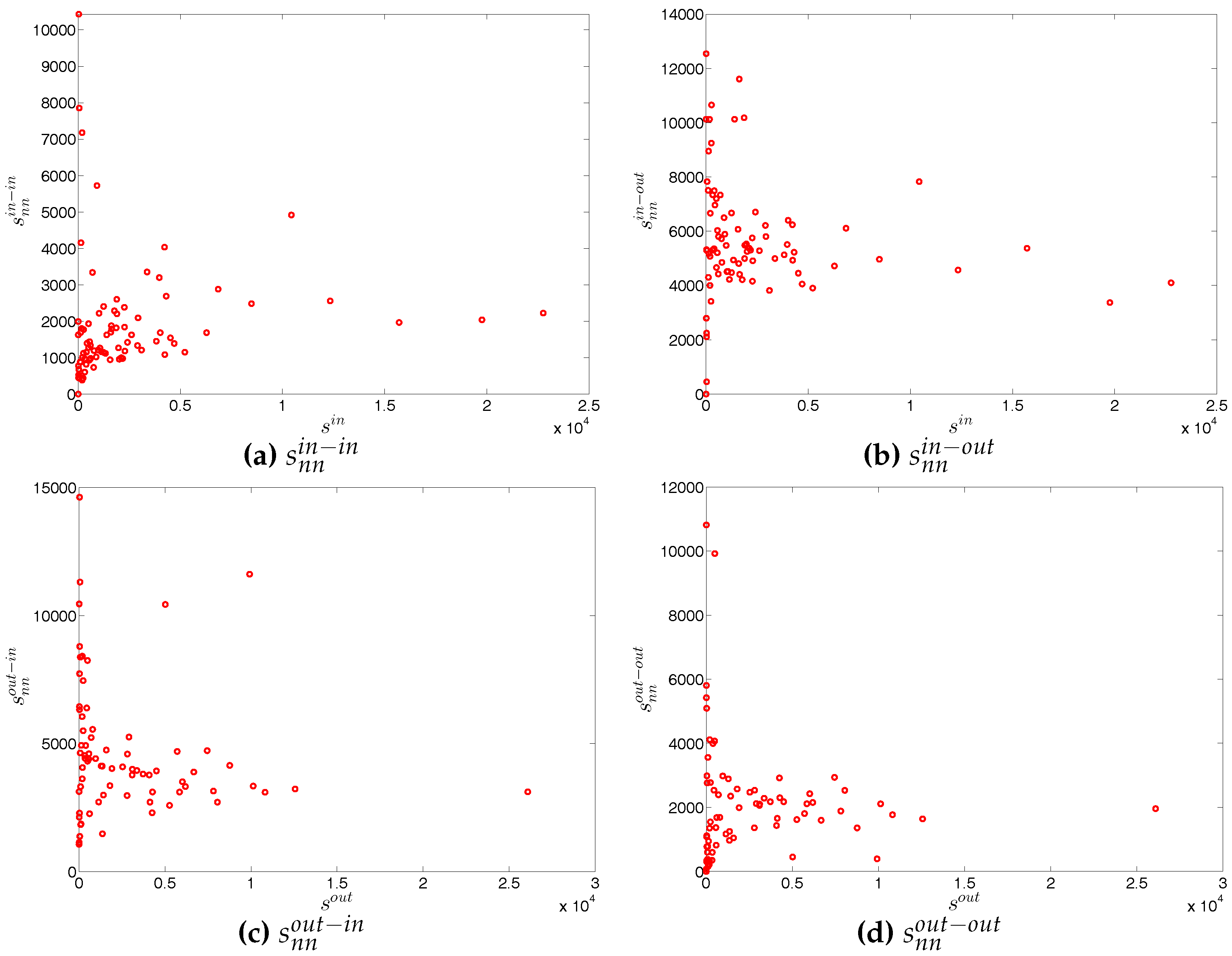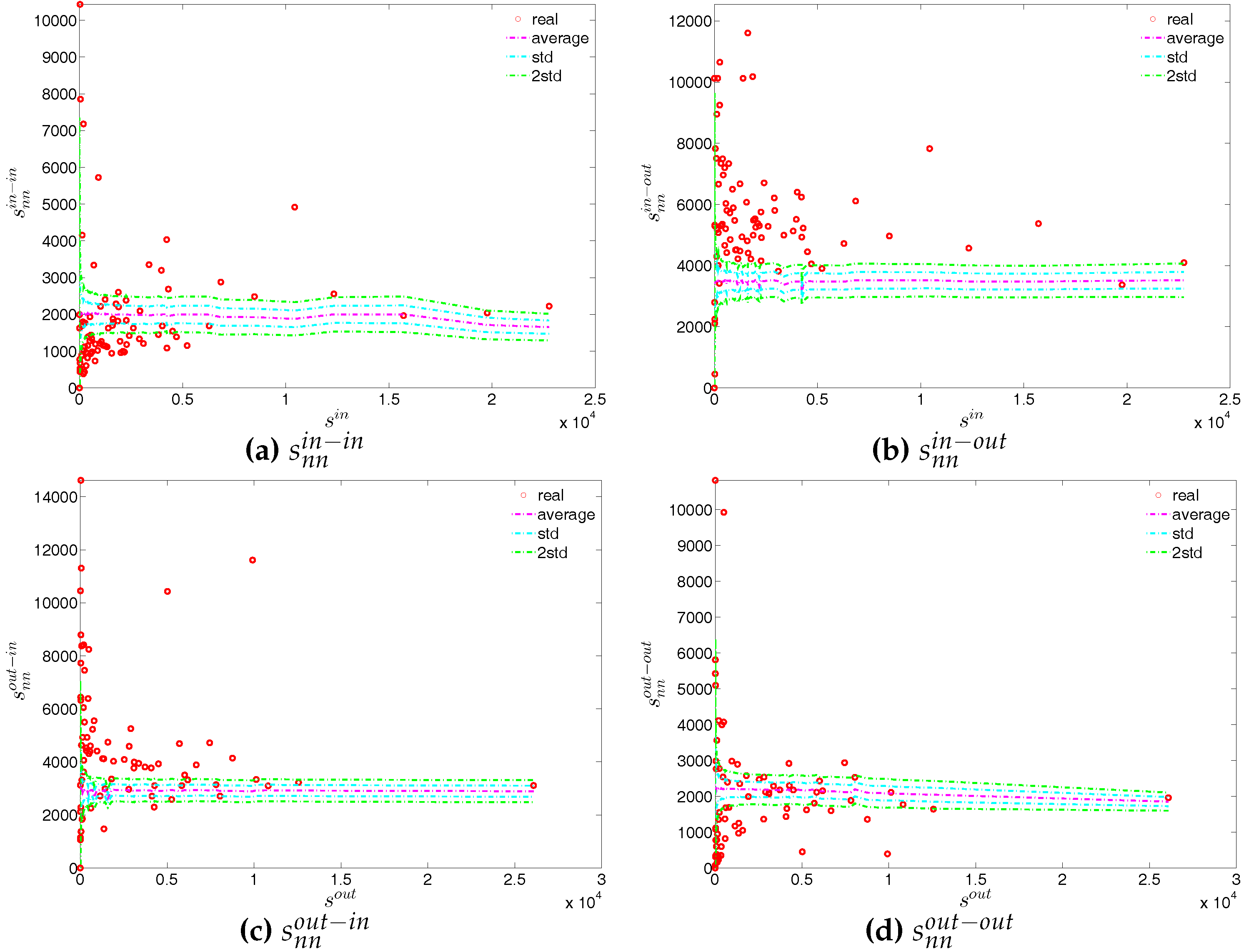Figure 1.
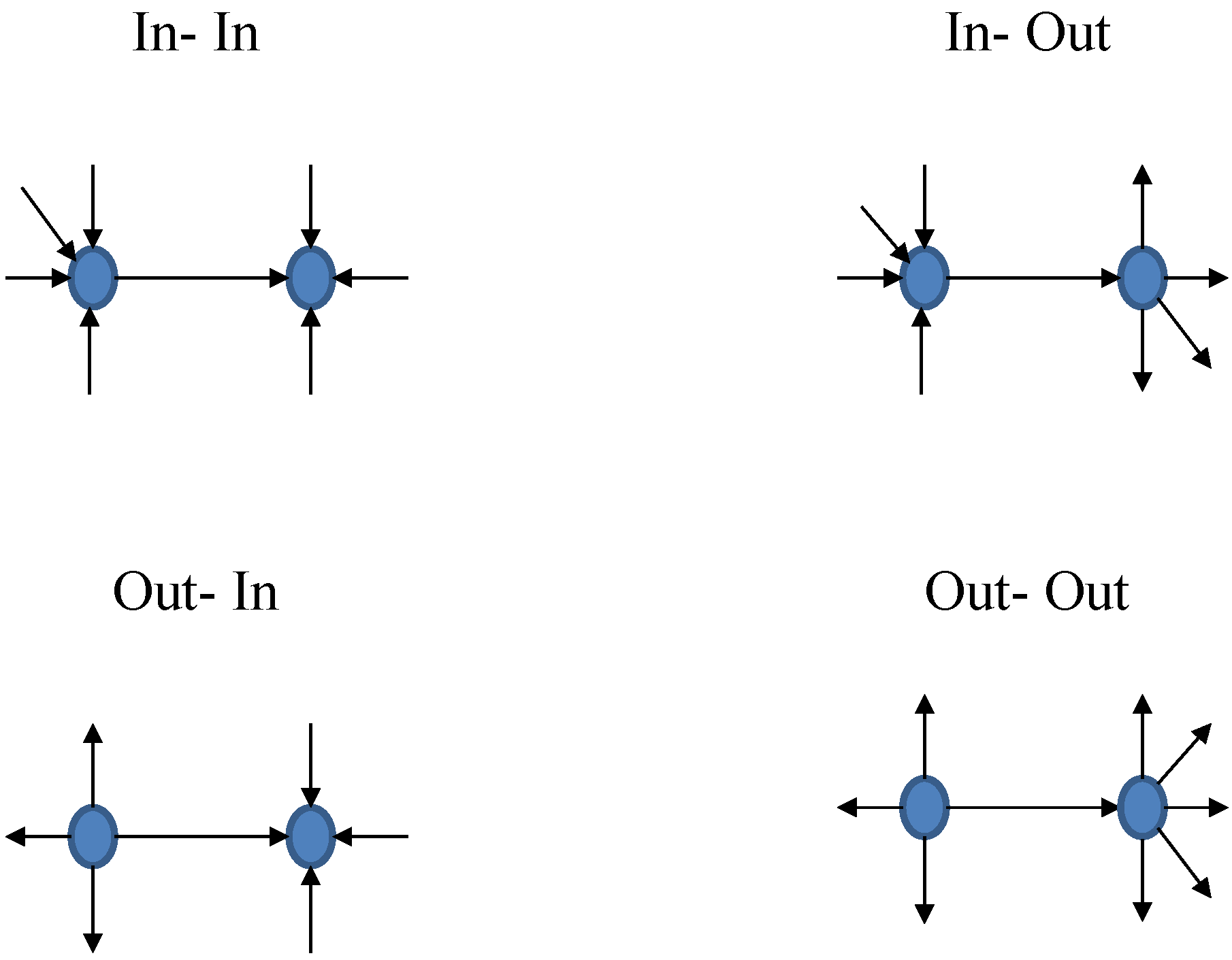
Degree-degree dependencies in the directed version.Degree-degree dependencies in the directed version.
Figure 1.
Degree-degree dependencies in the directed version.Degree-degree dependencies in the directed version.
Figure 2.
Directed triangles and the corresponding (binary) clusterings associated with a node i. (a) Cycle clustering; (b) Middleman clustering; (c) In clustering; (d) Out clustering.Directed triangles and the corresponding clusterings.
Figure 2.
Directed triangles and the corresponding (binary) clusterings associated with a node i. (a) Cycle clustering; (b) Middleman clustering; (c) In clustering; (d) Out clustering.Directed triangles and the corresponding clusterings.
Figure 3.
The evolution of the size and the density of the electronic market for interbank deposits (e-MID) network. The left y-axis shows the number of active banks (in blue) and the right y-axis shows density (in green).
Figure 3.
The evolution of the size and the density of the electronic market for interbank deposits (e-MID) network. The left y-axis shows the number of active banks (in blue) and the right y-axis shows density (in green).
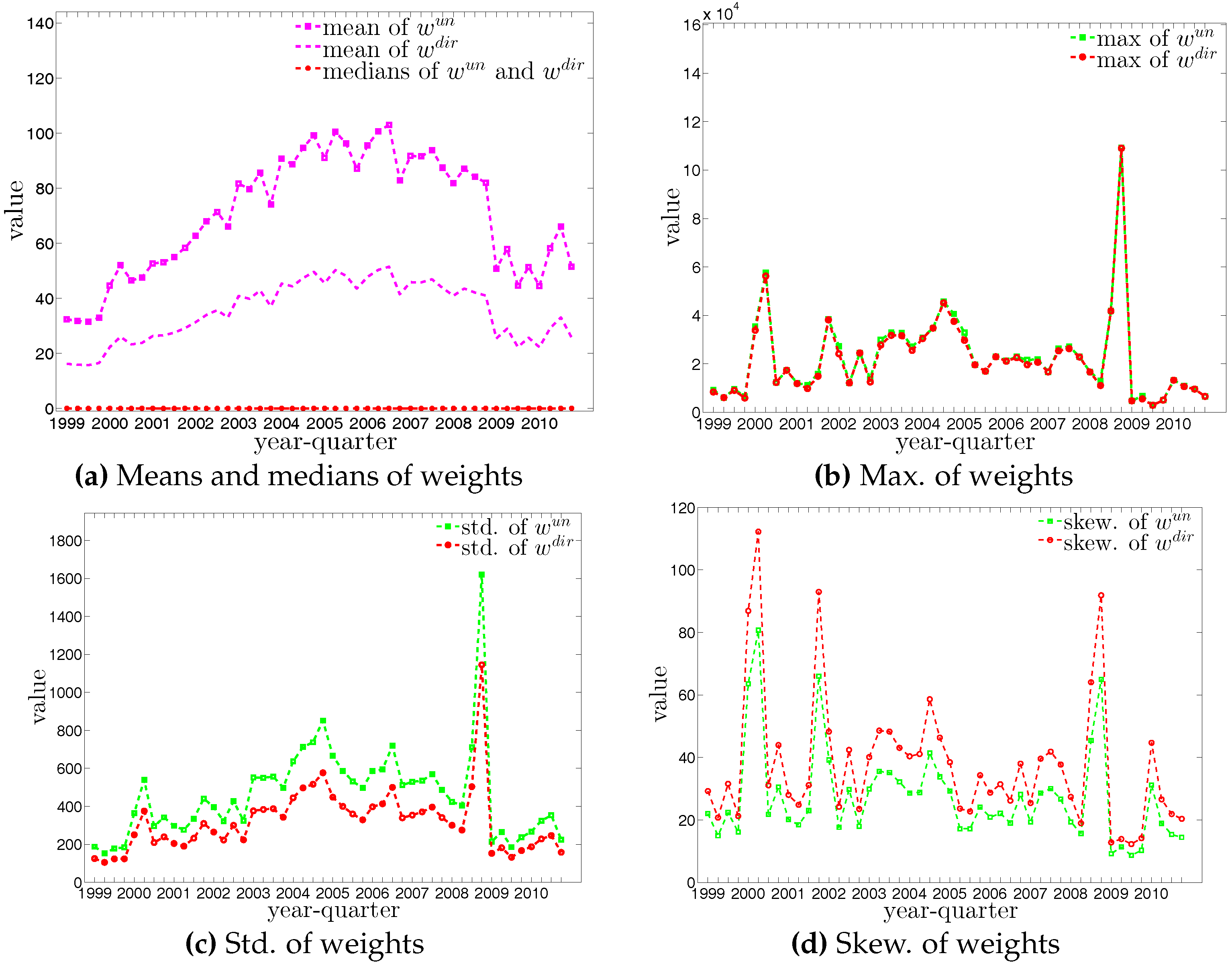
Figure 4.
The evolution of the basic statistics of weights in the undirected version () and in directed version ().
Figure 4.
The evolution of the basic statistics of weights in the undirected version () and in directed version ().
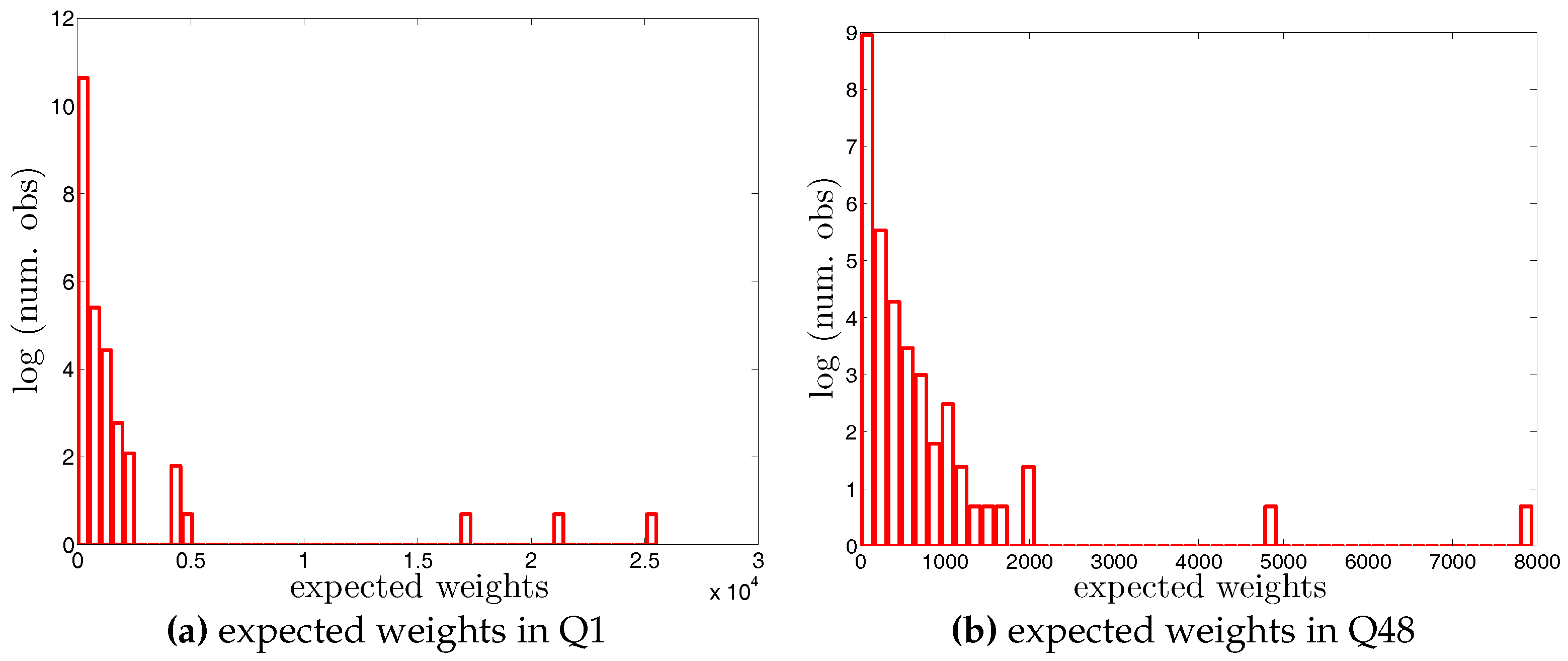
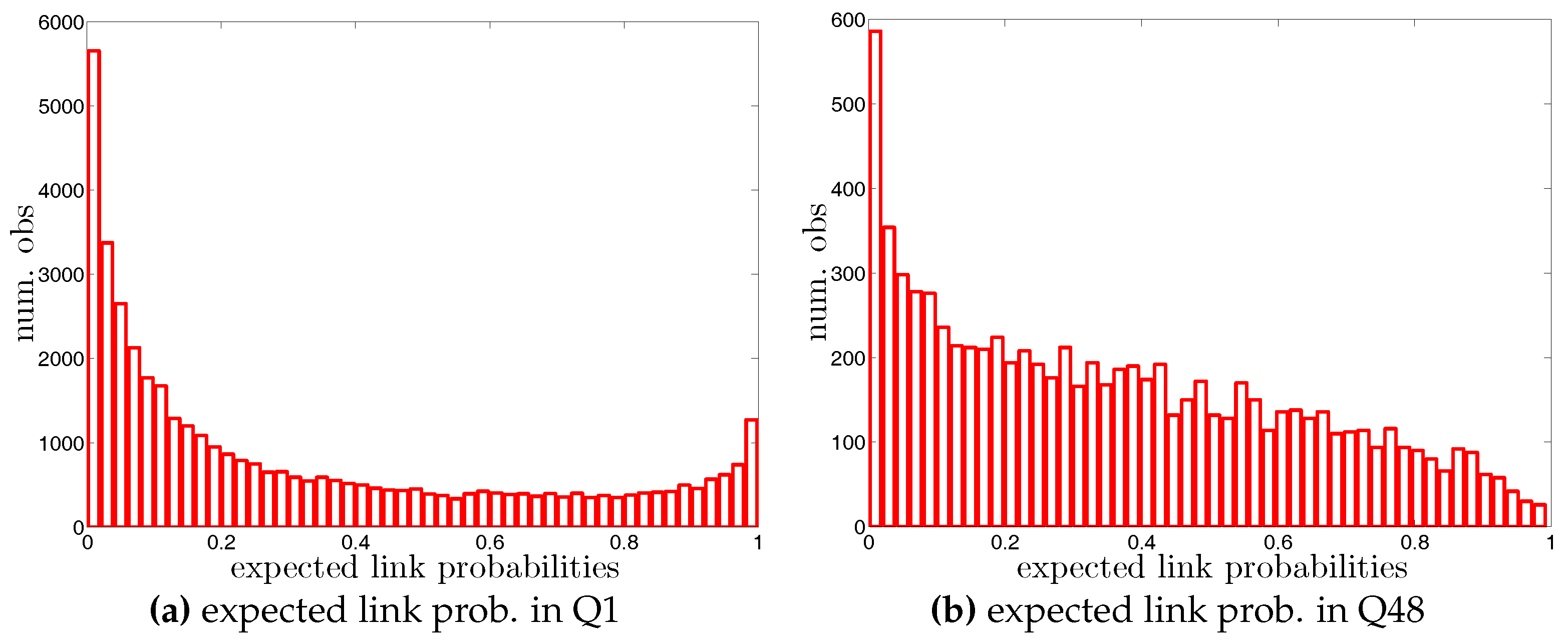
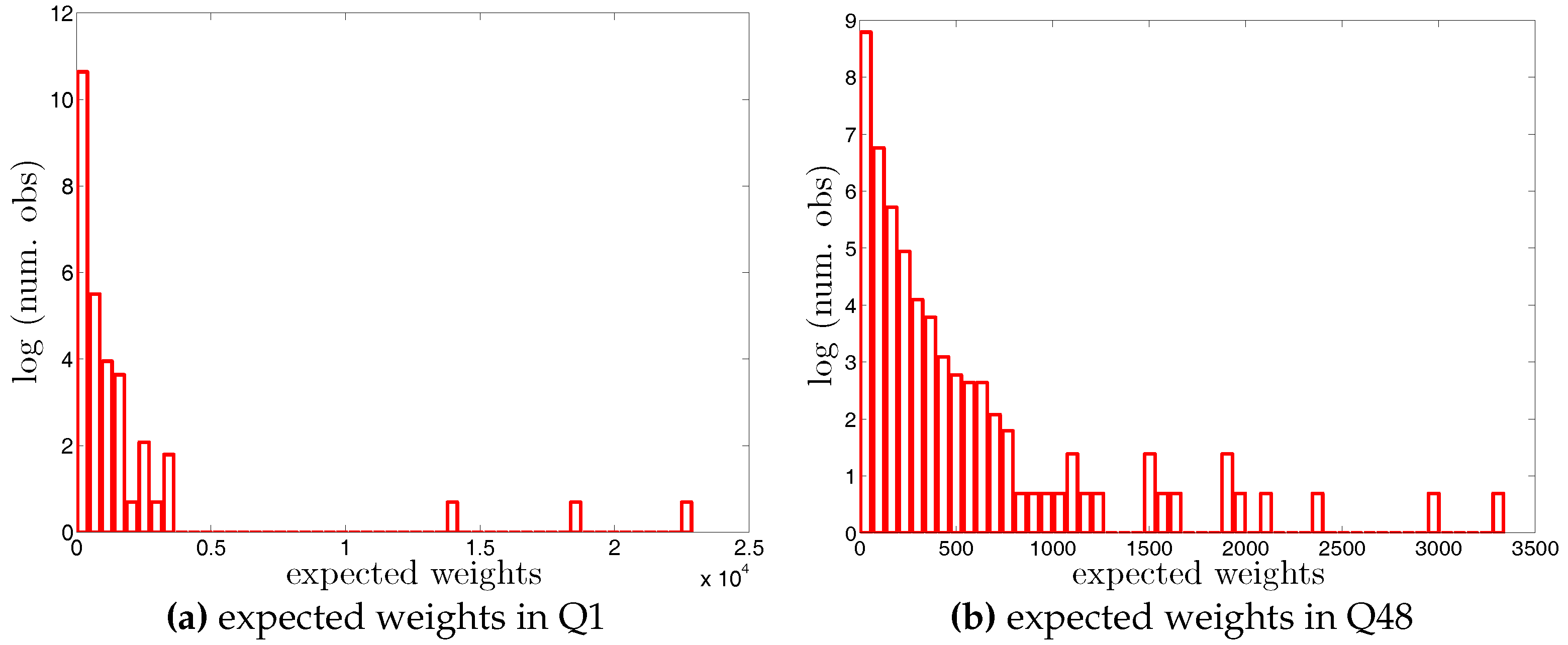
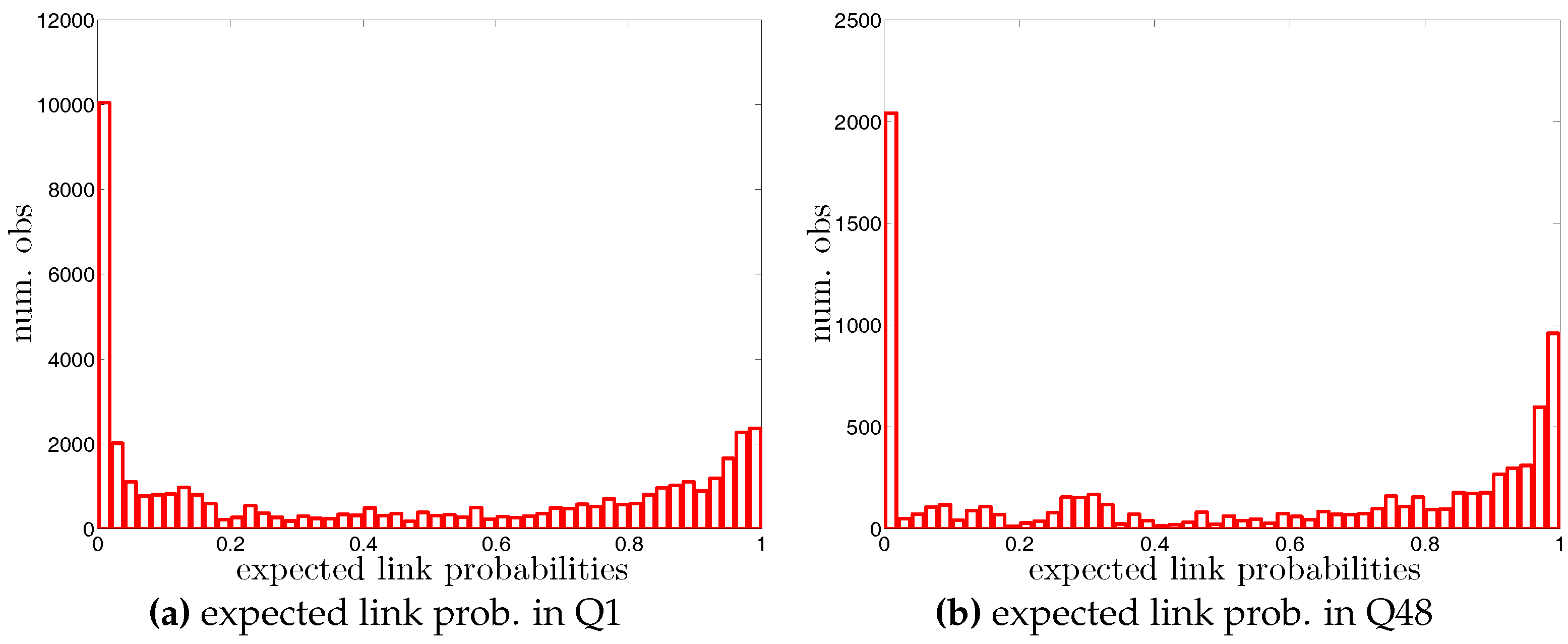
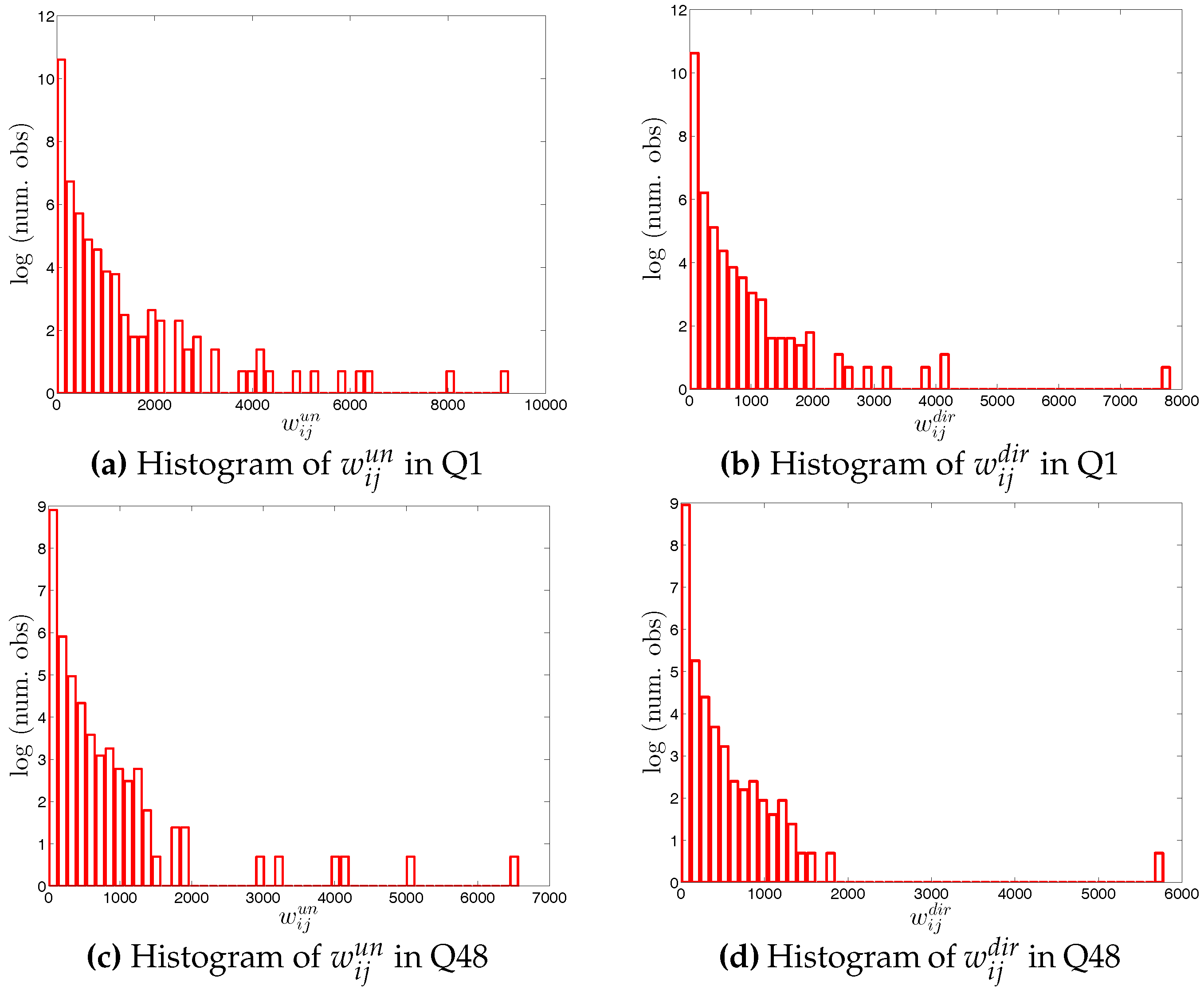
Figure 5.
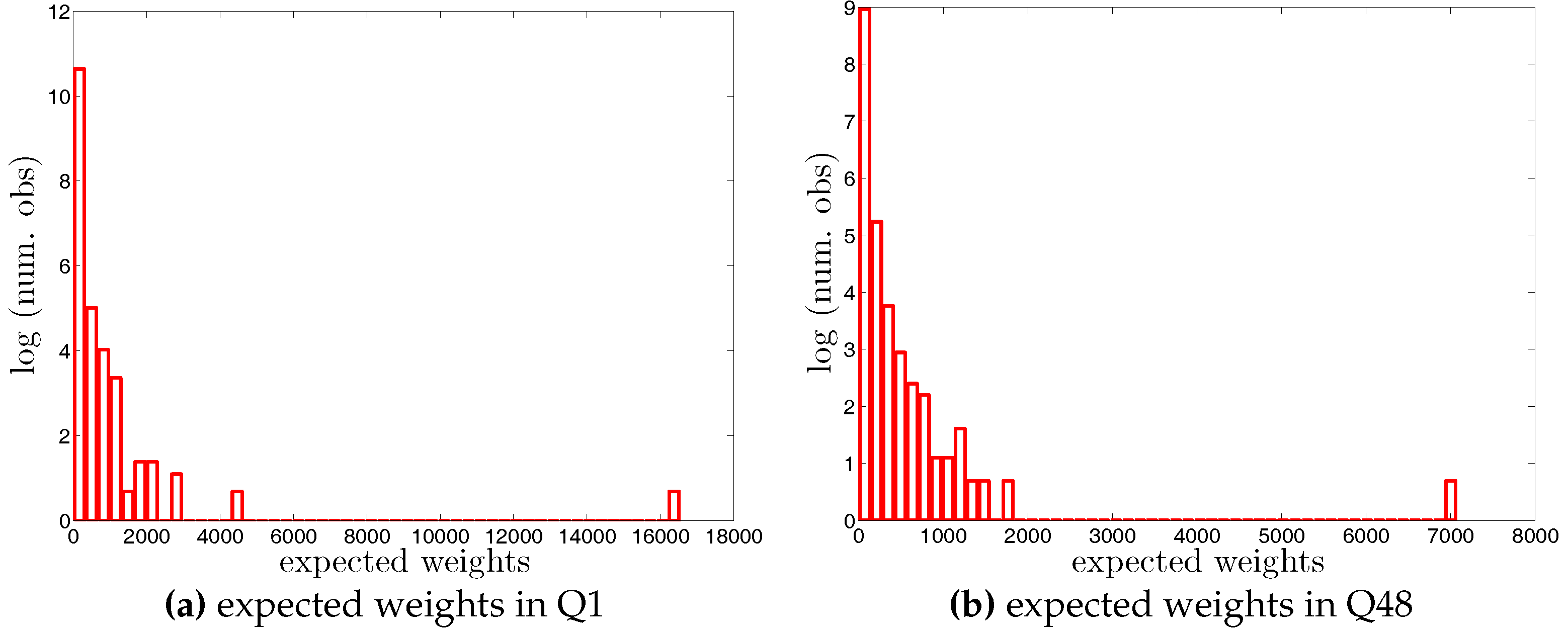
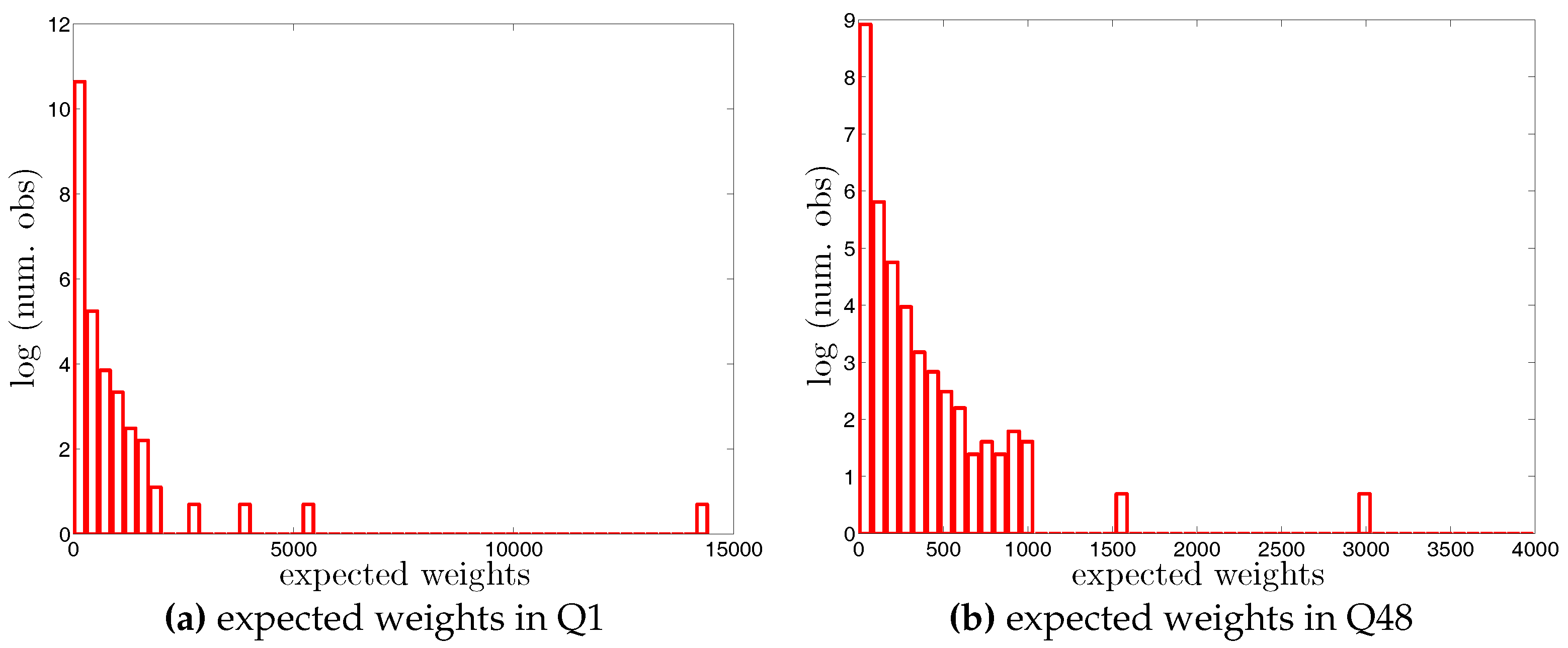
Histograms of weights (i.e., in the undirected version and in the directed version) in two example quarters, Q1 and Q48. Note that for the sake of readability, we plot the number of the observations in log scale.
Figure 5.
Histograms of weights (i.e., in the undirected version and in the directed version) in two example quarters, Q1 and Q48. Note that for the sake of readability, we plot the number of the observations in log scale.
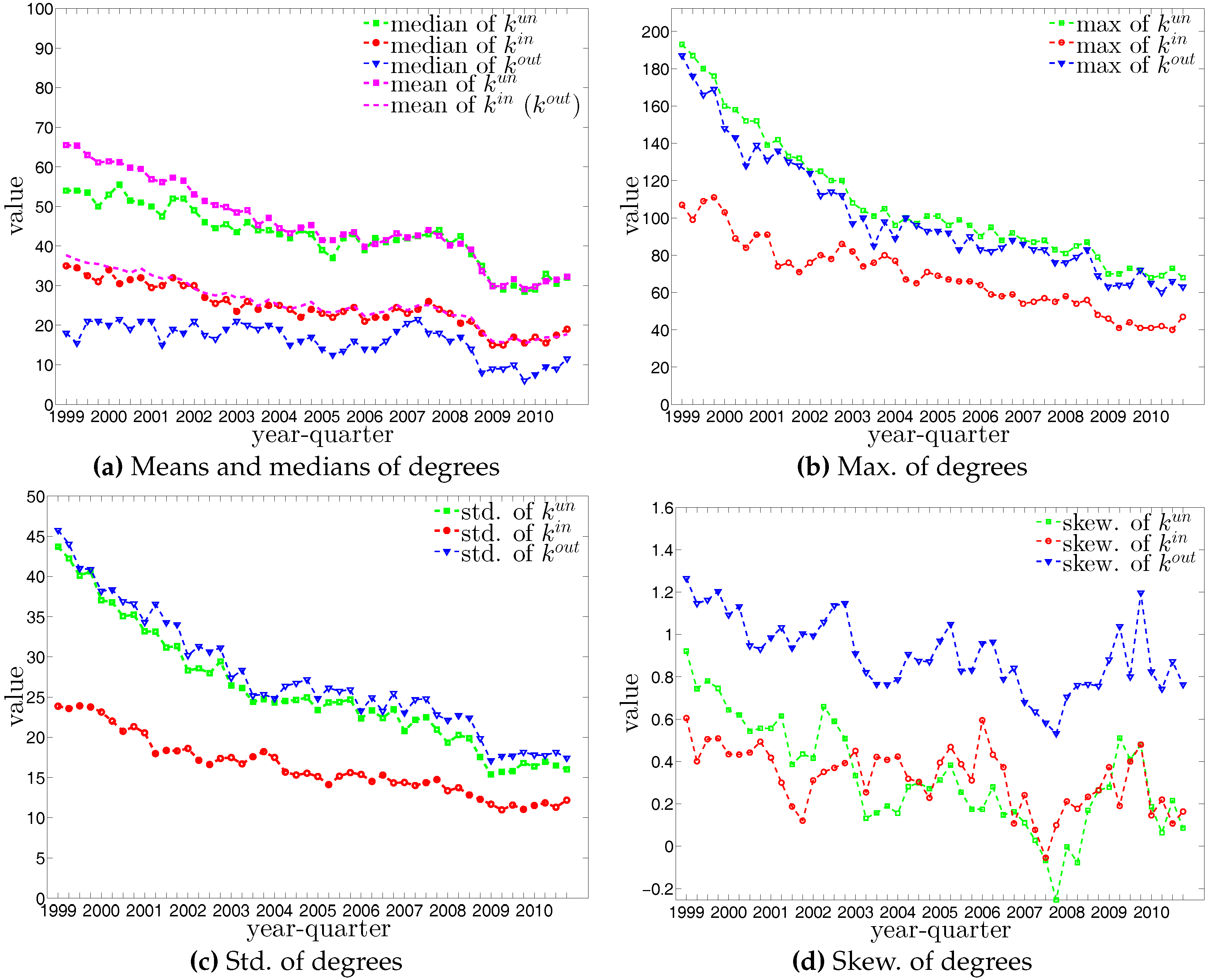
Figure 6.
The evolution of the basic statistics of degrees. Note that, by definition, the mean values of and are identical.
Figure 6.
The evolution of the basic statistics of degrees. Note that, by definition, the mean values of and are identical.
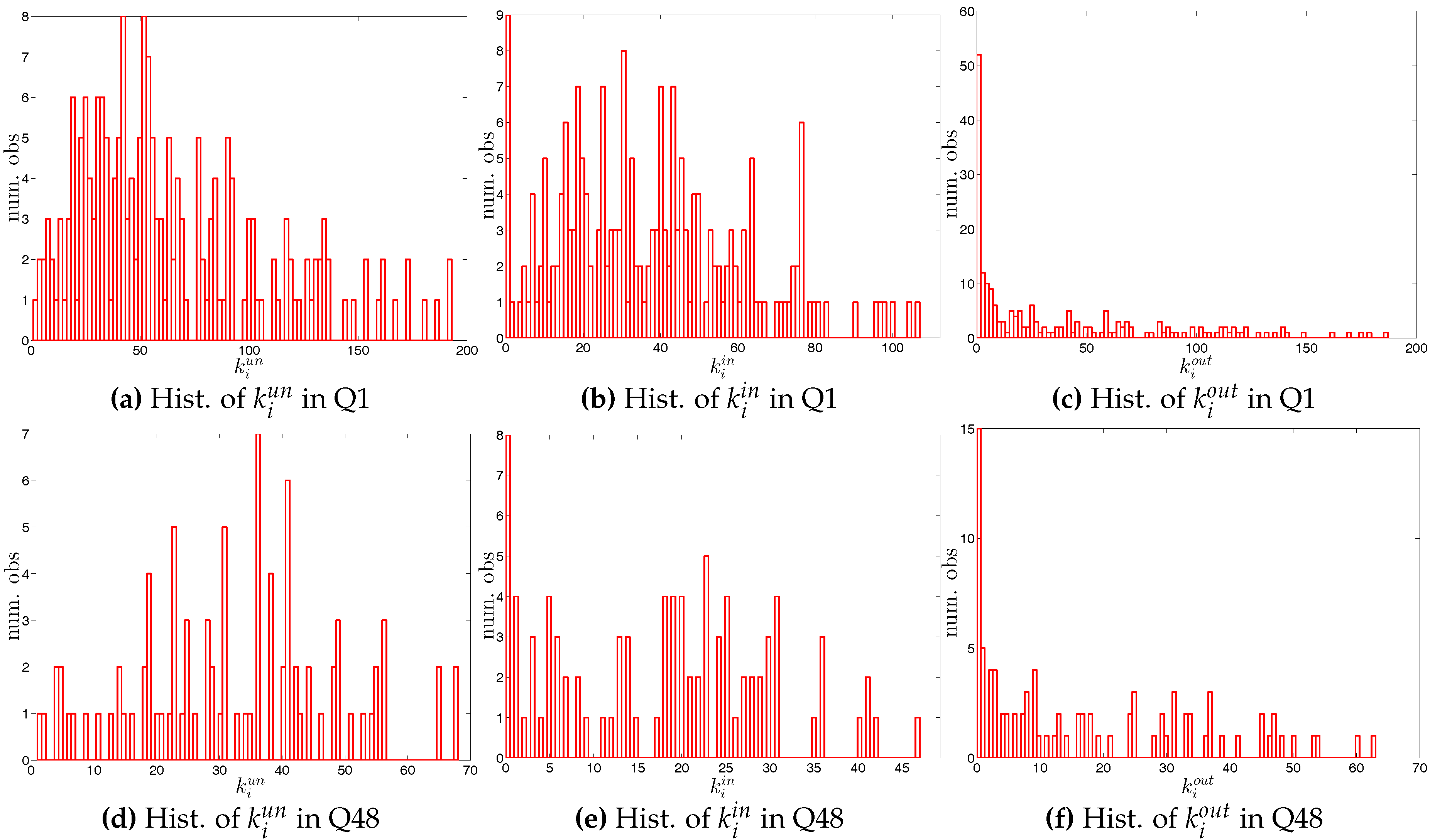
Figure 7.
Histograms of degrees in two example quarters, Q1 and Q48.
Figure 7.
Histograms of degrees in two example quarters, Q1 and Q48.
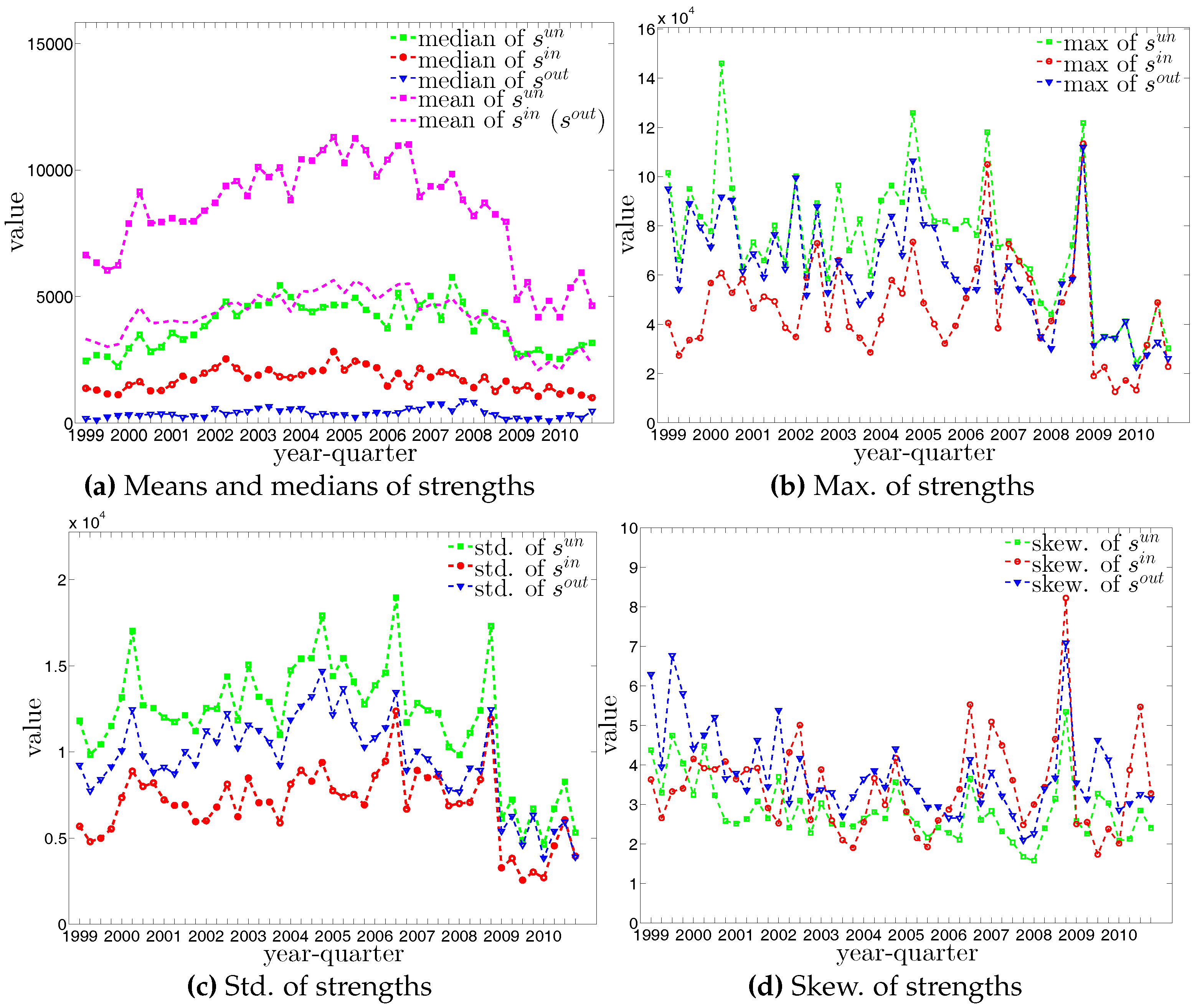
Figure 8.
The evolution of the basic statistics of strengths. Note that, by definition, the mean values of and are identical.
Figure 8.
The evolution of the basic statistics of strengths. Note that, by definition, the mean values of and are identical.
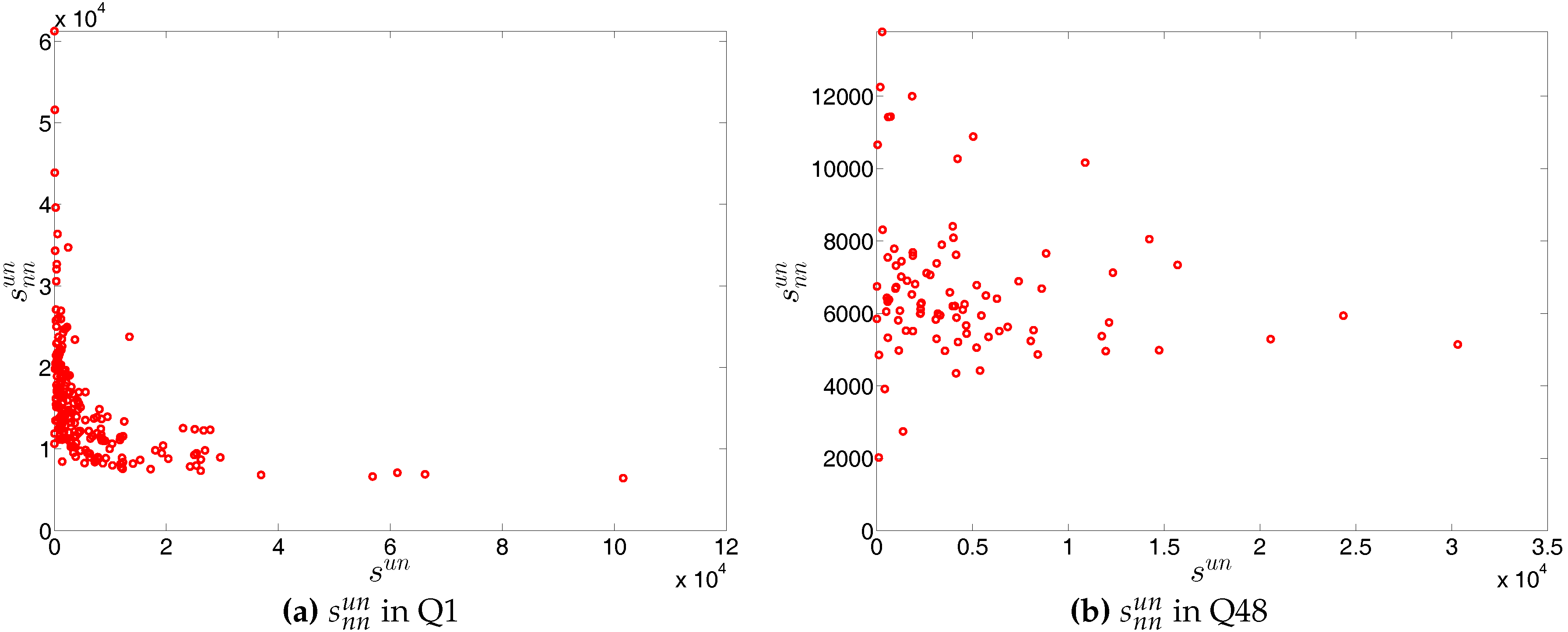
Figure 9.
Histograms of strengths in two example quarters, Q1 and Q48.
Figure 9.
Histograms of strengths in two example quarters, Q1 and Q48.
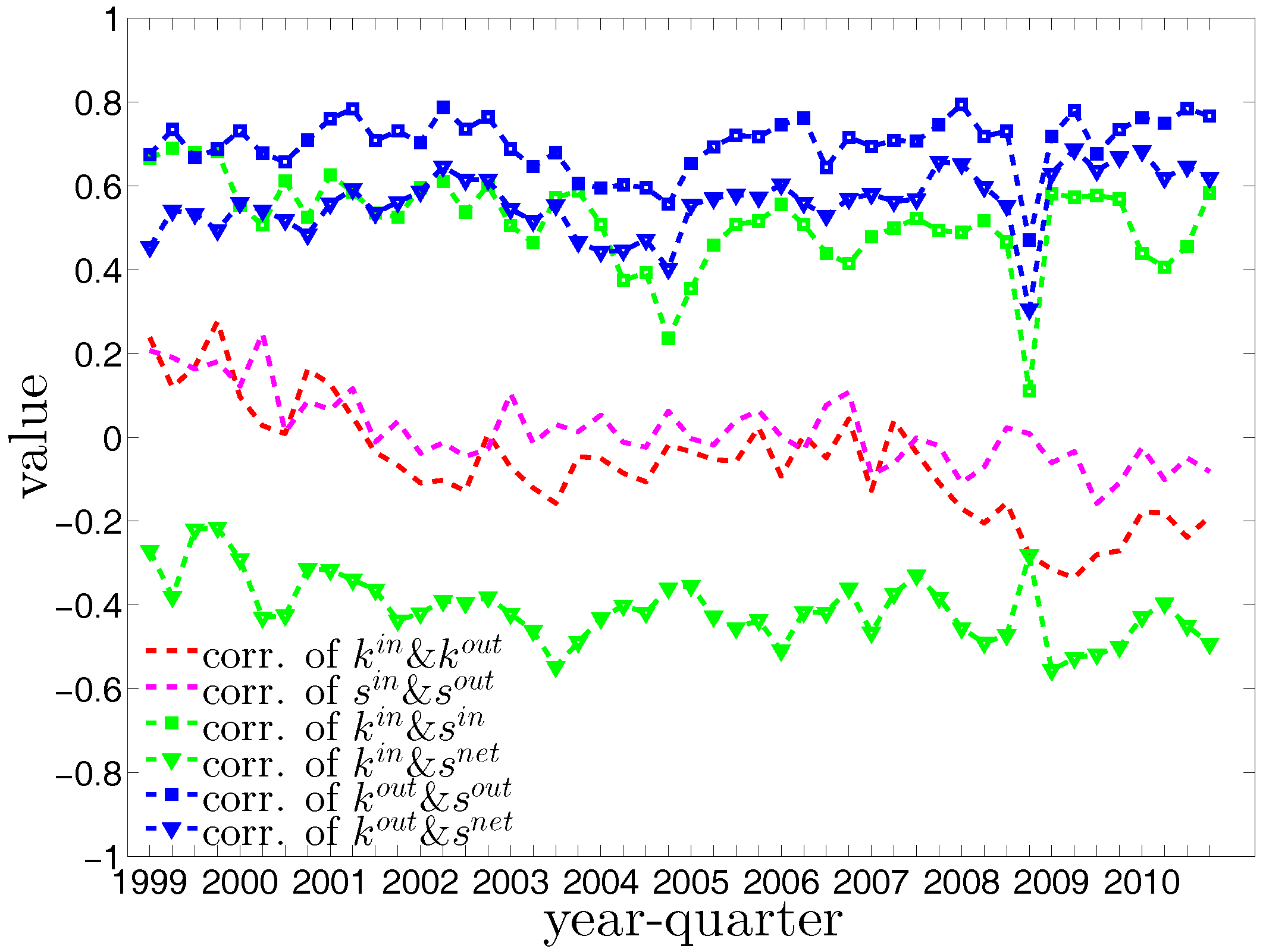
Figure 10.
The evolution of the Pearson correlation coefficients between degrees and strengths.
Figure 10.
The evolution of the Pearson correlation coefficients between degrees and strengths.
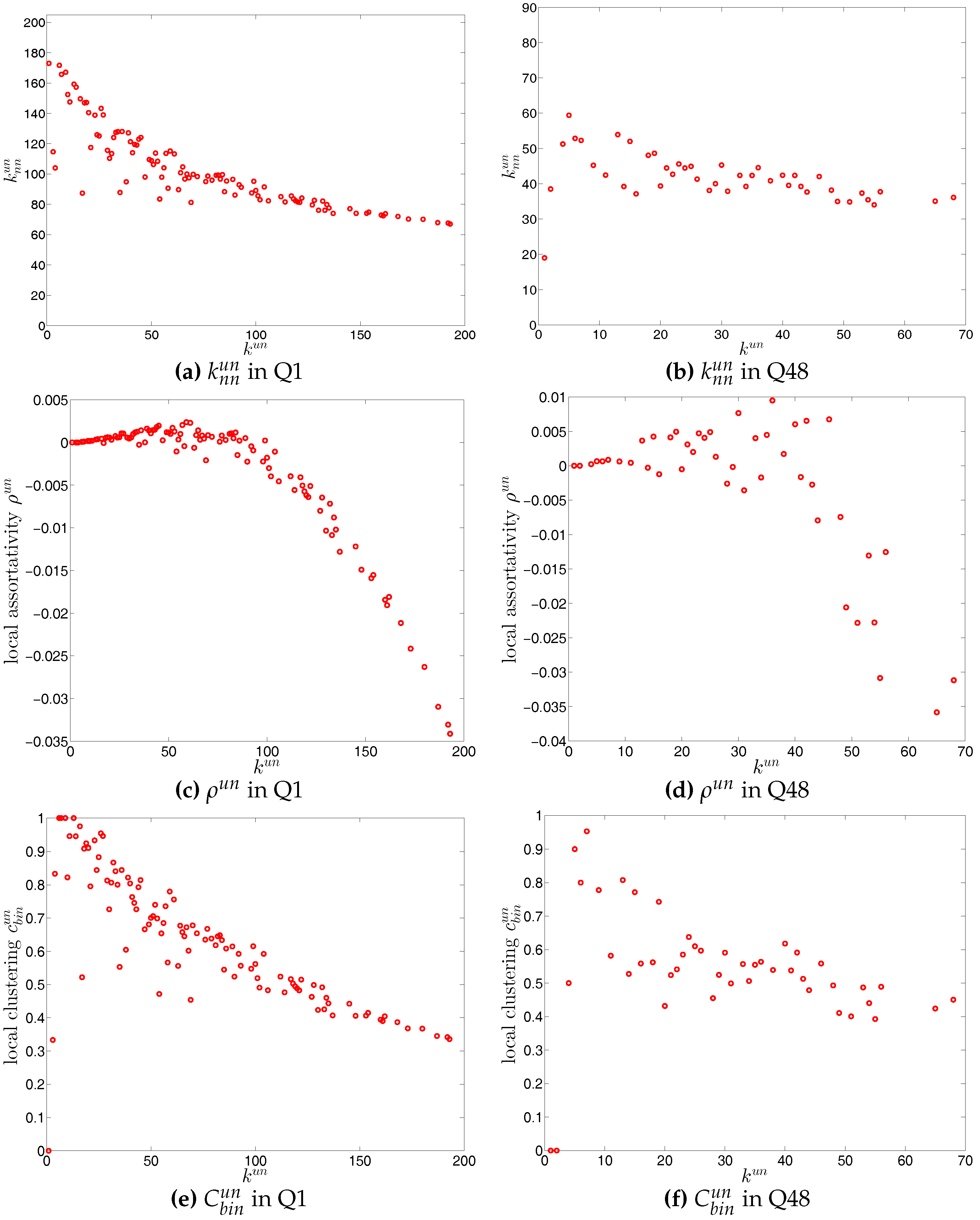
Figure 11.
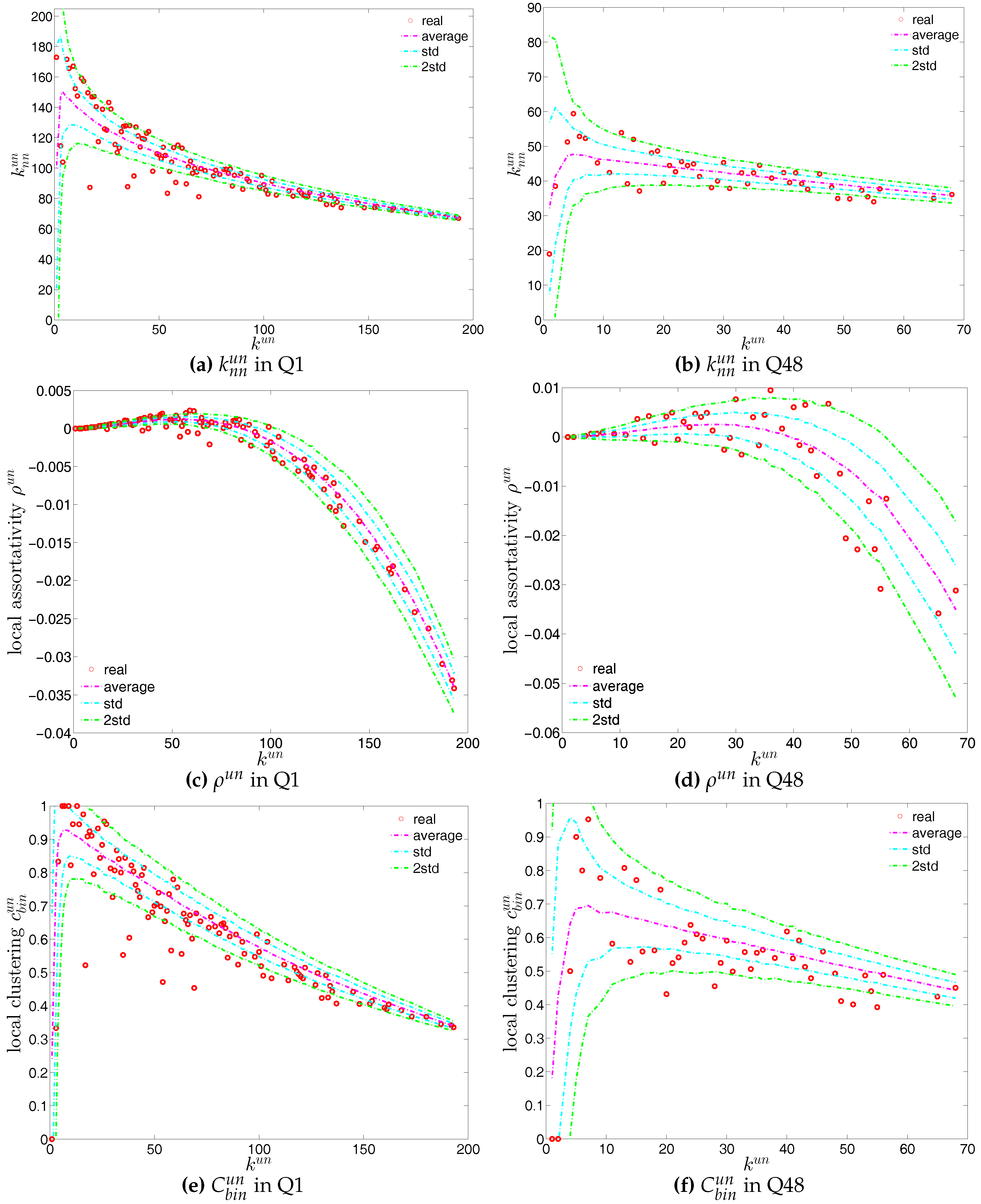
Average degree of the nearest neighbors (ANND) (a,b), local assortativity (c,d), and local clustering coefficients (e,f) in the undirected binary e-MID network, in Q1 and Q48.Average degrees of nearest neighbors, local assortativity, and local clustering coefficients in the undirected binary e-MID network, in Q1 and Q48.
Figure 11.
Average degree of the nearest neighbors (ANND) (a,b), local assortativity (c,d), and local clustering coefficients (e,f) in the undirected binary e-MID network, in Q1 and Q48.Average degrees of nearest neighbors, local assortativity, and local clustering coefficients in the undirected binary e-MID network, in Q1 and Q48.
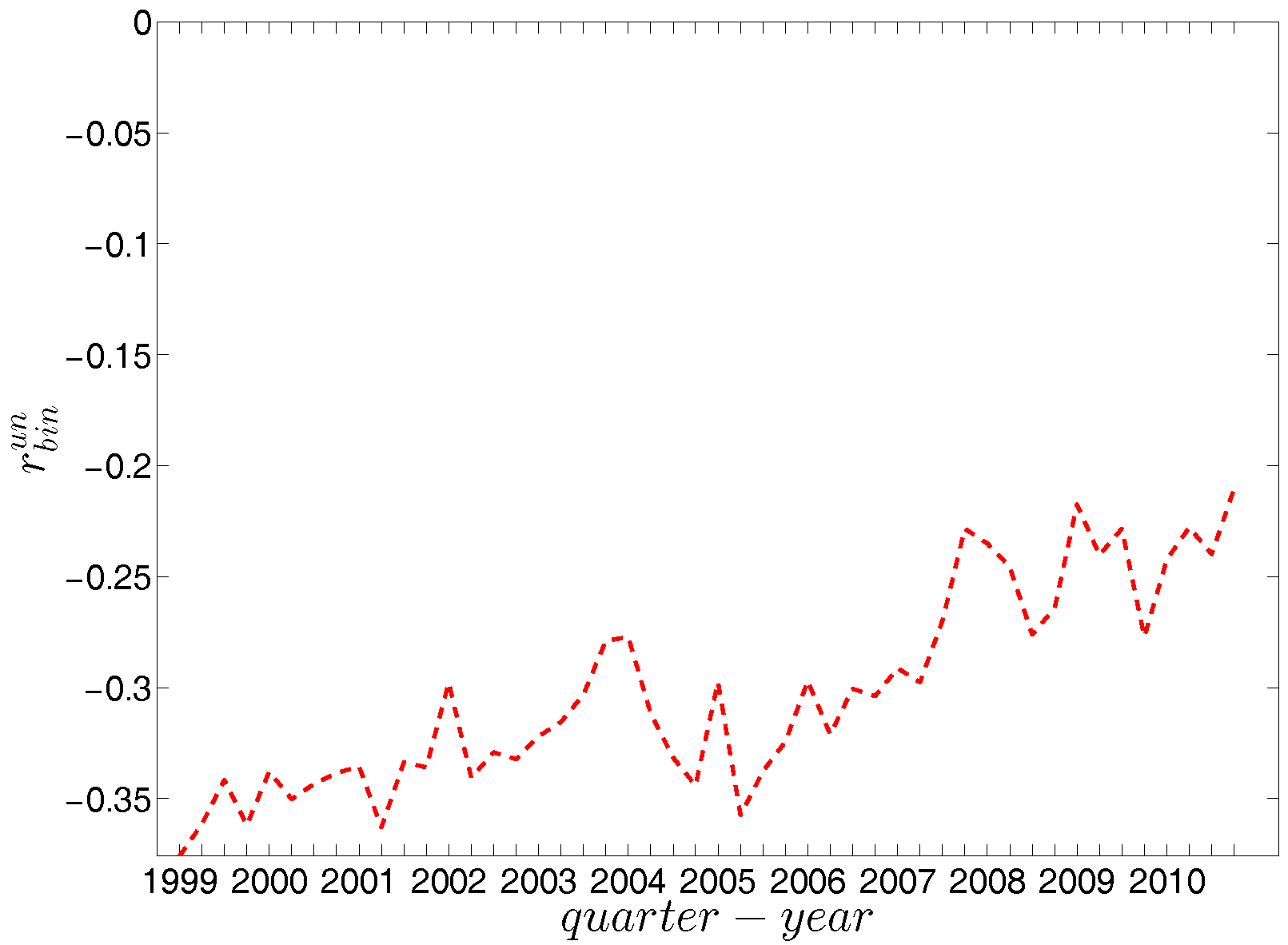
Figure 12.
Evolution of the overall assortativity indicator in the undirected binary e-MID network.
Figure 12.
Evolution of the overall assortativity indicator in the undirected binary e-MID network.
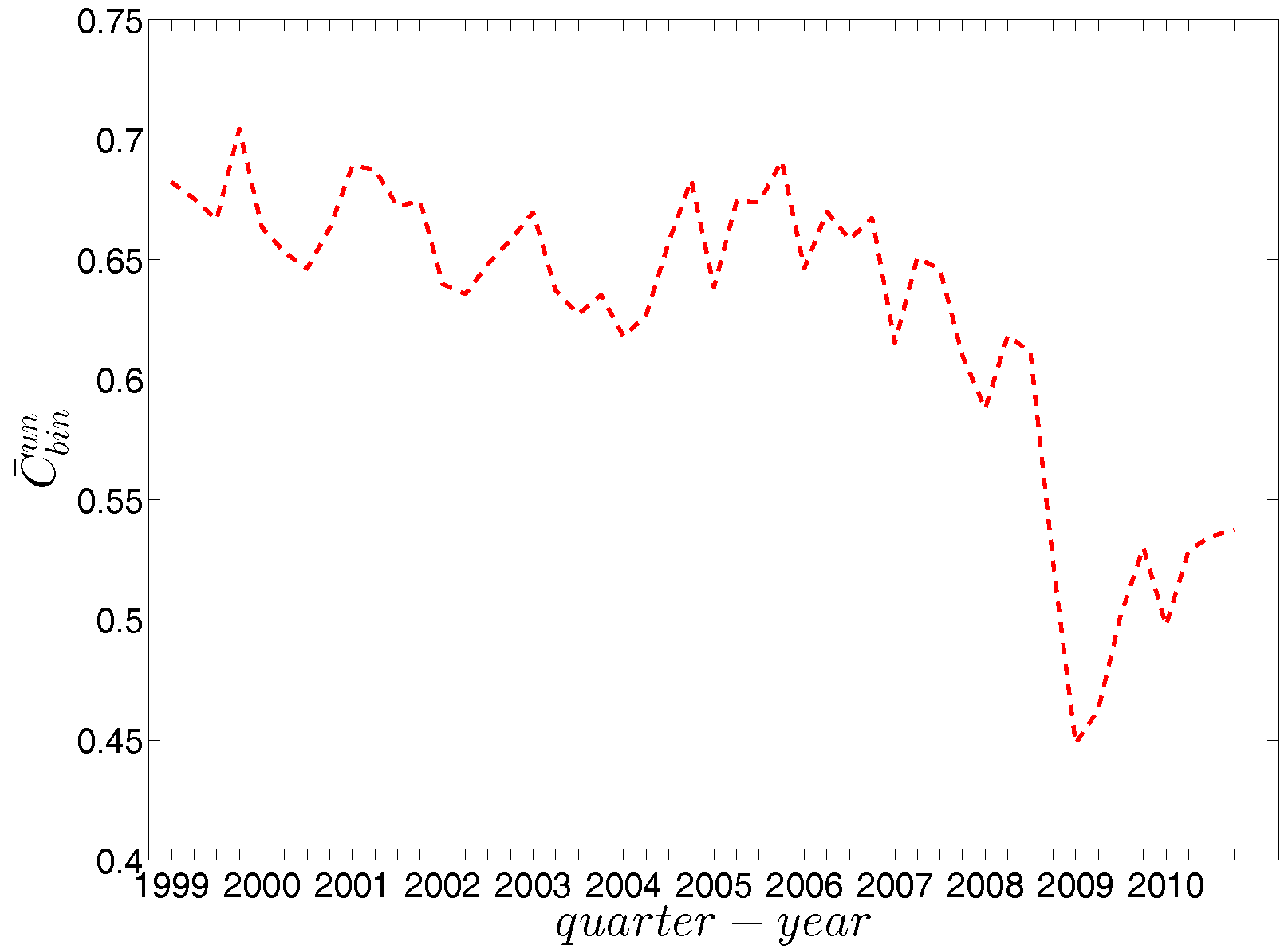
Figure 13.
Evolution of the average of local clustering coefficients (i.e., ) in the undirected binary e-MID network.
Figure 13.
Evolution of the average of local clustering coefficients (i.e., ) in the undirected binary e-MID network.
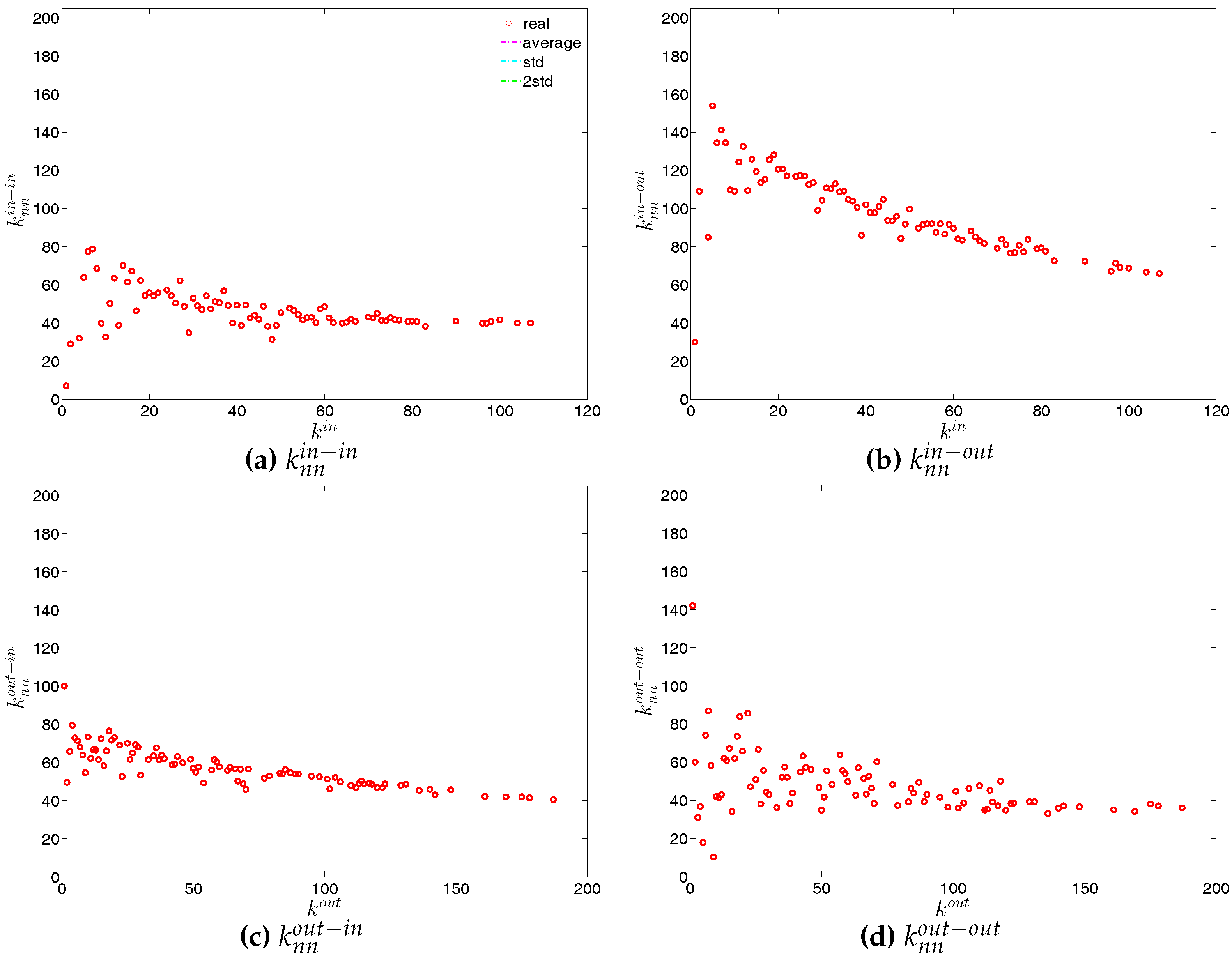
Figure 14.
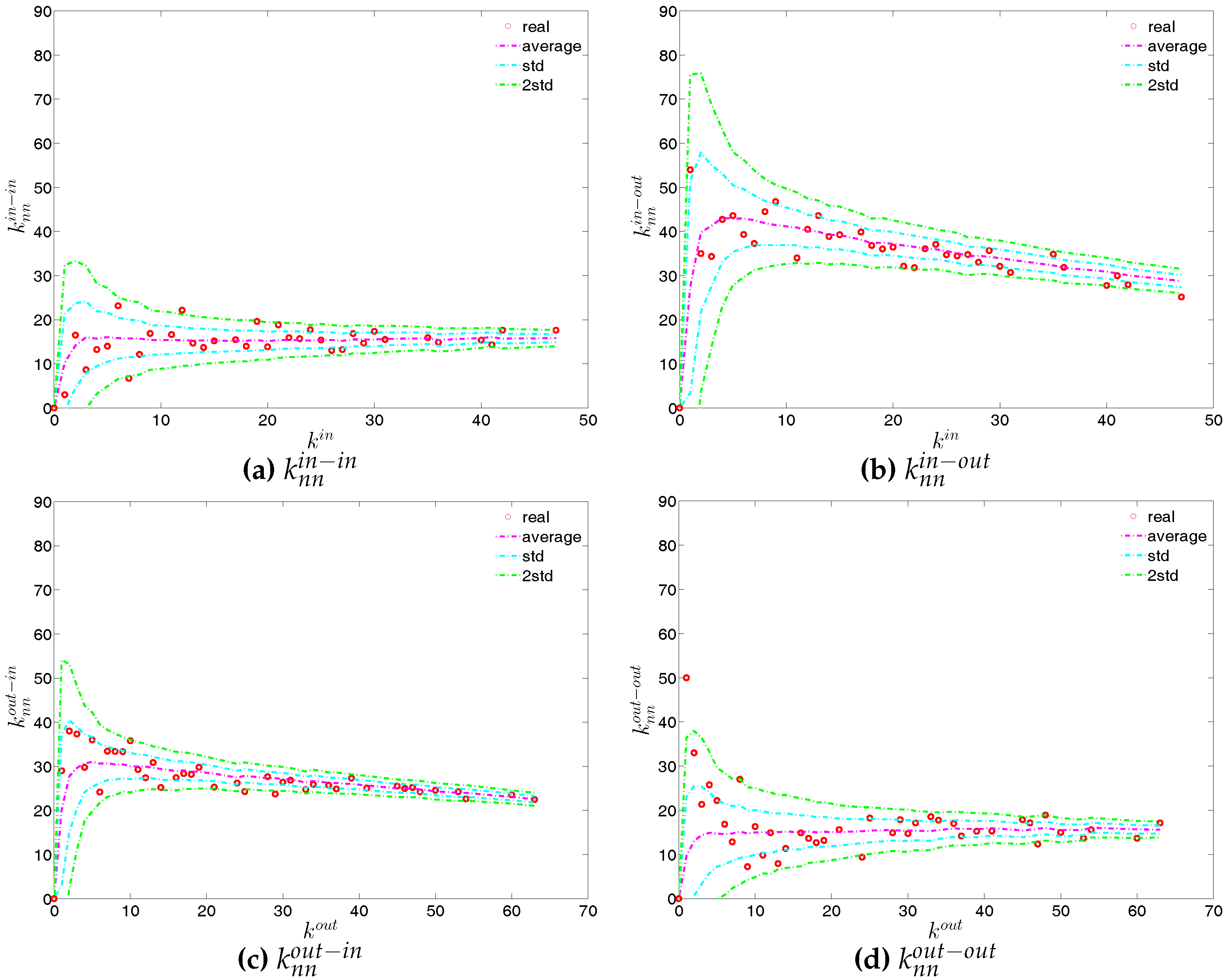
ANND in the directed binary e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 14.
ANND in the directed binary e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 15.
ANND in the directed binary e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 15.
ANND in the directed binary e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
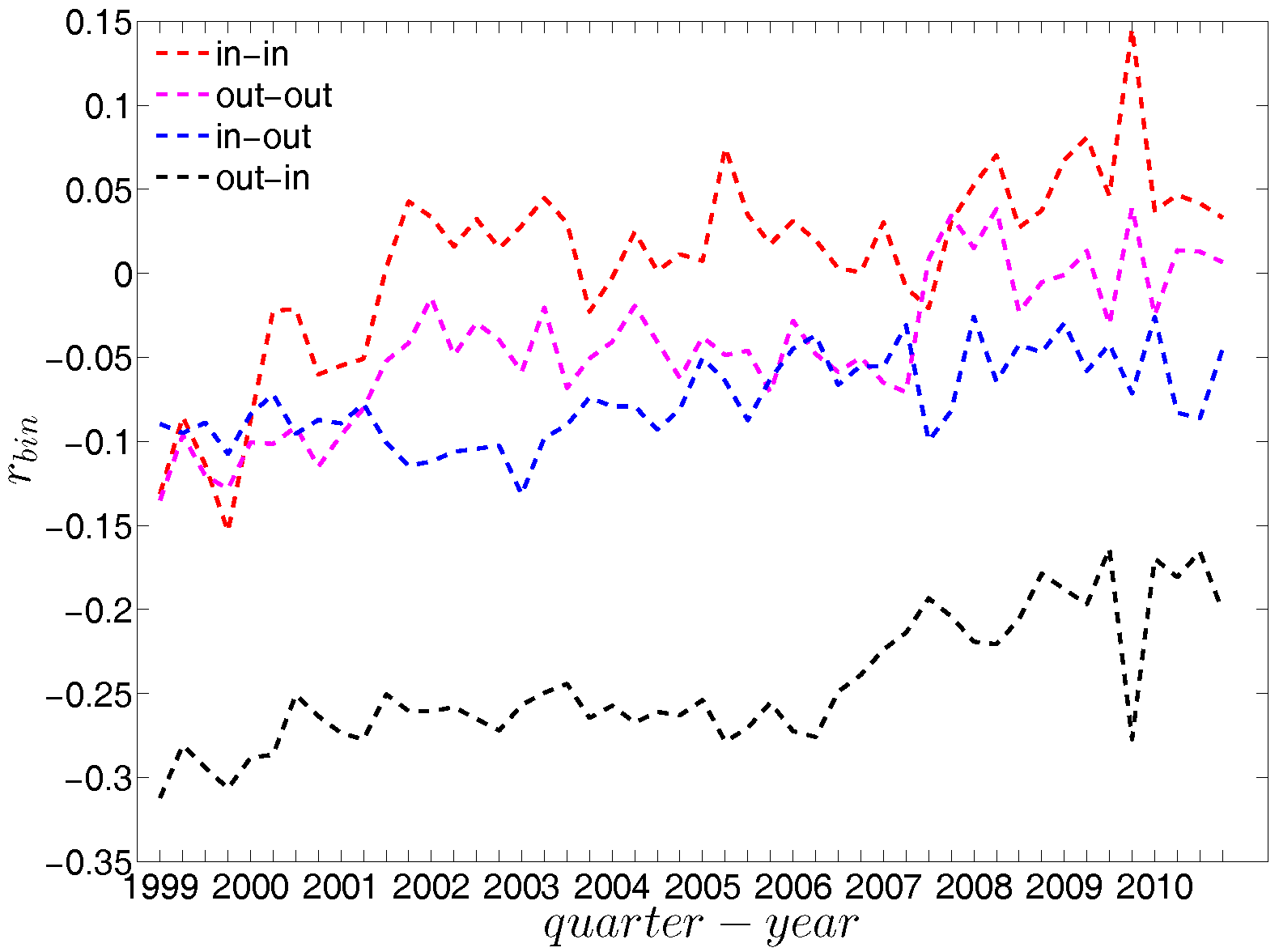
Figure 16.
Evolution of the overall assortativity indicators in the directed binary e-MID network.Evolution of the overall assortativity indicators in the directed binary e-MID network.
Figure 16.
Evolution of the overall assortativity indicators in the directed binary e-MID network.Evolution of the overall assortativity indicators in the directed binary e-MID network.
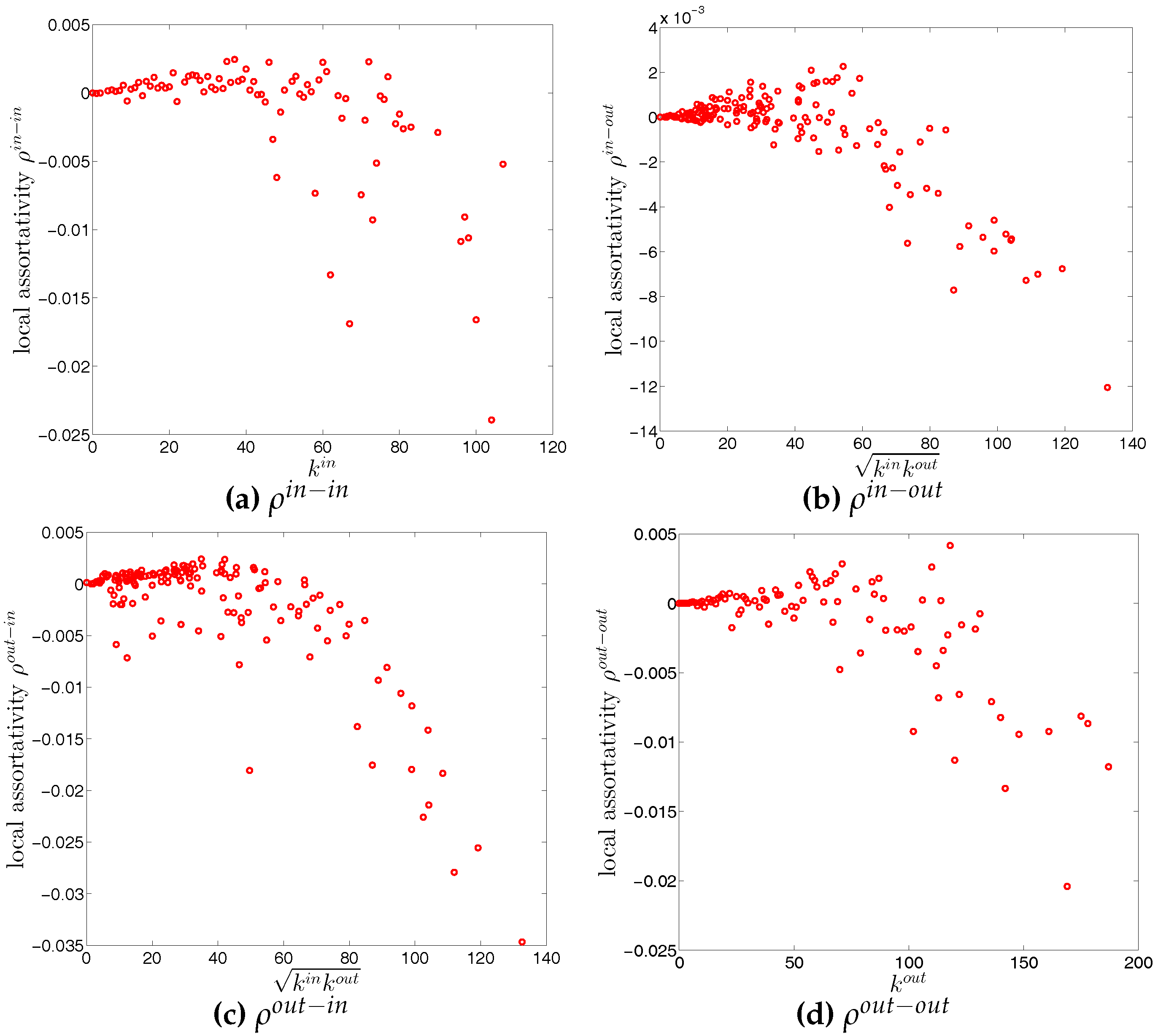
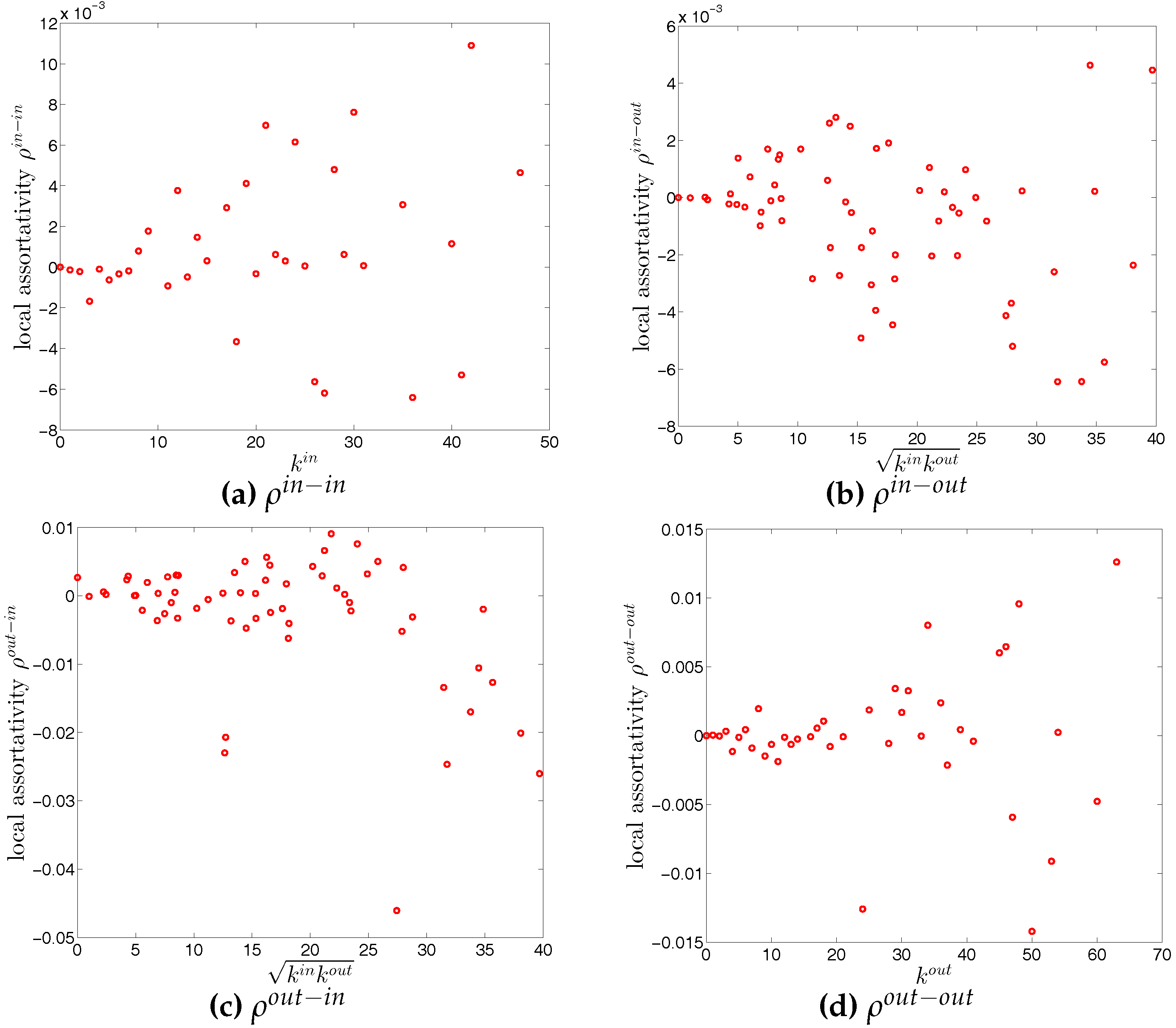
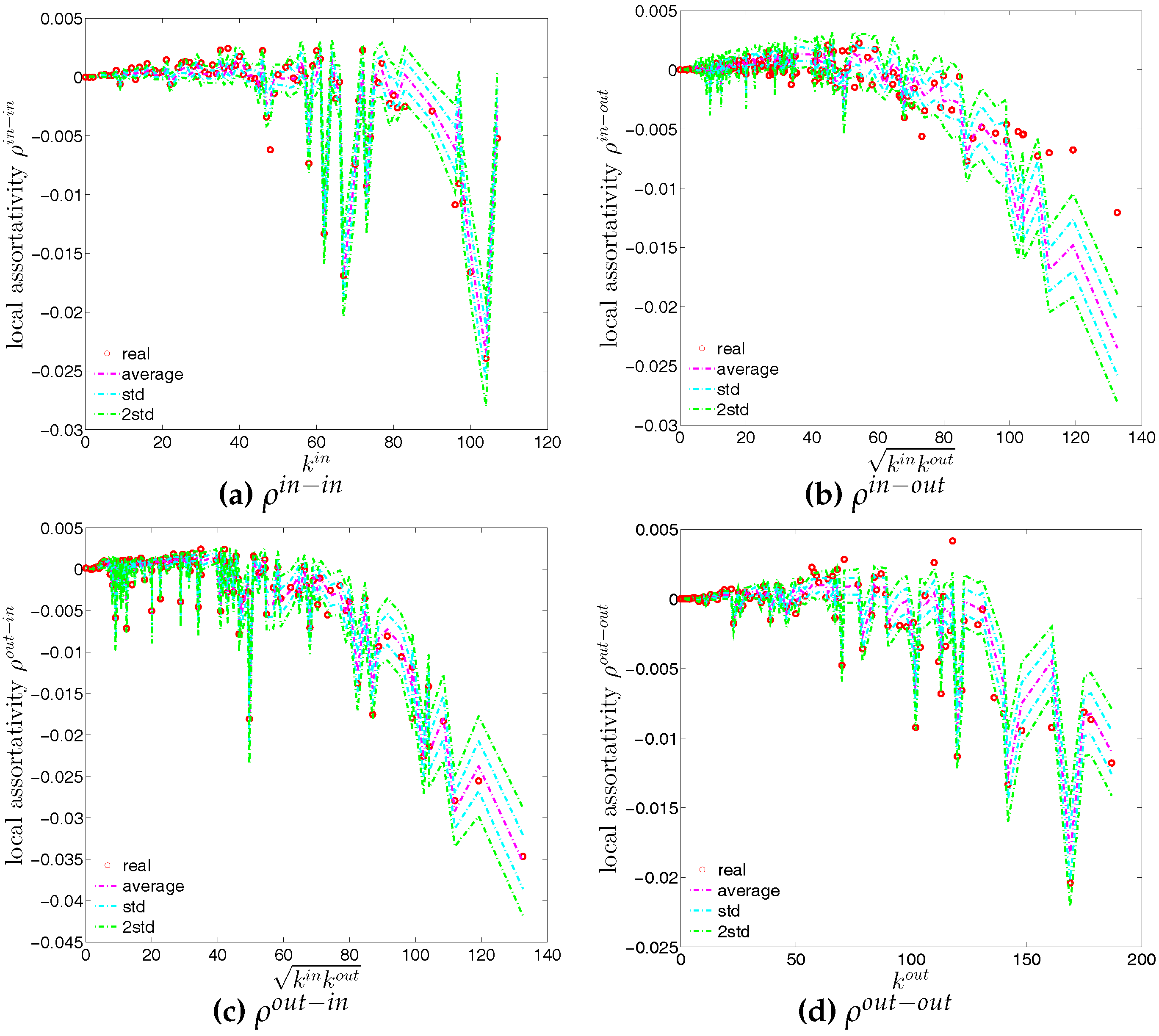
Figure 17.
Local assortativity in the directed binary e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 17.
Local assortativity in the directed binary e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
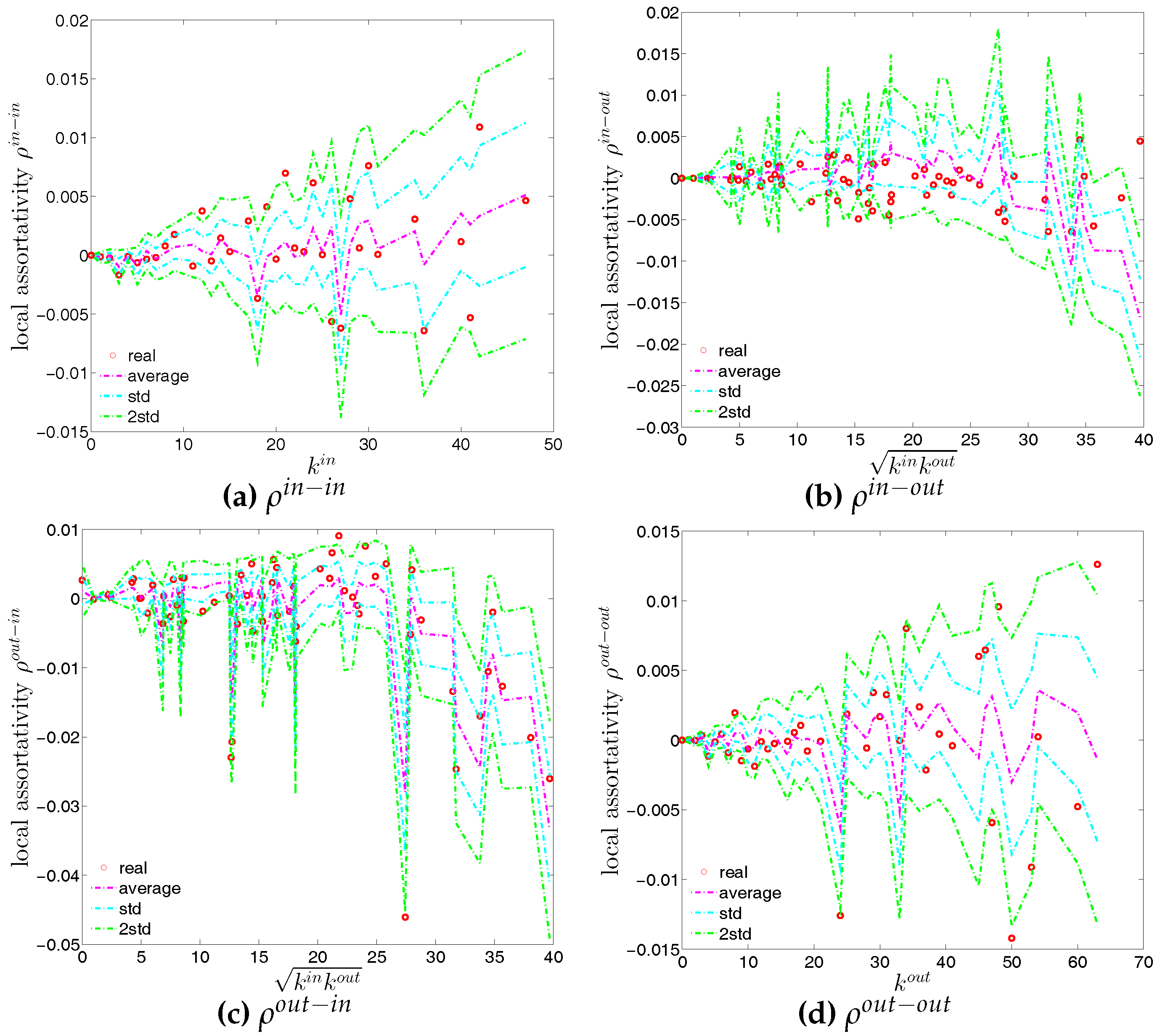
Figure 18.
Local assortativity in the directed binary e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 18.
Local assortativity in the directed binary e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
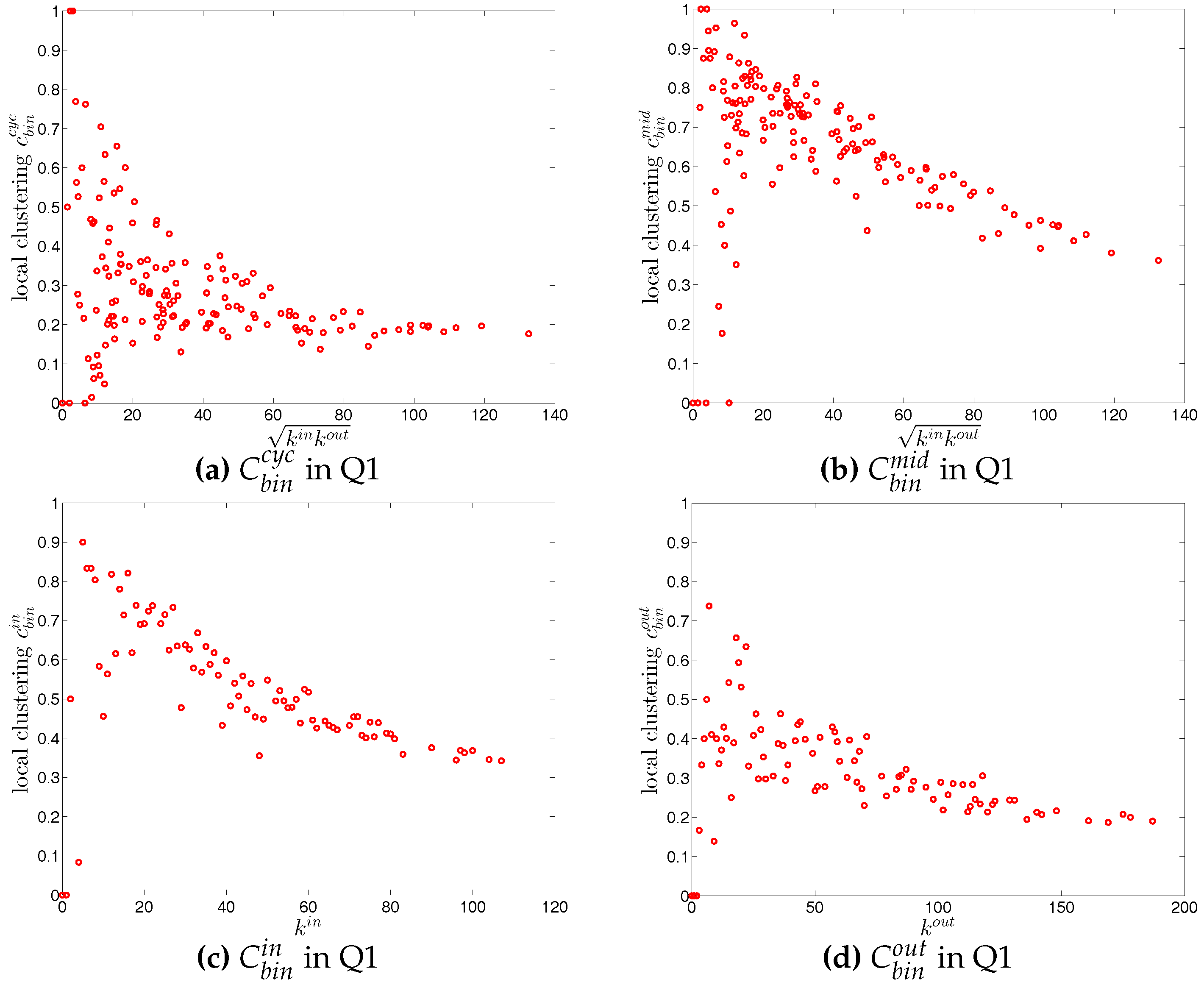
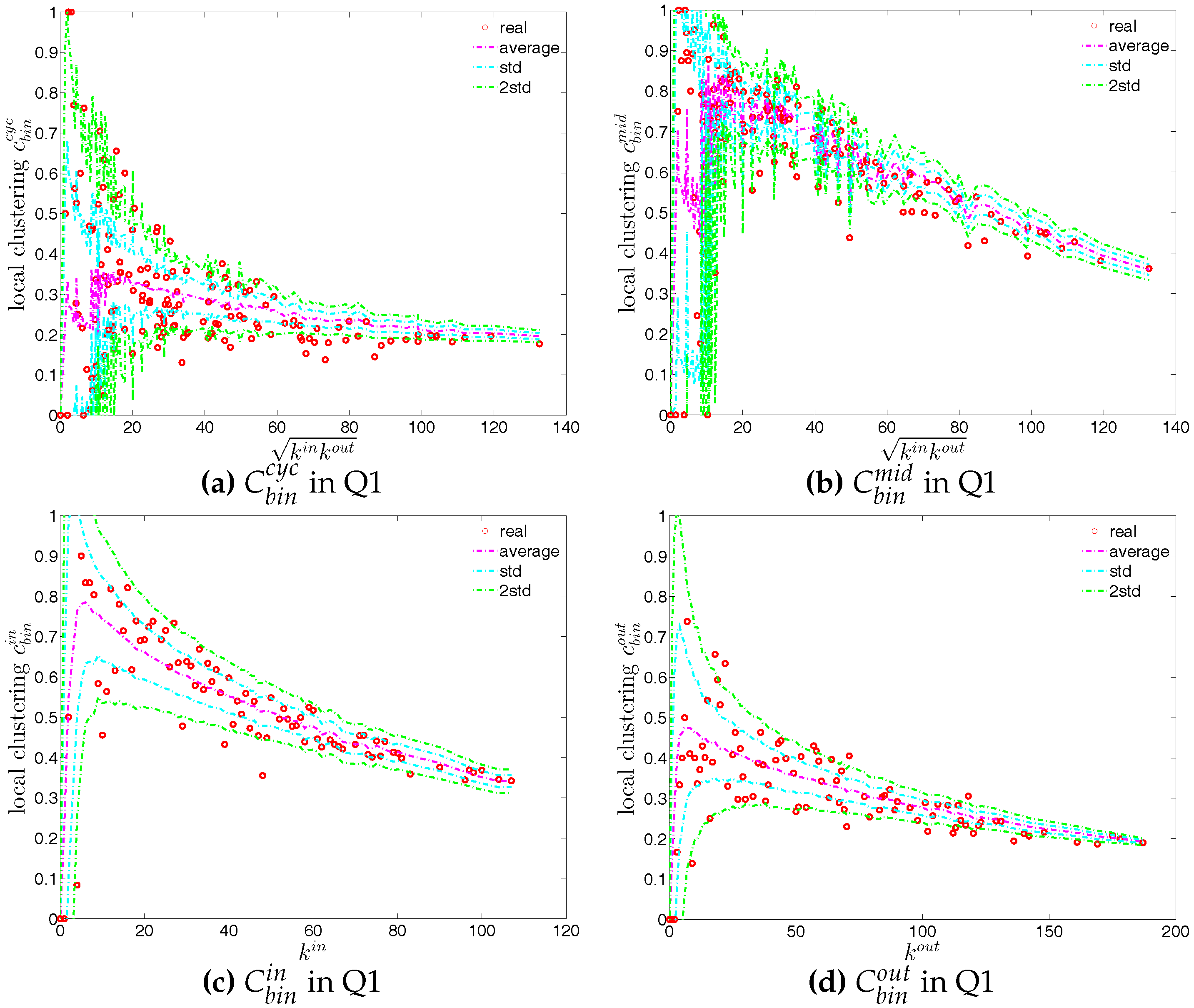
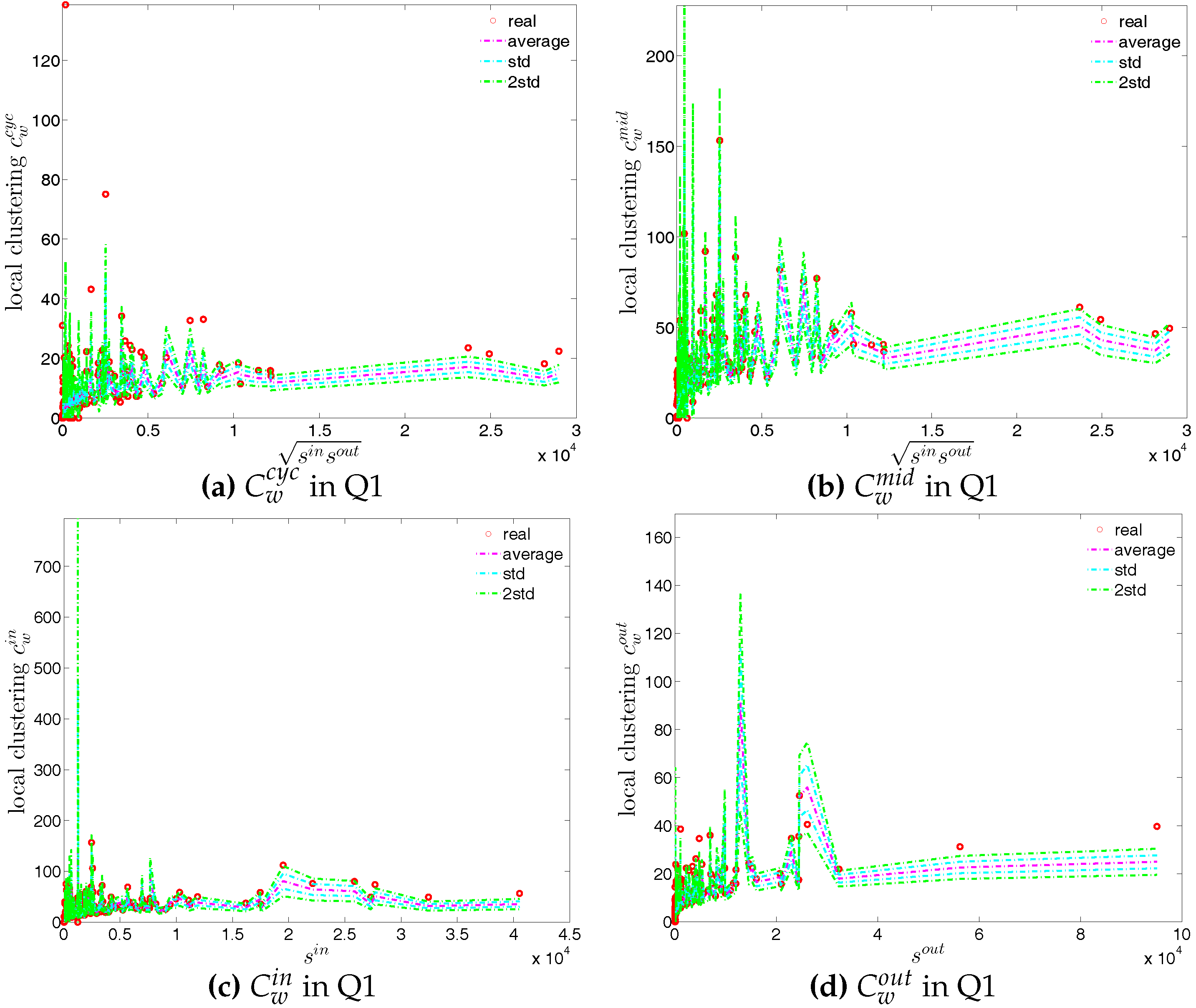
Figure 19.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the directed binary e-MID network, in Q1.
Figure 19.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the directed binary e-MID network, in Q1.
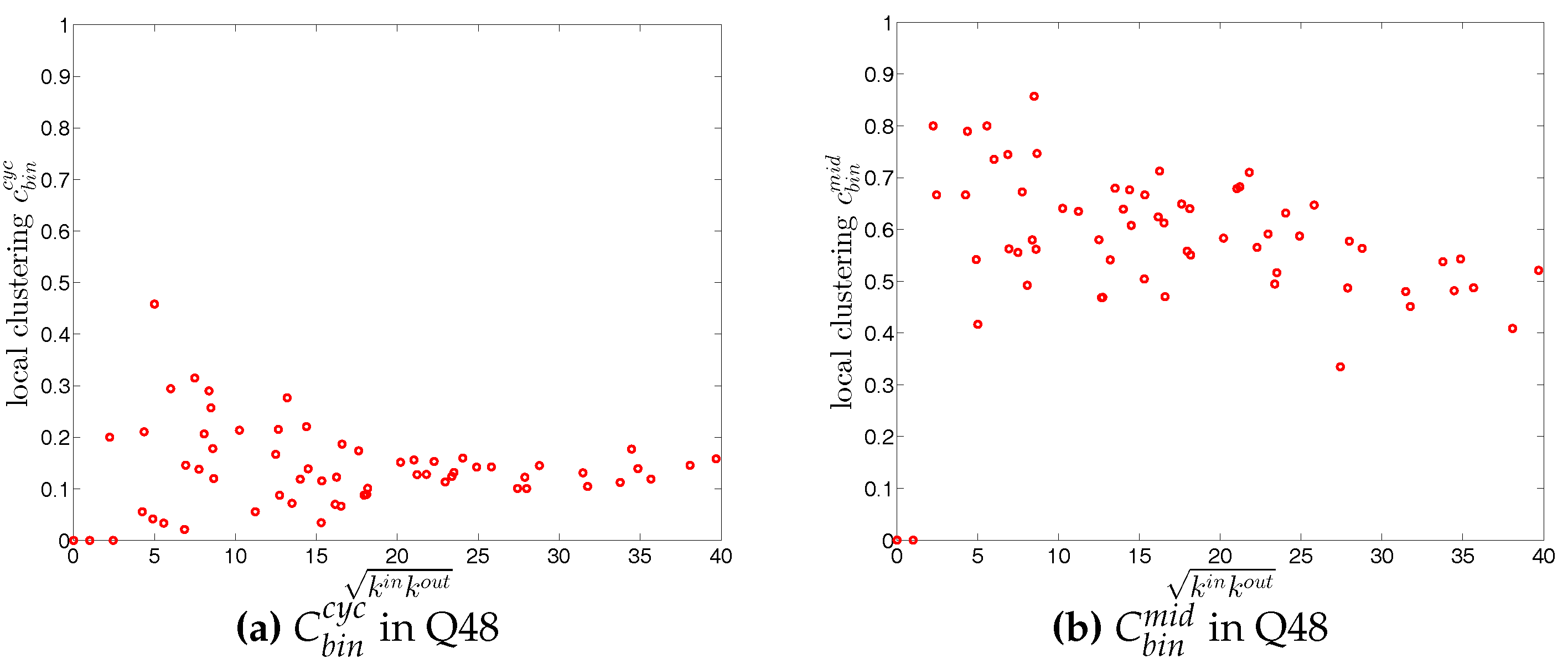
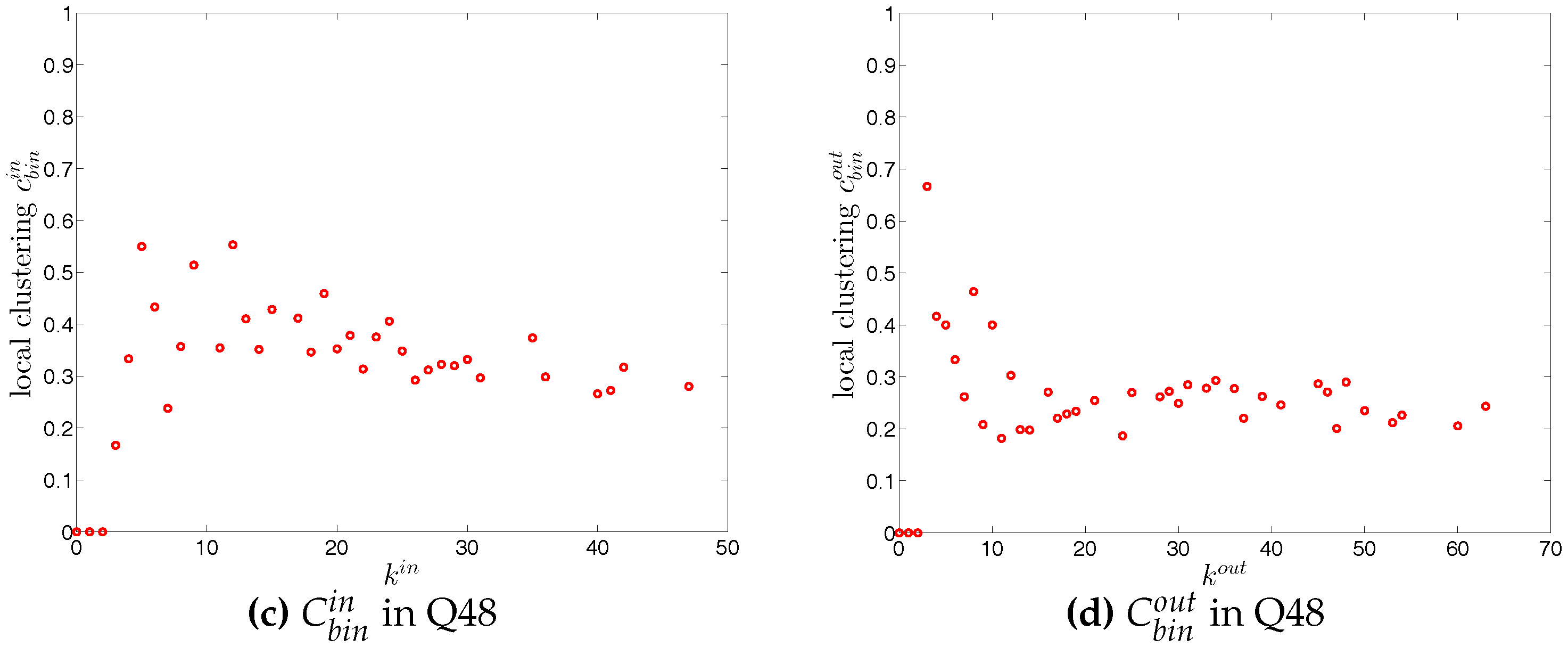
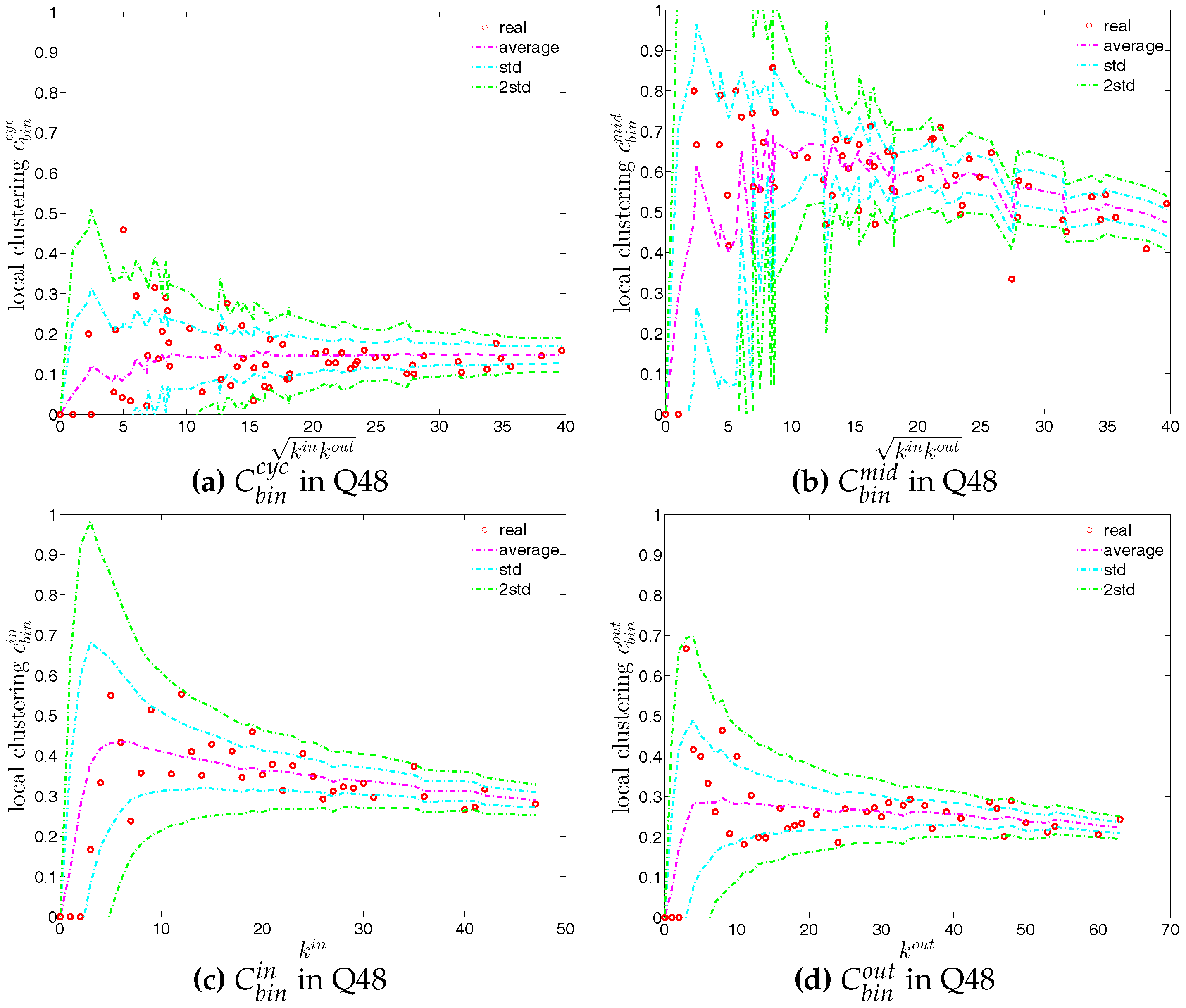
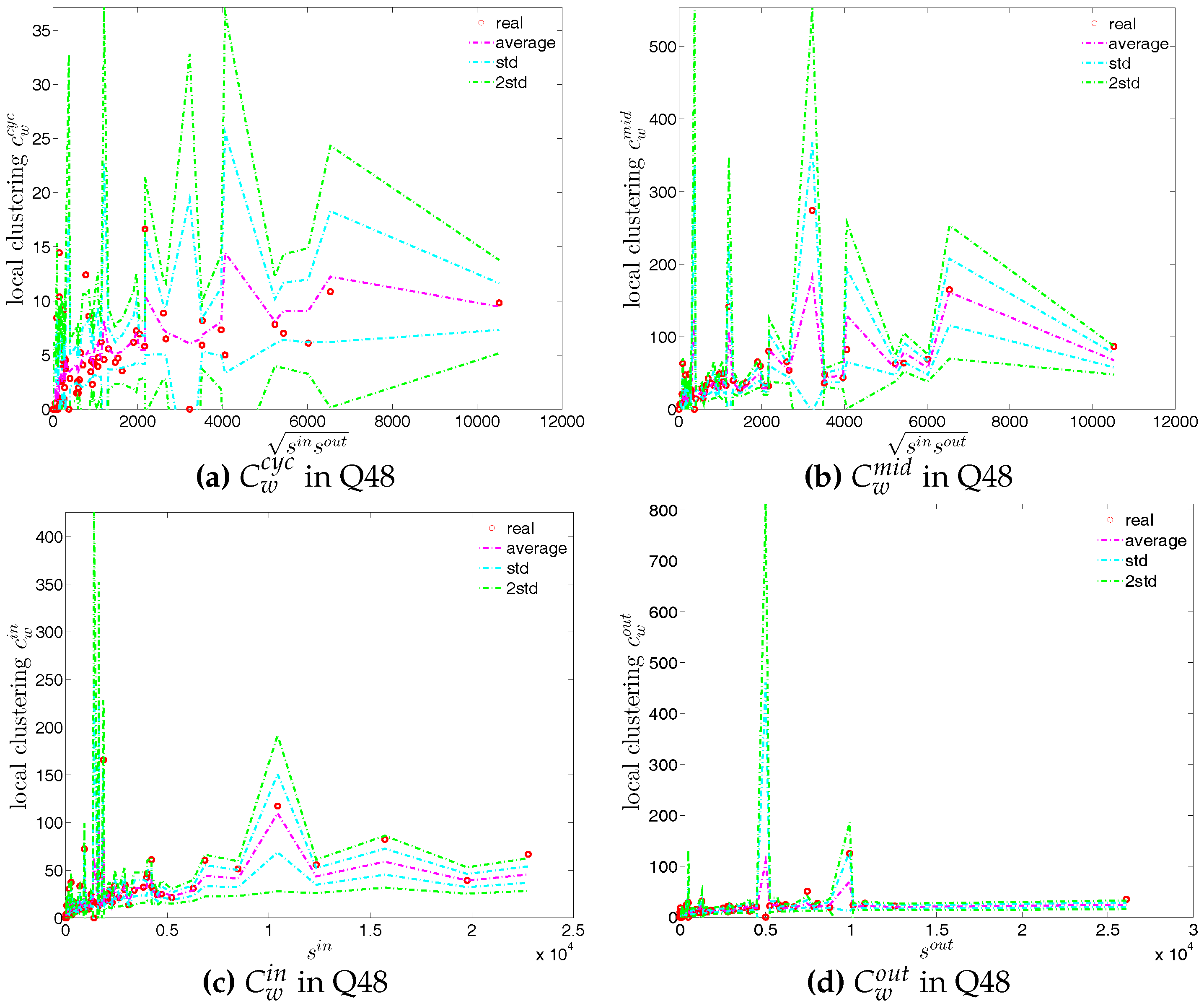
Figure 20.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the directed binary e-MID network, in Q48.
Figure 20.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the directed binary e-MID network, in Q48.
Figure 21.
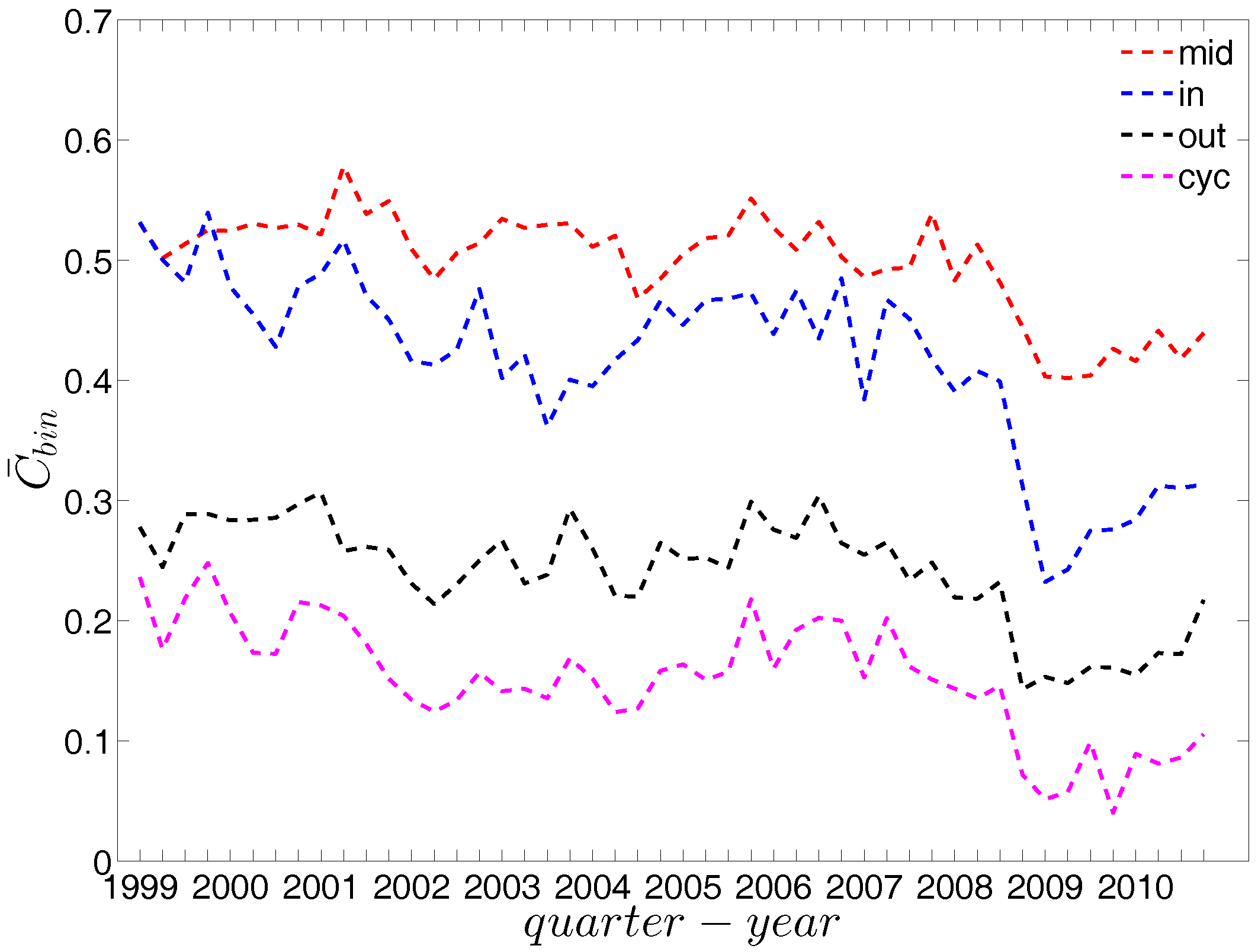
Evolution of the averages of local clustering coefficients (i.e., , , , and ) in the directed binary e-MID network.
Figure 21.
Evolution of the averages of local clustering coefficients (i.e., , , , and ) in the directed binary e-MID network.
Figure 22.
(a,b) ANND; (c,d) local assortativity ; (e,f) local clustering coefficients in the observed e-MID network and in the UBCM, in Q1 and Q48.
Figure 22.
(a,b) ANND; (c,d) local assortativity ; (e,f) local clustering coefficients in the observed e-MID network and in the UBCM, in Q1 and Q48.
Figure 23.
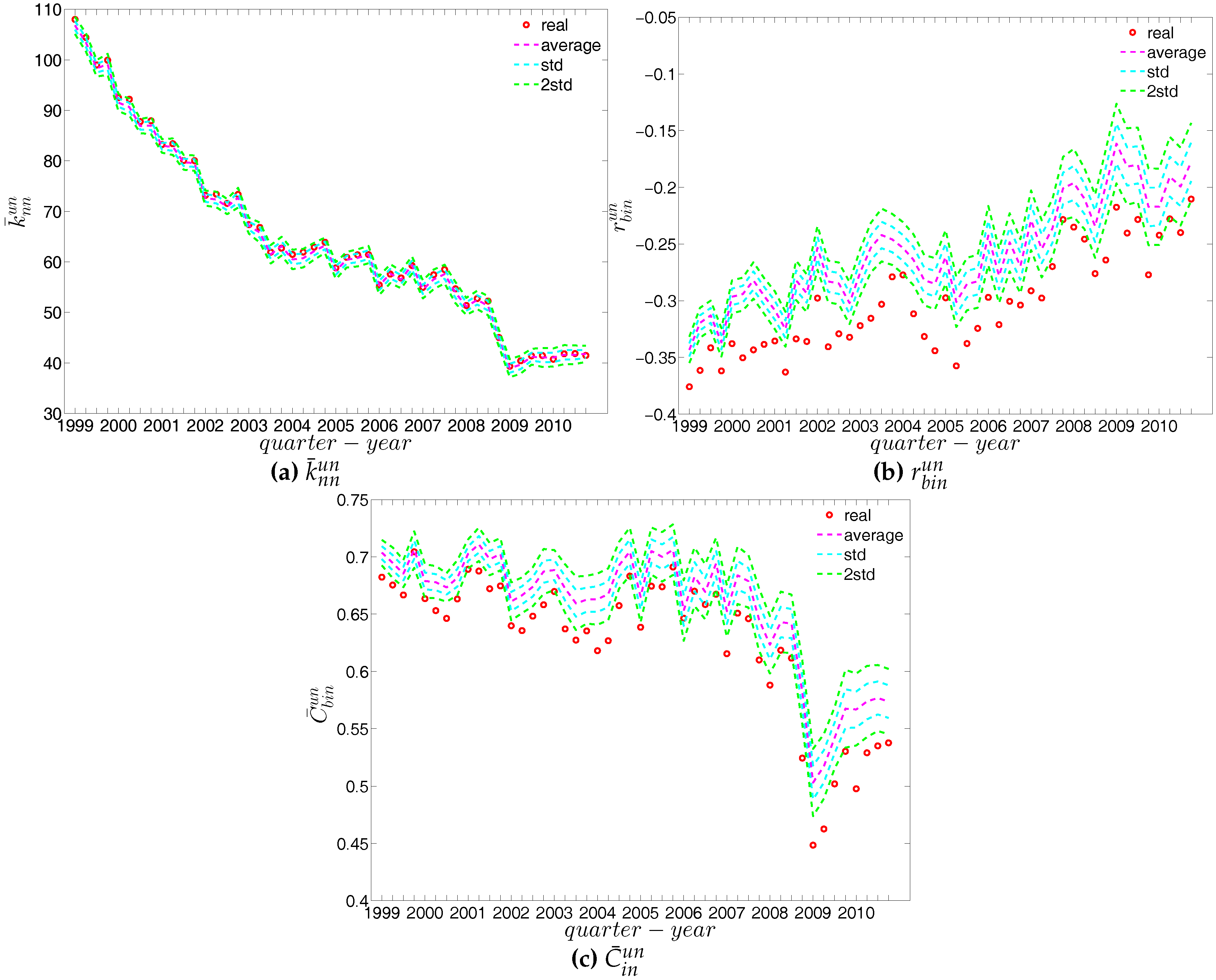
Evolution of (a) ; (b) ; and (c) in the observed e-MID network and in the undirected binary configuration model (UBCM).
Figure 23.
Evolution of (a) ; (b) ; and (c) in the observed e-MID network and in the undirected binary configuration model (UBCM).
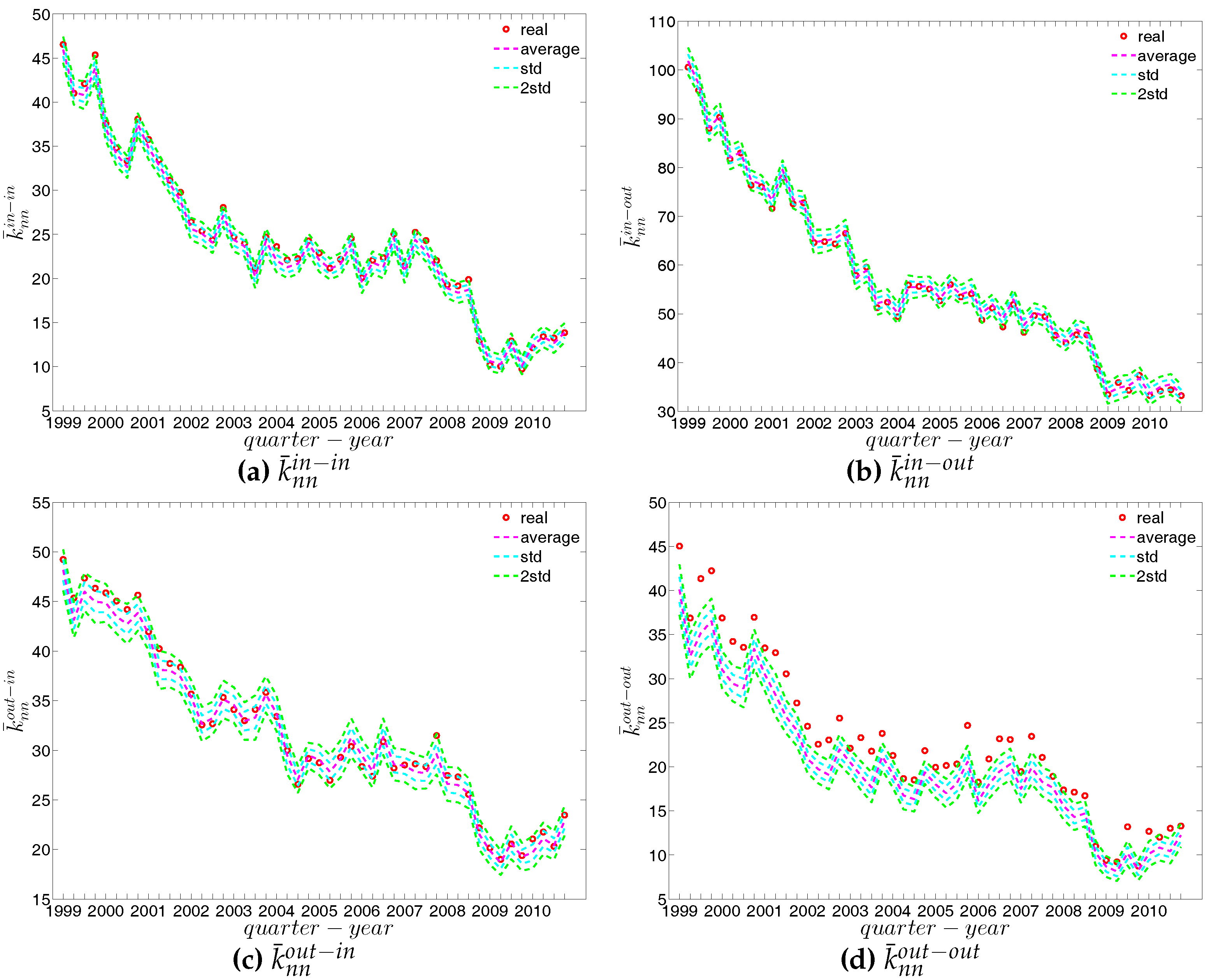
Figure 24.
ANND in the observed e-MID network and in the DBCM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 24.
ANND in the observed e-MID network and in the DBCM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 25.
ANND in the observed e-MID network and in the DBCM, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 25.
ANND in the observed e-MID network and in the DBCM, in Q48. (a) ; (b) ; (c) ; (d) .
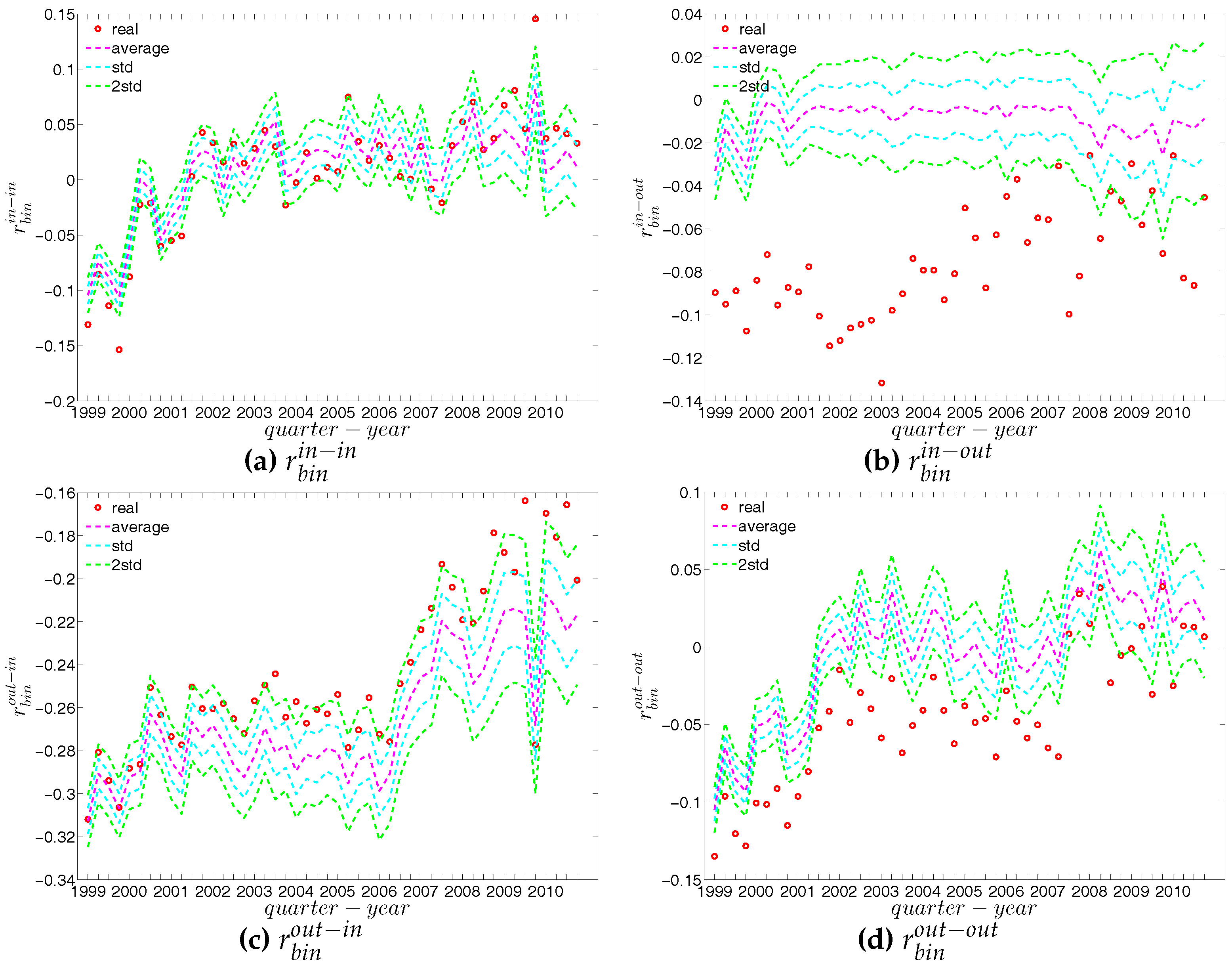
Figure 26.
Local assortativity in the observed e-MID network and in the DBCM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 26.
Local assortativity in the observed e-MID network and in the DBCM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 27.
Local assortativity in the observed e-MID network and in the DBCM, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 27.
Local assortativity in the observed e-MID network and in the DBCM, in Q48. (a) ; (b) ; (c) ; (d) .
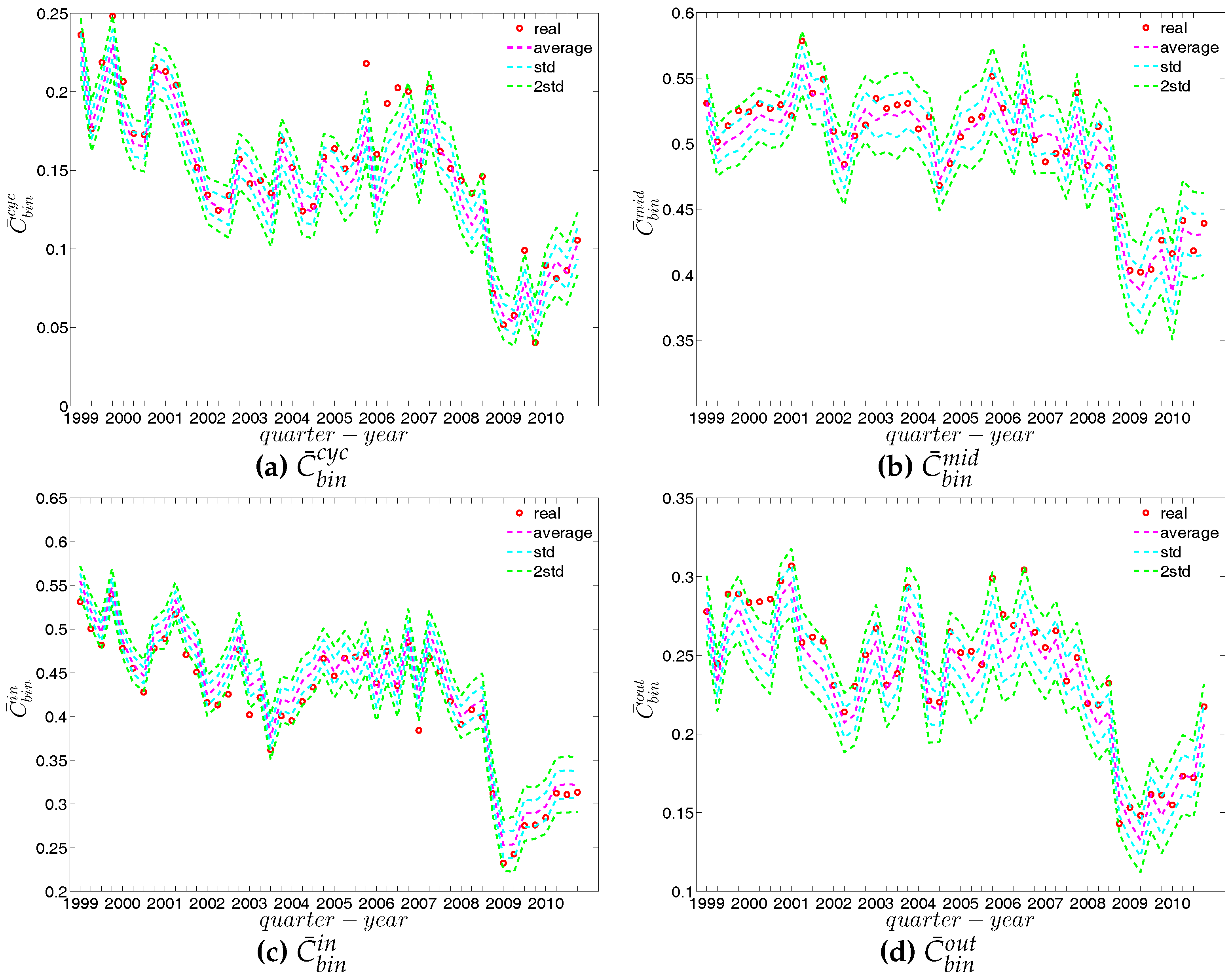
Figure 28.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the observed e-MID network and in DBCM, in Q1.
Figure 28.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the observed e-MID network and in DBCM, in Q1.
Figure 29.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the observed e-MID network and in DBCM, in Q48.
Figure 29.
Local clustering coefficients (a) ; (b) ; (c) ; (d) in the observed e-MID network and in DBCM, in Q48.
Figure 30.
Evolution of the averages of ANNDs in the observed e-MID network and in the DBCM. (a) ; (b) ; (c) ; (d) .
Figure 30.
Evolution of the averages of ANNDs in the observed e-MID network and in the DBCM. (a) ; (b) ; (c) ; (d) .
Figure 31.
Evolution of the global assortativity indicators in the observed e-MID network and in the DBCM. (a) ; (b) ; (c) ; (d) .
Figure 31.
Evolution of the global assortativity indicators in the observed e-MID network and in the DBCM. (a) ; (b) ; (c) ; (d) .
Figure 32.
Evolution of the averages of clustering coefficients in the observed e-MID network and in the DBCM. (a) ; (b) ; (c) ; (d) .
Figure 32.
Evolution of the averages of clustering coefficients in the observed e-MID network and in the DBCM. (a) ; (b) ; (c) ; (d) .
Figure 33.
Average strength of the nearest neighbors (ANNS) in the undirected weighted e-MID network, in Q1 and Q48.
Figure 33.
Average strength of the nearest neighbors (ANNS) in the undirected weighted e-MID network, in Q1 and Q48.
Figure 34.
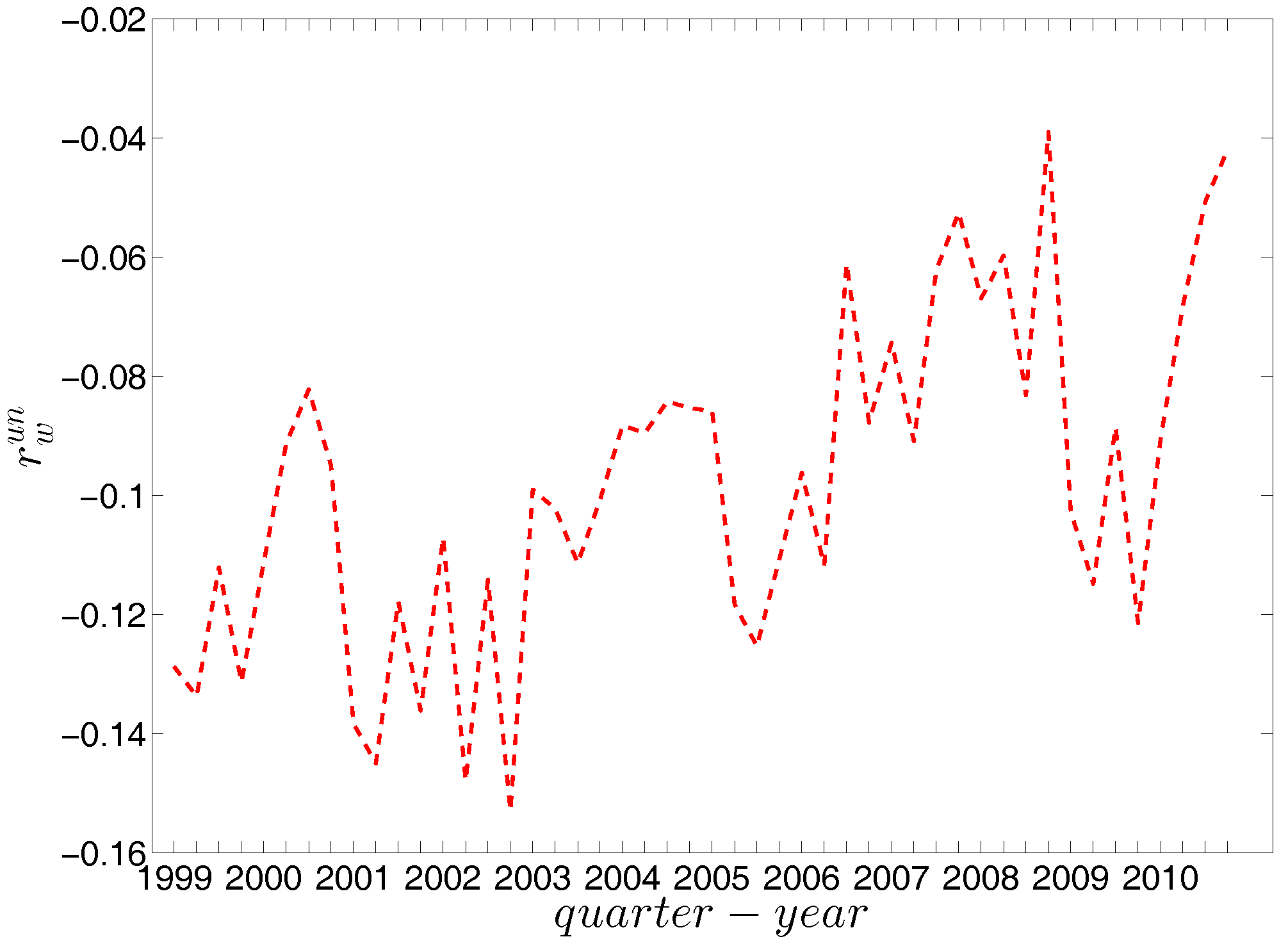
Evolution of global weighted assortativity in the undirected weighted e-MID network.
Figure 34.
Evolution of global weighted assortativity in the undirected weighted e-MID network.
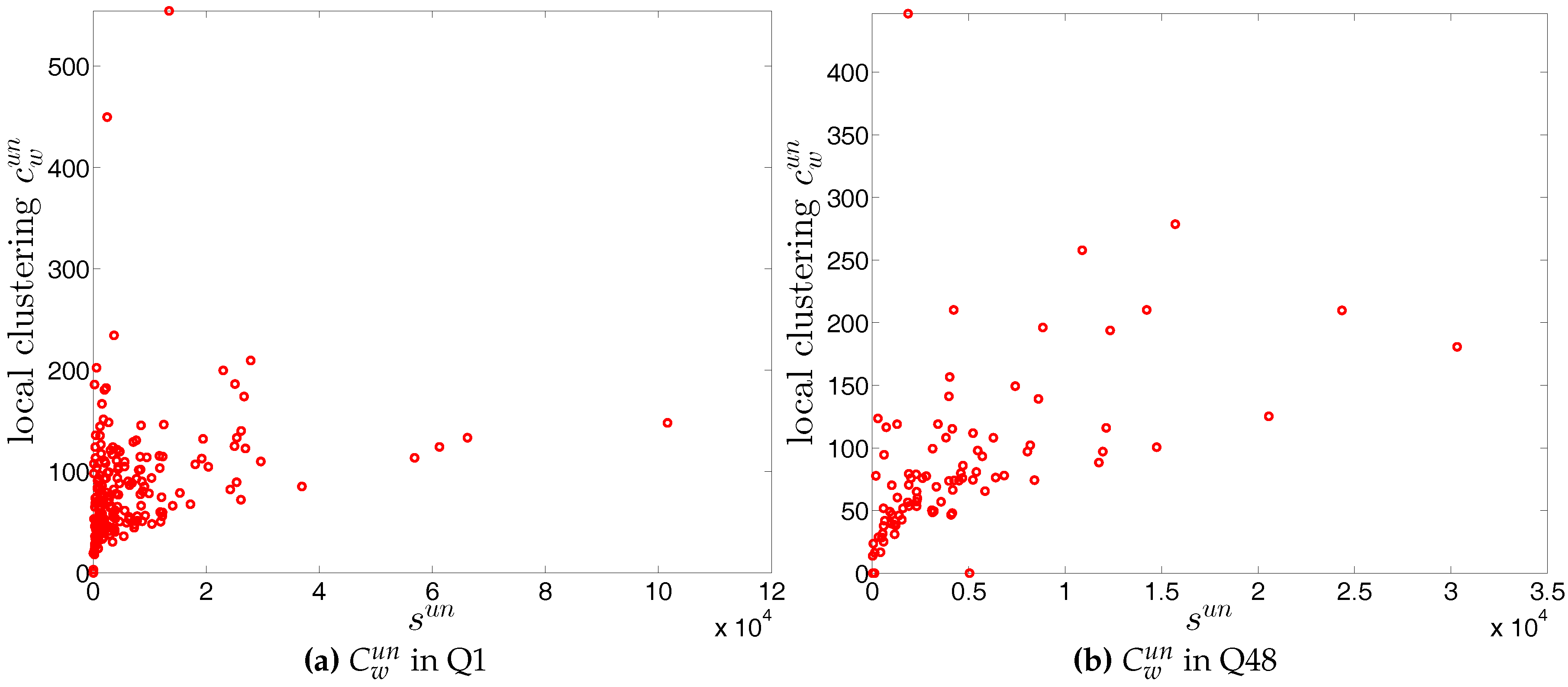
Figure 35.
Local clustering coefficients in the undirected weighted e-MID network, in Q1 and Q48.
Figure 35.
Local clustering coefficients in the undirected weighted e-MID network, in Q1 and Q48.
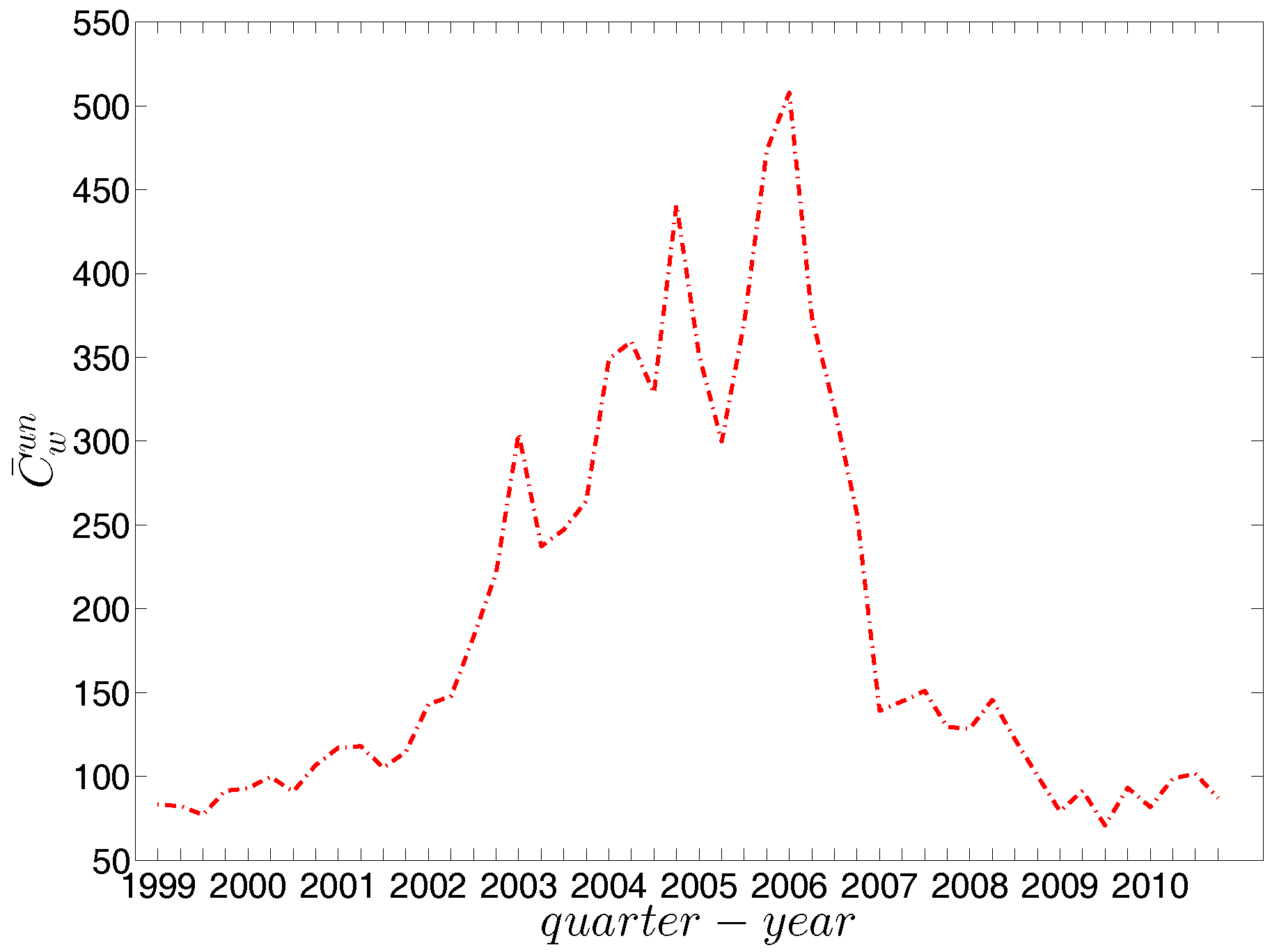
Figure 36.
Evolution of the average of local weighted clustering coefficients (i.e., ) in the undirected weighted e-MID network.
Figure 36.
Evolution of the average of local weighted clustering coefficients (i.e., ) in the undirected weighted e-MID network.
Figure 37.
ANNSs in the directed weighted e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 37.
ANNSs in the directed weighted e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 38.
ANNSs in the directed weighted e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 38.
ANNSs in the directed weighted e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 39.
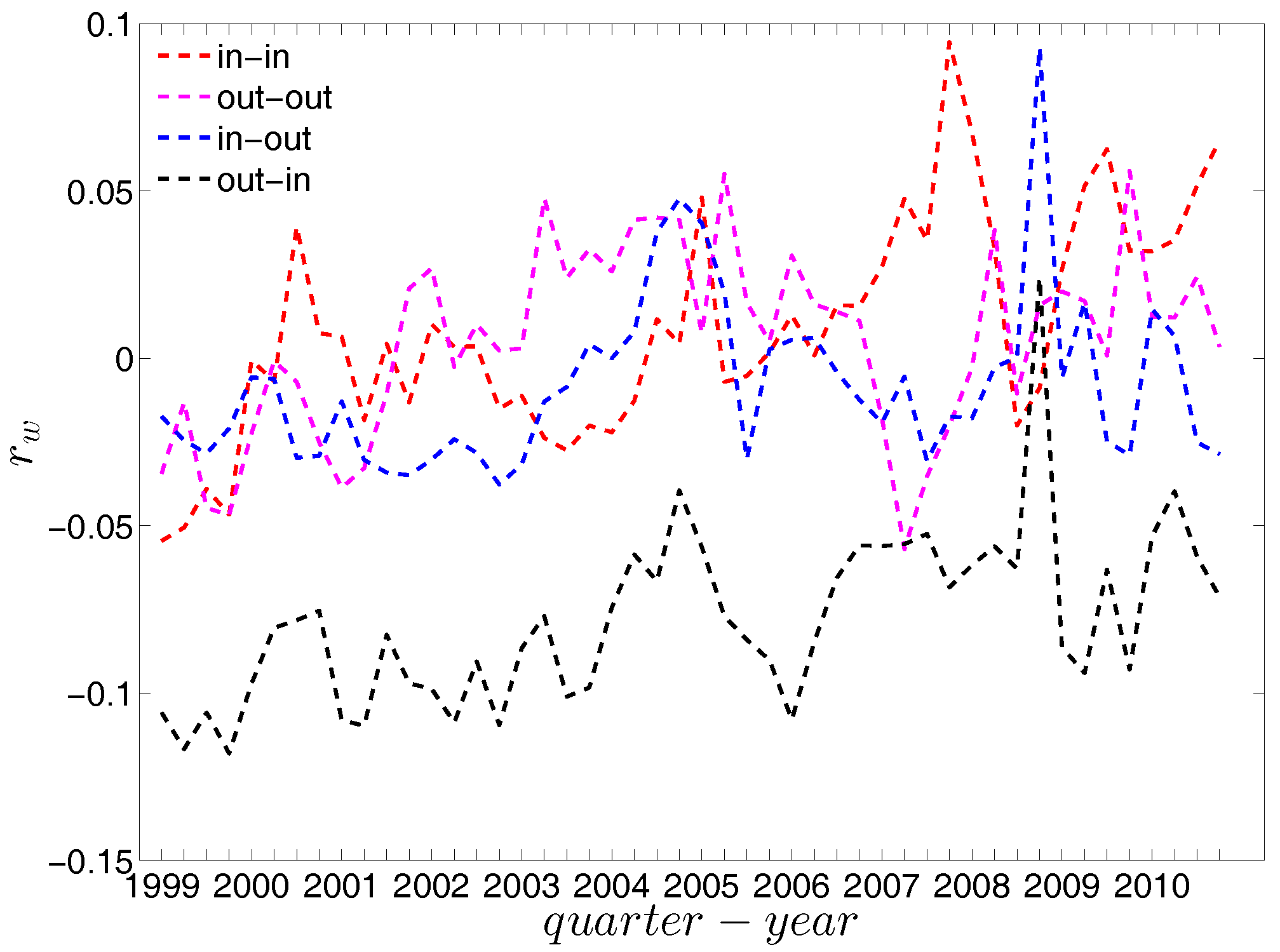
Evolution of the directed weighted assortativity indicators, i.e., , , , and in the directed weighted e-MID network.
Figure 39.
Evolution of the directed weighted assortativity indicators, i.e., , , , and in the directed weighted e-MID network.
Figure 40.
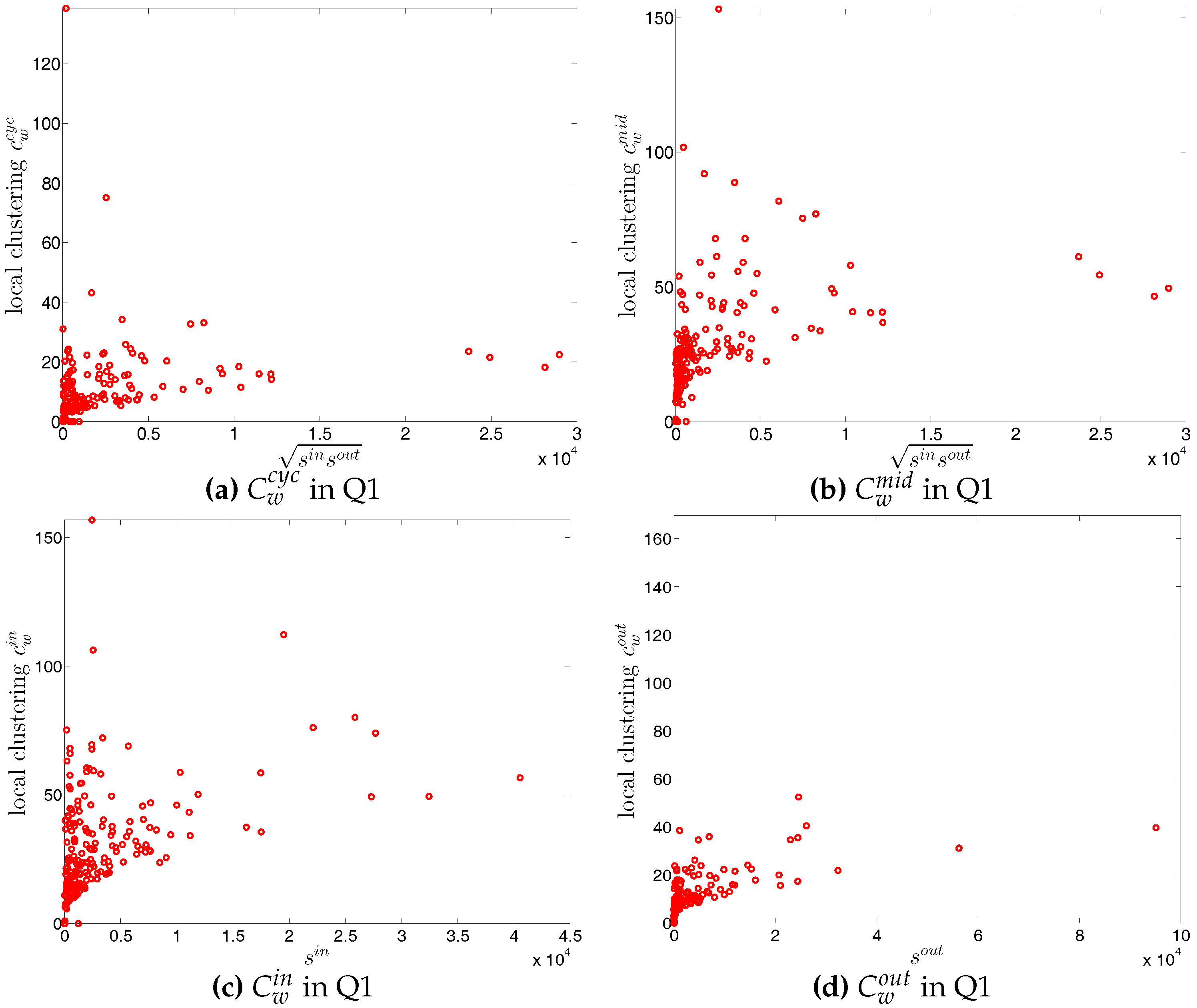
Local weighted clustering coefficients in the directed weighted e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 40.
Local weighted clustering coefficients in the directed weighted e-MID network, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 41.
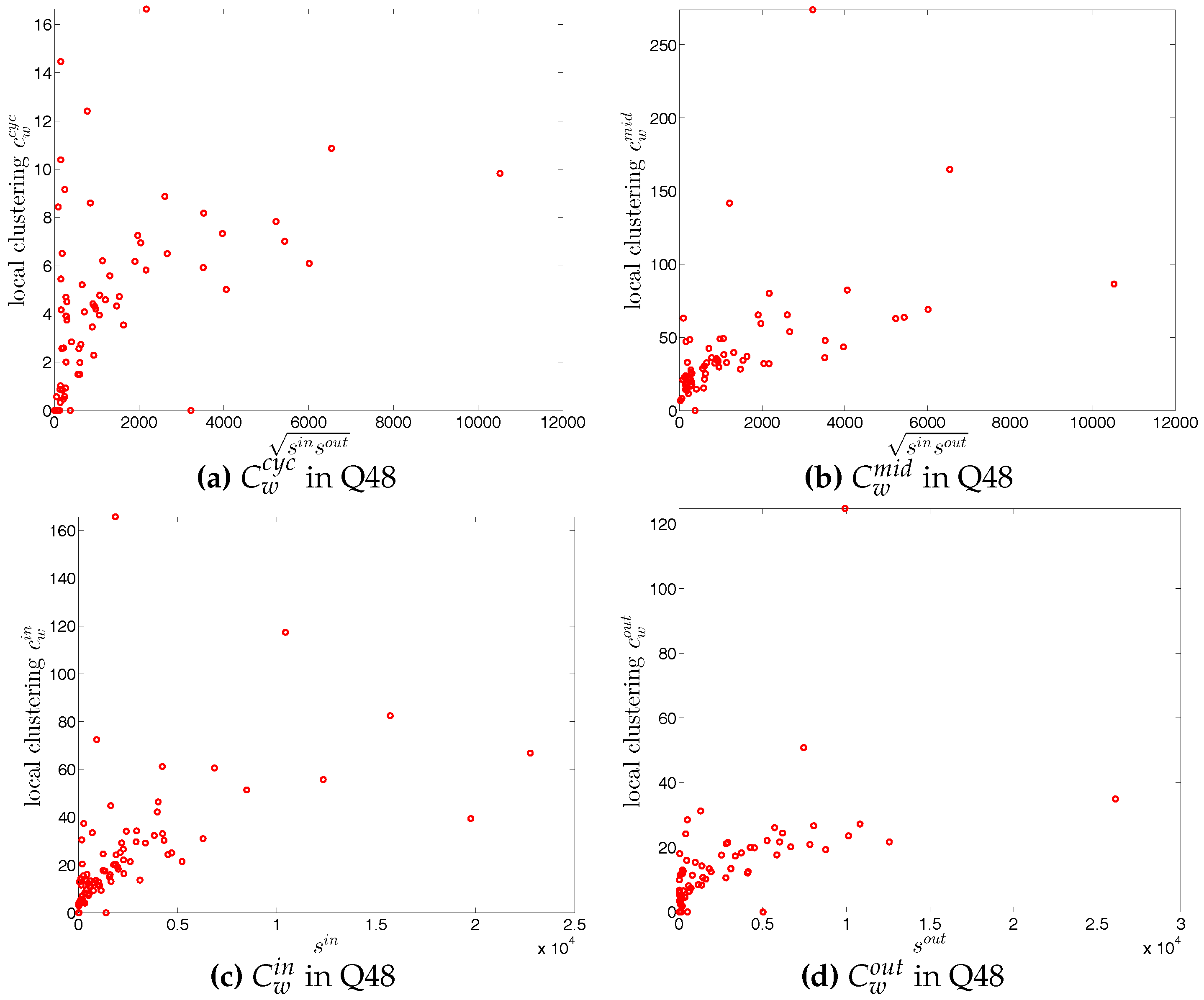
Local weighted clustering coefficients in the directed weighted e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 41.
Local weighted clustering coefficients in the directed weighted e-MID network, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 42.
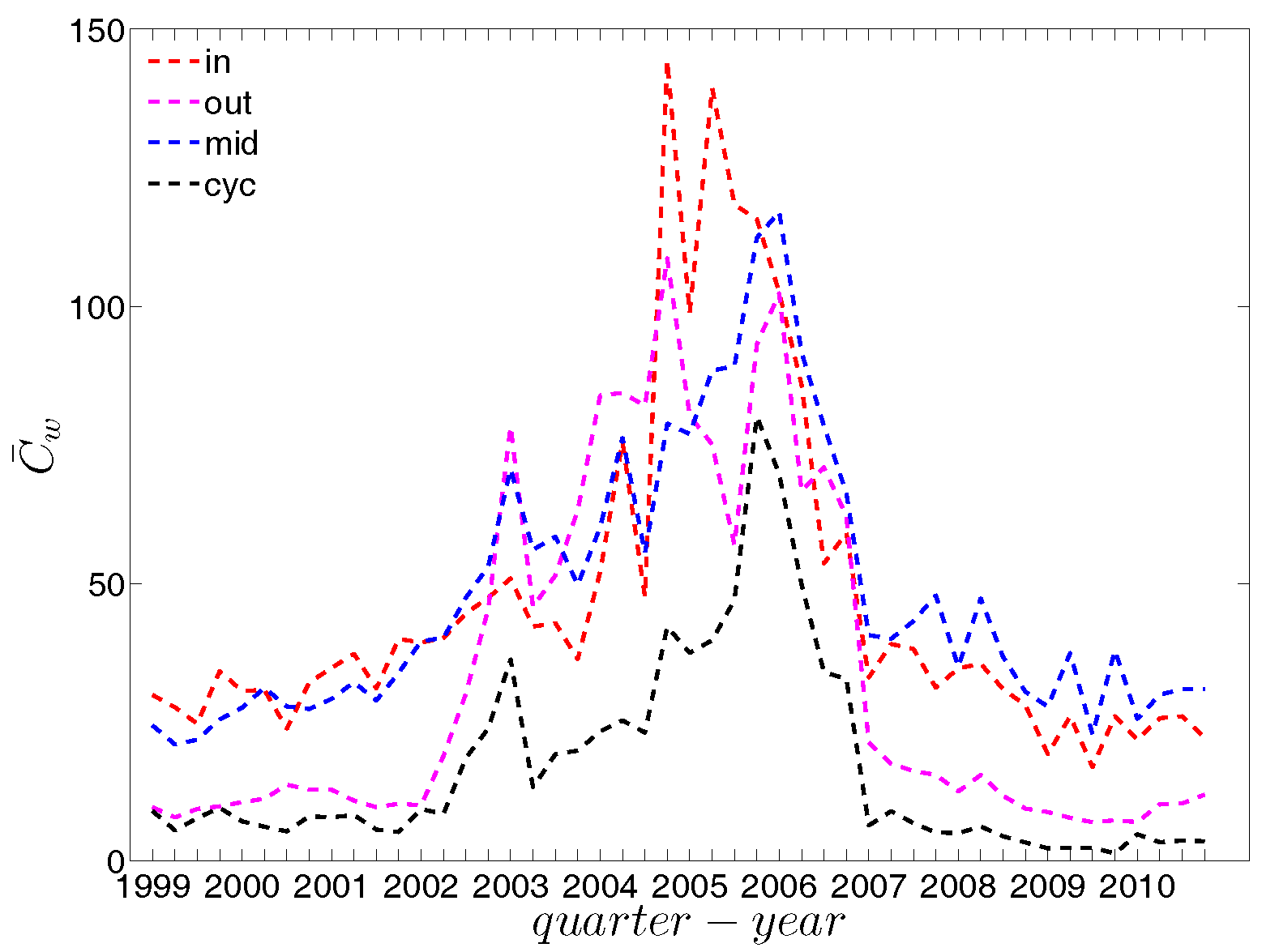
Evolution of the averages of local weighted clustering coefficients, i.e., , , , and in the directed weighted e-MID network.
Figure 42.
Evolution of the averages of local weighted clustering coefficients, i.e., , , , and in the directed weighted e-MID network.
Figure 43.
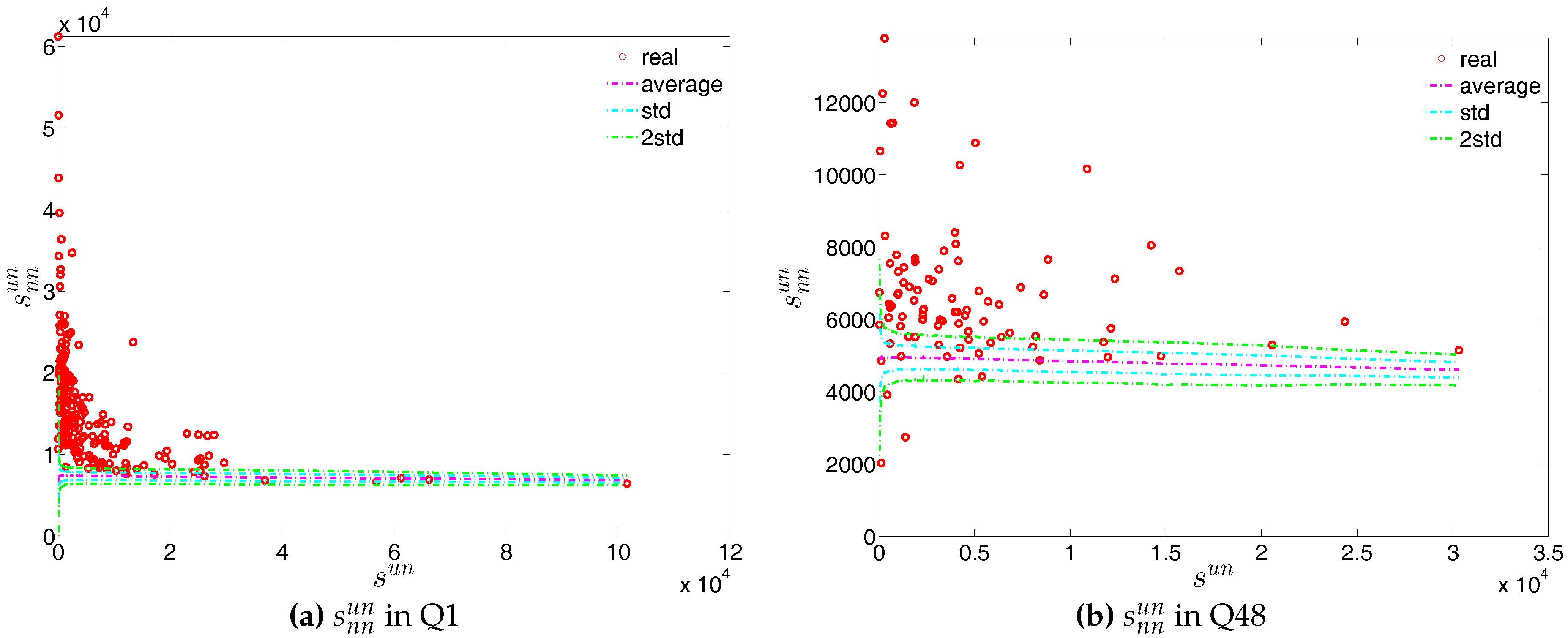
ANNS in the observed e-MID network and in the UWCM, in Q1 and Q48.
Figure 43.
ANNS in the observed e-MID network and in the UWCM, in Q1 and Q48.
Figure 44.
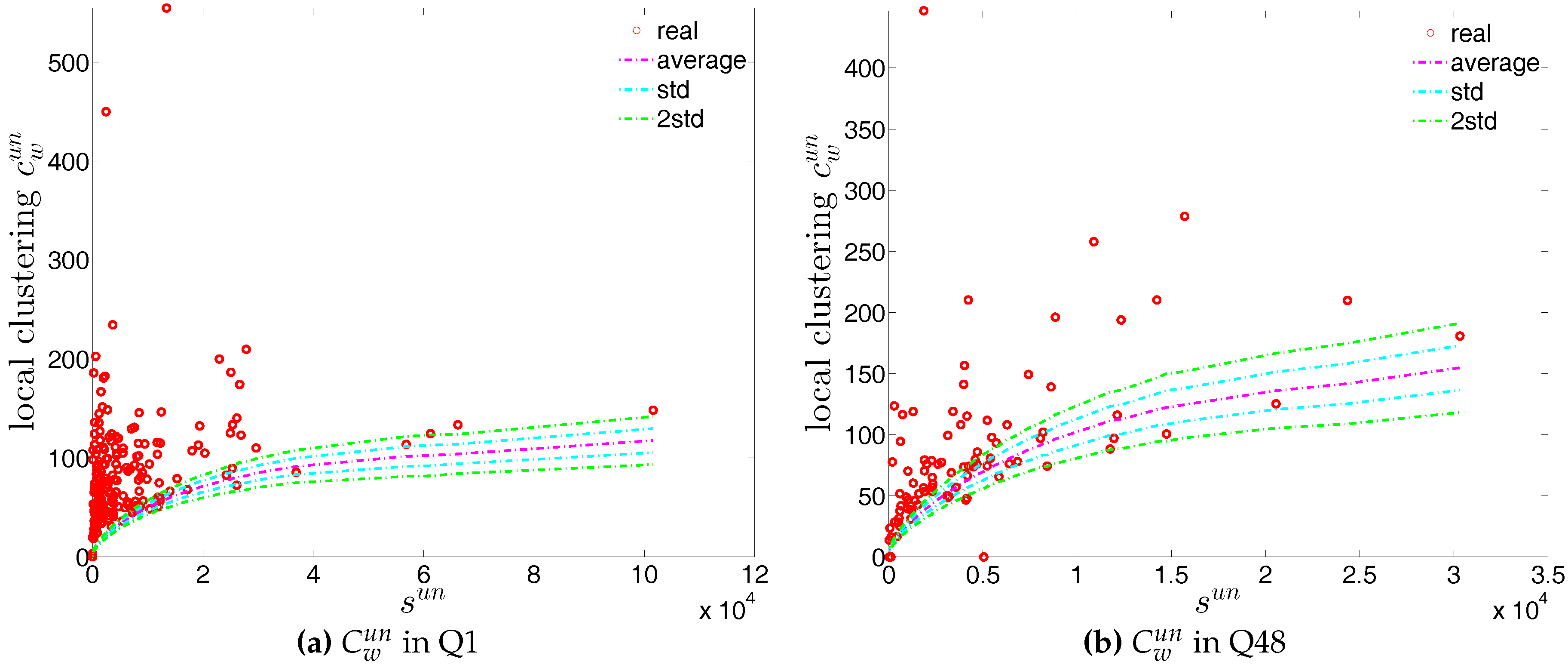
Local weighted clustering coefficients in the observed e-MID network and in the UWCM, in Q1 and Q48.
Figure 44.
Local weighted clustering coefficients in the observed e-MID network and in the UWCM, in Q1 and Q48.
Figure 45.
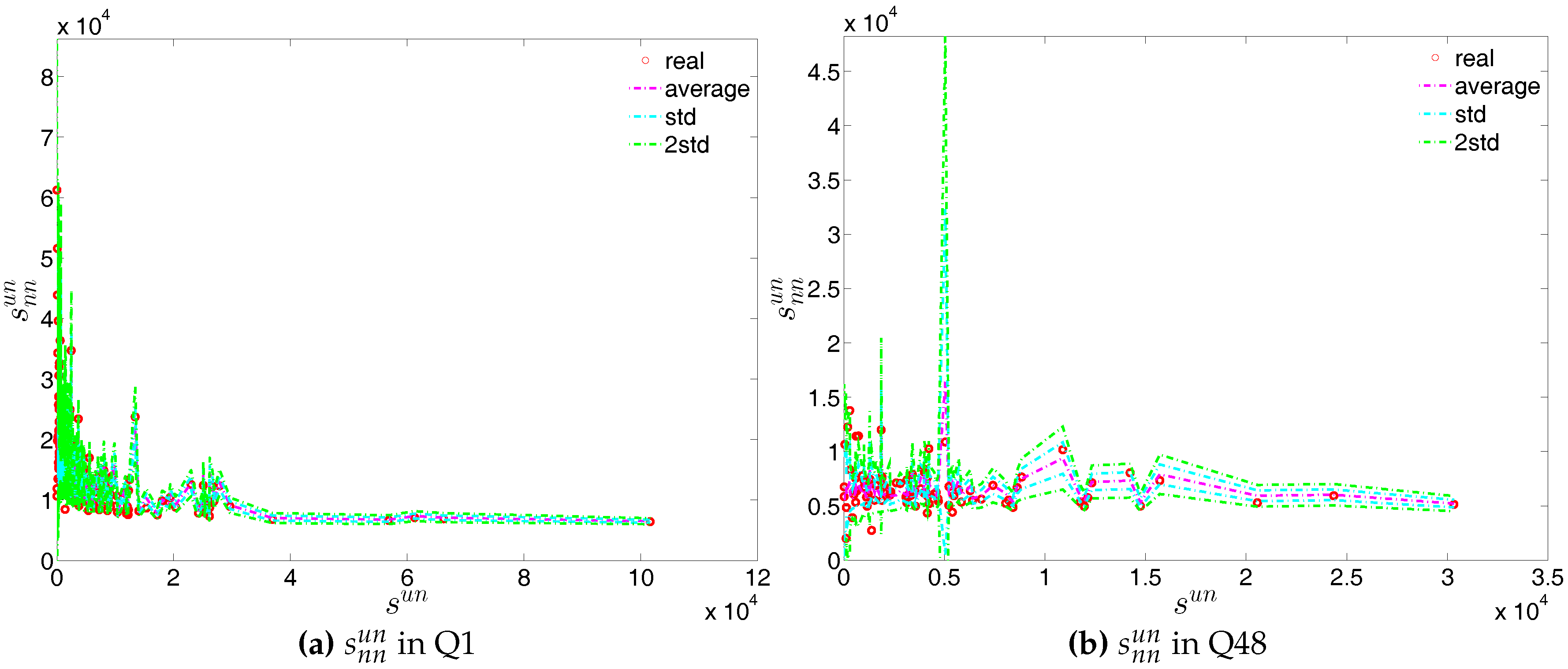
ANNS in the observed e-MID network and in the UECM, in Q1 and Q48.
Figure 45.
ANNS in the observed e-MID network and in the UECM, in Q1 and Q48.
Figure 46.
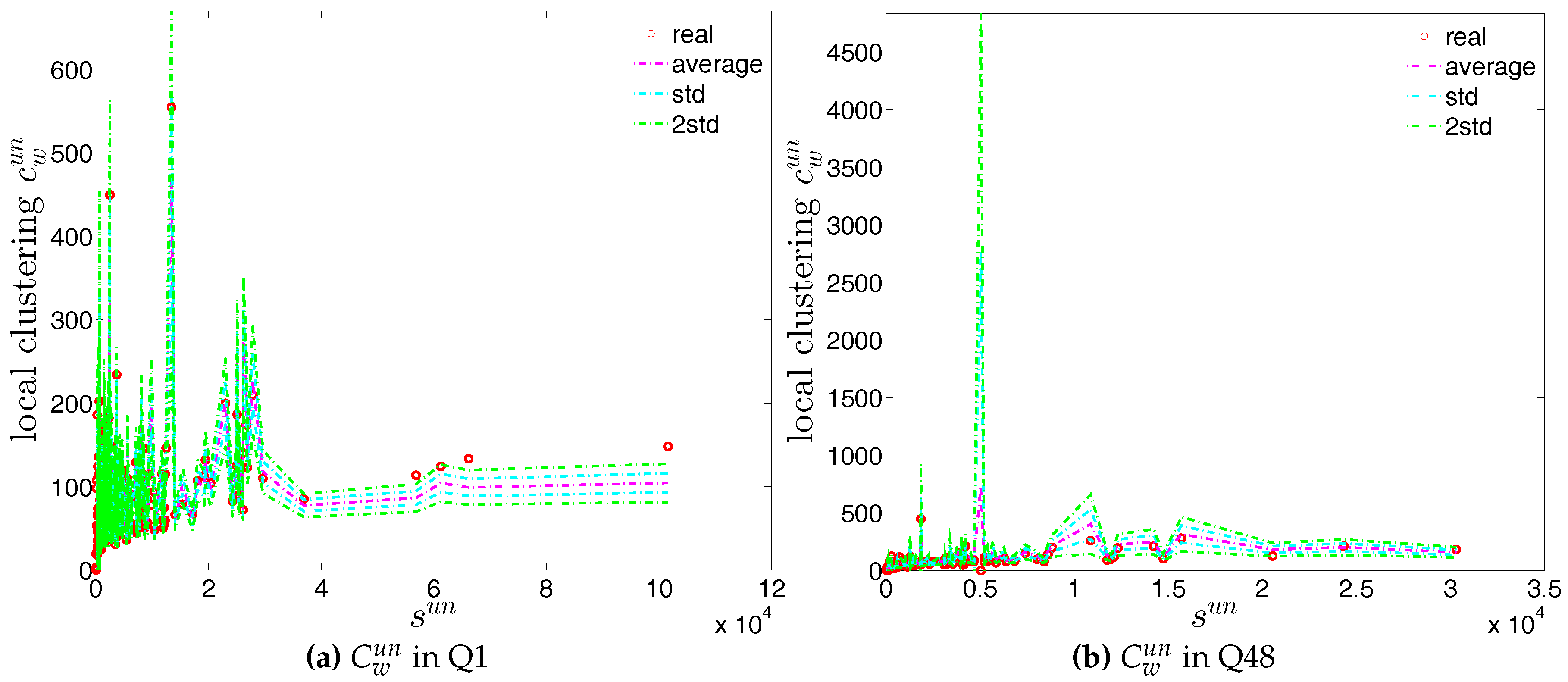
Local weighted clustering coefficients in the observed e-MID network and in the UECM, in Q1 and Q48.
Figure 46.
Local weighted clustering coefficients in the observed e-MID network and in the UECM, in Q1 and Q48.
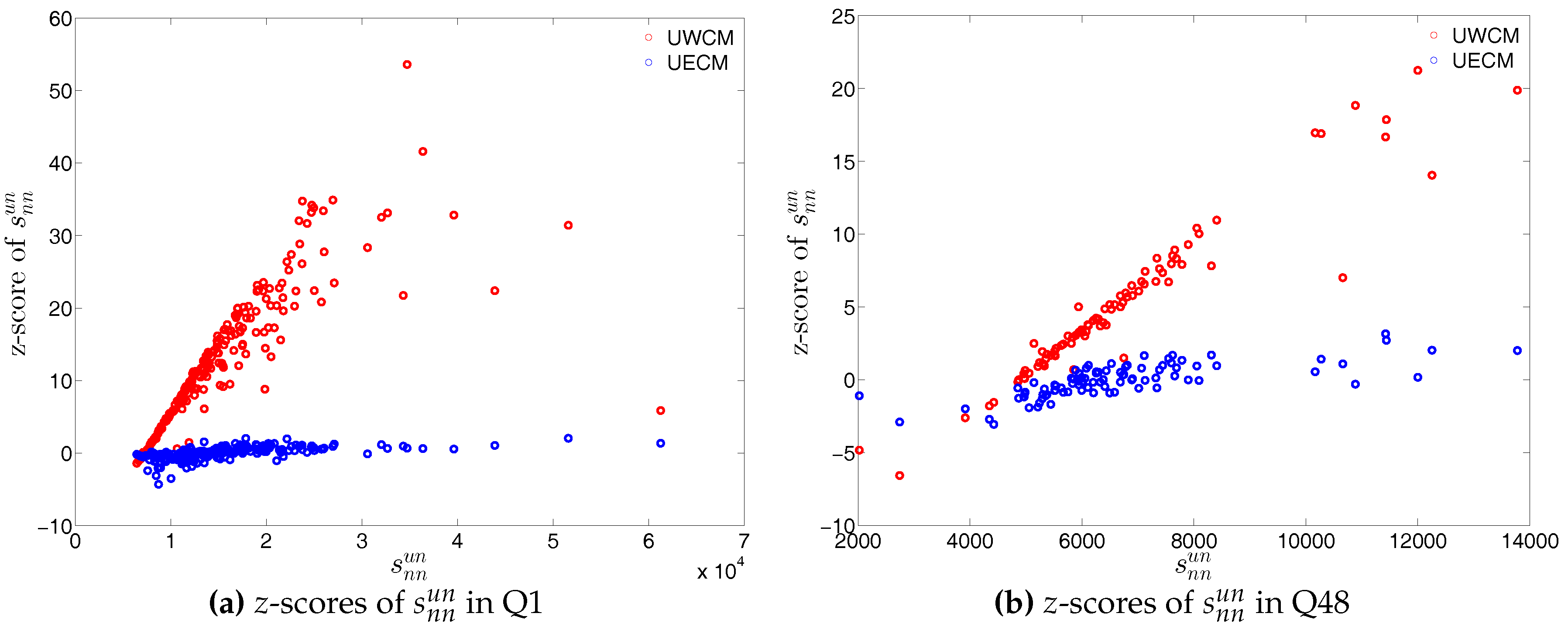
Figure 47.
z-scores of vs. in the UWCM and the UECM, in Q1 and in Q48. Panel (a) for z-scores of in Q1; panel (b) for z-scores of in Q48.
Figure 47.
z-scores of vs. in the UWCM and the UECM, in Q1 and in Q48. Panel (a) for z-scores of in Q1; panel (b) for z-scores of in Q48.
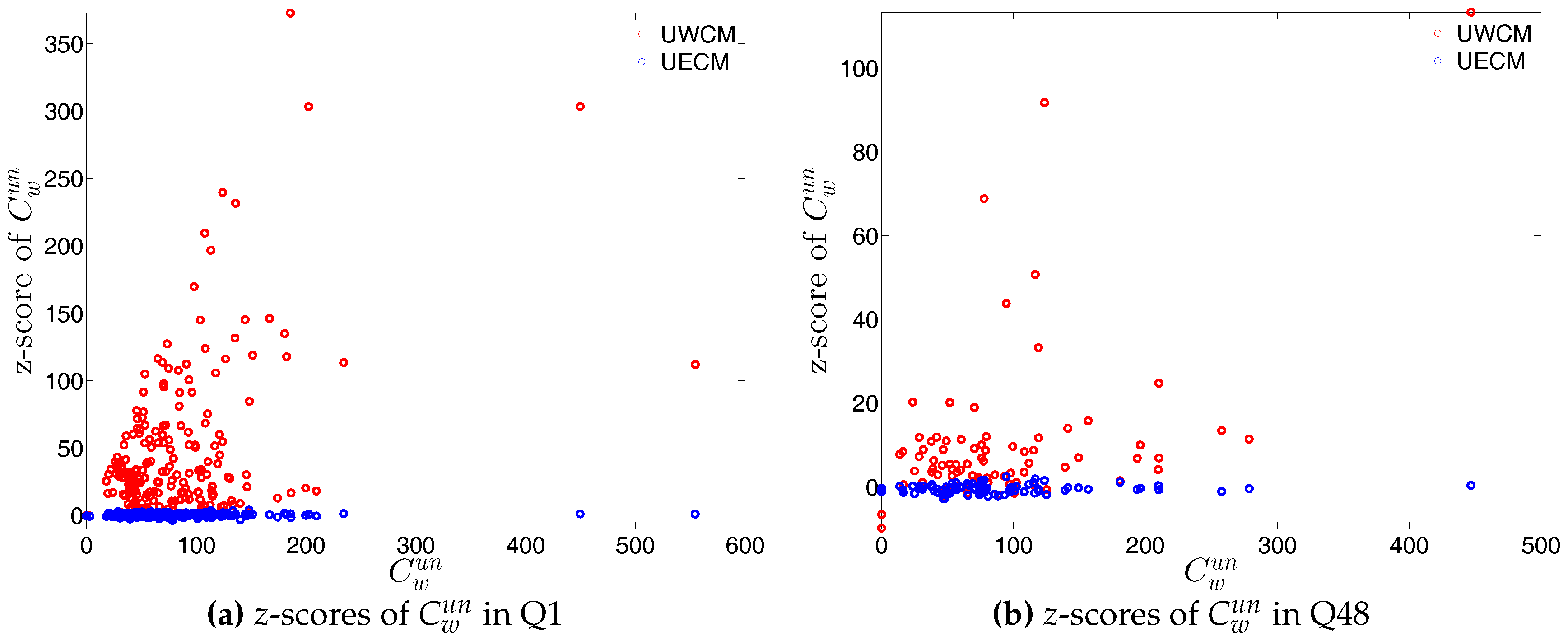
Figure 48.
z-scores of vs. in the UWCM and the UECM. (a) for z-scores of in Q1; (b) for z-scores of in Q48.
Figure 48.
z-scores of vs. in the UWCM and the UECM. (a) for z-scores of in Q1; (b) for z-scores of in Q48.
Figure 49.
Evolution of (a) ; (b) ; and (c) in the observed e-MID network and in the UWCM.
Figure 49.
Evolution of (a) ; (b) ; and (c) in the observed e-MID network and in the UWCM.
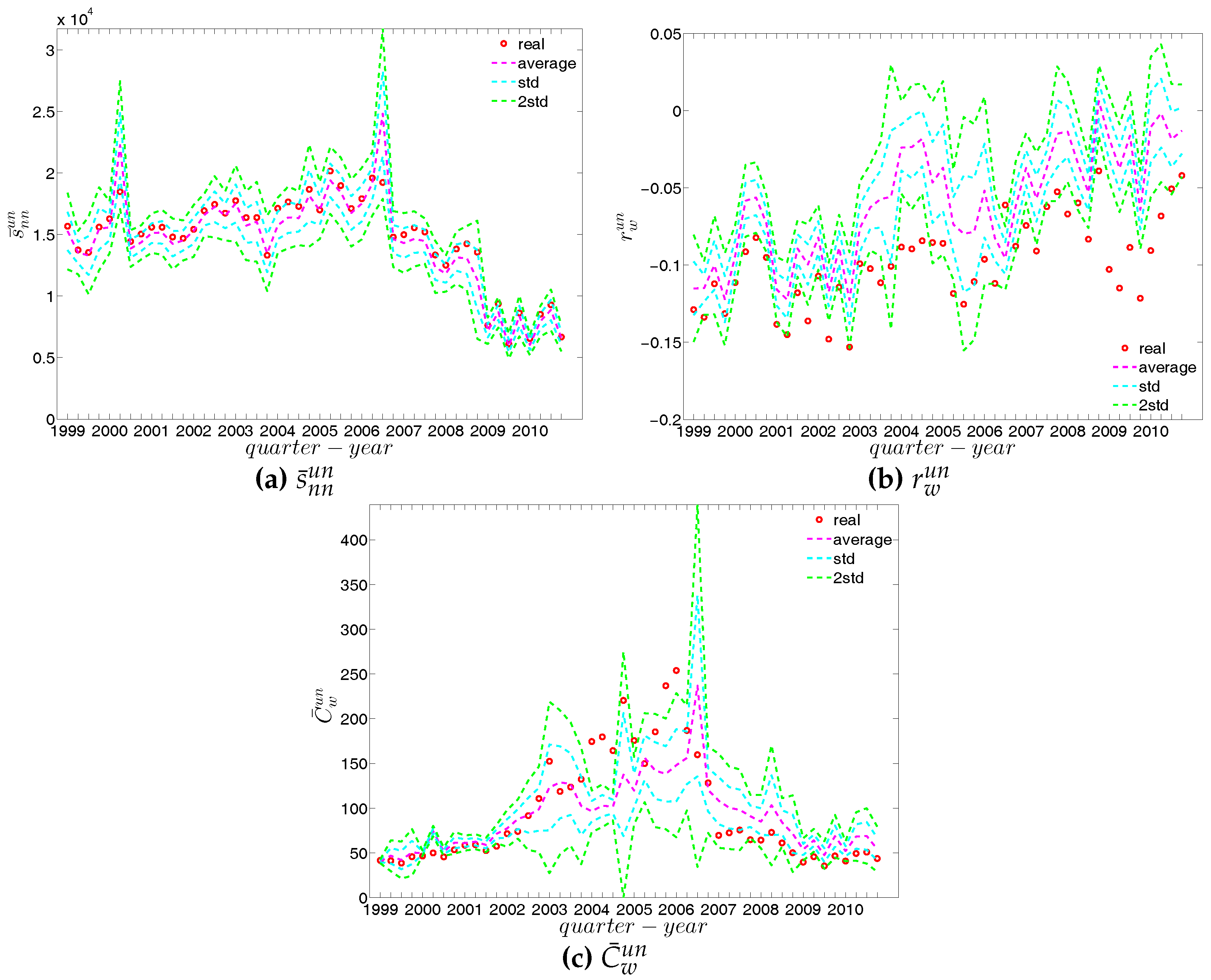
Figure 50.
Evolution of (a) ; (b) ; and (c) in the observed e-MID network and in the UECM.
Figure 50.
Evolution of (a) ; (b) ; and (c) in the observed e-MID network and in the UECM.
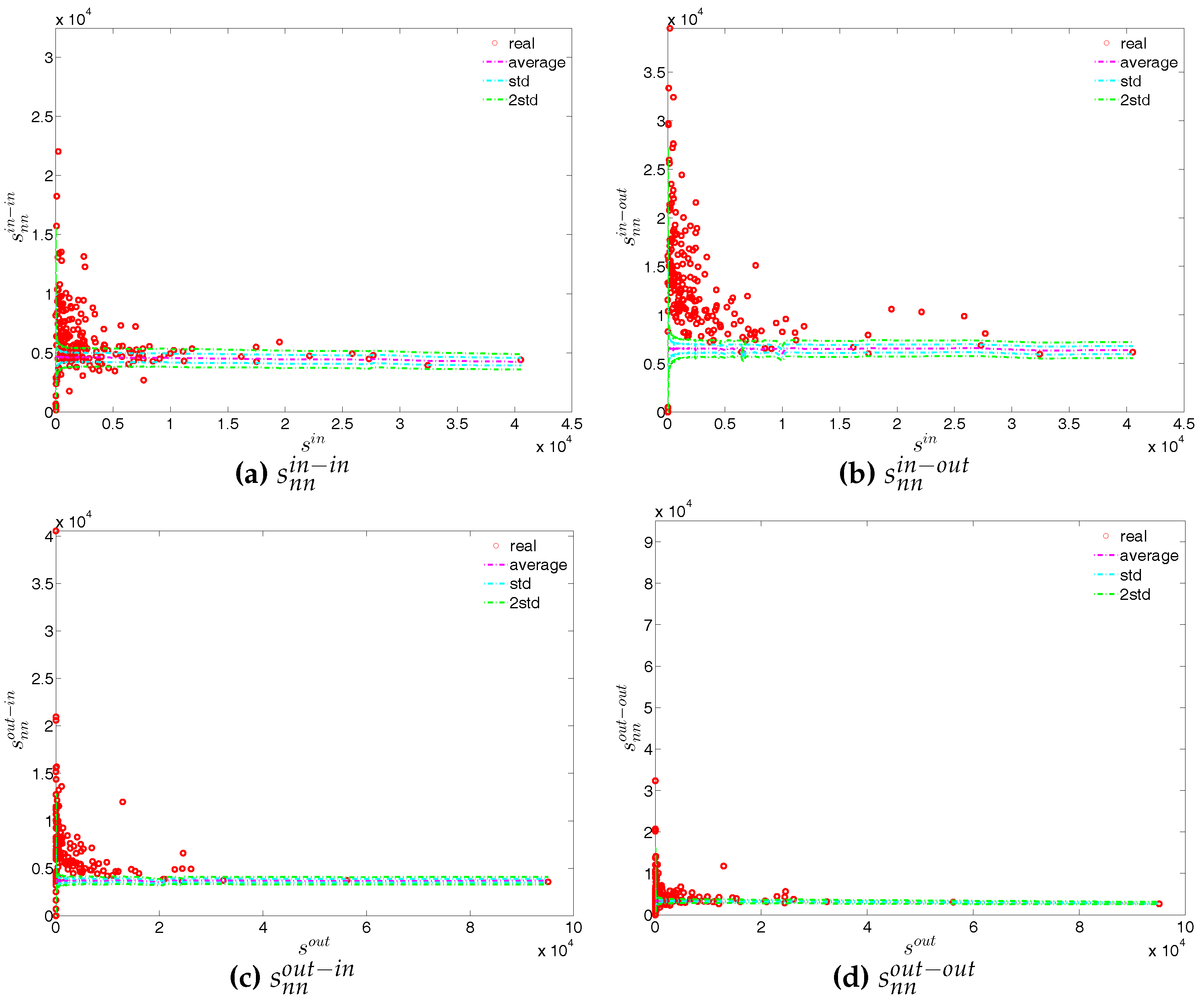
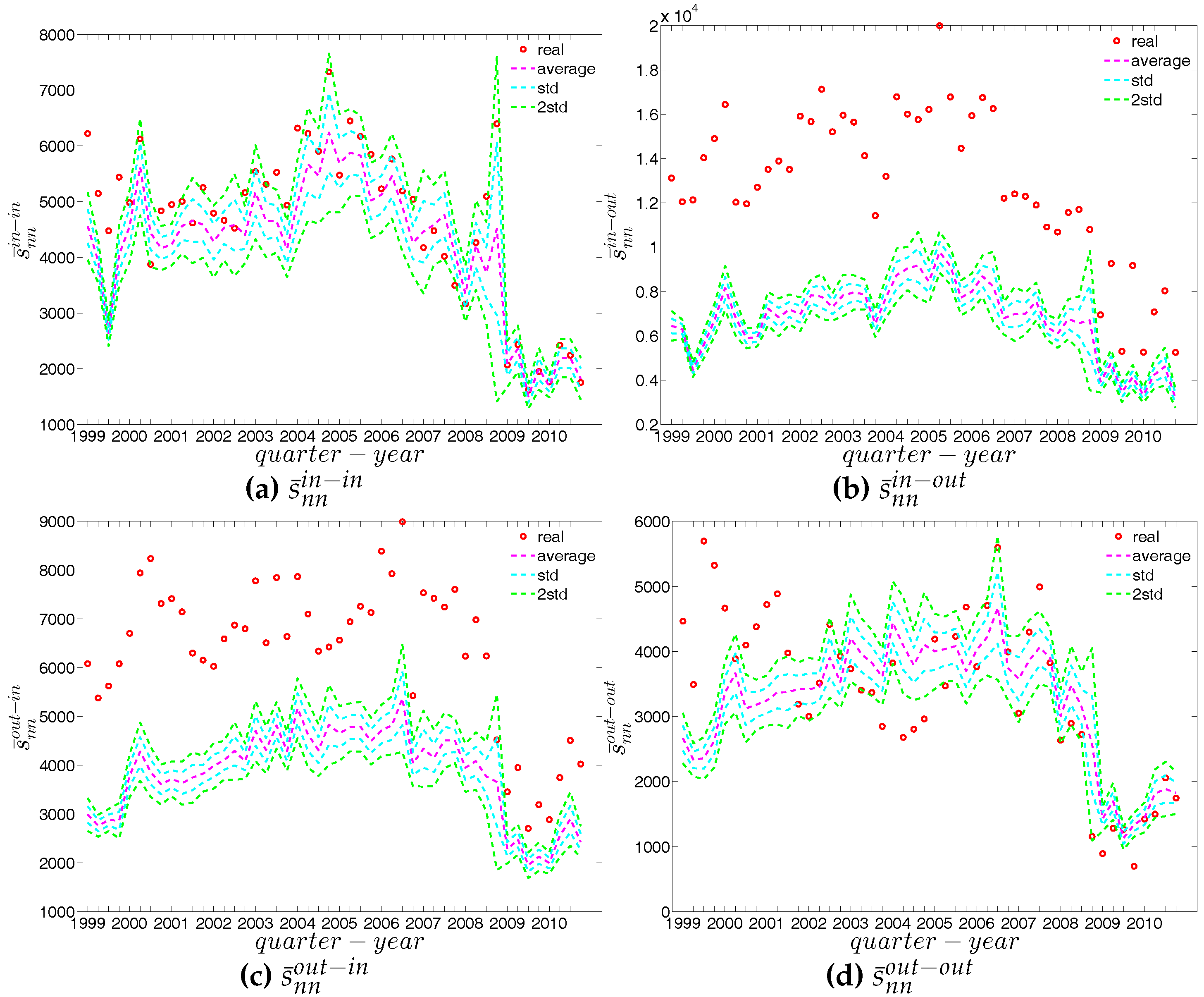
Figure 51.
ANNSs in the observed e-MID network and in the DWCM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 51.
ANNSs in the observed e-MID network and in the DWCM, in Q1. (a) ; (b) ; (c) ; (d) .
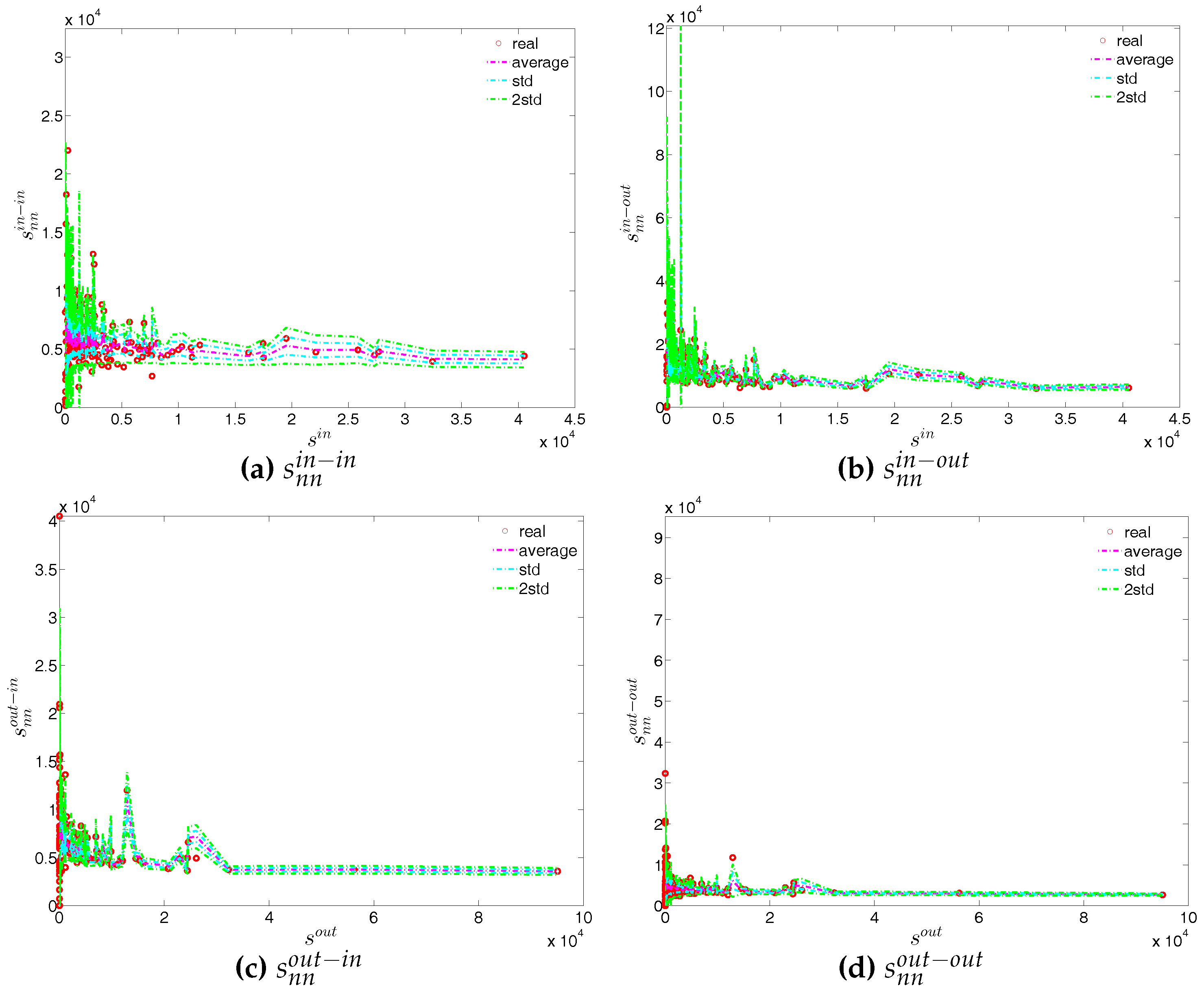
Figure 52.
ANNSs in the observed e-MID network and in the DWCM, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 52.
ANNSs in the observed e-MID network and in the DWCM, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 53.
ANNSs in the observed e-MID network and in the DECM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 53.
ANNSs in the observed e-MID network and in the DECM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 54.
ANNSs in the observed e-MID network and in the DECM, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 54.
ANNSs in the observed e-MID network and in the DECM, in Q48. (a) ; (b) ; (c) ; (d) .
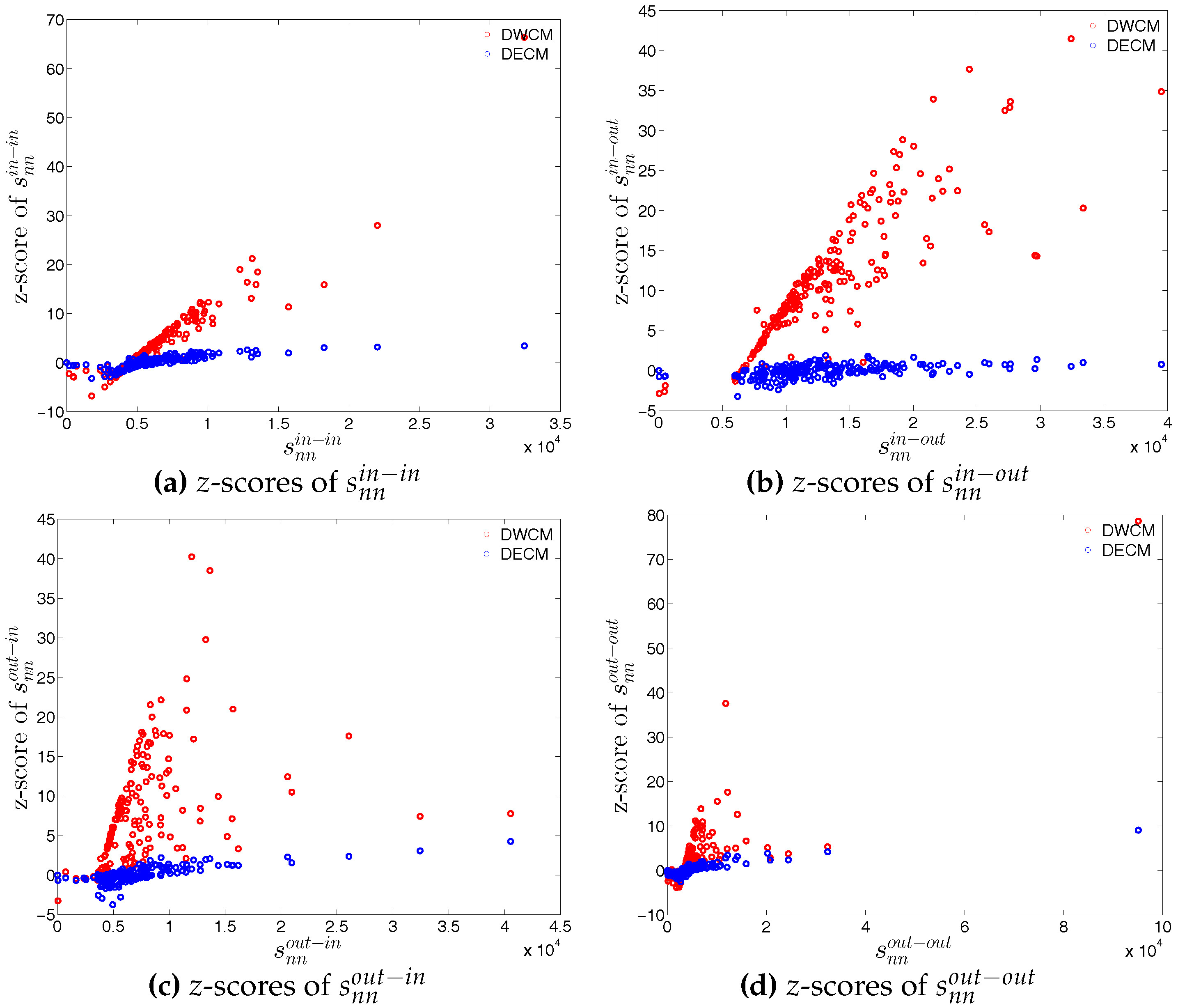
Figure 55.
z-scores of ANNSs vs. ANNSs, in the DWCM and DECM models, in Q1. (a) for ; (b) for ; (c) for ; (d) for .
Figure 55.
z-scores of ANNSs vs. ANNSs, in the DWCM and DECM models, in Q1. (a) for ; (b) for ; (c) for ; (d) for .
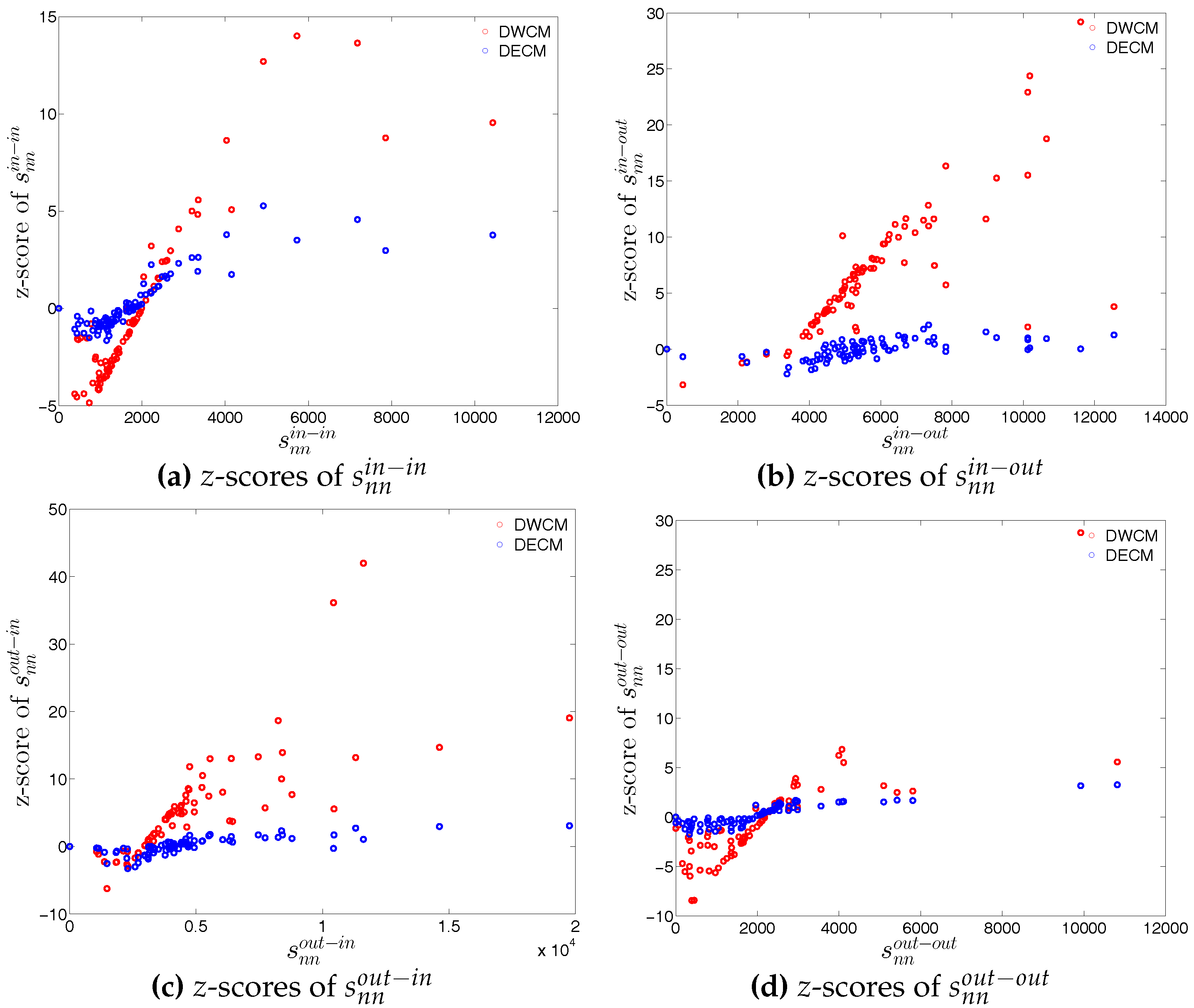
Figure 56.
z-scores of ANNSs vs. ANNSs, in the DWCM and DECM models, in Q48. (a) for ; (b) for ; (c) for ; (d) for .
Figure 56.
z-scores of ANNSs vs. ANNSs, in the DWCM and DECM models, in Q48. (a) for ; (b) for ; (c) for ; (d) for .
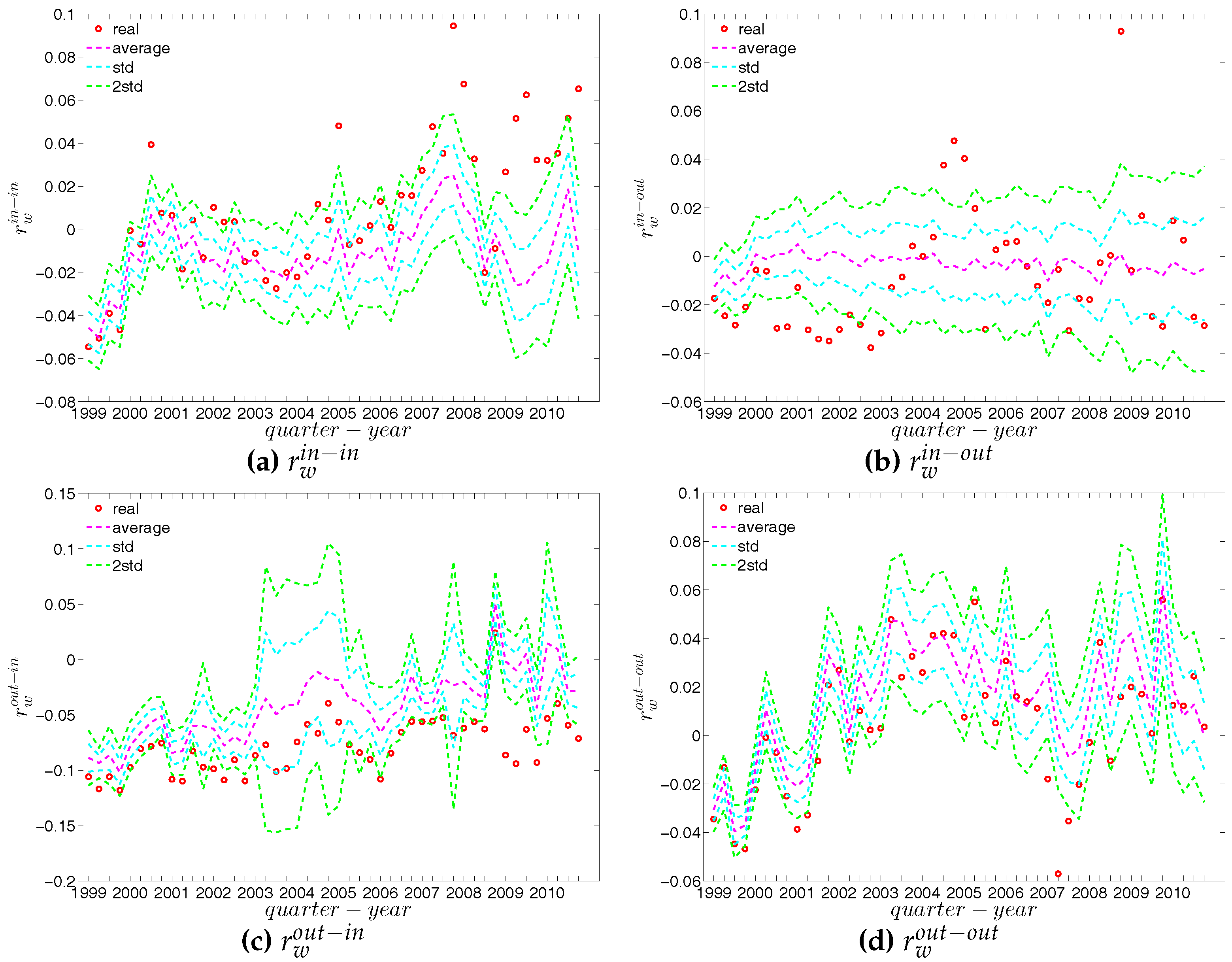
Figure 57.
Local weighted clustering coefficients in the observed e-MID network and in the DWCM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 57.
Local weighted clustering coefficients in the observed e-MID network and in the DWCM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 58.
Local weighted clustering coefficients in the observed e-MID network and in the DWCM, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 58.
Local weighted clustering coefficients in the observed e-MID network and in the DWCM, in Q48. (a) ; (b) ; (c) ; (d) .
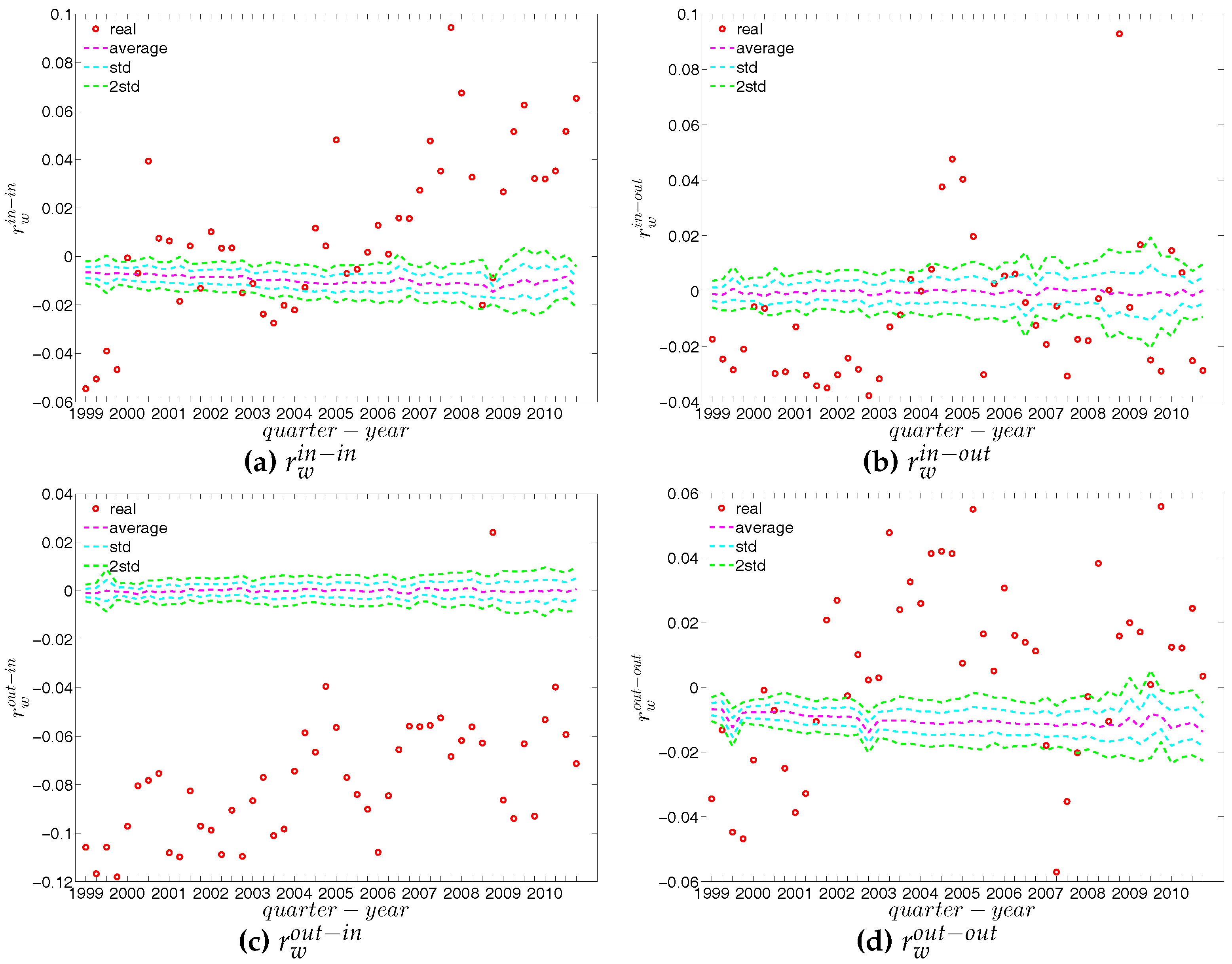
Figure 59.
Local weighted clustering coefficients in the observed e-MID network and in the DECM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 59.
Local weighted clustering coefficients in the observed e-MID network and in the DECM, in Q1. (a) ; (b) ; (c) ; (d) .
Figure 60.
Local weighted clustering coefficients in the observed e-MID network and in the DECM, in Q48. (a) ; (b) ; (c) ; (d) .
Figure 60.
Local weighted clustering coefficients in the observed e-MID network and in the DECM, in Q48. (a) ; (b) ; (c) ; (d) .
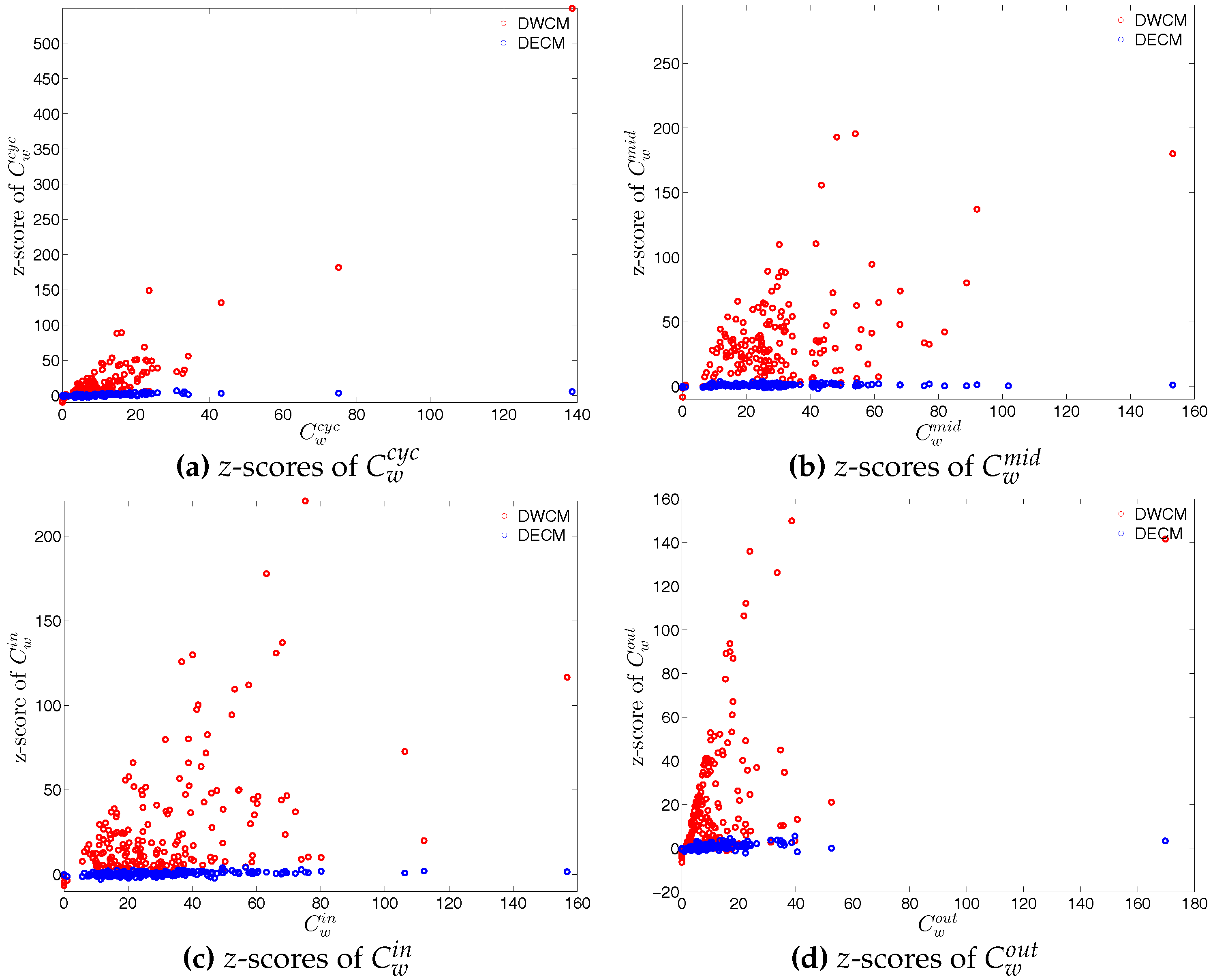
Figure 61.
z-scores of vs. , evaluated under the DWCM and DECM models, in Q1. (a) for ; (b) for ; (c) for ; (d) for .
Figure 61.
z-scores of vs. , evaluated under the DWCM and DECM models, in Q1. (a) for ; (b) for ; (c) for ; (d) for .
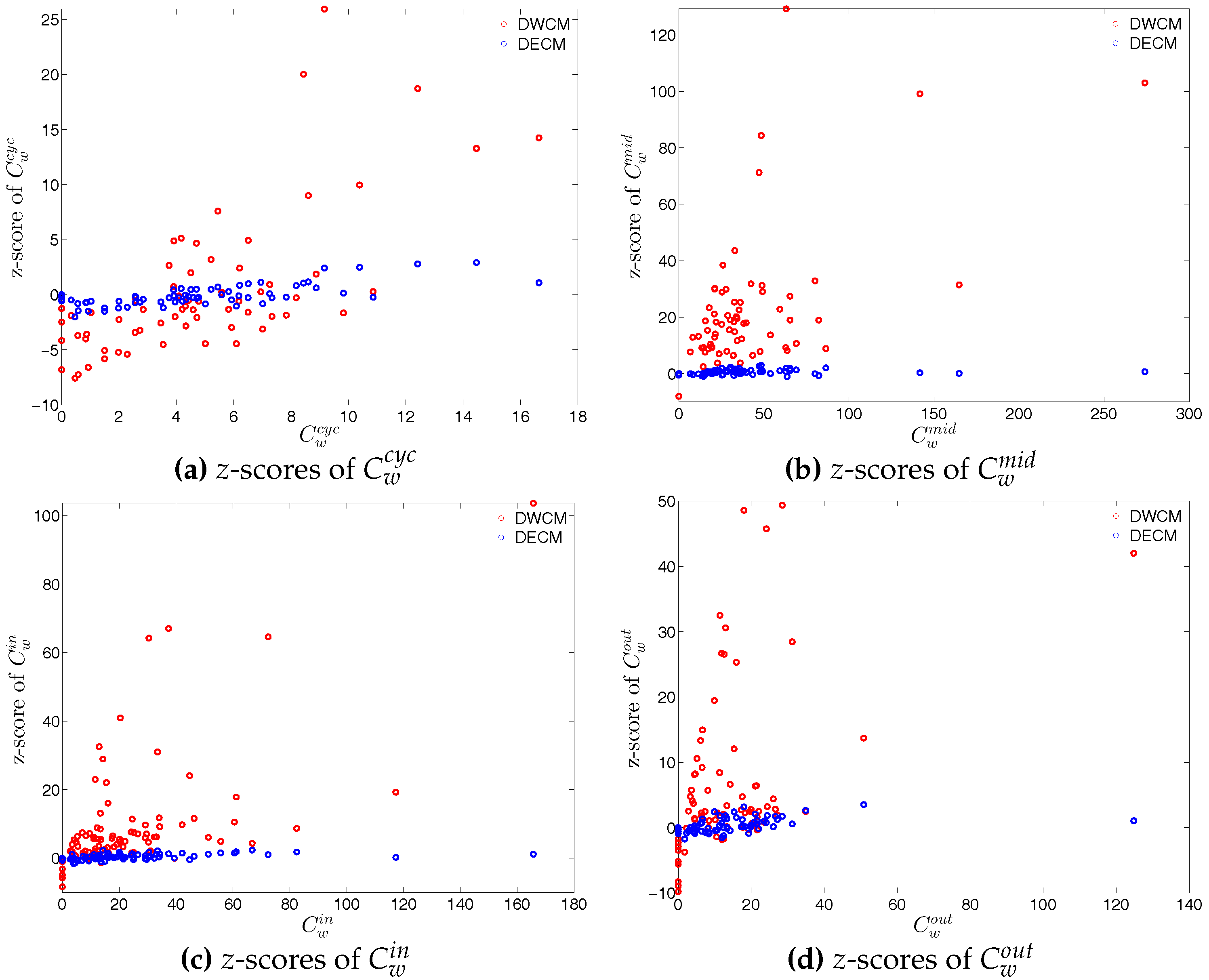
Figure 62.
z-scores of vs. , evaluated under the DWCM and DECM models, in Q48. (a) for ; (b) for ; (c) for ; (d) for .
Figure 62.
z-scores of vs. , evaluated under the DWCM and DECM models, in Q48. (a) for ; (b) for ; (c) for ; (d) for .
Figure 63.
Evolution of the averages of ANNSs in the observed e-MID network and in the DWCM. (a) ; (b) ; (c) ; (d) .
Figure 63.
Evolution of the averages of ANNSs in the observed e-MID network and in the DWCM. (a) ; (b) ; (c) ; (d) .
Figure 64.
Evolution of the global weighted assortativity indicators in the observed e-MID network and in the DWCM. (a) ; (b) ; (c) ; (d) .
Figure 64.
Evolution of the global weighted assortativity indicators in the observed e-MID network and in the DWCM. (a) ; (b) ; (c) ; (d) .
Figure 65.
Evolution of the averages of local weighted clustering coefficients in the observed e-MID network and in the DWCM. (a) ; (b) ; (c) ; (d) .
Figure 65.
Evolution of the averages of local weighted clustering coefficients in the observed e-MID network and in the DWCM. (a) ; (b) ; (c) ; (d) .
Figure 66.
Evolution of the averages of ANNSs in the observed e-MID network and in the DECM. (a) ; (b) ; (c) ; (d) .
Figure 66.
Evolution of the averages of ANNSs in the observed e-MID network and in the DECM. (a) ; (b) ; (c) ; (d) .
Figure 67.
Evolution of the global weighted assortativity indicators in the observed e-MID network and in the DECM. (a) ; (b) (b); (c) ; (d) .
Figure 67.
Evolution of the global weighted assortativity indicators in the observed e-MID network and in the DECM. (a) ; (b) (b); (c) ; (d) .
Figure 68.
Evolution of the averages of local weighted clustering coefficients in the observed e-MID network and in the DECM. (a) ; (b) ; (c) ; (d) .
Figure 68.
Evolution of the averages of local weighted clustering coefficients in the observed e-MID network and in the DECM. (a) ; (b) ; (c) ; (d) .
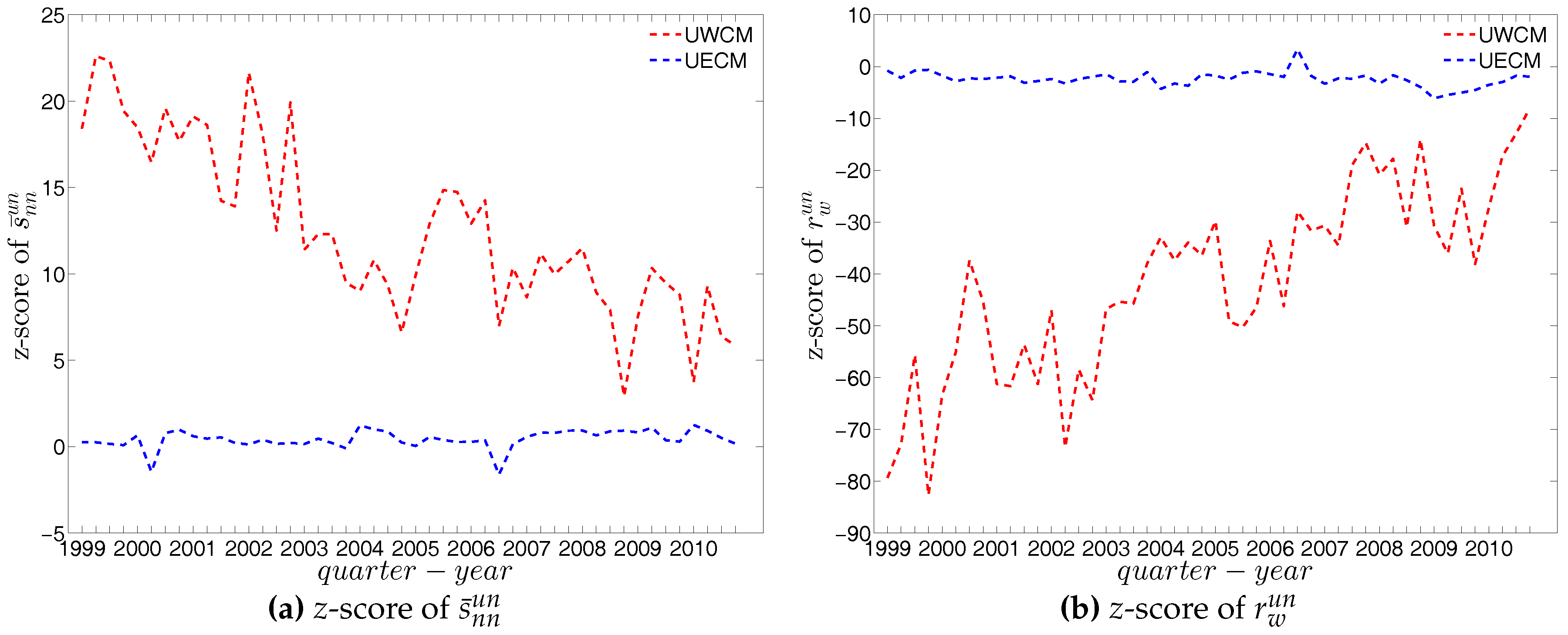
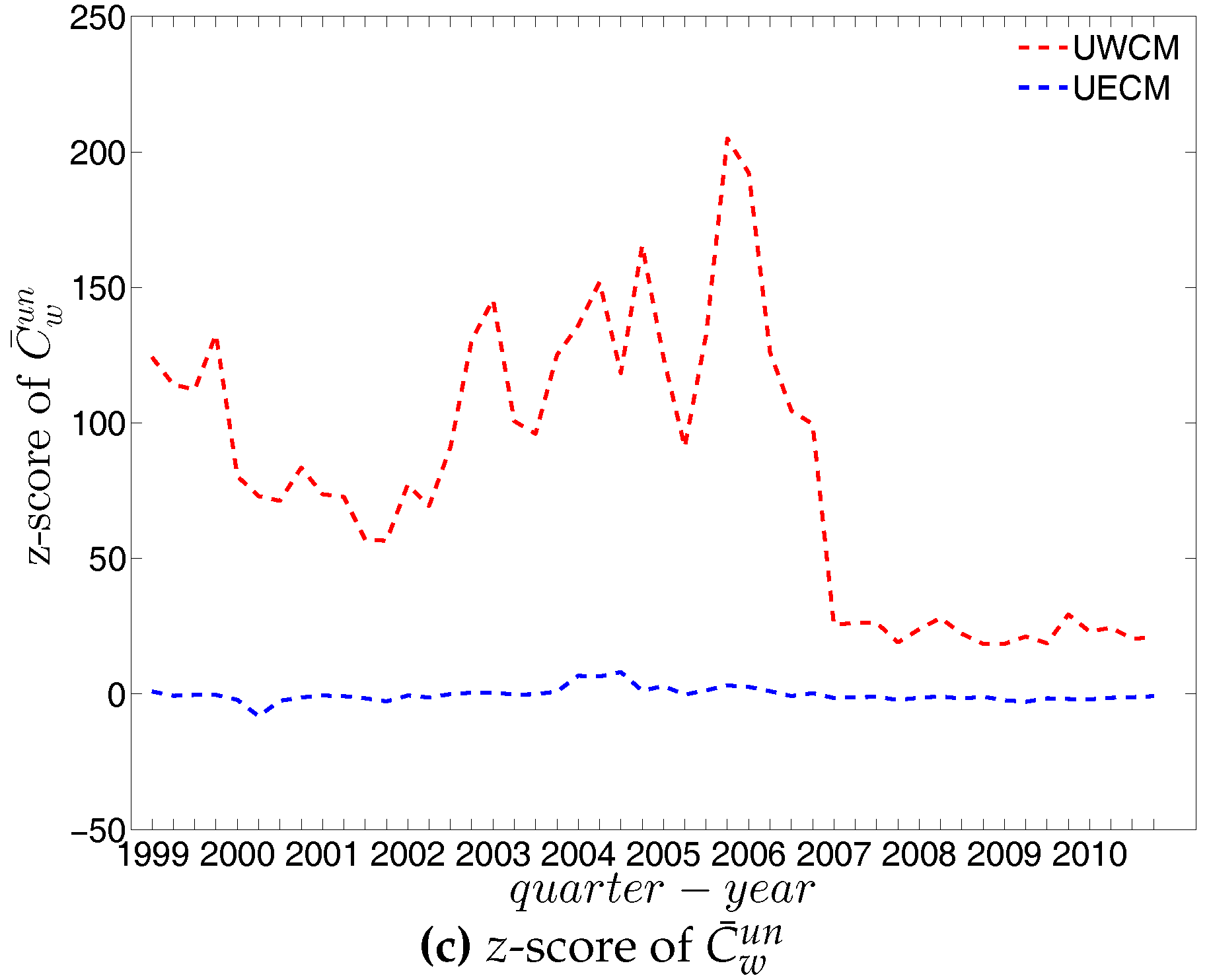
Figure 69.
Evolution of the z-scores for (a) ; (b) ; and (c) evaluated under the UWCM (red dashed lines) and the UECM (blue dashed lines).
Figure 69.
Evolution of the z-scores for (a) ; (b) ; and (c) evaluated under the UWCM (red dashed lines) and the UECM (blue dashed lines).
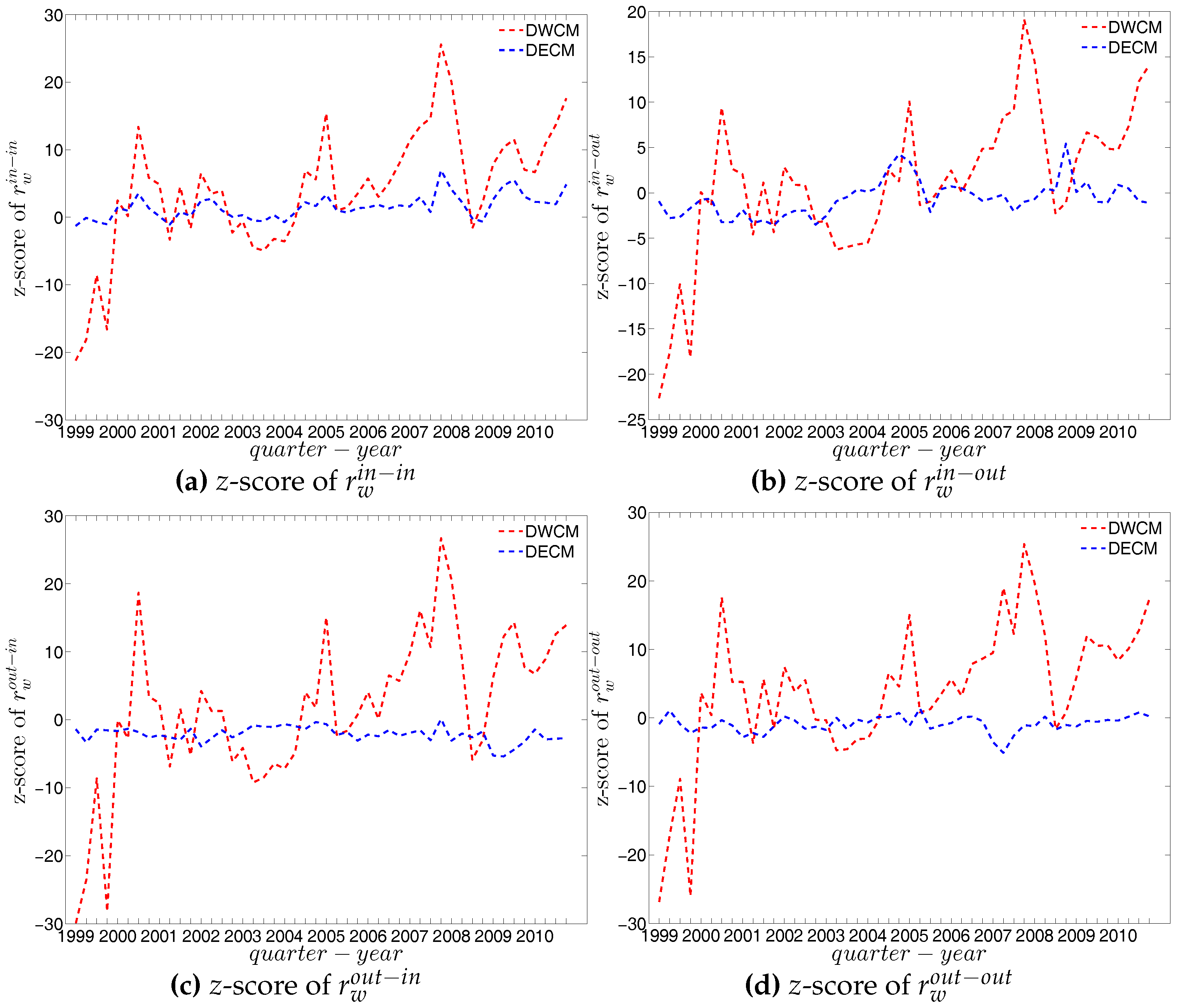
Figure 70.
Evolution of the z-scores for (a) ; (b) ; (c) , and (d) evaluated under the DWCM (red dashed lines) and the DECM (blue dashed lines).
Figure 70.
Evolution of the z-scores for (a) ; (b) ; (c) , and (d) evaluated under the DWCM (red dashed lines) and the DECM (blue dashed lines).
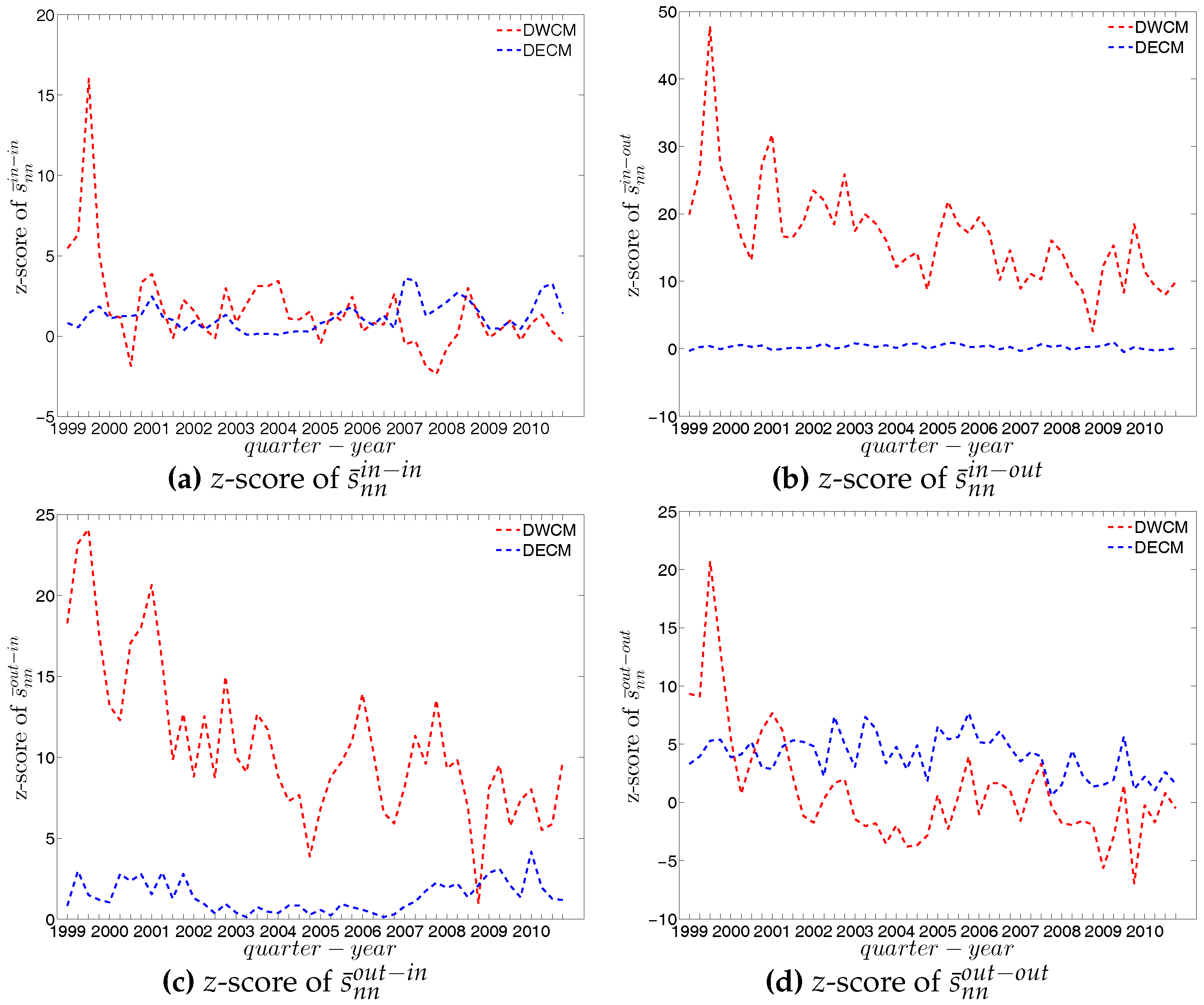
Figure 71.
Evolution of the z-scores for (a) ; (b) ; (c) ; and (d) evaluated under the DWCM (red dashed lines) and the DECM (blue dashed lines).
Figure 71.
Evolution of the z-scores for (a) ; (b) ; (c) ; and (d) evaluated under the DWCM (red dashed lines) and the DECM (blue dashed lines).
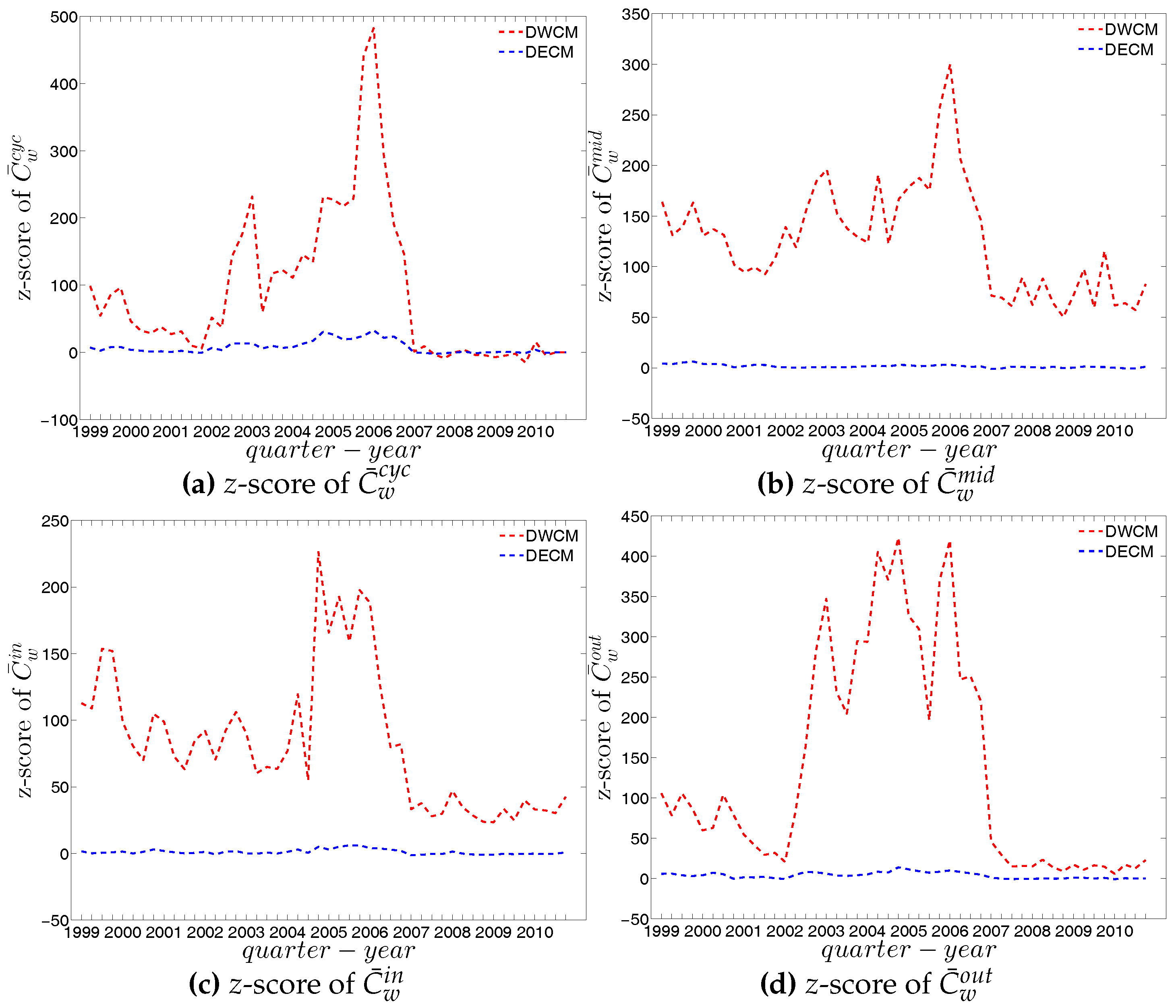
Figure 72.
Evolution of the z-scores for (a) ; (b) ; (c) ; and (d) evaluated under the DWCM (red dashed lines) and the DECM (blue dashed lines).
Figure 72.
Evolution of the z-scores for (a) ; (b) ; (c) ; and (d) evaluated under the DWCM (red dashed lines) and the DECM (blue dashed lines).