Classification of Fractal Signals Using Two-Parameter Non-Extensive Wavelet Entropy
Abstract
:1. Introduction
2. Materials and methods
2.1. The Representation of Fractal Signals by Wavelets
2.2. A Nonextensive Wavelet -Entropy of Fractal Signals
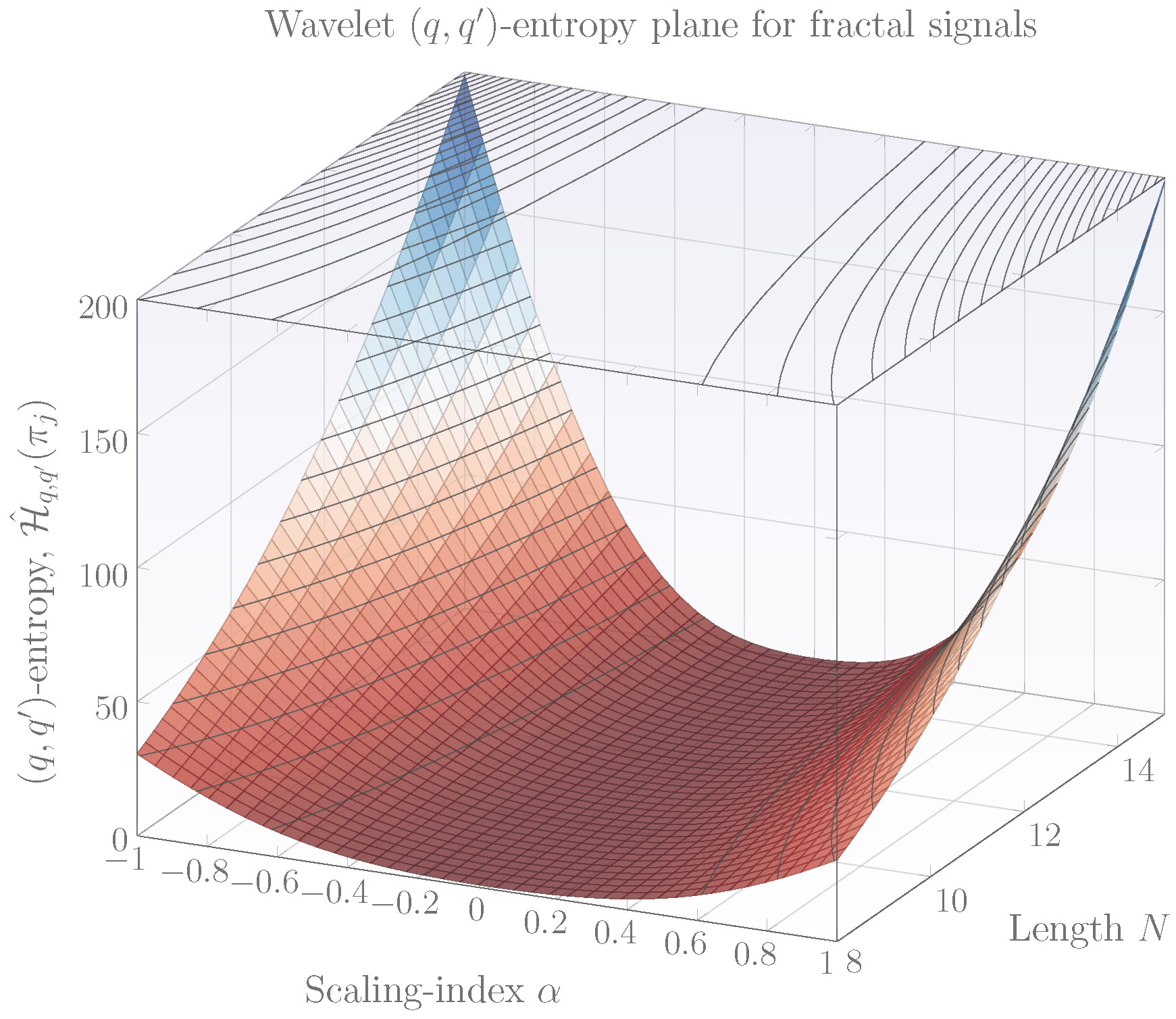
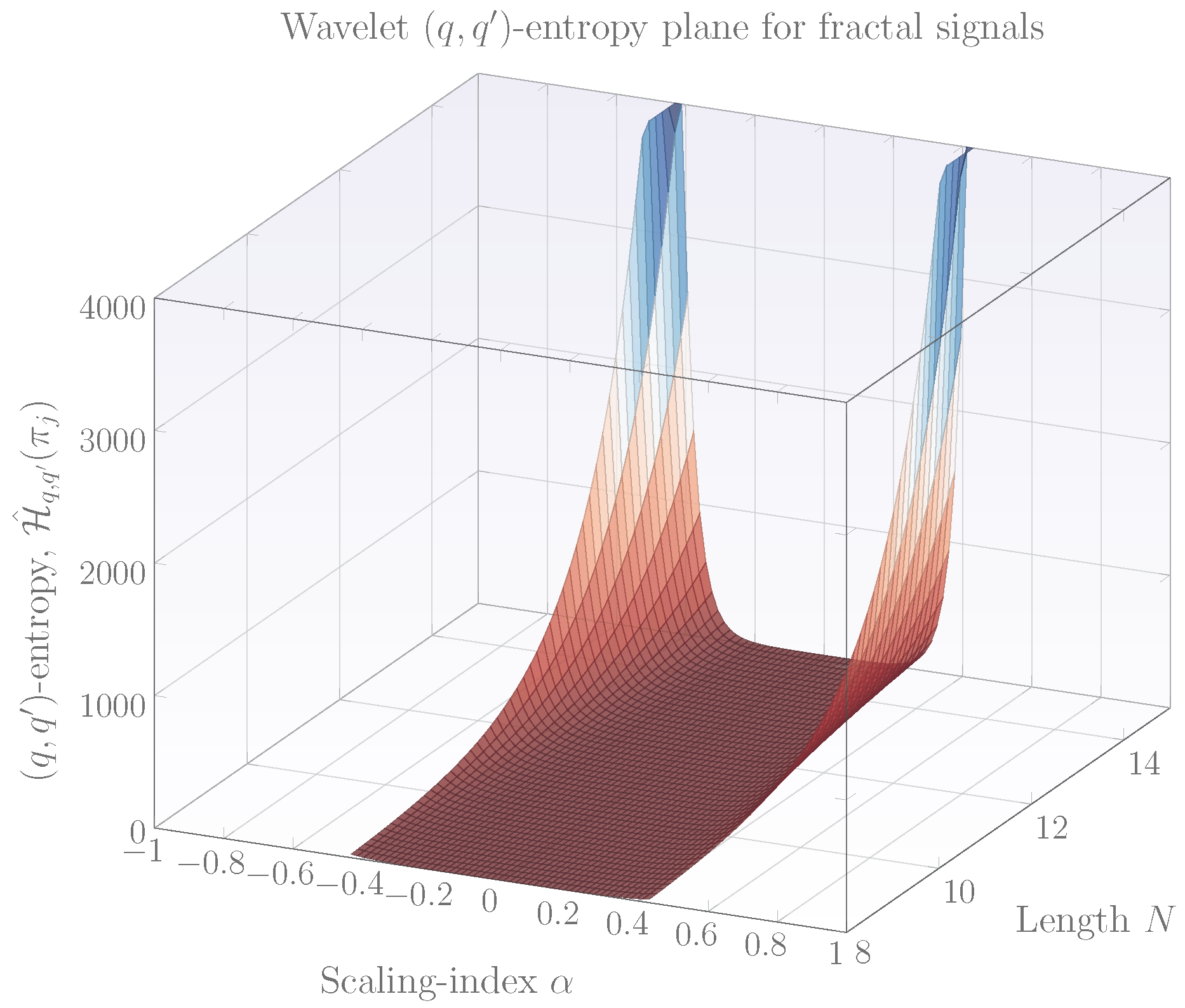
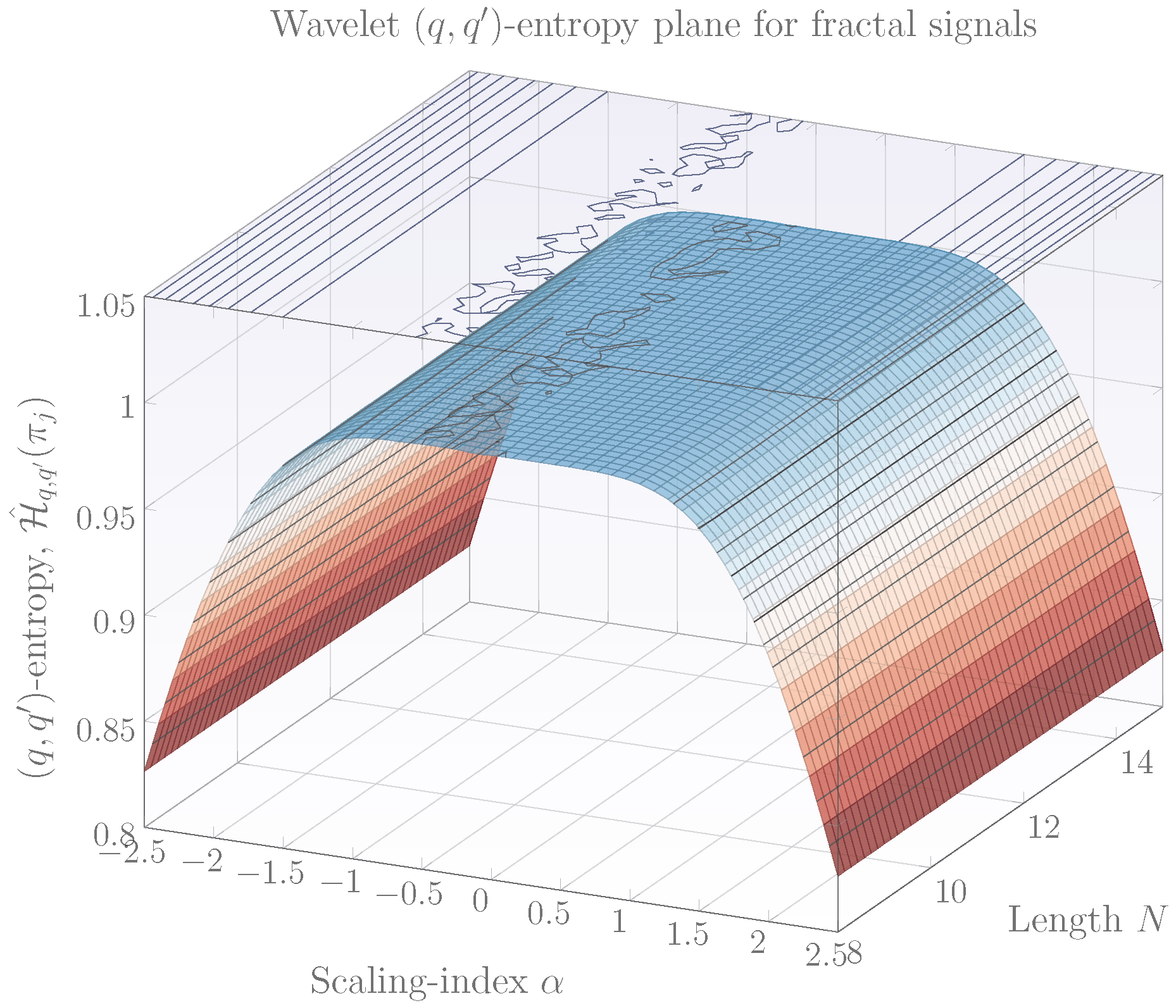
2.3. The Behaviour of Wavelet -Entropy for Various Pairs
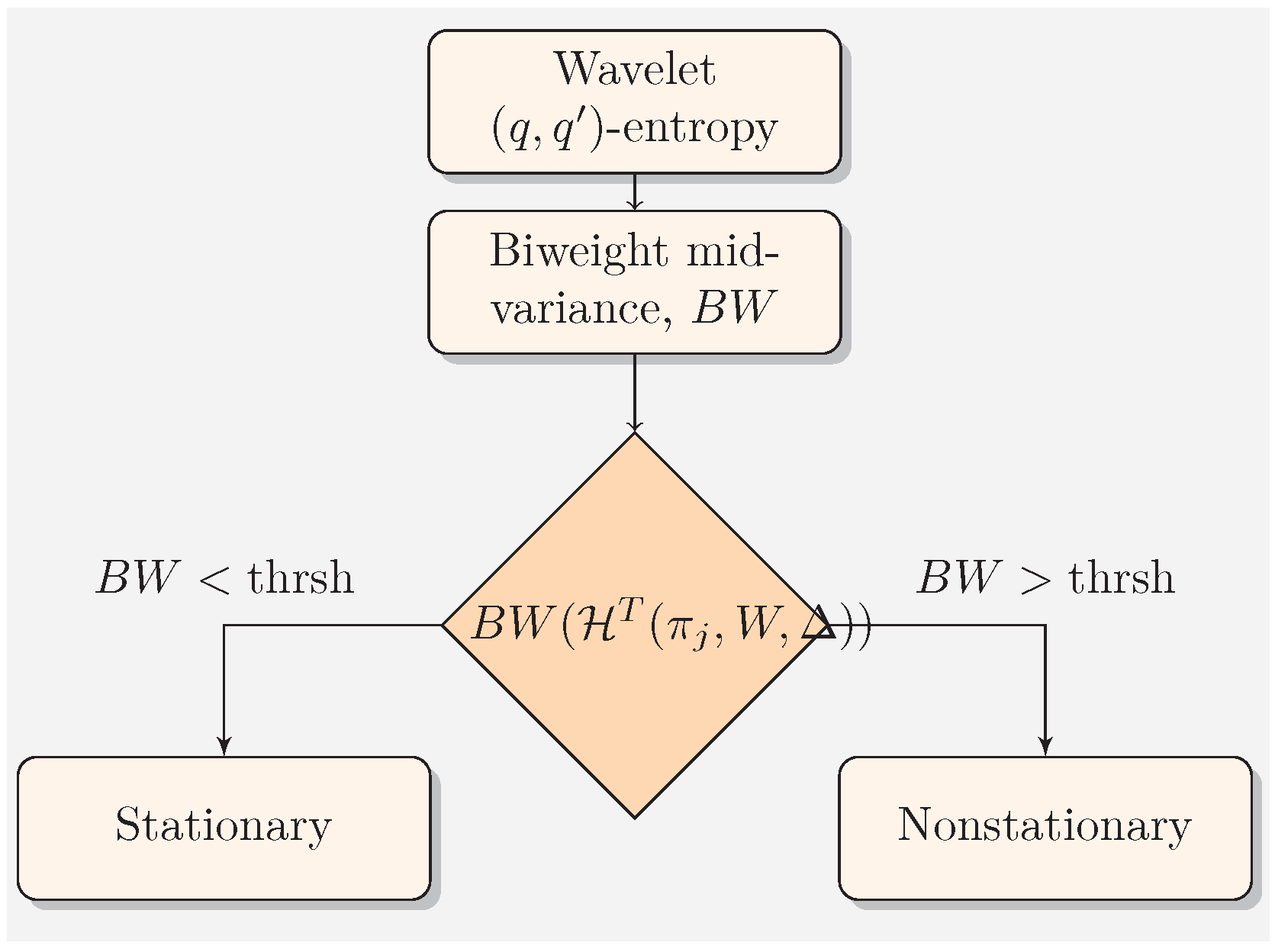
2.4. The Classification of Fractal Signals with Wavelet -Entropy
3. Results
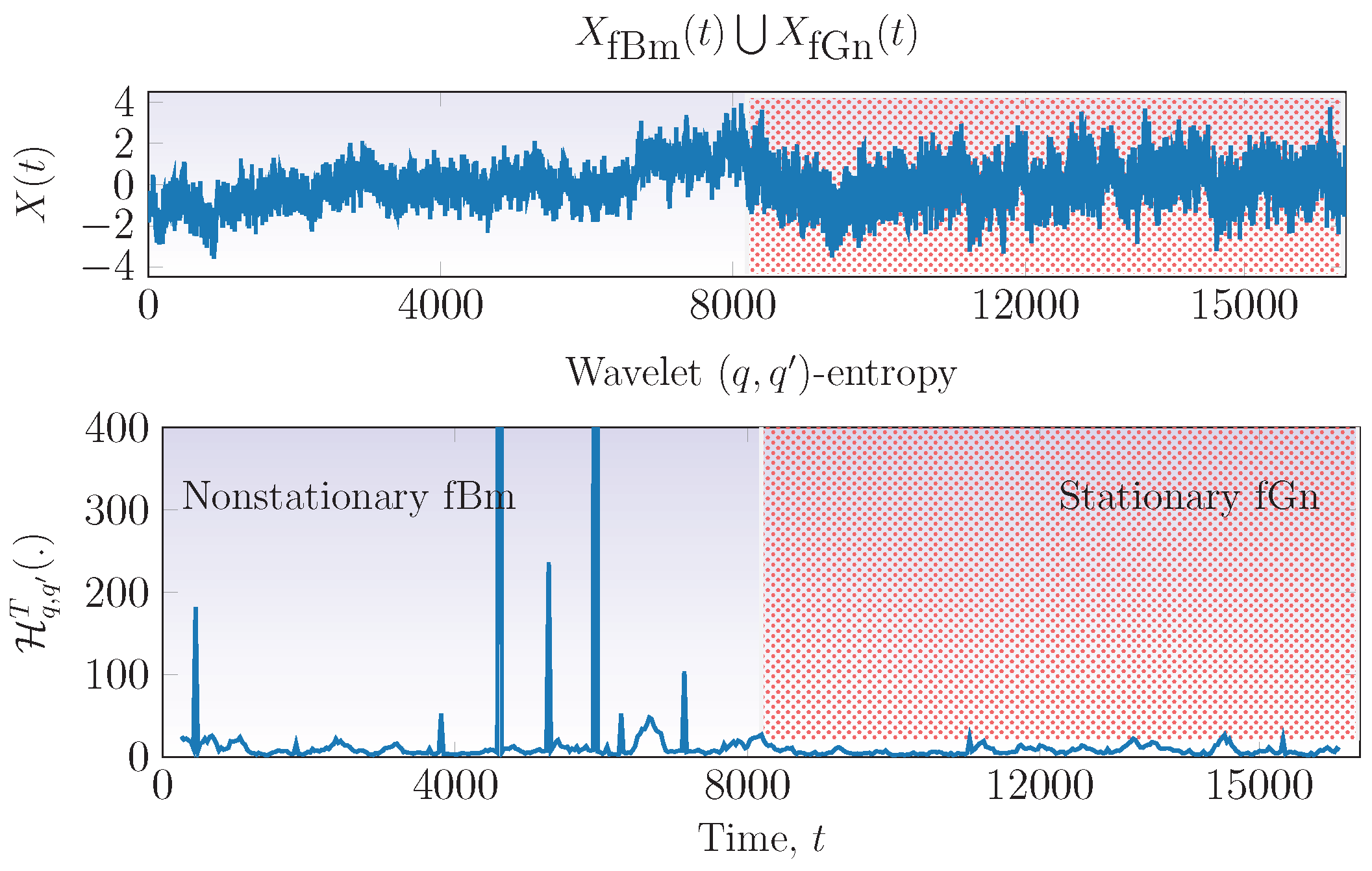
3.1. Experimental Results
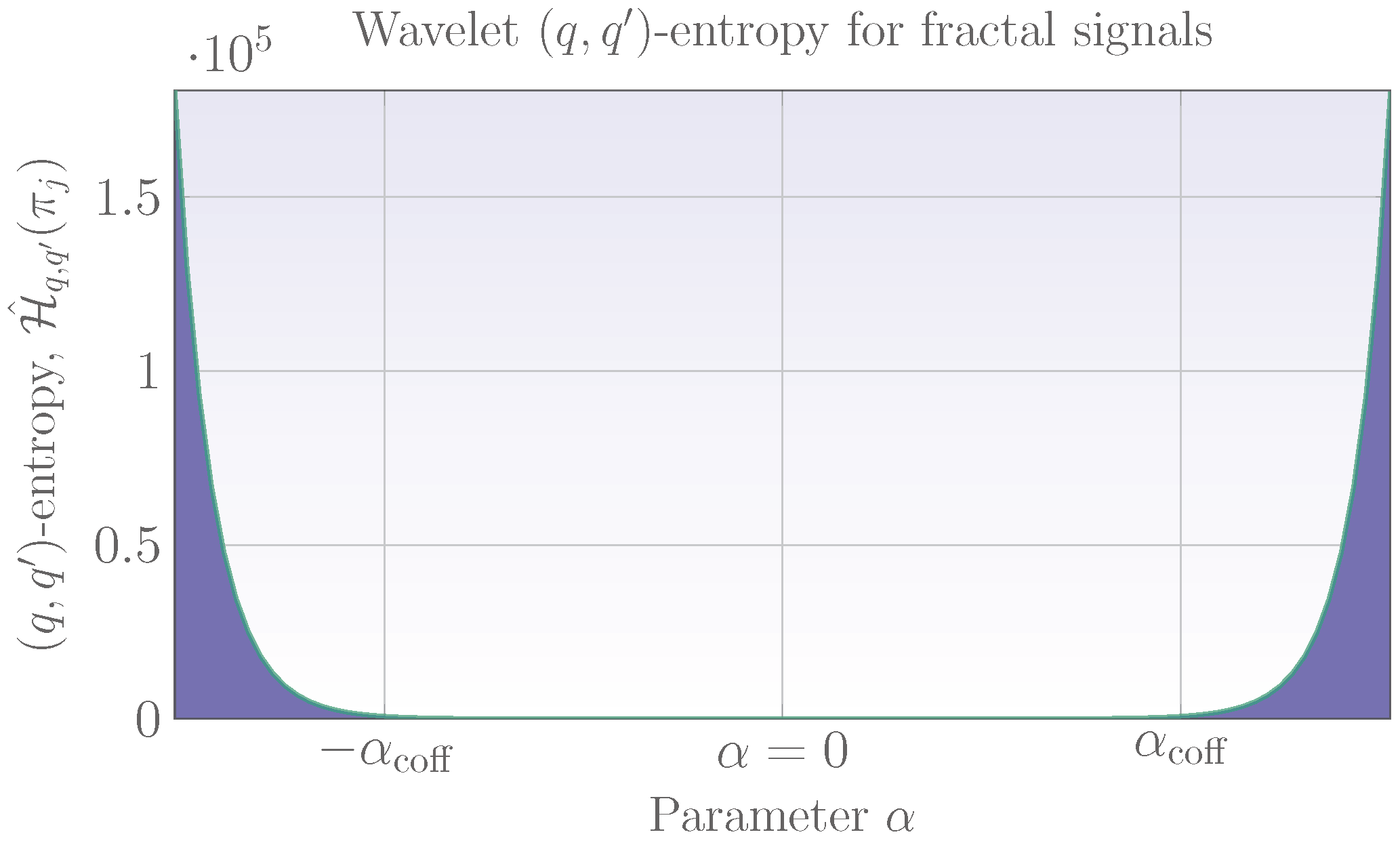
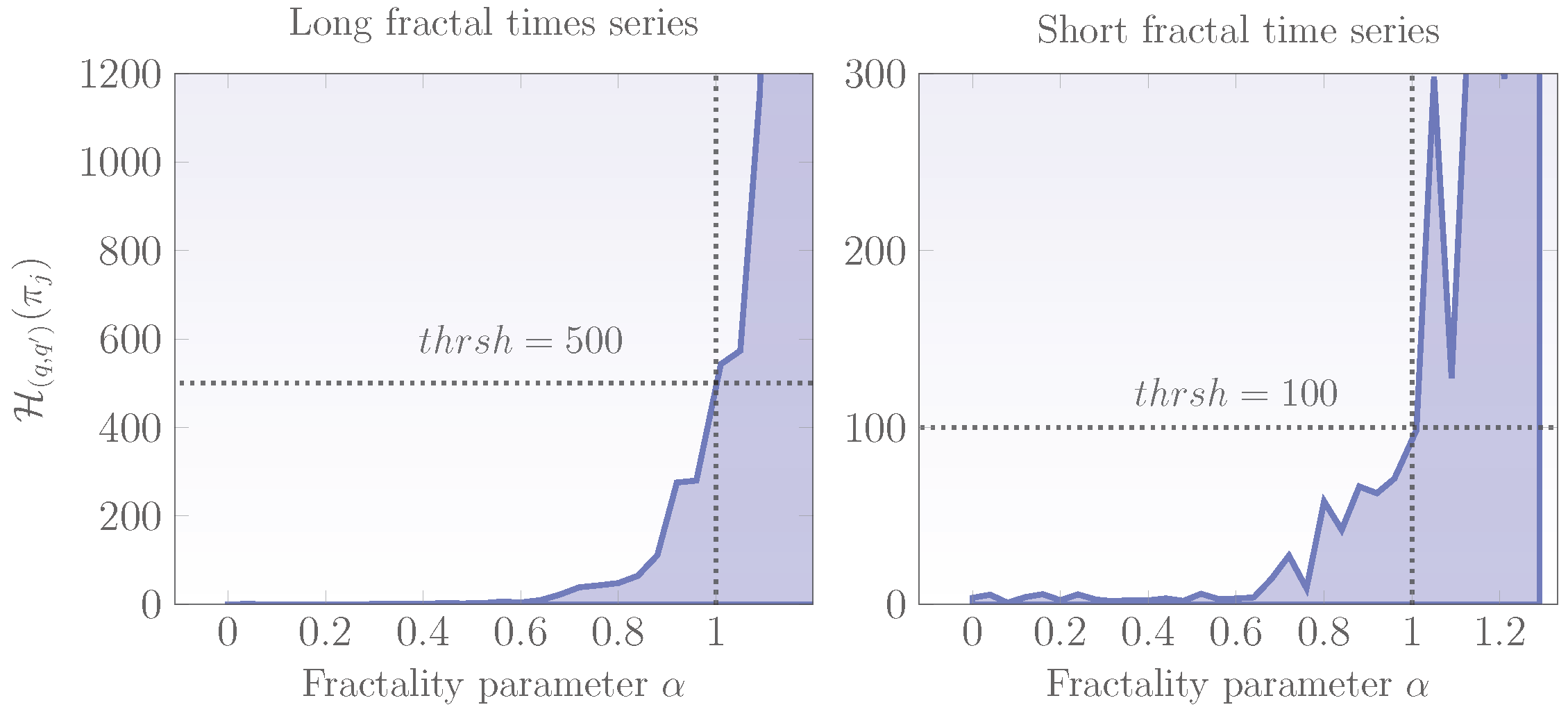
3.2. The Threshold for Long and Short Fractal Time Series
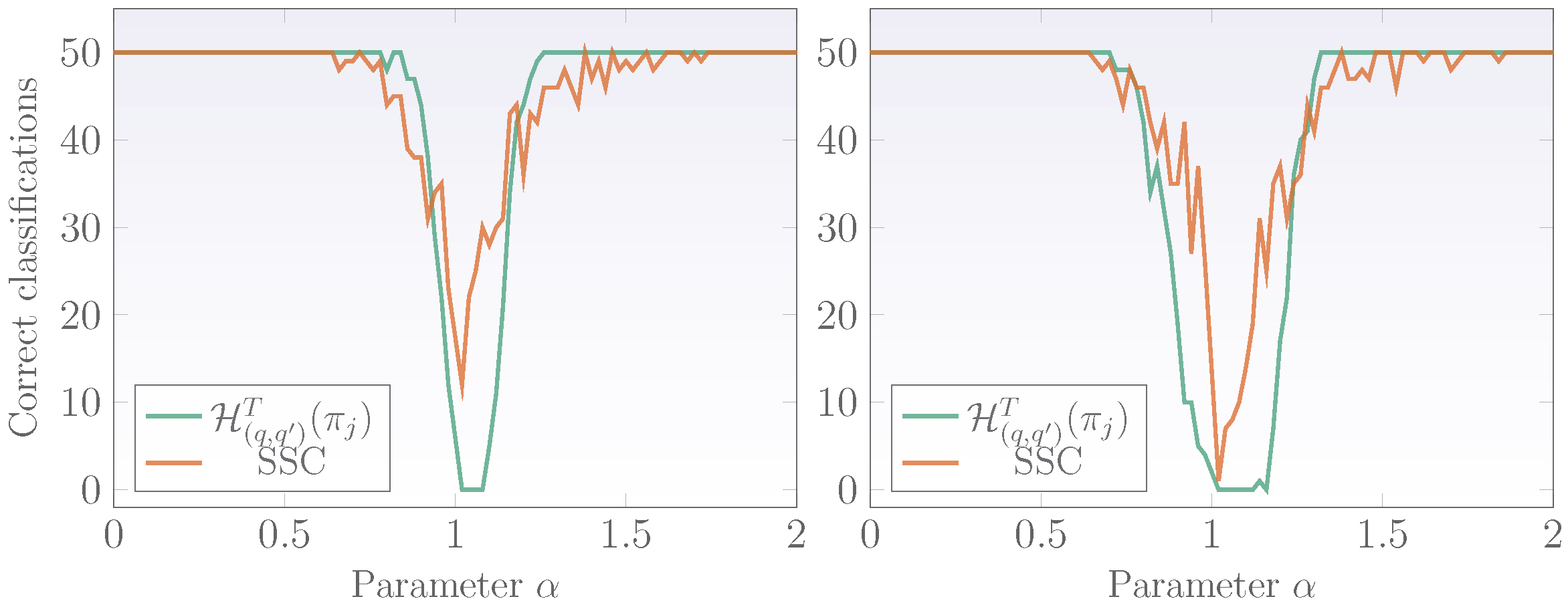
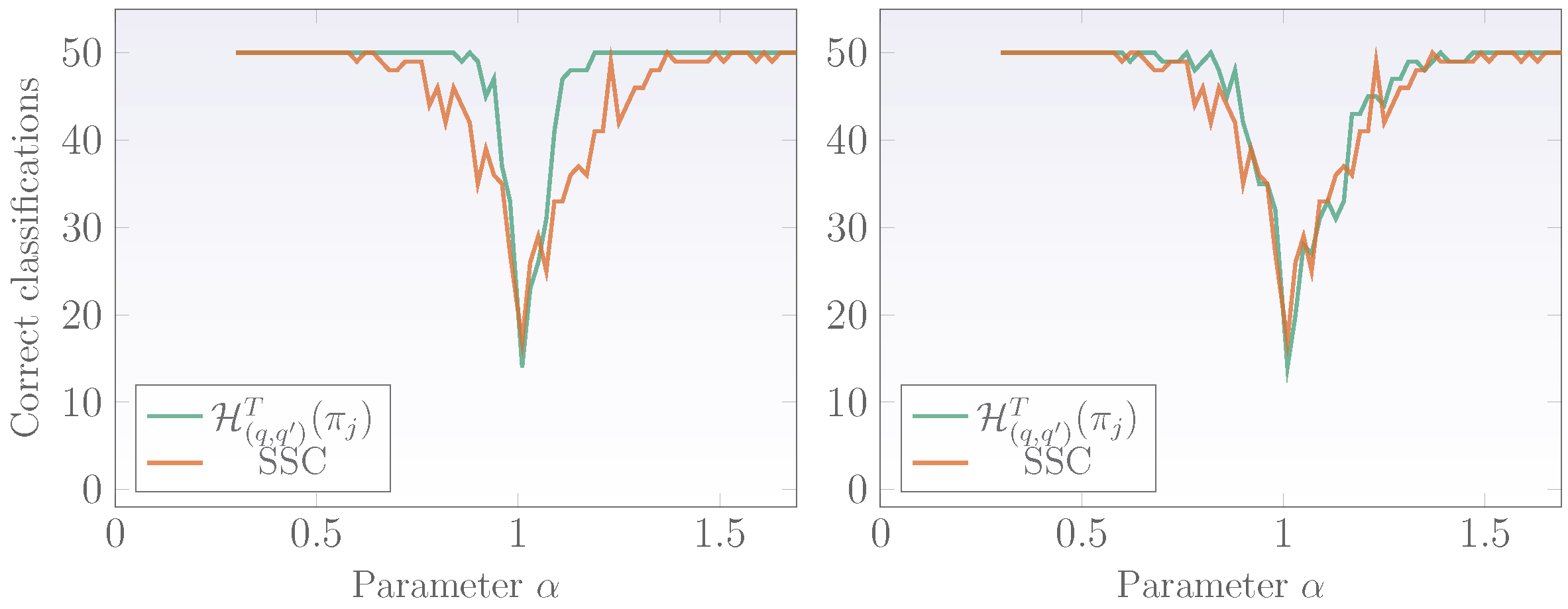
3.3. Comparison with the Standard SSC Technique
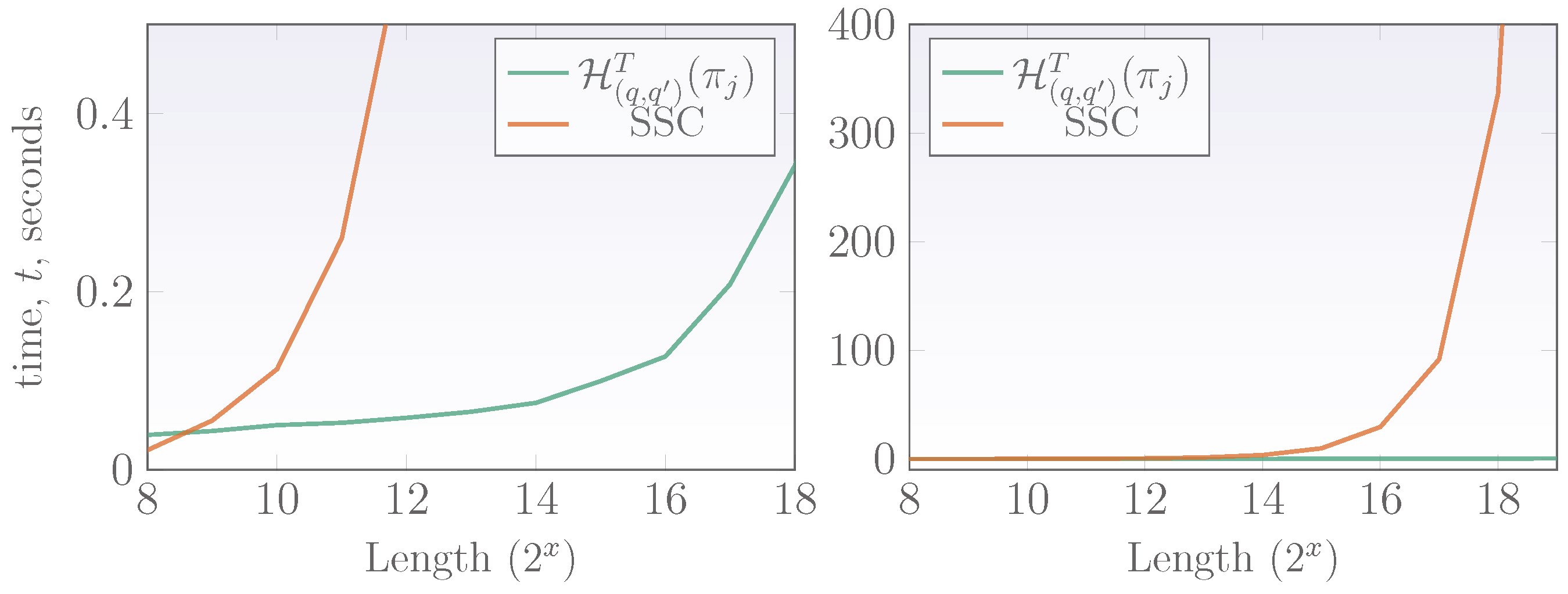
3.4. Computational Complexity
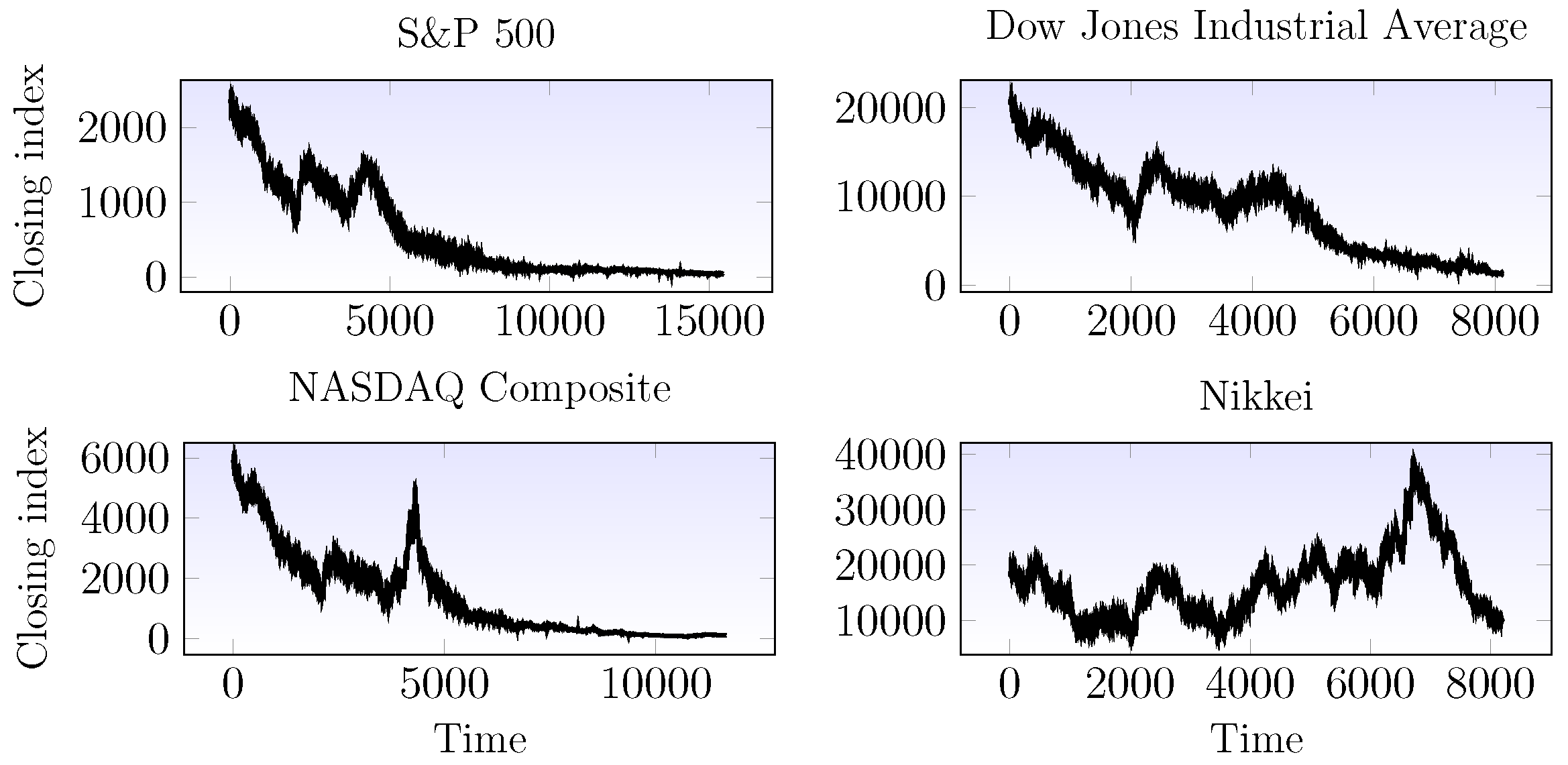
3.5. Application to Financial Time Series
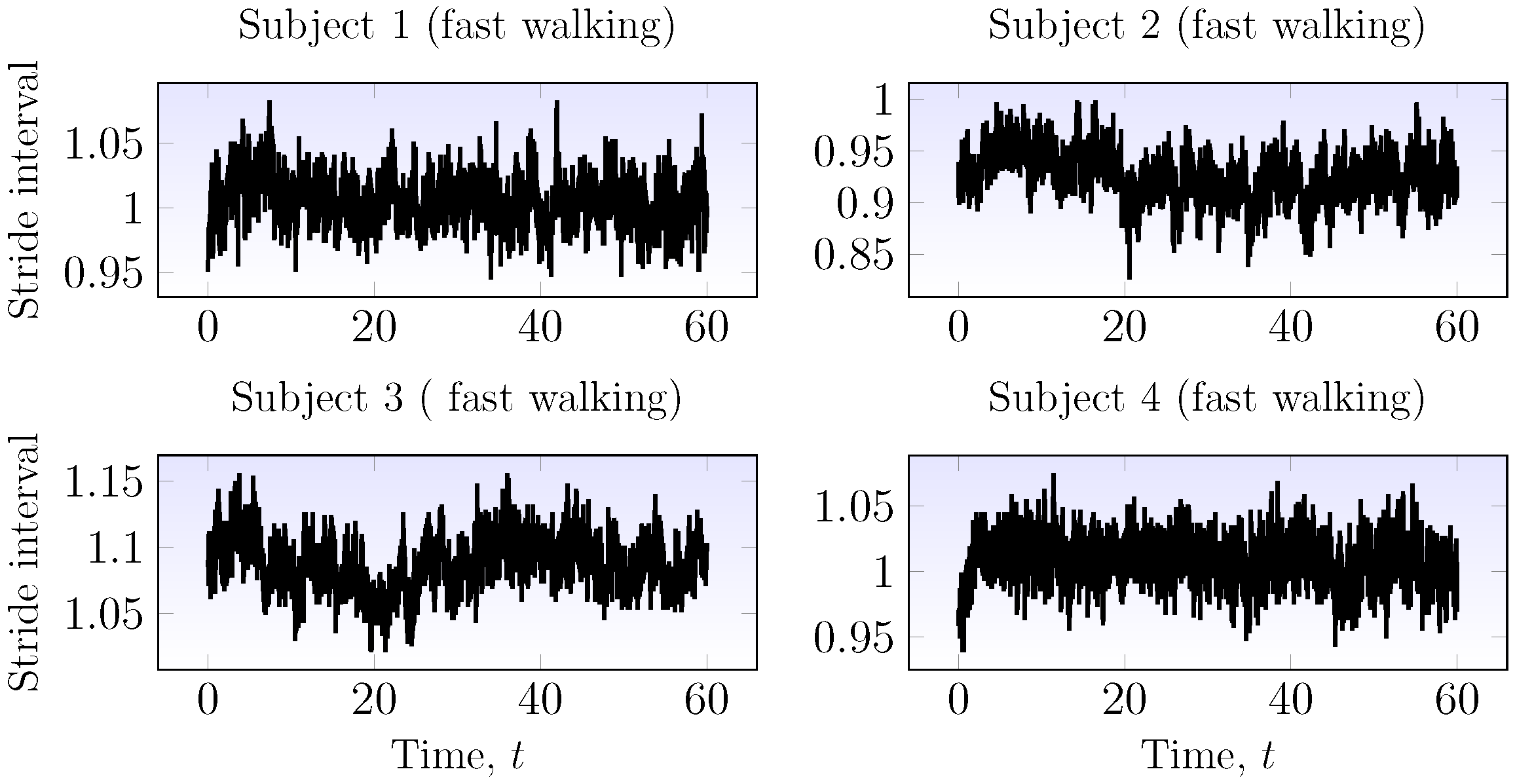
3.6. Application to Physiological Time Series
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Martín-Montoya, L.A.; Aranda-Camacho, N.M.; Quimbary, C.J. Long-range correlations and trends in Colombian seismic time series. Physica A 2015, 421, 124–133. [Google Scholar] [CrossRef]
- Molino-Minero-Re, E.; García-Nocetti, F.; Benítes-Pérez, H. Application of a time-scale local Hurst exponent analysis to time series. Digit. Signal Process. 2015, 37, 92–99. [Google Scholar] [CrossRef]
- Van Orden, G.C.; Holden, J.G.; Turvey, M.T. Human cognition and 1/f scaling. J. Exp. Psychol. Gen. 2005, 134, 117–123. [Google Scholar] [CrossRef] [PubMed]
- Szolgayova, E.; Laaha, G.; Bloschl, G.; Bucher, C. Factors influencing long range dependence in streamflow of European rivers. Hydrol. Process. 2014, 28, 1573–1586. [Google Scholar] [CrossRef]
- Holden, J.G.; Riley, M.A.; Gao, J.; Torre, K. Fractal Analyses: Statistical and methodological innovations and best practices. Fractal Physiol. 2013, 4, 97. [Google Scholar]
- Serinaldi, F. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Physica A 2010, 389, 2770–2781. [Google Scholar] [CrossRef]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L.R. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef] [PubMed]
- Beran, J.; Sherman, R.; Taqqu, M.S.; Willinger, W. Long-Range Dependence in Variable-Bit-Rate Video Traffic. IEEE Trans. Commun. 1995, 43, 1566–1579. [Google Scholar] [CrossRef]
- Hausdorf, J.M.; Zemany, L.; Peng, C.K.; Goldberger, A.L. Maturation of Gait Dynamics: Stride to stride variability and its temporal organization in children. J. Appl. Physiol. 1999, 86, 1040–1047. [Google Scholar]
- Deligneres, D.; Torre, K.; Lemoine, L. Methodological issues in the application of monofractal analyses in psychological and behavioral research. Nonlinear Dyn. Psychol. Life Sci. 2005, 9, 451–477. [Google Scholar]
- Rea, W.; Oxley, L.; Reale, M.; Brown, J. Not all estimators are born equal: The empirical properties of some estimators of long-memory. Math. Comput. Simul. 2013, 93, 29–42. [Google Scholar] [CrossRef]
- Stadnitski, T. Measuring Fractality. Front. Physiol. 2012, 3, 127. [Google Scholar] [CrossRef] [PubMed]
- Eke, A.; Hermán, P.; Bassingthwaighte, J.B.; Raymond, G.; Percival, D.B.; Cannon, M.; Balla, I.; Ikrényi, C. Physiological Time Series: Distinguishing Fractal Noises and Motions. Pflug. Arch. 2000, 439, 403–415. [Google Scholar] [CrossRef]
- Ramirez Pacheco, J.; Torres Román, D.; Toral Cruz, H. Distinguishing Stationary/Nonstationary Scaling Processes Using Wavelet Tsallis q-Entropies. Math. Probl. Eng. 2012, 2012, 1–18. [Google Scholar] [CrossRef]
- Bonachela, J.; Hinrichsen, H.; Muñoz, M.A. Entropy estimates of small data sets. J. Phys. A Math. Gen. 2008, 41, 202001. [Google Scholar] [CrossRef]
- Kumar, U.; Kumar, V.; Kapur, J.N. Normalized measures of entropy. Int. J. Gen. Syst. 1986, 12, 55–69. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.R.; Plastino, A. Tsallis-like information measures and the analysis of complex signals. Physica A 2000, 275, 262–271. [Google Scholar] [CrossRef]
- Vignat, C.; Bercher, J.F. Analysis of signals in the Fisher-Shannon information plane. Phys. Lett. A 2003, 312, 27–33. [Google Scholar] [CrossRef]
- Rakjović, M. Entropic nonextensivity as a measure of time series complexity. Physica A 2004, 340, 327–333. [Google Scholar] [CrossRef]
- Romera, E.; Dehesa, J.S. The Fisher-Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- Romera, E.; Nagy, A. Fisher-Rényi entropy product and information plane. Phys. Lett. A 2008, 372, 6823–6825. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; López-Rosa, S.; Flores-Gallegos, N. Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 2010, 12, 7108–7116. [Google Scholar] [CrossRef] [PubMed]
- Lovallo, M.; Telesca, L. Complexity measures and information planes of X-ray astrophysical sources. J. Stat. Mech. Theory Exp. 2011, 3, P03029. [Google Scholar] [CrossRef]
- Zunino, L.; Perez, D.G.; Garavaglia, M.; Rosso, O.A. Wavelet Entropy of Stochastic Processes. Physica A 2007, 379, 503–512. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Rosso, O.A.; Basar, E.; Schumann, M. Wavelet entropy in event-related potentials: A new method shows ordering of EEG oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Pacheco, J.; Toral-Cruz, H.; Rizo-Domínguez, L.; Cortez-González, J. Generalized Wavelet Fisher’s Information of 1/f Signals. Adv. Math. Phys. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Rosso, O.A.; Zunino, L.; Pérez, D.G. Extracting features of Gaussian self-similar stochastic processes using wavelet-based information tools. Phys. Rev. E 2007, 76, 061114. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.X.; Sun, Z.S. Structural damage identification by using wavelet entropy. Eng. Struct. 2008, 30, 2840–2849. [Google Scholar] [CrossRef]
- Voss, R.F. Evolution of long-range fractal correlations and 1/f noise in DNA base sequences. Phys. Rev. Lett. 1992, 68, 3805. [Google Scholar] [CrossRef] [PubMed]
- De Felice, A.; D’Addio, G.; Cesarelli, M.; Balzano, G.; Accardo, A. Fractal behaviour of heart rate variability reflects abnormal respiration patterns in OSAS patients. Eur. Respir. J. 2013, 42, P2560. [Google Scholar]
- Deligneres, D.; Ramdani, S.; Lemoine, L.; Torre, K.; Fortes, M.; Ninot, G. Fractal Analyses of short time series: A re-assessment of classical methods. J. Math. Psychol. 2006, 50, 525–544. [Google Scholar] [CrossRef]
- Abry, P.; Veitch, D. Wavelet Analysis of Long-Range Dependent Traffic. IEEE Trans. Inf. Theory 1998, 44, 2–15. [Google Scholar] [CrossRef]
- Veitch, D.; Abry, P. A Wavelet Based Joint Estimator of the Parameters of Long-Range Dependence. IEEE Trans. Inf. Theory 1999, 45, 878–897. [Google Scholar] [CrossRef]
- Mandelbrot, B.; van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: Measures of weak and strong persistence. J. Stat. Plan. Inference 1999, 80, 173–196. [Google Scholar] [CrossRef]
- Gallant, J.C.; Moore, I.D.; Hutchinson, M.F.; Gessler, P. Estimating the Fractal Dimension of Profiles: A Comparison of Methods. Math. Geol. 1994, 26, 455–481. [Google Scholar] [CrossRef]
- Pilgram, B.; Kaplan, D.T. A comparison of estimators for 1/f noise. Physica D 1998, 114, 108–122. [Google Scholar] [CrossRef]
- Goupillaud, P.; Grossmann, A.; Morlet, J. Cycle-octave and related transforms in seismic signal analysis. Geoexploration 1984, 23, 85–102. [Google Scholar] [CrossRef]
- Hudgins, L.; Friehe, C.A.; Mayer, M.E. Wavelet Transforms and Atmospheric Turbulence. Phys. Rev. Lett. 1993, 71, 3279–3283. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.; Kovacevic, J. Wavelets: The Mathematical Background. Proc. IEEE 1996, 84, 514–522. [Google Scholar] [CrossRef]
- Stoev, S.; Taqqu, M.S.; Park, C.; Marron, J.S. On the Wavelet Spectrum Diagnostic for Hurst Parameter Estimation in the Analysis of Internet Traffic. Comput. Netw. 2005, 48, 423–445. [Google Scholar] [CrossRef]
- Zunino, L.; Pérez, D.G.; Martin, M.T.; Plastino, A.; Garavaglia, M.; Rosso, O.A. Characterization of Gaussian Self-similar stochastic processes using wavelet-based information tools. Phys. Rev. E 2007, 75, 021115. [Google Scholar] [CrossRef] [PubMed]
- Perez, D.G.; Zunino, L.; Martin, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Model-free stochastic processes studied with q-wavelet-based information tools. Phys. Lett. A 2007, 364, 259–266. [Google Scholar] [CrossRef]
- Ramirez-Pacheco, J.; Torres-Roman, D. Cosh window behaviour of wavelet Tsallis q-entropies in 1/fα signals. Electron. Lett. 2011, 47, 186–187. [Google Scholar] [CrossRef]
- Soltani, S.; Simard, P.; Boichu, D. Estimation of the self-similarity parameter using the wavelet transform. Signal Process. 2004, 84, 117–123. [Google Scholar] [CrossRef]
- Shen, H.; Zhu, Z.; Lee, T.C.M. Robust estimation of the self-similarity parameter in network traffic using the wavelet transform. Signal Process. 2007, 87, 2111–2124. [Google Scholar] [CrossRef]
- Flandrin, P. Wavelet Analysis and Synthesis of Fractional Brownian Motion. IEEE Trans. Inf. Theory 1992, 38, 910–917. [Google Scholar] [CrossRef]
- Bardet, J.M. Statistical Study of the Wavelet Analysis of Fractional Brownian Motion. IEEE Trans. Inf. Theory 2002, 48, 991–999. [Google Scholar] [CrossRef]
- Pesquet-Popescu, B. Statistical Properties of the Wavelet Decomposition of certain Non-Gaussian Self-Similar Processes. Signal Process. 1999, 75, 303–322. [Google Scholar] [CrossRef]
- Borges, E.P. A family of nonextensive entropies. Phys. Lett. A 1998, 246, 399–402. [Google Scholar] [CrossRef]
- Davies, R.B.; Harte, D.S. Test for Hurst Effect. Biometrika 1987, 74, 95–101. [Google Scholar] [CrossRef]
- Bayraktar, E.; Poor, H.V.; Sircar, K.R. Estimating the fractal dimension of the S&P 500 index using wavelet analysis. Int. J. Theor. Appl. Financ. 2004, 7, 615–643. [Google Scholar]
- Zunino, L.; Tabak, B.M.; Figliola, A.; Perez, D.G.; Garavaglia, M.; Rosso, O.A. A multifractal approach for stock market inefficiency. Physica A 2008, 387, 6558–6566. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Purdon, P.L.; Peng, C.K.; Ladin, Z.V.; Wei, J.Y.; Goldberger, A.L. Fractal dynamics of human gait: Stability of long-range correlations in stride interval fluctuations. J. Appl. Physiol. 1996, 80, 1448–1457. [Google Scholar] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Pacheco, J.C.; Trejo-Sánchez, J.A.; Cortez-González, J.; Palacio, R.R. Classification of Fractal Signals Using Two-Parameter Non-Extensive Wavelet Entropy. Entropy 2017, 19, 224. https://doi.org/10.3390/e19050224
Ramírez-Pacheco JC, Trejo-Sánchez JA, Cortez-González J, Palacio RR. Classification of Fractal Signals Using Two-Parameter Non-Extensive Wavelet Entropy. Entropy. 2017; 19(5):224. https://doi.org/10.3390/e19050224
Chicago/Turabian StyleRamírez-Pacheco, Julio César, Joel Antonio Trejo-Sánchez, Joaquin Cortez-González, and Ramón R. Palacio. 2017. "Classification of Fractal Signals Using Two-Parameter Non-Extensive Wavelet Entropy" Entropy 19, no. 5: 224. https://doi.org/10.3390/e19050224
APA StyleRamírez-Pacheco, J. C., Trejo-Sánchez, J. A., Cortez-González, J., & Palacio, R. R. (2017). Classification of Fractal Signals Using Two-Parameter Non-Extensive Wavelet Entropy. Entropy, 19(5), 224. https://doi.org/10.3390/e19050224





