Abstract
This article proposes a methodology for the classification of fractal signals as stationary or nonstationary. The methodology is based on the theoretical behavior of two-parameter wavelet entropy of fractal signals. The wavelet -entropy is a wavelet-based extension of the -entropy of Borges and is based on the entropy planes for various q and ; it is theoretically shown that it constitutes an efficient and effective technique for fractal signal classification. Moreover, the second parameter provides further analysis flexibility and robustness in the sense that different pairs can analyze the same phenomena and increase the range of dispersion of entropies. A comparison study against the standard signal summation conversion technique shows that the proposed methodology is not only comparable in accuracy but also more computationally efficient. The application of the proposed methodology to physiological and financial time series is also presented along with the classification of these as stationary or nonstationary.
1. Introduction
Fractal signals are ubiquitous in nature [1,2,3,4,5,6] and many aspects of these processes appear in hardly any field of science [3,4,7,8,9,10]. An important research topic within the fractal theory concerns the estimation of fractal signals [5,6,11,12], specifically, the fractality parameter. Within fractal signal analysis and estimation, fractal signal classification (i.e., the classification of signals as stationary or nonstationary) plays an important role since it determines the type of estimator to be used, the form of important statistics such as correlations and moments and also the smoothness of sample paths [7,10,12,13,14]. Some authors have even claimed that the signal classification should be considered as the primary step for fractal signal analysis [13] and have devised methodologies for the classification of fractal processes. Many techniques have attempted to classify fractal signals as stationary or nonstationary. The signal summation conversion (SSC) [7,13] is a technique based on the observed behavior of the power spectral density (PSD) estimator when estimating the fractality parameter in the range . The PSD underestimates fractal signals in a range of the fractality exponent and therefore an additional technique is used instead (scaled window variance (SWV)). SSC is therefore a PSD-based technique and is described in detail in [7,13]. The fractal signal classification scheme based on wavelet Tsallis q-entropy was first proposed in [14] and takes advantage of the particular behavior of entropies (nonextensive Tsallis) for fractal signals. Both techniques, however, are subject to inaccuracies in the stationary/nonstationary limit () but unlike the SSC methodology, the wavelet Tsallis q-entropy technique appears to be more computationally efficient [14], therefore it is more appropriate for long signals. In this article, two-parameter nonextensive wavelet entropy is proposed for the fractal signal classification problem. The concept of entropy, as applied to statistical mechanics, measures the information content or uncertainty of a random signal or system [15,16]. The entropy of a signal, in their diverse functionals, has been proposed to solve a handful of problems across the numerous fields of science. For instance, the well-known Shannon, Rényi and Tsallis entropies have been used in [17,18,19] to assess the complexities associated to random and nonlinear phenomena. The literature has also witnessed the rise of more elaborate information theory functionals which consist of the product of complexity/entropy measures and allow for greater flexibility and the possibility to analyze a wider range of phenomena. Current applications of the aforementioned entropic measures include but are not limited to the analysis of two-electron systems [20] and their extension to many electron systems [21]. Also, information planes are being applied to randomness and the localization of molecules [22] and for the analysis of X-ray astrophysical sources [23]. With the advent of multiscale analyses, more precise and fast information theory quantifiers have been proposed. The so-called wavelet entropy [24,25] constitutes an extension of the Shannon entropy using a probability function obtained from the wavelet representation of the signal. Extensions of the wavelet entropy include the wavelet q-entropy using a Tsallis functional and the generalized wavelet Fisher’s information [26]. The analysis of a signal in their wavelet domain has many advantages including the possibility to handle nonstationarities and to adjust the analyses to selective signal resolutions. Wavelet information tools have found applications in various fields including physiology, e.g., for electroencephalogram (EEG) and electrocardiogram (ECG) signal analysis [25,27], and physics [27], among others [28]. Wavelet information tools, therefore embody a field that is under constant development and may offer significant tools and advantages for signal and system analysis. This article, as mentioned above, proposes a methodology that uses the observed behavior of wavelet -entropies of fractal signals for the classification of these as stationary or nonstationary. The motivation behind the use of the wavelet -entropy stems from the fact that fractal signals experiment constant entropies over time while nonstationary fractal signals display variable entropies across time. In addition, parameter provides further analysis flexibility and the ability to use different configurations of the pair to analyze the same phenomena. Moreover, wavelet -entropy constitutes a generalization of the wavelet entropy and wavelet q-entropy approaches and therefore, the results reported in the literature using these entropies may be replicated with the wavelet -entropy. The rest of the article is organized as follows: Section 2 provides a review of some important results regarding the wavelet analysis of fractal signals and presents some important properties of the wavelet -entropy as well. The signal classification problem is also presented and a brief description of the techniques available for performing this is given. Section 3 presents some results regarding the classification of fractal signals using the wavelet -entropy and Section 4 presents a comparison study with the SSC using synthesized fractal signals and the application of the proposed methodology in gait and financial time series. Finally Section 5 concludes the article.
2. Materials and methods
2.1. The Representation of Fractal Signals by Wavelets
Fractal signals are ubiquitous in nature and are representative models for the phenomena occurring in deoxyribonucleic acid (DNA) sequences [29], heart-beat time series [30], and mood and self-steem [31], among others. The PSD is the traditional approach used in the literature to define a fractal process. In fact, a fractal signal is defined as a process for which their PSD is:
where is a constant, is the fractality parameter and represent the lower and upper bounds upon which (1) holds [32,33]. Many stochastic processes can be used to model the power-law behavior of the PSD of fractal processes (as given in Equation (1)). The pure-power-law (PPL) process, the fractional auto-regressive integrated moving-average (f-ARIMA) time series and the well-known fractional Brownian motion (fBm) and fractional Gaussian noise (fGn) are examples of fractal stochastic processes [34]. In this contribution, the classification of fractal signals as stationary or nonstationary is considered. Two types of fractal stochastic processes are studied, the fGn/fBm family and the PPL family of random signals. FBm is a Gaussian process which is self-similar and nonstationary [6,35,36]. FBm is defined in terms of two interrelated concepts, the correlation function which is given by:
with and spectral density function (SDF) which satisfies the following relation:
Equation (3) implies that the fBm is a fractal signal with [6,36]. FGn, on the other hand, is a differenced version of fBm and is stationary, Gaussian, self-similar and has a PSD of the form [6,11,35,36,37]:
with . In the limit of , the PSD of fGn behaves as and therefore is a fractal signal with . The PPL family of stochastic processes is defined as a process for which their PSD is:
for . When , the PPL process is stationary and when , it is nonstationary. The fGn/fBm and the PPL families of processes behave similarly although they differ in their PSD. Wavelet analysis, originally proposed in geophysics [38], decomposes a signal in terms of small waves and permits to compute the so-called multiresolution analysis [39,40]. For random signals, the wavelet spectrum [41] permits computation of many interesting quantities such as the relative wavelet energy (RWE) which basically represents a probability function for the signal under study [24,42]. The wavelet spectrum of fractal signals was obtained in the work of Abry and Veitch [32,33] and can be computed using the following relation,
where is the Fourier integral of the mother wavelet , is the PSD of the process , the expectation operator and is the discrete wavelet transform (DWT) of the process at time k and wavelet scale j [32,33]. Using the PSD of fractal signals given by Equation (1) and substituting it into Equation (6) results in the wavelet spectrum of fractal signals,
where C is a constant. Equation (7) has been used for the estimation of the fractality exponent [32] and also for computing wavelet-based information tools [14,24,25,42,43,44]. For further information on wavelets and in the wavelet analysis of fractal signals refer to [32,33,39,40,45,46,47,48,49] and references therein.
2.2. A Nonextensive Wavelet -Entropy of Fractal Signals
In this article, a methodology for the classification of fractal signals based on the behavior of their wavelet -entropy is proposed. The wavelet -entropy is an extension (to the time-scale domain) of the -entropy first proposed by Borges in [50]. In order to obtain a closed-form expression for the wavelet -entropy of fractal signals, their RWE is computed. The RWE of fractal signals was obtained in [24] using the wavelet spectrum equation of (7) and results in:
where . Note that in (8) for represents a probability mass function (pmf) in the sense that , and therefore many information theory quantifiers can be obtained for fractal signals using this relation. The application of (8) into the definition of -entropy [50] and given by the relation,
results in the wavelet -entropy of fractal signals which is given by,
and can also be expressed as,
Equation (11) represents the wavelet -entropy of fractal signals and the expression in (11) represents a polynomial of order which for any , is given by:
When , the standard (normalized) wavelet Tsallis q-entropy presented in [25,27,44] is obtained and with and , the wavelet entropy of [24] results. Therefore, with the use of wavelet -entropy, the results previously obtained with wavelet entropy and wavelet Tsallis-q-entropy can be replicated. The motivation with the use of the two-parameter entropy lies in the increased flexibility and robustness which can be achieved by the parameter .
2.3. The Behaviour of Wavelet -Entropy for Various Pairs
Equation (11) is of particular importance since it allows to construct the so-called entropy planes which permit to visualize the behavior of entropies for different q, , N and . A diversity of entropy planes can be obtained, however, they can be grouped into the following types for the case of fractal signal classification. Figure 1 shows an entropy plane constructed by setting the parameter , , using several N and . Note from the figure that in the limit of , entropies are small and appear to be zero, however their true value is:
and therefore the well-known Gaussian noise exhibits the smallest -entropy. In general, whenever , fractal signals neighboring will also be regarded as processes experiencing small constant entropies. Fractal signals with fractality parameter lying outside this interval will have a wavelet -entropy that differs from and when computed in sliding windows they lead to a signal which varies with higher dispersion over time. Therefore, whenever or , behavior such as that one obtained in Figure 1 is observed. Note that for this case, the wavelet -entropy behaves as a whitening filter which regards signals in a specific range as noise. The range of constant entropies can be scaled or comprised according to q and , this means that by setting fixed and varying q, a different region of constant entropies is observed. Note that setting the constant region of wavelet -entropies in the fractality interval allows to distinguish stationary processes from nonstationary ones simply by observing whether their entropies are constant or varying and consequently a simple yet powerful classification technique may be devised. A particular advantage of wavelet -entropy over their related wavelet q-entropy and wavelet entropy approaches is their ability to analyze the same phenomena using a different pair. This implies increased analysis flexibility and robustness. Figure 2 displays a wavelet entropy plane for fractal signals when (or when ). In this case, the entropies are similar to the entropies of Figure 1, and experiment roughly two classes of behavior in the same way as the that observed in Figure 1, the first is associated with constant entropies in a range of the fractality parameters while the second is for varying entropies (for signals with fractality parameter lying outside the constant range). Unlike the entropies of Figure 1, the entropies observed in Figure 2 exhibit a faster increase outside the interval of constant entropies. The width of constant entropies can be set with parameter q, and in the same way, can be used to classify fractal signals as stationary or nonstationary. It is important to note that the classification of fractal signals is not limited to the stationary/nonstationary case but can also be performed for classifying fractal signals as short-memory and long-memory and also to classify extended fBms from fBms as well, however the present contribution only considers the stationary/nonstationary case. Finally, a third way to classify fractal processes as stationary or nonstationary can also be obtained when the wavelet -entropy has and . Note that this corresponds to the case of wavelet Tsallis q-entropies and the wavelet entropy plane is identical to the one presented in [14]. Figure 3 displays the wavelet entropies for these values of q and along with their contour plots. The wavelet -entropy plane of Figure 3 displays constant (maximum) entropies in a range of the fractality parameter and decreasing entropies outside this interval. This behavior can also be used for fractal signal classification, however, it is more restricted in the sense that the range of variation of entropies is small compared to previous -pairs and hence the classification is more complex. Consequently, for the problem of fractal signal classification behavior such as that observed in Figure 1 or Figure 2 is preferred. In the following, the methodology based on the wavelet -entropy for fractal signal classification is described.
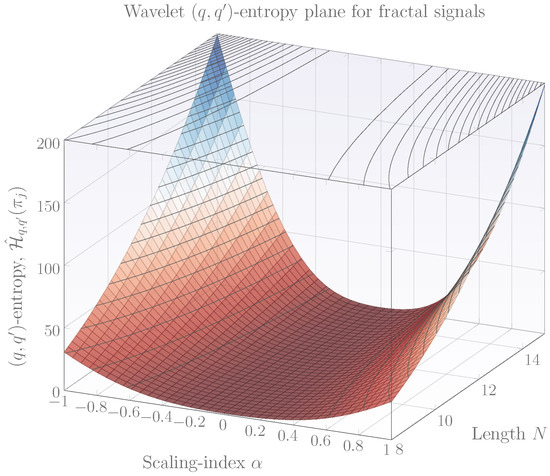
Figure 1.
Wavelet -entropy for fractal signals of parameter . Parameters q and are set to and respectively. Length N is given in powers of 2.
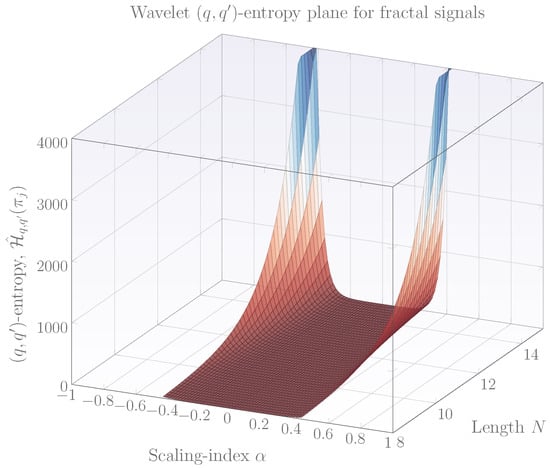
Figure 2.
Wavelet -entropy for fractal signals of parameter . Parameters q and are set to and respectively. Length N is given in powers of 2.
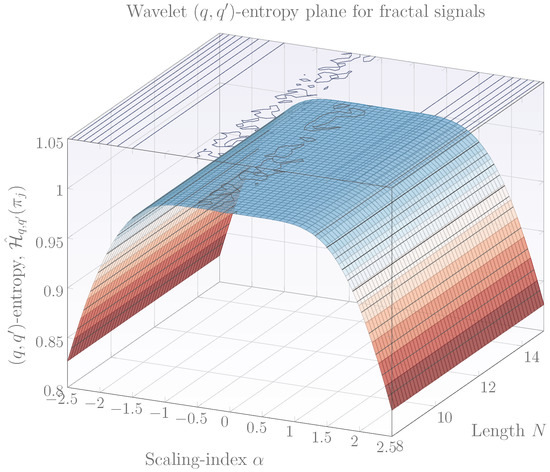
Figure 3.
Wavelet -entropy for signals. Parameters q and are set to and . Scaling index range is and the length of the signal ranges in the interval .
2.4. The Classification of Fractal Signals with Wavelet -Entropy
The theoretical wavelet -entropy planes obtained previously give insight into the characteristics of entropies for fractal signals. The behavior of these entropies, for selected values of q and , permit to devise a simple methodology for the classification of fractal signals as stationary or nonstationary. However, as mentioned above, the fractal signal classification using wavelet -entropies is not only limited to the stationary/nonstationary case but can also be used for the classification of other classes of fractal processes such as long-memory and short-memory and for fBm and extended fBm as well. Based on this, Figure 4 displays a generalization of the behavior observed in the wavelet -entropies of Figure 1 and Figure 2 and which may permit to classify fractal processes as stationary or nonstationary. First, observe that wavelet -entropies are constant over a region and fluctuate for processes whose fractality parameter lies outside this range. For the special case in which , wavelet -entropies distinguish stationary fractal processes from nonstationary ones. The classification is thus based on whether the observed signal wavelet -entropy fluctuates over a given threshold or not. In order to more efficiently capture the fluctuations of wavelet -entropies, these are computed in sliding windows of the form,
where is the wavelet -entropy operator over a sample of the signal and W denotes the window size, the sliding factor and . The use of sliding windows therefore allows for highlighting the fluctuations of entropies and this variation may be captured with a standard dispersion technique. Since the standard deviation is not robust to peaks and other anomalies within the data, the biweight midvariance is used instead since it constitutes a robust estimator of the dispersion within a signal. The biweight midvariance () of a sample is defined according to the following relation:
where , c is typically 9, MAD is the usual median absolute deviation and is the number of points which satisfy the condition. Wavelet -entropy therefore fluctuates for nonstationary processes and remains constant for stationary ones. The estimation of entropies by sliding windows permits to emphasize further the fluctuations and these fluctuations can be quantified with the biweight midvariance. In theory, wavelet -entropies for stationary processes are constant, however, in practice, they also fluctuate and a threshold is set in order to classify fractal processes. Based on this, Figure 5 presents the proposed scheme for classifying fractal signals as stationary or nonstationary using wavelet -entropies.
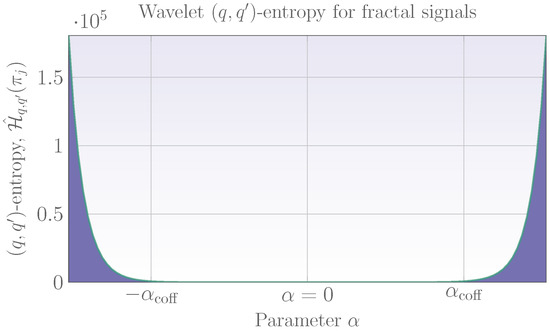
Figure 4.
Wavelet entropy plane when (or ). Constant regions are observed in and variable regions outside this interval.
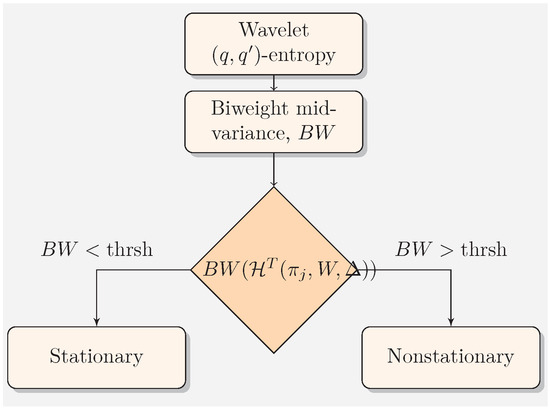
Figure 5.
Fractal signal classification scheme using wavelet -entropy and the biweight midvariance technique.
First, wavelet -entropies are computed in sliding windows and then the fluctuation is estimated using the biweight midvariance technique. Finally, a decision is taken on whether the biweight midvariance is greater or smaller than a given threshold. In case the biweight midvariance is greater than the threshold, the process is regarded as nonstationary otherwise the process is stationary. The advantages of the proposed scheme is that overall the process is computationally efficient and therefore fast for classifying long fractal signals. In the following, a simulation experiment to test the efficacy of the proposed methodology is presented together with a comparison study against the standard SSC technique.
3. Results
3.1. Experimental Results
Figure 5 presented the proposed fractal signal classification scheme based on wavelet -entropies. Note from Figure 5 that a process is regarded as nonstationary whenever , otherwise, the process is stationary. To get an idea of the fluctuations experimented by the wavelet entropies of nonstationary and stationary processes, Figure 6 displays the wavelet -entropies (, ) of two concatenated fractal signals, the first nonstationary fBm and the second stationary fGn. Note that the fBm signal experiences a higher fluctuation with peaks while the fGn presents a lower variation. In biweight midvariance terms, the first presents a higher than the second and the scheme of Figure 5 may distinguish between these two signals straightforwardly. The fractality parameter of the first is and for the second . The fractal signal classification problem has been regarded in the literature as of primary importance, however, all fractal signal classification techniques experiment errors in the limit of . In the following the threshold is determined for long and short time series for fixed values and a comparison of the proposed technique with the standard SSC is presented.
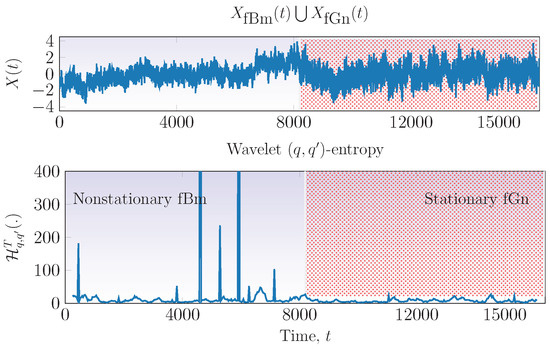
Figure 6.
Classification of signals as stationary or nonstationary. Top plot: concatenated nonstationary and stationary signal, first half part is a nonstationary signal (fractional Brownian motion (fBm) with ) and second half corresponds to a stationary one (fractional Gaussian noise (fGn) with ). Bottom plot: wavelet -entropy of concatenated signal computed in sliding windows with , and .
3.2. The Threshold for Long and Short Fractal Time Series
In order to obtain the threshold for classifying fractal signals as stationary or nonstationary, an experimental setup using synthesized fGn and fBm random signals was devised. In fact, for every fractal signal with parameter in the range , 50 traces were generated and for each, the was estimated and averaged. A plot of versus the averaged can be used to select the required threshold for the given q and . The threshold is determined for both long and short fractal time series and can be used to classify fractal signals as stationary or nonstationary. Figure 7 displays the results of the experimental setup and also the proposed value of for long and short time series. Notice that should be set to 500 for long time series and for short ones. In the following, a comparison of the wavelet -entropy based scheme for signal classification against the standard SSC is presented.
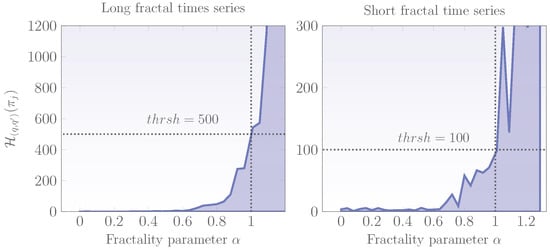
Figure 7.
Determination of the optimal threshold for long and short time series. For convenience only the range is shown and every plot was obtained using and and .
3.3. Comparison with the Standard SSC Technique
As previously mentioned, SSC is a well-known technique for classifying fractal signals as stationary or nonstationary. SSC refines the estimation of PSD in the limit of and within this limit it applies the bdSWV to enhance the estimations. In this interval, SSC basically converts a fGn signal into a fBm and an fBm into an extended fBm via a cumulative sum. The next step in the SSC algorithm is to obtain an estimate of H (). When , the signal is regarded as stationary and when it is nonstationary. For further details on the SSC and some comparison with the PSD technique refer to the work of Eke [13]. In the following, a comparison study of the SSC and the proposed technique based on wavelet -entropies is presented. To perform this comparison, exact fractal signals with known fractality parameters are synthesized. The method employed to generate these fractal signals is known as the Davies and Harte (DHM) technique and the algorithm is detailed further in [51]. The R package fractal includes the DHM and is used to synthesize fGn, fBm and PPL signals with length and , in the range of the fractality parameter and in steps of . For each , 50 fractal signals are generated and classified using the SSC and the methodology based on wavelet -entropies. Finally, the number of correct classifications against the fractality parameter is plotted and the accuracy of each methodology compared. The idea behind the use of PPL signals and the family of fGn/fBm signals stems from the fact that PPL signals represent fractal signals with exact power-law behavior while the fGn/fBm family are approximately fractal. Figure 8 displays the results of both techniques (SSC and wavelet -entropies) using signals of fGn/fBm type. In this experimental study, wavelet -entropy values were set with , , and the threshold with for long signals and for short ones. Left plot corresponds to long signals () while the plot on the right corresponds to short-length fGn/fBm signals (). For long and short signals, the methodology based on wavelets tends to have a lower range of misclassifications but has a weaker behavior when the fractality parameter approaches the limit.
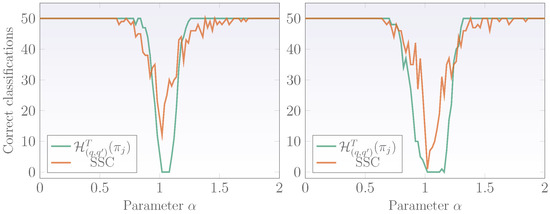
Figure 8.
Classification of synthesized fGn and fBm signals using wavelet -entropy and signal summation conversion (SSC). Left plot corresponds to signals with length and right plot to signals with .
Figure 9, presents the classification results of both techniques when using PPL signals of length (left plot) and (right plot). For long PPL signals, the methodology based on wavelet -entropies presents better performance than the SSC technique while for short PPL signals it is slightly better but overall is statistically similar as the SSC. In summary, the technique based on wavelet -entropies constitutes a fractal signal classification methodology which presents similar classifications as those observed for the SSC, however is more robust in the sense that it permits not only to classify stationary and nonstationary signals but can also be applied for the long-memory/short-memory signal classification problem. In addition, the technique based on wavelet -entropies is computationally efficient and can be used to classify long signals fast and accurately.
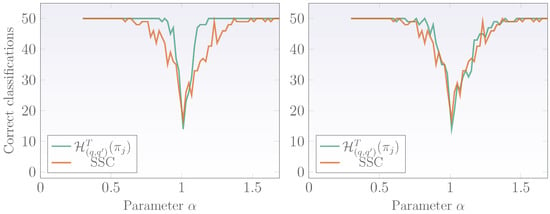
Figure 9.
Classification of synthesized pure-power-law (PPL) signals as stationary or nonstationary using wavelet -entropy and SSC. Left plot corresponds to long signals with length and right plot to short-length signals with .
3.4. Computational Complexity
Wavelet -entropy based signal classification display similar results as that of SSC for long and short fBm/fGn and PPL fractal signals. SSC, however is slower than the proposed technique and not recommended for long signals. As a matter of fact since the DWT is and the nonextensive entropies within the DWT signal take , then the overall complexity of wavelet -entropy is . SSC on the other hand employs a cumulative sum which is and an fast Fourier transform (FFT) technique for the PSD which is , therefore, it is extremely slow and prohibitive for long signals.
3.5. Application to Financial Time Series
Fractal models have been applied to several financial time series from stock market indices [52] to stock market inefficiency [53]. In the following, classification of stock market indices either as stationary fractal models or nonstationary ones is performed using the method based on wavelet -entropy. For the classification, the parameters are set to , , and . The estimated biweight midvariances for these time series are: 120,657.5, 94,943.44, 242,874.8 and 109,040.7 for SP&500, Dow Jones, NASDAQ and Nikkei respectively (Figure 10 displays the studied time series). As can be noted all these stock market indices are nonstationary and can be modeled by the fBm signal.
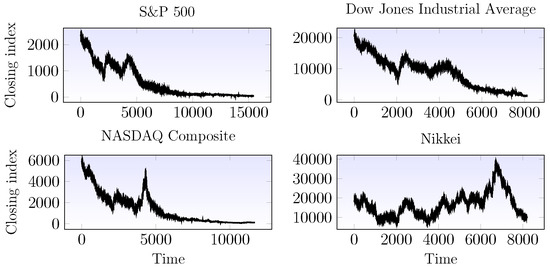
Figure 10.
Stock market closing indices. Top left plot displays the S&P index from January 1956 to 21 April 2017. Top right plot displays the Dow Jones Industrial Average time series from February 1985 to 21 April 2017. Finally bottom left and right plots display the indices for the NASDAQ and Nikkei indices.
3.6. Application to Physiological Time Series
Many physiological and biomedical time series are modeled by fractal time series. Gait time series (gait dynamics) are example physiological signals for which fractal models have been applied [54]. In the following, the classification of stride interval (gait dynamics) time series using wavelet -entropy is performed. For the classification, the parameters are set to , , and . The time series consist of stride intervals of four young and healthy subjects walking fast during an hour-long interval. The time series are plotted in Figure 11. The biweight midvariances are and for the si01, si02, si03 and si04 subjects and clearly indicate that these time series are stationary.
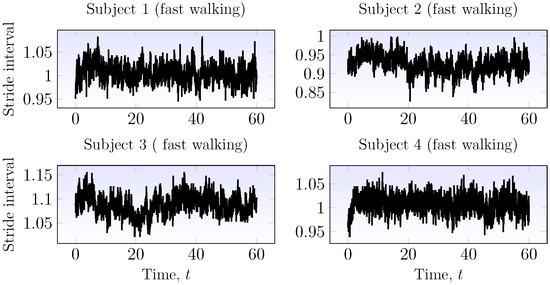
Figure 11.
Stride interval time series from four healthy, young adults walking during a period of an hour in a 400-m oval.
4. Discussion
Figure 8 and Figure 9 showed the classification rates of the proposed technique and the SSC for fGn, fBm and PPL signals. Both techniques present advantages and disadvantages. For instance, the technique based on wavelet -entropies have less variation range, however, it presents no correct classifications in the limit of . Overall, both techniques present similar classifications and can be regarded as statistically similar with respect to the number of correct classifications. Despite these similarities, the wavelet -entropy technique has two additional advantages, it is computationally efficient and can be used to classify other types of fractal processes. As a matter of fact, the proposed technique provides a classification in a fraction of a second for long signals while the SSC is slow. Figure 12 displays the average time required to classify a signal as stationary or nonstationary using the SSC and the proposed technique. Note that the SSC may require almost an hour to classify a signal with length elements. Therefore, although both techniques are statistically similar, the technique based on wavelet -entropies permits to classify signals more rapidly. This accurate and fast classification is important is fields such as computer networking, physics among others.
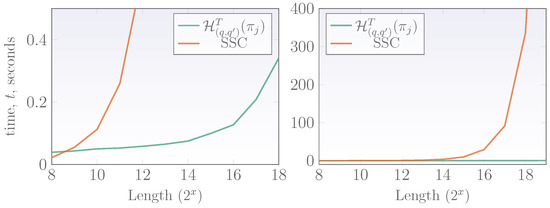
Figure 12.
Average times for obtaining a classification using the proposed technique based on wavelet -entropies and the SSC. Left plot displays a comparison between these techniques while the plot on the right shows the classification times of SSC.
5. Conclusions
In this article, a methodology for the classification of fractal signals as stationary or nonstationary was proposed. The proposed methodology is based on two-parameter wavelet entropy which operates as a preprocessing technique, and the biweight midvariance which measures the fluctuations observed in the wavelet entropies. Theoretical wavelet information planes for these entropies were obtained and based on these, a classification scheme was devised to regard fractal signals as stationary or nonstationary. In fact, it was shown that nonstationary fractal signals experience fluctuations that are higher than those observed for stationary fractal signals and that this rationale can be used for the fractal signal classification problem. Experimental results using synthesized fractal signals demonstrate that the technique based on wavelet -entropies is not only comparable in accuracy to the SSC but is also computationally efficient, making it useful for the analysis of long fractal signals. Moreover, it was shown that unlike the SSC, the technique based on wavelet -entropies is more versatile in the sense that can be used for the classification of other types of fractal processes such as long-memory and short-memory. Furthermore, by setting (and also and ), the results obtained with wavelet Tsallis q-entropies and wavelet entropies can also be replicated with the wavelet -entropy. Finally, the application of the wavelet -entropy to real physiological and stock market time series indicated that the former are stationary while the latter are best modeled by nonstationary fractal processes.
Acknowledgments
Julio C. Ramírez-Pacheco thanks the support of CONACYT grant for project infrastructure and PROMEP grant. Joaquin Cortez-González thanks the support of PROFOCIE 2014. Joaquin Cortez thanks the support of PFCE 2016 and Sonora Institute of Technology through internal funding for research groups (CAs).
Author Contributions
Julio Ramírez-Pacheco and Joel Trejo-Sánchez conceived the idea. Julio Ramírez-Pacheco, Cortez-González and Ramón Palacio-Cinco designed the numerical experiments. Julio Ramírez-Pacheco and Ramón Palacio-Cinco programmed the simulations in R. All authors discussed the numerical results and write the article. All authors have read and approved the final version of the manuscript.
Conflicts of Interest
The authors declare that there is no conflict of interets regarding the publication of this paper.
References
- Martín-Montoya, L.A.; Aranda-Camacho, N.M.; Quimbary, C.J. Long-range correlations and trends in Colombian seismic time series. Physica A 2015, 421, 124–133. [Google Scholar] [CrossRef]
- Molino-Minero-Re, E.; García-Nocetti, F.; Benítes-Pérez, H. Application of a time-scale local Hurst exponent analysis to time series. Digit. Signal Process. 2015, 37, 92–99. [Google Scholar] [CrossRef]
- Van Orden, G.C.; Holden, J.G.; Turvey, M.T. Human cognition and 1/f scaling. J. Exp. Psychol. Gen. 2005, 134, 117–123. [Google Scholar] [CrossRef] [PubMed]
- Szolgayova, E.; Laaha, G.; Bloschl, G.; Bucher, C. Factors influencing long range dependence in streamflow of European rivers. Hydrol. Process. 2014, 28, 1573–1586. [Google Scholar] [CrossRef]
- Holden, J.G.; Riley, M.A.; Gao, J.; Torre, K. Fractal Analyses: Statistical and methodological innovations and best practices. Fractal Physiol. 2013, 4, 97. [Google Scholar]
- Serinaldi, F. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Physica A 2010, 389, 2770–2781. [Google Scholar] [CrossRef]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L.R. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef] [PubMed]
- Beran, J.; Sherman, R.; Taqqu, M.S.; Willinger, W. Long-Range Dependence in Variable-Bit-Rate Video Traffic. IEEE Trans. Commun. 1995, 43, 1566–1579. [Google Scholar] [CrossRef]
- Hausdorf, J.M.; Zemany, L.; Peng, C.K.; Goldberger, A.L. Maturation of Gait Dynamics: Stride to stride variability and its temporal organization in children. J. Appl. Physiol. 1999, 86, 1040–1047. [Google Scholar]
- Deligneres, D.; Torre, K.; Lemoine, L. Methodological issues in the application of monofractal analyses in psychological and behavioral research. Nonlinear Dyn. Psychol. Life Sci. 2005, 9, 451–477. [Google Scholar]
- Rea, W.; Oxley, L.; Reale, M.; Brown, J. Not all estimators are born equal: The empirical properties of some estimators of long-memory. Math. Comput. Simul. 2013, 93, 29–42. [Google Scholar] [CrossRef]
- Stadnitski, T. Measuring Fractality. Front. Physiol. 2012, 3, 127. [Google Scholar] [CrossRef] [PubMed]
- Eke, A.; Hermán, P.; Bassingthwaighte, J.B.; Raymond, G.; Percival, D.B.; Cannon, M.; Balla, I.; Ikrényi, C. Physiological Time Series: Distinguishing Fractal Noises and Motions. Pflug. Arch. 2000, 439, 403–415. [Google Scholar] [CrossRef]
- Ramirez Pacheco, J.; Torres Román, D.; Toral Cruz, H. Distinguishing Stationary/Nonstationary Scaling Processes Using Wavelet Tsallis q-Entropies. Math. Probl. Eng. 2012, 2012, 1–18. [Google Scholar] [CrossRef]
- Bonachela, J.; Hinrichsen, H.; Muñoz, M.A. Entropy estimates of small data sets. J. Phys. A Math. Gen. 2008, 41, 202001. [Google Scholar] [CrossRef]
- Kumar, U.; Kumar, V.; Kapur, J.N. Normalized measures of entropy. Int. J. Gen. Syst. 1986, 12, 55–69. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.R.; Plastino, A. Tsallis-like information measures and the analysis of complex signals. Physica A 2000, 275, 262–271. [Google Scholar] [CrossRef]
- Vignat, C.; Bercher, J.F. Analysis of signals in the Fisher-Shannon information plane. Phys. Lett. A 2003, 312, 27–33. [Google Scholar] [CrossRef]
- Rakjović, M. Entropic nonextensivity as a measure of time series complexity. Physica A 2004, 340, 327–333. [Google Scholar] [CrossRef]
- Romera, E.; Dehesa, J.S. The Fisher-Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- Romera, E.; Nagy, A. Fisher-Rényi entropy product and information plane. Phys. Lett. A 2008, 372, 6823–6825. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; López-Rosa, S.; Flores-Gallegos, N. Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 2010, 12, 7108–7116. [Google Scholar] [CrossRef] [PubMed]
- Lovallo, M.; Telesca, L. Complexity measures and information planes of X-ray astrophysical sources. J. Stat. Mech. Theory Exp. 2011, 3, P03029. [Google Scholar] [CrossRef]
- Zunino, L.; Perez, D.G.; Garavaglia, M.; Rosso, O.A. Wavelet Entropy of Stochastic Processes. Physica A 2007, 379, 503–512. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Rosso, O.A.; Basar, E.; Schumann, M. Wavelet entropy in event-related potentials: A new method shows ordering of EEG oscillations. Biol. Cybern. 2001, 84, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Pacheco, J.; Toral-Cruz, H.; Rizo-Domínguez, L.; Cortez-González, J. Generalized Wavelet Fisher’s Information of 1/f Signals. Adv. Math. Phys. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Rosso, O.A.; Zunino, L.; Pérez, D.G. Extracting features of Gaussian self-similar stochastic processes using wavelet-based information tools. Phys. Rev. E 2007, 76, 061114. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.X.; Sun, Z.S. Structural damage identification by using wavelet entropy. Eng. Struct. 2008, 30, 2840–2849. [Google Scholar] [CrossRef]
- Voss, R.F. Evolution of long-range fractal correlations and 1/f noise in DNA base sequences. Phys. Rev. Lett. 1992, 68, 3805. [Google Scholar] [CrossRef] [PubMed]
- De Felice, A.; D’Addio, G.; Cesarelli, M.; Balzano, G.; Accardo, A. Fractal behaviour of heart rate variability reflects abnormal respiration patterns in OSAS patients. Eur. Respir. J. 2013, 42, P2560. [Google Scholar]
- Deligneres, D.; Ramdani, S.; Lemoine, L.; Torre, K.; Fortes, M.; Ninot, G. Fractal Analyses of short time series: A re-assessment of classical methods. J. Math. Psychol. 2006, 50, 525–544. [Google Scholar] [CrossRef]
- Abry, P.; Veitch, D. Wavelet Analysis of Long-Range Dependent Traffic. IEEE Trans. Inf. Theory 1998, 44, 2–15. [Google Scholar] [CrossRef]
- Veitch, D.; Abry, P. A Wavelet Based Joint Estimator of the Parameters of Long-Range Dependence. IEEE Trans. Inf. Theory 1999, 45, 878–897. [Google Scholar] [CrossRef]
- Mandelbrot, B.; van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: Measures of weak and strong persistence. J. Stat. Plan. Inference 1999, 80, 173–196. [Google Scholar] [CrossRef]
- Gallant, J.C.; Moore, I.D.; Hutchinson, M.F.; Gessler, P. Estimating the Fractal Dimension of Profiles: A Comparison of Methods. Math. Geol. 1994, 26, 455–481. [Google Scholar] [CrossRef]
- Pilgram, B.; Kaplan, D.T. A comparison of estimators for 1/f noise. Physica D 1998, 114, 108–122. [Google Scholar] [CrossRef]
- Goupillaud, P.; Grossmann, A.; Morlet, J. Cycle-octave and related transforms in seismic signal analysis. Geoexploration 1984, 23, 85–102. [Google Scholar] [CrossRef]
- Hudgins, L.; Friehe, C.A.; Mayer, M.E. Wavelet Transforms and Atmospheric Turbulence. Phys. Rev. Lett. 1993, 71, 3279–3283. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.; Kovacevic, J. Wavelets: The Mathematical Background. Proc. IEEE 1996, 84, 514–522. [Google Scholar] [CrossRef]
- Stoev, S.; Taqqu, M.S.; Park, C.; Marron, J.S. On the Wavelet Spectrum Diagnostic for Hurst Parameter Estimation in the Analysis of Internet Traffic. Comput. Netw. 2005, 48, 423–445. [Google Scholar] [CrossRef]
- Zunino, L.; Pérez, D.G.; Martin, M.T.; Plastino, A.; Garavaglia, M.; Rosso, O.A. Characterization of Gaussian Self-similar stochastic processes using wavelet-based information tools. Phys. Rev. E 2007, 75, 021115. [Google Scholar] [CrossRef] [PubMed]
- Perez, D.G.; Zunino, L.; Martin, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Model-free stochastic processes studied with q-wavelet-based information tools. Phys. Lett. A 2007, 364, 259–266. [Google Scholar] [CrossRef]
- Ramirez-Pacheco, J.; Torres-Roman, D. Cosh window behaviour of wavelet Tsallis q-entropies in 1/fα signals. Electron. Lett. 2011, 47, 186–187. [Google Scholar] [CrossRef]
- Soltani, S.; Simard, P.; Boichu, D. Estimation of the self-similarity parameter using the wavelet transform. Signal Process. 2004, 84, 117–123. [Google Scholar] [CrossRef]
- Shen, H.; Zhu, Z.; Lee, T.C.M. Robust estimation of the self-similarity parameter in network traffic using the wavelet transform. Signal Process. 2007, 87, 2111–2124. [Google Scholar] [CrossRef]
- Flandrin, P. Wavelet Analysis and Synthesis of Fractional Brownian Motion. IEEE Trans. Inf. Theory 1992, 38, 910–917. [Google Scholar] [CrossRef]
- Bardet, J.M. Statistical Study of the Wavelet Analysis of Fractional Brownian Motion. IEEE Trans. Inf. Theory 2002, 48, 991–999. [Google Scholar] [CrossRef]
- Pesquet-Popescu, B. Statistical Properties of the Wavelet Decomposition of certain Non-Gaussian Self-Similar Processes. Signal Process. 1999, 75, 303–322. [Google Scholar] [CrossRef]
- Borges, E.P. A family of nonextensive entropies. Phys. Lett. A 1998, 246, 399–402. [Google Scholar] [CrossRef]
- Davies, R.B.; Harte, D.S. Test for Hurst Effect. Biometrika 1987, 74, 95–101. [Google Scholar] [CrossRef]
- Bayraktar, E.; Poor, H.V.; Sircar, K.R. Estimating the fractal dimension of the S&P 500 index using wavelet analysis. Int. J. Theor. Appl. Financ. 2004, 7, 615–643. [Google Scholar]
- Zunino, L.; Tabak, B.M.; Figliola, A.; Perez, D.G.; Garavaglia, M.; Rosso, O.A. A multifractal approach for stock market inefficiency. Physica A 2008, 387, 6558–6566. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Purdon, P.L.; Peng, C.K.; Ladin, Z.V.; Wei, J.Y.; Goldberger, A.L. Fractal dynamics of human gait: Stability of long-range correlations in stride interval fluctuations. J. Appl. Physiol. 1996, 80, 1448–1457. [Google Scholar] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).