Structure and Dynamics of Water at Carbon-Based Interfaces
Abstract
:1. Introduction
2. Liquid Water on Carbon-Based Interfaces
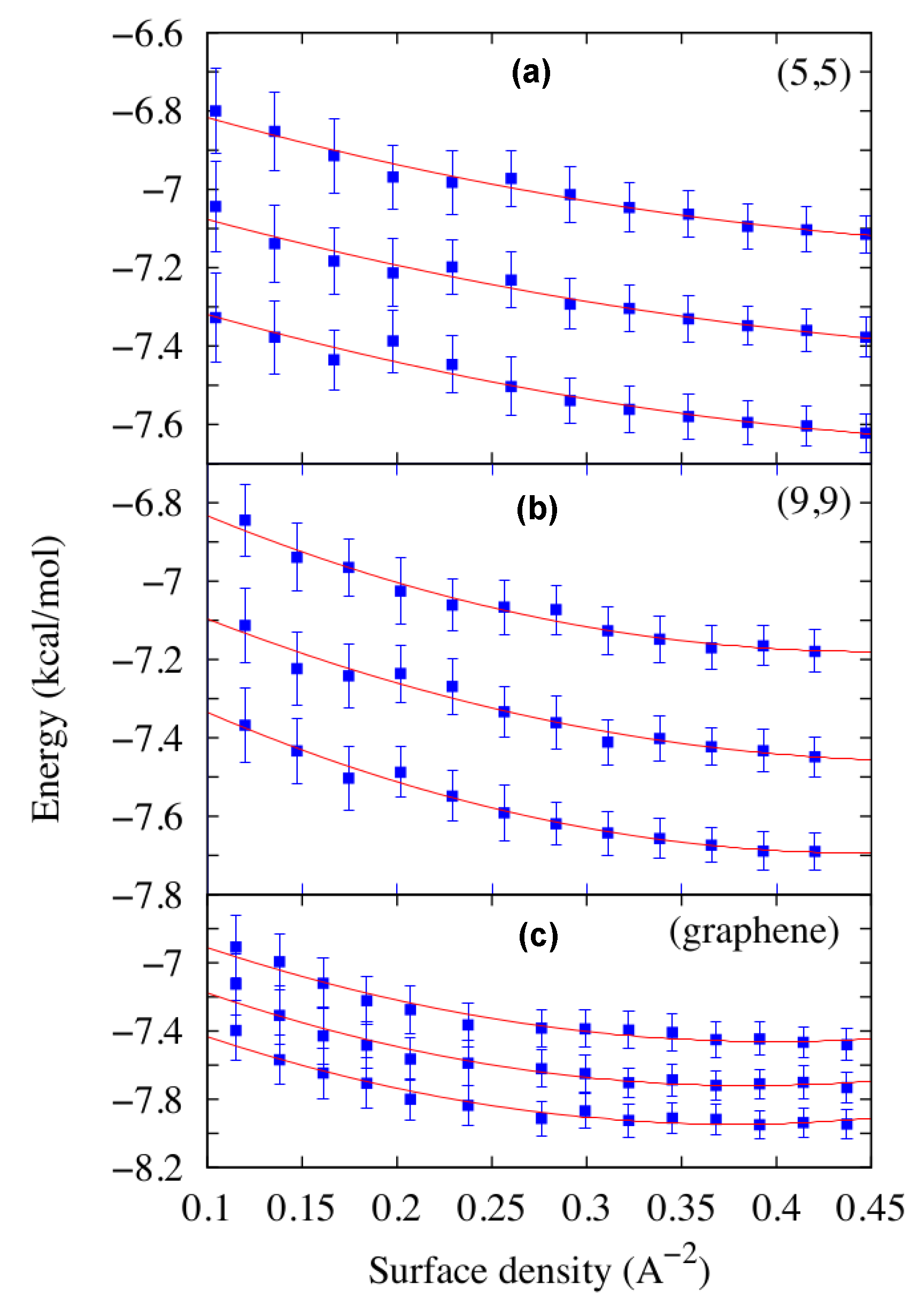
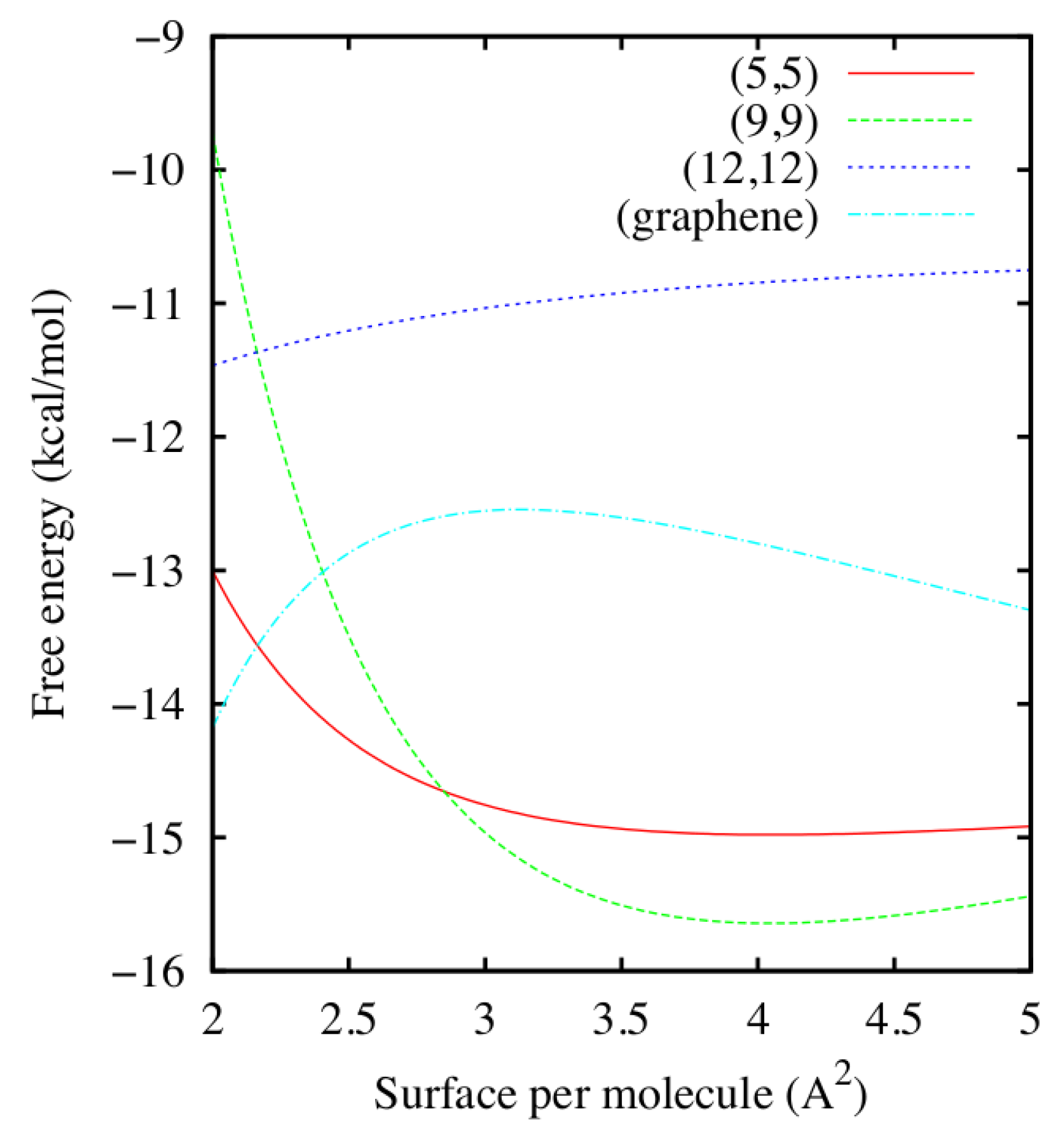
2.1. Thermodynamic Stability
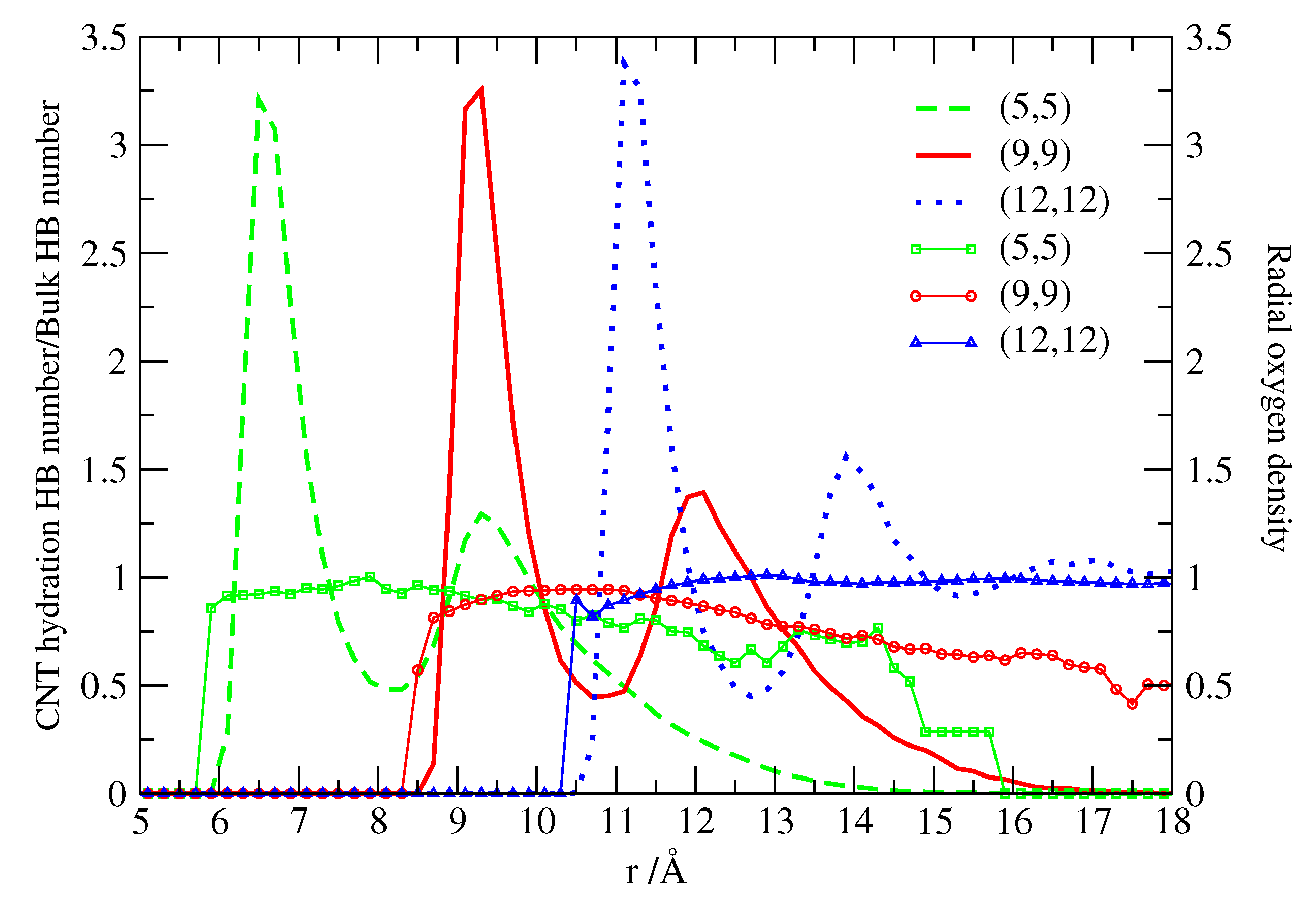
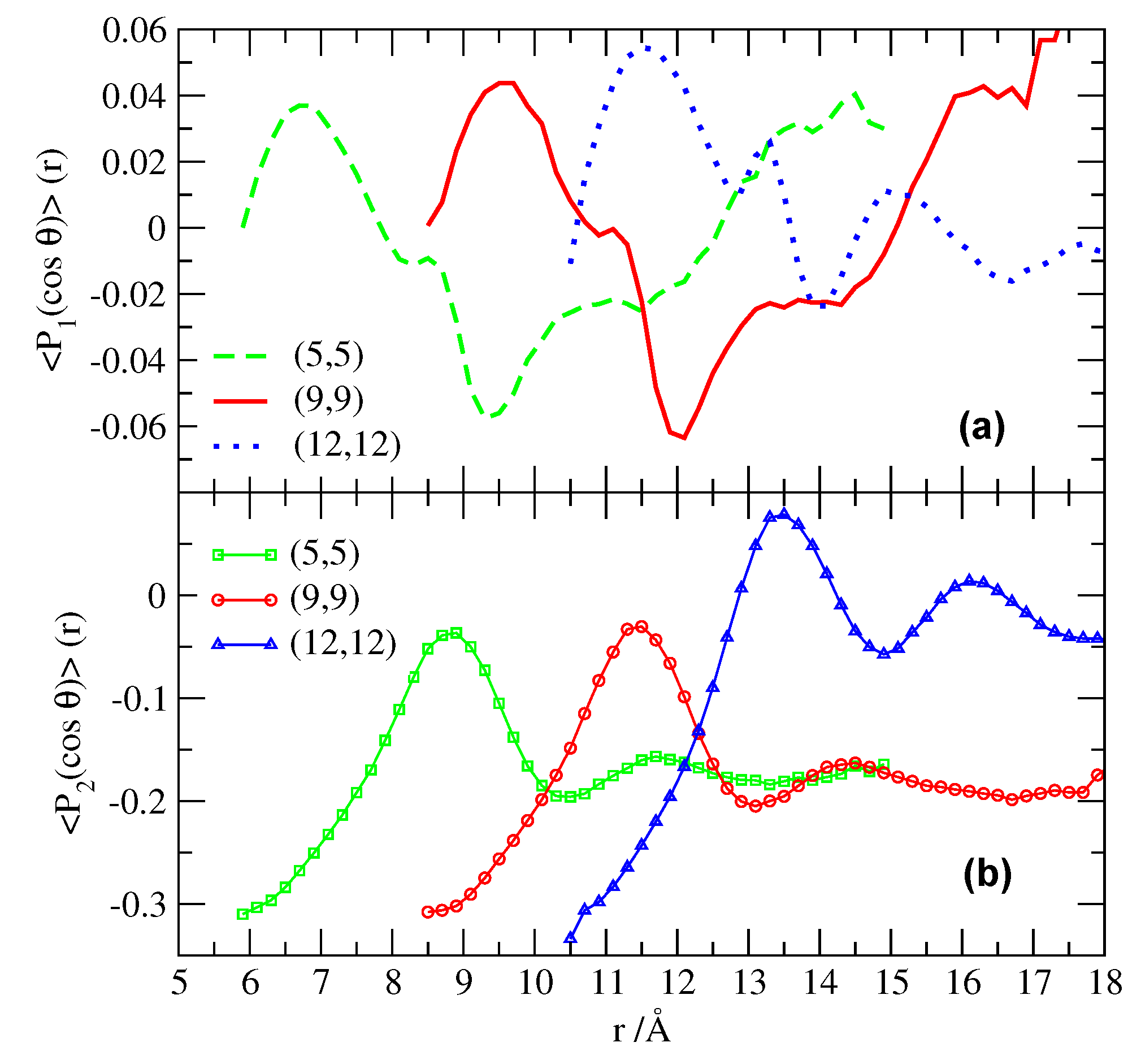
2.2. Structure and Hydrogen Bonding
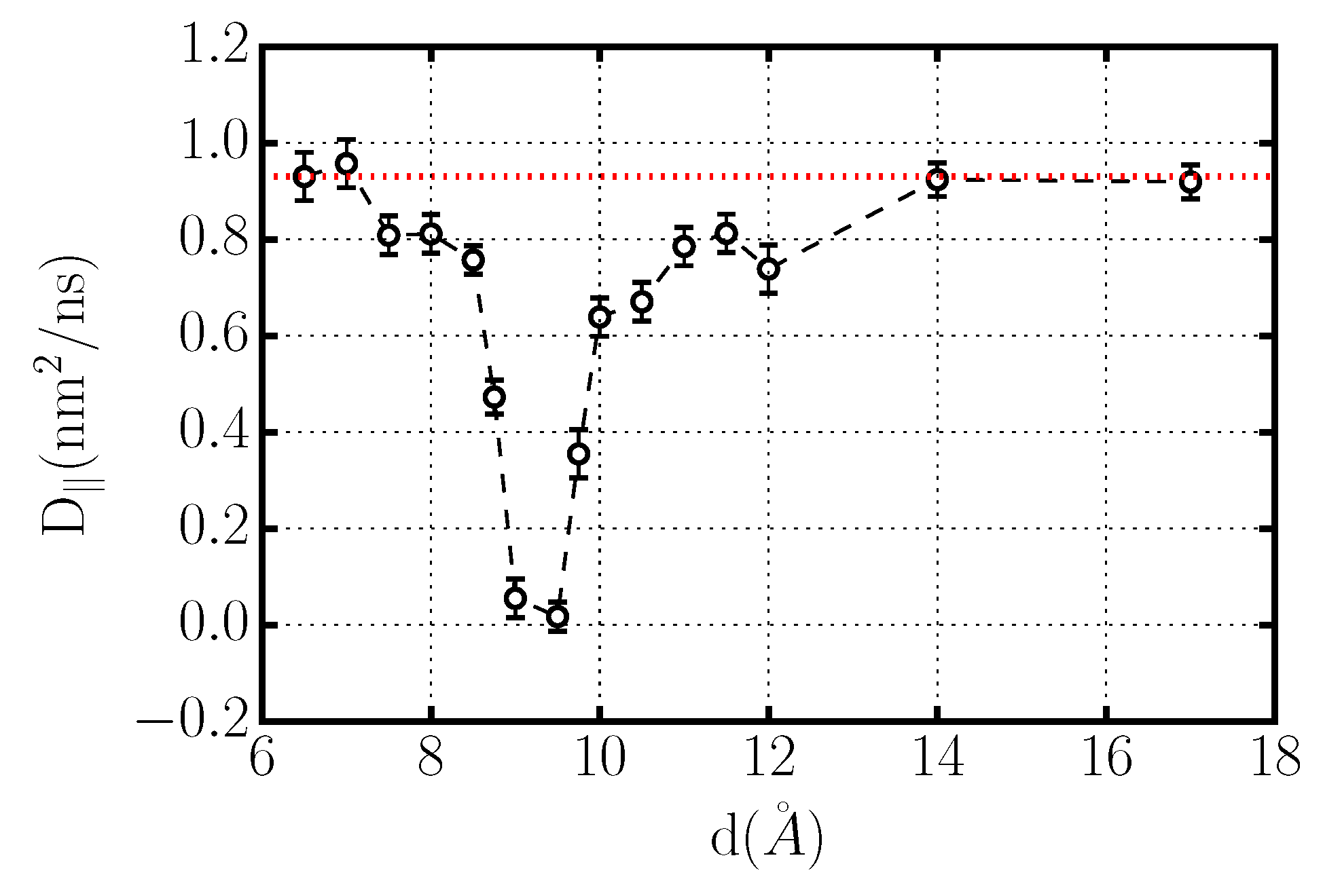
2.3. Diffusion Coefficients
2.3.1. Water inside CNTs
2.3.2. Water outside CNTs and on Flat Rigid Graphene
2.3.3. Water on Corrugated Graphene
3. Results
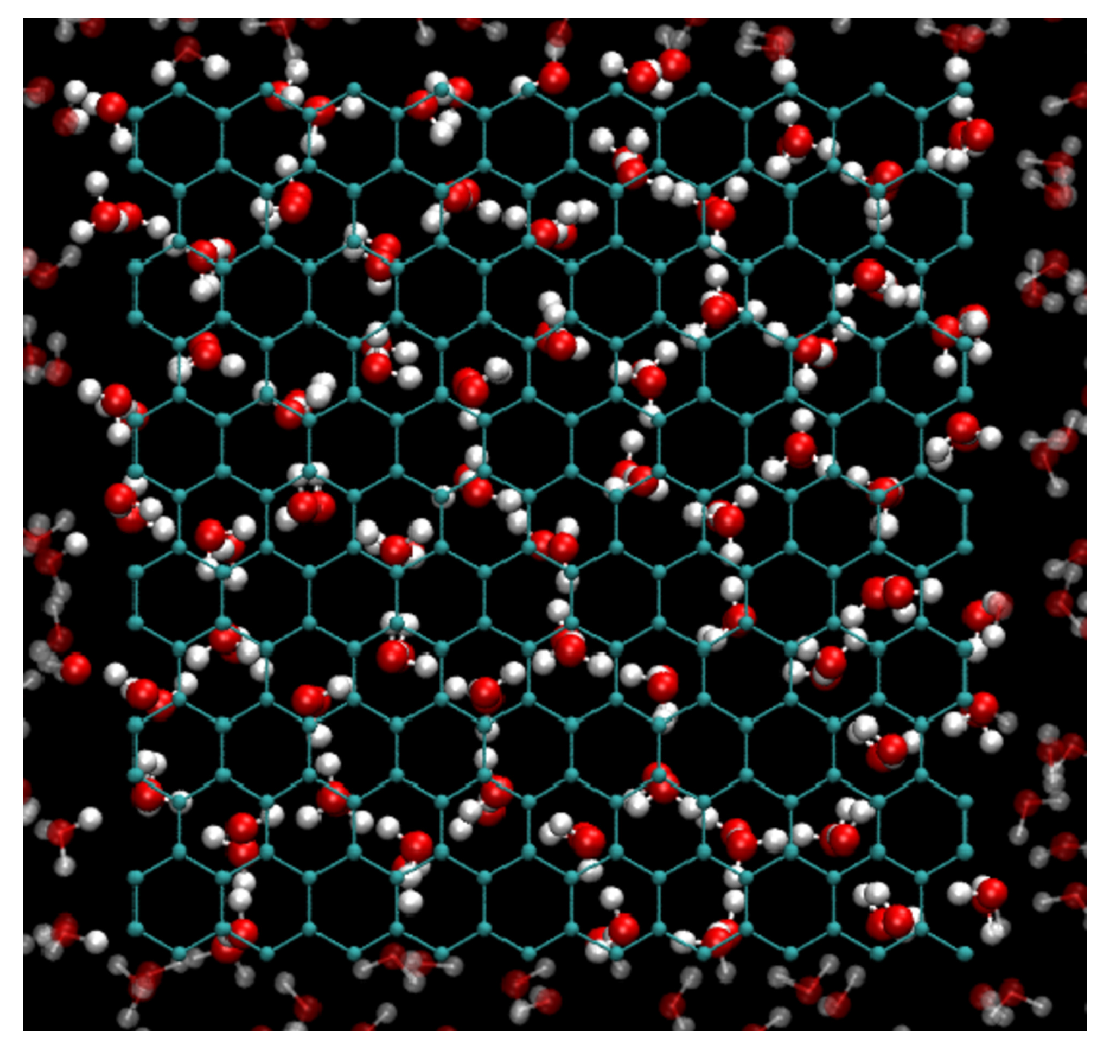
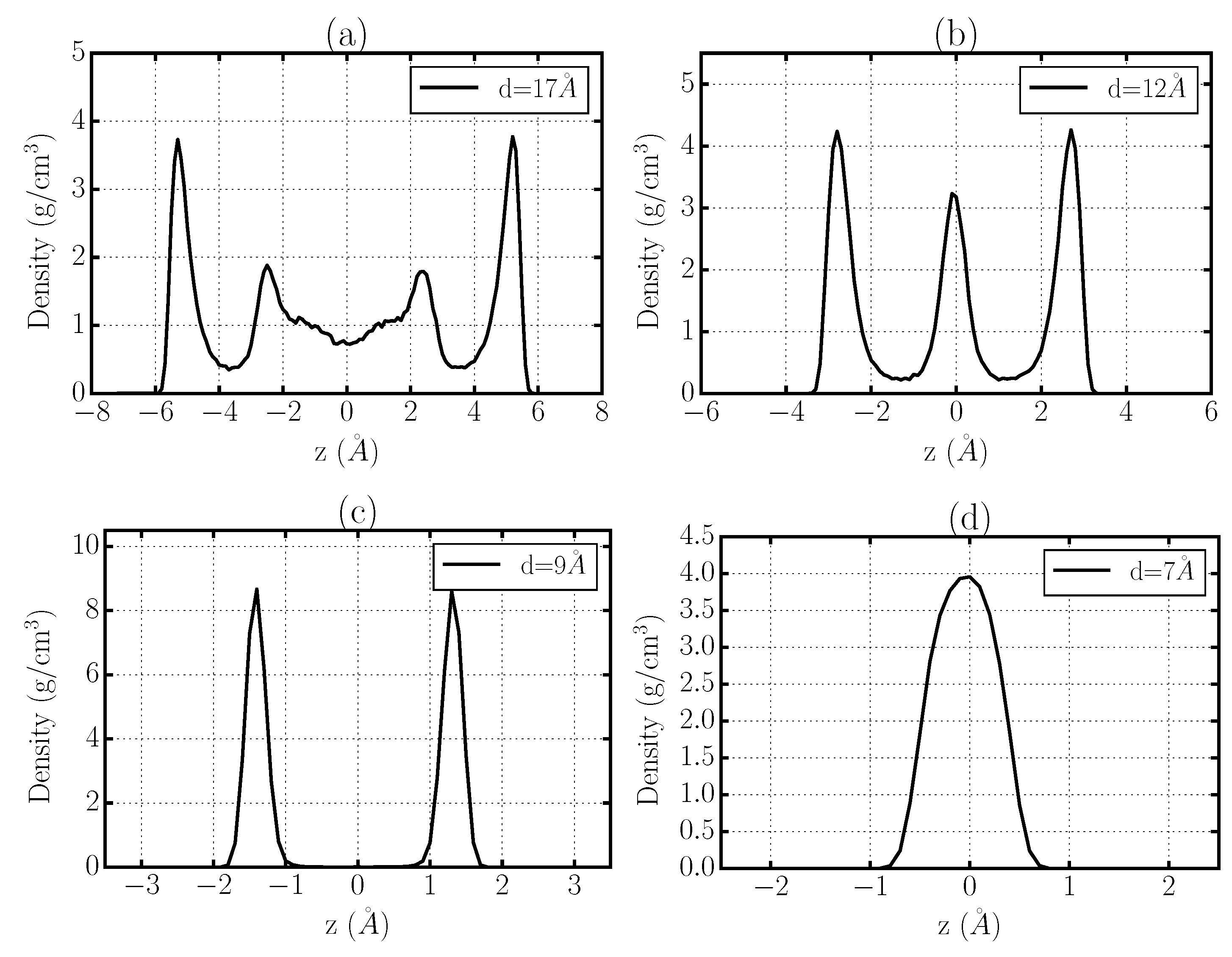
3.1. Crystallization of Water by Confinement between Graphene Plates
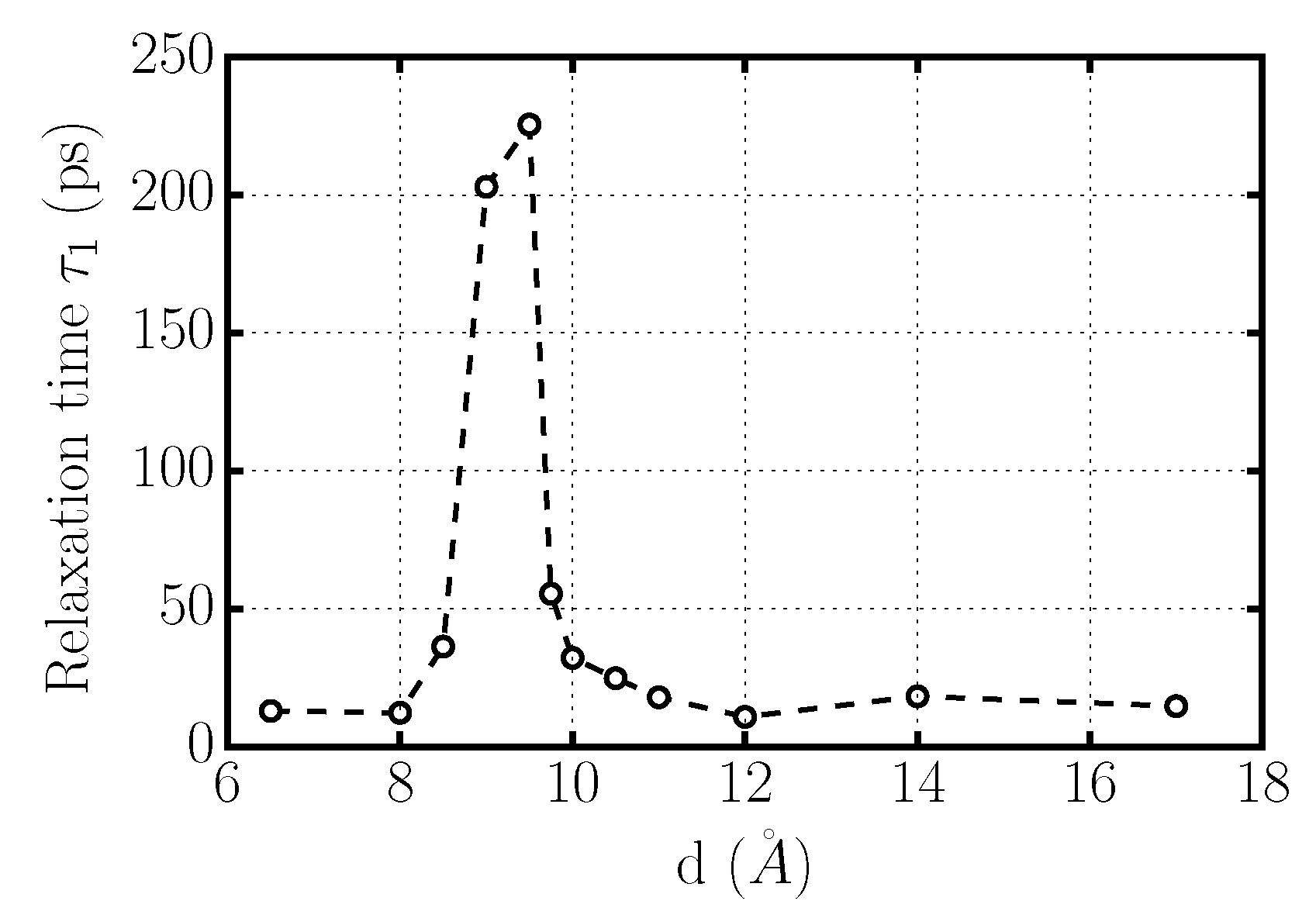
Dynamics of Confined Water
3.2. Structure of Confined Water
4. Computational Methods
4.1. Water Adsorbed at the Outside of Rigid CNTs and on Flat Graphene
4.2. Corrugated Graphene
4.3. Water Confined between Graphene Plates
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gileadi, E.; Kirowa-Eisner, E.; Penciner, J. Interfacial Electrochemistry; Addison-Wesley: Reading, MA, USA, 1975. [Google Scholar]
- Thiel, P.A.; Madey, T.E. The interaction of water with solid surfaces: fundamental aspects. Surf. Sci. Rep. 1987, 7, 211–385. [Google Scholar] [CrossRef]
- Butler, G.; Ison, H.C.K. Corrosion and Its Prevention in Waters; Reinhold: New York, NY, USA, 1966. [Google Scholar]
- Bartón, K. Protection against Atmosferic Corrosion: Theories and Methods; Wiley: London, UK, 1976. [Google Scholar]
- Turner, J.E.; Hendewerk, M.; Somorjai, G.A. The photodissociation of water by doped iron oxides: The unbiased p/n assembly. Chem. Phys. Lett. 1984, 105, 581–585. [Google Scholar] [CrossRef]
- Xue, G.; Xu, Y.; Ding, T.; Li, J.; Yin, J.; Fei, W.; Cao, Y.; Yu, J.; Yuan, L.; Gong, L.; et al. Water-evaporation-induced electricity with nanostructured carbon materials. Nat. Nano 2017. [Google Scholar] [CrossRef] [PubMed]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; Springer: Dordrecht, The Netherlands, 1978; pp. 257–268. [Google Scholar]
- Kim, J.; Lu, W.; Qiu, W.; Wang, L.; Caffey, M.; Zhong, D. Ultrafast hydration dynamics in the lipidic cubic phase: Discrete water structures in nanochannels. J. Phys. Chem. B 2006, 110, 21994–22000. [Google Scholar] [CrossRef] [PubMed]
- Tong, J.; Briggs, M.M.; McIntosh, T.J. Water permeability of aquaporin-4 channel depends on bilayer composition, thickness, and elasticity. Biophys. J. 2012, 103, 1899–1908. [Google Scholar] [CrossRef] [PubMed]
- Russo, C.J.; Passmore, L.A. Progress towards an optimal specimen support for electron cryomicroscopy. Curr. Opin. Struct. Biol. 2016, 37, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Gelb, L.D.; Gubbins, K.E.; Radhakrishnan, R.; Sliwinska-Bartowiak, M. Phase separation in confined systems. Rep. Prog. Phys. 1999, 62, 1573–1660. [Google Scholar] [CrossRef]
- Evans, R.; Marini Bettolo Marconi, U.; Tarazona, P. Fluids in narrow pores: Adsorption, capillary condensation, and critical points. J. Chem. Phys. 1986, 84, 2376–2399. [Google Scholar] [CrossRef]
- Bal, P.C.; Evans, R. Temperature dependence of gas adsorption on a mesoporous solid: Capillary criticality and hysteresis. Langmuir 1989, 5, 714–723. [Google Scholar] [CrossRef]
- Zangi, R.; Mark, A.E. Monolayer Ice. Phys. Rev. Lett. 2003, 91, 025502. [Google Scholar] [CrossRef] [PubMed]
- Zangi, R. Water confined to a slab geometry: A review of recent computer simulation studies. J. Phys. Condens. Matter 2004, 16, S5371–S5388. [Google Scholar] [CrossRef]
- Kumar, P.; Buldyrev, S.V.; Starr, F.W.; Giovambattista, N.; Stanley, H.E. Thermodynamics, structure, and dynamics of water confined between hydrophobic plates. Phys. Rev. E 2005, 72, 051503. [Google Scholar] [CrossRef] [PubMed]
- Vilanova, O.; Franzese, G. Structural and dynamical properties of nanoconfined supercooled water. arXiv, 2011; arXiv:1102.2864. [Google Scholar]
- Chen, J.; Schusteritsch, G.; Pickard, C.J.; Salzmann, C.G.; Michaelides, A. Two Dimensional Ice from First Principles: Structures and Phase Transitions. Phys. Rev. Lett. 2016, 116, 025501. [Google Scholar] [CrossRef]
- Corsetti, F.; Matthews, P.; Artacho, E. Structural and configurational properties of nanoconfined monolayer ice from first principles. Sci. Rep. 2016, 6, 18651. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.Y.; McCammon, J.A.; Rossky, P.J. The structure of liquid water at an extended hydrophobic surface. J. Chem. Phys. 1984, 80, 4448–4455. [Google Scholar] [CrossRef]
- Zhu, S.-B.; Robinson, G.W. Structure and dynamics of liquid water between plates. J. Chem. Phys. 1990, 94, 1403–1410. [Google Scholar] [CrossRef]
- Mamatkulov, S.I.; Khabibullaev, P.K.; Netz, R.R. Water at hydrophobic substrates: curvature, pressure, and temperature effects. Langmuir 2004, 20, 4756–4763. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, N.; Pettitt, B.M. On the mechanism of hydrophobic association of nanoscopic solutes. J. Am. Chem. Soc. 2005, 127, 3556–3567. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, N.; Pettitt, B.M. Dynamics of water trapped between hydrophobic solutes. J. Phys. Chem. B 2005, 109, 6422–6429. [Google Scholar] [CrossRef] [PubMed]
- Gallo, P.; Rovere, M. Anomalous dynamics of confined water at low hydration. J. Phys. Condens. Matter 2003, 15, 7625–7633. [Google Scholar] [CrossRef]
- Rovere, M.; Ricci, M.A.; Vellati, D.; Bruni, F. A molecular dynamics simulation of water confined in a cylindrical SiO2 pore. J. Chem. Phys. 1998, 108, 9859–9867. [Google Scholar] [CrossRef]
- Spohr, E. Computer simulation of the water/platinum interface. Dynamical results. Chem. Phys. 1990, 141, 87–94. [Google Scholar] [CrossRef]
- Rustad, J.R.; Felmy, A.R.; Bylaska, E.J. Molecular simulation of the magnetite-water interface. Geochim. Cosmochim. Acta 2003, 67, 1001–1016. [Google Scholar] [CrossRef]
- Martins, L.R.; Skaf, M.S.; Ladanyi, B.M. Solvation dynamics at the water/zirconia interface: Molecular dynamics simulations. J. Phys. Chem. B 2004, 108, 19687–19697. [Google Scholar] [CrossRef]
- Gordillo, M.C.; Martí, J. Molecular dynamics description of a layer of water molecules on a hydrophobic surface. J. Chem. Phys. 2002, 117, 3425–3430. [Google Scholar] [CrossRef]
- Striolo, A.; Chialvo, A.; Cummings, P.T.; Gubbins, K.E. Water adsorption in carbon-slit nanopores. Langmuir 2003, 19, 8583–8591. [Google Scholar] [CrossRef]
- Cabrera Sanfelix, P.; Holloway, S.; Kolasinski, K.W.; Darling, G.R. The structure of water on the (0001) surface of graphite. Surf. Sci. 2003, 532–535, 166–172. [Google Scholar] [CrossRef]
- Pertsin, A.; Grunze, M. Water-graphite interaction and behavior of water near the graphite surface. J. Phys. Chem. B 2004, 108, 1357–1364. [Google Scholar] [CrossRef]
- Gordillo, M.C.; Nagy, G.; Martí, J. Structure of water nanoconfined between hydrophobic surfaces. J. Chem. Phys. 2005, 123, 054707. [Google Scholar] [CrossRef] [PubMed]
- Hummer, G.; Rasaiah, J.C.; Noworyta, J.P. Water conduction through the hydrophobic channel of a carbon nanotube. Nature 2001, 414, 188–190. [Google Scholar] [CrossRef] [PubMed]
- Gordillo, M.C.; Martí, J. Water on the outside of carbon nanotube bundles. Phys. Rev. B. 2003, 67, 205425. [Google Scholar] [CrossRef]
- Striolo, A.; Chialvo, A.; Cummings, P.T.; Gubbins, K.E. Simulated water adsorption in chemically heterogeneous carbon nanotubes. J. Chem. Phys. 2006, 124, 074710. [Google Scholar] [CrossRef] [PubMed]
- Nagy, G. Water structure at the graphite (0001) surface by STM measurements. J. Electroanal. Chem. 1996, 409, 19–23. [Google Scholar] [CrossRef]
- Daio, T.; Bayer, T.; Ikuta, T.; Nishiyama, T.; Takahashi, K.; Takata, Y.; Sasaki, K.; Matthew Lyth, S. In-Situ ESEM and EELS Observation of Water Uptake and Ice Formation in Multilayer Graphene Oxide. Sci. Rep. 2015, 5, 11807. [Google Scholar] [CrossRef] [PubMed]
- Scodinu, A.; Fourkas, J.T. Comparison of the orientational dynamics of water confined in hydrophobic and hydrophilic nanopores. J. Phys. Chem. B 2002, 106, 10292–10295. [Google Scholar] [CrossRef]
- Teschke, O.; de Souza, E.F. Water molecular arrangement at air/water interfaces probed by atomic force microscopy. Chem. Phys. Lett. 2005, 403, 95–101. [Google Scholar] [CrossRef]
- Tombari, E.; Salvetti, G.; Ferrari, C.; Johari, G.P. Thermodynamic functions of water and ice confined to 2 nm radius pores. J. Chem. Phys. 2005, 122, 104712. [Google Scholar] [CrossRef] [PubMed]
- Ricci, M.A.; Bruni, F.; Gallo, P.; Rovere, M.; Soper, A.K. Water in confined geometries: experiments and simulations. J. Phys. Condens. Matter 2000, 12, A345–A350. [Google Scholar] [CrossRef]
- Janiak, C.; Scharmann, T.G.; Mason, S.A. Two-dimensional water and ice layers: Neutron diffraction studies at 278, 263, and 20 K. J. Am. Chem. Soc. 2002, 124, 14010–14011. [Google Scholar] [CrossRef] [PubMed]
- Kolesnikov, A.I.; Zanotti, J.-M.; Loong, C.-K.; Thiyagarajan, P.; Moravsky, A.P.; Loufty, R.O.; Burnham, C.J. Anomalously soft dynamics of water in a nanotube: a revelation of nanoscale confinement. Phys. Rev. Lett. 2004, 93, 035503. [Google Scholar] [CrossRef] [PubMed]
- Sliwinska-Bartkoviak, M.; Jazdzewska, M.; Huan, L.L.; Gubbins, K.E. Melting behavior of water in cylindrical pores: Carbon nanotubes and silica glasses. Phys. Chem. Chem. Phys. 2008, 10, 4909–4919. [Google Scholar] [CrossRef] [PubMed]
- Mouterde, T.; Lehoucq, G.; Xavier, S.; Checco, A.; Black, C.T.; Rahman, A.; Midavaine, T.; Clanet, C.; Quere, D. Antifogging abilities of model nanotextures. Nat. Mater. 2017. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.; Vasu, K.S.; Williams, C.D.; Gopinadhan, K.; Su, Y.; Cherian, C.; Dix, J.; Prestat, E.; Haigh, S.J.; Grigorieva, I.V.; et al. Tuneable Sieving of Ions Using Graphene Oxide Membranes. arXiv, 2017; arXiv:1701.05519. [Google Scholar]
- Gordillo, M.C.; Martí, J. Structure of water adsorbed on a single graphene sheet. Phys. Rev. B. 2008, 78, 075432. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
- Calero, C.; Gordillo, M.C.; Martí, J. Size effects on water adsorbed on hydrophobic probes at the nanometric scale. J. Chem. Phys. 2013, 138, 214702. [Google Scholar] [CrossRef] [PubMed]
- Werder, T.; Walther, J.H.; Jaffe, R.L.; Halicioglu, T.; Koumoutsakos, P. On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 2003, 107, 1345–1352. [Google Scholar] [CrossRef]
- Martí, J. Dynamic properties of hydrogen-bonded networks in supercritical water. Phys. Rev. E 2000, 61, 449–456. [Google Scholar] [CrossRef]
- Boero, M.; Terakura, K.; Ikeshoji, T.; Liew, C.C.; Parrinello, M. Hydrogen bonding and dipole moment of water at supercritical conditions: A first-principles molecular dynamics study. Phys. Rev. Lett. 2000, 85, 3245–3248. [Google Scholar] [CrossRef] [PubMed]
- Matubayasi, N.; Wakai, C.; Nakahara, M. Structural study of supercritical water. I. Nuclear magnetic resonance spectroscopy. J. Chem. Phys. 1997, 107, 9133–9140. [Google Scholar] [CrossRef]
- Martí, J.; Nagy, G.; Gordillo, M.C.; Guàrdia, E. Molecular simulation of liquid water confined inside graphite channels: Thermodynamics and structural properties. J. Chem. Phys. 2006, 124, 094703. [Google Scholar] [CrossRef] [PubMed]
- Nagy, G.; Gordillo, M.C.; Guàrdia, E.; Martí, J. Liquid water confined in carbon nanochannels at high temperatures. J. Phys. Chem. B 2007, 111, 12524–12530. [Google Scholar] [CrossRef] [PubMed]
- Cicero, G.; Grossman, J.K.; Schwegler, E.; Gygi, F.; Galli, G. Water confined in nanotubes and between graphene sheets: A first principle study. J. Am. Chem. Soc. 2008, 130, 1871–1878. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, N. On the Manifestation of Hydrophobicity at the Nanoscale. J. Phys. Chem. B 2008, 112, 6296–6300. [Google Scholar] [CrossRef] [PubMed]
- Madden, P.; Kivelson, D. A consistent molecular treatment of dielectric phenomena. Adv. Chem. Phys. 1984, 56, 467–566. [Google Scholar]
- Gilijamse, J.J.; Lock, A.J.; Bakker, H.J. Dynamics of confined water molecules. Proc. Natl. Acad. Sci. USA 2005, 102, 3202–3207. [Google Scholar] [CrossRef] [PubMed]
- Tummala, N.R.; Striolo, A. Hydrogen-Bond Dynamics for Water Confined in Carbon Tetrachloride-Acetone Mixtures. J. Phys. Chem. B 2008, 112, 10675–10683. [Google Scholar] [CrossRef] [PubMed]
- Martí, J.; Nagy, G.; Gordillo, M.C.; Guàrdia, E. Molecular dynamics simulation of liquid water confined inside graphite channels: Dielectric and dynamical properties. J. Phys. Chem. B 2006, 110, 23987–23994. [Google Scholar] [CrossRef] [PubMed]
- Martí, J.; Gordillo, M.C. Temperature effects on the static and dynamic properties of liquid water inside nanotubes. Phys. Rev. E 2001, 64, 021504. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Zhang, H.; Zheng, Y.; Zhang, Z. Nanoconfinement induced anomalous water diffusion inside carbon nanotubes. Microfluid. Nanofluid. 2011, 10, 1359–1364. [Google Scholar] [CrossRef]
- Zheng, Y.-G.; Ye, H.-F.; Zhang, Z.-Q.; Zhang, H.-W. Water diffusion inside carbon nanotubes: Mutual effects of surface and confinement. Phys. Chem. Chem. Phys. 2012, 14, 964–971. [Google Scholar] [CrossRef] [PubMed]
- Bordin, J.R.; de Oliveira, A.B.; Diehl, A.; Barbosa, M.C. Diffusion enhancement in core-softened fluid confined in nanotubes. J. Chem. Phys. 2012, 137, 084504. [Google Scholar] [CrossRef] [PubMed]
- de los Santos, F.; Franzese, G. Relations between the diffusion anomaly and cooperative rearranging regions in a hydrophobically nanoconfined water monolayer. Phys. Rev. E 2012, 85, 010602. [Google Scholar] [CrossRef] [PubMed]
- Gordillo, M.C.; Martí, J. Hydrogen bond structure of liquid water confined in nanotubes. Chem. Phys. Lett. 2000, 329, 341–345. [Google Scholar] [CrossRef]
- Holt, J.K.; Park, H.G.; Wang, Y.; Stadermann, M.; Artyukhin, A.B.; Grigoropoulos, C.P.; Noy, A.; Bakajin, O. Fast Mass Transport Through Sub-2-Nanometer Carbon Nanotubes. Science 2006, 312, 1034–1037. [Google Scholar] [CrossRef] [PubMed]
- Martí, J.; Gordillo, M.C. Time-dependent properties of liquid water isotopes adsorbed in carbon nanotubes. J. Chem. Phys. 2001, 114, 10486–10492. [Google Scholar] [CrossRef]
- Krynicki, K.; Green, C.D.; Sawyer, D.W. Pressure and temperature dependence of self-diffusion in water. Faraday Discuss. Chem. Soc. 1978, 66, 199–208. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Hausser, R.; Maier, G.; Noack, F. Kernmagnetische messungen von selbstdiffusions-koeffizienten in wasser und benzol bis zum kritischen punkt. Z. Naturforsch. A 1966, 21, 1410–1415. [Google Scholar] [CrossRef]
- Martí, J.; Gordillo, M.C. Structure and dynamics of liquid water adsorbed on the external walls of carbon nanotubes. J. Chem. Phys. 2003, 119, 12540–12546. [Google Scholar] [CrossRef]
- Martí, J.; Sala, J.; Guàrdia, E. Molecular dynamics simulations of water confined in graphene nanochannels: From ambient to supercritical environments. J. Mol. Liq. 2009, 153, 72–78. [Google Scholar] [CrossRef]
- Gordillo, M.C.; Martí, J. Effect of surface roughness on the static and dynamic properties of water adsorbed on graphene. J. Phys. Chem. B 2010, 114, 4583–4589. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Harder, E.; Berne, B.J. On the calculation of diffusion coefficients in confined fluids and interfaces with an application to the liquid-vapor interface of water. J. Phys. Chem. B 2004, 108, 6595–6602. [Google Scholar] [CrossRef]
- Martí, J.; Guàrdia, E.; Padró, J.A. Dielectric properties and infrared spectra of liquid water: Influence of the dynamic cross correlations. J. Chem. Phys. 1994, 101, 10883–10891. [Google Scholar] [CrossRef]
- Martí, J.; Padró, J.A.; Guàrdia, E. Molecular dynamics simulation of liquid water along the coexistence curve: Hydrogen bonds and vibrational spectra. J. Chem. Phys. 1996, 105, 639–649. [Google Scholar] [CrossRef]
- Algara-Siller, G.; Lehtinen, O.; Wang, F.C.; Nair, R.R.; Kaiser, U.; Wu, H.A.; Geim, A.K.; Grigorieva, I.V. Square ice in graphene nanocapillaries. Nature 2015, 519, 443–445. [Google Scholar] [CrossRef] [PubMed]
- Zangi, R.; Mark, E.A. Bilayer ice and alternate liquid phases of confined water. J. Chem. Phys. 2003, 119, 1694–1700. [Google Scholar] [CrossRef]
- Giovambattista, N.; Rossky, P.J.; Debenedetti, P.G. Phase transitions induced by nanoconfinement in liquid water. Phys. Rev. Lett. 2009, 102, 050603. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Choi, M.Y.; Kumar, P.; Stanley, H.E. Phase transitions in confined water nanofilms. Nat. Phys. 2010, 6, 685–689. [Google Scholar] [CrossRef]
- Giovambattista, N.; Rossky, P.J.; Debenedetti, P.G. Effect of pressure on the phase behavior and structure of water confined between nanoscale hydrophobic and hydrophilic plates. Phys. Rev. E 2006, 73, 041604. [Google Scholar] [CrossRef] [PubMed]
- Abascal, J.L.F.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef] [PubMed]
- Rozmanov, D.; Kusalik, P.G. Transport coefficients in the TIP4P-2005 water model. J. Chem. Phys. 2012, 136, 044507. [Google Scholar] [CrossRef] [PubMed]
- Vega, C.; Abascal, J.L.F. Relation between the melting temperature and the temperature of maximum density for the most common models of water. J. Chem. Phys. 2005, 123, 144504. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, M.; Alam, M.P.; Chakravarty, C. Thermodynamic, Diffusional, and Structural Anomalies in Rigid-Body Water Models. J. Phys. Chem. B 2011, 115, 6935–6945. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Gr. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comp. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N · log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Fasolino, A.; Los, J.H.; Katsnelson, M.I. Intrinsic ripples in graphene. Nat. Mat. 2006, 6, 858–861. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Abedpour, N.; Neek-Amal, M.; Asgari, R.; Shahbazi, F.; Nafari, N.; Tabar, M.R.R. Roughness of undoped graphene and its short-range induced gauge field. Phys. Rev. B 2007, 76, 195407. [Google Scholar] [CrossRef]
- Bao, W.; Miao, F.; Chen, Z.; Zhang, H.; Jang, W.; Dames, C.; Lau, C.N. Controlled ripple texturing of suspended graphene and ultrathin graphite membranes. Nat. Nanotechnol. 2009, 4, 562–566. [Google Scholar] [CrossRef] [PubMed]
- Martí, J.; Padró, J.A.; Guàrdia, E. Molecular dynamics calculation of the infrared spectra in liquid H2O-D2O mixtures. J. Mol. Liq. 1994, 62, 17–31. [Google Scholar] [CrossRef]
- Toukan, K.; Rahman, A. Molecular-dynamics study of atomic motions in water. Phys. Rev. B 1985, 31, 2643–2648. [Google Scholar] [CrossRef]
- Martí, J. Analysis of the hydrogen bonding and vibrational spectra of supercritical model water by molecular dynamics simulations. J. Chem. Phys. 1999, 110, 6876–6886. [Google Scholar] [CrossRef]
- Kostov, M.K.; Cheng, H.; Cooper, A.C.; Pez, G.P. Influence of carbon curvature on molecular adsorptions in carbon-based materials: A force field approach. Phys. Rev. Lett. 2002, 89, 146105. [Google Scholar] [CrossRef] [PubMed]
- Berkowitz, M.L. Ewald summation for systems with slab geometry. J. Chem. Phys. 1999, 111, 3155–3162. [Google Scholar]
- Spohr, E. Effect of electrostatic boundary conditions and system size on the interfacial properties of water and aqueous solutions. J. Chem. Phys. 1997, 107, 6342–6348. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
| System | l (nm) | D (nm) | Nw |
|---|---|---|---|
| (5,5) CNT | 7.62 (Z-axis) | 0.66 | 835 |
| (9,9) CNT | 6.43 (Z-axis) | 1.22 | 935 |
| (12,12) CNT | 8.33 (Z-axis) | 1.63 | 4500 |
| Graphene | 3.19 × 3.40 | - | 1252 |
| Bulk water | - | - | 1000 |
| CNT (n,m) | Dtotal | Dz−axis | Dxy−plane |
|---|---|---|---|
| (6,6) | 2.5 | 4.3 | 1.6 |
| (8,8) | 3.2 | 3.5 | 3.0 |
| (10,10) | 3.1 | 3.8 | 2.7 |
| H2O (bulk) | 2.6 | - | - |
| Experimental | 2.3 | - | - |
| CNT (n,m) | Dz |
|---|---|
| (5,5) | 4.9 |
| (9,9) | 4.9 |
| (12,12) | 4.6 |
| Graphene | 4.6 |
| Bulk unconstrained | 5.8 |
| Distortion Amplitude (Å) | Type of Distortion | Water-Graphene | Bulk Region | Water-Vacuum |
|---|---|---|---|---|
| 0 | None | 3.3 | 3.1 | 3.6 |
| 0.7 | Random | 2.8 | 2.1 | 3.2 |
| 0.7 | Equation (8) | 2.8 | 2.3 | 3.7 |
| 0.7 | Equation (9) | 2.8 | 2.1 | 3.6 |
| 0.7 | Equation (7) | 2.6 | 2.2 | 3.3 |
| 5 | Equation (8) | 2.6 | 2.2 | 4.3 |
| 5 | Equation (9) | 2.6 | 2.2 | 4.2 |
| 5 | Equation (7) | 2.6 | 2.2 | 4.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martí, J.; Calero, C.; Franzese, G. Structure and Dynamics of Water at Carbon-Based Interfaces. Entropy 2017, 19, 135. https://doi.org/10.3390/e19030135
Martí J, Calero C, Franzese G. Structure and Dynamics of Water at Carbon-Based Interfaces. Entropy. 2017; 19(3):135. https://doi.org/10.3390/e19030135
Chicago/Turabian StyleMartí, Jordi, Carles Calero, and Giancarlo Franzese. 2017. "Structure and Dynamics of Water at Carbon-Based Interfaces" Entropy 19, no. 3: 135. https://doi.org/10.3390/e19030135
APA StyleMartí, J., Calero, C., & Franzese, G. (2017). Structure and Dynamics of Water at Carbon-Based Interfaces. Entropy, 19(3), 135. https://doi.org/10.3390/e19030135







