Permutation Entropy: New Ideas and Challenges
Abstract
:1. Introduction
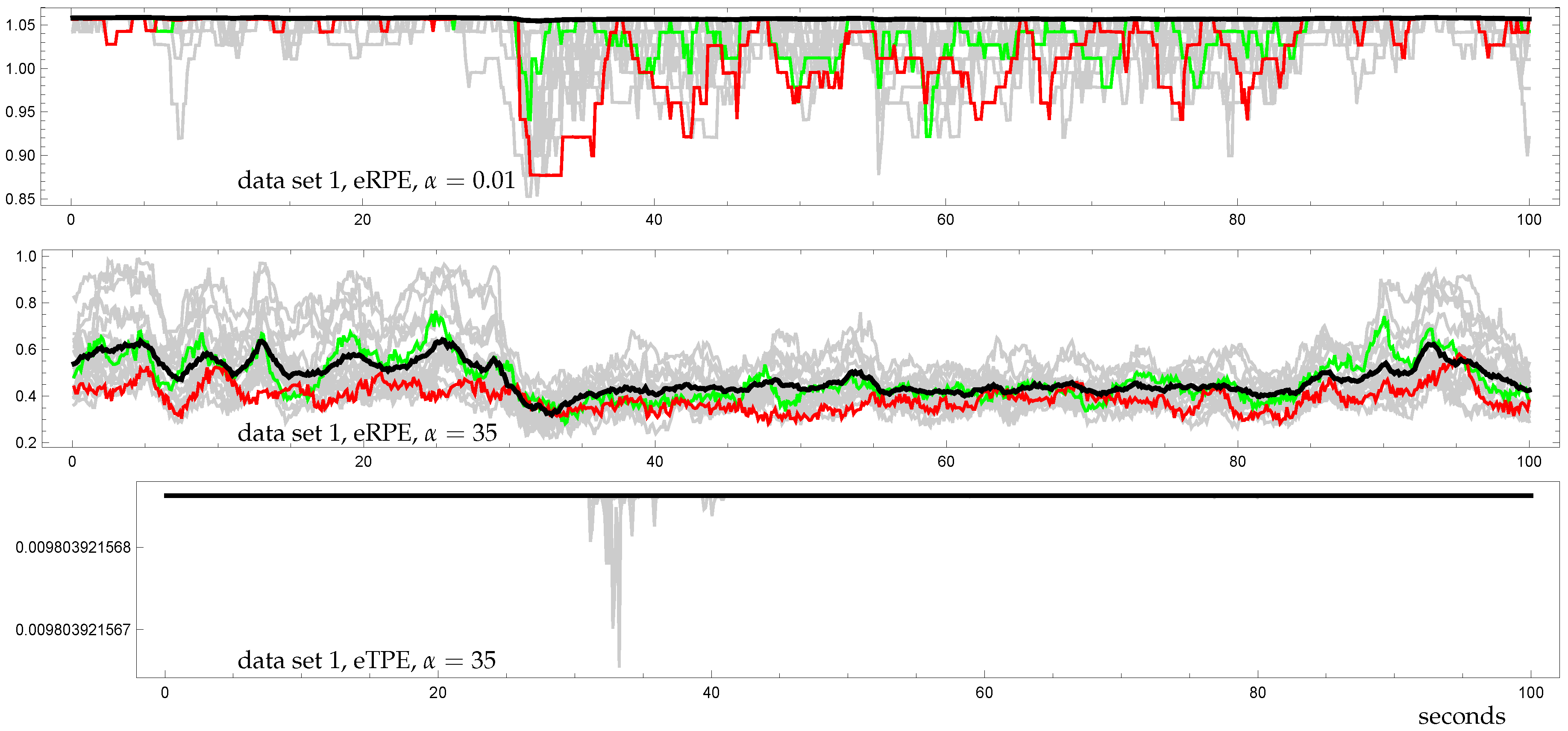
2. Some Theoretical Background
2.1. The Kolmogorov–Sinai Entropy
2.2. Observables and Ordinal Partitioning
2.3. No Information Loss
2.4. Conditional Entropy of Ordinal Patterns
2.5. Permutation Entropy
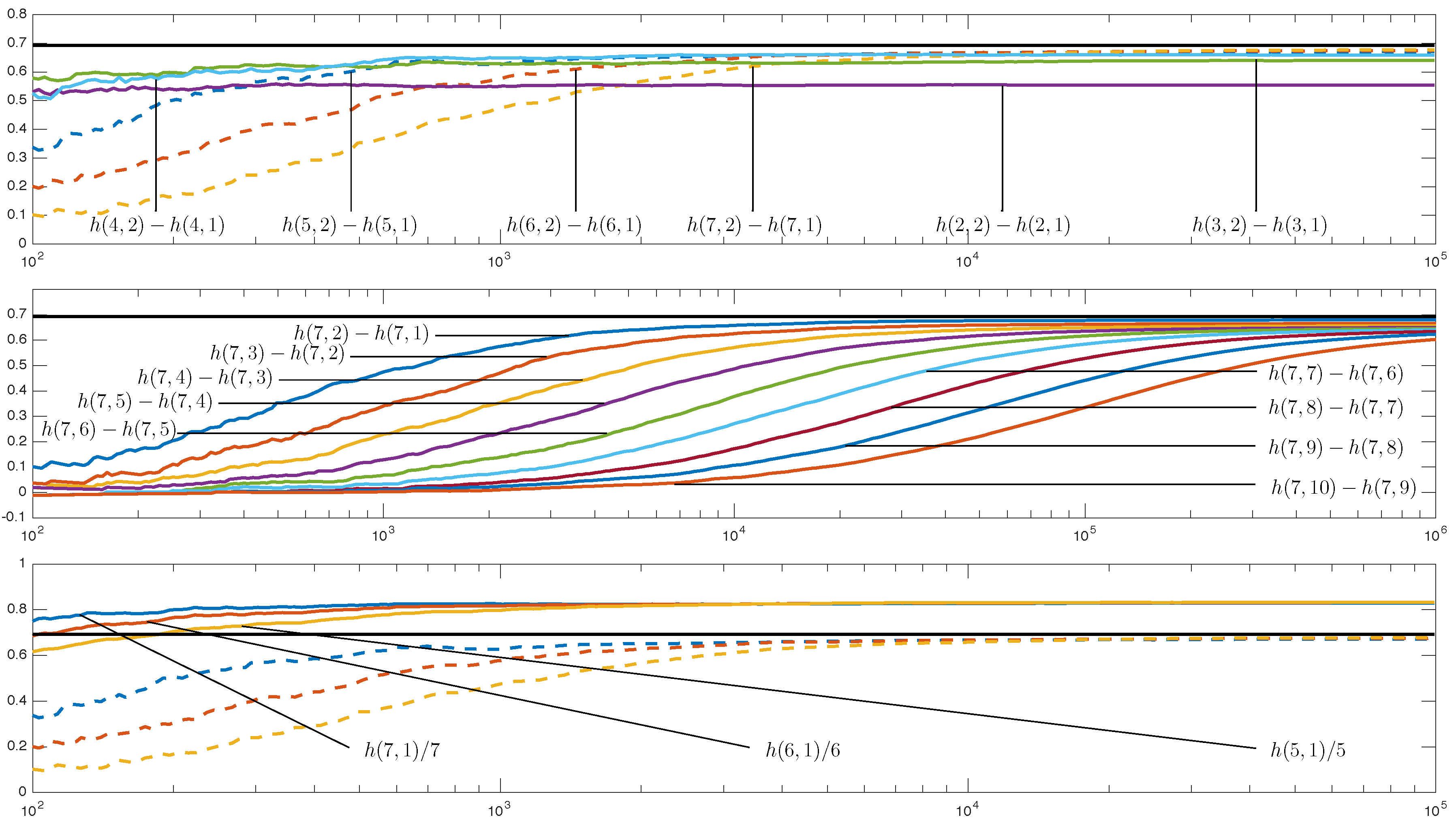
2.6. The Practical Viewpoint
3. Generalizations Based on the Families of Renyi and Tsallis Entropies
3.1. The Concept
3.2. Some Properties
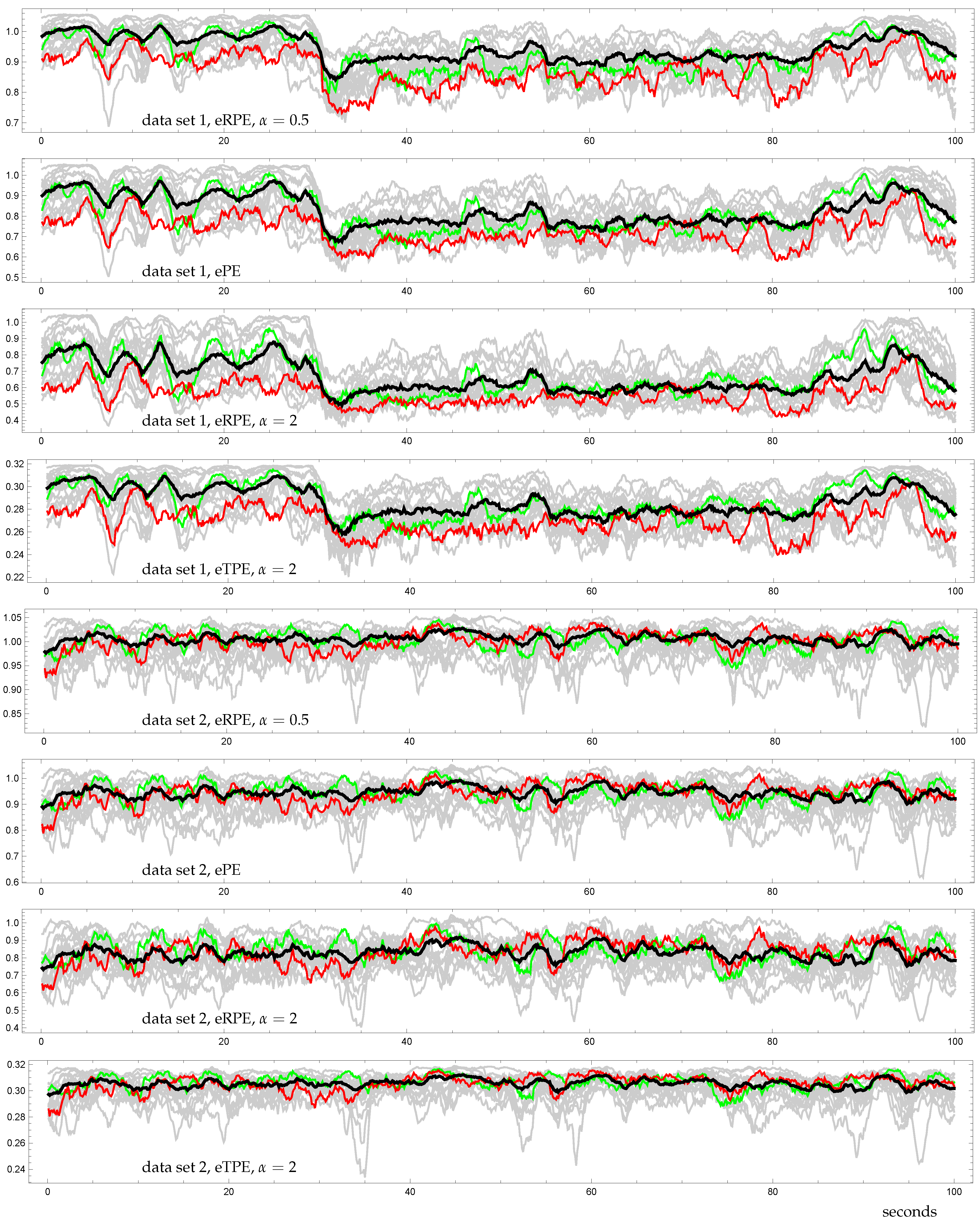
3.3. Demonstration
4. Classification on the Base of Different Entropies
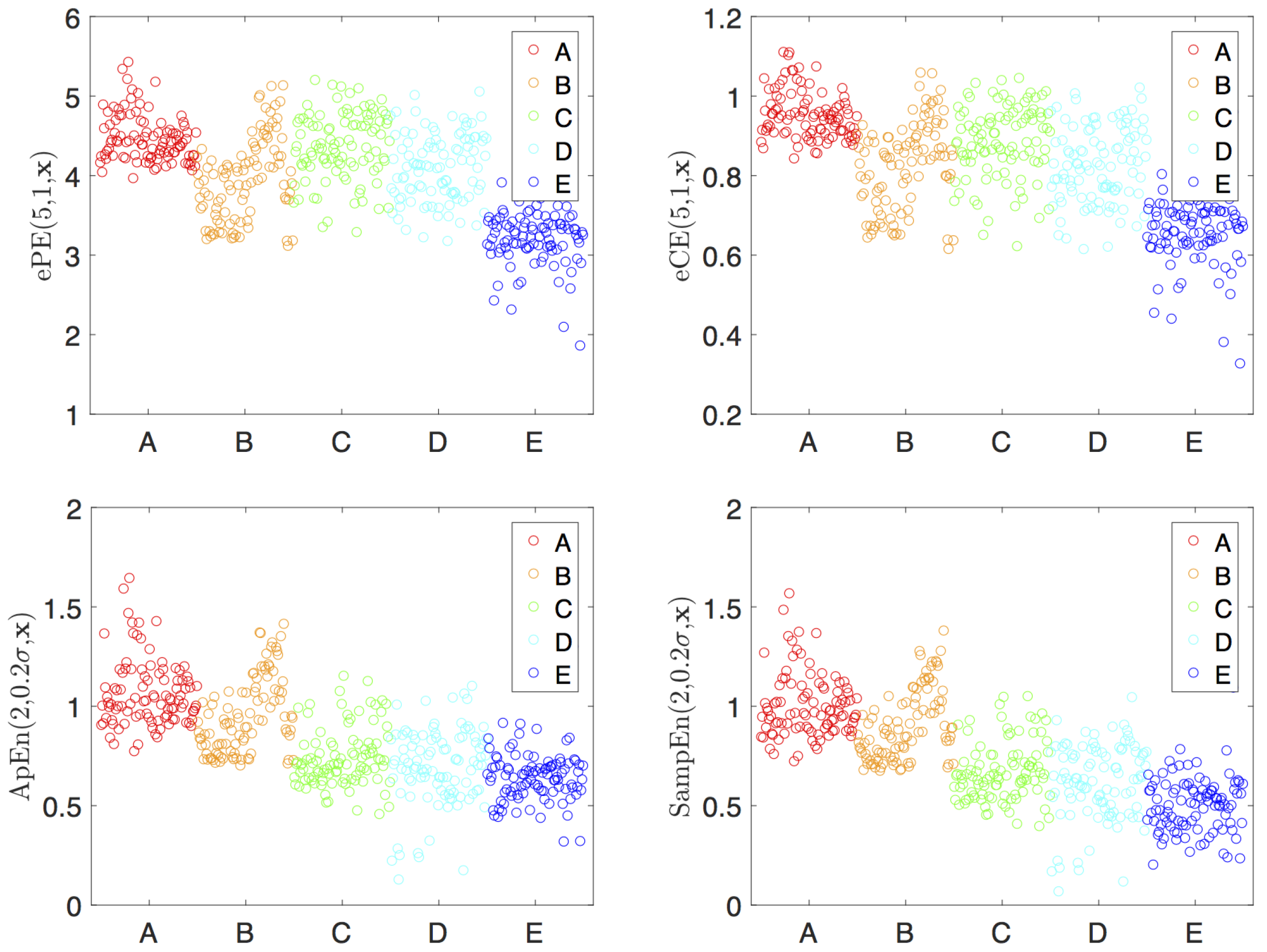
4.1. The Data
- group A: surface EEG’s recorded from healthy subjects with open eyes,
- group B: surface EEG’s recorded from healthy subjects with closed eyes,
- group C: intracranial EEG’s recorded from subjects with epilepsy during a seizure-free period from within the epileptogenic zone,
- group D: intracranial EEG’s recorded from subjects with epilepsy during a seizure-free period from hippocampal formation of the opposite hemisphere of the brain,
- group E: intracranial EEG’s recorded from subjects with epilepsy during a seizure period.
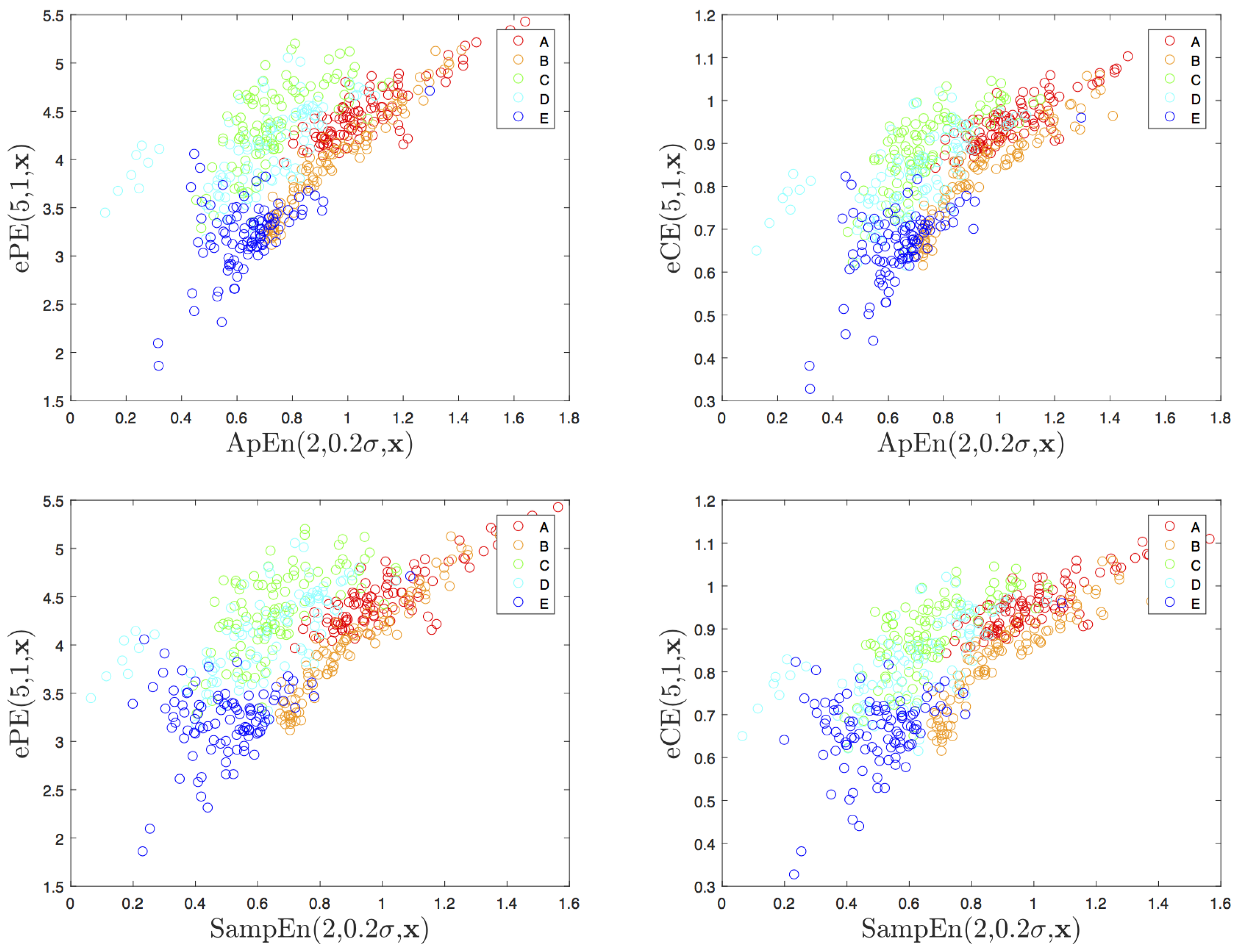
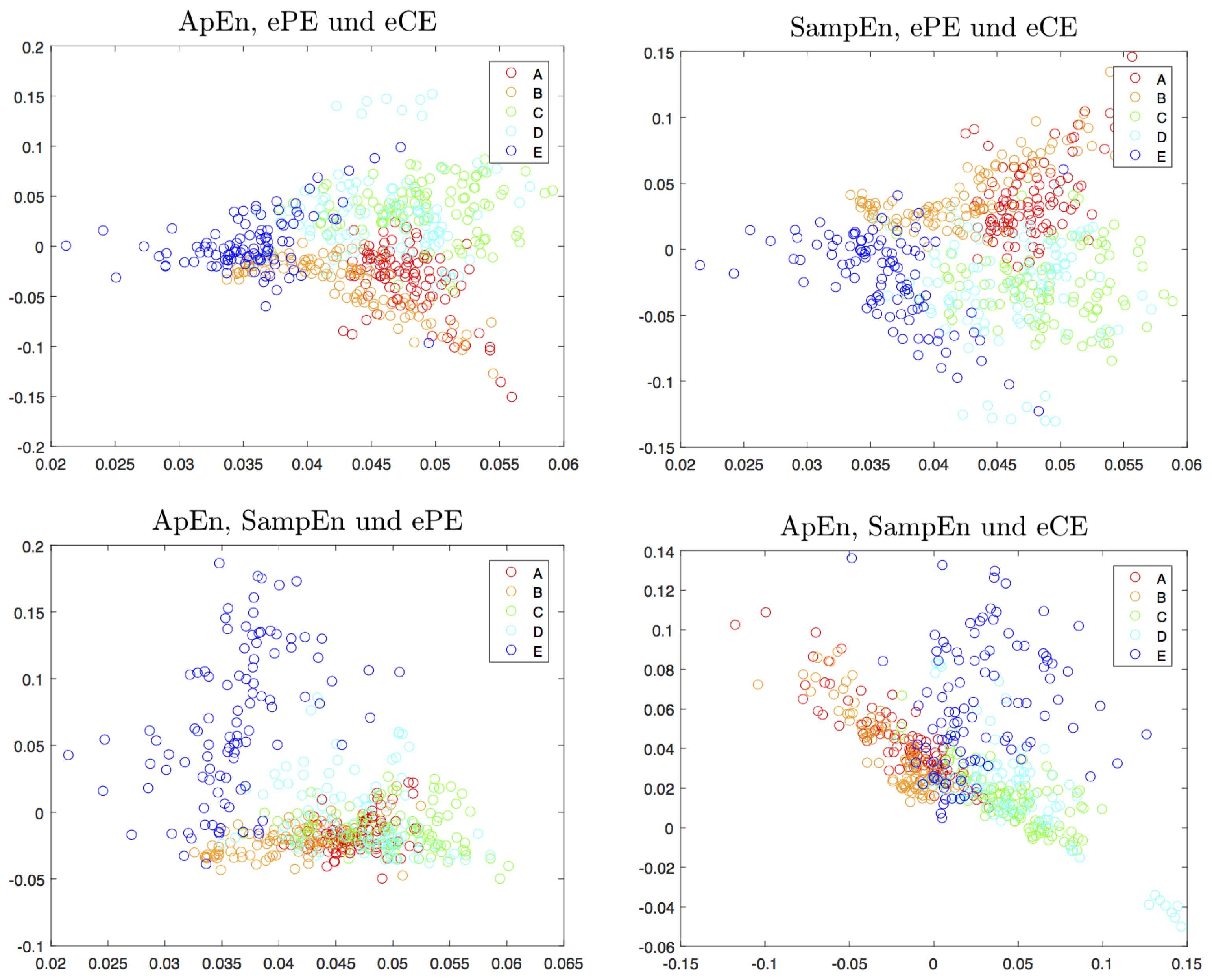
4.2. Visualization and Classification for Delay One
4.3. Other Delays
5. Resume
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bandt, C.; Pompe, B. Permutation entropy—A natural complexity measure for time series. Phys. Rev. E 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Keller, K.; Kurths, J. (Eds.) Recent progress in symbolic dynamics and permutation complexity. Ten years of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 247–257.
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K.; Unakafova, V.A. Ordinal symbolic analysis and its application to biomedical recordings. Philos. Trans. R. Soc. A 2015, 373, 20140091. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M. Permutation Complexity in Dynamical Systems; Springer: Berlin-Heidelberg, Germany, 2010. [Google Scholar]
- Keller, K.; Lauffer, H. Symbolic analysis of high-dimensional time series. Int. J. Bifurc. Chaos 2003, 13, 2657–2668. [Google Scholar] [CrossRef]
- Bandt, C.; Keller, G.; Pompe, B. Entropy of interval maps via permutations. Nonlinearity 2002, 15, 1595–1602. [Google Scholar] [CrossRef]
- Liu, X.-F.; Wang, Y. Fine-grained permutation entropy as a measure of natural complexity for time series. Chin. Phys. B 2009, 18, 2690–2695. [Google Scholar]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Keller, K.; Unakafov, A.M.; Unakafova, V.A. Ordinal Patterns, Entropy, and EEG. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Bian, C.; Qin, C.; Ma, Q.D.Y.; Shen, Q. Modified permutation-entropy analysis of heartbeat dynamics. Phys. Rev. E 2012, 85, 021906. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Perez, D.G.; Kowalski, A.; Martín, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Brownian motion, fractional Gaussian noise, and Tsallis permutation entropy. Physica A 2008, 387, 6057–6068. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Y.; Sun, X.; Li, D.; Voss, L.J.; Sleigh, J.W.; Hagihira, S.; Li, X. EEG entropy measures in anesthesia. Front. Comput. Neurosci. 2015, 9, 00016. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of EEG recordings during sevoflurane anesthesia. J. Neural Eng. 2010, 7, 046010. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Li, J.; Liu, X.; Li, X. Dynamic characteristics of absence EEG recordings with multiscale permutation entropy analysis. Epilepsy Res. 2013, 104, 246–252. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Escudero, J. Improved multiscale permutation entropy for biomedical signal analysis: Interpretation and application to electroencephalogram recordings. Biomed. Signal Process. 2016, 23, 28–41. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E 2012, 86, 046210. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Ribeiro, H.V. Discriminating image textures with the multiscale two-dimensional complexity-entropy causality plane. Chaos Solitons Fract. 2016, 91, 679–688. [Google Scholar] [CrossRef]
- Unakafov, A.M.; Keller, K. Conditional entropy of ordinal patterns. Physica D 2013, 269, 94–102. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Rieke, C.; Mormann, F.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef] [PubMed]
- Unakafova, V.A.; Keller, K. Efficiently Measuring Complexity on the Basis of Real-World Data. Entropy 2013, 15, 4392–4415. [Google Scholar] [CrossRef]
- Walters, P. An Introduction to Ergodic Theory; Springer: New York, NY, USA, 1982. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Lecture Notes in Mathematics; Dynamical Systems and Turbulence; Rand, D.A., Young, L.S., Eds.; Springer: New York, NY, USA, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Gutman, J. Takens’ embedding theorem with a continuous observable. arXiv 2016. [Google Scholar]
- Antoniouk, A.; Keller, K.; Maksymenko, S. Kolmogorov-Sinai entropy via separation properties of order-generated σ-algebras. Discrete Contin. Dyn. Syst. A 2014, 34, 1793–1809. [Google Scholar]
- Keller, K.; Maksymenko, S.; Stolz, I. Entropy determination based on the ordinal structure of a dynamical system. Discrete Contin. Dyn. Syst. B 2015, 20, 3507–3524. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Young, L.-S. Mathematical theory of Lyapunov exponents. J. Phys. A Math. Theor. 2013, 46, 1–17. [Google Scholar] [CrossRef]
- Caballero, M.V.; Mariano, M.; Ruiz, M. Draft: Symbolic Correlation Integral. Getting Rid of the Proximity Parameter. Available online: http://data.leo-univ-orleans.fr/media/seminars/175/WP_208.pdf (accessed on 14 February 2017).
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
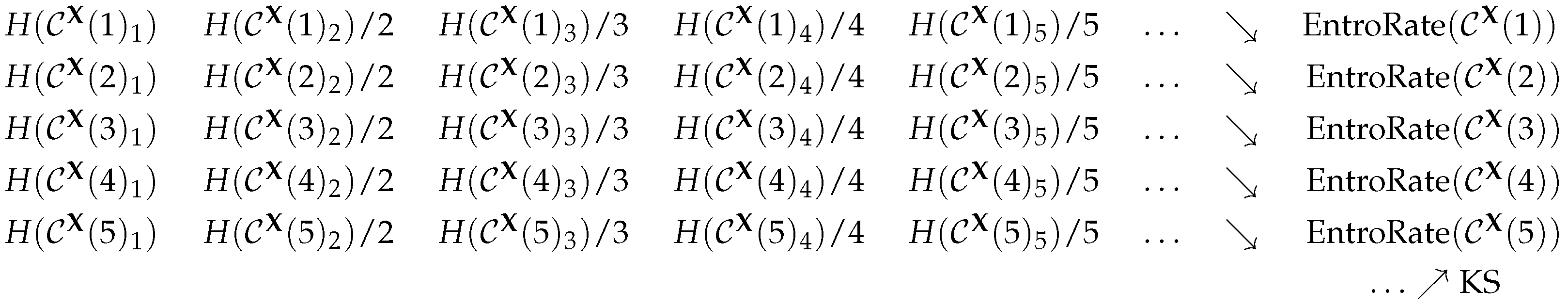
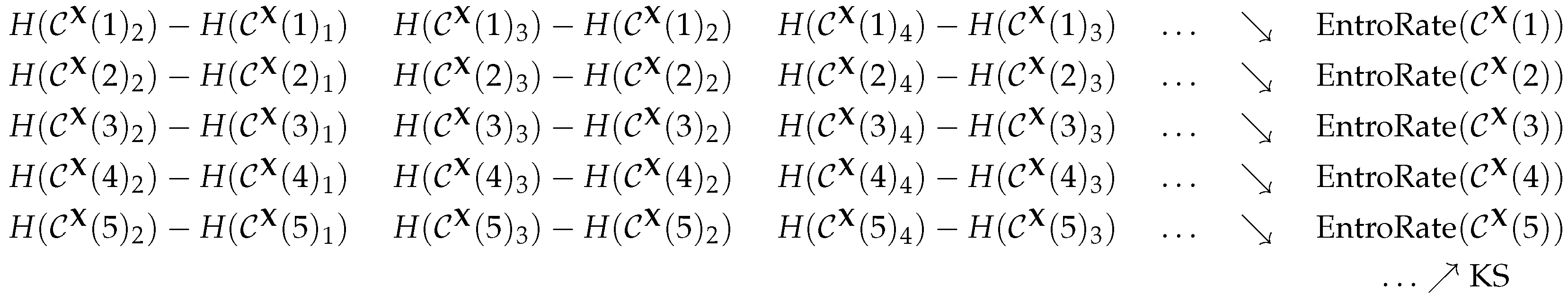

| α | 2 | 250 | ||||||
|---|---|---|---|---|---|---|---|---|
| Fp2 | ||||||||
| T3 | ||||||||
| P3 |
| Entropy | Classification Accuracy (In %) |
|---|---|
| ApEn | 31.0 |
| SampEn | 37.8 |
| ePE | 32.0 |
| eCE | 30.0 |
| Entropy | Classification Accuracy (In %) |
|---|---|
| ApEn & SampEn | 51.0 |
| ApEn & ePE | 58.0 |
| ApEn & eCE | 61.8 |
| SampEn & ePE | 64.0 |
| SampEn & eCE | 64.6 |
| ePE & eCE | 48.2 |
| Entropy | Classification Accuracy (In %) |
|---|---|
| ApEn & SampEn & ePE | 67.4 |
| ApEn & SampEn & eCE | 66.8 |
| ApEn & ePE & eCE | 65.4 |
| SampEn & ePE & eCE | 71.8 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation Entropy: New Ideas and Challenges. Entropy 2017, 19, 134. https://doi.org/10.3390/e19030134
Keller K, Mangold T, Stolz I, Werner J. Permutation Entropy: New Ideas and Challenges. Entropy. 2017; 19(3):134. https://doi.org/10.3390/e19030134
Chicago/Turabian StyleKeller, Karsten, Teresa Mangold, Inga Stolz, and Jenna Werner. 2017. "Permutation Entropy: New Ideas and Challenges" Entropy 19, no. 3: 134. https://doi.org/10.3390/e19030134
APA StyleKeller, K., Mangold, T., Stolz, I., & Werner, J. (2017). Permutation Entropy: New Ideas and Challenges. Entropy, 19(3), 134. https://doi.org/10.3390/e19030134






