Discrepancies between Conventional Multiscale Entropy and Modified Short-Time Multiscale Entropy of Photoplethysmographic Pulse Signals in Middle- and Old- Aged Individuals with or without Diabetes
Abstract
:1. Introduction
2. Methods
2.1. Study Population
2.2. Study Protocol
2.3. Calculation of Bilateral Fingertips PPG Pulse Amplitude Series
2.3.1. Detrending of PPGA Series Signal
2.3.2. Coarse-Grained Process and SE
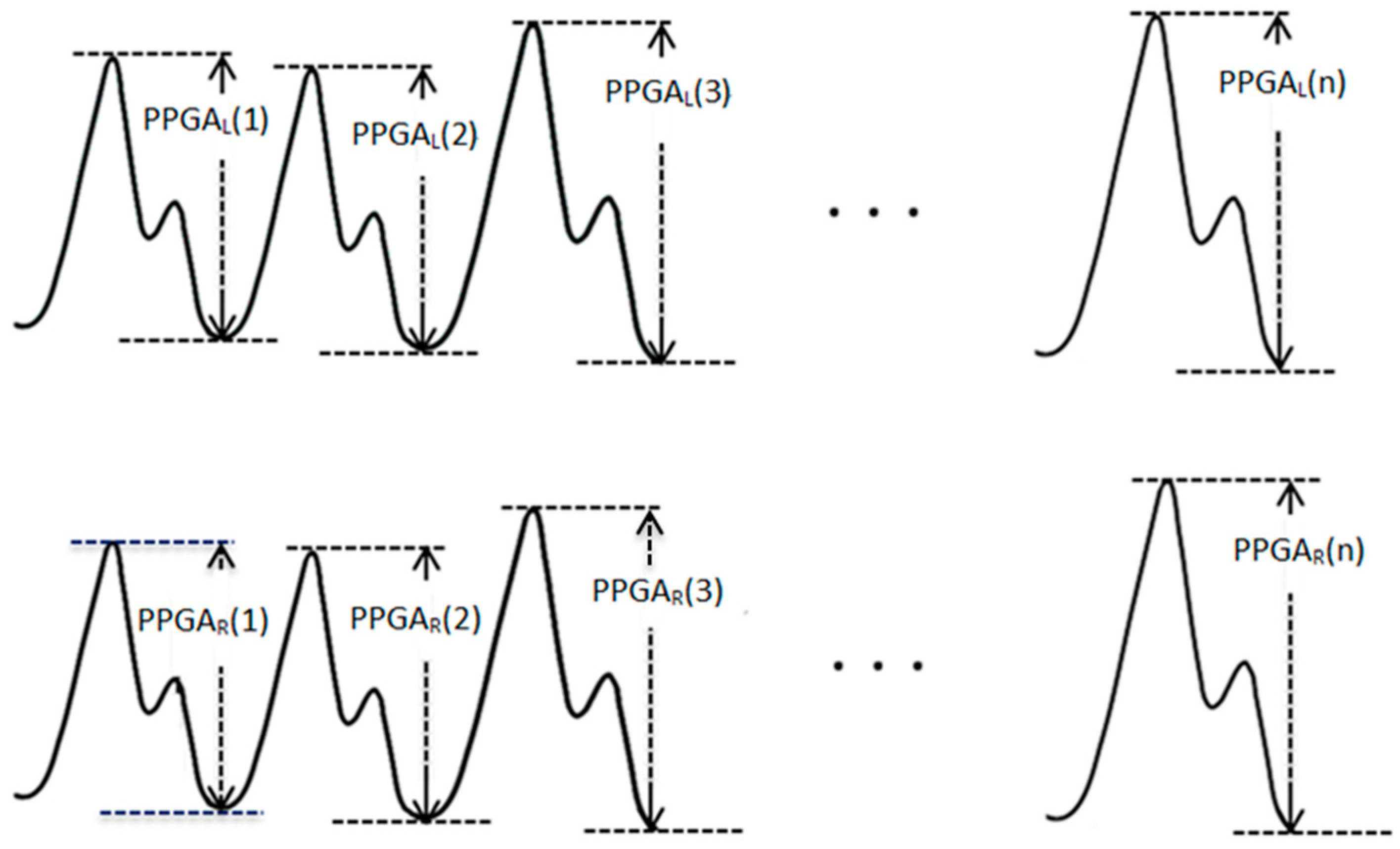
2.3.3. The cMSE of Bilateral Fingertips PPG Series Signal
- (a)
- Define the data series x(n) with length N and the two parameters of m and r (where m = Embedded dimension of the vector; r = tolerance). N = 1000 and 1500 for nPPGAL(i) and nPPGAR(j), respectively. In addition, m = 2 and r = 0.15 were set according to previous Costa et al. study recommendation [13].
- (b)
- Define N − m + 1 vectors, each of size m, composed as follows:
- (c)
- Define as the maximum value: . Calculate the number of within distance and calculate the ratio of the number to the total for each value of and an average to all points is defined as:
- (d)
- Increase the embedded dimension to m + 1, gives:
- (e)
- Therefore, SE is defined as:
2.3.4. The sMSE of Bilateral Fingertips PPG Series Signal
2.3.5. The PPGA-Based cMSE and sMSE Index
2.4. Statistical Analysis
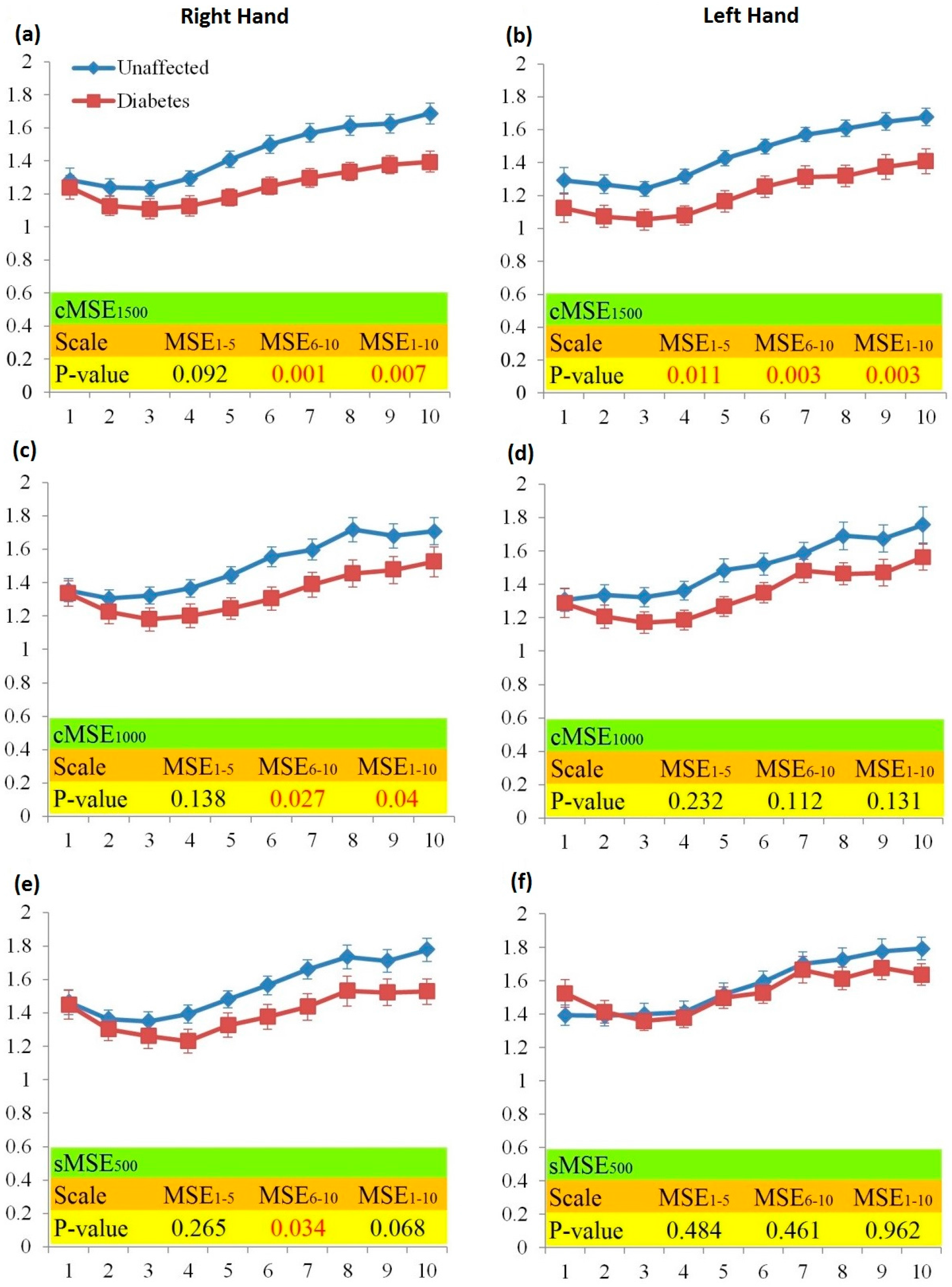
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Physica A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lee, K.Y.; Lin, S.G. Modified multiscale entropy for short-term time series analysis. Physica A 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Choi, Y.S. Assessment of Multiscale Information for Short Physiological Time Series. Int. J. Electr. Comput. Energ. Electron. Commun. Eng. 2016, 10, 117–120. [Google Scholar]
- Chang, Y.C.; Wu, H.T.; Chen, H.R.; Liu, A.B.; Yeh, J.J.; Lo, M.T.; Tsao, J.H.; Tang, C.J.; Tsai, I.T.; Sun, C.K.; et al. Application of a Modified Entropy Computational Method in Assessing the Complexity of Pulse Wave Velocity Signals in Healthy and Diabetic Subjects. Entropy 2014, 16, 4032–4043. [Google Scholar] [CrossRef]
- Yang, C.C.; Wu, H.T.; Chuang, W.Y.; Liu, T.C.; Tsai, I.T.; Chen, J.J.; Sun, C.K. Application of Short-Time MSE in Assessing Impact of Acupuncture on Peripheral Blood Flow and Autonomic Activities in Normal and Overweight Subjects. J. Med. Biol. Eng. 2016, 36, 386–395. [Google Scholar] [CrossRef]
- Wu, H.T.; Lee, C.Y.; Liu, C.C.; Liu, A.B. Multiscale cross-approximate entropy analysis as a measurement of complexity between ECG R-R interval and PPG pulse amplitude series among the normal and diabetic subjects. Comput. Math. Methods Med. 2013, 2013, 231762. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.T.; Liu, C.C.; Lo, M.T.; Hsu, P.C.; Liu, A.B.; Chang, K.Y.; Tang, C.J. Multiscale cross-approximate entropy analysis as a measure of complexity among the aged and diabetic. Comput. Math. Methods Med. 2013, 2013, 324325. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Huang, N.E.; Long, S.R.; Peng, C.K. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Klein, R.; Klein, B.E.; Moss, S.E.; Cruickshanks, K.J. Relationship of hyperglycemia to the long-term incidence and progression of diabetic retinopathy. Arch. Intern. Med. 1994, 154, 2169–2178. [Google Scholar] [CrossRef] [PubMed]
- Bash, L.D.; Selvin, E.; Steffes, M.; Coresh, J.; Astor, B.C. Poor glycemic control in diabetes and the risk of incident chronic kidney disease even in the absence of albuminuria and retinopathy: Atherosclerosis Risk in Communities (ARIC) Study. Arch. Intern. Med. 2008, 168, 2440–2447. [Google Scholar] [CrossRef] [PubMed]
- Young, R.J.; Ewing, D.J.; Clarke, B.F. Nerve function and metabolic control in teenage diabetics. Diabetes 1983, 32, 142–147. [Google Scholar] [CrossRef] [PubMed]
- Hemmingsen, B.; Lund, S.S.; Gluud, C.; Vaag, A.; Almdal, T.P.; Hemmingsen, C.; Wetterslev, J. Targeting intensive glycaemic control versus targeting conventional glycaemic control for type 2 diabetes mellitus. Cochrane Database Syst. Rev. 2013, 11, 008143. [Google Scholar]
- Maiorana, A.; O’Driscoll, G.; Cheetham, C.; Dembo, L.; Stanton, K.; Goodman, C.; Taylor, R.; Green, D. The effect of combined aerobic and resistance exercise training on vascular function in type 2 diabetes. J. Am. Coll. Cardiol. 2001, 38, 860–866. [Google Scholar] [CrossRef]
- Fuchsjäger-Mayrl, G.; Pleiner, J.; Wiesinger, G.F.; Sieder, A.E.; Quittan, M.; Nuhr, M.J.; Francesconi, C.; Seit, H.P.; Francesconi, M.; Schmetterer, L.; et al. Exercise training improves vascular endothelial function in patients with type 1 diabetes. Diabetes Care 2002, 25, 1795–1801. [Google Scholar] [CrossRef] [PubMed]
- Balducci, S.; Iacobellis, G.; Parisi, L.; Di Biase, N.; Calandriello, E.; Leonetti, F.; Fallucca, F. Exercise training can modify the natural history of diabetic peripheral neuropathy. J. Diabetes Complicat. 2006, 20, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. On the analysis of fingertip photoplethysmogram signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Okutucu, S.; Karakulak, U.N.; Aytemir, K.; Oto, A. Heart rate recovery: A practical clinical indicator of abnormal cardiac autonomic function. Expert Rev. Cardiovasc. Ther. 2011, 9, 1417–1430. [Google Scholar] [CrossRef] [PubMed]
- Banthia, S.; Bergner, D.W.; Chicos, A.B.; Ng, J.; Pelchovitz, D.J.; Subacius, H.; Kadish, A.H.; Goldberger, J.J. Detection of cardiovascular autonomic neuropathy using exercise testing in patients with type 2 diabetes mellitus. J. Diabetes Complicat. 2013, 27, 64–69. [Google Scholar] [CrossRef] [PubMed]
| Unaffected (n = 35) | Diabetes (n = 35) | p-Value | |
|---|---|---|---|
| Male, % | 23 (51.43) | 24 (54.29) | 0.811 |
| Age, year | 59.74 (8.19) | 60.2 (6.58) | 0.798 |
| Height, m | 161.62 (8.48) | 169.82 (50.45) | 0.360 |
| Weight, kg | 67.82 (10.22) | 70.61 (14.73) | 0.372 |
| Waist circumference, cm | 88.47 (7.98) | 90.94 (12.39) | 0.336 |
| Pulse rate, beats/min | 73.42 (8.68) | 81.34 (10.93) | 0.002 |
| Systolic BP, mmHg | 127.94 (18.74) | 123.91 (16.13) | 0.349 |
| Diastolic BP, mmHg | 75.82 (10.84) | 74.23 (10.16) | 0.539 |
| HbA1c, % | 6.00 (0.39) | 8.74 (1.74) | 0.000 |
| Total cholesterol, mg/dL | 188.15 (35.48) | 182.06 (37.28) | 0.506 |
| Triglyceride, mg/dL | 111.18 (84.84) | 137.23 (69.40) | 0.187 |
| HDL-C, mg/dL | 47.24 (16.09) | 41.97 (17.78) | 0.218 |
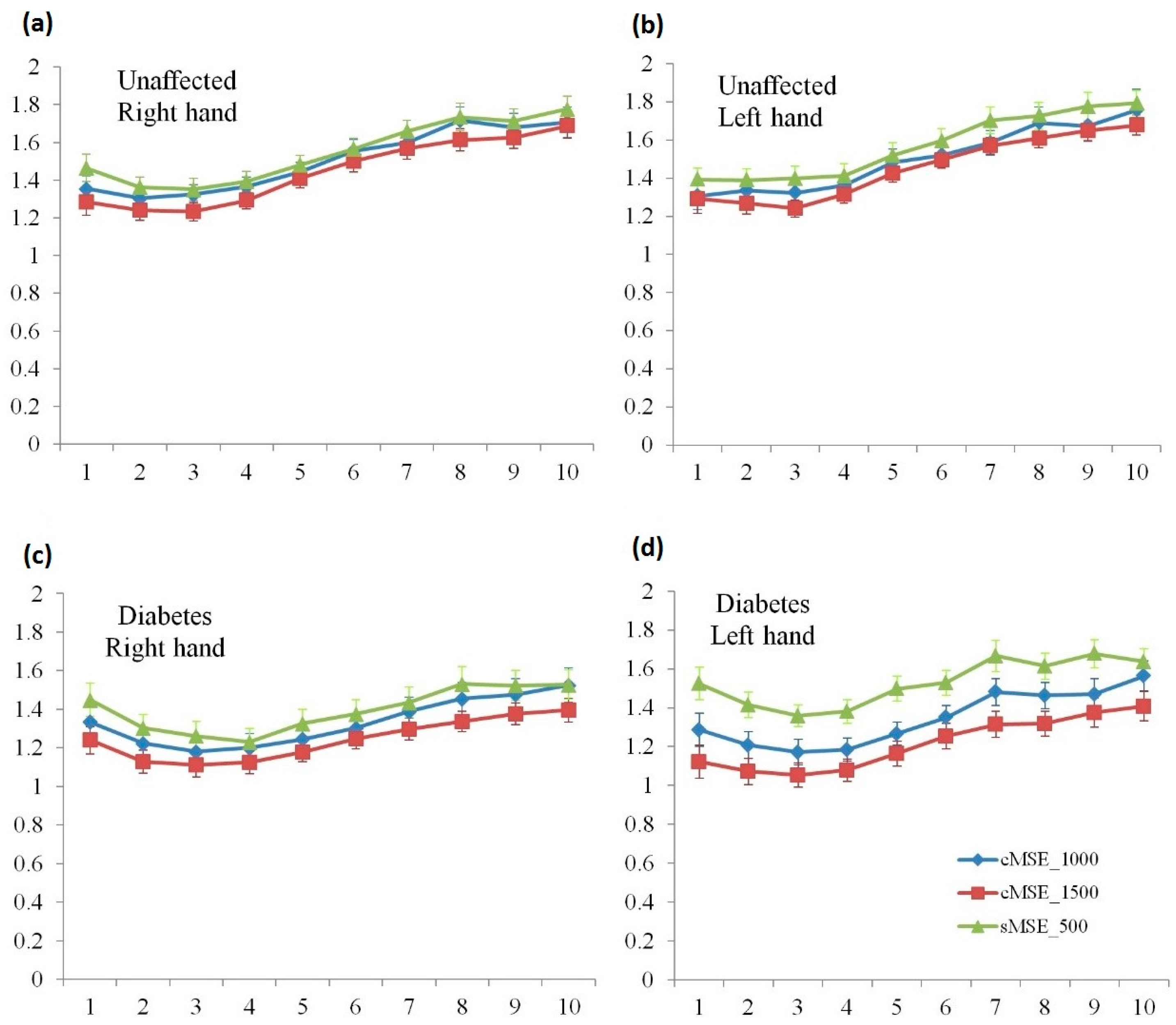
| Scale 1 | Scale 2 | Scale 3 | Scale 4 | Scale 5 | Scale 6 | Scale 7 | Scale 8 | Scale 9 | Scale 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Unaffected | ||||||||||
| right hand | ||||||||||
| cMSE1500 | 1.28 (0.07) | 1.24 (0.05) | 1.23 (0.05) | 1.29 (0.05) | 1.41 (0.05) | 1.50 (0.06) | 1.57 (0.06) | 1.61 (0.06) | 1.62 (0.06) | 1.69 (0.06) |
| sMSE500 | 1.46 (0.07) | 1.36 (0.05) | 1.35 (0.06) | 1.39 (0.05) | 1.48 (0.05) | 1.57 (0.06) | 1.66 (0.06) | 1.74 (0.07) | 1.71 (0.07) | 1.78 (0.07) |
| p-value | 0.082 | 0.10 | 0.12 | 0.16 | 0.30 | 0.40 | 0.26 | 0.19 | 0.32 | 0.34 |
| left hand | ||||||||||
| cMSE1500 | 1.29 (0.08) | 1.27 (0.06) | 1.24 (0.04) | 1.31 (0.04) | 1.43 (0.05) | 1.50 (0.04) | 1.57 (0.04) | 1.61 (0.05) | 1.65 (0.05) | 1.68 (0.05) |
| sMSE500 | 1.39 (0.06) | 1.39 (0.06) | 1.40 (0.06) | 1.41 (0.07) | 1.52 (0.06) | 1.60 (0.06) | 1.70 (0.07) | 1.73 (0.07) | 1.78 (0.08) | 1.79 (0.07) |
| p-value | 0.30 | 0.14 | 0.044 | 0.22 | 0.25 | 0.21 | 0.11 | 0.17 | 0.17 | 0.18 |
| Diabetes | ||||||||||
| right hand | ||||||||||
| cMSE1500 | 1.24 (0.07) | 1.13 (0.06) | 1.11 (0.06) | 1.13 (0.06) | 1.18 (0.05) | 1.25 (0.05) | 1.30 (0.06) | 1.34 (0.05) | 1.38 (0.06) | 1.39 (0.06) |
| sMSE500 | 1.45 (0.09) | 1.30 (0.07) | 1.26 (0.07) | 1.23 (0.07) | 1.33 (0.07) | 1.38 (0.07) | 1.44 (0.08) | 1.53 (0.09) | 1.52 (0.08) | 1.53 (0.08) |
| p-value | 0.080 | 0.078 | 0.16 | 0.33 | 0.14 | 0.21 | 0.20 | 0.086 | 0.15 | 0.21 |
| left hand | ||||||||||
| cMSE1500 | 1.12 (0.08) | 1.07 (0.07) | 1.05 (0.06) | 1.08 (0.06) | 1.16 (0.06) | 1.25 (0.06) | 1.31 (0.07) | 1.32 (0.07) | 1.37 (0.07) | 1.41 (0.08) |
| sMSE500 | 1.52 (0.08) | 1.41 (0.07) | 1.36 (0.06) | 1.38 (0.06) | 1.50 (0.06) | 1.53 (0.06) | 1.67 (0.08) | 1.61 (0.07) | 1.68 (0.07) | 1.64 (0.06) |
| p-value | 0.0020 | 0.0020 | 0.0020 | 0.0020 | 0.0020 | 0.0070 | 0.0030 | 0.0050 | 0.0070 | 0.031 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, G.-M.; Haryadi, B.; Yang, C.-M.; Chu, S.-C.; Yang, C.-C.; Wu, H.-T. Discrepancies between Conventional Multiscale Entropy and Modified Short-Time Multiscale Entropy of Photoplethysmographic Pulse Signals in Middle- and Old- Aged Individuals with or without Diabetes. Entropy 2017, 19, 132. https://doi.org/10.3390/e19030132
Lin G-M, Haryadi B, Yang C-M, Chu S-C, Yang C-C, Wu H-T. Discrepancies between Conventional Multiscale Entropy and Modified Short-Time Multiscale Entropy of Photoplethysmographic Pulse Signals in Middle- and Old- Aged Individuals with or without Diabetes. Entropy. 2017; 19(3):132. https://doi.org/10.3390/e19030132
Chicago/Turabian StyleLin, Gen-Min, Bagus Haryadi, Chieh-Ming Yang, Shiao-Chiang Chu, Cheng-Chan Yang, and Hsien-Tsai Wu. 2017. "Discrepancies between Conventional Multiscale Entropy and Modified Short-Time Multiscale Entropy of Photoplethysmographic Pulse Signals in Middle- and Old- Aged Individuals with or without Diabetes" Entropy 19, no. 3: 132. https://doi.org/10.3390/e19030132
APA StyleLin, G.-M., Haryadi, B., Yang, C.-M., Chu, S.-C., Yang, C.-C., & Wu, H.-T. (2017). Discrepancies between Conventional Multiscale Entropy and Modified Short-Time Multiscale Entropy of Photoplethysmographic Pulse Signals in Middle- and Old- Aged Individuals with or without Diabetes. Entropy, 19(3), 132. https://doi.org/10.3390/e19030132








