Abstract
In this paper, firstly, manifold consisting of all symmetric positive-definite matrices is introduced based on matrix information geometry; Secondly, the geometrical structures of information submanifold of are presented including metric, geodesic and geodesic distance; Thirdly, the information resolution with sensor networks is presented by three classical measurement models based on information submanifold; Finally, the bearing-only tracking by single sensor is introduced by the Fisher information matrix. The preliminary analysis results introduced in this paper indicate that information submanifold is able to offer consistent and more comprehensive means to understand and solve sensor network problems for targets resolution and tracking, which are not easily handled by some conventional analysis methods.
1. Introduction
As an interesting research area in matrix information geometry, symmetric positive-definite (SPD) matrices offer detailed analysis and comprehensive results by considering them as geometrical objects [1,2,3]. Meanwhile, it also can be found that some applications are related to SPD matrices of real numbers [4,5,6,7]. In the last thirty years, its applications have spanned several discipline areas such as information theory, systems theory, control theory, signal processing and mathematical programming [8,9,10,11,12,13,14,15]. Considering the set of all SPD matrices as a manifold , by defining affine Riemannian metric on , ones can find that becomes a complete Riemannian manifold (Hadamard space) [16]. Thus, for any two points on , there exists the shortest curve, namely, geodesic connecting them. It is remarkable that ones can obtain an explicit expression of the geodesic on to conveniently calculate the geodesic distance [3].
Fisher information matrix (FIM) is one of important contents in the probability theory and statistics [17,18]. Since a FIM is a symmetric positive-definite matrix, the set of all Fisher information matrices (FIMs) corresponding to a given probability distribution family is a submanifold of , which is called the information submanifold of . Thus, some properties including metric and geodesic about the information submanifold can be obtained through the differential geometrical theory of . In addition, for the sensor networks, the resolve ability of multiple closely spaced targets with a given sensor measurement model is a basic concept about the sensor systems and an extremely important aspect of their over-all performance [19,20]. Some sensor measurement models have been introduced in [21,22,23]. The information resolution based on statistical manifold is introduced in [24,25] which cannot give an geodesic explicitly expressed in general. Meanwhile, as a very important issue for sensor networks, target tracking has also been investigated [22,23,26]. In this paper, the above two aspects are considered by the information submanifold for sensor networks. Accordingly, by virtue of information submanifold, we give the analysis of sensor networks to gain a better understanding and more comprehensive investigation of sensor system issues for target resolution and tracking. In particular, the information distance (IFD) between two targets is used to measure target resolvability in the region covered by the sensor system and is exactly calculated by the geodesic on . Comparing with some classical resolution, such as normal resolution defined by half-power width, Kullback-Leibler divergence defined by distance-like measurement, the presented information resolution is defined by the information submanifold with geodesic distance not Euclidean distance (Ed), which can show the geometrical property of the measurement models more efficiently. It is also compared with the Rao geodesic distance which is defined by statistical manifold through three classical sensor network measurement models in this paper. The simulation results indicate that the presented information resolution has the similar efficient as Rao geodesic distance and less computation complexity because of the application of Fisher information and the geodesic explicitly expressed for any two FIMs.
The outline of this paper is organized as follows. In Section 2, the geometrical structures of are stated briefly. The information submanifold theory is presented in Section 3. The target resolution and tracking with some classical measurement models based on the geodesic distance on the information submanifold are presented and analyzed in Section 4. Finally, some conclusions are given at Section 5.
2. Manifold of Symmetric Positive-Definite Matrices
In this section, basic materials including some definitions and results about manifold of the SPD matrices are reviewed [8,16]. These will be used throughout this paper. Let denote the space of all real symmetric matrices, and the set of all SPD matrices is considered as a manifold
where means that the quadratic form for all . Then, the exponential mapping from to is usually given by
It is well known that and if . When , the logarithmic mapping can be given by
In particular, if . Another important fact is that
For a given matrix , the Riemannian metric is defined by
where are two tangent vectors over at A and denotes the trace of object matrix. The positive definiteness of this metric is due to the fact that
Then, manifold with the Riemannian metric becomes a Riemannian manifold. The geodesic , with initial point and initial tangent vector , is given by
Let , then the geodesic connecting A and B is given by
The geodesic distance between A and B on is given by
where is the eigenvalue of matrix for . The mean in the Riemannian sense of two SPD matrices A and B is given by . If all belong to a single geodesic of , i.e., , we have
It can be seen that if and only if .
Proposition 1.
Let , then the geodesic distance between A and B is given by
where denotes the determinant of matrix A.
Proof.
For two SPD matrices
we get
By a direct calculation, we see that the eigenvalues of satisfy
and furthermore, we have
Finally, by (9), the geodesic distance between A and B can be obtained as (3) for any two SPD matrices. ☐
Proposition 2.
If A and B are diagonal matrices on , i.e., and , then the geodesic connecting A and B is given by
The corresponding geodesic distance is given by
Proof.
For two diagonal matrices
we can get
Therefore, by (4), the geodesic connecting A and B is given by
Meanwhile, because the eigenvalues of matrix are
by (9), the geodesic distance between A and B satisfies
☐
3. Information Submanifold
As well known that the probability distribution family is called a statistical model with probability density function (pdf) [27], if it satisfies the following regularity conditions:
- All the ’s have a common support so that for all , where X is the support.
- For every fixed θ, are linearly independent, where .
- The moments of random variables exist up to necessary orders.
- The partial derivatives and the integration with respect to the measure F can always be exchanged asfor any smooth functions .
Based on the theory of probability distribution, for a given pdf with , the FIM is defined by
where denotes the expectation with respect to the pdf . Particularly, for the multivariate normal distribution with the pdf
where and are the mean and the covariance of the distribution, respectively, we have
For the pdf , by the theory of differential geometry [28], it is easy to know that the set
is a submanifold of . Then, we can give the following definition.
Definition 1.
For a given pdf , the determinant of FIM , i.e., , is called Fisher information of , while the set is called information submanifold of for the given probability distribution family M.
Proposition 3.
For the exponential family with the pdf
we have
In fact, for the exponential family with the pdf (28) where is the natural coordinate system, are independent function, and is the potential function which is independent to x, by direct calculation we can get
From (4), suppose that and are two FIMs corresponding to the same statistical model, then the geodesic connecting A and B is given by
From (9), the corresponding geodesic distance is given by
which is also called information distance (IFD) between and , where is the eigenvalue of matrix .
3.1. The Information Submanifold for the Normal Distribution
In particular, for the normal distribution with the pdf
where , μ and σ are the mean and the variance, respectively, by (24), we can get the FIM as
which is positive-definite diagonal matrix.
Proposition 4.
Suppose that and , where and . The geodesic connecting A and B is given by
The geodesic distance between A and B is
Proof.
By (16) and (35), we can easily obtain that
☐
Proposition 5.
Suppose that , are m FIMs corresponding the normal distribution, then the Riemannian mean of them is given by
and the geometric mean is given by
Proof.
From (35), for any , we have . Therefore, for any m FIMs , they are all belong to . Then, by (10), we can get the Riemannian mean as
Meanwhile, the geometric mean is given by
☐
3.2. The Information Submanifold for the Von Mises Distribution
In probability theory and directional statistics, the von Mises (voM) distribution which is also known as the circular normal distribution or Tikhonov distribution is an important continuous probability distribution on the circle. For the voM distribution with the angle variable given by
where , and is the modified Bessel function of integer order r satisfying
the components of the FIM with are respectively
Similarly as the last subsection, let and be two FIMs for voM distribution where , then by a calculation from (3), we can see that the geodesic connecting A and B satisfies
where
The geodesic distance between A and B is given by
3.3. The Information Submanifold for Curved Gaussian Distribution
For the curved Gaussian distribution with the pdf [29]
where with and . By (29), we can get the corresponding FIM
and it’s inverse matrix
As the same time, let and be two FIMs for curved Gaussian distribution where , then by (3), we can get the geodesic connecting A and B
The geodesic distance between A and B is given as
where .
4. Application of Information Submanifold for Sensor Networks
4.1. Information Resolution Based on Information Submanifold
In this subsection, the information resolution based on information submanifold is served as a new metric to measure the intrinsic similarities of the corresponding information matrix and is optimal to determine such resolution with respect to the underlying similitude which generates the manifold of SPD matrices based on differential geometry. It is defined on the basis of consideration of information distance connecting two relative FIMs for two measurement results. According to the definition, a new resolution cell denoted as is a geodesic ball described by the set of equidistant points from the center θ in an information submanifold which is defined by a measurement model . Therefore, we have the following definition.
Definition 2.
For a given measurement model with pdf and a known target state θ with , the set
is called information resolution cell, where given by (32) is the IFD of the two targets and δ is the radius of the information resolution cell which is called the information resolution limit.
Given a minimal resolution limit value for a sensor network, we can distinguish two targets by the information resolution , i.e., if , the two targets can be distinguished, otherwise, we cannot distinguish them so that regard them as one target. In the following three subsections, we will use three classical measurement models, i.e., range-bearing measurement model, two-bearings measurement model and three dimensional (3D) range-bearings measurement model, to show the effectiveness of information resolution based on information submanifold.
4.1.1. Range-Bearing Measurement
As well known that, assume that the sensor is located at the origin of coordinate , the range-bearing measurement model can be represented as
where with , and . It should be noted that the term appeared in the diagonal of range component to take into account the fact that the amplitude of the radar echo signal attenuates according to the fourth power of the target range. Then, we can see that the sensor measurement x satisfies the Gaussian distribution with the mean and covariance matrix given by
According to the FIM above, we can obtain an information submanifold corresponding to the range-bearing measurement model and calculate the information distance between any two measured target states for determining whether they can be resolved or not.
Assume that the area of interest is with and . The sensor is located at and the known target is located at . At the same time, without loss of generality, we assume that the detection target is on the same plane with and the sensor.
Figure 1a shows the information distance between two closely spaced targets and for range-bearing measurement sensor network. Figure 1b is the contour map of Figure 1a. A same plot is generated in Figure 2a in Rao geodesic distance based on information matrix metric (). And the contour map generated via in the same scenario as in Figure 1b is given in Figure 2b. From this, we can see that the IFD increases with the area centered at the location of . At the same time, we can know that the change of IFD is more larger when the detected target is closer to the sensor . Clearly, the uncertainty area is under a given threshold to the value of IFD and target can be distinguished from target when it is outside this area. There are sixteen targets with Ed, and IFD as shown in Table 1 corresponding to and , respectively. It can be seen that the IFD is increasing with the Ed between and , especially when is moving to close the sensor. Meanwhile, we can also know that the IFD is different for two detected targets with the same Ed to , and the closer the Ed of one target to is, the bigger the IFD to is in generally. For example, setting and with the same and to for , however the relationship of the IFD is which indicates that the presented information resolution is more efficient and accurate than others for this measurement system. In addition, if the minimal resolution limit is given as for the samples in Table 1, the four targets and cannot be distinguished with , and the others can be distinguished. For target , we can get the similar analysis results as .
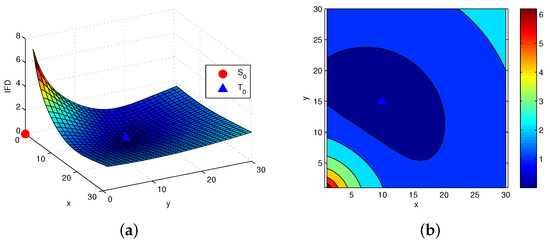
Figure 1.
(a) IFD between two closely spaced targets for range-bearing measurement model; (b) The contour map of Figure 1a.
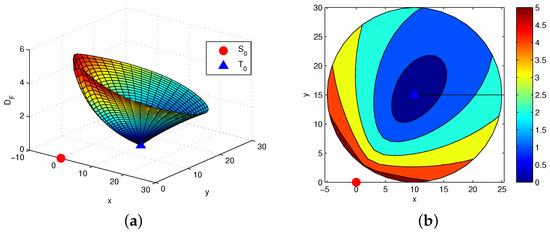
Figure 2.
(a) between two closely spaced targets for range-bearing measurement model; (b) The contour map of Figure 2a.

Table 1.
and IFD with for range-bearing measurement model.
4.1.2. Two-Bearings Measurement
Suppose that two sensors and are located at and respectively. The sensors can observe two bearings of the target and each of the measurement satisfies the voM distribution, i.e.,
where , and κ is a constant. Sine the sensor measurements are independent, each voM distribution is with common concentration parameter κ and the measurement at ith sensor has circular mean , then the bearing measurements satisfy the joint distribution with the pdf
where is the local coordinate. Then, by (24), we can obtain the corresponding FIM as
Thus, we can obtain an information submanifold corresponding to the two-bearings measurement model and calculate the information distance between two measured target states.
Assume that the area of interest is and . The two sensors are located at , and , respectively. The target is located at . Without loss of generality, we also assume that the detection target is on the same plane with and the sensors.
Figure 3a shows the information distance between two spaced targets and for the two-bearings measurement sensor network. Figure 3b is the contour map of Figure 3a. A same plot is generated in Figure 4a in Rao geodesic distance based on information matrix metric. And the contour map generated via in the same scenario as in Figure 1b is given in Figure 4b. Accordingly, it is easy to know that the IFD increases with the area centered at the location of . At the same time, we can know that the change of IFD is more larger when the detected target is closer to the line connecting the sensor and . Clearly, the uncertainty area is under a given threshold to the value of IFD and target can be distinguished from target when it is outside this area. As shown in Table 2 with and , for the selected samples, we can also get the similar property which is given in the last subsection. For example, setting and with the same , the corresponding relationships about and IFD are and , respectively. Thus, we can know that the presented information resolution has the same efficient as the Rao geodesic distance for the measurement model. Meanwhile, based on the geometrical property of this measurement model, i.e., the closer the detected target to the line is, the bigger the change of the Fisher information is, it can be seen that the presented method is more accuracy than others for this measurement model. Similarly, for a given minimal resolution limit , there are only and which cannot be distinguished from , while the all targets can be distinguished from under the same situations.
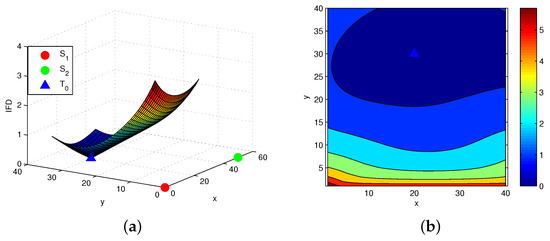
Figure 3.
(a) IFD between two closely spaced targets for two-bearings measurement model; (b) The contour map of Figure 3a.
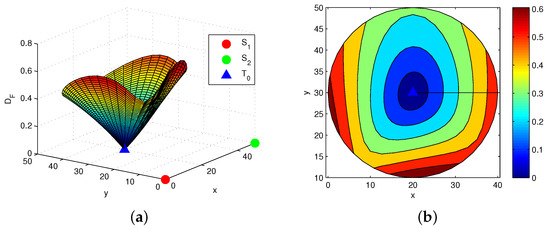
Figure 4.
(a) between two closely spaced targets for two-bearings measurement model; (b) The contour map of Figure 4a.

Table 2.
and IFD for two-bearings measurement model.
4.1.3. 3D Range-Bearings Measurement
Using a similar method, we consider the 3D positioning model in this subsection. Let the range, azimuth and altitude angle of the target be τ, α and β, respectively. In the network of single conventional sensor measurement model, the state of a target is simply represented by its location, i.e., . The sensor can observe range and bearings of the target, and then the measurement model can be written as
where τ, α and β denote the range, angle of rotation and angle of altitude of the measurement subject to an additive zero-mean Gaussian noise with the covariance , respectively. Therefore, the measurement x obeys a normal distribution with the mean and the covariance respectively satisfying
where , and are the standard deviations of range and bearings measurement noise, respectively. By (26), we can calculate the FIM elements of model (62) respectively as follows
By the six equations above, we can calculate the geodesic distance between any two information matrices corresponding to the 3D measurement model. Assume that the area of interest is , , and . Then, the sensor is located at , and the reference target is located at . In addition, we assume that the moving target is on the same plane with for simplifying the simulation results.
Figure 5a shows the information distance between two closely spaced targets and for 3D range and angle measurement sensor network and Figure 5b is the contour map of Figure 5a. From this we can know that the IFD increases with the area centered at the location of . The closer that target to is, the smaller the IFD is. For a given resolution limit , we can easily know that two targets whether can be distinguished or not by calculating the IFD between them, i.e., there are two detection points or one point. A same plot is generated in Figure 6a in Rao geodesic distance based on information matrix metric. And the contour map generated via in the same scenario is given in Figure 6b. For some samples as shown in Table 3 with and , the similar analysis results can be also obtained as the 2D range-bearing measurement model. For example, by a given minimal resolution limit , there are only and which cannot be distinguished from and only which cannot be distinguished from with the presented method.
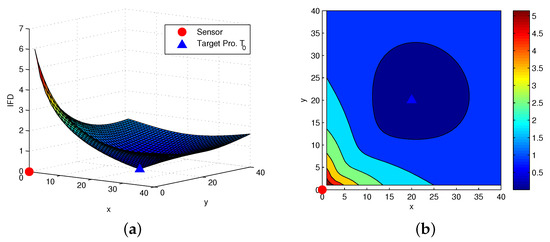
Figure 5.
(a) between two closely spaced targets for 3D range-bearings measurement sensor network; (b) The contour map of Figure 5a.
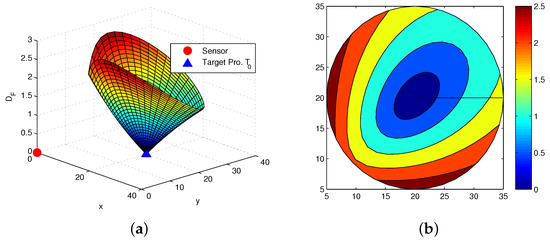
Figure 6.
(a) between two closely spaced targets for 3D range-bearings measurement sensor network; (b) The contour map of Figure 6a.

Table 3.
and IFD with for 3D range-bearings measurement sensor network.
Remark 1.
From the analysis with the three sensor systems above, it illustrates the sensing ability of the sensor networks to distinguish two closely spaced targets. A minimal detectable information distance may be identify in the maps for a given resolution limit . If information distance between two targets is below the given threshold, the two closely spaced targets may not be distinguished by the sensor system and are considered as one target. Otherwise, we can distinguish them as two different targets. In addition, compared with some classical resolution, information resolution based on information submanifold and information resolution based on statistical manifold are all defined throughout geodesic distance and can all show the geometric property of sensor networks measurement system. It should be noted that, because there is no explicit geodesic expression on statistical manifold in general, the geodesic calculation has very high complexity and is approximately handled by the Euclidean distance sometimes. Thus, it would be some cause of calculation error for target resolvability, especially when the two targets is not fairly close to each other. However, the information distance based on information submanifold is only related to FIMs corresponding to the targets states and can be calculated by an explicit geodesic expression on . Meanwhile, the presented resolution in this paper can show the Fisher information and the measurement models more effectively.
4.2. Bearing-Only Tracking With Single Sensor
In this subsection, we present a new tracking method based on information submanifold for bearing-only tracking with a single sensor. By (59)∼(62), as a function of the second sensor location, the determinant of the FIM can be given by
where , and .
For the given locations of the two sensors, we can get the Fisher information for the detection target by (70) which represents the volume of the amount of information. Under the same situation as in the last subsection, the target information map and the contour map for the two-bearings passive sensor networks can be obtained as shown in Figure 7a,b on a logarithm scale. From the two figures, it can be seen that the amount of the information is very little and even almost is zero nearby the straight line passing through the two sensors. In fact, the target can not be located in this region due to the bearing-only measurement. In order to eliminate the unmeasurable area and obtain the maximal Fisher information, we can move the sensor with respect to the target. If the trajectory of the target moving is known, the sensor would have an optimal scheduling such that maximal target information. Therefore, we make the following parameter replacement using the polar coordinate
where r and denote the step length and the direction of the sensor movement, respectively. Substituting (71) into (70), we see that (70) becomes
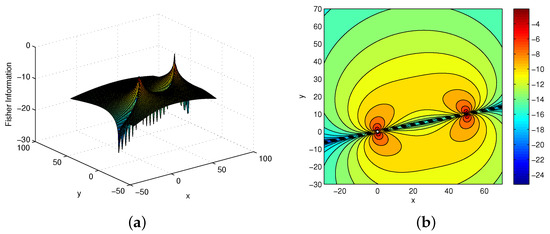
Figure 7.
(a) Target information for the sensor network with two-bearings passive sensor networks; (b) The contour map of target information.
Taking the partial derivative of (72) with respect to and setting it to be zero, we can obtain the optimal sensor heading course which satisfies the following expression
Without loss of generality, let the Line-of-Sight from the sensor to the target be the baseline direction of the coordinate systems. The optimal sensor moving direction based on (73) can be simplified as
where .
Assume that the initial state of the sensor locates at , and the location of the target is . Then, we can get the polar relation map about the optimal moving direction and the moving radius r as Figure 8.
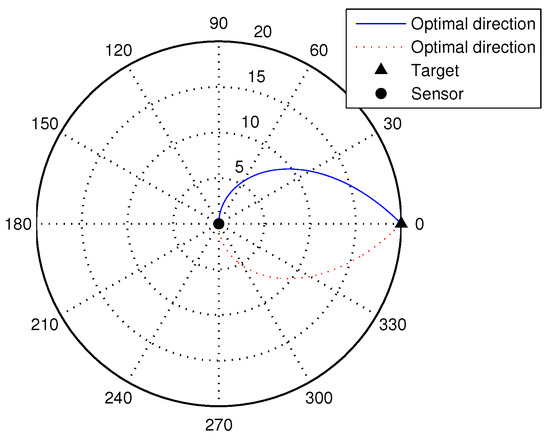
Figure 8.
Optimal sensor movement direction for given radius.
As described in Figure 8, the optimal direction of the sensor changes from to with the increase of the length of tracking radius. And when the radius equals to the distance between the target and the sensor, i.e., , the optimal direction is . Therefore, we can select the optimal direction based on the radius of the sensor which we design in the practical applications.
5. Conclusions
In this paper, we have proposed the information submanifold and its applications for sensor networks based on SPD matrices. Three simple examples corresponding three probability distributions are calculated with the geodesic and geodesic distance. The problems of target resolution and tracking with a single sensor based on the information submanifold are analyzed and computed through two classical sensor networks models. The simulation results have shown that the proposed method yields very effective performance in practical environments. Our future work will focus on the applications of the curvature of the information submanifold for the management and tracking of the sensor networks.
Acknowledgments
This subject is supported by the National Natural Science Foundation of China (No. 61179031).
Author Contributions
Hao Xu conceived and designed the experiments; Hao Xu performed the experiments; Hao Xu and Huafei Sun analyzed the data; Aung Naing Win contributed reagents/materials/analysis tools; Hao Xu and Huafei Sun wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fiori, S. Learning the Fre’chet Mean over the Manifold of Symmetric Positive-Definite Matrices. Cognit. Comput. 2009, 1, 279–291. [Google Scholar] [CrossRef]
- Harandi, M.T.; Salzmann, M.; Hartley, R. From Manifold to Manifold: Geometry-Aware Dimensionality Reduction for SPD Matrices; Springer: Basel, Switzerland, 2014; Volume 8690, pp. 17–32. [Google Scholar]
- Arsigny, V.; Fillard, P.; Pennec, X.; Ayache, N. Geometric Means in a Novel Vector Space Structures on Symmetrics Positive-Definite Matrices. Siam J. Matrix Anal. Appl. 2007, 29, 328–347. [Google Scholar] [CrossRef]
- Le Bihan, D. Diffusion MNR Imaging. Magn. Reson. Q. 1991, 7, 1–30. [Google Scholar] [PubMed]
- Fillard, P.; Arsigny, V.; Pennec, X.; Hayashi, K.M.; Thompson, P.M.; Ayache, N. Measuring Brain Variability by Extrapolating Sparse Tensor Fields Measured on Sulcal Lines. Neuroimage 2007, 34, 639–650. [Google Scholar] [CrossRef] [PubMed]
- Harandi, M.T.; Sanderson, C.; Hartley, R.; Lovell, B.C. Sparse Coding and Dictionary Learning for Symmetric Positive Definite Matrices: A Kernel Approach. Lect. Notes Comput. Sci. 2012, 7573, 216–229. [Google Scholar]
- Jayasumana, S.; Hartley, R.; Salzmann, M.; Li, H.; Harandi, M. Kernel Methods on the Riemannian Manifold of Symmetric Positive Definite Matrices. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 73–80.
- Moakher, M. A Differential Geometric Approach to The Geometric Mean of Symmetric Positive-Definite Matrices. Siam J. Matrix Anal. Appl. 2005, 26, 735–747. [Google Scholar] [CrossRef]
- Hall, B. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Menendez, M.L.; Morales, D.; Pardo, L.; Salicrij, M. Statistical Test Based on Geodesic Distances. Appl. Math. Lett. 1995, 8, 65–69. [Google Scholar] [CrossRef]
- Fiori, S. A Theory for Learning by Weight Flow on Stiefel-Grassman Manifold. Neural Comput. 2001, 13, 1625–1647. [Google Scholar] [CrossRef]
- Fiori, S. Solving Minimal-Distance Problems over the Manifold of Real-Symplectic Matrices. Siam J. Matrix Anal. Appl. 2011, 32, 938–968. [Google Scholar] [CrossRef]
- Bini, D.A.; Iannazzo, B. Computing the Karcher Mean of Symmetric Positive Definite Matrices. Stat. Methodol. 2007, 4, 341–353. [Google Scholar] [CrossRef]
- Barbaresco, F. Interactions Between Symmetric Cones and Information Geometrics: Bruhat-Tits and Siegel Spaces Models for High Resolution Autregressive Doppler Imagery. Springer Lect. Notes Comput. Sci. 2009, 5416, 124–163. [Google Scholar]
- Barbaresco, F. Innovative Tools for Radar Signal Processing based on Cartan’s Geometry of SPD Matrices and Information Geometry. In Proceedings of the IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 26–30.
- Nielsen, F.; Bhatia, R. Matrix Information Geometry; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mahata, K.; Schoukens, J.; de Cock, A. Information Matrix and D-optimal Design with Gaussian Inputs for Wiener Model Identification. Automatica 2016, 69, 65–77. [Google Scholar] [CrossRef]
- Stoica, P.; Marzetta, T.L. Parameter Estimation Problems with Singular Information Matrices. IEEE Trans. Signal Proc. 2001, 49, 87–90. [Google Scholar] [CrossRef]
- Amari, A.; Weiss, A.J. Fundamental resolution limits of closely spaced random signals. IET Radar Sonar Navig. 2008, 2, 170–179. [Google Scholar] [CrossRef]
- Amari, A.; Weiss, A.J. Fundamental limitations on the resolution of deterministic signals. IEEE Trans. Signal Proc. 2008, 56, 5309–5318. [Google Scholar] [CrossRef]
- Hero, A.O., III; Castañón, D.; Cochran, D.; Kastella, K. Foundations and Applications of Sensor Management; Springer: New York, NY, USA, 2008. [Google Scholar]
- Nardone, S.C.; Aidala, V.J. Observability Criteria for Bearings-Only Target Motion Analysis. IEEE Trans. Autom. Control 1981, 17, 162–166. [Google Scholar] [CrossRef]
- Jauffret, C.; Pillon, D. Observability in Passive Target Motion Analysis. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1290–1300. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, X.; Caelli, T.; Li, X.; Moran, B. On Information Resolution of Radar Systems. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3084–3102. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, X.; Moran, B. Sensor Network Performance Evaluation in Statistical Manifolds. In Proceedings of the 2010 13th Conference on Information Fusion (FUSION), Edinburgh, UK, 26–29 July 2010.
- Barton, D.K.; Leonov, S.A. Radar Technology Encyclopedia; Artech House: Massachusetts, MA, USA, 1997. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Lang, S. Foundations of Differential Geometry; Springer: New York, NY, USA, 1999. [Google Scholar]
- Amari, S. Differential Geometry of Curved Exponential Families-Curvatures and Information Loss. Ann. Stat. 1982, 10, 357–385. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).