A Model of Mechanothermodynamic Entropy in Tribology
Abstract
:1. Thermodynamic Entropy
2. Thermomechanic Entropy
3. Entropy in Friction and Wear Processes
- (1)
- Adhesion of surfaces and films, associated with adhesive wear and adhesive friction, with entropy change:where interface surface energy γ is the work per unit area to create new surface area ∆AS and Tm is the local temperature of the media.
- (2)
- Plastic deformation, associated with abrasive wear, friction ploughing, and/or cutting, with entropy change:where Uc is work (plastic deformation or cutting) expended per unit volume ∆V affected, and Tm is temperature of the affected material media.
- (3)
- Fracture, associated with fatigue wear and surface damage, with entropy change:where a is crack length, G = −∂US/∂a is the energy release rate dependent on strain energy US, γo is surface energy, and Tcr is temperature of the cracked material at the crack tip.
- (4)
- Phase changes, associated with surface melting, and recrystallization of metals, with entropy change:where ∆H is the change in enthalpy—the latent heat absorbed or shed during the phase change—and Tphase is the temperature associated with the phase change.
- (5)
- Chemical reactions, associated with chemical and oxidation wear, with entropy change:where chemical affinity A depends on the chemical potentials ηi and stoichiometric coefficients κi of the reaction. Since the stoichiometry of the reaction relates changes of molar masses dN’i of reactants and products, extent of reaction ξ has differential change dξ = ± dN’i/κi where minus pertains to reactions, and plus to products.
- (6)
- Diffusion, associated with gradient induced migration of material, with entropy change similar to that for chemical reactions.
- (7)
- Mixing, which for tribology involves mixing of third body [22,23] material entrained between surfaces, with molar entropy change:Here R is the universal gas constant, Ni denotes molar masses of n species, and ratios Ni/N denote molar fractions.
- (8)
- Heat transfer, associated with diffusion of heat dQ from region of higher temperature Th to lower temperature Tl, with entropy change:
4. Entropy in Fatigue Damage Processes
5. Tribo-Fatigue Entropy
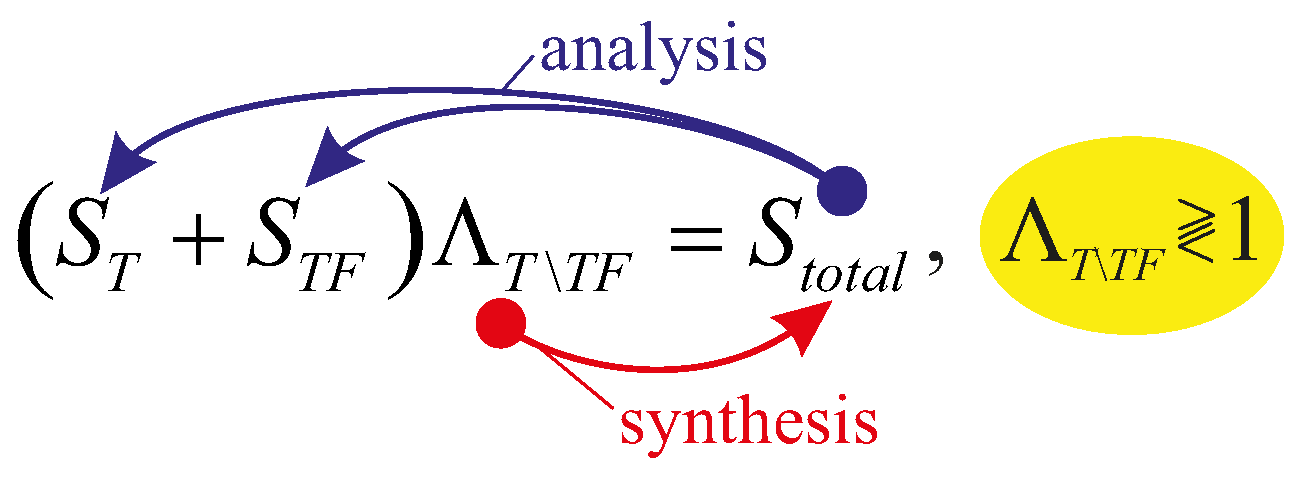
6. Mechanothermodynamic Entropy
7. Discussion of the Research Results
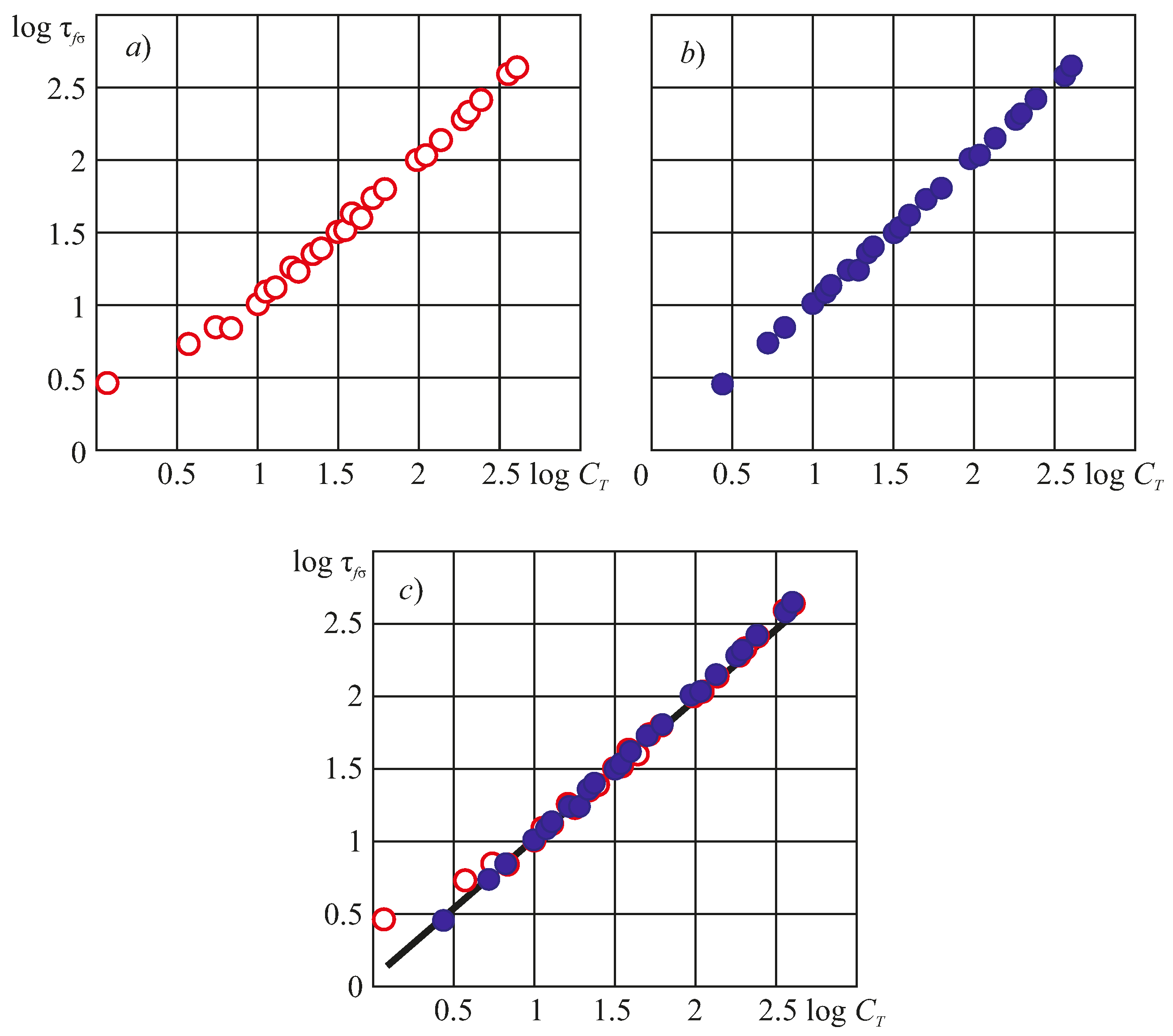
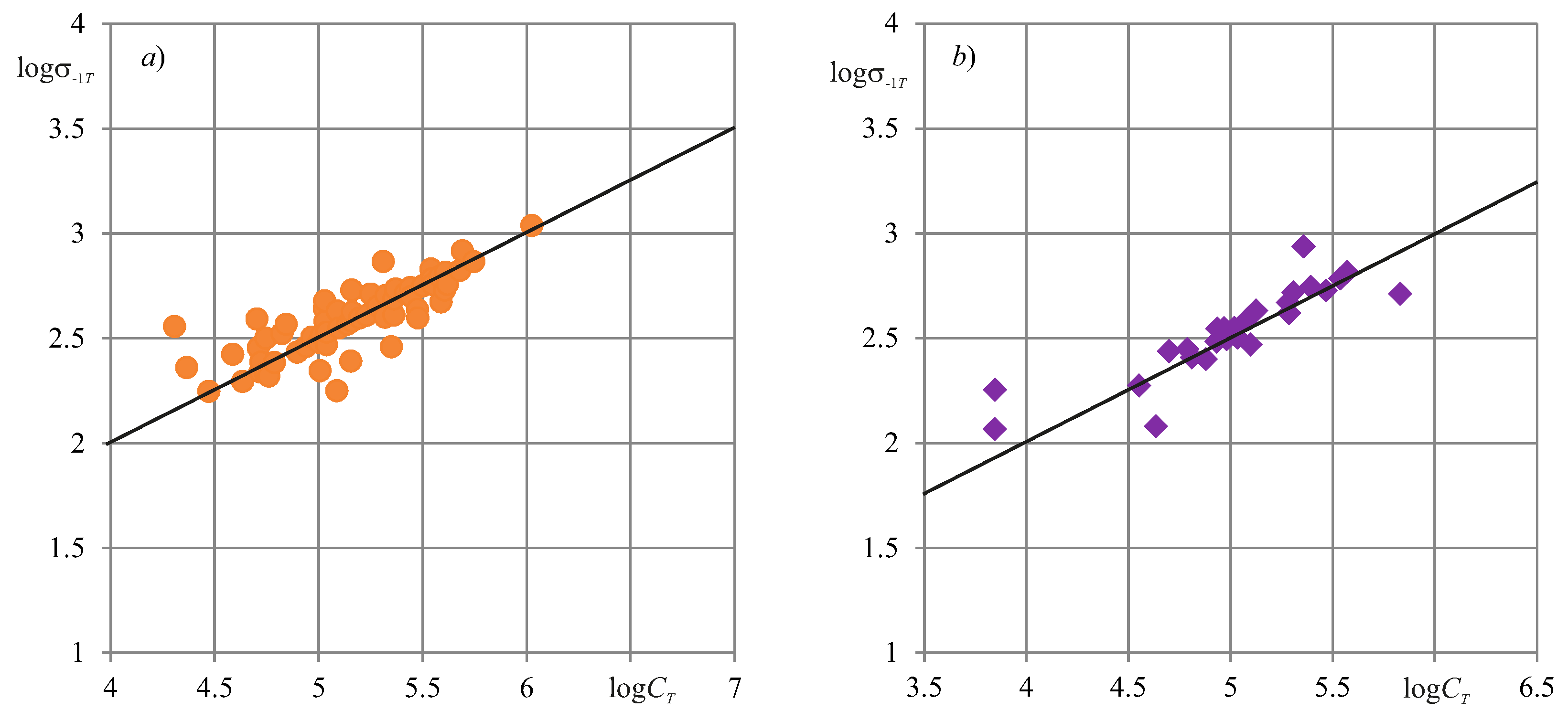
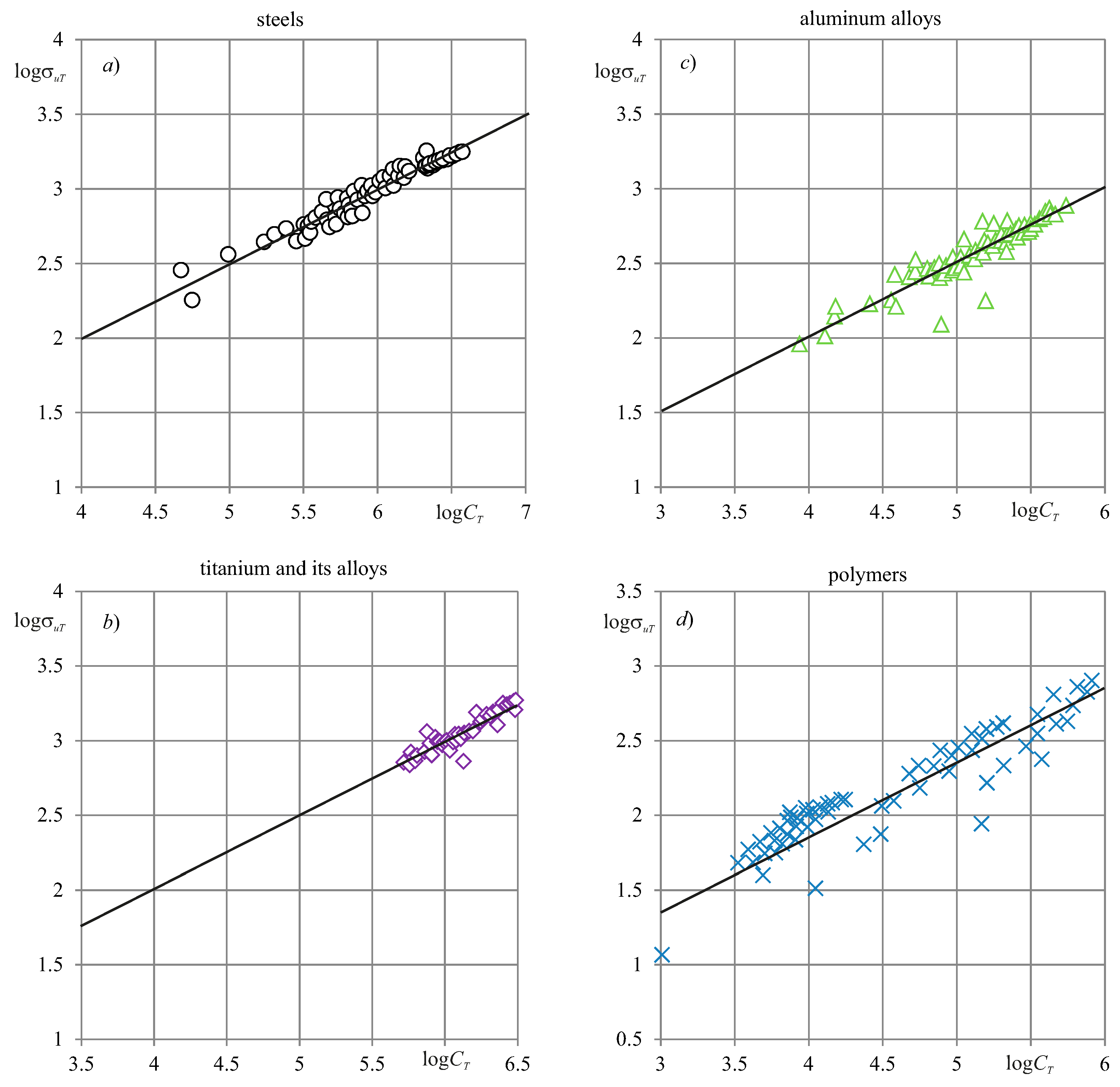
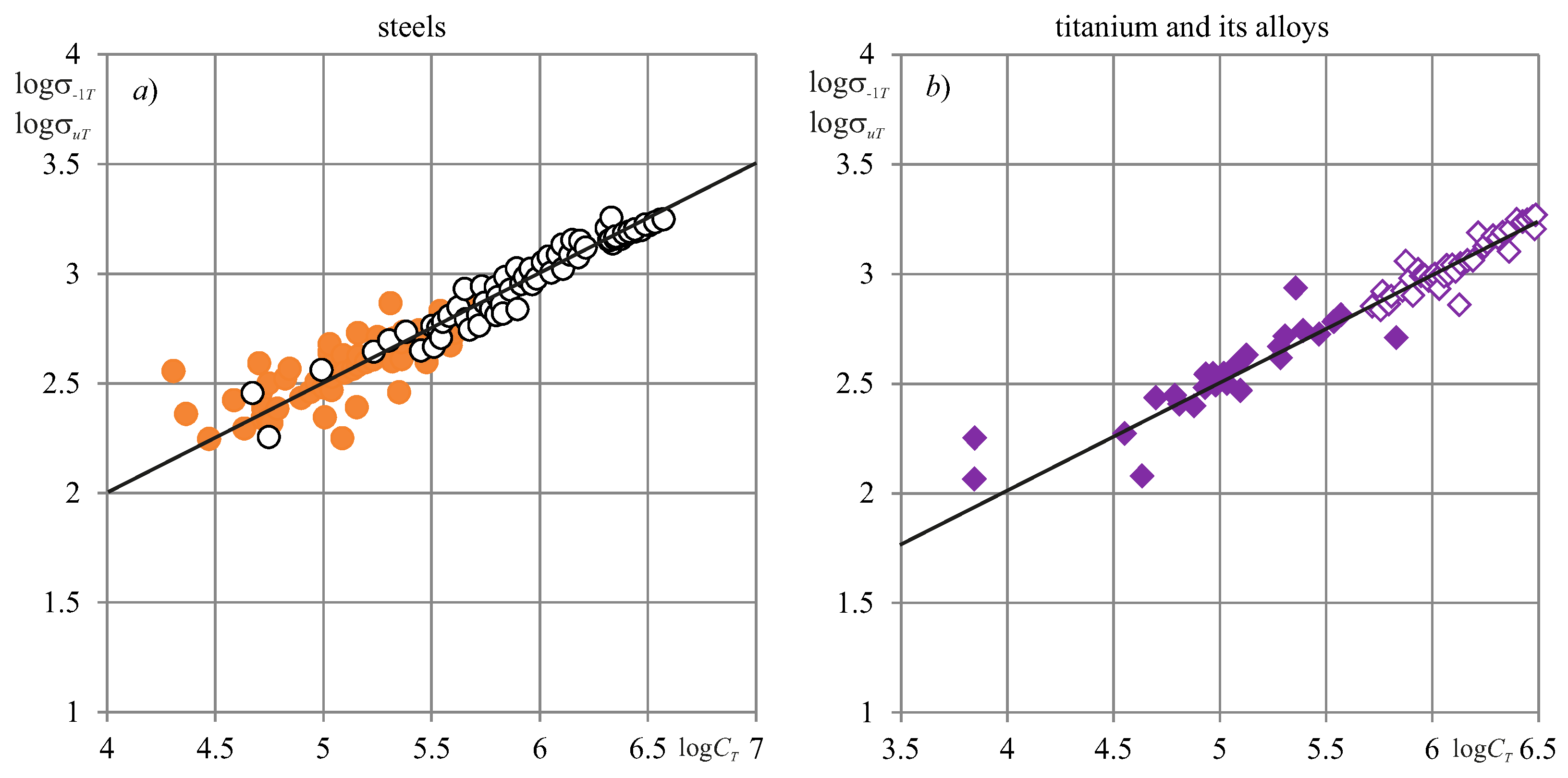
8. Experimental Verification
9. Conclusions
- (1)
- Thermodynamic thermomechanical entropies are specific characteristics of energy dissipation in the environment. In contrast tribo-fatigue entropy is athe specific characteristic of absorption of energy in the moving and deformable solid. Mechanothermodynamic entropy is a generalized characteristic of both energy absorption in a body and dissipation in an environment. It is generated by interacting forces of different nature (mechanical, thermodynamic, electrochemical, etc.).
- (2)
- The processes of friction, wear and fatigue in a general case generate mechanothermodynamic entropy, however irreversible damageability of moving and deformable solids caused by loads of different nature (mechanical, thermal, electrochemical, etc.) is most appropriately characterized by (internal) mechanothermodynamic entropy.
Author Contributions
Conflicts of Interest
References
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- Prokhorov, A.M. Physical Encyclopaedic Dictionary; Soviet Encyclopaedia: Moscow, Russia, 1983. (In Russian) [Google Scholar]
- Sosnovskiy, L.A. Mechanics of Wear-Fatigue Damage; BelSUT Press: Gomel, Belarus, 2007; p. 434. (In Russian) [Google Scholar]
- Sosnovskiy, L.A. Tribo-Fatigue: Wear-Fatigue Damage and Its Prediction (Foundations of Engineering Mechanics); Springer: Berlin/Heidelberg, Germany, 2005; p. 424. [Google Scholar]
- Sherbakov, S.S.; Sosnovskiy, L.A. Mechanics of Tribo-Fatigue Systems; BSU: Minsk, Belarus, 2010; p. 407. (In Russian) [Google Scholar]
- Sosnovskiy, L.A.; Sherbakov, S.S. Surprises of Tribo-Fatigue; Magic Book: Minsk, Belarus, 2009; p. 200. [Google Scholar]
- Mase, G. Theory and Problems of Continuum Mechanics; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Sedov, L.I. Mechanics of a Continuous Medium; Nauka: Moscow, 1973. (In Russian) [Google Scholar]
- Bryant, M.D. Entropy and Dissipative Processes of friction and Wear. FME Trans. 2009, 37, 55–60. [Google Scholar]
- Bryant, M.D. Unification of Friction and Wear. In Recent Developments in Wear Prevention, Friction and Lubrication; Nikas, G., Ed.; Old City Publishing: Philadelphia, PA, USA, 2010; pp. 159–196. [Google Scholar]
- Bryant, M.D.; Khonsari, M.M.; Ling, F.F. On the thermodynamics of degradation. Proc. R. Soc. Lond. A 2008, 464, 2001–2014. [Google Scholar] [CrossRef]
- Ling, F.F.; Bryant, M.D.; Doelling, K.L. On Irreversible Thermodynamics for Wear Prediction. Wear 2002, 253, 1165–1172. [Google Scholar] [CrossRef]
- Doelling, K.L.; Ling, F.F.; Bryant, M.D.; Heilman, B.P. An experimental study of the correlation between wear and entropy flow in machinery components. J. Appl. Phys. 2000, 88, 2999–3003. [Google Scholar] [CrossRef]
- Bryant, M.D.; Khonsari, M.M. Application of degradation-entropy generation theorem to dry sliding friction and wear. In Proceedings of the STLE/ASME International Joint Tribology Conference, Miami, FL, USA, 20–22 October 2008.
- Amiri, M.; Khonsari, M.M. On the Thermodynamics of Friction and Wear—A Review. Entropy 2010, 12, 1021–1049. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M.; Brahmeshwarkar, S. On the Relationship Between Wear and Thermal Response in Sliding Systems. Tribol. Lett. 2010, 38, 147–154. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. On the Prediction of Fatigue Crack Initiation in Rolling/Sliding Contacts with Provision for Loading Sequence Effect. Tribol. Int. 2011, 44, 1620–1628. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. A Comprehensive Fatigue Failure Criterion Based on Thermodynamic Approach. J. Compos. Mater. 2012, 46, 437–447. [Google Scholar] [CrossRef]
- Naderi, M.; Kahirdeh, A.; Khonsari, M.M. Dissipated Thermal Energy and Damage Evolution of Glass/Epoxy Using Infrared Thermography and Acoustic Emission. J. Compos. B Eng. 2012, 43, 1613–1620. [Google Scholar] [CrossRef]
- Aghdam, A.B.; Beheshti, A.; Khonsari, M.M. On the fretting crack nucleation with provision for size effect. Tribol. Int. 2012, 47, 32–43. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M.; Brakhmeshwarkar, S. An Application of Dimensional Analysis to Entropy-Wear Relationship. J. Tribol. 2012, 134, 011604. [Google Scholar] [CrossRef]
- Godet, M. Third-bodies in tribology. Wear 1990, 136, 29–45. [Google Scholar] [CrossRef]
- Richard, D.; Iordanoff, I.; Berthier, Y.; Renouf, M.; Fillot, N. Friction coefficient as a macroscopic view of local dissipation. J. Tribol. 2007, 129, 829–835. [Google Scholar] [CrossRef]
- Kozyrev, Y.P.; Sedakova, E.B. Application of a thermodynamic model for analysis of wear resistance of materials. J. Mach. Manuf. Reliab. 2008, 37, 60–62. [Google Scholar]
- Basaran, C.; Yan, C.Y. A Thermodynamic Framework for Damage Mechanics of Solder Joints. J. Electron. Packag. 1998, 120, 379–384. [Google Scholar] [CrossRef]
- Basaran, C.; Gunel, E.M. Damage Mechanics Unified Constitutive Modeling for Polymers. In Handbook of Damage Mechanics; Springer: New York, NY, USA, 2014. [Google Scholar]
- Basaran, C.; Nie, S.; Gomez, J.; Gunel, E.; Li, S.; Lin, M.; Tang, H.; Yan, C.; Yao, W.; Ye, H. Thermodynamic Theory for Damage Evolution in Solids. In Handbook of Damage Mechanics; Springer: New York, NY, USA, 2014. [Google Scholar]
- Basaran, C.; Nie, S. An Irreversible Thermodynamic Theory for Damage Mechanics of Solids. Int. J. Damage Mech. 2004, 13, 205–224. [Google Scholar] [CrossRef]
- Chandaroy, R.; Basaran, C. Damage Mechanics of Surface Mount Technology Solder Joints under Concurrent Thermal and Dynamic Loadings. J. Electron. Packag. 1999, 121, 61–68. [Google Scholar] [CrossRef]
- Tang, H.; Basaran, C. A Damage Mechanics Based Fatigue Life Prediction Model. J. Electron. Packag. 2003, 125, 120–125. [Google Scholar] [CrossRef]
- Basaran, C.; Tang, H.; Nie, S. Experimental Damage Mechanics of Microelectronics Solder Joints under Fatigue Loading. Mech. Mater. 2004, 36, 1111–1121. [Google Scholar] [CrossRef]
- Gomez, J.; Basaran, C. A Thermodynamics Based Damage Mechanics Constitutive Model for Low Cycle Fatigue Analysis of Microelectronics Solder Joints Incorporating Size Effect. Int. J. Solids Struct. 2005, 42, 3744–3772. [Google Scholar] [CrossRef]
- Gomez, J.; Lin, M.; Basaran, C. Damage Mechanics Modeling of Concurrent Thermal and Vibration Loading On Electronics Packaging. Multidiscip. Model. Mater. Struct. 2006, 2, 309–326. [Google Scholar] [CrossRef]
- Kim, D.; Dargush, G.; Basaran, C. A cyclic two-surface thermoplastic damage model with application to metallic plate dampers. Eng. Struct. 2013, 52, 608–620. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. A Thermodynamic Approach to Fatigue Damage Accumulation under Variable Loading. J. Mater. Sci. Eng. A 2010, 527, 6133–6139. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. An Experimental Approach to Low-Cycle Fatigue Damage Based on Thermodynamic Entropy. Int. J. Solids Struct. 2010, 4, 875–880. [Google Scholar]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. Lond. A 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Amiri, M. Introduction to Thermodynamics of Mechanical Fatigue; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Amiri, M.; Naderi, M.; Khonsari, M.M. An Experimental Approach to Evaluate the Critical Damage. Int. J. Damage Mech. 2011, 20, 89–112. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. On the Role of Entropy Generation in Processes Involving Fatigue. Entropy 2012, 14, 24–31. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. Thermodynamic Analysis of Fatigue Failure in a Composite Laminate. Mech. Mater. 2012, 46, 113–122. [Google Scholar] [CrossRef]
- Morrow, J. Cyclic Plastic Strain Energy and Fatigue of Metals. ASTM Int. 1965. [Google Scholar] [CrossRef]
- Liakat, A.; Khonsari, M. On the Anelasticity and Fatigue Fracture Entropy in High-cycle Metal Fatigue. J. Mater. Des. 2015, 82, 18–27. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. “Life Prediction of Metals Undergoing Fatigue Load Based on Temperature Evolution. J. Mater. Sci. Eng. A 2010, 527, 1555–1559. [Google Scholar] [CrossRef]
- Sosnovskiy, L.A.; Sherbakov, S.S. Mechanothermodynamical System and Its Behavior. Contin. Mech. Thermodyn. 2012, 24, 239–256. [Google Scholar] [CrossRef]
- Sosnovskiy, L.A. L-Risk (Mechanothermodynamics of Irreversible Damages); BelSUT Press: Gomel, Belarus, 2004; p. 317. (In Russian) [Google Scholar]
- Sosnovskiy, L.A.; Sherbakov, S.S. Principles of Mechanothermodynamics; BelSUT Press: Gomel, Belarus, 2013; p. 150. (In Russian) [Google Scholar]
- Sosnovskiy, L.A.; Sherbakov, S.S. Vibro-Impact in Rolling Contact. J. Sound Vib. 2007, 308, 489–503. [Google Scholar] [CrossRef]
- Shcherbakov, S.S. Modeling of the Damaged State by the Finite-Element Method on Simultaneous Action of Contact and Noncontact Loads. J. Eng. Phys. Thermophys. 2012, 85, 472–477. [Google Scholar] [CrossRef]
- Shcherbakov, S.S. State of Volumetric Damage of Tribo-Fatigue System. Strength Mater. 2013, 45, 171–178. [Google Scholar] [CrossRef]
- Zhuravkov, M.A.; Sherbakov, S.S.; Krupoderov, A.V. Modeling of volumetric damage of multielement clamp-knife-base tribo-fatigue system. J. Appl. Math. Mech. 2017, 97, 60–69. [Google Scholar] [CrossRef]
- Sosnovskiy, L.A.; Sherbakov, S.S. Mechanothermodynamics; Springer: Cham, Switzerland, 2016; p. 155. [Google Scholar]
- Sosnovskiy, L.A. Statistical Mechanics of Fatigue Damage; Nauka i Tekhnika: Minsk, Belarus, 1987; p. 288. (In Russian) [Google Scholar]
- Sosnovskiy, L.A.; Sherbakov, S.S. Mechanothermodynamic Entropy and Analysis of Damage State of Complex Systems. Entropy 2016, 18, 268. [Google Scholar] [CrossRef]
- KanagaKaruppiah, K.S.; Sundararajan, S.; Xu, Z.; Li, X. The effect of protein adsorption on the friction behavior of ultra-high molecular weight polyethylene. Tribol. Lett. 2006, 22, 181–188. [Google Scholar] [CrossRef]
- Li, X.; Nardi, P. Micro/nanomechanical characterization of a natural nanocomposite material—The shell of Pectinidae. Nanotechnology 2003, 15, 211–217. [Google Scholar] [CrossRef]
- Li, X.; Gao, H.; Scrivens, W.A.; Fei, D.; Thakur, V.; Sutton, M.A.; Reynolds, A.P.; Myrick, M.L. Structural and mechanical characterization of nanoclay-reinforced agarose nanocomposites. Nanotechnology 2005, 16, 2020–2029. [Google Scholar] [CrossRef] [PubMed]
- Kahirdeh, A.; Khonsari, M.M. Energy dissipation in the course of the fatigue degradation: Mathematical derivation and experimental quantification. Int. J. Solids Struct. 2015, 77, 74–85. [Google Scholar] [CrossRef]
- Ontiveros, V.; Amiri, M.; Kahirdeh, A.; Modarres, M. Thermodynamic entropy generation in the course of the fatigue crack initiation. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 423–434. [Google Scholar] [CrossRef]
- Sherbakov, S.S.; Zhuravkov, M.A. Interaction of Several Bodies as Applied to Solving Tribo-Fatigue Problems. Acta Mech. 2013, 224, 1541–1553. [Google Scholar] [CrossRef]
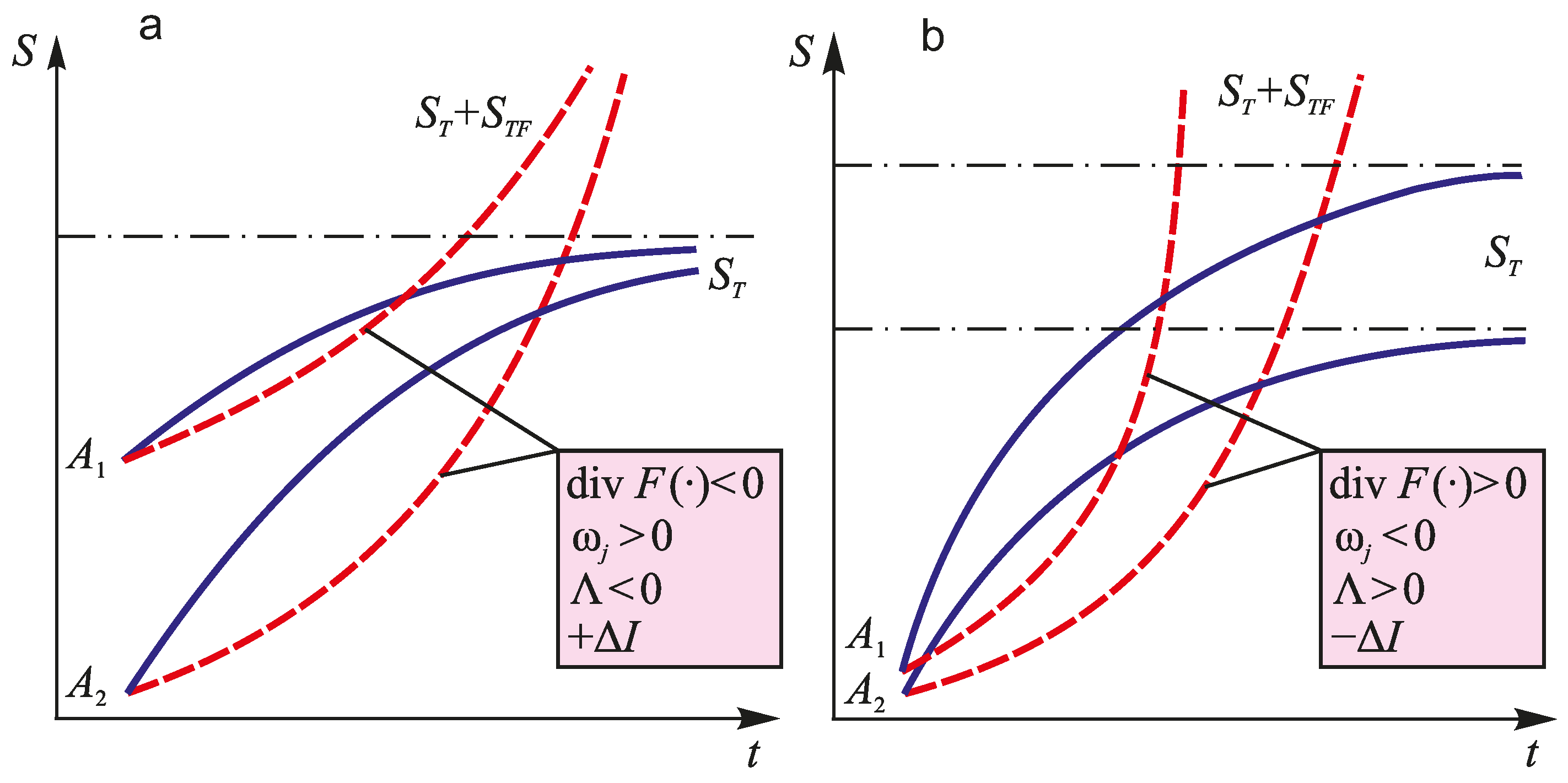
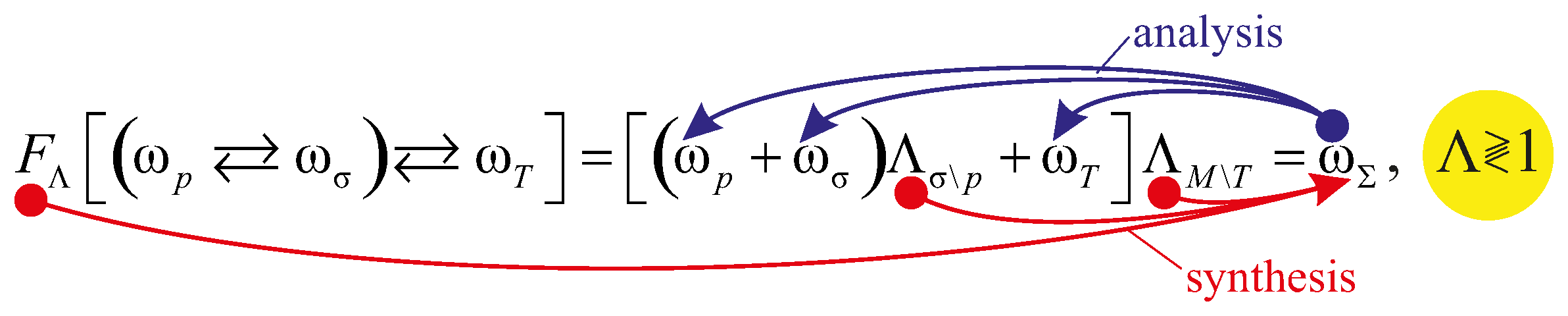
| Main Types of Systems States | Qualitative Characteristic of Damage | Parameter (Quantitative Characteristic) of Damage | Type of Evolution |
|---|---|---|---|
| A-state | Undamaged |  | |
| B-state | Damaged | 0 < < 1 | |
| C-state | Critical(limiting) | = 1 = |
| Parameter | Characteristic |
|---|---|
| div F(●) ⋛ 0 | Relative motion of physical points of matter or elements of a system (converging, diverging and other processes) |
| ωj ⋛ 0 | Nature of irreversible damageability (hardening, softening, etc.) |
| Λ ⋛ 1 | Direction and intensity of interaction of irreversible any-nature damages |
| Parameter | Parameter Value | |
|---|---|---|
| Steel 45 | Silumin | |
| U0, kJ/mole | 419 | 222 |
| Tmelt, K | 1773 | 830 |
| σ−1, MPa | 280 | 42 |
| τ−1, MPa | 170 | 30 |
| aT | 0.236 | 0.267 |
| aσ | 0.005 | 0.126 |
| aτ | 0.014 | 0.247 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sosnovskiy, L.A.; Sherbakov, S.S. A Model of Mechanothermodynamic Entropy in Tribology. Entropy 2017, 19, 115. https://doi.org/10.3390/e19030115
Sosnovskiy LA, Sherbakov SS. A Model of Mechanothermodynamic Entropy in Tribology. Entropy. 2017; 19(3):115. https://doi.org/10.3390/e19030115
Chicago/Turabian StyleSosnovskiy, Leonid A., and Sergei S. Sherbakov. 2017. "A Model of Mechanothermodynamic Entropy in Tribology" Entropy 19, no. 3: 115. https://doi.org/10.3390/e19030115
APA StyleSosnovskiy, L. A., & Sherbakov, S. S. (2017). A Model of Mechanothermodynamic Entropy in Tribology. Entropy, 19(3), 115. https://doi.org/10.3390/e19030115





