Brownian Dynamics Computational Model of Protein Diffusion in Crowded Media with Dextran Macromolecules as Obstacles
Abstract
:1. Introduction
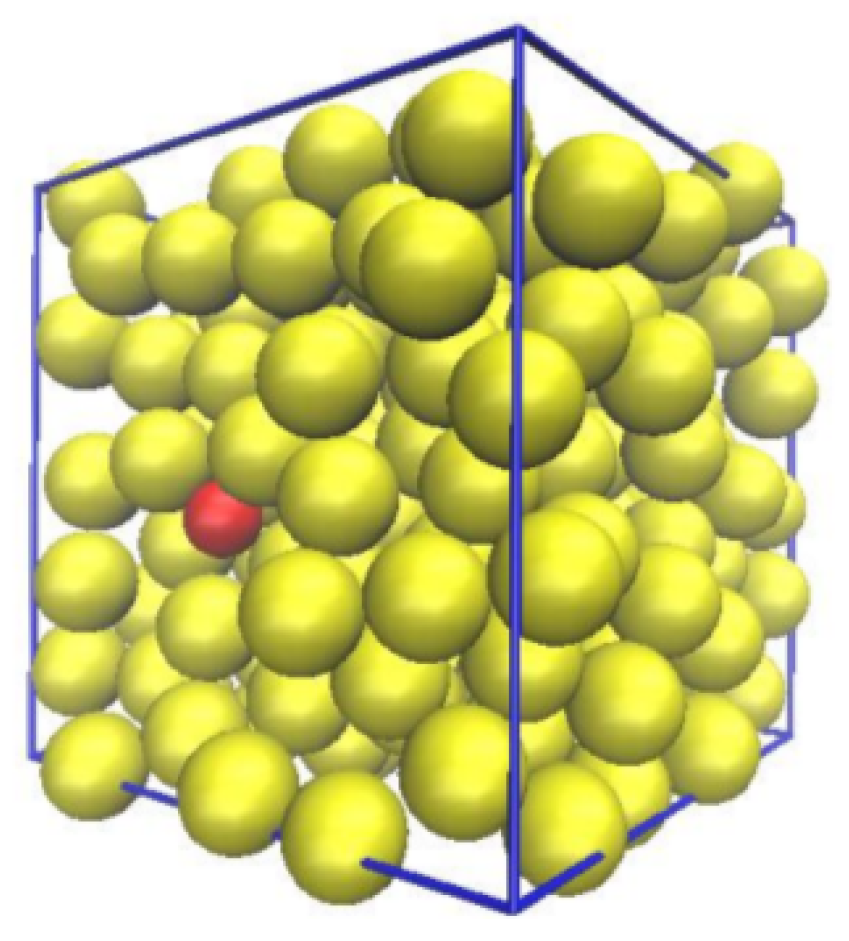
2. Methodology and System Parametrization
2.1. BD Simulations with HI
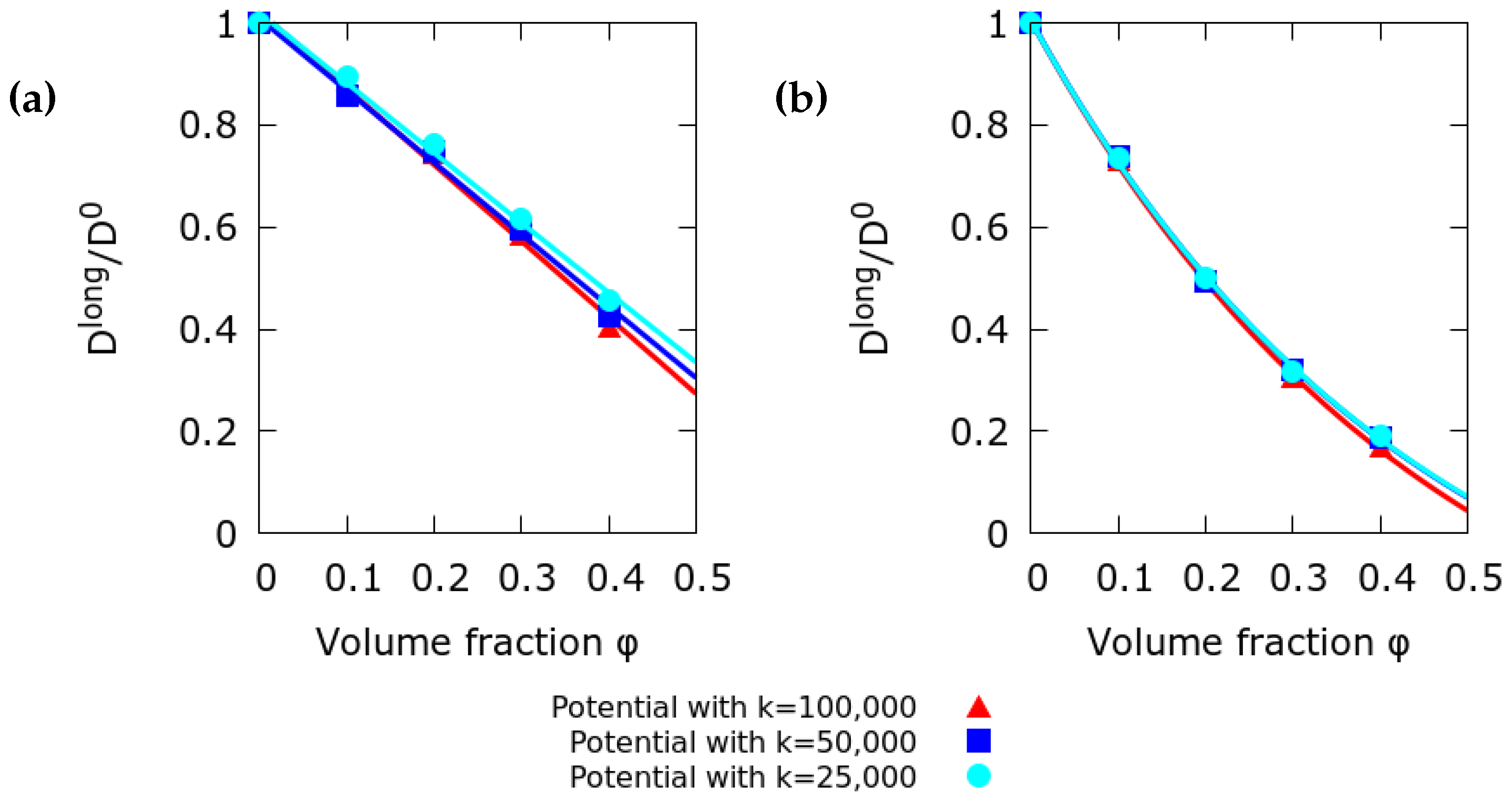
2.2. Effect of the Interaction Potential
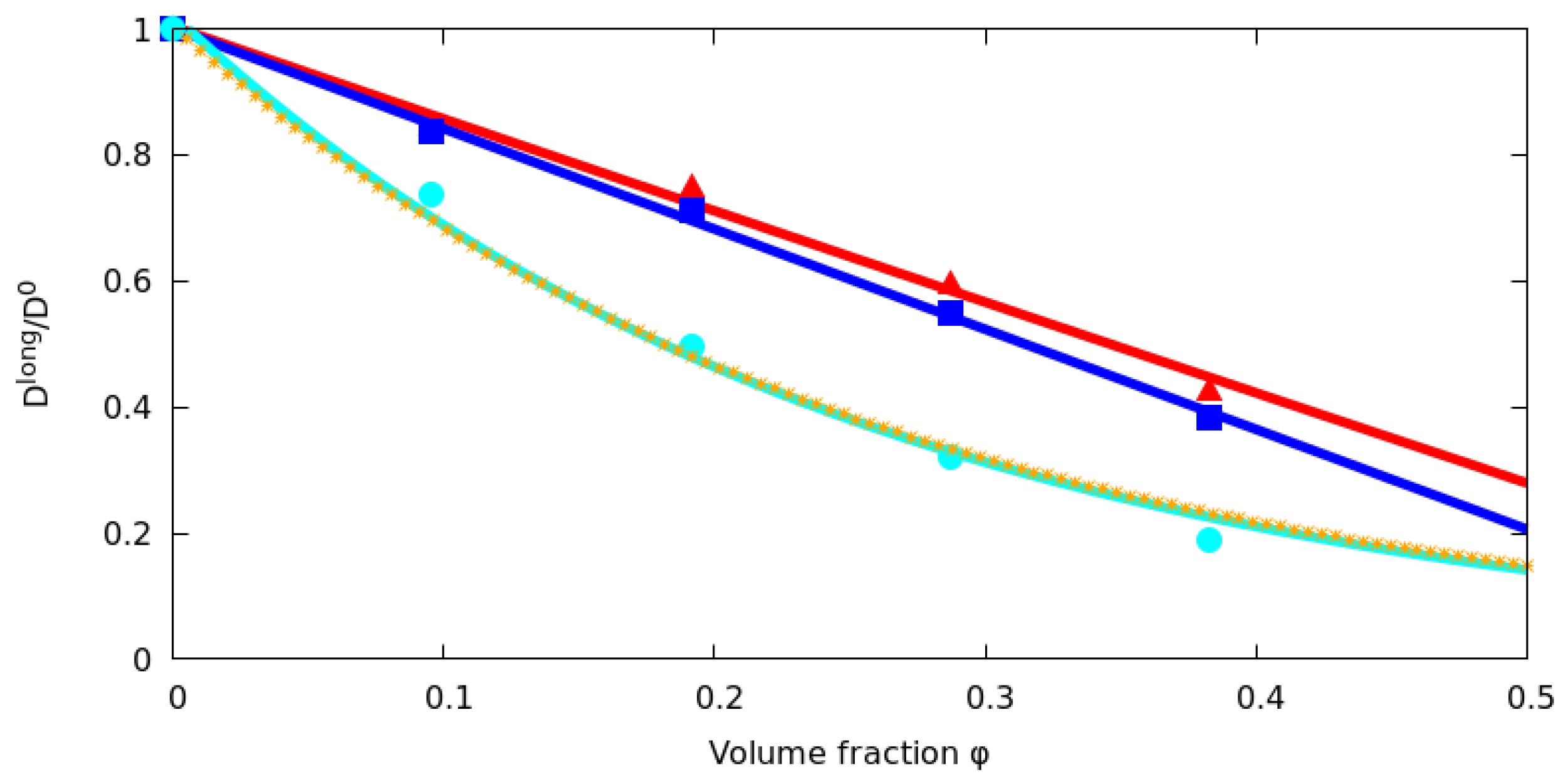
2.3. Effect of Long Range Hydrodynamic Interactions
2.4. Effect of the Difference in Size between Tracer and Obstacles
2.5. Dextran Model
3. Results and Discussion
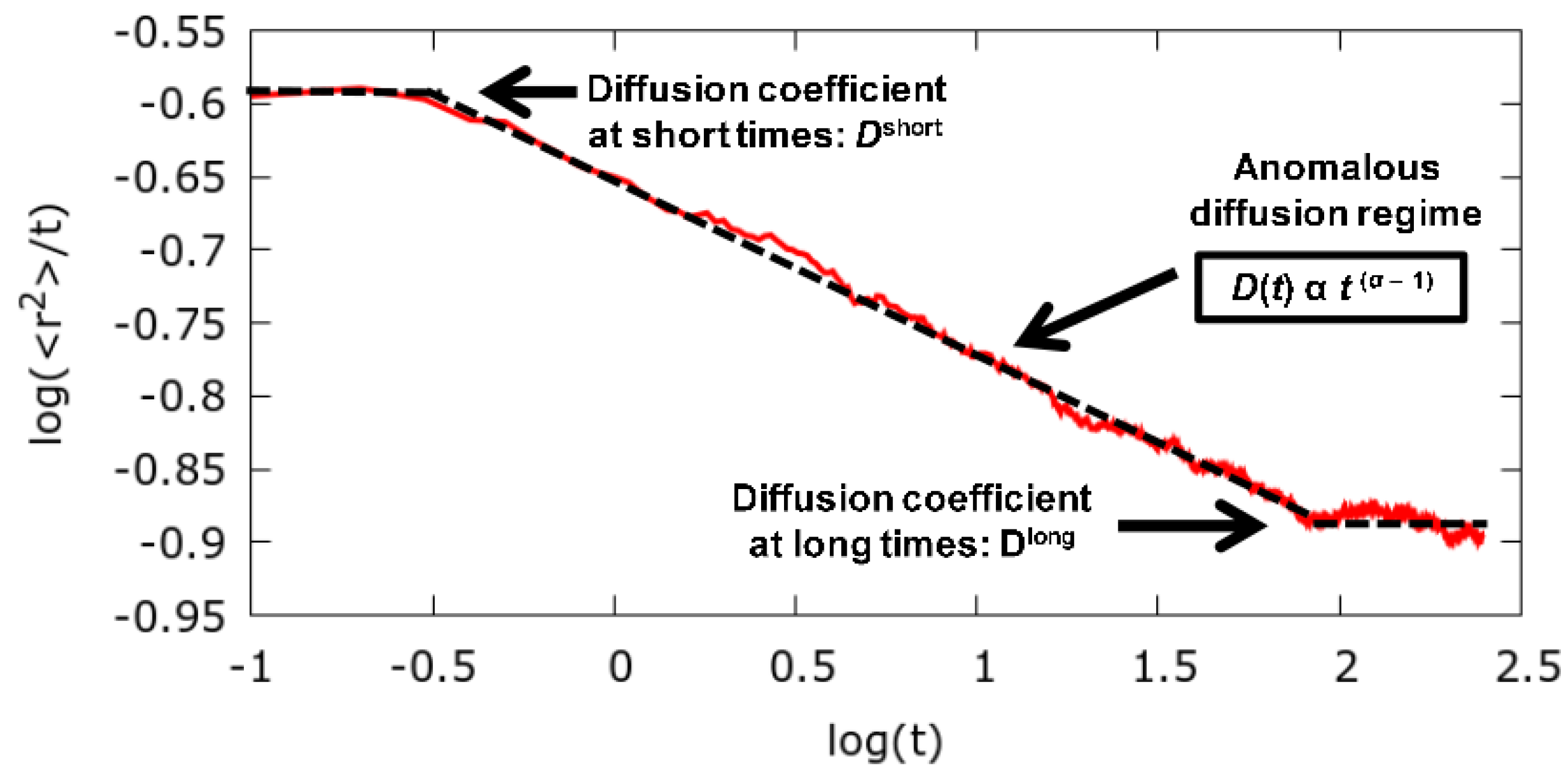
3.1. Long Time Diffusion Coefficient
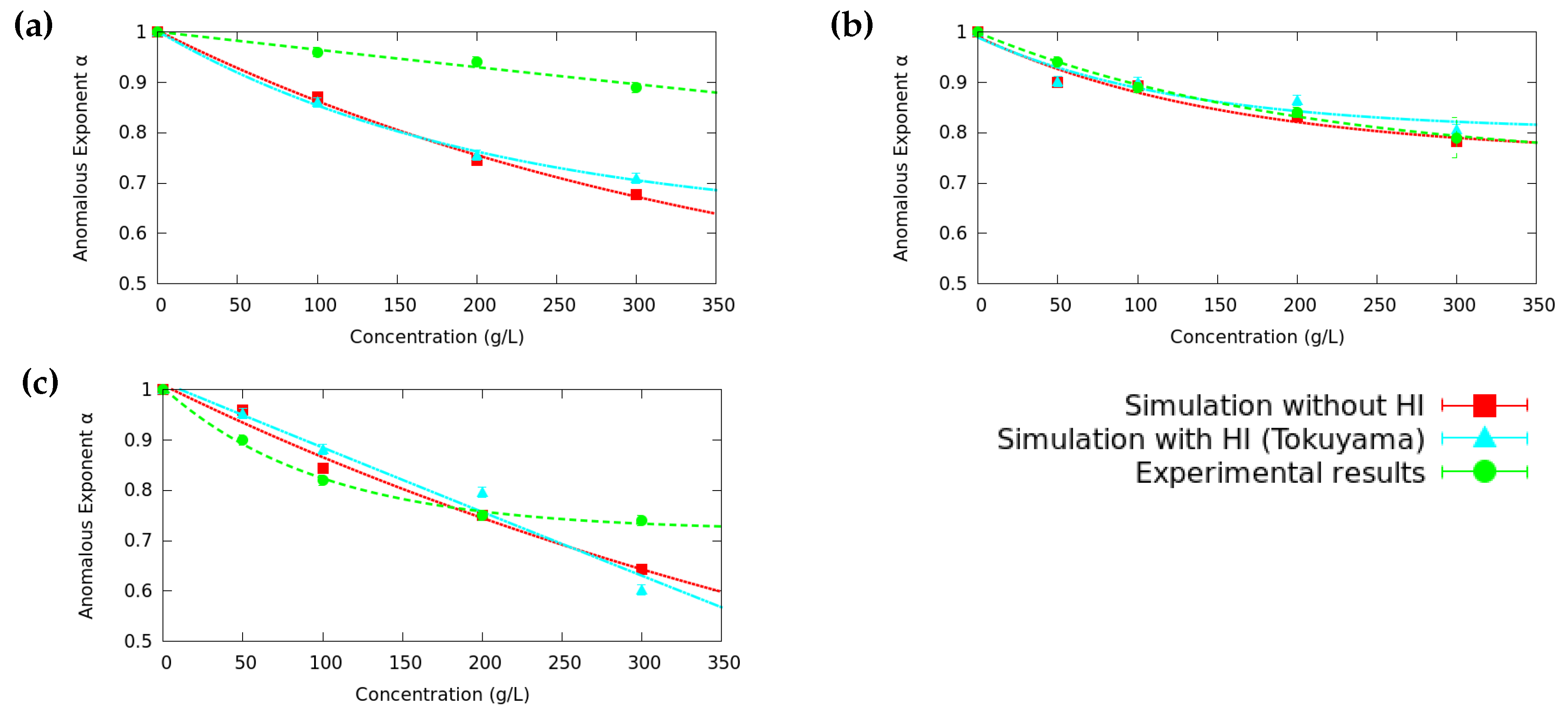
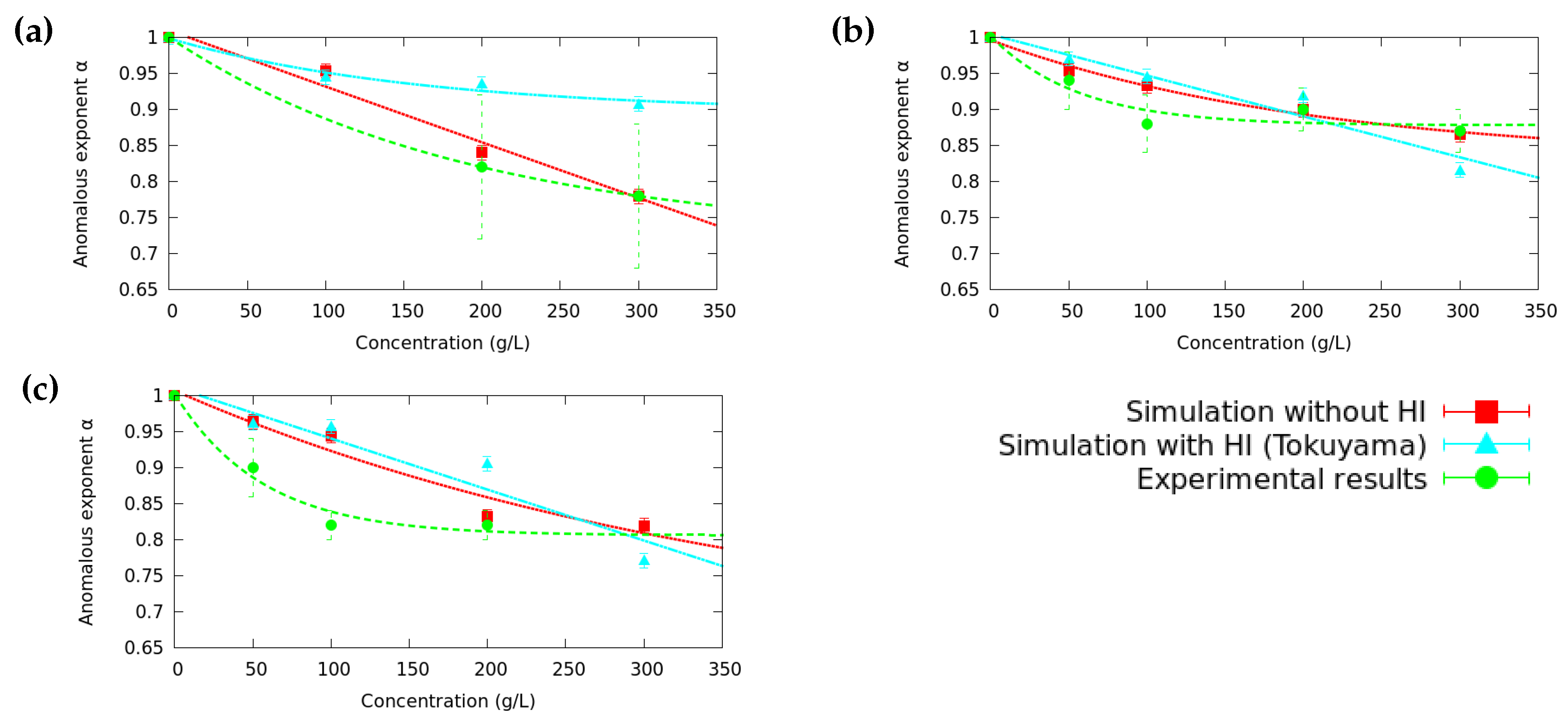
3.2. Anomalous Diffusion Exponent
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BD | Brownian Dynamics |
| FCS | Flourescence Correlation Spectroscopy |
| FRAP | Fluorescence Recovery After Photobleaching |
| HI | Hydrodynamic Interactions |
| RPY | Rotne–Prager–Yamakawa |
References
- Zhou, H.X.; Rivas, G.; Minton, A.P. Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008, 37, 375–397. [Google Scholar] [CrossRef] [PubMed]
- Ellis, R.J. Macromolecular crowding: Obvious but underappreciated. TRENDS BioChem. Sci. 2001, 26, 597–604. [Google Scholar] [CrossRef]
- Pastor, I.; Pitulice, L.; Balcells, C.; Vilaseca, E.; Madurga, S.; Isvoran, A.; Mas, F. Effect of crowding by Dextrans in enzymatic reactions. Biophys. Chem. 2014, 185, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Balcells, C.; Pastor, I.; Pitulice, L.; Hernández, C.; Via, M.; Garcés, J.L.; Madurga, S.; Vilaseca, E.; Isvoran, A.; Cascante, M.; et al. Macromolecular Crowding upon in-vivo-Like Enzyme-Kinetics: Effect of Enzyme-Obstacle Size Ratio. New J. Chem. 2015, 24, 3–16. [Google Scholar]
- Banks, D.S.; Fradin, C. Anomalous Diffusion of Proteins Due to Molecular Crowding. Biophys. J. 2005, 89, 2960–2971. [Google Scholar] [CrossRef] [PubMed]
- Pastor, I.; Vilaseca, E.; Madurga, S.; Garcés, J.L.; Cascante, M.; Mas, F. Diffusion of α-Chymiotrypsin in Solution-Crowded Media. A Flourescence Recovery After Photobleaching Study. J. Phys. Chem. 2010, 114, 4028–4034. [Google Scholar] [CrossRef] [PubMed]
- Vilaseca, E.; Pastor, I.; Isvoran, A.; Madurga, S.; Garcés, J.L.; Mas, F. Diffusion in macromolecular crowded media: Monte Carlo simulation of obstructed diffusion vs. FRAP experiments. Theor. Chem. Acc. 2011, 128, 795–805. [Google Scholar] [CrossRef]
- Elcock, A.H. Models of macromolecular crowding effects and the need of quantitative comparisons with experiment. Curr. Opin. Struct. Biol. 2010, 20, 196–206. [Google Scholar] [CrossRef] [PubMed]
- Vilaseca, E.; Isvoran, A.; Madurga, S.; Pastor, I.; Garceés, J.L.; Mas, F. New insights into diffusion in 3D crowded media by Monte Carlo simulations: Effect of size, mobility and spatial distribution of obstacles. Phys. Chem. Chem. Phys. 2011, 13, 7396–7407. [Google Scholar] [CrossRef] [PubMed]
- Hasnain, S.; McClendon, C.L.; Hsu, M.T.; Jacobson, M.P.; Bandyopadhyay, P. A New Coarse-Grained Model for E. coli Cytoplasm: Accurate Calculation of the Diffusion Coefficient of Proteins and Observation of Anomalous Diffusion. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Gomez, D.; Klumpp, S. Biochemical reactions in crowded environments: Revisiting the effects of volume exclusion with simulations. Front. Phys. 2015. [Google Scholar] [CrossRef]
- Yu, I.; Mori, T.; Ando, T.; Harada, R.; Jung, J.; Sugita, Y.; Feig, M. Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm. eLife 2016, 5, e19274. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J. Anomalous Diffusion Due to Obstacles: A Monte Carlo Study. Biophys. J. 1994, 66, 394–401. [Google Scholar] [CrossRef]
- Bauchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanics, model and physical application. Phys. Rep. 1990, 185, 127–293. [Google Scholar] [CrossRef]
- Elcock, A.H. Molecule-Centered Method for Accelerating the Calculation of Hydrodynamic Interactions in Brownian Dynamics Simulations Containing Many Flexible Biomolecules. J. Chem. Theory Comput. 2013, 9, 3224–3239. [Google Scholar] [CrossRef] [PubMed]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Rotne, J.; Prager, S. Variational treatment of hydrodynamic interaction in polymers. J. Chem. Phys. 1969, 50, 4831–4837. [Google Scholar] [CrossRef]
- Yamakawa, H.J. Transport properties of polymer chains in dilute solution: Hydrodynamic interaction. Chem. Phys. 1970, 53, 436–443. [Google Scholar] [CrossRef]
- Tokuyama, M.; Oppenheim, I. Dynamics of hard-sphere suspensions. Phys. Rev. E 1994, 50, R16. [Google Scholar] [CrossRef]
- Tokuyama, M.; Moriki, T.; Kimura, Y. Self-diffusion of biomolecules in solution. Phys. Rev. E 2011, 83, 081402. [Google Scholar] [CrossRef] [PubMed]
- Tokuyama, M. Mean-field theory of glass transitions. Physica A 2006, 364, 23–62. [Google Scholar] [CrossRef]
- Rodríguez, R.; Hernández, J.G.; García, J. Comparison of Brownian dynamics algorithms with hydrodynamic interactions. J. Chem. Phys. 2011, 135, 084116. [Google Scholar]
- Fixman, M. Implicit algorithm for Brownian Dynamics of Polymers. Macromolecules 1986, 19, 1195–1204. [Google Scholar] [CrossRef]
- Geyer, T.; Winter, U. An O(N2) approximation for hydrodynamic interactions in Brownian dynamics simulations. J. Chem. Phys. 2009, 130, 114905. [Google Scholar] [CrossRef] [PubMed]
- Zuk, P.J.; Wajnryb, E.; Mizerski, K.A.; Szymczak, P. Rotne–Prager–Yamakawa approximation for different-sized particles in application to macromolecular bead model. J. Fluid. Mech. 2014, 741, R5. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F.; Bossis, G. Dynamic simulation of hydrodynamically interacting particles. J. Fluid Mech. 1987, 180, 21–49. [Google Scholar] [CrossRef]
- Brady, J.F.; Bossis, G. Stokesian Dynamics. Annu. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Phillips, R.J.; Brady, J.F.; Bossis, G. Hydrodynamic transport properties of hard-sphere dispersions. I. Suspensions of freely mobile particles. Phys. Fluids 1988, 31, 3462–3472. [Google Scholar] [CrossRef]
- Ando, T.; Chow, E.; Skolnick, J. Dynamic simulation of concentrated macromolecular solutions with screened long-range hydrodynamic interactions: Algorithm and limitations. J. Chem. Phys. 2013, 139, 121922. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Weinstein, H. Toward realistic modeling of dynamic processes in cell signaling: Quantification of macromolecular crowding effects. J. Chem. Phys. 2007, 127, 155105. [Google Scholar] [CrossRef] [PubMed]
- Mereghetti, P.; Wade, R.C. Atomic Detail Brownian Dynamics Simulations of Concentrated Protein Solutions with a Mean Field Treatment of Hydrodynamic Interactions. J. Chem. Phys. 2012, 116, 8523–8533. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. The multivariate Langevin and Fokker–Planck equations. Am. J. Phys. 1996, 64, 1246–1257. [Google Scholar] [CrossRef]
- Mori, H. Transport, Collective Motion and Brownian Motion. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Dhont, J.K.G. Brownian motion of non-interacting particles. In An Introduction to Dynamics of Colloids; Elsevier: Amsterdam, The Netherlands, 1996; Chapter 2. [Google Scholar]
- Schöneberg, J.; Noé, F. ReaDDy—A Software for Particle-Based Reaction-Diffusion Dynamics in Crowded Cellular Environments. PLoS ONE 2013, 8, e74261. [Google Scholar] [CrossRef] [PubMed]
- Roosen-Runge, F.; Hennig, M.; Zhang, F.; Jacobs, R.M.; Sztucki, M.; Schober, H.; Seydel, T.; Schreiber, F. Protein self-diffusion in crowded solutions. Proc. Natl. Acad. Sci. USA 2011, 108, 11815–11820. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Zhou, H.X. Atomistic modeling of macromolecular crowding predicts modest increases in protein folding and binding stability. Biophys. J. 2009, 97, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Sastry, S.; Truskett, T.M.; Debenedetti, P.G.; Torquato, S.; Stillinger, F.H. Free volume in the hard sphere liquid. Mol. Phys. 1998, 95, 289–297. [Google Scholar] [CrossRef]
- Brady, J.F.; Phillips, R.J.; Lester, J.C.; Bossis, G. Dynamic simulation of hydrodynamically interacting suspensions. J. Fluid Mech. 1988, 195, 257–280. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Ewald sum of the Rotne–Prager tensor. J. Chem. Phys. 1986, 85, 1581–1582. [Google Scholar] [CrossRef]
- Ladd, A.J. Hydrodynamic transport coefficients of random dispersions of hard spheres. J. Chem. Phys. 1990, 93, 3484–3494. [Google Scholar] [CrossRef]
- Ortega, A.; Amorós, D.; de la Torre, J.G. Prediction of hydrodynamic and other solution properties of rigid proteins from atomic-and residue-level models. Biophys. J. 2011, 101, 892–898. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, J.K.; Wenby, B.; Meiselman, H.J.; Fisher, T.C. The Hydrodynamic Radii of Macromolecules and Their Effect on Red Blood Cell Aggregation. Biophys. J. 2004, 87, 4259–4270. [Google Scholar] [CrossRef] [PubMed]
- Fundueanu, G.; Nastruzzi, C.; Carpov, A.; Desbrieres, J.; Rinaudo, M. Physico-chemical characterization of Ca-alginate microparticles produced with different methods. Biomaterials 1999, 20, 1427–1435. [Google Scholar] [CrossRef]
- Sloan, J.W.; Alexander, B.H.; Lohmar, R.L.; Wolff, I.A.; Rist, C.E. Determination of dextran structure by periodate oxidation techniques. J. Am. Chem. Soc. 1954, 76, 4429–4434. [Google Scholar] [CrossRef]
- Sabatie, J.; Choplin, L.; Moan, M.; Doublier, J.L.; Paul, F.; Monsan, P. The effect of synthesis temperature on the structure of dextran NRRL B 512F. Carbohydr. Polym. 1988, 9, 87–101. [Google Scholar] [CrossRef]
- Schaefer, D.W. A unified model for the structure of polymers in semidilute solution. Polymer 1984, 25, 387–394. [Google Scholar] [CrossRef]
- Vilaseca, P.; Franzese, G. Softness dependence of the anomalies for the continuous shouldered well potential. J. Chem. Phys. 2010, 133, 084507. [Google Scholar] [CrossRef] [PubMed]
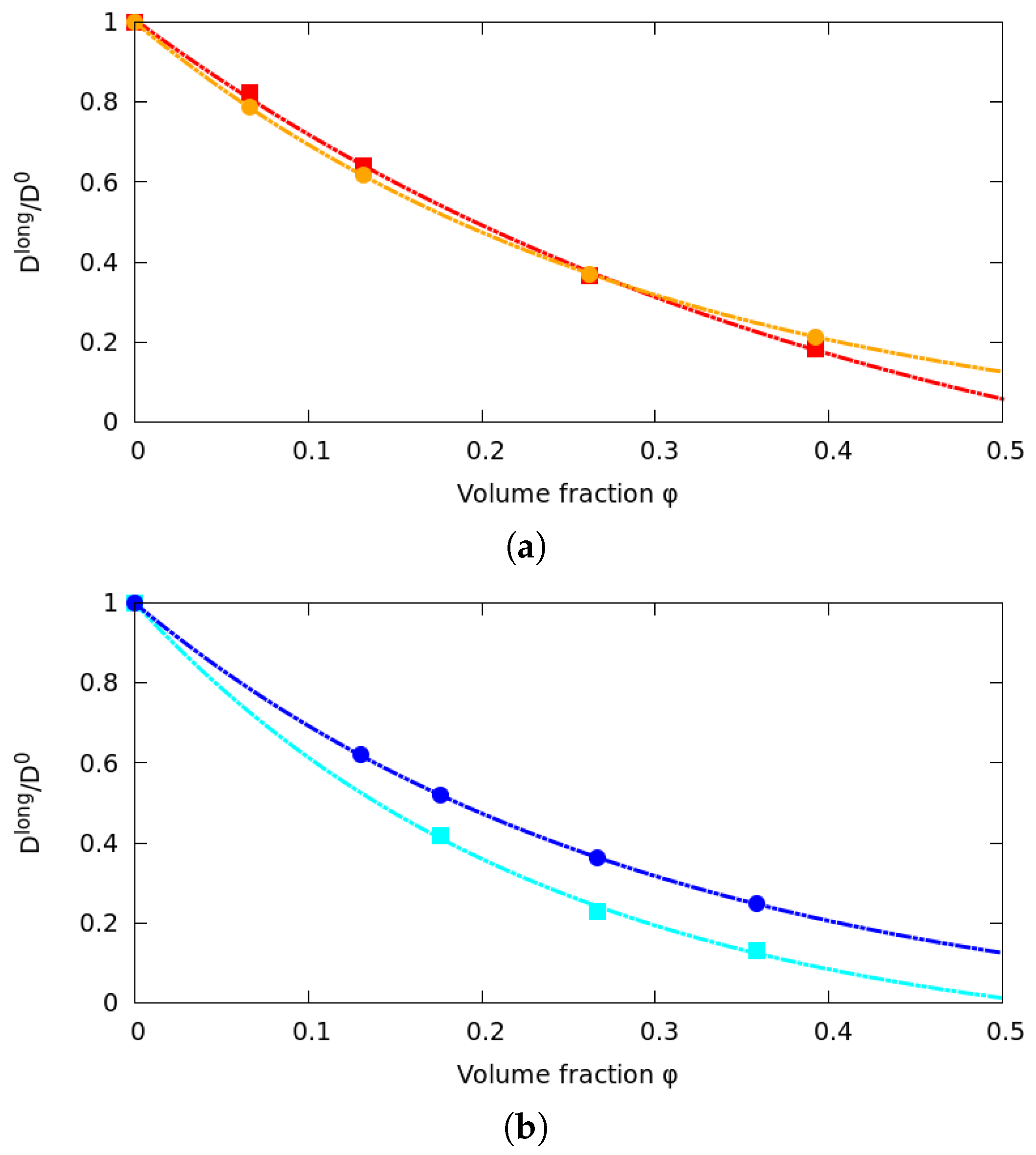
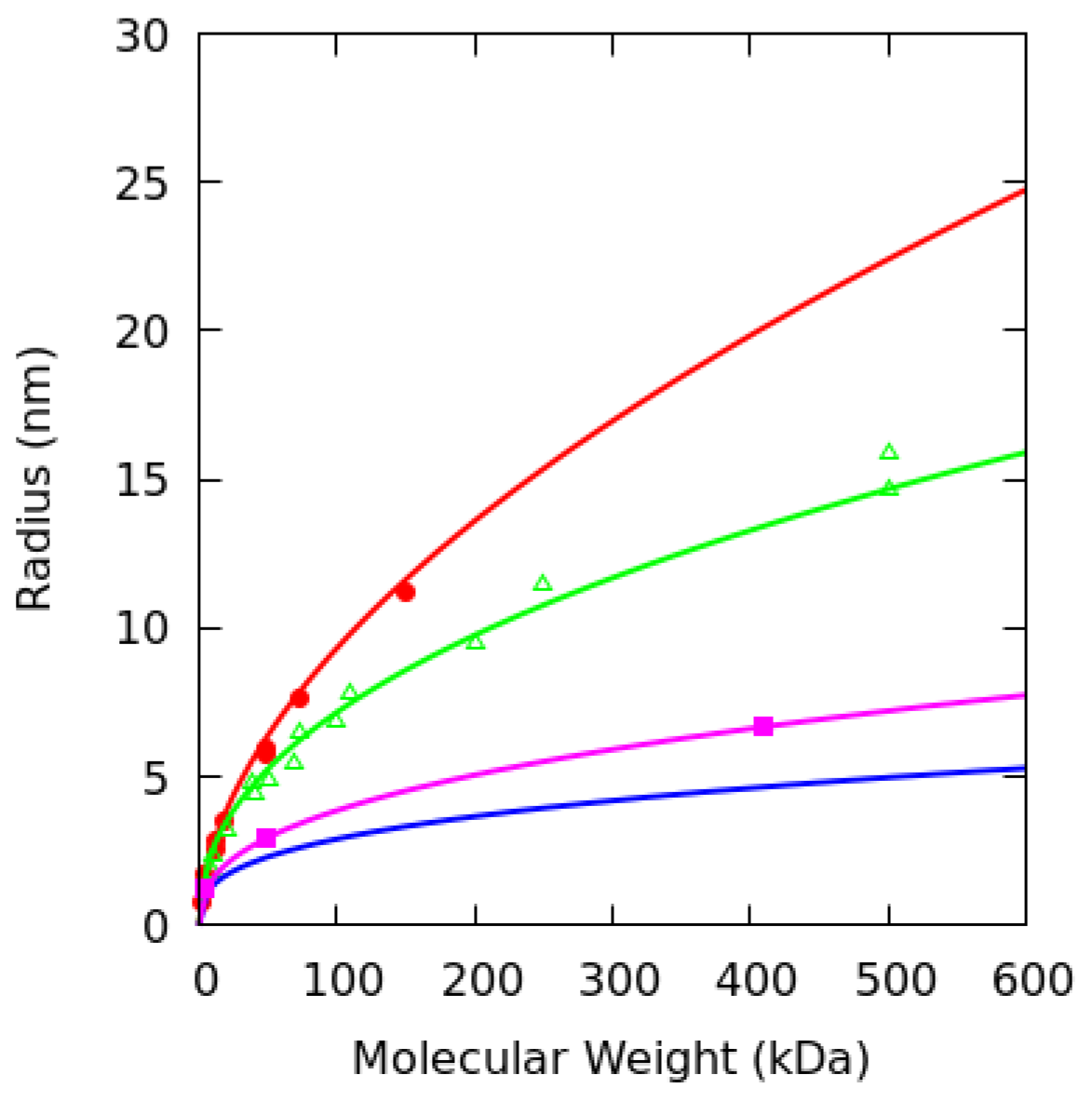
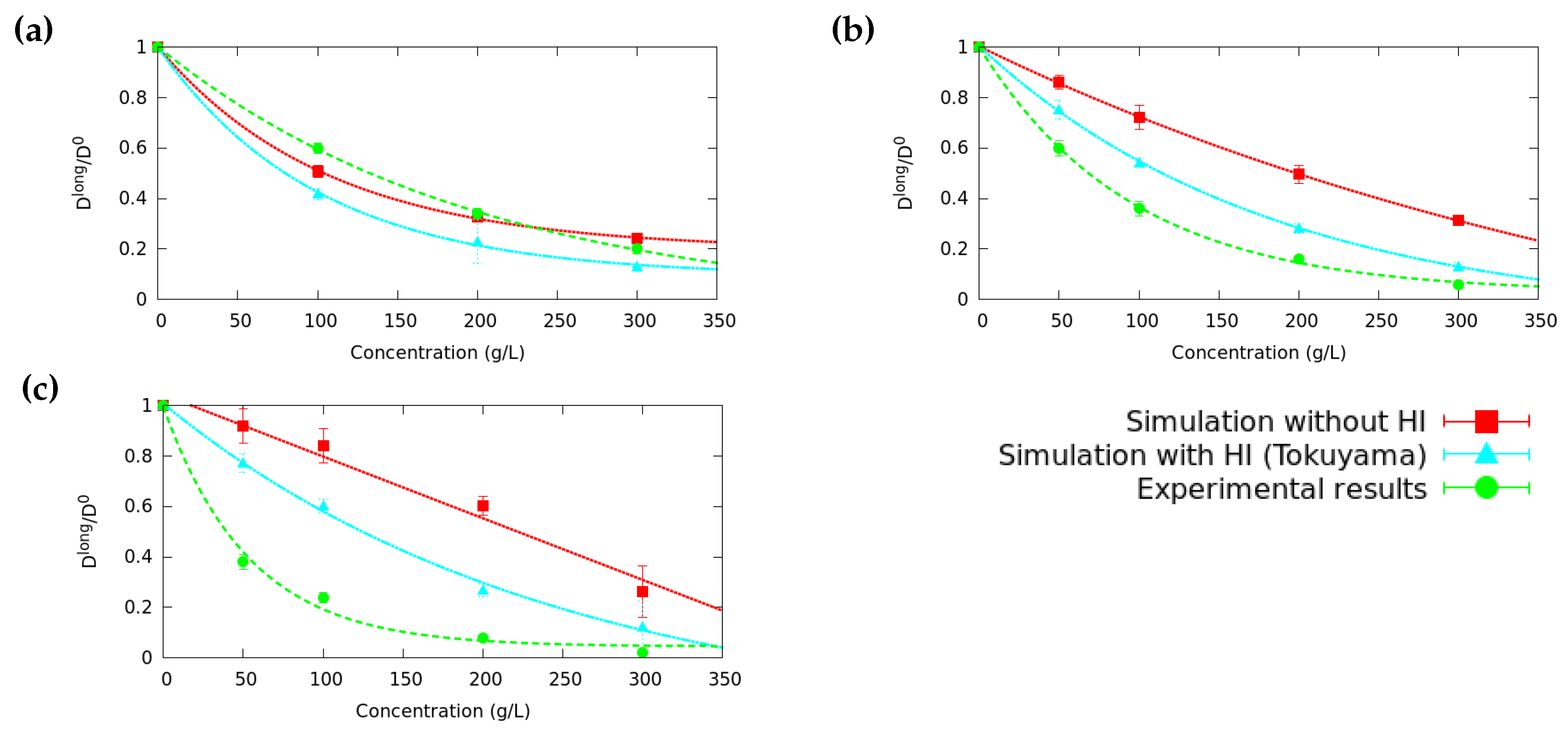
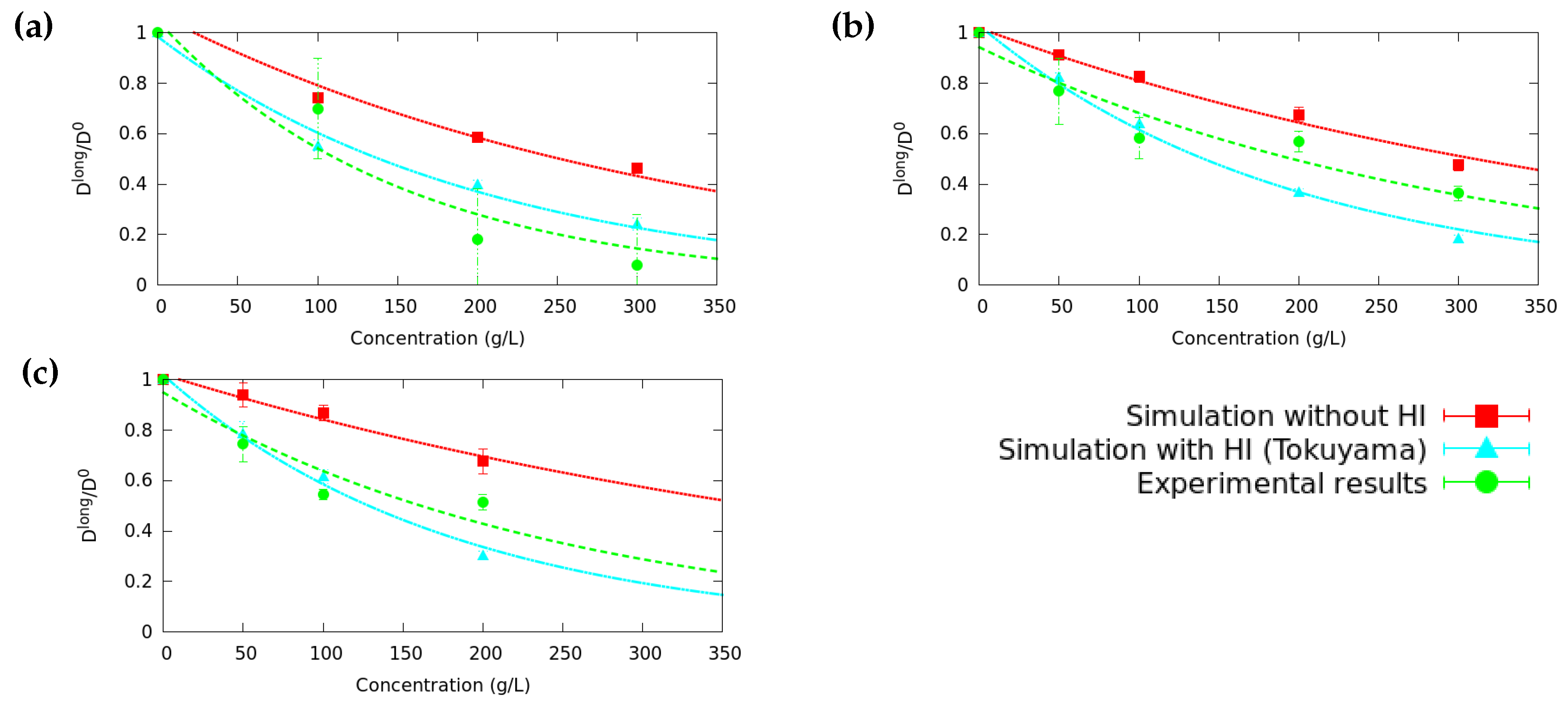
| K (nm·Da) | 0.018 ± 0.001 | 0.043 ± 0.002 | 0.063 | 0.045 |
| γ | 0.544 ± 0.005 | 0.445 ± 0.004 | 0.387 |
| Dextran | |||||
|---|---|---|---|---|---|
| D5 | 5.2 | 1.7 | 1.9 | 1.1 | 1.2 |
| D50 | 48.6 | 5.8 | 5.2 | 2.3 | 2.9 |
| D400 | 409.8 | 17 | 13.5 | 4.7 | 6.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco, P.M.; Via, M.; Garcés, J.L.; Madurga, S.; Mas, F. Brownian Dynamics Computational Model of Protein Diffusion in Crowded Media with Dextran Macromolecules as Obstacles. Entropy 2017, 19, 105. https://doi.org/10.3390/e19030105
Blanco PM, Via M, Garcés JL, Madurga S, Mas F. Brownian Dynamics Computational Model of Protein Diffusion in Crowded Media with Dextran Macromolecules as Obstacles. Entropy. 2017; 19(3):105. https://doi.org/10.3390/e19030105
Chicago/Turabian StyleBlanco, Pablo M., Mireia Via, Josep Lluís Garcés, Sergio Madurga, and Francesc Mas. 2017. "Brownian Dynamics Computational Model of Protein Diffusion in Crowded Media with Dextran Macromolecules as Obstacles" Entropy 19, no. 3: 105. https://doi.org/10.3390/e19030105
APA StyleBlanco, P. M., Via, M., Garcés, J. L., Madurga, S., & Mas, F. (2017). Brownian Dynamics Computational Model of Protein Diffusion in Crowded Media with Dextran Macromolecules as Obstacles. Entropy, 19(3), 105. https://doi.org/10.3390/e19030105







