Abstract
This paper analyses the complexity of multivariate electroencephalogram (EEG) signals in different frequency scales for the analysis and classification of focal and non-focal EEG signals. The proposed multivariate sub-band entropy measure has been built based on tunable-Q wavelet transform (TQWT). In the field of multivariate entropy analysis, recent studies have performed analysis of biomedical signals with a multi-level filtering approach. This approach has become a useful tool for measuring inherent complexity of the biomedical signals. However, these methods may not be well suited for quantifying the complexity of the individual multivariate sub-bands of the analysed signal. In this present study, we have tried to resolve this difficulty by employing TQWT for analysing the sub-band signals of the analysed multivariate signal. It should be noted that higher value of Q factor is suitable for analysing signals with oscillatory nature, whereas the lower value of Q factor is suitable for analysing signals with non-oscillatory transients in nature. Moreover, with an increased number of sub-bands and a higher value of Q-factor, a reasonably good resolution can be achieved simultaneously in high and low frequency regions of the considered signals. Finally, we have employed multivariate fuzzy entropy (mvFE) to the multivariate sub-band signals obtained from the analysed signal. The proposed Q-based multivariate sub-band entropy has been studied on the publicly available bivariate Bern Barcelona focal and non-focal EEG signals database to investigate the statistical significance of the proposed features in different time segmented signals. Finally, the features are fed to random forest and least squares support vector machine (LS-SVM) classifiers to select the best classifier. Our method has achieved the highest classification accuracy of 84.67% in classifying focal and non-focal EEG signals with LS-SVM classifier. The proposed multivariate sub-band fuzzy entropy can also be applied to measure complexity of other multivariate biomedical signals.
1. Introduction
Approximately 60 million people worldwide are affected by a neurological disorder known as epilepsy [1]. Electroencephalogram (EEG) signals are generally used for the medical investigations of the epilepsy disorder [2]. Epilepsy is broadly classified into two categories—namely, focal and generalized epilepsy. Focal epilepsy affects the limited area of the brain. It has been noticed that 20% patients of generalized epilepsy and 60% patients of focal epilepsy develop resistance to drugs and undergo surgery [3]. Hence, it would be of prime importance to localize the brain area affected by focal epilepsy for medical diagnosis. There are some presurgical localization methods—namely, positron emission tomography (PET) [4], magnetic resonance imaging (MRI) [5,6], and single photon emission computed tomography (SPECT) [7] are useful for locating epilepsy affected brain areas. The epileptogenic focus can also be located with the help of EEG signals before presurgical evaluation. The EEG signal based method for locating the epilepsy affected brain area is convenient. Moreover, EEG signals provide good temporal resolution.
Recording of focal (F) and non-focal (NF) EEG signals can be used to locate the brain area that is affected by epilepsy disease. The brain area from where first seizure EEG signal changes are identified gives rise to F EEG signals; on the other hand, the brain area that does not contribute to seizure onset generates NF EEG signals [8]. It should be noted that seizure segments are absent in F and NF types of EEG signals [8]. The non-stationary signal analysis techniques are suitable for EEG signal analysis [9]. In [8], the authors have found that F type EEG signals are more stationary, less random, and more nonlinear in comparison to the NF type of EEG signals. Recently, several automated signal processing based methods have been proposed that can detect the changes in the attributes of EEG signals prior to onset of the seizure and hence locate epileptogenic focus. In [10], for localizing epileptic events, the authors have used wavelet packet and time-frequency waveforms for the characterization of spikes in the electrocorticograph (ECoG) signals of 21 patients. In [11,12], the authors have analyzed delta asymmetry of EEG signals recorded from partial epilepsy patients in order to lateralize and localize epileptic focus. It has been found that, prior to neocortical epilepsy onset, the high frequency oscillations (HFO) (60–100 Hz) increase significantly, which can be a helpful measure for the localization of the seizure onset zone [13]. In [14], the authors employed empirical wavelet transform (EWT) [15] for the separation of EEG rhythms and projected the obtained EEG rhythms in two-dimensional (2D) reconstructed phase space (RPS). The authors measured the area of the EEG rhythms in 2D RPS plots corresponding to different levels of central tendency measure (CTM) values. These computed area parameters were fed to a least squares support vector machine (LS-SVM) classifier for the the detection of focal EEG signals.
In previous studies [16,17,18,19,20,21], the entropy based features have been found to be useful for the discrimination of F and NF EEG signals. In [16], the F and NF types of EEG signals were classified using delay permutation entropy (DPE) and support vector machine (SVM) classifier. The authors found that for the delay range 5 to 30, the NF type EEG signals have a higher DPE index in comparison to F type EEG signals. In [17], the authors decomposed EEG signals into numbers of intrinsic mode functions (IMFs) using the empirical mode decomposition (EMD) method [22]. They extracted average sample entropy (ASE) as well as average variance of instantaneous frequency (AVIF) features from the obtained IMFs in order to classify F and NF types of EEG signals. In [18], the authors have extracted several entropy features from the individual channel IMFs—namely, approximate entropy, Shannon entropy, sample entropy, Renyi’s entropy, phase entropy 1 and phase entropy 2 from the IMFs of EEG signals. They obtained the average of those entropy values of the same index IMFs of both of the channels in order to find final feature vectors. They measured the complexity of the IMFs in a spectral domain using average Renyi’s entropy and average Shannon entropy in a higher order spectral domain using average phase entropy 1 and average phase entropy 2. The authors also measured the self similarity of the IMFs using ASE and average approximate entropies. In [19], a method based on discrete wavelet transform (DWT) was proposed for the classification of F and NF types of EEG signals. The authors decomposed the EEG signals up to six levels using Daubechies order 4 (db4) wavelet and extracted several entropy features from the DWT coefficients. In [20], the authors analyzed F and NF types of EEG signals in the EMD-DWT domain and extracted spectral entropies—namely, Shannon entropy, log-energy entropy, and Renyi entropies for the discrimination of F and NF types of EEG signals. They obtained better discrimination of F and NF type of EEG signals with log-energy entropy in the EMD-DWT domain. In [21], F and NF types of EEG signals were decomposed using a time-frequency localized wavelet filter-bank and computed several entropy features followed by an LS-SVM classifier to classify F and NF types of EEG signals.
It should be noted that most of the previous methods performed the univariate analysis of F and NF types of EEG signals which do not consider the cross channel information present in the multivariate EEG signals. In this paper, we have tried to measure the complexity of bivariate F and NF types of EEG signals by considering two channels simultaneously to distinguish F and NF types of EEG signals. In [23,24], authors proposed multivariate multi-scale sample entropy based on the concept of coarse graining and multivariate embedding theory [25]. They applied the proposed method to the complexity analysis of bivariate physiological signals and three-dimensional (3D) wind speed signals. Though sample entropy and its multivariate extension algorithms are very popular, they may produce undefined or unreliable results for short-time series. The reason behind this can be explained as: sample entropy and its multivariate extension use vector similarity definitions based on Heaviside function. This creates a very rigid boundary with the set threshold denoted as r. Due to this rigid boundary, computed entropy value changes abruptly with even slight changes of threshold r. The sample entropy may also be undefined for no vector matching with very small threshold r [26,27]. To increase the statistical stability of entropy values of univariate signals, the fuzzy entropy has been proposed based on fuzzy theory [27,28]. The fuzzy entropy has been applied as a complexity measure for many signals such as biomedical signals [29,30,31] and bearing fault diagnosis [32]. As a generalized form of univariate fuzzy entropy, multivariate fuzzy entropy (mvFE) has also been proposed for the multivariate signals [33,34]. In [35], the authors have applied multivariate fuzzy measure entropy for the analysis of multivariate cardiovascular signals.
In this work, we propose tunable-Q wavelet transform (TQWT) [36] based multivariate sub-band fuzzy entropy measure and studied the effectiveness of the proposed technique for the discrimination of bivariate F and NF types of EEG signals. Figure 1 shows the block diagram of the proposed TQWT based multivariate sub-band fuzzy entropy. In Figure 1, SB 1, SB 2 and so on represent the obtained sub-band 1, sub-band 2 and so on, respectively, after decomposition with TQWT. It should be noted that the same indexed sub-bands of different channels belong to the same oscillatory level. After that, we have used two different classifiers to evaluate the performance of our proposed feature extraction method. Our proposed multivariate sub-band fuzzy entropy measure utilizes TQWT based filter-bank for quantifying the complexity of multivariate narrow band sub-band signals, which can be a generalized tool for measuring complexity of other multivariate signals with proper selection of the Q-parameter.
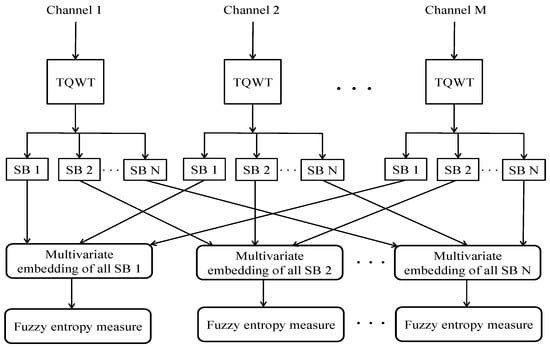
Figure 1.
TQWT based multivariate sub-band fuzzy entropy.
The rest of the paper is organised as follows: Section 2 gives a brief description of the EEG database used in this study. Section 3 discusses the computation of the existing mvFE, Section 4 describes the computation of proposed Q-based multivariate sub-band fuzzy entropy, and Section 5 discusses the statistical significance of the proposed features and experimental results. Finally, Section 6 concludes the paper.
2. Bern–Barcelona EEG Dataset
The proposed TQWT based multivariate sub-band fuzzy entropy has been studied on the publicly available Bern–Barcelona EEG database [8]. The database contains the intracranial EEG recordings of five patients who suffered from drug-resistant long-standing temporal lobe epilepsy. The studied database includes bivariate EEG signals of both F and NF categories. For each of the F and NF categories, the database contains 3750 pairs of bivariate EEG signals. The signals were recorded with a sampling rate of 512 Hz. The duration of each bivariate EEG signals is 20 s. In this study, the first 50 F and NF types of bivariate EEG signals are selected to find the optimal signal length that provides statistically significant discrimination between two classes. Finally, based on the outcome of the analysis of the first 50 F and NF EEG signals, we have chosen the optimum signal length and classified 3750 F and 3750 NF types of bivariate EEG signals.
3. Multivariate Fuzzy Entropy (mvFE)
The computation of mvFE can be summarised by the following steps [33]:
- Step 1: Generation of the multivariate composite embedded reconstruction from the s-variate time-series where , based on the Takens embedding theorem as follows [23,25]:where denotes embedding vector and represents time lag vector. For example, channel 1 () of a bivariate time series is expressed as and channel 2 () is expressed as with N number of samples for each time-series. If we consider and , then some of the composite delay vectors are expressed as , , etc.
- Step 2: Formation of composite delay vectors , where and .
- Step 3: Defining the distance as the maximum norm and computed between two composite delay vectors such as and .
- Step 4. Defining the fuzzy membership function as [33]:where d denotes computed distance between two composite delay vectors, r denotes chosen threshold parameter and represents fuzzy power.
- Step 5. Define the global quantity for a chosen fuzzy power and threshold r as [33]:
- Step 6. Increment of the dimensionality from m to in such a way so that the dimensionality of the other variables do not change, which is possible in s different ways, such as from to for .
- Step 7. Computation of by considering the increased dimensionality.
- Step 8. Finally, the computation of the mvFE can be expressed as follows [33]:
We have normalized each channels data to unit variance in order to maintain total variation same for all the considered multivariate series as suggested in [23]. In this work time lag () is considered as 1 where as embedding dimension () is taken as 2 for all the available channels. The value of threshold parameter (r) has been taken as 0.15 multiplied with standard deviation of normalized time series as suggested in [23]. The fuzzy power () is considered as 2 for computation of mvFE according to [33].
4. TQWT Based Multivariate Sub-Band Fuzzy Entropy
In this work, we have computed the mvFE of the sub-band signals falling in the same oscillatory levels. The sub-band signals of the individual channels have been obtained using TQWT. The TQWT is a special type of DWT and has found a wide range of applicability in biomedical signal analysis [37,38,39,40,41], bearing fault detection [42,43], and cross-terms reduction in time-frequency distribution [44]. The TQWT is useful to analyse oscillatory signals by adjusting input parameters—namely, Q, redundancy or over-sampling rate denoted by R [36], and number of decomposition levels denoted by J. The brief description of the input parameters are as follows:
For oscillatory signal analysis, the value of the parameter Q should be chosen high, as a result the wavelets generated will have more oscillations with narrow frequency responses as compared to their center frequencies. The high Q value is used for analysing oscillatory signals. The lower value of Q is used to analyse signals having piecewise smooth structures like transients. For a lower value of Q, generated wavelets have fewer oscillations and wider frequency responses compared to their center frequencies. The lower value of Q gives good frequency resolution in the low frequency region; on the other hand, higher value of Q is useful to get good frequency resolution in the high frequency region of the spectrum. This property of TQWT has been used to design a filter-bank that provides nearly uniform resolution for all frequency components in [44]. The designed filter-bank has been studied for the reduction of cross-terms in Wigner–Ville distribution based time-frequency analysis.
The parameter R localizes the wavelet in the time domain without changing its shape. For a fixed Q value, the overlap of the adjacent frequency responses increases with increased value of the redundancy parameter R. This results in the requirement of a higher number of levels to cover the entire frequency region.
The TQWT is built by the concept of two channel filter bank operation. Let the high-pass and low-pass scale factors be denoted by δ and γ, respectively, for the two-channel filter bank. The frequency response corresponding to low-pass filter in TQWT mathematically expressed as [36]:
The frequency response of the high-pass filter in TQWT can be mathematically expressed as [36]:
where is known as Daubechies filter frequency response [36]. Low-pass scale factor and high-pass scale factor are to be chosen in order to satisfy the condition .
The redundancy parameter (R), quality factor (Q), and maximum number of sub-bands () of TQWT are mathematically defined as [36]:
where N is the length of the analysed signal.
Detailed mathematical expressions of Q, R, center frequency () and bandwidth (B) of TQWT are provided in [36].
The TQWT based multivariate sub-band fuzzy entropy is computed as follows:
- All of the EEG signals corresponding to different channels are decomposed with the same input parameters using TQWT. The sub-band signals are reconstructed by performing inverse TQWT operation. This results in the same number of sub-band signals denoted by for every individual channel. The indexes j and s correspond to decomposition level and channel number, respectively.Figure 2 presents the F type EEG signal and its sub-band signals, and Figure 3 shows the NF type EEG signal and its associated sub-band signals obtained using TQWT ().
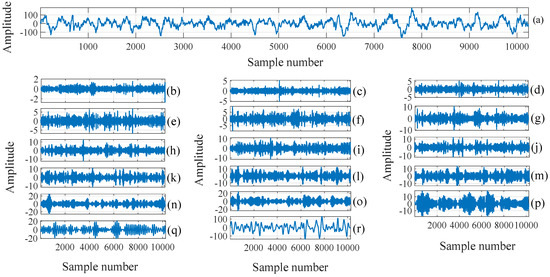 Figure 2. (a) Plot of F type EEG signal (channel “x”); (b–r) Plot of reconstructed sub-band signals obtained using TQWT.
Figure 2. (a) Plot of F type EEG signal (channel “x”); (b–r) Plot of reconstructed sub-band signals obtained using TQWT.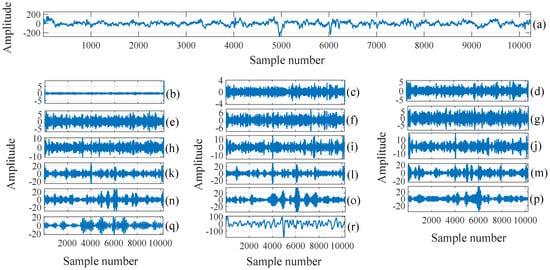 Figure 3. (a) Plot of NF type EEG signal (channel “x”); (b–r) Plot of reconstructed sub-band signals obtained using TQWT.
Figure 3. (a) Plot of NF type EEG signal (channel “x”); (b–r) Plot of reconstructed sub-band signals obtained using TQWT. - The mvFE described in the previous section has been computed for the sub-band signals of the same oscillatory levels belonging to different channels. As an example, sub-band 1 of different channels are used to compute mvFE and so on.
5. Results and Discussion
The Q-based multivariate sub-band fuzzy entropy described in the previous section has been applied to 50 F and NF types of bivariate EEG signals. We have studied four different segments of EEG signals of durations corresponding to 20 s, 10 s, 5 s, and 2 s, respectively, to find out the statistical significance of the computed features over different time spans. Table 1 and Table 2 present the results of the statistical analysis of the computed features. We have performed the Kruskal–Wallis statistical test [45] to find the statistical significance () of the computed features in different oscillatory levels of the analyzed signals. The Kruskal–Wallis statistical test has been used for finding the statistical significance of the features computed from EEG signals [14,46]. In this paper, we have fixed the redundancy parameter (R) as 3 and considered sufficiently many levels (at maximum ) for decomposition of EEG signals using TQWT. The Q parameter of TQWT has been varied from 1 to 4. It should be noted that, with increased value of Q parameter, the number of levels of decomposition (J) should also be increased to achieve sufficiently good resolution in low- and high-frequency regions of the spectrum.

Table 1.
Statistical analysis results of the proposed TQWT based multivariate sub-band fuzzy entropy computed for 20 s and 10 s duration segments.

Table 2.
Statistical analysis results of the proposed TQWT based multivariate sub-band fuzzy entropy computed for 5 s and 2 s duration segments.
In this study, for 20 s and 10 s duration segmented EEG signals, J has been considered as 16. For 5 s and 2 s duration segmented EEG signals, the maximum possible J has been considered as per Equation (6). In Table 1 and Table 2, we have reported the analysis of five sub-band signals that give the highest statistical significance for the discrimination of F and NF types of EEG signals. We have also reported the mean and standard deviation (SD) values of the proposed entropy features corresponding to those sub-band signals. It has been observed from Table 1 and Table 2 that neither of the entropy features by themselves sufficiently quantify the differences of F and NF kinds of EEG signals. In a few cases, the overlap of the computed entropy features are significantly high. This implies that a simple threshold applied on these parameters will not be sufficient to distinguish F and NF groups of EEG signals.
It is clearly observed from Table 1 and Table 2 that mvFE computed for NF types of EEG signals are higher than the F types of EEG signals in every considered segment for analysis. This supports the findings of the previous works studied using this database [18]. To present the comparison of the features in different considered segments, it has been found that with increased segment duration, the computed p-values are significantly lower than those for shorter segment durations. This implies that proposed Q-based multivariate sub-band fuzzy entropy features give better discrimination with longer segment size. The variation of the Q-parameter puts a significant impact on the computed features in different oscillatory levels. For a lower value of Q (), the p-values obtained for lower order sub-band signals are significantly lower than the p-values computed for higher order sub-band signals with mvFE features. When Q is chosen as high (), the mvFE features computed for higher order sub-band signals are statistically more significant to discriminate F and NF types of EEG signals. We have used confidence interval (CI) plots for showing the discrimination between F and NF types of EEG signals. In [47], CI plots were used for the discrimination of seizure, seizure-free, and healthy groups of EEG signals. In Figure 4, Figure 5, Figure 6 and Figure 7, we have shown the CI plots (99% confidence limits of the mean value) for different time segmented signals with different quality factors (Q varies from 1 to 4), where red and blue lines represent the F and NF groups of EEG signals. In Figure 4, we have shown the CI plot (with 99% confidence) for different values of the Q parameter when signal duration of 20 s is considered. It is clear from Figure 4 that with increased value of the Q parameter, the mvFE gives more discrimination in higher order sub-bands. It should be noted that we have not achieved significant discrimination in the first (highest frequency) and last (lowest frequency) sub-band signals irrespective of the value of Q parameter used. Figure 5, Figure 6 and Figure 7 show the CI plots (99% confidence) for 10 s, 5 s, and 2 s duration segmented EEG signals, respectively. It can be noticed from Figure 5, Figure 6 and Figure 7 that the discriminating ability of the proposed entropy features get reduced for shorter duration of the EEG signals. From the CI plot of Figure 7, it is obvious that F and NF groups of EEG signals are not distinguishable in most of the sub-band signals using 2 s duration segmented signals. Thus, keeping in mind the outcome of the above statistical analysis on 50 F and 50 NF EEG signals using our proposed features, we have considered 20 s signal duration to classify F and NF groups of EEG signals. It should be noted that all the available signals (3750 F and 3750 NF) in the Bern–Barcelona EEG database have been considered for classification work. To find the optimal subset of features, we have applied a wrapper based feature selection technique [48] available in the WEKA machine learning toolbox (Weka 3.6.13, University of Waikato, Hamilton, New Zealand) [49]. Finally, we have used two classifiers—namely, random forest classifier [50] (available in WEKA) and least squares support vector machine classifier (LS-SVM) [51] with Morlet wavelet [14,52] and radial basis function (RBF) kernels. The chosen values of kernel parameters ω and a for Morlet wavelet kernel are 0.5 and 6, respectively. The RBF [14] kernel parameter σ = 1 has been selected in this work. The performance of the proposed feature extraction method with the mentioned classifiers has been evaluated with a 10-fold cross-validation method [53]. The use of a 10-fold cross-validation method for the classification of biomedical signals is advantageous [14,54].
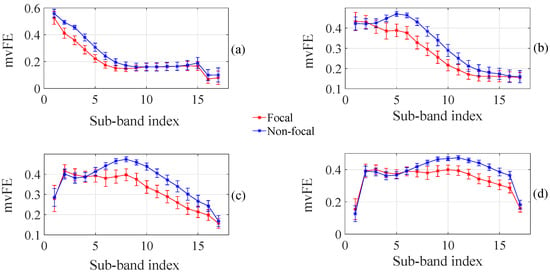
Figure 4.
Confidence interval plot of proposed TQWT based multivariate sub-band fuzzy entropy with 99% confidence for 20 s signal duration. (a) For ; (b) For ; (c) For ; (d) For .
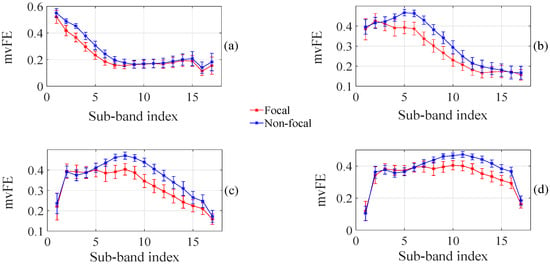
Figure 5.
Confidence interval plot of proposed TQWT based multivariate sub-band fuzzy entropy with 99% confidence for 10 s signal duration. (a) For ; (b) For ; (c) For ; (d) For .
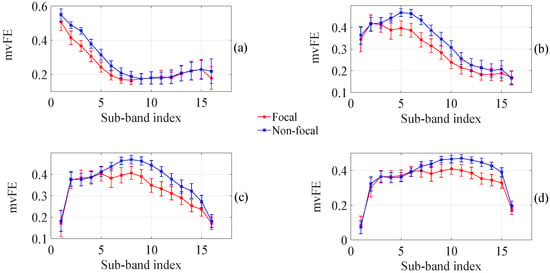
Figure 6.
Confidence interval plot of proposed TQWT based multivariate sub-band fuzzy entropy with 99% confidence for 5 s signal duration. (a) For ; (b) For ; (c) For ; (d) For .
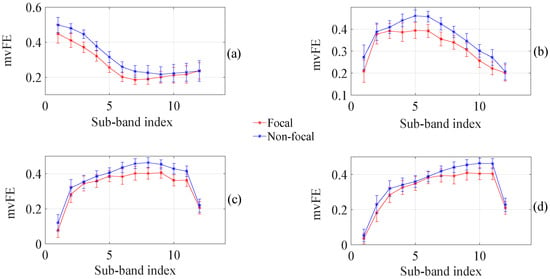
Figure 7.
Confidence interval plot of proposed TQWT based multivariate sub-band fuzzy entropy with 99% confidence for 2 s signal duration. (a) For ; (b) For ; (c) For ; (d) For .
Finally, we have computed three classification performance parameters [55]—namely, accuracy (Acc), sensitivity (Sens), and specificity (Spec). These parameters are defined as, Acc = (TP + TN)/(TP + TN + FP + FN), Sens = TP/(TP + FN), and Spec = TN/(TN + FP), where TP counts the number of truly detected F EEG signals, TN denotes the number of truly classified NF EEG signals, FN is the number of misclassified F EEG signals, and FP counts the number of wrongly classified NF EEG signals. In Table 3, we have presented the computed Acc, Sens, and Spec values of the mentioned classifiers for different considered value of Q parameter. It has been found from our current study that for each considered values of Q parameter, the performance of LS-SVM classifier is better than random forest classifiers in terms of the computed classification performance parameters—namely, Acc, Sens, and Spec. The highest obtained classification accuracy of random forest classier is 83.2% for . The LS-SVM classifier achieved the highest classification accuracy of 84.67% with Morlet wavelet kernel for . It is clear from Table 3 that obtained classification accuracies of LS-SVM classifier with RBF kernel for different values of Q parameters are slightly lower as compared with LS-SVM classifier with Morlet wavelet kernel. In the previous classification works [17,18,19,21] using this database, authors combined multiple entropy features to classify F and NF EEG signals. They averaged the computed entropy features in order to measure the complexity of bivariate F and NF EEG signals. However, in this work, we have used only mvFE to discriminate F and NF EEG signals. It should be noted that in spite of moderate values of the evaluated classification parameters, the proposed feature extraction method provided the platform to compute multivariate sub-band entropies for measuring the signal complexity in different frequency scales. Moreover, the filtering parameters (Q, R, and J) can be tuned optimally to achieve better discrimination between two classes of signals. Thus, the proposed multivariate sub-band entropy features can also be computed to measure the complexity of other multivariate signals of interest. In the future, other existing entropy features can also be explored in the proposed framework to measure the complexity of multivariate signals in multiple oscillatory levels.

Table 3.
Evaluated classification performance parameters using the proposed multivariate sub-band fuzzy entropy features.
6. Conclusions
A Q-based multivariate sub-band fuzzy entropy has been proposed in this paper. The proposed entropy measure is based on the TQWT method. The proposed method was applied for the discrimination of F and NF types of EEG signals. To evaluate the statistical significance of the proposed features, the Kruskal–Wallis statistical test was applied. The proposed feature extraction method has been applied to different time-segmented EEG signals. It was found that the computed mvFE features are statistically more significant for longer duration EEG signals. The proposed feature extraction method decomposed EEG signals prior to the computation of mvFE. Thus, different values of the Q parameter generated distinct filter banks and resulted in distinct entropy values. The effectiveness of the proposed feature extraction method was presented using CI plots for different time segmented signals to discriminate F and NF types of EEG signals. Finally, we have used two classifiers to evaluate the discrimination ability of our proposed feature extraction method.
The proposed TQWT parameter based mvFE has provided statistically significant discrimination between F and NF classes of EEG signals. The developed method needs to be studied in a large EEG database that includes recordings of long durations from a larger number of subjects before applying it for clinical purposes. It should be noted that the proposed TQWT based mvFE structure is not only limited for analysis of bivariate F and NF EEG signals but can also find applicability in other classes of multivariate physiological signals corresponding to normal and abnormal classes.
Author Contributions
Ram Bilas Pachori and U. Rajendra Acharya formulated the research problem. Abhijit Bhattacharyya carried out the research work. Abhijit Bhattacharyya drafted the manuscript and all authors edited the manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Witte, H.; Iasemidis, L.D.; Litt, B. Special issue on epileptic seizure prediction. IEEE Trans. Biomed. Eng. 2003, 50, 537–539. [Google Scholar] [CrossRef]
- Acharya, U.R.; Sree, S.V.; Swapna, G.; Martis, R.J.; Suri, J.S. Automated EEG analysis of epilepsy: A review. Knowl. Based Syst. 2013, 45, 147–165. [Google Scholar] [CrossRef]
- Pati, S.; Alexopoulos, A.V. Pharmacoresistant epilepsy: From pathogenesis to current and emerging therapies. Cleve Clin. J. Med. 2010, 77, 457–467. [Google Scholar] [CrossRef] [PubMed]
- Savic, I.; Thorell, J.O.; Roland, P. [11C] Flumazenil positron emission tomography visualizes frontal epileptogenic regions. Epilepsia 1995, 36, 1225–1232. [Google Scholar] [CrossRef] [PubMed]
- Seeck, M.; Lazeyras, F.; Michel, C.M.; Blanke, O.; Gericke, C.; Ives, J.; Delavelle, J.; Golay, X.; Haenggeli, C.A.; De Tribolet, N.; et al. Non-invasive epileptic focus localization using EEG-triggered functional MRI and electromagnetic tomography. Electroencephalogr. Clin. Neurophysiol. 1998, 106, 508–512. [Google Scholar] [CrossRef]
- Woermann, F.G.; Vollmar, C. Clinical MRI in children and adults with focal epilepsy: A critical review. Epilepsy Behav. 2009, 15, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Newton, M.R.; Berkovic, S.F.; Austin, M.C.; Rowe, C.C.; McKay, W.J.; Bladin, P.F. SPECT in the localisation of extratemporal and temporal seizure foci. J. Neurol. Neurosurg. Psychiatry 1995, 59, 26–30. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Schindler, K.; Rummel, C. Nonrandomness, nonlinear dependence, and nonstationarity of electroencephalographic recordings from epilepsy patients. Phys. Rev. E 2012, 86, 046206. [Google Scholar] [CrossRef] [PubMed]
- Pachori, R.B.; Sircar, P. EEG signal analysis using FB expansion and second-order linear TVAR process. Signal Process. 2008, 88, 415–420. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Alcántara, R.; Medina, V. Analysis and localization of epileptic events using wavelet packets. Med. Eng. Phys. 2001, 23, 623–631. [Google Scholar] [CrossRef]
- Panet-Raymond, D.; Gotman, J. Asymmetry in delta activity in patients with focal epilepsy. Electroencephalogr. Clin. Neurophysiol. 1990, 75, 474–481. [Google Scholar] [CrossRef]
- Marciani, M.G.; Stefanini, F.; Stefani, N.; Maschio, M.C.; Gigli, G.L.; Roncacci, S.; Caltagirone, C.; Bernardi, G. Lateralization of the epileptogenic focus by computerized EEG study and neuropsychological evaluation. Int. J. Neurosci. 1992, 66, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Worrell, G.A.; Parish, L.; Cranstoun, S.D.; Jonas, R.; Baltuch, G.; Litt, B. High-frequency oscillations and seizure generation in neocortical epilepsy. Brain 2004, 127, 1496–1506. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, A.; Sharma, M.; Pachori, R.B.; Sircar, P.; Acharya, U.R. A novel approach for automated detection of focal EEG signals using empirical wavelet transform. Neural Comput. Appl. 2016, 1–11. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Zhu, G.; Li, Y.; Wen, P.P.; Wang, S.; Xi, M. Epileptogenic focus detection in intracranial EEG based on delay permutation entropy. AIP Conf. Proc. 2013, 1559, 31–36. [Google Scholar]
- Sharma, R.; Pachori, R.B.; Gautam, S. Empirical mode decomposition based classification of focal and non-focal EEG signals. In Proceedings of the 2014 International Conference on Medical Biometrics, Shenzhen, China, 30 May–1 June 2014; pp. 135–140.
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. An integrated index for the identification of focal electroencephalogram signals using discrete wavelet transform and entropy measures. Entropy 2015, 17, 5218–5240. [Google Scholar] [CrossRef]
- Das, A.B.; Bhuiyan, M.I.H. Discrimination and classification of focal and non-focal EEG signals using entropy-based features in the EMD-DWT domain. Biomed. Signal Process. Control 2016, 29, 11–21. [Google Scholar] [CrossRef]
- Sharma, M.; Dhere, A.; Pachori, R.B.; Acharya, U.R. An automatic detection of focal EEG signals using new class of time-frequency localized orthogonal wavelet filter banks. Knowl. Based Syst. 2017, 118, 217–227. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Physica D 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, K.; Zhao, L.; Liu, F.; Zheng, D.; Liu, C.; Liu, S. Analysis of heart rate variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. An efficient automated technique for CAD diagnosis using flexible analytic wavelet transform and entropy features extracted from HRV signals. Expert Syst. Appl. 2016, 63, 165–172. [Google Scholar] [CrossRef]
- Zhao, L.; Wei, S.; Zhang, C.; Zhang, Y.; Jiang, X.; Liu, F.; Liu, C. Determination of sample entropy and fuzzy measure entropy parameters for distinguishing congestive heart failure from normal sinus rhythm subjects. Entropy 2015, 17, 6270–6288. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy. Mech. Mach. Theory 2013, 70, 441–453. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Refined composite multivariate generalized multiscale fuzzy entropy: A tool for complexity analysis of multichannel signals. Physica A 2017, 465, 261–276. [Google Scholar] [CrossRef]
- Azami, H.; Smith, K.; Escudero, J. MEMD-enhanced multivariate fuzzy entropy for the evaluation of complexity in biomedical signals. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 3761–3764.
- Zhao, L.; Wei, S.; Tang, H.; Liu, C. Multivariable fuzzy measure entropy analysis for heart rate variability and heart sound amplitude variability. Entropy 2016, 18, 430. [Google Scholar] [CrossRef]
- Selesnick, I.W. Wavelet transform with tunable Q-factor. IEEE Trans. Signal Process. 2011, 59, 3560–3575. [Google Scholar] [CrossRef]
- Patidar, S.; Pachori, R.B.; Upadhyay, A.; Acharya, U.R. An integrated alcoholic index using tunable-Q wavelet transform based features extracted from EEG signals for diagnosis of alcoholism. Appl. Soft Comput. 2017, 50, 71–78. [Google Scholar] [CrossRef]
- Patidar, S.; Pachori, R.B.; Acharya, U.R. Automated diagnosis of coronary artery disease using tunable-Q wavelet transform applied on heart rate signals. Knowl. Based Syst. 2015, 82, 1–10. [Google Scholar] [CrossRef]
- Patidar, S.; Pachori, R.B.; Garg, N. Automatic diagnosis of septal defects based on tunable-Q wavelet transform of cardiac sound signals. Expert Syst. Appl. 2015, 42, 3315–3326. [Google Scholar] [CrossRef]
- Patidar, S.; Pachori, R.B. Segmentation of cardiac sound signals by removing murmurs using constrained tunable-Q wavelet transform. Biomed. Signal Process. Control 2013, 8, 559–567. [Google Scholar] [CrossRef]
- Patidar, S.; Pachori, R.B. Classification of cardiac sound signals using constrained tunable-Q wavelet transform. Expert Syst. Appl. 2014, 41, 7161–7170. [Google Scholar] [CrossRef]
- Luo, J.; Yu, D.; Liang, M. A kurtosis-guided adaptive demodulation technique for bearing fault detection based on tunable-Q wavelet transform. Meas. Sci. Technol. 2013, 24, 055009. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Pachori, R.B.; Nishad, A. Cross-terms reduction in the Wigner–Ville distribution using tunable-Q wavelet transform. Signal Process. 2016, 120, 288–304. [Google Scholar] [CrossRef]
- Freund, R.J.; Wilson, W.J. Statistical Methods; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Pachori, R.B. Discrimination between ictal and seizure-free EEG signals using empirical mode decomposition. J. Res. Lett. Signal Process. 2008, 2008. [Google Scholar] [CrossRef]
- Adeli, H.; Ghosh-Dastidar, S.; Dadmehr, N. A wavelet-chaos methodology for analysis of EEGs and EEG subbands to detect seizure and epilepsy. IEEE Trans. Biomed. Eng. 2007, 54, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Jiao, L. Wavelet support vector machine. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 34–39. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1145.
- Bhattacharyya, A.; Pachori, R.B. A multivariate approach for patient specific EEG seizure detection using empirical wavelet transform. IEEE Trans. Biomed. Eng. 2017. [Google Scholar] [CrossRef] [PubMed]
- Azar, A.T.; El-Said, S.A. Performance analysis of support vector machines classifiers in breast cancer mammography recognition. Neural Comput. Appl. 2014, 24, 1163–1177. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).