Bayesian Nonlinear Filtering via Information Geometric Optimization

Abstract

In this paper, Bayesian nonlinear filtering is considered from the viewpoint of information geometry and a novel filtering method is proposed based on information geometric optimization. Under the Bayesian filtering framework, we derive a relationship between the nonlinear characteristics of filtering and the metric tensor of the corresponding statistical manifold. Bayesian joint distributions are used to construct the statistical manifold. In this case, nonlinear filtering can be converted to an optimization problem on the statistical manifold and the adaptive natural gradient descent method is used to seek the optimal estimate. The proposed method provides a general filtering formulation and the Kalman filter, the Extended Kalman filter (EKF) and the Iterated Extended Kalman filter (IEKF) can be seen as special cases of this formulation. The performance of the proposed method is evaluated on a passive target tracking problem and the results demonstrate the superiority of the proposed method compared to various Kalman filter methods.

1. Introduction

Filtering problems arise in various applications such as signal processing, automatic control and financial time series. The goal of nonlinear filtering is to estimate the state of a nonlinear dynamic process based on noisy observation. In the last several decades, the Kalman filter has become a standard method for linear dynamic systems subject to linear measurements, which can provide a perfect analytical solution in the optimal operation. However, it is not suitable for the nonlinear cases of filtering problems. Along with the spirit of Kalman filter, the approximation methods have been proposed for the nonlinear filtering, such as the Extended Kalman filter (EKF) [1], Unscented Kalman filter (UKF) [2], Gauss–Hermite Kalman filter (GHKF) [3], and Cubature Kalman filter (CKF) [4]. All these methods can be induced by the Bayesian approach with different approximations [5] for nonlinear cases. Apart from the aforementioned methods, the sequential Monte Carlo technique approximating for the Bayesian probability density functions (PDFs) is another feasible approach, for instance, the particle filtering (PF) [6] which uses the particle representations of probability distributions. Within the Bayesian framework, the nonlinear filtering can be converted to Bayesian filtering, and the procedure of filtering consists of two steps: state propagation and measurement update. Correspondingly, the state propagation provides the prior information for the state, and the measurement update integrates the prior information and the conditional measurement to obtain the posterior PDF of the state. In particular, the nonlinear and non-Gaussian conditions will make the measurement update more difficult and the solution of posterior PDFs intractable.

Because Bayesian posterior PDF plays a key role in nonlinear filtering, the study of Bayesian posterior PDF has attracted increasing attentions over the past few decades. Conventionally, the linear minimum mean square error (LMMSE) estimator and maximum a posteriori (MAP) estimator have played major roles in estimating posterior PDF. For the LMMSE estimator, it approximates the posterior mean and covariance matrix by its estimator and its mean square error matrix, respectively. Usually, the EKF, UKF and CKF can be derived from the LMMSE estimator. Besides, an adaptable recursive method named recursive update filter (RUF) has been derived based on the principle of LMMSE [7,8], which overcomes some of the limitations of the EKF. Being different from the LMMSE, the MAP estimator has estimated the posterior mean and obtained the covariance matrix by linearizing the measurement function around the MAP estimator. The well-known iterated EKF (IEKF), which is induced by using the Gauss–Newton optimization [9] or Levenberg–Marquardt (LM) [10] method, can be interpreted as a MAP estimator. With the variational approach employing for MAP optimization, the variational Kalman filter (VKF) [11] has been proposed. By using the Newton–Raphson iterative optimization steps to yield an approximate MAP estimation, the generalized iterated Kalman filter (GIKF) [12] algorithm has been presented to handle the nonlinear stochastic discrete-time system with state-dependent multiplicative estimation. Generally speaking, the MAP estimator methods need the iterative procedures to obtain the final estimation, and these iterative methods for nonlinear filtering have better performance. As the IEKF outperforms EKF and UKF, as shown by Lefebvre [13], the Iterated UKF (IUKF) [14] performs better than the UKF in the estimation of state and the corresponding covariance matrix.

Recently, Morelande [15] has adopted the Kullback–Leibler (KL) divergence as the metric to analyze the difference between the true joint posterior PDFs of the state conditional on the measurement and the approximation posterior PDFs. Actually, this metric can be used to derive new algorithms. The iterated posterior linearization filter (IPLF) [16] can be seen as an approximate recursive KL divergence minimization procedure. The adaptive unscented Gaussian likelihood approximation filter (AUGLAF) [17] selects the best approximation to the posterior PDFs based on the KL divergence. The KL partitioned update Kalman filter (KLPUKF) [18] uses KL divergence to measure the nonlinearity of the measurement. In essence, the KL divergence, also known as relative entropy, is a quantity in information theory. This optimization criterion of information theory has already been applied in signal processing. By utilizing the information theoretic quantities to capture the higher-order statistics, we can obtain the significant performance improvement. Meanwhile, another optimization criterion in information theoretic learning (ITL), i.e., maximum correntropy criterion (MCC), has been introduced for the filtering problems. With this criterion involving in the existing filtering framework, some new Kalman-type filters have been proposed, such as maximum correntropy Kalman filter (MCKF) [19], maximum correntropy unscented Kalman filter (MCUKF) [20], robust information filter based on maximum correntropy criterion [21].

Enlightened by the information theoretic quantities applied in nonlinear filtering, we consider the nonlinear filtering from the information geometric viewpoint. Information geometry, which was originally proposed by Amari [22], has become a new mathematical tool for the study on manifold of probability distributions. The combination of information theory and differential geometry opens a new perspective to study the geometric structure of information theory and provides a new way to deal with the existing statistical problems. In this paper, we will study the nonlinear filtering by using information geometric method. By using the joint PDFs of the measurement and the state to construct the statistical manifold, the nonlinear characteristics can be represented as the geometric quantities, such as metric tensor, and the filtering problems are converted to the optimization problems on the statistical manifold. In this way, the nonlinear filtering can be progressed by the information geometric optimization method, and it will induce an iterative procedure for estimation. The natural gradient descent [23] method is used to seek the optimal estimation across the statistical manifold, and the distance defined on the statistical manifold is utilized to design as the stopping criterion to achieve the goal of filtering.

The paper is organized as follows. Firstly, we give a brief description for Bayesian filtering and information geometry in Section 2 and Section 3, respectively. Then, the adaptive natural gradient descent method on the statistical manifold is presented to derive the new nonlinear filtering algorithm in Section 4. Further discussion about our proposed method will be given in Section 5, and the numerical simulations are implemented to demonstrate the performance in Section 6. Finally, conclusions are made in Section 7.

2. Bayesian Filtering

Bayesian principle provides a general approach for nonlinear filtering, and this approach is called as Bayesian filtering [5]. Bayesian filtering converts the state and measurement from the state-space to probability distribution. The goal of Bayesian filtering is to estimate the state of a nonlinear dynamic process conditional on measurement. The formulations of Bayesian filtering are

$$p\left({\mathit{x}}_k|{\mathit{y}}_{k-1}\right)=\int p\left({\mathit{x}}_k|{\mathit{x}}_{k-1}\right)p\left({\mathit{x}}_{k-1}|{\mathit{y}}_{k-1}\right)d{\mathit{x}}_{k-1}$$

(1)

$$p\left({\mathit{x}}_k|{\mathit{y}}_k\right)=\frac{p\left({\mathit{y}}_k|{\mathit{x}}_k\right)p\left({\mathit{x}}_k|{\mathit{y}}_{k-1}\right)}{\int p\left({\mathit{y}}_k|{\mathit{x}}_k\right)p\left({\mathit{x}}_k|{\mathit{y}}_{k-1}\right)d{\mathit{x}}_k}$$

(2)

with the probability densities as follows

$${\mathit{x}}_k|{\mathit{x}}_{k-1}\sim p\left(\mathit{x};\mathit{f}\left({\mathit{x}}_{k-1}\right),\mathbf{Q}\right)$$

(3)

$${\mathit{y}}_k|{\mathit{x}}_k\sim p\left(\mathit{y};\mathit{h}\left({\mathit{x}}_k\right),\mathbf{R}\right)$$

(4)

which correspond to the general state-space model formulation

$${\mathit{x}}_k=\mathit{f}\left({\mathit{x}}_{k-1}\right)+{\mathit{u}}_{\mathit{k}}$$

(5)

$$\begin{array}{cc}\hfill {\mathit{y}}_k& =\mathit{h}\left({\mathit{x}}_k\right)+{\mathit{v}}_{\mathit{k}}\hfill \end{array}$$

(6)

where $\mathit{f}$ and $\mathit{h}$ denote the state transition and measurement functions, and the covariance matrix $\mathbf{Q}$ and $\mathbf{R}$ correspond to the zero mean Gaussian noise ${\mathit{u}}_k$ and ${\mathit{v}}_k$, respectively.

For the Bayesian filtering problem, Equation (1) represents the state propagation, while Equation (2) represents the measurement update. Because it is usually intractable to calculate analytically for Bayesian posterior distribution, the optimization methods are used to avoid the troublesome integral and address this problem in a computationally feasible way, such as the MAP. Compared with the LMMSE method, the advantage of the MAP method is that there is no need to solve the integral operations in Bayesian posterior distribution. Further, when we consider these PDFs, the information geometry [22] provides an alternative approach, and the optimization on the statistical manifold can be utilized to derive the new filtering algorithm.

3. Information Geometry

3.1. Riemannian Metric Tensor

Consider a parameterized family of probability density as $\mathcal{S}=\{p\left(\mathit{y}|\mathit{\theta }\right),\mathit{\theta }={({\theta }_1,\cdots ,{\theta }_n)}^{\mathrm{T}}\in \Theta \}$, where $\mathit{y}\in {\mathbb{R}}^m$ is a measurable random variable, $\mathit{\theta }$ is the parameter to be estimated, and $p\left(\mathit{y}|\mathit{\theta }\right)$ is the conditional PDF of $\mathit{y}$ given $\mathit{\theta }$. With the parameter $\mathit{\theta }$ acting as the coordinate system, $\mathcal{S}$ can be regarded as an n-dimensional manifold. When the Fisher information matrix (FIM) [24]

$$\begin{array}{cc}\hfill {\left[\mathbf{F}\left(\mathit{\theta }\right)\right]}_{ij}& \triangleq {\mathbf{E}}_{\mathit{y}|\mathit{\theta }}\left[\frac{\partial \log p\left(\mathit{y}|\mathit{\theta }\right)}{\partial {\theta }_i}\frac{\partial \log p\left(\mathit{y}|\mathit{\theta }\right)}{\partial {\theta }_j}\right]\hfill \\ & =-{\mathbf{E}}_{\mathit{y}|\mathit{\theta }}\left[\frac{{\partial }^2\log p\left(\mathit{y}|\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}\right]\hfill \end{array}$$

(7)

is defined as the Riemannian metric tensor, $\mathcal{S}$ is a statistical manifold. Usually, this metric tensor in statistical manifold is also called as Fisher metric tensor [25]. ${\mathbf{E}}_{\mathit{y}|\mathit{\theta }}\left[·\right]$ denotes the expectation with respect to $p\left(\mathit{y}|\mathit{\theta }\right)$.

When $\mathit{\theta }$ has the prior PDF $p\left(\mathit{\theta }\right)$, the Bayesian principle can be used to characterize the joint PDF $p\left(\mathit{y},\mathit{\theta }\right)$ of $\mathit{y}$ and $\mathit{\theta }$. The Fisher metric tensor for Bayesian problems is defined as follows [24]

$$\begin{array}{cc}\hfill {\left[\mathbf{G}\left(\mathit{\theta }\right)\right]}_{ij}& \triangleq -{\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\frac{{\partial }^2\log p\left(\mathit{y},\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}\right]\hfill \\ & =-{\mathbf{E}}_{\mathit{y}|\mathit{\theta }}{\mathbf{E}}_{\mathit{\theta }}\left[\frac{{\partial }^2\log p\left(\mathit{y}|\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}\right]-{\mathbf{E}}_{\mathit{\theta }}\left[\frac{{\partial }^2\log p\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}\right]\hfill \end{array}$$

(8)

where ${\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[·\right]$ and ${\mathbf{E}}_{\mathit{\theta }}\left[·\right]$ denote the the expectations with respect to $p\left(\mathit{y},\mathit{\theta }\right)$ and $p\left(\mathit{\theta }\right)$, respectively.

This Fisher metric tensor (8) is the expected Fisher information on the measurement plus the negative Hessian of the log-prior on the parameter. The first part of Equation (8) characterizes the measurement conditional on the parameter, while the second part includes the effect of prior information on the parameter. In other words, the two terms of Equation (8) correspond to the information obtained from the measurement and the prior distribution of the parameter, respectively.

Besides, the Fisher metric tensor is relative with the Bayesian posterior Cramér–Rao Bounds (PCRB), which is applicable to multidimensional nonlinear, possible non-Gaussian, dynamical systems [26]. From the viewpoint of statistical inference, we can measure the performance of estimation by using the Bayesian PCRB. The PCRB on the estimation error has the formulation as

$$\begin{array}{c}\hfill \mathbf{PCRB}\triangleq {\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\left(\widehat{\mathit{\theta }}\left(\mathit{y}\right)-\mathit{\theta }\right){\left(\widehat{\mathit{\theta }}\left(\mathit{y}\right)-\mathit{\theta }\right)}^{\mathrm{T}}\right]\ge {\mathbf{G}}^{-1}\left(\mathit{\theta }\right)\end{array}$$

(9)

where $\widehat{\mathit{\theta }}\left(\mathit{y}\right)$ denotes the estimate of $\mathit{\theta }$, and $\mathbf{G}\left(\mathit{\theta }\right)$ is the $n\times n$ Fisher information matrix with the elements defined in the Equation (8) The inequality $“\ge ”$ means that the difference $\mathbf{PCRB}-{\mathbf{G}}^{-1}\left(\mathit{\theta }\right)$ is a positive semidefinite matrix. This inequality is used to describe the estimation error bound. Usually, in application, the covariance matrix of the estimation is approximated by the inverse of Fisher information matrix.

3.2. Natural Gradient Descent

The gradient method is a general approach for solving optimization problem. For most of the problems that estimate the parameter $\mathit{\theta }$ in Euclidean space, the gradient descent update is defined as

$$\begin{array}{c}\hfill {\widehat{\mathit{\theta }}}^i={\widehat{\mathit{\theta }}}^{i-1}-{\nabla }_{\mathit{\theta }}L\left({\widehat{\mathit{\theta }}}^{i-1}\right)\end{array}$$

(10)

where ${\nabla }_{\mathit{\theta }}L$ is the gradient of convex differentiable objective function L, and it determines the update direction for next iterative step. However, it is not suitable for the Riemannian manifold, because of the curvature of the manifold. Based on the Riemannian metric tensor, the gradient on Riemannian manifold has been proposed as ${\tilde{\nabla }}_{\mathit{\theta }}L\left(\mathit{\theta }\right)={\mathbf{G}}^{-1}\left(\mathit{\theta }\right){\nabla }_{\mathit{\theta }}L\left(\mathit{\theta }\right)$ known as the natural gradient. Thus, the natural gradient descent update on the Riemannian manifold as

$$\begin{array}{c}\hfill {\widehat{\mathit{\theta }}}^i={\widehat{\mathit{\theta }}}^{i-1}-{\eta }_i{\mathbf{G}}^{-1}\left({\widehat{\mathit{\theta }}}^{i-1}\right){\nabla }_{\mathit{\theta }}L\left({\widehat{\mathit{\theta }}}^{i-1}\right)\end{array}$$

(11)

where $\mathbf{G}\left(\mathit{\theta }\right)$ is the Riemannian metric tensor associated with the estimated parameter $\mathit{\theta }$, i is the number of iterative steps and the parameter ${\eta }_i\in \left(0,1\right]$ denotes the step-size parameter for iterative update. The natural gradient descent multiples the inverse of Riemannian metric tensor by the gradient of objective function. It takes into account the direction of steepest descent on the Riemannian manifold, which involves the curvature of the manifold. It has been proven that steps along the direction of the natural gradient descent is the steepest descent on the Riemannian manifold [27]. The natural gradient method has been used in many application, such as nonlinear estimation [28]. In addition, the natural gradient desecent is Fisher Efficient [23]. Luo et al. [29] has analyzed the convergence and bound properties of natural gradient descent method. After the natural gradient descent method constructing the iterative update procedure, the stopping conditions have to set to obtain the final estimate. Usually, the distance between two successive estimates has been used for these conditions.

3.3. Divergence and Distance

In Euclidean space, the distance can be used to describe the difference between two quantities, and it is defined by Euclidean norm as $\parallel \Delta \mathit{\theta }\parallel =\sqrt{<\Delta \mathit{\theta },\Delta \mathit{\theta }>}=\sqrt{\Delta {\mathit{\theta }}^{\mathrm{T}}\Delta \mathit{\theta }}$. While in the Riemannian manifold, the distance is defined with Riemannian metric tensor $\mathbf{G}\left(\mathit{\theta }\right)$ as ${\parallel \Delta \mathit{\theta }\parallel }_{\mathbf{G}\left(\mathit{\theta }\right)}=\sqrt{<\Delta \mathit{\theta },\Delta \mathit{\theta }{>}_{\mathbf{G}\left(\mathit{\theta }\right)}}=\sqrt{\Delta {\mathit{\theta }}^{\mathrm{T}}\mathbf{G}\left(\mathit{\theta }\right)\Delta \mathit{\theta }}$. In statistical manifold with Fisher metric tensor instead of Riemannian metric tensor, Amari [30] has defined the squared distance between two nearby distributions $p(\mathit{y},\mathit{\theta })$ and $p(\mathit{y},\mathit{\theta }+\Delta \mathit{\theta })$ as

$$d{s}^2=\Delta {\mathit{\theta }}^{\mathrm{T}}\mathbf{G}\left(\mathit{\theta }\right)\Delta \mathit{\theta }=<\Delta \mathit{\theta },\Delta \mathit{\theta }{>}_{\mathbf{G}\left(\mathit{\theta }\right)}$$

(12)

Besides, the KL divergence has provided another means to measure the similarity of two nearby probability distributions. The KL divergence is defined as

$${\mathrm{D}}_{\mathrm{KL}}\left(p\parallel q\right)=\int p\left(\mathit{y}\right)\log \left(\frac{p\left(\mathit{y}\right)}{q\left(\mathit{y}\right)}\right)$$

(13)

where p and q denote two probability densities. The KL divergence is also called relative entropy as in information theory. As for the KL divergence, it is a good measure of difference with the desired mathematical properties [31].

Let q approximate the neighborhood p as $q\left(\mathit{y},\mathit{\theta }\right)=p\left(\mathit{y},\mathit{\theta }+\Delta \mathit{\theta }\right)$, and the Taylor expansion gives an approximation of the KL divergence by

$$\begin{array}{c}{\mathrm{D}}_{\mathrm{KL}}\left(p\left(\mathit{y},\mathit{\theta }\right)\parallel p\left(\mathit{y},\mathit{\theta }+\Delta \mathit{\theta }\right)\right)={\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\log \left\{\frac{p\left(\mathit{y},\mathit{\theta }\right)}{p\left(\mathit{y},\mathit{\theta }+\Delta \mathit{\theta }\right)}\right\}\right]\hfill \\ ={\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\log p\left(\mathit{y},\mathit{\theta }\right)\right]-{\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\log p\left(\mathit{y},\mathit{\theta }+\Delta \mathit{\theta }\right)\right]\hfill \\ \approx {\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\log p\left(\mathit{y},\mathit{\theta }\right)\right]-{\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\log p\left(\mathit{y},\mathit{\theta }\right)+\sum _{i=1}^m\frac{\partial \log p\left(\mathit{y},\mathit{\theta }\right)}{\partial {\mathit{\theta }}_i}\Delta {\mathit{\theta }}_i+\frac{1}{2}\sum _{i,j=1}^m\frac{{\partial }^2\log p\left(\mathit{y},\mathit{\theta }\right)}{\partial {\mathit{\theta }}_i\partial {\mathit{\theta }}_j}\Delta {\mathit{\theta }}_i\Delta {\mathit{\theta }}_j\right]\hfill \\ =-{\mathbf{E}}_{\mathit{y},\mathit{\theta }}\left[\frac{1}{2}\sum _{i,j=1}^m\frac{{\partial }^2\log p\left(\mathit{y},\mathit{\theta }\right)}{\partial {\mathit{\theta }}_i\partial {\mathit{\theta }}_j}\Delta {\mathit{\theta }}_i\Delta {\mathit{\theta }}_j\right]\hfill \\ =\frac{1}{2}\Delta {\mathit{\theta }}^{\mathrm{T}}\mathbf{G}\left(\mathit{\theta }\right)\Delta \mathit{\theta }\hfill \end{array}$$

(14)

where $\mathbf{G}\left(\mathit{\theta }\right)$ denotes the Fisher metric tensor of statistical manifold, $\Delta {\mathit{\theta }}_i$ denotes the i-th scalar of $\Delta \mathit{\theta }$. In the equation, $\mathbf{E}\left[\frac{\partial \log p\left(\mathit{y},\mathit{\theta }\right)}{\partial \mathit{\theta }}\right]=0$ [22] has been used. From this relationship, we can note that the KL divergence has included the second order information of probability density. Compared with the Amari’s squared distance, the KL divergence has local behavior that it is approximately a half of the squared distance for the statistical manifold, which coincides with the geodesic distance for infinitesimal distances [32]. With the help of divergence and distance, we can measure how close between two estimates from the viewpoint of statistical manifold.

For the particular statistical manifold of multivariate Gaussian, it has the explicit formulation of probability density

$$\begin{array}{c}\hfill p(\mathit{y};\mathit{\mu },\mathbf{\Sigma })=\frac{\exp \left[-\frac{1}{2}{(\mathit{y}-\mathit{\mu })}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}(\mathit{y}-\mathit{\mu })\right]}{\sqrt{{\left(2\pi \right)}^{m}det(\mathbf{\Sigma })}}\end{array}$$

(15)

where $\mathit{y}$ is the random variable, $\mathit{\mu }\in {\mathbb{R}}^m$ and $\mathbf{\Sigma }\in Sym\left(m\right)$ denote the mean and the covariance matrix, respectively. $Sym\left(m\right)$ is the space of real symmetric $m\times m$ positive-definite matrix. The mean and the covariance matrix are the unknown parameters to be estimated. The statistical manifold is constructed by the probability density as $\mathcal{S}=\left\{p\left(\mathit{y};\mathit{\mu },\mathbf{\Sigma }\right),\left(\mathit{\mu },\mathbf{\Sigma }\right)\in {\mathbb{R}}^m\times Sym\left(m\right)\right\}$. The logarithm likelihood of the multivariate Gaussian can be re-written as

$$\begin{array}{c}\hfill \ell =\log p\left(\mathit{y};\mathit{\mu },\mathbf{\Sigma }\right)=-\frac{1}{2}{(\mathit{y}-\mathit{\mu })}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}(\mathit{y}-\mathit{\mu })-\frac{1}{2}\log det(\mathbf{\Sigma })-\frac{m}{2}\log \left(2\pi \right)\end{array}$$

(16)

Consider $\mathit{\mu }$ and $\mathbf{\Sigma }$ as the mutual independent parameters, the first order partial derivatives of ℓ with respect to $\mathit{\mu }$ and $\mathbf{\Sigma }$ are

$$\begin{array}{c}\hfill {\nabla }_{\mathit{\mu }}={\mathbf{\Sigma }}^{-1}\left(\mathit{y}-\mathit{\mu }\right)\end{array}$$

(17)

$$\begin{array}{cc}\hfill {\nabla }_{\mathbf{\Sigma }}\ell & =\frac{\partial \left(-\frac{1}{2}\mathrm{tr}\left[{\mathbf{\Sigma }}^{-1}\left(\mathit{y}-\mathit{\mu }\right){\left(\mathit{y}-\mathit{\mu }\right)}^{\mathrm{T}}\right]\right)}{\partial \mathbf{\Sigma }}+\frac{\partial \left(-\frac{1}{2}\log det\left(\mathbf{\Sigma }\right)\right)}{\partial \mathbf{\Sigma }}\hfill \\ & =\frac{1}{2}{\mathbf{\Sigma }}^{-1}\left(\mathit{y}-\mathit{\mu }\right){\left(\mathit{y}-\mathit{\mu }\right)}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}-\frac{1}{2}{\mathbf{\Sigma }}^{-1}\hfill \end{array}$$

(18)

then, we can compute the second order partial derivatives of ℓ as follows

$${\nabla }_{\mathit{\mu }}{\left[{\nabla }_{\mathit{\mu }}\ell \right]}^{\mathrm{T}}=-{\mathbf{\Sigma }}^{-1}$$

(19)

$${\nabla }_{\mathbf{\Sigma }}{\left[{\nabla }_{\mathbf{\Sigma }}\ell \right]}^{\mathrm{T}}=\frac{\partial {\mathbf{\Sigma }}^{-1}}{\partial \mathbf{\Sigma }}\left(\mathit{y}-\mathit{\mu }\right){\left(\mathit{y}-\mathit{\mu }\right)}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}-\frac{1}{2}\frac{\partial {\mathbf{\Sigma }}^{-1}}{\partial \mathbf{\Sigma }}$$

(20)

The Fisher metric tensor with respect to $\mathit{\mu }$ is

$$\begin{array}{c}\hfill {\mathbf{F}}_{\mathit{\mu }}=-{\mathbf{E}}_{\mathit{y}}\left[{\nabla }_{\mathit{\mu }}{\left[{\nabla }_{\mathit{\mu }}\ell \right]}^{\mathrm{T}}\right]={\mathbf{\Sigma }}^{-1}\end{array}$$

(21)

and the Fisher metric tensor with respect to $\mathbf{\Sigma }$ is

$$\begin{array}{cc}\hfill {\mathbf{F}}_{\mathbf{\Sigma }}& =-{\mathbf{E}}_{\mathit{y}}\left[{\nabla }_{\mathbf{\Sigma }}{\left[{\nabla }_{\mathbf{\Sigma }}\ell \right]}^{\mathrm{T}}\right]\hfill \\ & =-\frac{\partial {\mathbf{\Sigma }}^{-1}}{\partial \mathbf{\Sigma }}\mathbf{\Sigma }{\mathbf{\Sigma }}^{-1}+\frac{1}{2}\frac{\partial {\mathbf{\Sigma }}^{-1}}{\partial \mathbf{\Sigma }}=\frac{1}{2}{\mathbf{\Sigma }}^{-1}\otimes {\mathbf{\Sigma }}^{-1}\hfill \end{array}$$

(22)

where ⊗ denotes the Kronecker product.

With ${\mathbf{E}}_{\mathit{y}}\left[{\nabla }_{\mathit{\mu }}\ell {\nabla }_{\mathbf{\Sigma }}{\ell }^{\mathrm{T}}\right]={\mathbf{E}}_{\mathit{y}}{\left[{\nabla }_{\mathbf{\Sigma }}\ell {\nabla }_{\mathit{\mu }}{\ell }^{\mathrm{T}}\right]}^{\mathrm{T}}=\mathbf{0}$, we can obtain the distance

$$\begin{array}{cc}\hfill d{s}^2& =\Delta {\mathit{\mu }}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\Delta \mathit{\mu }+\frac{1}{2}{\left(\mathrm{vec}\left(\Delta \mathbf{\Sigma }\right)\right)}^{\mathrm{T}}\left({\mathbf{\Sigma }}^{-1}\otimes {\mathbf{\Sigma }}^{-1}\right)\mathrm{vec}\left(\Delta \mathbf{\Sigma }\right)\hfill \\ & =\Delta {\mathit{\mu }}^{\mathrm{T}}{\mathbf{\Sigma }}^{-1}\Delta \mathit{\mu }+\frac{1}{2}\mathrm{tr}\left[{\left({\mathbf{\Sigma }}^{-1}\Delta \mathbf{\Sigma }\right)}^2\right]\hfill \end{array}$$

(23)

where m is the dimension of data $\mathit{y}$, $\Delta \mathit{\mu }$ and $\Delta \mathbf{\Sigma }$ denote the variations of $\mathit{\mu }$ and $\mathbf{\Sigma }$, respectively. In the above procedure of deriving, the following equations [33] have been used

$$\mathrm{tr}\left(\mathbf{ABCD}\right)={\left(\mathrm{vec}\left({\mathbf{D}}^{\mathrm{T}}\right)\right)}^{\mathrm{T}}\left({\mathbf{C}}^{\mathrm{T}}\otimes \mathbf{A}\right)\mathrm{vec}\left(\mathbf{B}\right)$$

(24)

$$\frac{\partial \mathrm{tr}\left(\mathbf{A}{\mathbf{X}}^{-1}\mathbf{B}\right)}{\partial \mathbf{X}}=-{\mathbf{X}}^{-1}\mathbf{BA}{\mathbf{X}}^{-1}$$

(25)

$$\frac{\partial \log det\mathbf{X}}{\partial \mathbf{X}}={\mathbf{X}}^{-1}$$

(26)

$$\frac{\partial {\mathbf{X}}^{-1}}{\partial \mathbf{X}}=-\left({\mathbf{X}}^{-\mathrm{T}}\otimes {\mathbf{X}}^{-1}\right)$$

(27)

where $\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D},\mathbf{X}$ are matrices.

The distance between two quantities on statistical manifold is corresponding to the KL divergence between two probability densities. When we compare two quantities on statistical manifold, the distance can measure their similarity. The shorter distance means the smaller divergence of two probability densities. This can be used to describe the convergence of estimation.

Conventionally, the gradient method will process an iterative procedure to estimate the state, and the distance between two estimates is used to measure the convergence of the algorithm. Intuitionally, the convergence on statistical manifold is that the difference between two probability distributions corresponding to two estimates is very small. In the iterative estimation procedure, the convergence means that two successive estimates are almost equivalent, or, in practice, the distance between two estimates is less than a certain value.

4. Natural Gradient Descent Filtering

For the Bayesian filtering, the posterior distribution plays the key role in the procedure. However, the close-form of posterior PDFs is intractable because of the Bayesian integral. Usually, the optimization technique has been used to obtain the approximation formulation. In this section, we consider this problem from the information geometric perspective, and derive a new filtering method by using information geometric optimization technique.

In the Bayesian filtering, the state propagation (Equation (1)) can provide the prior information of state before the measurement update. The prior PDF is Gaussian density when the state transition function is linear. While the state function is nonlinear, the prior PDF is non-Gaussian. Here, we focus on the measurement update step, and make an effort to use information geometric optimization for the posterior PDF. Similar to the usual Gaussian filtering, the Gaussian density is used to approximate the non-Gaussian density in the step of state propagation [16], which has the formulation as

$$\begin{array}{c}\hfill p\left({\mathit{x}}_k|{\mathit{y}}_{k-1}\right)\approx \mathcal{N}\left({\mathit{x}}_k;{\widehat{\mathit{x}}}_k^{-},{\mathbf{\Sigma }}_k\right)\end{array}$$

(28)

where ${\widehat{\mathit{x}}}_k^{-}$ and ${\mathbf{\Sigma }}_k$ denote the mean and covariance matrix of the prior PDF after state propagation. It means that the k-time state ${\mathit{x}}_k$ based on the $k-1$-time measurement ${\mathit{y}}_{k-1}$. With the k-time measurement likelihood function, i.e., the conditional probability density of the measurement ${\mathit{y}}_k$ given ${\mathit{x}}_k$ is

$$\begin{array}{c}\hfill p\left({\mathit{y}}_k|{\mathit{x}}_k\right)=\mathcal{N}\left({\mathit{y}}_k;\mathit{h}\left({\mathit{x}}_k\right),\mathbf{R}\right)\end{array}$$

(29)

We can obtain the Bayesian posterior probability density by substituting Equations (28) and (29) into Equation (2). The numerical optimization is used to obtain the approximative solution for Bayesian integral. Similar to MAP, the optimization is reformulated as

$$\begin{array}{cc}\hfill {\widehat{\mathit{x}}}_k& =\arg \underset{{\mathit{x}}_k}{max}p\left({\mathit{x}}_k|{\mathit{y}}_k\right)=\arg \underset{{\mathit{x}}_k}{min}L\left({\mathit{x}}_k\right)\hfill \end{array}$$

(30)

where $L\left({\mathit{x}}_k\right)=-\log p\left({\mathit{y}}_k|{\mathit{x}}_k\right)-\log p\left({\mathit{x}}_k|{\mathit{y}}_{k-1}\right)$ denotes the negative logarithm likelihood function of posterior distribution, which neglects the terms independent of the ${\mathit{x}}_k$.

Consider the statistical manifold $\mathcal{S}=\{p\left({\mathit{y}}_k,{\mathit{x}}_k\right),{\mathit{x}}_k\in {\mathbb{R}}^n\}$ constructed by the joint probability density $p\left({\mathit{y}}_k,{\mathit{x}}_k\right)$, the natural logarithm maps the statistical manifold to $\mathbb{R}$ as $\log :\mathcal{S}\to \mathbb{R}$. Given a point ${\widehat{\mathit{x}}}_k$, the Fisher metric tensor of $\mathcal{S}$ at ${\widehat{\mathit{x}}}_k$ can be calculated as

$$\begin{array}{cc}\hfill \mathbf{G}\left({\widehat{\mathit{x}}}_k\right)& ={\mathbf{E}}_{{\mathit{y}}_k,{\mathit{x}}_k}\left[-{\nabla }_{{\mathit{x}}_k}{\left[{\nabla }_{{\mathit{x}}_k}\log p\left({\mathit{y}}_k,{\mathit{x}}_k\right)\right]}^{\mathrm{T}}\right]\hfill \\ & ={\mathbf{E}}_{{\mathit{x}}_k}{\mathbf{E}}_{{\mathit{y}}_k|{\mathit{x}}_k}\left[{\mathit{e}}_y^{\mathrm{T}}{\mathbf{R}}^{-1}{\nabla }_{{\mathit{x}}_k}^{{\mathit{x}}_k}\mathit{h}\left({\widehat{\mathit{x}}}_k\right)+{\nabla }_{{\mathit{x}}_k}\mathit{h}{\left({\widehat{\mathit{x}}}_k\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}{\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\widehat{\mathit{x}}}_k\right)+{\mathbf{\Sigma }}_k^{-1}\right]\hfill \\ & ={\mathbf{E}}_{{\mathit{x}}_k}\left[{\nabla }_{{\mathit{x}}_k}\mathit{h}{\left({\widehat{\mathit{x}}}_k\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}{\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\widehat{\mathit{x}}}_k\right)\right]+{\mathbf{\Sigma }}_k^{-1}\hfill \\ & ={\nabla }_{{\mathit{x}}_k}\mathit{h}{\left({\widehat{\mathit{x}}}_k\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}{\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\widehat{\mathit{x}}}_k\right)+{\mathbf{\Sigma }}_k^{-1}\hfill \end{array}$$

(31)

where ${\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\mathit{x}}_k\right)=\frac{\partial \mathit{h}\left({\mathit{x}}_k\right)}{\partial {\mathit{x}}_k}\in {\mathbb{R}}^m\times {\mathbb{R}}^n$ denotes the first order partial derivative of $\mathit{h}$ with respect to ${\mathit{x}}_k$, and ${\mathit{e}}_y=\mathit{h}\left({\mathit{x}}_k\right)-{\mathit{y}}_k$ represents the error of the measurement prediction with the state estimation ${\mathit{x}}_k={\widehat{\mathit{x}}}_k$.

From Equation (31), we can note that the Fisher metric tensor consists of two parts: the measurement information and the prior information of the state. It also means that the curvature of the statistical manifold is affected by the measurement data and the prior information. It is evident that the effect of nonlinear measurement is reflected by the first terms of the Fisher metric tensor. Equation (31) establishes the relationship between the nonlinear measurement and the metric tensor.

Since the joint PDFs construct the statistical manifold, the minimization of $L\left({\mathit{x}}_k\right)$ is converted to the optimization on the statistical manifold for the best estimation. This optimization on statistical manifold considers the measurement and state in a unified approach, and the natural gradient descent method can be used to seek the optimal estimation on the manifold along geodesic lines.

By computing the first order partial derivative of $L\left({\mathit{x}}_k\right)$, we can obtain the gradient

$$\begin{array}{cc}\hfill {\nabla }_{{\mathit{x}}_k}L\left({\mathit{x}}_k\right)& ={\nabla }_{{\mathit{x}}_k}\mathit{h}{\left({\mathit{x}}_k\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathit{e}}_y+{\mathbf{\Sigma }}_k^{-1}{\mathit{e}}_x\hfill \end{array}$$

(32)

where ${\mathit{e}}_y=\mathit{h}\left({\mathit{x}}_k\right)-{\mathit{y}}_k$ and ${\mathit{e}}_x={\mathit{x}}_k-{\widehat{\mathit{x}}}_k^{-}$ denote the individual error of the measurement prediction and the state estimation.

Since ${\mathbf{R}}^{-1}$ is a symmetric positive-definite diagonal matrix, ${\nabla }_{{\mathit{x}}_k}\mathit{h}{\left({\widehat{\mathit{x}}}_k\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}{\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\widehat{\mathit{x}}}_k\right)$ is positive semi-definite. Note that ${\mathbf{\Sigma }}_k^{-1}$ is positive, so $\mathbf{G}\left({\mathit{x}}_k\right)$ is nonsingular. Thus, the natural gradient of the statistical manifold is defined as

$$\begin{array}{c}\hfill {\mathbf{G}}^{-1}\left({\widehat{\mathit{x}}}_k\right){\nabla }_{{\mathit{x}}_k}L\left({\widehat{\mathit{x}}}_k\right)={\left({\nabla }_{{\mathit{x}}_k}\mathit{h}{\left({\widehat{\mathit{x}}}_k\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}{\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\widehat{\mathit{x}}}_k\right)+{\mathbf{\Sigma }}_k^{-1}\right)}^{-1}\left({\nabla }_{{\mathit{x}}_k}\mathit{h}{\left({\widehat{\mathit{x}}}_k\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathit{e}}_y+{\mathbf{\Sigma }}_k^{-1}{\mathit{e}}_x\right)\end{array}$$

(33)

With the natural gradient descent on the statistical manifold, we can update the state estimation

$$\begin{array}{cc}\hfill {\widehat{\mathit{x}}}_k^{+}& ={\widehat{\mathit{x}}}_k^{-}-\eta {\mathbf{G}}^{-1}\left({\widehat{\mathit{x}}}_k^{-}\right){\nabla }_{{\mathit{x}}_k}L\left({\widehat{\mathit{x}}}_k^{-}\right)\hfill \\ & ={\widehat{\mathit{x}}}_k^{-}-\eta {\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{H}+{\mathbf{\Sigma }}_k^{-1}\right)}^{-1}\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\right)\left(\mathit{h}\left({\widehat{\mathit{x}}}_k^{-}\right)-{\mathit{y}}_k\right)\hfill \end{array}$$

(34)

and the covariance matrix is approximated by the inverse of the Fisher metric tensor

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Sigma }}}_{\mathbf{k}}& ={\mathbf{G}}^{-1}\left({\widehat{\mathit{x}}}_k^{-}\right)={\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{H}+{\mathbf{\Sigma }}_k^{-1}\right)}^{-1}\hfill \end{array}$$

(35)

where $\mathbf{H}={\left.{\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\mathit{x}}_k\right)\right|}_{{\mathit{x}}_k={\widehat{\mathit{x}}}_k^{-}}$ is the Jacobian matrix of measurement function $\mathit{h}$.

Usually, one step cannot achieve the best estimation, so more steps must be utilized to achieve the final estimation. The states are updated iteratively in state space, while the corresponding posterior probabilities are moving across the statistical manifold.

To sum it up, we can construct an iterative estimation of state through the natural gradient descent method

$$\begin{array}{cc}\hfill {\widehat{\mathit{x}}}_k^{i+1}& ={\widehat{\mathit{x}}}_k^i-{\eta }_i{\mathbf{G}}^{-1}\left({\widehat{\mathit{x}}}_k^i\right){\nabla }_{{\mathit{x}}_k}L\left({\widehat{\mathit{x}}}_k^i\right)\hfill \\ & ={\widehat{\mathit{x}}}_k^i-{\eta }_i{\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{H}}_i+{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}\right)}^{-1}\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}\left(\mathit{h}\left({\widehat{\mathit{x}}}_k^i\right)-{\mathit{y}}_k\right)+{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}({\widehat{\mathit{x}}}_k^i-{\widehat{\mathit{x}}}_k^0)\right)\hfill \\ & ={\widehat{\mathit{x}}}_k^i+{\eta }_i{\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{H}}_i+{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}\right)}^{-1}\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}\left({\mathit{y}}_k-\mathit{h}\left({\widehat{\mathit{x}}}_k^i\right)\right)-{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}({\widehat{\mathit{x}}}_k^i-{\widehat{\mathit{x}}}_k^0)\right)\hfill \end{array}$$

(36)

which corresponds to the moving from $p\left({\mathit{y}}_k,{\widehat{\mathit{x}}}_k^i\right)$ to $p\left({\mathit{y}}_k,{\widehat{\mathit{x}}}_k^{i+1}\right)$ on statistical manifold. In Equation (36), ${\mathbf{H}}_i={\nabla }_{{\mathit{x}}_k}\mathit{h}\left({\mathit{x}}_k\right){|}_{{\mathit{x}}_k={\widehat{\mathit{x}}}_k^i}$, and ${\widehat{\mathit{x}}}_k^0={\widehat{\mathit{x}}}_{\mathit{k}}^{-}$ is the prior information of state provided by the state propagation. Meanwhile, the error covariance matrix associated with ${\widehat{\mathit{x}}}_k^{i+1}$ is approximated by the inverse of Fisher metric tensor

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Sigma }}}_k^{i+1}& ={\mathbf{G}}^{-1}\left({\widehat{\mathit{x}}}_k^i\right)={\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{H}}_i+{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}\right)}^{-1}\hfill \end{array}$$

(37)

Therefore, we can obtain the iterative posterior mean and covariance matrix as $({\widehat{\mathit{x}}}_k^{i+1},{\widehat{\mathbf{\Sigma }}}_k^{i+1})$. When the stopping criteria are satisfied, the iterative procedure will be terminated, and the filtered state will be achieve.

4.1. Adaptive Step-Size

In this iterative procedure, there are some parameters that must be taken into account. One of them is the step-size parameter, which describes the update step-size in each iterated step. It can be a fixed value through the whole iterative procedure. As an alternative, the step-size is initialized and adjusted in each iteration. There are many strategies to adjust the value of step-size in order to achieve the sufficient decrease during the iterative procedure. In our proposed method, the value of step-size can be obtained by an exact line search [34]

$$\begin{array}{c}\hfill {\eta }_i=\arg \underset{0<\eta \le 1}{min}L\left({\widehat{\mathit{x}}}_k^i+\eta \times {\tilde{\nabla }}_{{\mathit{x}}_k}L\left({\widehat{\mathit{x}}}_k^i\right)\right)\end{array}$$

(38)

where ${\tilde{\nabla }}_{{\mathit{x}}_k}L\left({\widehat{\mathit{x}}}_k^i\right)$ denotes the natural gradient. In each iteration, the searching direction described by the natural gradient is fixed, and we just need to select the parameter $\eta$. Usually, the candidates of $\eta$ can be generated randomly.

4.2. Stopping Criterion

In the iterative procedure, the number of steps can be fixed as a constant. However, it has not considered the convergence and may lead to additional computational burden. Alternatively, the number of steps is acquired according to certain stopping criterion of the iterative procedure. As in the conventional IEKF, the stopping criterion is that the distance of the state estimates between two successive iterations is smaller than a given constant $\alpha$, that is,

$$\begin{array}{c}\hfill \parallel {\widehat{\mathit{x}}}_k^{i+1}-{\widehat{\mathit{x}}}_k^i{\parallel }^2=\langle {\widehat{\mathit{x}}}_k^{i+1}-{\widehat{\mathit{x}}}_k^i,{\widehat{\mathit{x}}}_k^{i+1}-{\widehat{\mathit{x}}}_k^i\rangle <\alpha \end{array}$$

(39)

While the distance $\parallel {\widehat{\mathit{x}}}_k^{i+1}-{\widehat{\mathit{x}}}_k^i{\parallel }^2$ is defined in Euclidean space, the counterpart in Riemannian manifold is

$$\begin{array}{c}\hfill \parallel {\widehat{\mathit{x}}}_k^{i+1}-{\widehat{\mathit{x}}}_k^i{\parallel }_{\mathbf{G}}^2={\langle {\widehat{\mathit{x}}}_k^{i+1}-{\widehat{\mathit{x}}}_k^i,{\widehat{\mathit{x}}}_k^{i+1}-{\widehat{\mathit{x}}}_k^i\rangle }_{\mathbf{G}}\end{array}$$

(40)

We can use this distance to measure the convergence on the statistical manifold. Owing to the equivalence between manifold distance and KL divergence, we also can utilize the KL divergence to measure the convergence. Here, we adopt the KL divergence (Equation (14)) instead of the distance in stopping criterion, i.e.,

$${\mathrm{D}}_{\mathrm{KL}}\left(p({\mathit{y}}_k,{\widehat{\mathit{x}}}_k^i)\parallel p({\mathit{y}}_k,{\widehat{\mathit{x}}}_k^{i+1})\right)<\frac{\gamma }{2}$$

(41)

Furthermore, it also describe the divergence between two probability densities of successive iterations. When the convergence is achieved, the divergence level is very low.

5. Discussion

5.1. Comparison with KF

When the conditions of state-space model have become linear and Gaussian, i.e., $\mathit{f}\left({\mathit{x}}_{k-1}\right)=\mathbf{F}{\mathit{x}}_{k-1}$ and $\mathit{h}\left({\mathit{x}}_k\right)=\mathbf{H}{\mathit{x}}_k$, the Fisher metric is

$$\begin{array}{c}\mathbf{G}\left({\mathit{x}}_k\right)={\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{H}+{\mathbf{\Sigma }}_k^{-1}\hfill \end{array}$$

(42)

It is independent of the state ${\mathit{x}}_k$, which means that the metric tensor is a constant across the statistical manifold. Thus, we need only one step to estimate the state and the step-size is full step by setting $\eta =1$. The natural gradient descent filtering (NGDF) is simplified as

$$\begin{array}{cc}\hfill {\widehat{\mathit{x}}}_k& ={\widehat{\mathit{x}}}_k^{-}-{\left.{\mathbf{G}}^{-1}\left({\mathit{x}}_k\right)\nabla L\left({\mathit{x}}_k\right)\right|}_{{\mathit{x}}_k={\widehat{\mathit{x}}}_k^{-}}\hfill \\ & ={\widehat{\mathit{x}}}_k^{-}-{\left.{\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{H}+{\mathbf{\Sigma }}_k^{-1}\right)}^{-1}\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathit{e}}_y+{\mathbf{\Sigma }}_k^{-1}{\mathit{e}}_x\right)\right|}_{{\mathit{x}}_k={\widehat{\mathit{x}}}_k^{-}}\hfill \\ & ={\widehat{\mathit{x}}}_k^{-}+\left({\mathbf{\Sigma }}_k{\mathbf{H}}^{\mathrm{T}}\right){\left(\mathbf{H}{\mathbf{\Sigma }}_k{\mathbf{H}}^{\mathrm{T}}+\mathbf{R}\right)}^{-1}({\mathit{y}}_k-\mathbf{H}{\mathit{x}}_k^{-})\hfill \end{array}$$

(43)

where $\mathit{h}\left({\mathit{x}}_k\right)=\mathbf{H}{\mathit{x}}_k$, ${\mathit{e}}_y=\mathbf{h}\left({\mathit{x}}_k\right)-{\mathit{y}}_k$, and ${\mathit{e}}_x={\mathit{x}}_k-{\widehat{\mathit{x}}}_k^{-}$. When the first order partial derivative is calculated at the point of prior estimation, ${\mathit{e}}_x$ will be zero. Besides, the matrix inversion lemma (Equation (48)) has been used. Equation (43) is the same as the measurement update of conventional Kalman filter, while the Kalman gain is defined as $\mathbf{K}=\left({\mathbf{\Sigma }}_k{\mathbf{H}}^{\mathrm{T}}\right){\left(\mathbf{H}{\mathbf{\Sigma }}_k{\mathbf{H}}^{\mathrm{T}}+\mathbf{R}\right)}^{-1}$. Meanwhile, the error covariance matrix (Equation (37)) can be calculated as

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Sigma }}}_k& ={\mathbf{G}}^{-1}\left(x_k\right)={\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{H}+{\mathbf{\Sigma }}_k^{-1}\right)}^{-1}\hfill \\ & ={\mathbf{\Sigma }}_k-{\mathbf{\Sigma }}_k{\mathbf{H}}^{\mathrm{T}}{\left(\mathbf{H}{\mathbf{\Sigma }}_k{\mathbf{H}}^{\mathrm{T}}+\mathbf{R}\right)}^{-1}\mathbf{H}{\mathbf{\Sigma }}_k\hfill \\ & ={\mathbf{\Sigma }}_k-\mathbf{K}\left(\mathbf{H}{\mathbf{\Sigma }}_k{\mathbf{H}}^{\mathrm{T}}+\mathbf{R}\right){\mathbf{K}}^{\mathrm{T}}\hfill \end{array}$$

(44)

Compared with the state estimation and error covariance matrix in Kalman filter, our method NGDF is equivalent to the Kalman filter when the conditions are linear and Gaussian. As for the EKF, NGDF has made the linear approximation for nonlinear case, so it has a similar formulation to Kalman filter.

5.2. Comparison with IEKF

Furthermore, if we set the step-size parameter as $\eta =1$ in the NGDF, the update of state is reformulated as

$$\begin{array}{cc}\hfill {\widehat{\mathit{x}}}_k^{i+1}& ={\widehat{\mathit{x}}}_k^i+{\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{H}}_i+{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}\right)}^{-1}\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}\left({\mathit{y}}_k-\mathit{h}\left({\widehat{\mathit{x}}}_k^i\right)\right)-{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}({\widehat{\mathit{x}}}_k^i-{\widehat{\mathit{x}}}_k^0)\right)\hfill \\ & ={\widehat{\mathit{x}}}_k^i+{\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{H}}_i+{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}\right)}^{-1}{\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}\left({\mathit{y}}_k-\mathit{h}\left({\widehat{\mathit{x}}}_k^i\right)\right)-{\left({\mathbf{H}}_i^{\mathrm{T}}{\mathbf{R}}^{-1}{\mathbf{H}}_i+{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}\right)}^{-1}{\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}({\widehat{\mathit{x}}}_k^i-{\widehat{\mathit{x}}}_k^0)\hfill \\ & ={\widehat{\mathit{x}}}_k^i+{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}{\left({\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}+\mathbf{R}\right)}^{-1}\left({\mathit{y}}_k-\mathit{h}\left({\widehat{\mathit{x}}}_k^i\right)\right)-\left({\widehat{\mathbf{\Sigma }}}_k^i-{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}{\left({\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}+\mathbf{R}\right)}^{-1}{\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i\right){\left({\widehat{\mathbf{\Sigma }}}_k^i\right)}^{-1}\left({\widehat{\mathit{x}}}_k^i-{\widehat{\mathit{x}}}_k^0\right)\hfill \\ & ={\widehat{\mathit{x}}}_k^0+{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}{\left({\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}+\mathbf{R}\right)}^{-1}\left({\mathit{y}}_k-\mathit{h}\left({\widehat{\mathit{x}}}_k^i\right)\right)+{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}{\left({\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}+\mathbf{R}\right)}^{-1}{\mathbf{H}}_i\left({\widehat{\mathit{x}}}_k^i-{\widehat{\mathit{x}}}_k^0\right)\hfill \\ & ={\widehat{\mathit{x}}}_k^0+{\mathbf{K}}_i\left({\mathit{y}}_k-\mathit{h}\left({\widehat{\mathit{x}}}_k^i\right)+{\mathbf{H}}_i\left({\widehat{\mathit{x}}}_k^i-{\widehat{\mathit{x}}}_k^0\right)\right)\hfill \end{array}$$

(45)

where ${\mathbf{K}}_i={\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}{\left({\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}+\mathbf{R}\right)}^{-1}$, and the covariance matrix is approximated by the inverse of the Fisher metric tensor

$$\begin{array}{c}\hfill {\widehat{\mathbf{\Sigma }}}_k^{i+1}={\mathbf{G}}^{-1}\left({\widehat{\mathit{x}}}_k^i\right)={\widehat{\mathbf{\Sigma }}}_k^i-{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}{\left({\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i{\mathbf{H}}_i^{\mathrm{T}}+\mathbf{R}\right)}^{-1}{\mathbf{H}}_i{\widehat{\mathbf{\Sigma }}}_k^i\end{array}$$

(46)

In the above procedure, the two forms of the matrix inversion lemma

$${({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{H}+{\mathbf{\Sigma }}^{-1})}^{-1}{\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}=\mathbf{\Sigma }{\mathbf{H}}^{\mathrm{T}}{(\mathbf{H}\mathbf{\Sigma }{\mathbf{H}}^{\mathrm{T}}+\mathbf{R})}^{-1}$$

(47)

$${\left({\mathbf{H}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{H}+{\mathbf{\Sigma }}^{-1}\right)}^{-1}=\mathbf{\Sigma }-\mathbf{\Sigma }{\mathbf{H}}^{\mathrm{T}}{\left(\mathbf{H}\mathbf{\Sigma }{\mathbf{H}}^{\mathrm{T}}+\mathbf{R}\right)}^{-1}\mathbf{H}\mathbf{\Sigma }$$

(48)

have been used.

Obviously, the aforementioned iterative procedure in the NGDF is the same as the IEKF method, when we set $\eta =1$ for the step-size parameter. However, the step-size of the NGDF is usually adjusted according to the objective function. The adjustment of step-size may make the NGDF improve the accuracy of estimation. This will be illustrated in the following experiments.

5.3. Comparison with GIKF

Apart from the natural gradient method, the Newton–Raphson method is another gradient method. Hu [12] has proposed the GIKF based on Newton–Raphson method. It should be noted that the natural gradient method is completely different from the Newton–Raphson method. The natural gradient multiples the inverse of the Riemannian metric tensor by the gradient, while the Newton–Raphson multiples the inverse of the Hessian matrix by the gradient. The Riemannian metric tensor is the metric of the underlying space independent of the objective function to be approximated, but the Hessian matrix is dependent on the objective function or the parameter coordinate. Thus, the natural gradient, which using Riemannian metric tensor instead of the Hessian matrix, is more robust [28].

5.4. Relationship with Riemannian Manifold MCMC

Except the MAP technique, the Monte Carlo technique is an alternative method to obtain the integral in Bayesian filtering. Usually, the Sequence Monte Carlo (SMC) and the Markov chain Monte Carlo (MCMC) are two widely used methods. The SMC has been used in the filtering problems, which is also called as PF. The MCMC method is a fundamental tool to generate samples from a posterior density in Bayesian data analysis and inference, and it is robust and excellent for nonlinear filtering and manifold learning. Recently, the geometric concepts are introduced into the MCMC method. As we take the underlying geometric structure into account for the recursive estimation based on PDFs, the Riemannian manifold is used in the MCMC method. This method has been induced by the Girolami [35] as

$$\begin{array}{c}\hfill {\mathit{\theta }}^{n+1}={\mathit{\theta }}^n+\frac{{\epsilon }^2}{2}{\mathbf{G}}^{-1}\left({\mathit{\theta }}^n\right){\nabla }_{\mathit{\theta }}\ell \left({\mathit{\theta }}^n\right)+\epsilon \sqrt{{\mathbf{G}}^{-1}\left({\mathit{\theta }}^n\right)}{\mathbf{z}}^n\end{array}$$

(49)

where $\epsilon \in (0,1]$ denotes the step-size of integration, and the random variable satisfies $\mathbf{z}\sim \mathcal{N}(\mathbf{z};\mathbf{0},\mathbf{I})$. The sampling mechanism can be rewritten as Gaussian form $\mathcal{N}\left(\mathit{\theta };\mathit{\mu }({\mathit{\theta }}^n,\epsilon ),\Sigma ({\mathit{\theta }}^n,\epsilon )\right)$, where

$$\begin{array}{cc}\hfill \mathit{\mu }({\mathit{\theta }}^n,\epsilon )& ={\mathit{\theta }}^n+\frac{{\epsilon }^2}{2}{\mathbf{G}}^{-1}\left({\mathit{\theta }}^n\right){\nabla }_{\mathit{\theta }}\ell \left({\mathit{\theta }}^n\right)\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill \Sigma ({\mathit{\theta }}^n,\epsilon )& ={\epsilon }^2{\mathbf{G}}^{-1}\left({\mathit{\theta }}^n\right)\hfill \end{array}$$

(51)

These are similar to our proposed filtering method. The state update is processed by the natural gradient method, and the covariance matrix is approximated by the inverse of the Riemannian metric tensor. Compared with our proposed method, the difference is the step-size in state update and the decaying factor for the Riemannian metric tensor. The reason is that the Riemannian manifold MCMC is derived by the Hamilton dynamics and Langevin diffusion, while our proposed method is derived by information geometric optimization on statistical manifold. In addition, the metric tensor plays an important role in Riemannian manifold, and the natural gradient method provides the general approach for optimization.

6. Simulation

In this section, we compare the classical filtering methods including EKF, IEKF and RUF with our method NGDF in the application of passive target tracking [14,36]. The EKF has just one step in the update procedure, and the IEKF is an iterative filtering method derived by the Netwon method. The RUF [7,8] is an another iterative filtering method derived by the LMMSE, not the MAP, and it has the fixed number of steps.

For the system setting, the state at time instant k is ${\mathbf{x}}_k={\left[x_k,{\dot{x}}_k,y_k,{\dot{y}}_k\right]}^{\mathrm{T}}$ consisting of position vector ${\left[x_k,y_k\right]}^{\mathrm{T}}$ and velocity vector ${\left[{\dot{x}}_k,{\dot{y}}_k\right]}^{\mathrm{T}}$, while the measurement at same instant is $\mathbf{z}\left(k\right)={[{\mathit{\theta }}_k,{\dot{\mathit{\theta }}}_k,{\dot{f}}_k]}^{\mathrm{T}}$ consisting of bearing ${\mathit{\theta }}_k$, bearing rate ${\dot{\mathit{\theta }}}_k$, and Doppler rate ${\dot{f}}_k$.

The state equation is linear and represented as

$$\begin{array}{c}\hfill {\mathit{x}}_k=\mathbf{F}{\mathit{x}}_{k-1}+\mathbf{G}{\mathbf{v}}_k\end{array}$$

(52)

where

$$\begin{array}{c}\hfill \mathbf{F}={\mathbf{I}}_2\otimes \left(\begin{array}{cc}1& \tau \\ 0& 1\end{array}\right)\end{array}\begin{array}{c}\hfill \mathbf{G}={\mathbf{I}}_2\otimes \left(\begin{array}{c}0.5{\tau }^2\\ \tau \end{array}\right)\end{array}$$

(53)

where ${\mathbf{I}}_2$ is a $2\times 2$ identity matrix, ⊗ is the Kronecker product, $\tau$ is the sampling time, and ${\mathbf{v}}_k={\left[v_{x_k},v_{y_k}\right]}^{\mathrm{T}}$ is zero-mean process noise with covariance matrix ${\mathbf{Q}}_k$.

The measurement equation is

$$\begin{array}{ccc}\hfill {\mathbf{z}}_k& =\hfill & \left[\begin{array}{c}{\mathit{\theta }}_k\\ {\dot{\mathit{\theta }}}_k\\ {\dot{f}}_k\end{array}\right]=\left[\begin{array}{c}\arctan \left(y_k/x_k\right)\\ \left({\dot{y}}_k{x}_k-{\dot{x}}_k{y}_k\right)/r_k^2\\ -{\left({\dot{y}}_k{x}_k-{\dot{x}}_k{y}_k\right)}^2/\left(\lambda r_k^3\right)\end{array}\right]+\left[\begin{array}{c}{n}_{{\mathit{\theta }}_k}\\ n_{{\dot{\mathit{\theta }}}_k}\\ n_{{\dot{f}}_k}\end{array}\right]\hfill \\ & \triangleq \hfill & \mathbf{h}\left({\mathbf{x}}_k\right)+{\mathbf{n}}_k\hfill \end{array}$$

(54)

where $r_k=\sqrt{x_k^2+y_k^2}$, $\lambda$ denotes the wavelength of received signal, and $n_{{\theta }_k},n_{{\dot{\theta }}_k},n_{{\dot{f}}_k}$ are mutually independent zero-mean Gaussian distributed noises with covariance matrix ${\mathbf{R}}_k=\mathrm{diag}[{\sigma }_{\theta }^2,{\sigma }_{\dot{\theta }}^2,{\sigma }_{\dot{f}}^2]$. Here, we treat $x_k,y_k$ as the coordinate of target, and ${\mathbf{z}}_k$ as the measurement, which are different from the notations in the above sections.

In this simulation, we consider 200 time steps for tracking, and $\tau =0.5\mathrm{s}$, $\lambda =0.1\mathrm{m}$, $\mathbf{Q}=\mathrm{diag}([{(9\mathrm{m}/{\mathrm{s}}^2)}^2,{(2\mathrm{m}/{\mathrm{s}}^2)}^2])$. The prior PDF at time 0 is $p\left({\mathit{x}}_0\right)=\mathcal{N}\left({\mathit{x}}_0;{\mathit{\mu }}_0,{\mathbf{\Sigma }}_0\right)$, where ${\mathit{\mu }}_0={[800\mathrm{m},-50\mathrm{m}/\mathrm{s},300\mathrm{m},10\mathrm{m}/\mathrm{s}]}^{\mathrm{T}}$, and

$${\mathbf{\Sigma }}_0=\left[\begin{array}{cccc}{\sigma }_x^2& 0& \rho {\sigma }_x{\sigma }_y& 0\\ 0& {\sigma }_v^2& 0& 0\\ \rho {\sigma }_x{\sigma }_y& 0& {\sigma }_y^2& 0\\ 0& 0& 0& {\sigma }_v^2\end{array}\right]$$

(55)

where ${\sigma }_x=500\mathrm{m}$, ${\sigma }_y=200\mathrm{m}$, $\rho =0.95$, and ${\sigma }_v=100\mathrm{m}/\mathrm{s}$.

We carry out the numerical experiment considering two aspects: the first is different initialization parameters in filtering method for the same track, while the second is different tracks with different noise level. The normalization root mean square error (RMSE) of position and velocity are utilized to illustrate the performance of tracking. They are defined as follows

$$\begin{array}{cc}\hfill {\mathrm{RMSE}}_{\mathrm{Pos}}& =\frac{\sqrt{{\left(x-\widehat{x}\right)}^2+{\left(y-\widehat{y}\right)}^2}}{\sqrt{x^2+y^2}}\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill {\mathrm{RMSE}}_{\mathrm{Vel}}& =\frac{\sqrt{{\left(v_x-{\widehat{v}}_x\right)}^2+{\left(v_y-{\widehat{v}}_y\right)}^2}}{\sqrt{v_x^2+v_y^2}}\hfill \end{array}$$

(57)

where ${\left[x,v_x,y,v_y\right]}^{\mathrm{T}}$ denotes the true state, and ${\left[\widehat{x},{\widehat{v}}_x,\widehat{y},{\widehat{v}}_y\right]}^{\mathrm{T}}$ is estimation state. For the filtering methods, we set $\gamma =1$ in the stopping criterion (41) for our proposed method, while $\alpha =1$ in (39) for the IEKF. In the iterative methods (IEKF, RUF and NGDF), the max number of iterative steps is $N=30$.

Firstly, we set the measurement noise variances as ${\sigma }_{\theta }=2\times {10}^{-4}\mathrm{rad}$, ${\sigma }_{\dot{\theta }}={10}^{-5}\mathrm{rad}/\mathrm{s}$ and ${\sigma }_{\dot{f}}=0.05\mathrm{Hz}/\mathrm{s}$, and select a track as Figure 1a. We carry out 100 Monte Carlo runs for filtering, and average over different realizations to obtain the tracking and normalized position RMSE. In each Monte Carlo runs, the initial filtered state at time 0 is generated random according to the prior PDF. Usually, they are different. 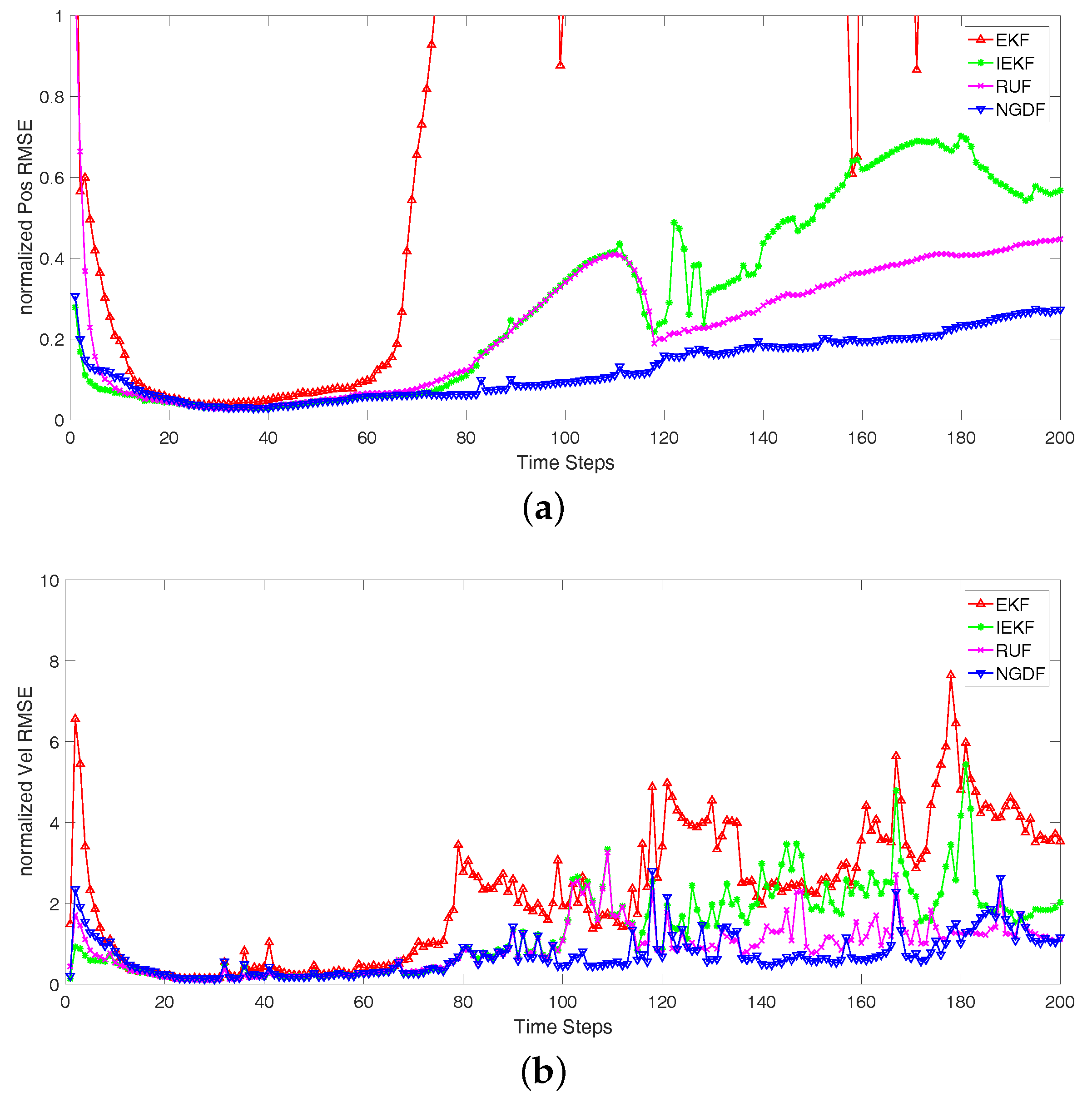After filtering, the results are shown in Figure 1. In this figure, we can note that the different initial state has influenced the first few steps, and will perform well in the follow steps. In addition, the changeable trajectory can lead to the performance of tracking degradation. In this comparing experiment, we can know that the filtered track by our filtering method is closer to the true track than the other methods, and the normalized position RMSE of our method is lower than the others. Comparing the iterative filtering methods with EKF, the iterative methods have better performance. This is because that the iterative methods have utilized the more iterative steps to hold the nonlinear measurement function, and they are more accurate than the nonlinear processing in EKF methods.

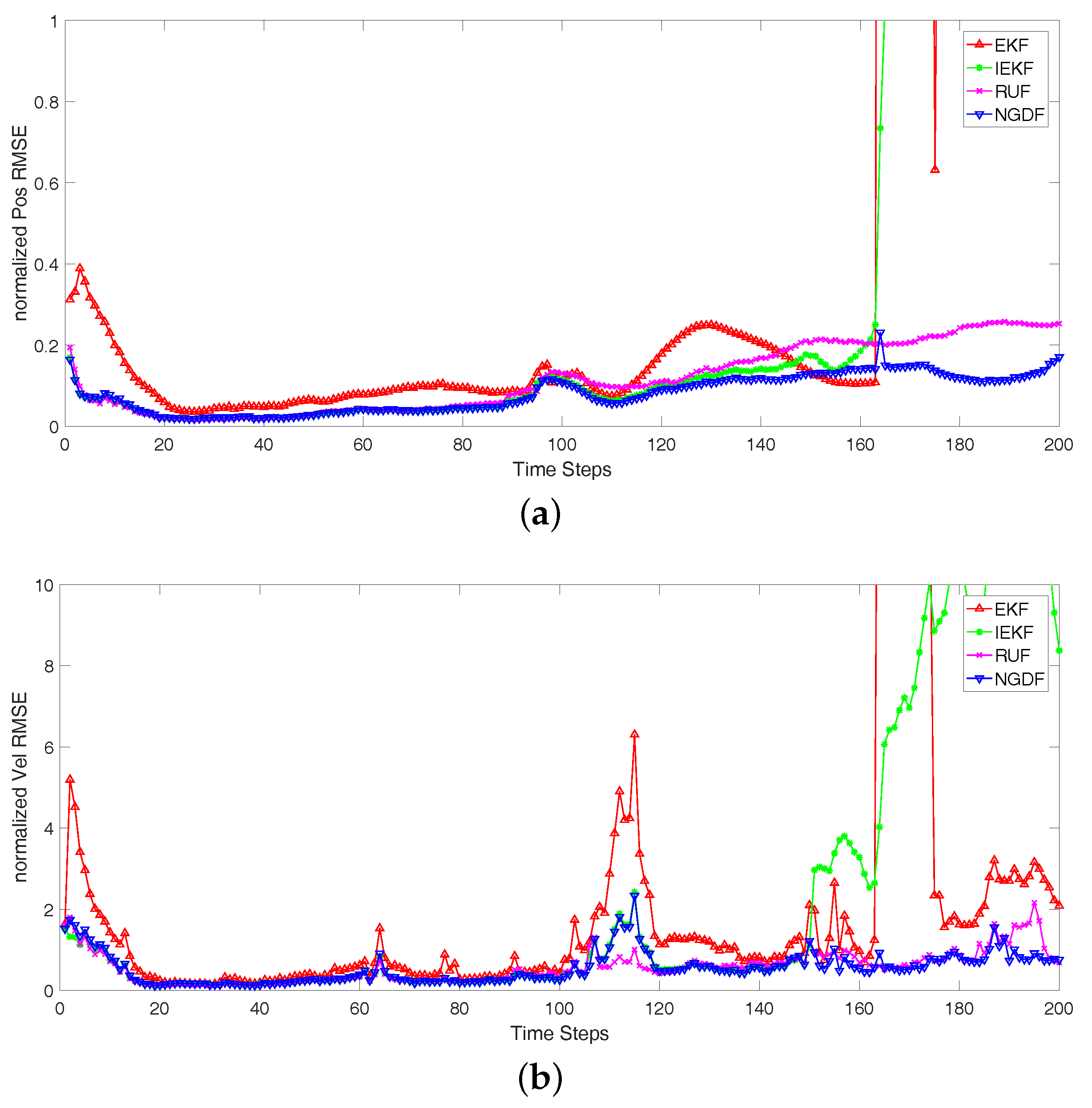
Secondly, we consider different tracks with different noise level. We carry out 100 Monte Carlo runs for the tracks, and take the average over different realizations of the tracks and the corresponding filtered states. The initial true state is random generated according to the prior PDF of state. Because the random initial state is used in each track and the state noise is imposed on state at each time step, the tracks will be different for the Monte Carlo runs. In the Bayesian filtering framework, we focus on the measurement update, and the different measurement noise is considered in this paper. We analyze the three scenarios that differ in the measurement noise variances:

• Scenario 1: ${\sigma }_{\theta }=2\times {10}^{-4}\mathrm{rad}$, ${\sigma }_{\dot{\theta }}={10}^{-5}\mathrm{rad}/\mathrm{s}$ and ${\sigma }_{\dot{f}}=0.05\mathrm{Hz}/\mathrm{s}$;
• Scenario 2: ${\sigma }_{\theta }=2\times {10}^{-6}\mathrm{rad}$, ${\sigma }_{\dot{\theta }}={10}^{-5}\mathrm{rad}/\mathrm{s}$ and ${\sigma }_{\dot{f}}=0.05\mathrm{Hz}/\mathrm{s}$;
• Scenario 3: ${\sigma }_{\theta }=2\times {10}^{-6}\mathrm{rad}$, ${\sigma }_{\dot{\theta }}={10}^{0.1}\mathrm{rad}/\mathrm{s}$ and ${\sigma }_{\dot{f}}={10}^{-3}\mathrm{Hz}/\mathrm{s}$.

The normalized RMSEs of position and velocity are shown in Figure 2, Figure 3 and Figure 4, and the number of iterative steps is shown in Figure 5. The results in Figure 2, Figure 3 and Figure 4 show that the iterative methods perform better than the EKF, and our proposed method NGDF outperforms other two iterative methods IEKF and RUF in the estimations of position and velocity. Our method has the stable performance that the normalized position RMSEs keep a lower level. The EKF method has the bad performance that it diverges at some times. Comparing with the estimation of velocity, the performance of four filtering methods fluctuate greatly. These are limited by the measurement of radar system. The position measurement can be obtained directly, while the velocity measurement is obtained indirectly that also need the position measurement. The error of position measurement and estimation also influence the velocity estimation. In this case, our method has small fluctuation comparing with the other methods. From Figure 2, Figure 3 and Figure 4, the EKF fluctuates greatly. It means that the EKF method diverges in many cases, and it is not suitable for this tracking problems with the nonlinear measurement. Meanwhile, the IEKF has some jump points. This is because the iterative estimation has not converged, but the stopping criterion is satisfied. Besides, we can note the performance of the RUF method. It has a stable performance second only to our method. However, it has far more computational burden than our method and the EKF and IEKF method shown in Figure 5.

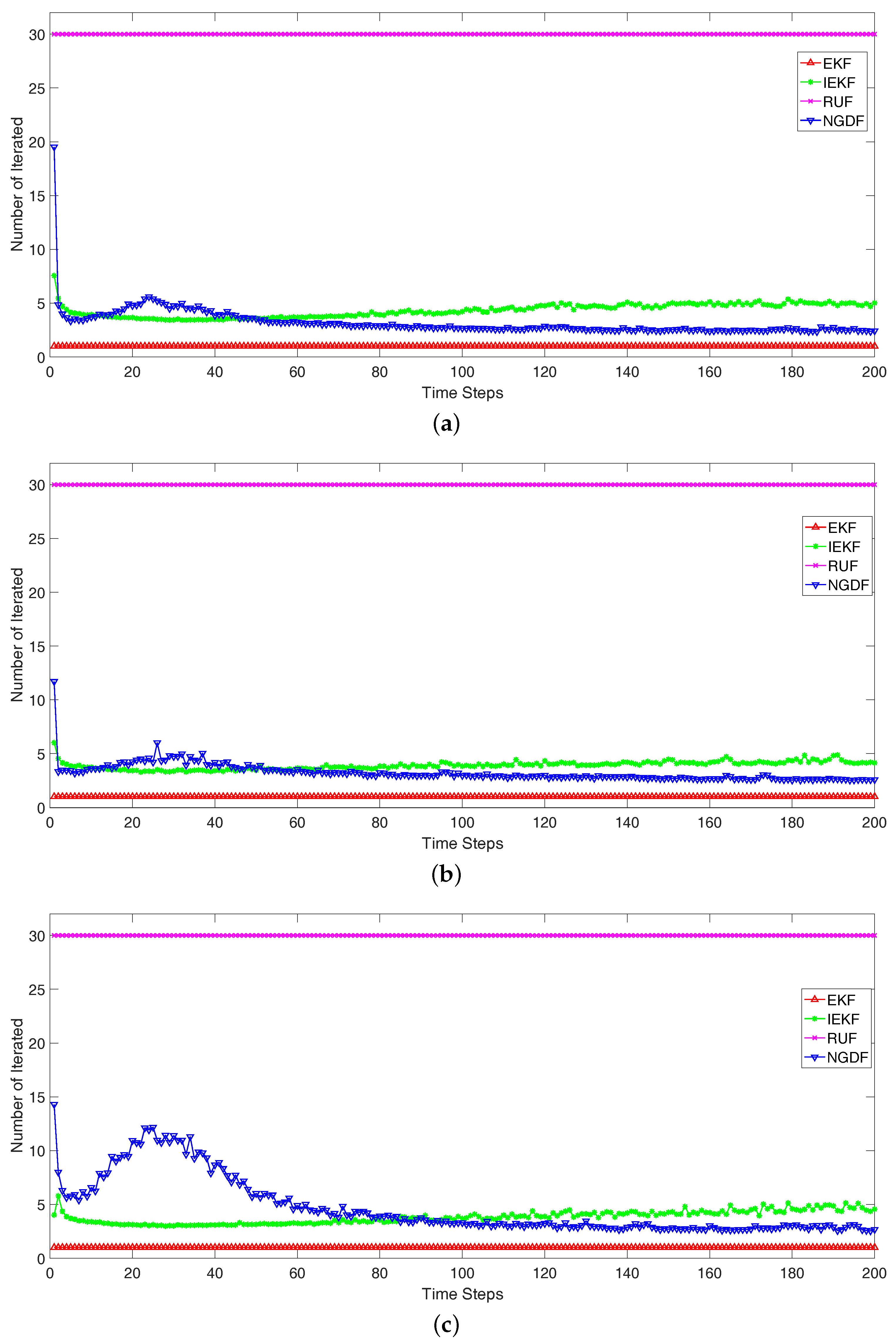
To measure the computational burden, we compare the number of iteration intuitively. The average number of iteration in each time step is shown in Figure 5. In the simulation, the EKF uses one step to obtain the filtered state in each time step, i.e., the iteration number is $N=1$. The RUF is an iterative method, which has fixed iteration number as $N=30$. For these three scenarios, the iteration number of the IEKF is about $N=5$, while the iteration number of NGDF is roughly less than $N=4$ in Figure 5a,b. In Figure 5c, the number of iteration of NGDF is more than IEKF before the time steps 80, but lower in the succedent time steps. These results can reflect the computational burden. In each time step, the computational burden of RUF is 30 times than the EKF, while the IEKF is about 5 times and NGDF is less 4 times. Comparing the IEKF and NGDF method, the step-size of NGDF is adaptive, which leads to the less steps and more robust estimation. While the IEKF uses the full step-size, which may fluctuate or delay the stopping time. Besides, we compare the execution times in milliseconds for the Scenario 1. The four methods are implemented with the Matlab on a Intel Core i7 laptop. The average of the execution times based on the 100 monte carlo runs are: EKF (11.5 s), IEKF (38.4 s), NGDF (26.4 s) and RUF (187.6 s). In addition, it should be noted that these times are computed for the whole filtering procedure which achieve filtering from the beginning of time steps to the end. We can conclude that the lowest computational burden is achieved by our proposed method.

In this simulation, we also note that the performance may be become bad after a certain tracking steps. This is because that the resolution limit of radar system measurement. The resolution limit of measurement will influence the accuracy of the measurement, thus make some effect on the estimation state. This is why that the tracking of radar system has a tracking time interval. Exceeding the time interval, the tracking performance is unavailable. In addition, the level of noise has influenced the track and estimation. The lower level of state noise may make the track tend to be fixed, while the lower level of measurement noise may make the measurement is more available. They can make the estimation more accurate, but there have no significant and determination relationship between noise level and filtering. This is because the nonlinear function between state and measurement. Usually for the filtering problems, we have made some simplification and considered some case to compare the filtering methods.

To sum up, in this simulation, our method is the filtering method with highest performance than the other methods. It has a stable performance, and the increase in performance of our method does not imply a much higher computational burden compared to other iterative methods.

7. Conclusions

In this paper, we have derived a novel filtering method by utilizing the information geometric approach. The filtering problem has been converted to an optimization on the statistical manifold constructed by the joint PDFs of Bayesian filtering, and the adaptive natural gradient descent method is used to search the optimal estimation. In the filtering procedure, curvature characteristic brought about by the nonlinearity of the observation operator $\mathit{h}$ is considered carefully by the Fisher metric tensor. For the Bayesian filtering, the Fisher metric tensor consists of measurement likelihood and prior information of state. For the linear case, the metric is constant, while variable in the nonlinear case. Then, the adaptive natural gradient descent technique is used to derive the iterative filtering, and the KL divergence is employed in the stopping criterion. Furthermore, the conventional Kalman filter, EKF and IEKF are the special formulations of our proposed method under certain conditions. With adaptive step-size and KL divergence stopping criterion, the proposed method has made some improvement over EKF, IEKF and RUF.

For the Bayesian nonlinear filtering, the posterior density may be non-Gaussian. There are two reasons bringing about the non-Gaussian cases. The first reason is that non-Gaussian observation densities make the posterior density non-Gaussian. An optimal filter has been proposed to address this problem [37]. It can modify the Kalman filter to handle the non-Gaussian observation density. The second reason is that nonlinear measurement makes the Gaussian densities become non-Gaussian. The Monte Carlo method can be used to solve this problem with large computational burden.

In the derivation of our method, we can note that the information geometric optimization for filtering can be extended to some non-Gaussian case, such as the exponential density. When the density has the analytic form, the metric can be computed, and the information geometric optimization can be used to derive the filtering method. Besides, we can use the fact that the non-Gaussian density can be approximated by the sum of some Gaussian densities to convert the non-Gaussian density into the Gaussian density, then the proposed method in this paper can be utilized in each Gaussian density component. In future work, we will continue to combine the information geometric optimization with non-Gaussian filtering, and provide some approaches for addressing the problems of non-Gaussian density in the filtering.