Capacity Bounds on the Downlink of Symmetric, Multi-Relay, Single-Receiver C-RAN Networks
Abstract
:1. Introduction
2. Preliminaries and Problem Setup
2.1. Notation
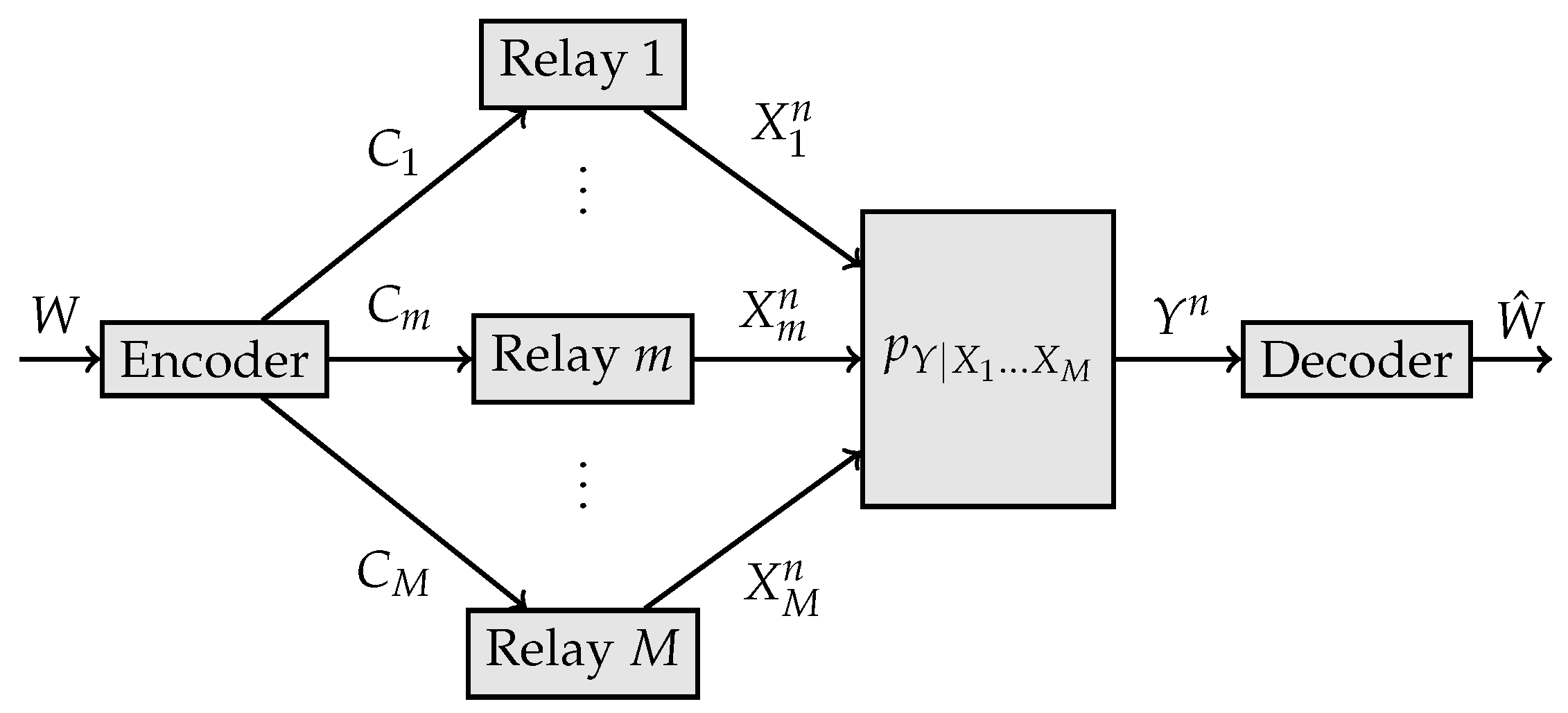
2.2. Model
3. A Lower Bound
3.1. Codebook Construction
3.2. Encoding
3.3. Relay Mapping at Relay m,
3.4. Decoding
4. An Upper Bound
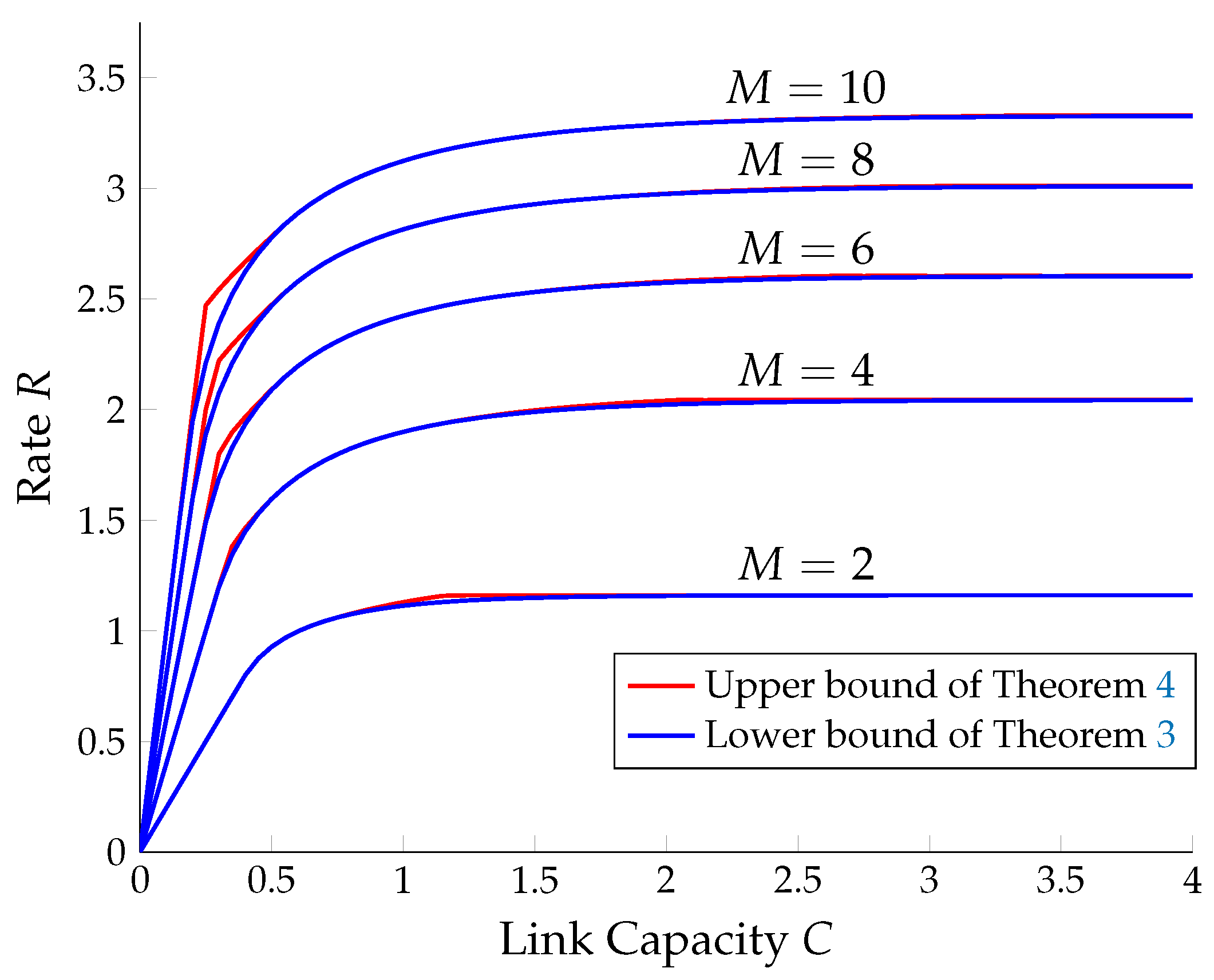
5. The Symmetric Gaussian C-RAN
- If then
- Otherwise, is the unique solution of in:and we have:
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Analysis of the Achievable Scheme
- (12) holds for indices where . We show that this event has a vanishing error probability as if we have (14). Since the codebook is symmetric with respect to all messages, we assume without loss of generality that and . Fix the sets such that . Consider the case whereWe denote the set of index tuples satisfying (A1) by . We have:where denotes and denotes . In Step (a), we use that (i) is “almost independent” of and (ii) the random sequences , and , are mutually “almost independent”. Note that we use the term “almost independent”, rather than independent, because we have assumed and ; i.e., we implicitly have a conditional probability and conditioned on , claims (i)–(ii) may not hold if we insist on exact independence. This issue has been dealt with in [21,22,23], and following similar arguments, one can show that (i) and (ii) hold with “almost independence”. The probability of the considered error event is thus arbitrarily close to zero for large enough n if:Inequality (A3) is satisfied by (14) when we choose . Note that the inequalities with are redundant.
Appendix B. Simplification for Symmetric Networks with Symmetric Distributions
Appendix C. Proof of Theorem 2
References
- Park, S.H.; Simeone, O.; Sahin, O.; Shamai, S. Fronthaul compression for cloud radio access networks: Signal processing advances inspired by network information theory. IEEE Signal Proc. Mag. 2014, 31, 69–79. [Google Scholar] [CrossRef]
- Yu, W. Cloud radio-access networks: Coding strategies, capacity analysis, and optimization techniques. In Proceedings of the Communications Theory Workshop, Toronto, ON, Canada, 6 May 2016. [Google Scholar]
- Peng, M.; Wang, C.; Lau, V.; Poor, H.V. Fronthaul-constrained cloud radio access networks: Insights and challenges. IEEE Wirel. Commun. 2015, 22, 152–160. [Google Scholar] [CrossRef]
- Dai, B.; Yu, W. Sparse beamforming and user-centric clustering for downlink cloud radio access network. IEEE Access 2014, 2, 1326–1339. [Google Scholar]
- Park, S.H.; Simeone, O.; Sahin, O.; Shamai, S. Joint precoding and multivariate backhaul compression for the downlink of cloud radio access networks. IEEE Trans. Signal Proc. 2013, 61, 5646–5658. [Google Scholar] [CrossRef]
- Patil, P.; Yu, W. Hybrid compression and message-sharing strategy for the downlink cloud radio-access network. In Proceedings of the Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 9–14 February 2014; pp. 1–6. [Google Scholar]
- Liu, N.; Kang, W. A new achievability scheme for downlink multicell processing with finite backhaul capacity. In Proceedings of the IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 1006–1010. [Google Scholar]
- Wang, C.; Wigger, M.A.; Zaidi, A. On achievability for downlink cloud radio access networks with base station cooperation. arXiv, 2016; arXiv:1610.09407. [Google Scholar]
- Yang, T.; Liu, N.; Kang, W.; Shamai, S. An upper bound on the sum capacity of the downlink multicell processing with finite backhaul capacity. arXiv, 2016; arXiv:1609.00833. [Google Scholar]
- Traskov, D.; Kramer, G. Reliable communication in networks with multi-access interference. In Proceedings of the Information Theory Workshop, Tahoe City, CA, USA, 2–6 September 2007; pp. 343–348. [Google Scholar]
- Kang, W.; Liu, N.; Chong, W. The Gaussian multiple access diamond channel. IEEE Trans. Inf. Theory 2015, 61, 6049–6059. [Google Scholar] [CrossRef]
- Saeedi Bidokhti, S.; Kramer, G. Capacity bounds for diamond networks with an orthogonal broadcast channel. IEEE Trans. Inf. Theory 2016, 62, 7103–7122. [Google Scholar] [CrossRef]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Venkataramani, R.; Kramer, G.; Goyal, V.K. Multiple description coding with many channels. IEEE Trans. Inf. Theory 2006, 49, 2106–2114. [Google Scholar] [CrossRef]
- Saeedi Bidokhti, S.; Kramer, G. Capacity bounds for a class of diamond networks. In Proceedings of the International Symposium Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 1196–1200. [Google Scholar]
- Ozarow, L. On a source-coding problem with two channels and three receivers. Bell Syst. Tech. J. 1980, 59, 1909–1921. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Thomas, J. Feedback can at most double Gaussian multiple access channel capacity. IEEE Trans. Inf. Theory 1987, 33, 711–716. [Google Scholar] [CrossRef]
- Lee, S.H.; Zhao, W.; Khisti, A. Secure degrees of freedom of the Gaussian diamond-wiretap channel. IEEE Trans. Inf. Theory 2017, 63, 496–508. [Google Scholar] [CrossRef]
- Zou, S.; Liang, Y.; Lai, L.; Shamai, S. An information theoretic approach to secret sharing. IEEE Trans. Inf. Theory 2015, 61, 3121–3136. [Google Scholar] [CrossRef]
- Minero, P.; Lim, S.H.; Kim, Y.H. A unified approach to hybrid coding. IEEE Trans. Inf. Theory 2005, 61, 1509–1523. [Google Scholar] [CrossRef]
- Grover, P.; Wagner, A.B.; Sahai, A. Information embedding meets distributed control. arXiv, 2010; arXiv:1003.0520. [Google Scholar]
- Saeedi Bidokhti, S.; Prabhakaran, V.M. Is non-unique decoding necessary? IEEE Trans. Inf. Theory 2014, 60, 2594–2610. [Google Scholar] [CrossRef]
- Willems, F.; van der Meulen, E. The discrete memoryless multiple-access channel with cribbing encoders. IEEE Trans. Inf. Theory 1985, 31, 313–327. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeedi Bidokhti, S.; Kramer, G.; Shamai, S. Capacity Bounds on the Downlink of Symmetric, Multi-Relay, Single-Receiver C-RAN Networks. Entropy 2017, 19, 610. https://doi.org/10.3390/e19110610
Saeedi Bidokhti S, Kramer G, Shamai S. Capacity Bounds on the Downlink of Symmetric, Multi-Relay, Single-Receiver C-RAN Networks. Entropy. 2017; 19(11):610. https://doi.org/10.3390/e19110610
Chicago/Turabian StyleSaeedi Bidokhti, Shirin, Gerhard Kramer, and Shlomo Shamai. 2017. "Capacity Bounds on the Downlink of Symmetric, Multi-Relay, Single-Receiver C-RAN Networks" Entropy 19, no. 11: 610. https://doi.org/10.3390/e19110610
APA StyleSaeedi Bidokhti, S., Kramer, G., & Shamai, S. (2017). Capacity Bounds on the Downlink of Symmetric, Multi-Relay, Single-Receiver C-RAN Networks. Entropy, 19(11), 610. https://doi.org/10.3390/e19110610





.png)
