Robust and Sparse Regression via γ-Divergence
Abstract
:1. Introduction
2. Regression Based on -Divergence
2.1. -Divergence for Regression
2.2. Estimation for -Regression
3. Parameter Estimation Procedure
3.1. MM Algorithm for Sparse -Regression
3.2. Sparse -Linear Regression
| Algorithm 1 Sparse -linear regression. |
|
3.3. Robust Cross-Validation
4. Robust Properties
4.1. Homogeneous Contamination
4.2. Heterogeneous Contamination
4.3. Redescending Property
5. Numerical Experiment
5.1. Regression Models for Simulation
5.2. Performance Measure
5.3. Comparative Methods
5.4. Details of Our Method
5.4.1. Initial Points
5.4.2. How to Choose Tuning Parameters
5.5. Result
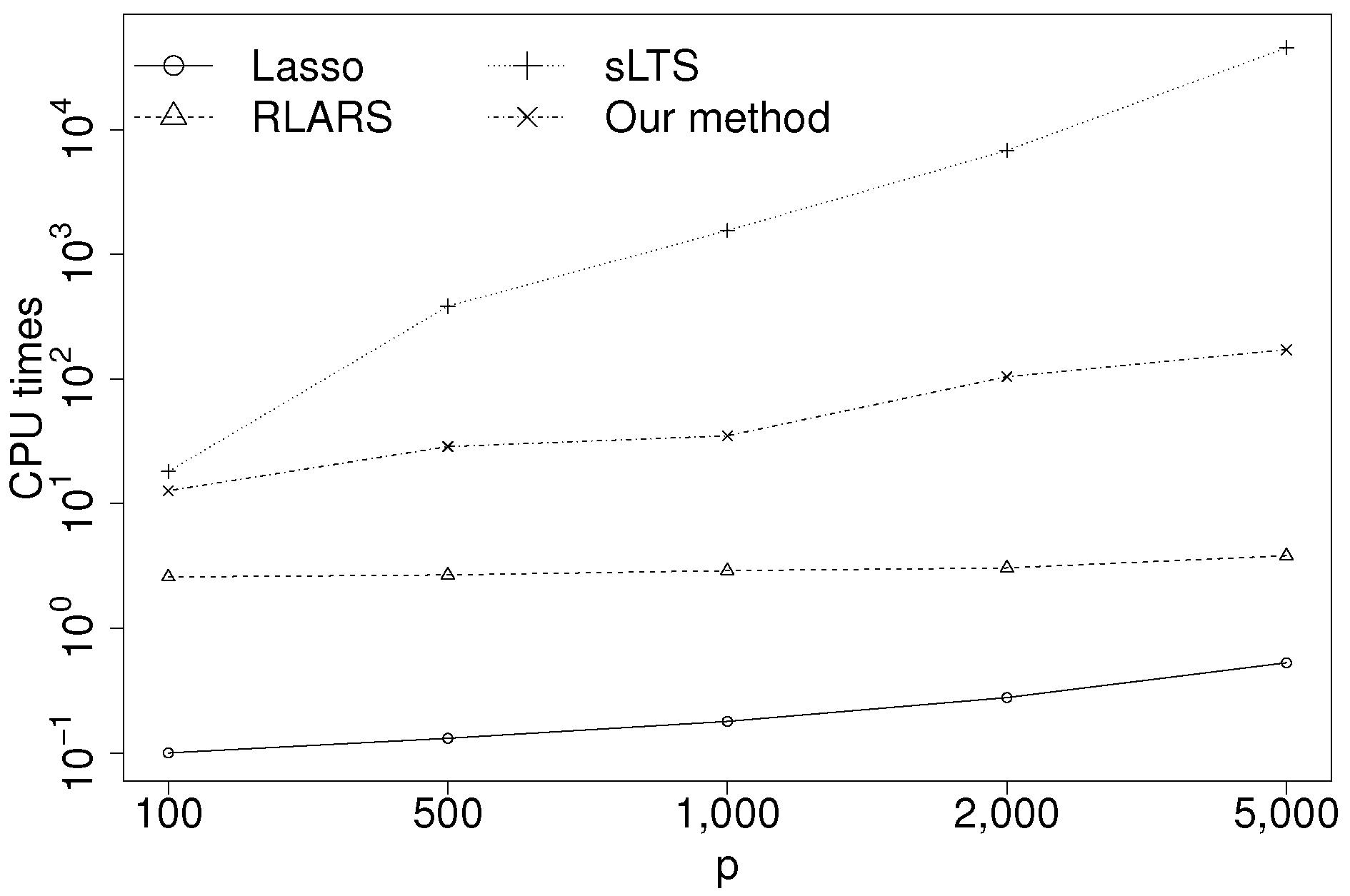
5.6. Computational Cost
6. Real Data Analyses
6.1. NCI-60 Cancer Cell Panel
6.2. Protein Homology Dataset
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar]
- Khan, J.A.; Van Aelst, S.; Zamar, R.H. Robust linear model selection based on least angle regression. J. Am. Stat. Assoc. 2007, 102, 1289–1299. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar]
- Alfons, A.; Croux, C.; Gelper, S. Sparse least trimmed squares regression for analyzing high-dimensional large data sets. Ann. Appl. Stat. 2013, 7, 226–248. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Least Median of Squares Regression. J. Am. Stat. Assoc. 1984, 79, 871–880. [Google Scholar] [CrossRef]
- Windham, M.P. Robustifying model fitting. J. R. Stat. Soc. Ser. B 1995, 57, 599–609. [Google Scholar]
- Basu, A.; Harris, I.R.; Hjort, N.L.; Jones, M.C. Robust and efficient estimation by minimising a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef]
- Jones, M.C.; Hjort, N.L.; Harris, I.R.; Basu, A. A Comparison of related density-based minimum divergence estimators. Biometrika 2001, 88, 865–873. [Google Scholar] [CrossRef]
- Fujisawa, H.; Eguchi, S. Robust Parameter Estimation with a Small Bias Against Heavy Contamination. J. Multivar. Anal. 2008, 99, 2053–2081. [Google Scholar] [CrossRef]
- Basu, A.; Shioya, H.; Park, C. Statistical Inference: The Minimum Distance Approach; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Kanamori, T.; Fujisawa, H. Robust estimation under heavy contamination using unnormalized models. Biometrika 2015, 102, 559–572. [Google Scholar] [CrossRef]
- Cichocki, A.; Cruces, S.; Amari, S.I. Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization. Entropy 2011, 13, 134–170. [Google Scholar] [CrossRef]
- Samek, W.; Blythe, D.; Müller, K.R.; Kawanabe, M. Robust Spatial Filtering with Beta Divergence. In Advances in Neural Information Processing Systems 26; Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; pp. 1007–1015. [Google Scholar]
- Hunter, D.R.; Lange, K. A tutorial on MM algorithms. Am. Stat. 2004, 58, 30–37. [Google Scholar] [CrossRef]
- Hirose, K.; Fujisawa, H. Robust sparse Gaussian graphical modeling. J. Multivar. Anal. 2017, 161, 172–190. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the Elastic Net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Höfling, H.; Tibshirani, R. Pathwise coordinate optimization. Ann. Appl. Stat. 2007, 1, 302–332. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction; Springer: New York, NY, USA, 2010. [Google Scholar]
- Maronna, R.A.; Martin, D.R.; Yohai, V.J. Robust Statistics: Theory and Methods; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef]
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 3.04 | 9.72 | 0.936 | 0.909 | 3.1 | 1.05 | 0.952 | 0.918 |
| RLARS | 0.806 | 6.46 | 0.936 | 0.949 | 0.718 | 6.7 | 0.944 | 0.962 |
| sLTS (, 80 grids) | 0.626 | 1.34 | 1.0 | 0.964 | 0.599 | 1.05 | 1.0 | 0.966 |
| sLTS (, 80 grids) | 0.651 | 1.71 | 1.0 | 0.961 | 0.623 | 1.33 | 1.0 | 0.961 |
| sLTS (, 80 grids) | 0.685 | 2.31 | 1.0 | 0.957 | 0.668 | 1.76 | 1.0 | 0.961 |
| sparse -linear reg ( = 0.1) | 0.557 | 6.71 | 1.0 | 0.966 | 0.561 | 6.99 | 1.0 | 0.965 |
| sparse -linear reg ( = 0.5) | 0.575 | 8.25 | 1.0 | 0.961 | 0.573 | 9.05 | 1.0 | 0.959 |
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 3.55 | 6.28 | 0.904 | 0.956 | 3.37 | 6.08 | 0.928 | 0.961 |
| RLARS | 0.88 | 3.8 | 0.904 | 0.977 | 0.843 | 4.46 | 0.9 | 0.986 |
| sLTS (, 80 grids) | 0.631 | 7.48 | 1.0 | 0.972 | 0.614 | 5.77 | 1.0 | 0.976 |
| sLTS (, 80 grids) | 0.677 | 1.03 | 1.0 | 0.966 | 0.632 | 7.08 | 1.0 | 0.973 |
| sLTS (, 80 grids) | 0.823 | 2.34 | 0.998 | 0.96 | 0.7 | 1.25 | 1.0 | 0.967 |
| sparse -linear reg () | 0.58 | 4.19 | 1.0 | 0.981 | 0.557 | 3.71 | 1.0 | 0.977 |
| sparse -linear reg () | 0.589 | 5.15 | 1.0 | 0.979 | 0.586 | 5.13 | 1.0 | 0.977 |
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 8.07 | 6.72 | 0.806 | 0.903 | 8.1 | 3.32 | 0.8 | 0.952 |
| RLARS | 2.65 | 1.54 | 0.75 | 0.963 | 2.09 | 1.17 | 0.812 | 0.966 |
| sLTS (, 80 grids) | 10.4 | 2.08 | 0.886 | 0.709 | 11.7 | 2.36 | 0.854 | 0.67 |
| sLTS (, 80 grids) | 2.12 | 3.66 | 0.972 | 0.899 | 2.89 | 5.13 | 0.966 | 0.887 |
| sLTS (, 80 grids) | 1.37 | 1.46 | 0.984 | 0.896 | 1.53 | 1.97 | 0.976 | 0.909 |
| sparse -linear reg ( = 0.1) | 1.13 | 9.16 | 0.964 | 0.97 | 0.961 | 5.38 | 0.982 | 0.977 |
| sparse -linear reg ( = 0.5) | 1.28 | 1.5 | 0.986 | 0.952 | 1.00 | 8.48 | 0.988 | 0.958 |
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 8.11 | 3.4 | 0.77 | 0.951 | 8.02 | 6.51 | 0.81 | 0.91 |
| RLARS | 3.6 | 1.7 | 0.71 | 0.978 | 2.67 | 1.02 | 0.76 | 0.984 |
| sLTS (, 80 grids) | 11.5 | 1.16 | 0.738 | 0.809 | 11.9 | 1.17 | 0.78 | 0.811 |
| sLTS (, 80 grids) | 3.34 | 3.01 | 0.94 | 0.929 | 4.22 | 4.08 | 0.928 | 0.924 |
| sLTS (, 80 grids) | 4.02 | 3.33 | 0.892 | 0.903 | 4.94 | 4.44 | 0.842 | 0.909 |
| sparse -linear reg () | 2.03 | 1.45 | 0.964 | 0.924 | 3.2 | 2.86 | 0.94 | 0.936 |
| sparse -linear reg () | 1.23 | 7.69 | 0.988 | 0.942 | 3.13 | 2.98 | 0.944 | 0.94 |
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 2.48 | 5.31 | 0.982 | 0.518 | 2.84 | 5.91 | 0.98 | 0.565 |
| RLARS | 0.85 | 6.58 | 0.93 | 0.827 | 0.829 | 7.97 | 0.91 | 0.885 |
| sLTS (, 80 grids) | 0.734 | 5.21 | 0.998 | 0.964 | 0.684 | 3.76 | 1.0 | 0.961 |
| sLTS (, 80 grids) | 0.66 | 1.78 | 1.0 | 0.975 | 0.648 | 1.59 | 1.0 | 0.961 |
| sLTS (, 80 grids) | 0.734 | 2.9 | 1.0 | 0.96 | 0.66 | 1.74 | 1.0 | 0.962 |
| sparse -linear reg ( = 0.1) | 0.577 | 8.54 | 1.0 | 0.894 | 0.545 | 5.44 | 1.0 | 0.975 |
| sparse -linear reg ( = 0.5) | 0.581 | 7.96 | 1.0 | 0.971 | 0.546 | 5.95 | 1.0 | 0.977 |
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 2.39 | 2.57 | 0.988 | 0.696 | 2.57 | 2.54 | 0.944 | 0.706 |
| RLARS | 1.01 | 5.44 | 0.896 | 0.923 | 0.877 | 4.82 | 0.898 | 0.94 |
| sLTS (, 80 grids) | 0.708 | 1.91 | 1.0 | 0.975 | 0.790 | 3.40 | 0.994 | 0.97 |
| sLTS (, 80 grids) | 0.683 | 1.06 | 1.0 | 0.975 | 0.635 | 7.40 | 1.0 | 0.977 |
| sLTS (, 80 grids) | 1.11 | 1.13 | 0.984 | 0.956 | 0.768 | 2.60 | 0.998 | 0.968 |
| sparse -linear reg () | 0.603 | 5.71 | 1.0 | 0.924 | 0.563 | 3.78 | 1.0 | 0.979 |
| sparse -linear reg () | 0.592 | 5.04 | 1.0 | 0.982 | 0.566 | 4.05 | 1.0 | 0.981 |
| , , | , , | |||||||
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 2.81 | 6.88 | 0.956 | 0.567 | 3.13 | 7.11 | 0.97 | 0.584 |
| RLARS | 2.70 | 7.69 | 0.872 | 0.789 | 2.22 | 6.1 | 0.852 | 0.855 |
| sLTS (, 80 grids) | 3.99 | 1.57 | 0.856 | 0.757 | 4.18 | 1.54 | 0.878 | 0.771 |
| sLTS (, 80 grids) | 3.2 | 1.46 | 0.888 | 0.854 | 2.69 | 1.08 | 0.922 | 0.867 |
| sLTS (, 80 grids) | 6.51 | 4.62 | 0.77 | 0.772 | 7.14 | 5.11 | 0.844 | 0.778 |
| sparse -linear reg ( = 0.1) | 1.75 | 3.89 | 0.974 | 0.725 | 1.47 | 2.66 | 0.976 | 0.865 |
| sparse -linear reg ( = 0.5) | 1.68 | 3.44 | 0.98 | 0.782 | 1.65 | 3.58 | 0.974 | 0.863 |
| , , | , , | |||||||
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 2.71 | 3.32 | 0.964 | 0.734 | 2.86 | 3.05 | 0.974 | 0.728 |
| RLARS | 3.03 | 4.59 | 0.844 | 0.876 | 2.85 | 4.33 | 0.862 | 0.896 |
| sLTS (, 80 grids) | 3.73 | 7.95 | 0.864 | 0.872 | 4.20 | 8.17 | 0.878 | 0.87 |
| sLTS (, 80 grids) | 4.45 | 1.23 | 0.85 | 0.886 | 3.61 | 8.95 | 0.904 | 0.908 |
| sLTS (, 80 grids) | 9.05 | 4.24 | 0.66 | 0.853 | 8.63 | 3.73 | 0.748 | 0.864 |
| sparse -linear reg () | 1.78 | 1.62 | 0.994 | 0.731 | 1.82 | 1.62 | 0.988 | 0.844 |
| sparse -linear reg () | 1.79 | 1.69 | 0.988 | 0.79 | 1.77 | 1.51 | 0.996 | 0.77 |
| , , | , , | |||||||
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 0.621 | 1.34 | 1.0 | 0.987 | 0.621 | 1.12 | 1.0 | 0.987 |
| RLARS | 0.551 | 7.15 | 0.996 | 0.969 | 0.543 | 6.74 | 0.996 | 0.971 |
| sLTS (, 40 grids) | 0.954 | 4.47 | 1.0 | 0.996 | 0.899 | 4.53 | 1.0 | 0.993 |
| sparse -linear reg ( = 0.1) | 0.564 | 7.27 | 1.0 | 0.878 | 0.565 | 6.59 | 1.0 | 0.908 |
| sparse -linear reg ( = 0.5) | 0.59 | 1.0 | 1.0 | 0.923 | 0.584 | 8.47 | 1.0 | 0.94 |
| , , | , , | |||||||
| Methods | RMSPE | MSE | TPR | TNR | RMSPE | MSE | TPR | TNR |
| Lasso | 0.635 | 7.18 | 1.0 | 0.992 | 0.624 | 6.17 | 1.0 | 0.991 |
| RLARS | 0.55 | 3.63 | 0.994 | 0.983 | 0.544 | 3.48 | 0.996 | 0.985 |
| sLTS (, 40 grids) | 1.01 | 3.76 | 1.0 | 0.996 | 0.909 | 2.47 | 1.0 | 0.996 |
| sparse -linear reg () | 0.584 | 4.45 | 1.0 | 0.935 | 0.573 | 3.99 | 1.0 | 0.938 |
| sparse -linear reg () | 0.621 | 6.55 | 1.0 | 0.967 | 0.602 | 5.58 | 1.0 | 0.966 |
| Methods | RTMSPE | Selected Variables |
|---|---|---|
| Lasso | 1.058 | 52 |
| RLARS | 0.936 | 18 |
| sLTS | 0.721 | 33 |
| Our method () | 0.679 | 29 |
| Our method () | 0.700 | 30 |
| Trimming Fraction | ||||
|---|---|---|---|---|
| Methods | 1% | 5% | 10% | Selected Variables |
| Lasso | 10.697 | 9.66 | 8.729 | 22 |
| RLARS | 10.473 | 9.435 | 8.527 | 27 |
| sLTS | 10.614 | 9.52 | 8.575 | 21 |
| Our method () | 10.461 | 9.403 | 8.481 | 44 |
| Our method () | 10.463 | 9.369 | 8.419 | 42 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawashima, T.; Fujisawa, H. Robust and Sparse Regression via γ-Divergence. Entropy 2017, 19, 608. https://doi.org/10.3390/e19110608
Kawashima T, Fujisawa H. Robust and Sparse Regression via γ-Divergence. Entropy. 2017; 19(11):608. https://doi.org/10.3390/e19110608
Chicago/Turabian StyleKawashima, Takayuki, and Hironori Fujisawa. 2017. "Robust and Sparse Regression via γ-Divergence" Entropy 19, no. 11: 608. https://doi.org/10.3390/e19110608
APA StyleKawashima, T., & Fujisawa, H. (2017). Robust and Sparse Regression via γ-Divergence. Entropy, 19(11), 608. https://doi.org/10.3390/e19110608




