Abstract
The aim of this paper is to show that the Tsallis-type (q-additive) entropic chain rule allows for a wider class of entropic functionals than previously thought. In particular, we point out that the ensuing entropy solutions (e.g., Tsallis entropy) can be determined uniquely only when one fixes the prescription for handling conditional entropies. By using the concept of Kolmogorov–Nagumo quasi-linear means, we prove this with the help of Darótzy’s mapping theorem. Our point is further illustrated with a number of explicit examples. Other salient issues, such as connections of conditional entropies with the de Finetti–Kolmogorov theorem for escort distributions and with Landsberg’s classification of non-extensive thermodynamic systems are also briefly discussed.
1. Introduction
During the last two decades, complex dynamical systems have undergone an important conceptual shift. The catalyst was the infusion of new ideas from the theory of critical phenomena (scaling laws), (multi-)fractals and trees, the renormalization group, random matrix theory and information theory. On the other hand, the usual Boltzmann–Gibbs statistics, while successful in describing stationary systems characterized by ergodicity or metric transitivity, fails to reproduce the statistical behavior of many real-world complex systems in biology, astrophysics, geology and economic and social sciences. In recent years, the use of a new paradigm known as generalized statistics has become very popular in complex systems. The notion “generalized statistics” refers to statistical systems that are described via broad, (semi-)heavy-tailed distributions. Examples include generalized hyperbolic distributions, Meixner distributions, Weibull distributions and various power-law tail distributions (e.g., Zipf–Pareto, Lévy or Tsallis-type distributions). In particular, the statistics associated with power-law tails accounts for a rich class of phenomena observed in many real-world systems ranging from financial markets, physics and biology to geoscience (see, e.g., [1,2] and the citations therein).
Currently, there is a number of key techniques for dealing with generalized-statistics-based complex systems. Among these one can especially mention: (a) innate general statistics approaches such as the q-deformed thermostatistics of Tsallis [1], the superstatistics of Beck et al. [3] and various generalized non-extensive entropies [4,5,6,7,8]; (b) information-theoretic concepts such as the information theory of Rényi [9,10], transfer entropies [11,12], complexity theory [1,13] or information geometry [14]. Particularly the concept of entropy, both in its information-theoretic and combinatorial disguise, plays a central role here. It is, however, clear that entropy can provide meaningful and technically-sound modus operandi only if there is a good guiding principle behind its formulation. Admittedly, from a mathematical point of view, the most satisfactory prescriptions are based on axiomatization of entropy or, preferably, on some operationally-viable coding theorem.
In the present paper, we focus on the axiomatic underpinning of pseudo-additive entropies that are currently being actively investigated in the context of non-equilibrium statistical physics and information theory (both classical and quantum) [1,2,15,16]. Among pseudo-additive entropies, we select and put under a deeper scrutiny a subclass of the so-called q-additive entropies. In this framework, we show that commonly-used axioms for q-additive entropies are prone to have multiplicity of distinct solutions with a common cause residing in the way that conditional entropies are handled. To do so, we extend arguments from [17] and demonstrate that the existence of different solutions is related to the Kolmogorov–Nagumo quasi-linear means and Darótzy’s mapping theorem. This formal side of our exposition is further bolstered by a number of explicit examples of entropic functionals that all satisfy the same q-additive entropic chain rules.
The structure of the paper is as follows. After this Introduction, we present in Section 2 a concise overview of some standard (pseudo-)additive entropic rules, which yield degenerate solutions for entropic functionals. This will be important in Section 3 where the same phenomenon will be observed in the context of entropic chain rules. Despite their higher restrictiveness, the chain rules still lead to degenerate solutions, and this fact is present even in the (more sophisticated) q-additive entropic chain rules as demonstrated in Section 4. In Section 5, we identify the root cause of this situation in the way that conditional entropies are handled. In particular, with the help of Darótzy’s mapping, we prove that any potential degeneracy at the level of additive entropic rules is automatically reflected also at the level of q-additivity. Additionally, we show that the analogous situation holds between normal and q-additive entropic chain rules whenever conditional entropies involved are defined via the Kolmogorov–Nagumo quasi-linear means. We close Section 5 by proving the de Finetti–Kolmogorov theorem for escort distributions. This allows demonstrating how more restrictive the q-additive entropic chain rules are in comparison with simple q-additive rules. Finally, Section 6 summarizes our results and discusses some further consequences.
2. Entropic (Pseudo-)Additivity Rules
2.1. Some (Pseudo-)Additivity Rules
Suppose X and Y are two events, e.g., messages, having and as the possible number of states, respectively. The two events taken together form a joint event that we denote as . If X and Y are independent of each other, every combination of X and Y’s values is a possible joint event, and so, . In this case, the entropy for a composite bipartite system , the joint entropy , is additive, i.e.,
On the other hand, if the events are not independent (and do not interact), it may be that some combinations of X and Y are not allowed (i.e., ), so that the joint entropy may be less than , a property known as the subadditivity of the entropy. This would mean that a system increases its entropy by splitting up into separate systems. This so-called fragmentation is typical, e.g., in entangled quantum systems [18]. We will have more to say about this in Section 5.
In practice, the entropy behavior in a number of independent bipartite systems cannot be easily grasped via simple additivity prescription (1). The reasons behind this might be the fact that some marginal states (e.g., surface states) are neglected or that the long-range correlations are invalidating the assumption of independence, and the concept of independence is used only as a convenient approximation. Whatever the reason, the modus operandi in these cases is to resort to some simple one-parameter deformation of the additivity rule that grasps in one way or another the non-additive contributions. Such deformations are known as pseudo-additive entropic forms. The most commonly-used versions are; Tsallis-type additivity [1]:
Landsberg-type additivity [19]:
-additivity [1,20] (used, e.g., in anti-de Sitter/conformal field theory (AdS/CFT) correspondence):
Masi–Czachor-type supra-additivity [21], etc.
Let us point out that it might happen that the above (pseudo-)additivity rules hold also for more generic joint systems for which . In such cases, one speaks about (pseudo-)extensivity [6]. Since the (pseudo-)extensivity is more a characteristic property of the actual interaction/correlation between X and Y rather than entropy itself, we shall not dwell on this issue here. Let us just mention that the actual form of non-extensivity and the value of parameters can be often connected to some specific physical phenomena [8,22]. In Section 3, we will see that, from a strictly mathematical standpoint, it is logically more satisfactory to deal with dependent, but non-interacting systems. In such cases, the above (pseudo-)additivity rules will be replaced with more restrictive entropy chain rules.
2.2. Degeneracy in Solutions
It is well known that there is a number of “logically consistent”, but form-inequivalent entropic functionals satisfying the simple additivity rule (1). Examples are provided by Shannon entropy (and ensuing Gibbs and von Neumann entropies) or Rényi entropy. In this connection, we should emphasize perhaps a less known fact that a similar situation holds also for pseudo-additivity. For instance, by assuming that with X is associated probability , then the Tsallis-type pseudo-additivity rule (2) is not only satisfied with Tsallis entropy:
as one would expect, but also with Landsberg’s entropy [19]:
or with Behara–Chawla -entropy [23]:
On the same footing, one may show that the (AdS/CFT) -additivity is satisfied with a class of the so-called Segal entropies [24]. Let us finally stress that the actual range of admissible q’s in (5)–(7) could be restricted by imposing some further conditions (going beyond Tsallis-type additivity rule), e.g., expansibility, concavity [1], Schur concavity [25], Lesche stability [26], robustness [27], etc. Here, we shall not dwell on this issue.
2.3. Uniqueness Issue: Part I
At this stage, there are two points that should be noted. First, the above (pseudo-)additive forms (1)–(4) are true only for independent events. Second, one could entertain the idea that when the entropic chain rules (which employ also the conditional entropy ) are used instead, then their higher restrictiveness could remove the unwanted degeneracy and lead to a single unique solution. This might seem as a good strategy particularly because the entropic chain rule with ensuing is of practical relevance in a number of areas. In this connection, one can mention applications in:
- information theory, where it describes input-output information of the (quantum) communication channel and enters in the data processing inequality [28],
- non-equilibrium and complex dynamics, where it enters in the May–Wigner criterion for the stability of dynamical systems and helps to estimate the connectivity of the network of system exchanges [29],
- time series and data analysis, where it describes transfer entropies in bivariate time series and the degree of synchronization between two signals [12].
In the following two sections, we will see what the entropic chain rules and their pseudo-additive extensions can really say about the uniqueness of entropic functionals.
3. Entropic Chain Rule
Additive Entropic Chain Rule: Some Fundamentals
Let us consider two generally dependent events. The elementary (Shannon-type) entropic chain rule for ensuing random events X and Y reads:
where is a single-random event entropy, is joint entropy and represents the related conditional entropy of Y given X. The meaning of the chain rule (8) is depicted in Figure 1.
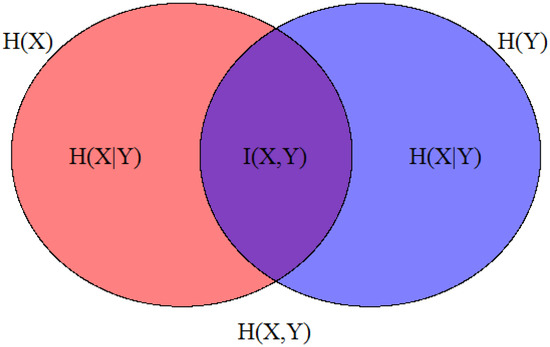
Figure 1.
Entropy Venn diagram for two random events. The symbol denotes the mutual information, i.e., .
By induction, one can generalize the previous relation (8) to:
At this stage, we can ask ourselves the following question. By imposing simple consistency conditions, such as:
- continuity, i.e., when is a continuous function of all arguments,
- maximality, i.e., when for given n, is maximal for and
- expansibility, i.e., when ,
to what extent is (with the above chain rule) unique? We might notice in passing that the above consistency conditions are nothing but Kolmogorov Axioms 1–3; see, e.g., [5]. It might perhaps come as a surprise that the uniqueness is not guarantied, at least not unless one prescribes how to handle conditional entropies.
To understand this point better, let us state the basic defining properties of :
- iff Y is completely determined by X, e.g., (g is some function),
- entropic Bayes’ rule,
- “second law of thermodynamics”,
- if Y and X are independent (sometimes “if and only if” is required).
These properties still allow for some additional flexibility. Examples might be provided with Shannon’s solution and Rényi’s solution that both share the same chain condition (9) and the above defining conditions for . In particular, for Shannon’s entropy, the conditional entropy of X given Y is constructed in two steps:
i.e., is defined via the linear mean. In contrast, in the case of Rényi’s entropy, the conditional entropy of X given Y is defined by means of the quasi-linear Kolmogorov–Nagumo (KN) mean [30,31] in the following two-step sequence [32]:
Here, the KN function reads [9,31]:
Particularly noteworthy is the appearance of the so-called escort distribution [32,33]:
in Equation (11). Interestingly, a need for in the definition of was already observed by Rényi in the 1960s [32]; some 30 years before the escort distribution was officially introduced in [33].
4. q-Additive Entropic Chain Rule
Uniqueness Issue: Part II
In analogy with the preceding section, one defines the q-additive entropic chain rule for two random generally dependent events X and Y as:
By induction, one can generalize this to an n-partite system as:
We can ask again a similar question as before, namely: To what extent is (subject to the above chain rule) unique?
As before, we should not be surprised to learn that the uniqueness is not guarantied unless is specified. Indeed, the q-additive entropic chain rule together with consistency conditions:
- iff Y is completely determined by X, e.g., ,
- q-entropic Bayes’ rule (The explicit form of the function depends on the type of q deformation. For instance, for q additivity, we have .),
- “second law of thermodynamics”,
- if Y and X are independent,
are not enough to fix the unique form of . Examples include: (a) Tsallis entropy where the conditional entropy of X given Y is defined as [34]:
i.e., is defined via the linear (escort) mean, (b) Frank–Daffertshofer entropy [35], where the conditional entropy is defined as:
with the KN function , i.e., is obtained via quasi-linear KN mean, (c) Sharma–Mittal entropy [36], where the conditional entropy is given by:
Here, and , i.e., is again defined the via quasi-linear KN mean. For more details on the applications of and , see [35,37,38].
5. Theoretical Justification of Degeneracy
From the previous examples, one may observe that the multiplicity of possible entropic functionals that are compatible with ordinary entropic chain rules and/or q-additive chain rules can be associated (at least in part) with a specific choice of the KN average, which enters the definition of . In this connection, the reader should note that KN averages do not spoil any of the defining properties of listed in Section 3 and Section 4.
The aim of this section is to show that whenever a degeneracy exists at the level of ordinary entropic chain rules (as it always does in accordance with Section 3), then one can systematically generate degeneracy at the level of q-additive chain rules. To this end, we prove the following theorem:
Theorem 1.
Darótzy’s mapping is a monotonic mapping such that:
is parameterized by and γ, so that:
Statement: Let us have the additive chain rule with defined with KN function . Darótzy’s mapping then generates the q-additive chain rule (provided we set ) where new is defined via KN function .
Proof of Theorem 1.
First, proof of the validity of Darótzy’s mapping is by a simple inspection. Second, let us assume that certain entropic functional with defined via some KN function satisfies additive chain rule:
Darótzy’s mapping then ensures that the entropic functional satisfies:
with:
The actual values of a and are immaterial for the q-additivity as the Darótzy mapping generates q-additivity only via parameter . The last line shows that the new conditional entropy is defined via KN function , while the escort parameter r is generally unrelated to q. Consequently, the ensuing q-additive entropy represents a three-parametric functional with parameters , r and q (apart from parameters originating from the KN function ). ☐
The core idea of Theorem 1 can be phrased as follows: if there exist two different entropy functionals for a given additive chain rule with two different KN-related conditional entropies, then one can use Darótzy’s mapping to map these two solutions to another two solutions that solve the q-additive chain rule. Simple examples of this mechanism are provided when we apply Darótzy’s mapping to both Shannon entropy and Rényi entropy. In the first case, we obtain the entropy:
while in the second case we have:
which is nothing but the Tsallis entropy . Both and satisfy the q-additive chain rules provided the corresponding conditional entropies are defined via KN functions and , respectively.
Along the same lines, one can apply two different Darótzy’s mappings to the same seeding entropy to get two distinct solutions for the same q-additive chain rule. For instance, when we apply to Rényi entropy Darótzy’s mappings with , we obtain the Frank–Daffertshofer entropy (17). When , we obtain the Sharma–Mittal entropy (18). For some further details on this issue, see, e.g., [4].
Darótzy’s mapping can also be directly used to generate from (simple) additive entropies new q-additivity entropies. However, many of such newly generated entropic functionals are inconsistent as they do not satisfy the entropy chain rule in the sense that there is no consistent definition of conditional entropy for them. This is the content of our second theorem, which highlights some tricky points related to joint escort distributions.
Theorem 2.
de Finetti–Kolmogorov relation and escort distributions: when working with escort distributions, the joint distributions derived from the original joint distributions do not satisfy the de Finetti–Kolmogorov relation, i.e., the analogue of (here and are marginal and conditional distributions, respectively).
Proof of Theorem 2.
By using the standard de Finetti–Kolmogorov relation for original distributions, i.e., , we may write the following chain of relations:
Here is the correct would-be joint escort distribution. Note that is not the escort of and iff events are independent [17]. ☐
An important upshot of this theorem is that some entropies (particularly those born out of escort distributions) might satisfy simple q-additivity, but not necessarily the q-additive entropic chain rule. The reason is that the more restrictive chain rule is sensitive to the failure of the de Finetti–Kolmogorov relation for joint escort distributions. A typical example is provided by the Jizba–Arimitsu entropy [17,25,39]:
where is the KN function . Because satisfies the simple additivity rule for independent events, Darótzy’s mapping ensures that satisfies the q-additivity. On the other hand, does not satisfy the simple chain rule due to failure of the de Finetti–Kolmogorov relation for joint events. Consequently, is not q-extensive.
In this connection, we might recall Landsberg’s classification of non-extensive thermodynamics. In 1990s P.T. Landsberg classified types of thermodynamics according to all possible functional properties of the entropy [19]. By defining entropy classes:
- Superadditivity, S: ,
- Homogeneity, H: ,
- Concavity, C: .
Landsberg concluded that there are only six logically-consistent thermodynamic classes: , , , , , . Types are are logically impossible [19]; see Figure 2.
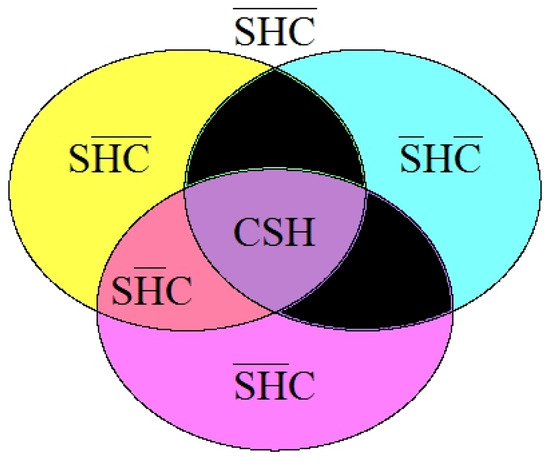
Figure 2.
Venn diagram for Landsberg’s thermodynamic types.
This classification is, however, based entirely on entropies for independent events. Since the entropic (pseudo-)additivity rule and chain rule for a given system do not need to follow the same pattern (e.g., they do not need to be both q-additive), the entropy class might change when conditional probabilities are included. For instance, according to Landsberg, should, for , belong to the class, while the corresponding chain-rule generalization allows for flipping between S and ; see [17].
6. Conclusions
In this paper, we have studied the uniqueness of entropic functionals under their composition laws. We have first recalled a well-known fact that many standard pseudo-additive entropic rules allow for a wide class of distinct entropic functionals. This is, of course, an unpleasant feature as the entropy should be (within a prescribed operational or axiomatic framework) a unique quantifier of ignorance, chaoticity, entanglement, etc. Since pseudo-additive laws employ only independent events, one might hope that the use of entropic chain rules (which deal also with dependent events) would restrict, or potentially even eliminate, the unwanted degeneracy. Here, we have specifically concentrated on a sub-class of pseudo-additive rules, the so-called q-additive entropic chain rules, and have shown that though some entropy functionals indeed cease to exist in this restrictive framework, one still finds degeneracy. The root cause behind this can be traced down to the way that a conditional entropy is handled. There is, in fact, a flexibility in the definition of permissible ’s. We have shown how such permissible ’s for any desired q-additive entropic chain rule can be systematically generated with the help of KN quasi-linear means and Darótzy’s mapping theorem. This formal side of our exposition was further bolstered by a number of explicit examples of entropic functionals that all satisfy the same q-additive entropic chain rules.
In view of the results obtained, the natural question presents itself: What is a defining property of the currently popular concept of non-extensive statistics [1]? Is it, (a) pseudo-additivity (as indicated by Landsberg’s classification), (b) the pseudo-additive chain rule (with generalized conditional entropies) or (c) power-law-type entropy maximizers. This question still awaits a satisfactory answer.
Acknowledgments
Both P.J.and J.K. were supported by the Czech Science Foundation Grant No. 17-33812L. J.K. was also supported by the Austrian Science Fund, Grant No. I 3073-N32.
Author Contributions
Both P.J. and J.K. participated equally on theoretical calculations and on the writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviation is used in this manuscript:
| KN | Kolmogorov–Nagumo |
References
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Naudts, J. Generalised Thermostatistics; Springer: London, UK, 2011. [Google Scholar]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Karmeshu, J. (Ed.) Entropy Measures, Maximum Entropy Principle and Emerging Applications; Springer: Berlin, Germany, 2003. [Google Scholar]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. EPL Europhys. Lett. 2011, 93, 50006-p1–50006-p6. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. When do generalized entropies apply? How phase space volume determines entropy. EPL Europhys. Lett. 2011, 96, 50003-p1–50005-p6. [Google Scholar] [CrossRef]
- Tempesta, P. Group entropies, correlation laws, and zeta functions. Phys. Rev. E 2011, 84, 021121-1–021121-10. [Google Scholar] [CrossRef] [PubMed]
- Biró, T.; Barnaföldi, G.; Ván, P. New entropy formula with fluctuating reservoir. Phys. A 2015, 417, 215–220. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. The world according to Rényi: Thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]
- Jizba, P.; Ma, Y.; Hayes, A.; Dunningham, J. One-parameter class of uncertainty relations based on entropy power. Phys. Rev. E 2016, 93, 060104(R)-1–060104(R)-5. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Jizba, P.; Kleinert, H.; Shefaat, M. Rényi’s information transfer between financial time series. Phys. A 2012, 391, 2971–2989. [Google Scholar] [CrossRef]
- Eom, Y.-H.; Jo, H.-H. Using friends to estimate heavy tails of degree distributions in large-scale complex networks. Sci. Rep. 2015, 5, 09752-1–09752-9. [Google Scholar] [CrossRef] [PubMed]
- Bercher, J.-F. Some properties of generalized Fisher information in the context of nonextensive thermostatistics. Phys. A 2013, 392, 3140–3154. [Google Scholar] [CrossRef]
- Short, A.J.; Wehner, S. Entropy in general physical theories. New J. Phys. 2010, 12, 033023. [Google Scholar] [CrossRef]
- Majhi, A. Non-extensive statistical mechanics and black hole entropy from quantum geometry. arXiv, 2017; arXiv:1703.09355. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. Remarks on “Comments on ’On q-non-extensive statistics with non-Tsallisian entropy” [Physica A 466 (2017) 160]. Phys. A 2017, 468, 238–243. [Google Scholar] [CrossRef]
- Schumacher, B.; Westmoreland, M. Quantum Processes, Systems, and Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Landsberg, P.T. Entropies Galore! Braz. J. Phys. 1999, 29, 46–49. [Google Scholar] [CrossRef]
- Vos, G. Generalized additivity in unitary conformal field theories. Nucl. Phys. B 2015, 899, 91–111. [Google Scholar] [CrossRef]
- Masi, M. A step beyond Tsallis and Renyi entropies. Phys. Lett. A 2005, 338, 217–224. [Google Scholar] [CrossRef]
- Korbel, J. Rescaling the nonadditivity parameter in Tsallis thermostatistics. Phys. Lett. A 2017, 381, 2588–2592. [Google Scholar] [CrossRef]
- Behara, M.; Chawla, J.S. Generalized gamma entropy. Sel. Stat. Can. 1974, 2, 15–38. [Google Scholar]
- Ochs, W.; Spohn, H.A. Characterization of the Segal entropy. Rep. Math. Phys. 1978, 14, 75–87. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. On q-non-extensive statistics with non-Tsallisian entropy. Phys. A 2016, 444, 808–827. [Google Scholar] [CrossRef]
- Lesche, B. Instabilities of Rényi entropies. J. Stat. Phys. 1982, 27, 419–422. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S.; Tsallis, C. On the robustness of q-expectation values and Rényi entropy. EPL Europhys. Lett. 2009, 85, 20005-p1–20005-p6. [Google Scholar] [CrossRef]
- Campbell, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Hastings, H.M. The May-Wigner stability theorem. J. Theor. Biol. 1982, 97, 155–166. [Google Scholar] [CrossRef]
- Nagumo, M. Über eine Classe der Mittelwerte. Jpn. J. Math. 1930, 7, 71–79. [Google Scholar] [CrossRef]
- Aczél, J. Lectures on Functional Equations an dtheir Applications; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Rényi, A. Selected Papers of Alfred Rényi; Akademia Kiado: Budapest, Hungary, 1976. [Google Scholar]
- Beck, C.; Schlögl, F. Thermodynamics of Chaotic Systems: An Introduction; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Abe, S. Axioms and uniqueness theorem for Tsallis entropy. Phys. Lett. A 2000, 271, 74–79. [Google Scholar] [CrossRef]
- Frank, T.D.; Daffertshofer, A. Exact time-dependent solutions of the Renyi Fokker-Planck equation and the Fokker-Planck equations related to the entropies proposed by Sharma and Mittal. Phys. A 2000, 285, 351–366. [Google Scholar] [CrossRef]
- Sharma, B.D.; Mittal, D.P. New non-additive measures of entropy for discrete probability distributions. J. Math. Sci. 1975, 10, 28–40. [Google Scholar]
- Aktürk, O.Ü.; Aktürk, E.; Tomak, M. Can Sobolev inequality be written for Sharma-Mittal entropy? Int. J. Theor. Phys. 2008, 47, 3310–3320. [Google Scholar] [CrossRef]
- Kosztołowicz, T.; Lewandowska, K.D. First-passage time for subd-diffusion: The nonadditive entropy approach versus the fractional model. Phys. Rev. E 2012, 86, 021108-1–021108-11. [Google Scholar] [CrossRef] [PubMed]
- Çankaya, M.N.; Korbel, J. On statistical properties of Jizba–Arimitsu hybrid entropy. Phys. A 2017, 474, 1–10. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).