Kovacs-Like Memory Effect in Athermal Systems: Linear Response Analysis
Abstract
:1. Introduction
2. Linear Theory for Kovacs-Like Memory Effects
2.1. General Markovian Dynamics
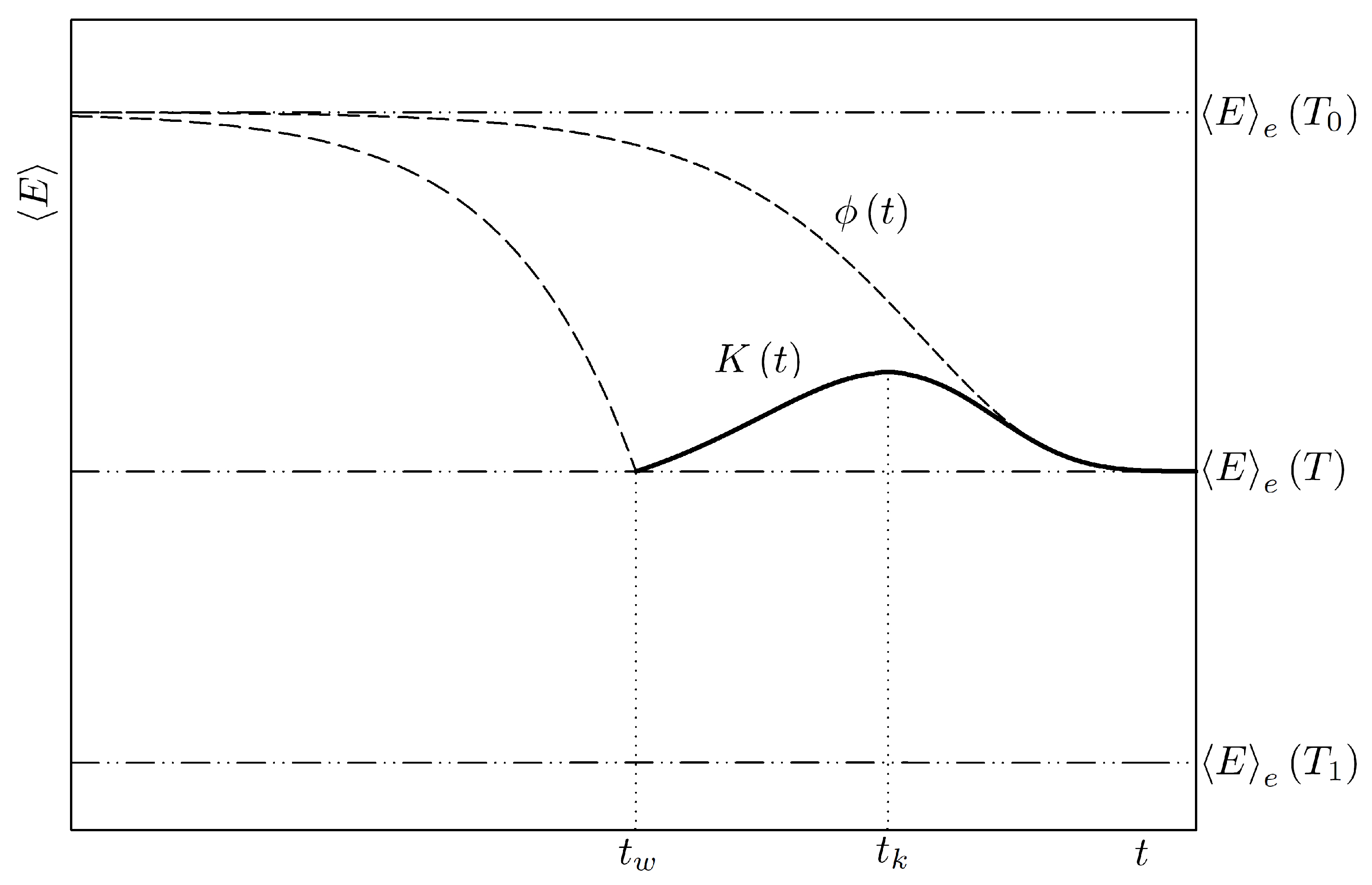
2.2. The Kovacs Protocol: Linear Response Analysis from the Master Equation
2.3. Linear Response from the Equations for the Moments
3. A Lattice Model with Conserved Momentum and Non-Conserved Energy
3.1. Definition of the Model: Kinetic Description
3.2. First Sonine Approximation
3.3. Kovacs Hump in Linear Response
3.4. Nonlinear Kovacs Hump
4. Numerical Results
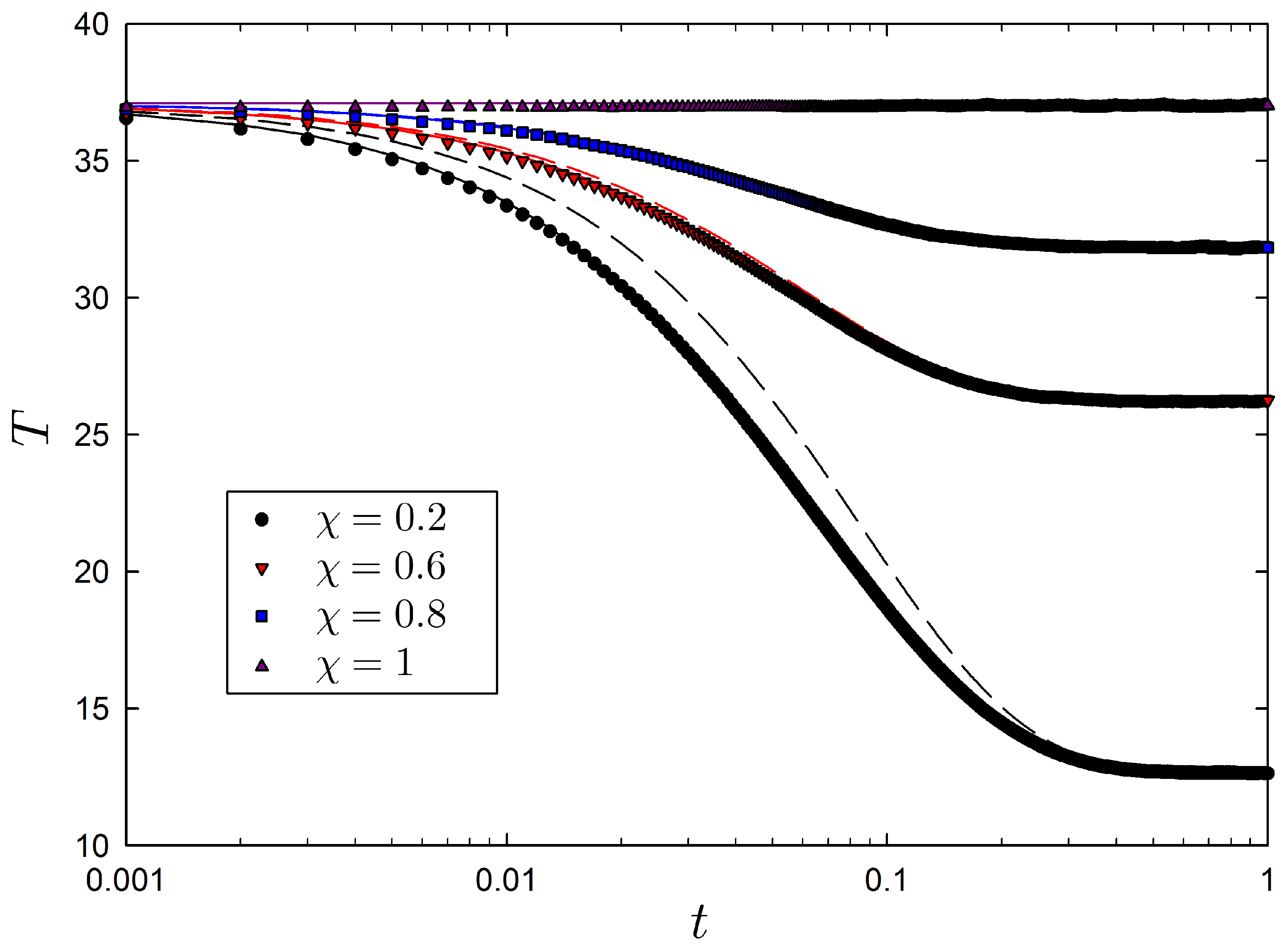
4.1. Validation of the Evolution Equations and Linear Relaxation
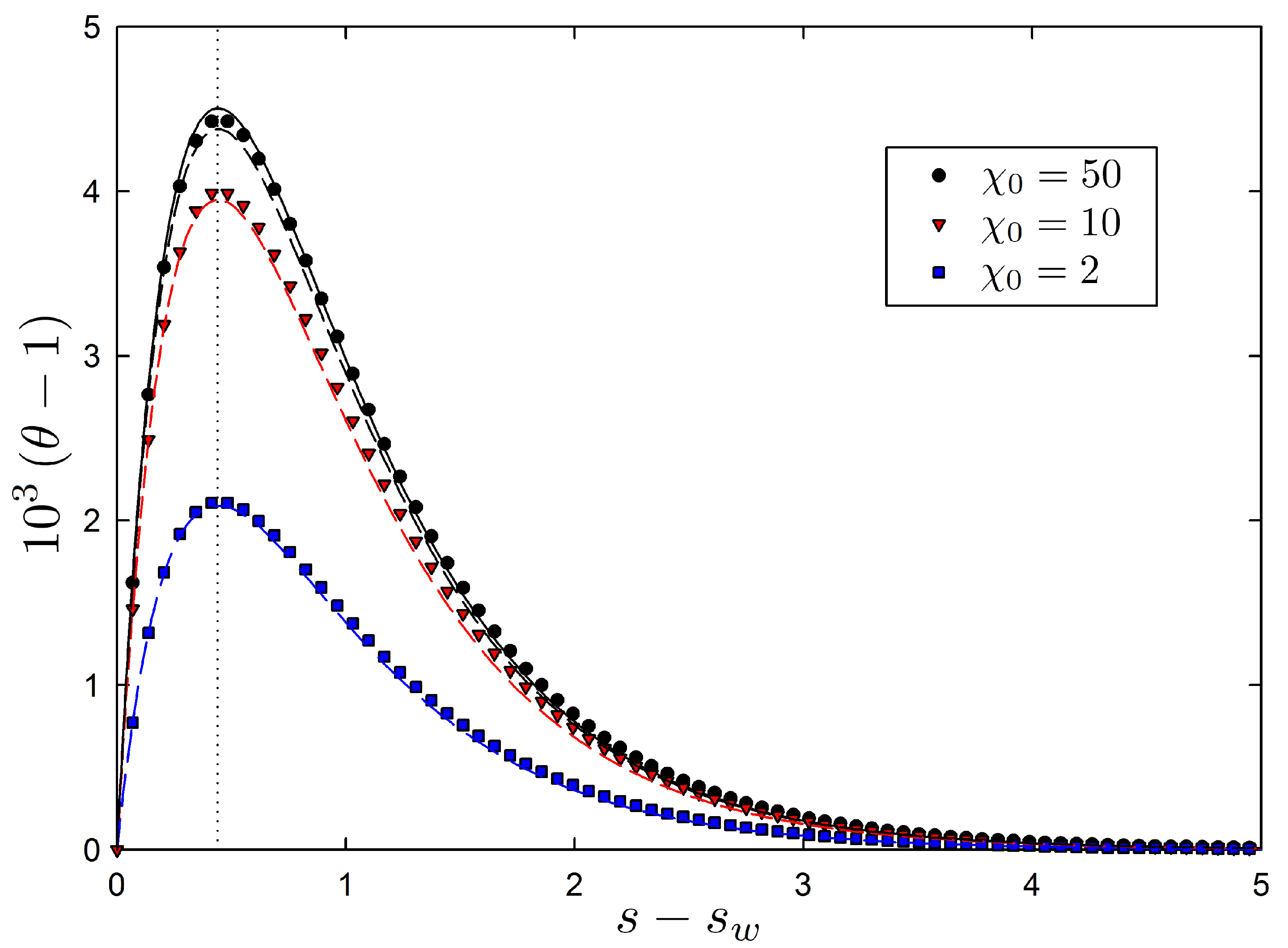
4.2. Kovacs Hump
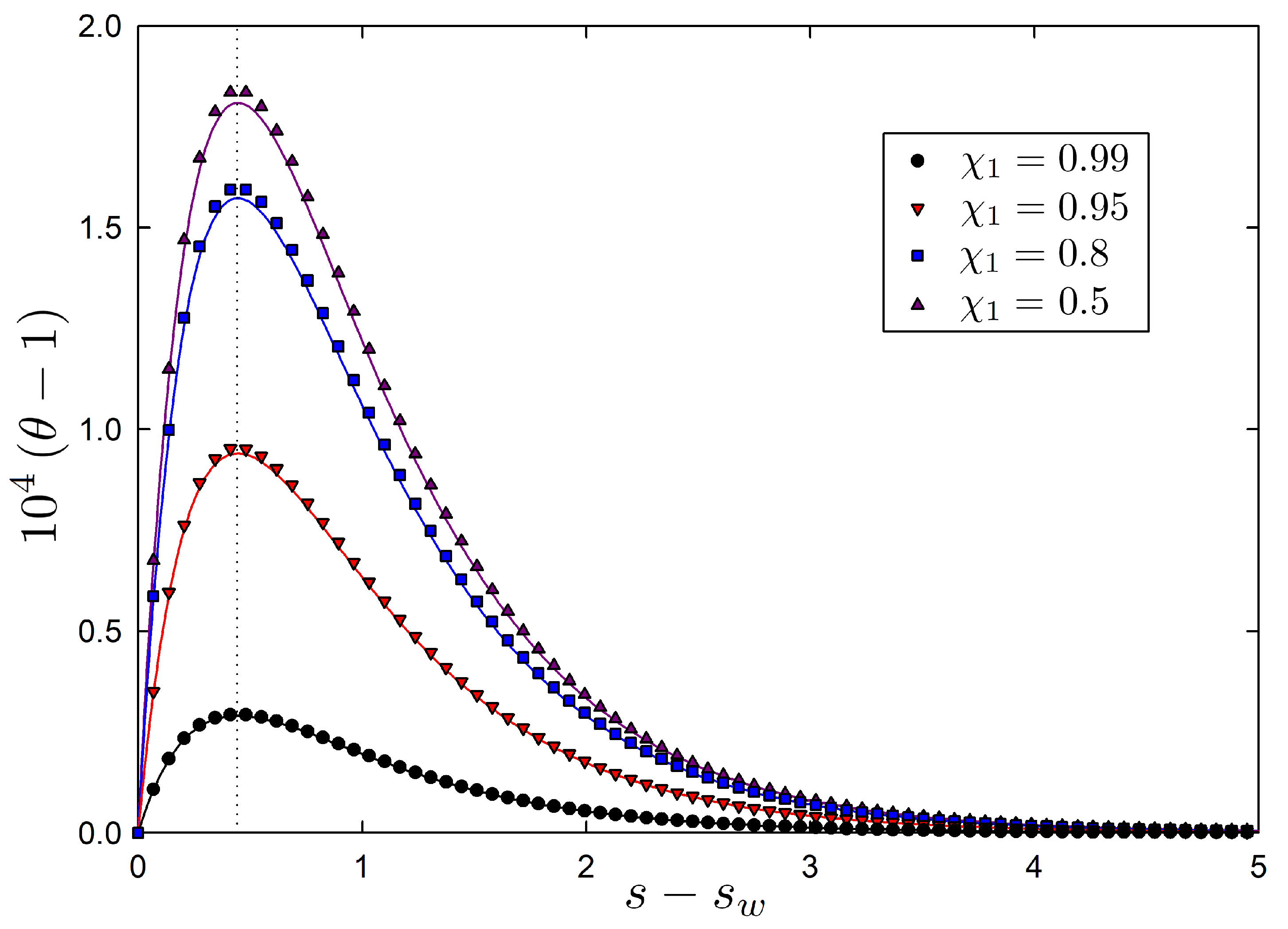
4.2.1. Linear Response
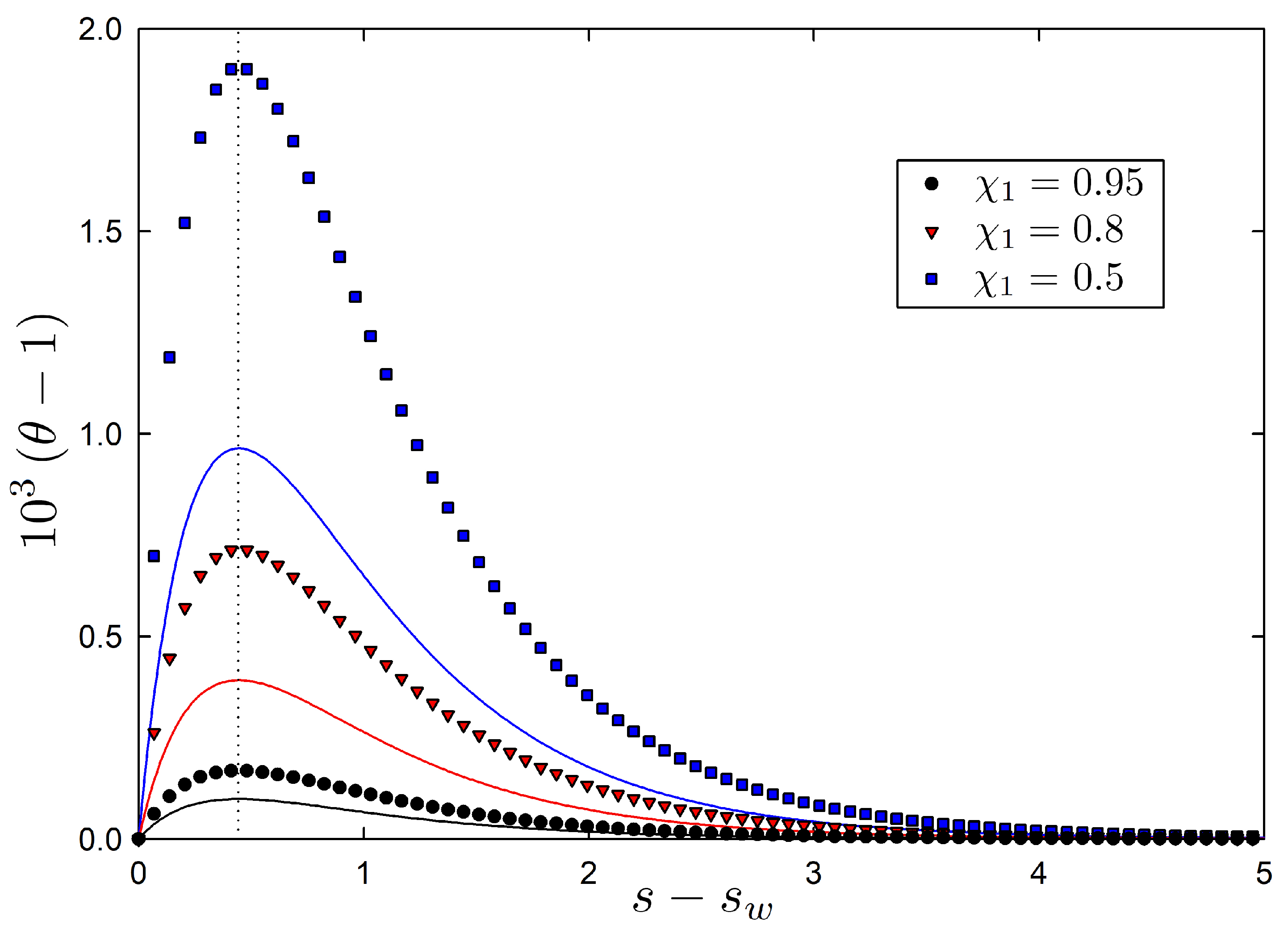
4.2.2. Nonlinear Regime
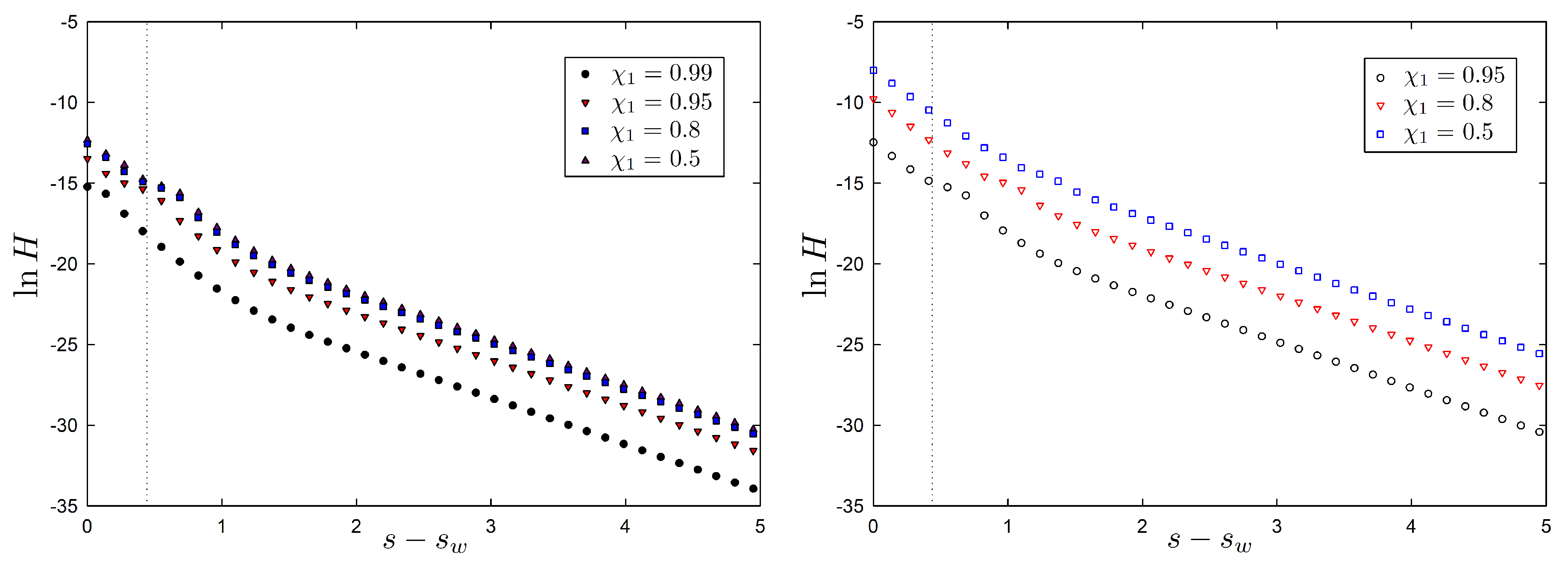
4.3. Monotonicity of an H-Functional
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Simulation Algorithm
- At time , a random “free time” is extracted with an exponential probability density , where depends on the state of the system ;
- Time is advanced by such a free time ;
- A pair is chosen to collide with probability ;
- All particles are heated by the stochastic thermostat, by adding independent Gaussian random numbers of zero mean and variance to their velocities;
- In order to conserve momentum, the mean value of the random numbers generated in the previous step is subtracted from the velocities of all particles;
- The process is repeated from Step 1.
References
- Kovacs, A.J.; Aklonis, J.J.; Hutchinson, J.M.; Ramos, A.R. Isobaric volume and enthalpy recovery of glasses. II. A transparent multiparameter theory. J. Polym. Sci. 1979, 17, 1097–1162. [Google Scholar] [CrossRef]
- Bertin, E.M.; Bouchaud, J.P.; Drouffe, J.M.; Godreche, C. The Kovacs effect in model glasses. J. Phys. A 2003, 36, 10701. [Google Scholar] [CrossRef]
- Buhot, A. Kovacs effect and fluctuation–dissipation relations in 1D kinetically constrained models. J. Phys. A 2003, 36, 12367. [Google Scholar] [CrossRef]
- Mossa, S.; Sciortino, F. Crossover (or Kovacs) effect in an aging molecular liquid. Phys. Rev. Lett. 2004, 92, 045504. [Google Scholar] [CrossRef] [PubMed]
- Aquino, G.; Leuzzi, L.; Nieuwenhuizen, T.M. Kovacs effect in a model for a fragile glass. Phys. Rev. B 2006, 73, 094205. [Google Scholar] [CrossRef]
- Prados, A.; Brey, J.J. The Kovacs effect: A master equation analysis. J. Stat. Mech. 2010, 2010, 368–369. [Google Scholar] [CrossRef]
- Diezemann, G.; Heuer, A. Memory effects in the relaxation of the Gaussian trap model. Phys. Rev. E 2011, 83, 031505. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-García, M.; Prados, A. Kovacs effect in the one-dimensional Ising model: A linear response analysis. Phys. Rev. E 2014, 89, 012140. [Google Scholar] [CrossRef] [PubMed]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Pöschel, T.; Luding, S. Granular Gases Vol. 564 of Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Van Noije, T.P.C.; Ernst, M.H. Velocity distributions in homogeneous granular fluids: The free and the heated case. Granul. Matter 1998, 1, 57–64. [Google Scholar] [CrossRef]
- Prados, A.; Trizac, E. Kovacs-Like Memory Effect in Driven Granular Gases. Phys. Rev. Lett. 2014, 112, 198001. [Google Scholar] [CrossRef] [PubMed]
- Trizac, E.; Prados, A. Memory effect in uniformly heated granular gases. Phys. Rev. E 2014, 90, 012204. [Google Scholar] [CrossRef] [PubMed]
- Lahini, Y.; Gottesman, O.; Amir, A.; Rubinstein, S.M. Nonmonotonic Aging and Memory Retention in Disordered Mechanical Systems. Phys. Rev. Lett. 2017, 118, 085501. [Google Scholar] [CrossRef] [PubMed]
- Kürsten, R.; Sushkov, V.; Ihle, T. Giant Kovacs-Like Memory Effect for Active Particles. Phys. Rev. Lett. 2017, in press. [Google Scholar]
- Lasanta, A.; Manacorda, A.; Prados, A.; Puglisi, A. Fluctuating hydrodynamics and mesoscopic effects of spatial correlations in dissipative systems with conserved momentum. New J. Phys. 2015, 17, 083039. [Google Scholar] [CrossRef]
- Manacorda, A.; Plata, C.A.; Lasanta, A.; Puglisi, A.; Prados, A. Lattice Models for Granular-Like Velocity Fields: Hydrodynamic Description. J. Stat. Phys. 2016, 164, 810–841. [Google Scholar] [CrossRef]
- Plata, C.A.; Manacorda, A.; Lasanta, A.; Puglisi, A.; Prados, A. Lattice models for granular-like velocity fields: Finite-size effects. J. Stat. Mech. 2016, 2016, 093203. [Google Scholar] [CrossRef]
- Marconi, U.M.B.; Puglisi, A.; Vulpiani, A. About an H-theorem for systems with non-conservative interactions. J. Stat. Mech. 2013, 2013, 114–124. [Google Scholar] [CrossRef]
- García de Soria, M.I.; Maynar, P.; Mischler, S.; Mouhot, C.; Rey, T.; Trizac, E. Towards an H-theorem for granular gases. J. Stat. Mech. 2015, 2014, P11009. [Google Scholar] [CrossRef]
- Plata, C.A.; Prados, A. Global stability and H-theorem in lattice models with nonconservative interactions. Phys. Rev. E 2017, 95, 052121. [Google Scholar] [CrossRef] [PubMed]
- Brey, J.J.; Prados, A. Stretched exponential decay at intermediate times in the one-dimentional Ising model at low temperatures. Physica A 1993, 197, 569–582. [Google Scholar] [CrossRef]
- Prasad, V.V.; Sabhapandit, S.; Dhar, A.; Narayan, O. Driven inelastic Maxwell gas in one dimension. Phys. Rev. E 2017, 95, 022115. [Google Scholar] [CrossRef] [PubMed]
- Ben-Naim, E.; Krapivsky, P.L. The inelastic Maxwell model. In Granular Gas Dynamics; Pöschel, T., Brilliantov, N., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2003; Volume 624, pp. 65–94. [Google Scholar]
- Ernst, M.H.; Trizac, E.; Barrat, A. The rich behavior of the Boltzmann equation for dissipative gases. EPL 2006, 76, 56–62. [Google Scholar] [CrossRef]
- Montanero, J.M.; Santos, A. Computer simulation of uniformly heated granular fluids. Granul. Matter 2000, 2, 53–64. [Google Scholar] [CrossRef]
- Maynar, P.; García de Soria, M.I.; Trizac, E. Fluctuating hydrodynamics for driven granular gases. Eur. Phys. J. Spec. Top. 2009, 179, 123–139. [Google Scholar] [CrossRef]
- Prasad, V.V.; Sabhapandit, S.; Dhar, A. High-energy tail of the velocity distribution of driven inelastic Maxwell gases. EPL 2013, 104, 54003. [Google Scholar] [CrossRef]
- Plata, C.A.; Prados, A. Kinetic description of a class of systems with non-conservative interactions. 2018; unpublished. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972. [Google Scholar]
- Falasco, G.; Baiesi, M. Temperature response in nonequilibrium stochastic systems. EPL 2016, 113, 20005. [Google Scholar] [CrossRef]
- Falasco, G.; Baiesi, M. Nonequilibrium temperature response for stochastic overdamped systems. New J. Phys. 2016, 18, 043039. [Google Scholar] [CrossRef]
- Lippiello, E.; Corberi, F.; Sarracino, A.; Zannetti, M. Nonlinear response and fluctuation-dissipation relations. Phys. Rev. E 2008, 78, 041120. [Google Scholar]
- Brey, J.J.; Prados, A. Normal solutions for master equations with time-dependent transition rates: Application to heating processes. Phys. Rev. E 1993, 47, 1541. [Google Scholar] [CrossRef]
- Bortz, A.B.; Kalos, M.H.; Lebowitz, J.L. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comput. Phys. 1975, 17, 10–18. [Google Scholar] [CrossRef]
- Prados, A.; Brey, J.J.; Sánchez-Rey, B. A dynamical Monte Carlo algorithm for master equations with time-dependent transition rates. J. Stat. Phys. 1997, 89, 709–734. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plata, C.A.; Prados, A. Kovacs-Like Memory Effect in Athermal Systems: Linear Response Analysis. Entropy 2017, 19, 539. https://doi.org/10.3390/e19100539
Plata CA, Prados A. Kovacs-Like Memory Effect in Athermal Systems: Linear Response Analysis. Entropy. 2017; 19(10):539. https://doi.org/10.3390/e19100539
Chicago/Turabian StylePlata, Carlos A., and Antonio Prados. 2017. "Kovacs-Like Memory Effect in Athermal Systems: Linear Response Analysis" Entropy 19, no. 10: 539. https://doi.org/10.3390/e19100539
APA StylePlata, C. A., & Prados, A. (2017). Kovacs-Like Memory Effect in Athermal Systems: Linear Response Analysis. Entropy, 19(10), 539. https://doi.org/10.3390/e19100539





