Abstract
We investigate the stationary and dynamic properties of the celebrated Nosé–Hoover dynamics of many-body interacting Hamiltonian systems, with an emphasis on the effect of inter-particle interactions. To this end, we consider a model system with both short- and long-range interactions. The Nosé–Hoover dynamics aim to generate the canonical equilibrium distribution of a system at a desired temperature by employing a set of time-reversible, deterministic equations of motion. A signature of canonical equilibrium is a single-particle momentum distribution that is Gaussian. We find that the equilibrium properties of the system within the Nosé–Hoover dynamics coincides with that within the canonical ensemble. Moreover, starting from out-of-equilibrium initial conditions, the average kinetic energy of the system relaxes to its target value over a size-independent timescale. However, quite surprisingly, our results indicate that under the same conditions and with only long-range interactions present in the system, the momentum distribution relaxes to its Gaussian form in equilibrium over a scale that diverges with the system size. On adding short-range interactions, the relaxation is found to occur over a timescale that has a much weaker dependence on system size. This system-size dependence of the timescale vanishes when only short-range interactions are present in the system. An implication of such an ultra-slow relaxation when only long-range interactions are present in the system is that macroscopic observables other than the average kinetic energy when estimated in the Nosé–Hoover dynamics may take an unusually long time to relax to its canonical equilibrium value. Our work underlines the crucial role that interactions play in deciding the equivalence between Nosé–Hoover and canonical equilibrium.
1. Introduction
Often, one needs in studies in nonlinear dynamics and statistical physics to investigate the dynamical properties of a many-body interacting Hamiltonian system evolving under the condition of a constant temperature. For example, one might be interested in studying the dynamical properties of the system in canonical equilibrium at a certain temperature T, with the temperature being proportional to the average kinetic energy of the system by virtue of the Theorem of Equipartition (In this work, we measure temperatures in units of the Boltzmann constant). To this end, one may devise a dynamics having a temperature as a dynamical parameter that is designed to relax an initial configuration of the system to canonical equilibrium at temperature , and then make the choice . A common practice is to employ a Langevin dynamics, i.e., a noisy, dissipative dynamics that mimics the interaction of the system with an external heat bath at temperature in terms of a deterministic frictional force and an uncorrelated, Gaussian-distributed random force added to the equation of motion [1]. In this approach, one then tunes suitably the strength of the random force such that the Langevin dynamics relaxes at long times to canonical equilibrium at temperature . The presence of dissipation renders the dynamics to be irreversible in time. A complementary approach to such a noisy, dissipative dynamics was pioneered by Nosé and Hoover, in which the dynamics is fully deterministic and time-reversible, while achieving the same objective of relaxing the system to canonical equilibrium at the desired temperature [2,3]; for a review, see [4,5]. The time evolution under the condition of relaxation at long times to canonical equilibrium at a given temperature is said to represent isokinetic ensemble dynamics when taking place according to the Nosé–Hoover equation of motion and to represent Langevin/canonical ensemble dynamics when taking place following the Langevin equation of motion.
To illustrate in detail the distinguishing feature of the Nosé–Hoover vis-à-vis Langevin dynamics, consider an interacting N-particle system characterized by the set of canonical coordinates and conjugated momenta. The particles, which we take for simplicity to have the same mass m, interact with one another via the two-body interaction potential . In the following, we consider ’s and ’s to be one-dimensional variables for reasons of simplicity. Our analysis, however, extends straightforwardly to higher dimensions. The Hamiltonian of the system is given by
where the first term on the right-hand side stands for the kinetic energy of the system.
In the approach due to Langevin, the dynamical equations of the system are given by
where t denotes time, is the dissipation constant, while is a Gaussian, white noise satisfying
Here, the overbars denote averaging over noise realizations, while characterizes the strength of the noise. The dynamics (2) are evidently not time-reversal invariant. Choosing ensures that the dynamics (2) relaxes at long times to the canonical distribution at given by [1]
in which the kinetic energy density of the system fluctuates around the average value .
In the approach due to Nosé and Hoover, a degree of freedom s augmenting the set is introduced, which is taken to characterize an external heat reservoir that interacts with the system through the momenta ’s. The Hamiltonian of the combined system is given by
where Q is the mass and is the conjugated momentum of the additional degree of freedom. The dynamics of the system is given by the following Hamilton equations of motion:
It may be easily checked that unlike dynamics (2), dynamics (6) is invariant under time reversal. In terms of new variables
and rescaled time
one obtains from the Hamilton Equations (6) the following dynamics:
where is the kinetic energy, while we have defined
From Equations (9)–(12), we observe that a complete description of the time evolution of the system is given in terms of Equations (9), (10), and (12), without any reference to Equation (11) for s, so that, as far as the description of the system is concerned, the variable s is an irrelevant one that may be ignored. We note in passing that a different, but closely related, Hamiltonian giving directly the Nosé-Hoover equations of motion but without any time scaling, as in Equation (8), is discussed in [6]. We will from now on drop the tilde over time in order not to overload the notation. Let us note that, in terms of the variables ’s, the Hamiltonian (5) takes the form
From Equation (12), we find that, in the stationary state ), the kinetic energy of the system equals (the extra factor of unity takes care of the presence of the additional degree of freedom s). For large , we then have the desired result: an ensemble of initial conditions under the evolution given by Equations (9), (10), and (12) evolves at long times to a stationary state in which the average kinetic energy density has the value . The quantity in Equation (12) denotes a relaxation timescale over which the kinetic energy relaxes to its target value. Beyond the average kinetic energy, it has been demonstrated by invoking the phase space continuity equation that the distribution
is a stationary state of the Nosé–Hoover dynamics [3]. It then follows that the corresponding stationary distribution for the system variables is the canonical equilibrium distribution:
normalized as . Thus, the dynamics (9)–(12) that includes the additional dynamical variable s nevertheless preseves the canonical equilibrium distribution of the system. A general formalism for constructing modified Hamiltonian dynamical systems that preserve a canonical equilibrium distribution on adding a time evolution equation for a single additional thermostat variable is discussed in [7].
Equation (16) implies that the single-particle momentum distribution , defined such that gives the probability that a randomly chosen particle has its momentum between p and , is a Gaussian distribution with mean zero and width equal to :
Consequently, the moments , with , satisfy .
In the above backdrop, the principal objective of this work is to answer the question: what is the effect of inter-particle interactions on the relaxation properties of the Nosé–Hoover dynamics? More specifically, considering a system embedded in a d-dimensional space, we ask: do systems with long-range interactions, in which the inter-particle interaction decays slower than , behave in a similar way to short-range systems that have the inter-particle interaction decaying faster than ? How does the timescale over which the phase space distribution relaxes to its canonical equilibrium form behave in the two cases, and, in particular, is there a system-size dependence in the timescale for long-range systems with respect to short-range ones? Studying these issues is particularly relevant and timely in the wake of recent surge in interest across physics in long-range interacting (LRI) systems.
LRI systems may display a notably distinct thermodynamic behavior with respect to short-range ones [8,9,10,11,12]. These systems are characterized by a two-body interaction potential that decays asymptotically with inter-particle separation r as , with in d spatial dimensions. The limit corresponds to the case of mean–field interaction. Examples of LRI systems are self-gravitating systems, plasmas, fluid dynamical systems, and some spin systems. One of the striking dynamical features resulting from long-range interactions is the occurrence of non-equilibrium quasi-stationary states (QSSs) during relaxation of LRI systems towards equilibrium. These states have lifetimes that diverge with the number of particles constituting the system, so that, in the thermodynamic limit, the system remains trapped in QSSs and does not attain equilibrium. Only for a finite number of particles do the QSSs eventually evolve towards equilibrium. Even in equilibrium, LRI systems may exhibit features such as ensemble inequivalence and a negative heat capacity in the microcanonical ensemble that are unusual for short-range systems.
In this work, we address our aforementioned queries within the ambit of a model system comprising classical -spins occupying the sites of a one-dimensional periodic lattice and interacting via a long-range (specifically, a mean–field interaction in which every spin interacts with every other and a short-range (specifically, a nearest-neighbor interaction in which every spin interacts with its left and right neighbors) interaction. With an aim to study the equilibrium properties as well as relaxation towards equilibrium, we simulate the Nosé–Hoover dynamics of the model by integrating the corresponding equations of motion in time. A signature of canonical equilibrium is a single-particle momentum distribution that is Gaussian (see Equation (17)). We find that the equilibrium properties of our model system evolving under the Nosé–Hoover dynamics coincide with those within the canonical ensemble. As regards relaxation towards canonical equilibrium, we observe that starting from out-of-equilibrium initial conditions, the average kinetic energy of the system relaxes to its target canonical-equilibrium value over a size-independent timescale. However, quite surprisingly, our results indicate that under the same conditions and with only long-range interactions present in the system, the momentum distribution relaxes to its Gaussian form in equilibrium over a scale that diverges with the system size. On adding short-range interactions, the relaxation is found to occur over a timescale that has a much weaker dependence on system size. This system-size dependence vanishes when only short-range interactions are present in the system. An implication of such an ultra-slow relaxation when only long-range interactions are present in the system is that macroscopic observables other than the average kinetic energy when estimated in the Nosé–Hoover dynamics may take an unusually long time to relax to its canonical equilibrium value. Our work underlines the crucial role that interactions play in deciding the equivalence between Nosé–Hoover and canonical equilibrium.
The paper is organized as follows. In Section 2, we describe the model of study. In Section 3, we obtain the so-called caloric curve of the model within the canonical ensemble, which we eventually invoke in later parts of the paper to decide on the equivalence of the equilibrium properties of the Nosé–Hoover dynamics and canonical equilibrium. In Section 4, we present results from simulations of the Nosé–Hoover dynamics of the model, and discuss the implications and relevance of the results. The paper ends with conclusions in Section 5.
2. Model of Study
Our system of study comprises a one-dimensional periodic lattice of N sites. Each site of the lattice is occupied by a unit-inertia rotor characterized by its angular coordinate and the corresponding conjugated momentum , with . One may also think of the rotors as representing classical -spins. Note that both of the ’s and the ’s are one-dimensional variables. There exist both a long-range (specifically, a global or a mean–field) coupling and a short-range (specifically, nearest-neighbor) coupling between the rotors. Thus, a rotor on site j interacts with strength with rotors on all the other sites and with strength K with the rotor occupying the -th and the -th site. The Hamiltonian of the system is given by [13,14]
Note that, for , the Hamiltonian (18) reduces to that of the widely-studied Hamiltonian mean–field (HMF) model [15], which is regarded as a paradigmatic model to study statics and dynamics of LRI systems [10]. On the other hand, for , the model (18) reduces to a short-ranged model in one dimension.
In the following, we take both the mean–field coupling J and the short-range coupling K to be positive, thereby modeling ferromagnetic global and nearest-neighbor couplings. Consequently, both the long-range and the short-range coupling between the rotors favor an ordered state in which all the rotor angles are equal, thereby minimizing the potential energy contribution to the total energy. Such a tendency is, however, opposed by the kinetic energy contribution whose average in equilibrium may be characterized by a temperature by invoking the Theorem of Equipartition. Noting that, for a given N, the total potential energy is bounded from above while the total kinetic energy is not, one expects the system to show in equilibrium an ordered/magnetized phase at low energies/temperatures and a disordered/unmagnetized phase at high energies/temperatures. This scenario holds even with .
The amount of order in the system is characterized by the magnetization
which is a vector whose length m has the thermodynamic value in equilibrium denoted by that is nonzero in the ordered phase and zero in the disordered phase. For , the corresponding HMF model is known to display a second-order phase transition between a high-temperature unmagnetized phase and a low-temperature magnetized phase at the critical temperature , with the corresponding critical energy density being [10]. On the other hand, invoking the Landau’s argument for the absence of any phase transition at a finite temperature in a one-dimensional model with only short-range interactions, one may conclude for that the corresponding short-ranged model does not display any phase transitions, though it has been shown to have interesting dynamical effects [16]. For general , when both long-range and short-range interactions are present, the model displays a second-order phase transition between an ordered and a disordered phase [13,14]. Note that all the mentioned phase transitions are continuous. Although ensemble equivalence is not guaranteed for LRI systems, it has been argued that inequivalence arises when one has a first-order phase transition in the canonical ensemble, and not when one has a second-order transition [17]. Consequently, we may regard the phase diagram of model (18) to be equivalent within microcanonical and canonical ensembles. For an explicit demonstration of ensemble equivalence for the model (18), one may refer to [14].
In the following section, we will obtain the caloric curve of model (18) that relates the equilibrium internal energy with the equilibrium temperature of the system.
3. The Caloric Curve within the Canonical Ensemble
As mentioned in the preceding section, model (18) is known to have equivalent microcanonical and canonical ensemble descriptions in equilibrium. Consequently, in obtaining the caloric curve of the model, which will be invoked to decide the equivalence between the equilibrium properties of the Nosé–Hoover dynamics and canonical equilibrium, it will suffice to restrict our analysis to the canonical ensemble description of the model.
The Langevin/canonical ensemble dynamics (2) for the model (18) comprises the set of time-evolution equations
with the properties of the noise given by Equation (3) with . Within the microcanonical ensemble description of the system, the time evolution of the variables is given by Hamilton equations obtained from Equation (20) by setting to zero. The Nosé–Hoover dynamics of the variables is obtained from Equations (9) and (10) as
where the time evolution of the variable is given by Equation (12).
In order to derive the desired caloric curve of model (18) within the canonical ensemble, we start with the canonical partition function of the system at temperature T given by , with . Using Equation (18), we get
Using the Hubbard–Stratonovich transformation in Equation (22), we obtain
Writing , with real and given by , we get
In view of the invariance of the Hamiltonian (18) under rotation by an equal amount of all the ’s, we get [18]
In order to proceed further, we consider separately the cases and in the following.
3.1.
For , Equation (25) yields
In the thermodynamic limit, may be approximated by invoking the saddle-point method to perform the integration in z on the right-hand side; one gets
where the saddle-point value solves the equation
with being the modified Bessel function of first kind and of order n. It may be shown by following the arguments given in [18] that is nothing but the stationary magnetization . Equation (28) has a trivial solution valid at all temperatures, while a non-zero solution exists for [10]. In fact, the system shows a continuous transition, from a magnetized phase () at low temperatures to an unmagnetized phase () at high temperatures at the critical temperature [10].
3.2.
For , Equation (25) gives
where we may identify the factor with the canonical partition function of a periodic chain of N interacting angle-only rotors, where a rotor on each site interacts with strength K with the rotor on the left nearest-neighbor and the right nearest-neighbor site, and also with an external field of strength along the x direction.
One may evaluate by rewriting it in terms of a transfer operator as
Let denote the set of eigenvalues of the transfer operator . In other words, denoting the eigenfunctions of as , we have . In terms of , we obtain
Substituting Equation (36) in Equation (31), and approximating the integral on the right-hand side of the latter by the saddle-point method, one gets
where solves the saddle-point equation , with being the free-energy function:
The saddle-point equation may thus be written as
Equation (37) gives the dimensionless free energy per rotor, , as , where we have suppressed the dependence of on K. We thus have
Note that the free energy at a given temperature has a definite value given by Equation (40), and is obtained by substituting the saddle-point solution into the expression for the free-energy function .
In the thermodynamic limit, the internal energy density of the system is obtained as
Using Equation (39), and the fact that, as for , the quantity is nothing but the stationary magnetization , we get
with satisfying
To proceed, we need to find . We consider separately the cases and .
3.2.1.
In this case, it may be easily checked that the eigenvalues of are given by with the corresponding eigenvector given by plane waves [14]. Using , we conclude that . Equation (43) then yields , while Equation (42) gives
where we have used the result . Equation (44) is the desired caloric curve of the model (18) within the canonical ensemble for .
3.2.2.
In this case, not knowing the analytic forms of the eigenvalues of , we resort to a numerical scheme to estimate the largest eigenvalue . To this end, we discretize the angles over the interval as , with and for any large positive integer P (we choose ). The operator then takes the form of a matrix of size , whose largest eigenvalue may be estimated numerically by employing the so-called power method [19] (A FORTRAN90 library that implements the power method and is distributed under the GNU Lesser General Public License (GPL) is available at [20]). Noting that is a finite-dimensional real square matrix with positive entries, the application of the Perron–Frobenius theorem implies the existence of its largest eigenvalue that is real and non-degenerate. At given values of , once has been estimated numerically, we compute the free-energy function as a function of z by using Equation (38). We then find numerically the value of z at which the computed free-energy function attains its minimum value. As discussed above, this minimizer is the equilibrium magnetization of the system at the given values of . In order to obtain the caloric curve, one has to estimate numerically the derivative , and then use Equation (42).
4. Results and Discussion
In this section, we discuss the results on equilibrium as well as relaxation properties of model (18) obtained by performing numerical integration of the Nosé–Hoover equations of motion (21). The numerical integration involved using a fourth-order Runge–Kutta method with timestep .
4.1. Results in Equilibrium
Here, we discuss the Nosé–Hoover equilibrium properties for model (18). The initial condition corresponds to the ’s independently and uniformly distributed in and the ’s independently sampled from a Gaussian distribution with zero mean and width equal to 0.5. The initial value of the parameter is 2.0, while we have taken . In Figure 1, we consider the case when only long-range interactions are present in system (). Figure 1a shows for that the average kinetic energy relaxes at long times to the value , as desired. Figure 1b shows for the same value of that the average internal energy has the same value in the stationary state as the one in canonical equilibrium given by Equation (29); Figure 1c shows the single-particle momentum distribution in the stationary state. We observe that has the correct canonical-equilibrium form of a Gaussian distribution, which further corroborates the property of the Nosé–Hoover dynamics that the canonical distribution (16) is a stationary state of the dynamics. Figure 1d shows for a range of values of the temperature that the caloric curve obtained within the Nosé–Hoover dynamics in equilibrium coincides with that within the canonical ensemble given by Equation (29). Figure 1a–c refer to the system size , while Figure 1d refers to two system sizes, namely, and . The aforementioned observed properties of the Nosé–Hoover dynamics have been checked to hold for (i) the case when only short-range interactions are present in the system (see Figure 2 that corresponds to ), in which case the caloric curve within the canonical ensemble is given by Equation (44), and (ii) when both long- and short-range interactions are present in the system (data not shown; see, however, Figure 3c).
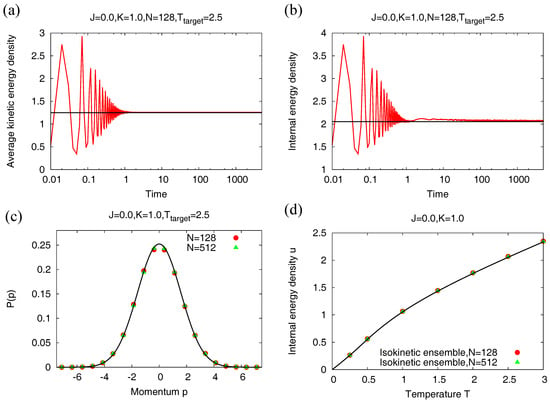
Figure 1.
Comparison of Nosé–Hoover and canonical equilibrium results for model (18) with (that is, with only short-range interactions). (a) variation of the average kinetic energy density with time. The black line denotes the value ; (b) variation of the internal energy density with time. The black line denotes the average internal energy density within the canonical ensemble given by Equation (44); (c) stationary single-particle momentum distribution obtained from momentum values measured at time . The black line denotes a Gaussian distribution with zero mean and width equal to ; (d) caloric curve for two system sizes, and . The black line shows the caloric curve within the canonical ensemble given by Equation (44). The data for the Nosé–Hoover dynamics are generated by integrating the equations of motion (21) using a fourth-order Runge–Kutta method with timestep equal to 0.01. The initial condition corresponds to the ’s independently and uniformly distributed in and the ’s independently sampled from a Gaussian distribution with zero mean and width equal to 0.5. The initial value of the parameter is 2, while we have taken .
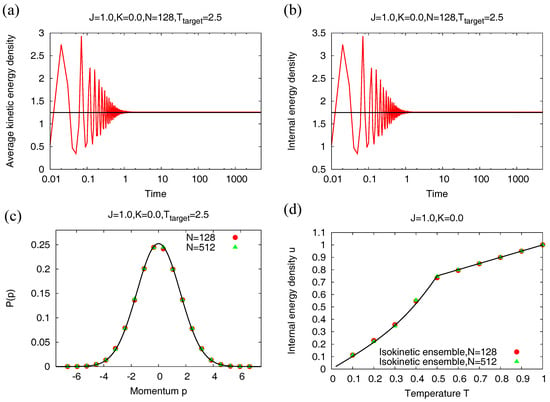
Figure 2.
Comparison of Nosé–Hoover and canonical equilibrium results for the model (18) with (that is, with only long-range interactions); (a) variation of the average kinetic energy density with time. The black line denotes the value ; (b) variation of the internal energy density with time. The black line denotes the average internal energy density within the canonical ensemble given by Equation (29); (c) stationary single-particle momentum distribution obtained from momentum values measured at time . The black line denotes a Gaussian distribution with zero mean and width equal to ; (d) caloric curve for two system sizes, and . The black line shows the caloric curve within the canonical ensemble given by Equation (29). The data for the Nosé–Hoover dynamics are generated by integrating the equations of motion (21) using a fourth-order Runge–Kutta method with timestep equal to 0.01. The initial condition corresponds to the ’s independently and uniformly distributed in and the ’s independently sampled from a Gaussian distribution with zero mean and width equal to 0.5. The initial value of the parameter is 2, while we have taken .
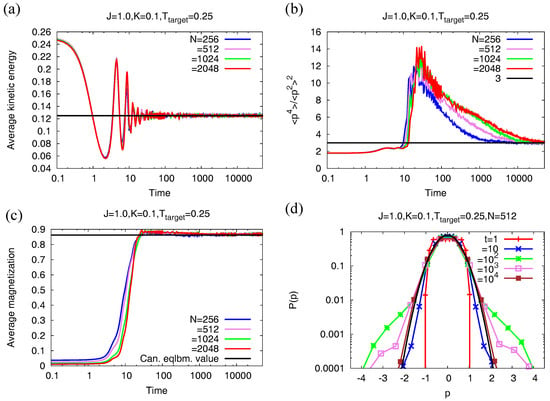
Figure 3.
Relaxation properties of the Nosé–Hoover dynamics for model (18) with . (a) variation of the average kinetic energy density with time, for four different system sizes. The black line denotes the value ; (b) variation of the ratio with time, for four different system sizes. The black line denotes the value 3 corresponding to a Gaussian distribution; (c) variation of the magnetization with time, again for four different system sizes. The black line denotes the canonical equilibriu m value obtained by the method described in Section 3.2.2; (d) single-particle momentum distribution as a function of time, for system size . The black line denotes a Gaussian distribution with zero mean and width equal to , Equation (17). The data for the Nosé–Hoover dynamics are generated by integrating the equations of motion (21) using a fourth-order Runge–Kutta method with timestep equal to 0.01. The initial condition corresponds to the ’s independently and uniformly distributed in and the ’s independently and uniformly distributed in . The initial value of the parameter is 2, while we have taken .
4.2. Results out of Equilibrium
Here, we discuss the relaxation properties of the Nosé–Hoover dynamics for model (18). The initial condition corresponds to the so-called water-bag distribution that has both and p uniformly distributed over given intervals [10]. We consider ’s to be independently and uniformly distributed in and the ’s to be independently and uniformly distributed in . The initial value of the parameter is 2.0, while we have taken .
Let us start with a discussion of the results in Figure 4 that corresponds to the case when only long-range interactions are present in the system (18). In Figure 4a, we see that, for four different system sizes, the average kinetic energy density relaxes at long times to the target value over a timescale that does not depend on the system size. A Gaussian distribution for the momentum, expected in canonical equilibrium, is characterized by a value 3 of the ratio (see Equation (17)). We see in Figure 4b that, in contrast to Figure 4a, this ratio, however, relaxes to the canonical equilibrium value over a time that depends on the system size, and which grows with increase of N. Figure 4c shows that the long-time magnetization value reached by the Nosé–Hoover dynamics coincides with the canonical equilibrium value for all system sizes. On the basis of these results, we conclude that, with only long-range interactions in system (18), only the second moment of the momentum distribution relaxes to its canonical equilibrium value over a size-independent timescale, while higher moments (and consequently, the whole of the momentum distribution) relax to their canonical equilibrium values over a time that grows with the system size. The latter fact is demonstrated in Figure 4d that shows for the time evolution of the single-particle momentum distribution.
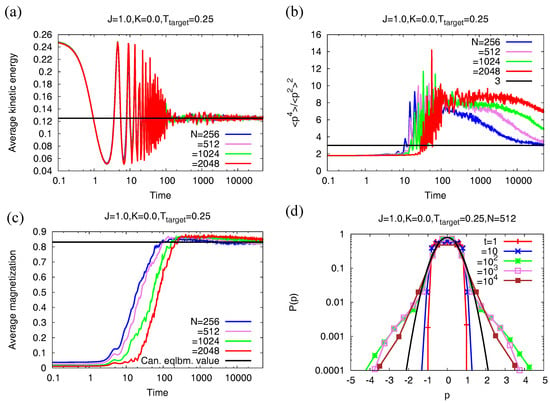
Figure 4.
Relaxation properties of the Nosé–Hoover dynamics for the model (18) with (that is, with only long-range interactions). (a) variation of the average kinetic energy density with time, for four different system sizes. The black line denotes the value ; (b) variation of the ratio with time, for four different system sizes. The black line denotes the value 3 corresponding to a Gaussian distribution; (c) variation of the magnetization with time, again for four different system sizes. The black line denotes the canonical equilibrium value given by Equation (28); (d) single-particle momentum distribution as a function of time, for system size . The black line denotes a Gaussian distribution with zero mean and width equal to , Equation (17). The data for the Nosé–Hoover dynamics are generated by integrating the equations of motion (21) using a fourth-order Runge–Kutta method with timestep equal to 0.01. The initial condition corresponds to the ’s independently and uniformly distributed in and the ’s independently and uniformly distributed in . The initial value of the parameter is 2, while we have taken .
The feature of a size-independent timescale for the relaxation of the average kinetic energy density to its canonical equilibrium value, observed in the case of purely long-range interactions in model (18), also holds on adding short-range interactions to the model and when the latter are the only interactions present in the system (see Figure 3a and Figure 5a). Moreover, in all cases, the long-time value of the magnetization matches with its canonical equilibrium value (see Figure 3c and Figure 5c). The most significant difference in the relaxation properties that is observed on adding short-range interactions may be inferred by comparing Figure 3b and Figure 4b: the very strong size-dependence observed in the relaxation of the ratio to its canonical equilibrium value gets substantially weakened on adding short-range interactions with coupling strength as low as compared to the value of the long-range coupling constant . Similar inference may be drawn from a comparison of Figure 3d and Figure 4d. This observation has an immediate and an important implication: additional short-range interactions speed up the relaxation of the momentum distribution towards canonical equilibrium. The aforementioned system-size dependence vanishes on turning off long-range interactions, so that the only remnant interactions in the system are the short-range ones (see Figure 5b,d).
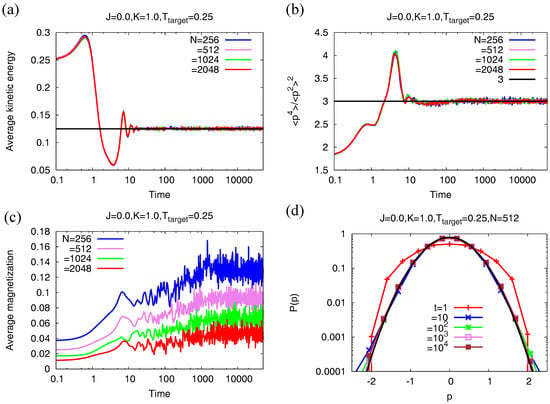
Figure 5.
Relaxation properties of the Nosé–Hoover dynamics for the model (18) with (that is, with only short-range interactions). (a) variation of the average kinetic energy density with time, for four different system sizes. The black line denotes the value ; (b) variation of the ratio with time, for four different system sizes. The black line denotes the value 3 corresponding to a Gaussian distribution; (c) variation of the magnetization with time, again for four different system sizes. The equilibrium magnetization goes to zero with increase of N as ; (d) single-particle momentum distribution as a function of time, for system size . The black line denotes a Gaussian distribution with zero mean and width equal to , Equation (17). The data for the Nosé–Hoover dynamics are generated by integrating the equations of motion (21) using a fourth-order Runge–Kutta method with timestep equal to 0.01. The initial condition corresponds to the ’s independently and uniformly distributed in and the ’s independently and uniformly distributed in . The initial value of the parameter is 2, while we have taken .
5. Conclusions
In this paper, we investigated the relaxation properties of the Nosé–Hoover dynamics of many-body interacting Hamiltonian systems, with an emphasis on the effect of inter-particle interactions. The dynamics aim to generate the canonical equilibrium distribution of a system at the desired temperature by employing time-reversible, deterministic dynamics. To pursue our study, we considered a representative model comprising N classical -spins occupying the sites of a one-dimensional periodic lattice. The spins interact with one another via both a long-range interaction, modelled as a mean–field interaction in which every spin interacts with every other, and a short-range one, modelled as a nearest-neighbor interaction in which every spin interacts with its left and right neighboring spins. We studied the Nosé–Hoover dynamics of the model through N-body integration of the corresponding equations of motion. Canonical equilibrium is characterized by a momentum distribution that is Gaussian. We found that the equilibrium properties of our model system evolving according to Nosé–Hoover dynamics are in excellent agreement with exact analytic results for the equilibrium properties derived within the canonical ensemble. Moreover, while starting from out-of-equilibrium initial conditions, the average kinetic energy of the system relaxes to its target value over a size-independent timescale. However, quite unexpectedly, we found that under the same conditions and with only long-range interactions present in the system, the momentum distribution relaxes to its Gaussian form in equilibrium over a scale that grows with N. The N-dependence gets weaker on adding short-range interactions, and vanishes when the latter are the only inter-particle interactions present in the system.
Viewed from the perspective of LRI systems, the slow relaxation observed within the Nosé–Hoover dynamics allows for drawing an analogy with a similar slow relaxation observed within the microcanonical dynamics of isolated LRI systems, a phenomenon that leads to the occurrence of nonequilibrium quasistationary states (QSSs) that have lifetimes diverging with the system size [10,21]. Within a kinetic theory approach, the QSSs are understood as stable, stationary solutions of the so-called Vlasov equation that governs the time evolution of the single-particle phase space distribution. The Vlasov equation is obtained as the first equation of the Bogoliubov–Born–Green–Yvon–Kirkwood (BBGKY) hierarchy by neglecting the correlation between particle trajectories, with corrections that decrease with an increase of N. For large but finite N, the eventual relaxation of QSSs towards equilibrium is understood as arising due to these finite-N corrections, the so-called collisional terms, to the Vlasov equation. In models in which the momentum variables are one-dimensional, it has been shown by analyzing the behavior of the dominant collisional term that Vlasov-stable phase-space distributions that are homogeneous in the coordinates evolve on times much larger than N, thereby leading for the distributions to characterize QSSs that have lifetimes diverging with N [8,11,22]. In light of the foregoing discussions, it is evidently pertinent and of immediate interest to invoke a kinetic theory approach and investigate in the context of the Nosé–Hoover dynamics of long-range systems whether additional short-range interactions play the role of collisional dynamics that speed up the relaxation of the system towards canonical equilibrium. Work in this direction is in progress and will be reported elsewhere.
The agreement reported in this paper in the value of the average kinetic energy computed in canonical equilibrium and within the Nosé–Hoover dynamics is reminiscent of a similar agreement in the large-system limit between ensemble and time averages predicted by Khinchin for the so-called sum-functions, that is, functions such as the kinetic energy that are sums of single-particle contributions [23]. The result was obtained for rarefied gases, which was later observed to also hold for systems with short-range interactions [24,25]. Our work hints at the validity of such a result even for long-range systems, as is evident from the agreement in the value of the average kinetic energy computed within the Nosé–Hoover dynamics and in canonical equilibrium (see Figure 4a). This point warrants a more detailed investigation that will be left for future studies.
Acknowledgments
This research did not receive any funding. The authors thank W. G. Hoover for fruitful email exchanges. Thanks are due to Leticia Cugliandolo for pointing out that a relaxation phenomenon similar to what is reported in this paper, namely, a fast relaxation of the kinetic energy and a much slower one of other observables, has also been observed in spin-glass systems.
Author Contributions
Shamik Gupta performed the analytical computations and numerical simulations and wrote the paper with inputs from Stefano Ruffo. Both of the authors contributed to the research work. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Nosé, S. A unified formulation of the constant temperature molecular-dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Morriss, G.P.; Dettmann, C.P. Thermostats: Analysis and application. Chaos 1998, 8, 321–336. [Google Scholar] [CrossRef] [PubMed]
- Klages, R. Microscopic Chaos, Fractals and Transport in Nonequilibrium Statistical Mechanics, monograph, Advanced Series in Nonlinear Dynamics Vol. 24; World Scientific: Singapore, 2017. [Google Scholar]
- Dettmann, C.P.; Morriss, G.P. Hamiltonian reformulation and pairing of Lyapunov exponents for Nosé-Hoover dynamics. Phys. Rev. E 1997, 55, 3693–3696. [Google Scholar] [CrossRef]
- Ramshaw, J.D. General formalism for singly thermostated Hamiltonian dynamics. Phys. Rev. E 2015, 92, 052138–052143. [Google Scholar] [CrossRef] [PubMed]
- Campa, A.; Dauxois, T.; Ruffo, S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 2009, 480, 57–159. [Google Scholar] [CrossRef]
- Bouchet, F.; Gupta, S.; Mukamel, D. Thermodynamics and dynamics of systems with long-range interactions. Physica A 2010, 389, 4389–4405. [Google Scholar] [CrossRef]
- Campa, A.; Dauxois, T.; Fanelli, D.; Ruffo, S. Physics of Long-Range Interacting Systems; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Levin, Y.; Pakter, R.; Rizzato, F.B.; Teles, T.N.; Benetti, F.P.C. Nonequilibrium statistical mechanics of systems with long-range interactions. Phys. Rep. 2014, 535, 1–60. [Google Scholar] [CrossRef]
- Gupta, S.; Ruffo, S. The world of long-range interactions: A bird’s eye view. Int. J. Mod. Phys. A 2017, 32, 1741018. [Google Scholar] [CrossRef]
- Campa, A.; Giansanti, A.; Mukamel, D.; Ruffo, S. Dynamics and thermodynamics of rotators interacting with both long- and short-range couplings. Physica A 2006, 365, 120–127. [Google Scholar] [CrossRef]
- Dauxois, T.; de Buyl, P.; Lori, L.; Ruffo, S. Models with short- and long-range interactions: The phase diagram and the reentrant phase. J. Stat. Mech. Theory Exp. 2010, 2010, P06015. [Google Scholar] [CrossRef]
- Antoni, M.; Ruffo, S. Clustering and relaxation in Hamiltonian long-range dynamics. Phys. Rev. E 1995, 52, 2361–2373. [Google Scholar] [CrossRef]
- Escande, D.; Kantz, H.; Livi, R.; Ruffo, S. Self-consistent check of the validity of Gibbs calculus using dynamical variables. J. Stat. Phys. 1994, 76, 605–626. [Google Scholar] [CrossRef]
- Bouchet, F.; Barré, J. Classification of phase transitions and ensemble inequivalence, in systems with long range interactions. J. Stat. Phys. 2005, 118, 1073–1105. [Google Scholar] [CrossRef]
- Gupta, S. Spontaneous collective synchronization in the Kuramoto model with additional non-local interactions. J. Phys. A: Math. Theor. 2017, 50, 424001. [Google Scholar] [CrossRef]
- Larson, R. Elementary Linear Algebra, 8th ed.; Cengage Learning: Boston, MA, USA, 2017. [Google Scholar]
- POWER_METHOD: The Power Method for Eigenvalues and Eigenvectors. Available online: http://people.sc.fsu.edu/~jburkardt/f_src/power_method/power_method.html (accessed on 14 October 2017).
- Yamaguchi, Y.Y.; Barré, J.; Bouchet, F.; Dauxois, T.; Ruffo, S. Stability criteria of the Vlasov equation and quasi-stationary states of the HMF model. Physica A 2004, 337, 36–66. [Google Scholar] [CrossRef]
- Bouchet, F.; Dauxois, T. Prediction of anomalous diffusion and algebraic relaxations for long-range interacting systems, using classical statistical mechanics. Phys. Rev. E 2005, 72, 045103. [Google Scholar] [CrossRef] [PubMed]
- Khinchin, A.I. Mathematical Foundations of Statistical Mechanics; Dover: New York, NY, USA, 1949. [Google Scholar]
- Mazur, P.; van der Linden, J. Asymptotic form of the structure function for real systems. J. Math. Phys. 1963, 4, 271–277. [Google Scholar] [CrossRef]
- Livi, R.; Pettini, M.; Ruffo, S.; Vulpiani, A. Chaotic behavior in nonlinear Hamiltonian systems and equilibrium statistical mechanics. J. Stat. Phys. 1987, 48, 539–559. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).