Bivariate Partial Information Decomposition: The Optimization Perspective
Abstract
:1. Introduction
2. Convex Optimization Basics
- (a)
- for some , (“feasible direction”); and
- (b)
- (“descent direction”).
- a subgradient g of f at x
- and an m-vector
2.1. Convex Optimization Through Interior Point Methods
3. Theoretical View on Bertschinger et al.’s Convex Program
3.1. The Feasible Region
- and are probability distributions.
- is non-empty. This is equivalent to for all .
- No element of X is “redundant”, i.e., for every we have both and .
3.2. The Objective Function and Optimality
- (a)
- If there is a with but , the f does not have a subgradient at q. Indeed, there is a feasible descent direction of f at q with directional derivative .
- (b)
- Otherwise—i.e., for all , only if —subgradients exist. For all , let be a probability distribution on . Suppose that, for all with ,Then g defined by , for all , is a subgradient of f at q.Moreover, is a subgradient iff there exists such a g with
- for all with ;
- for all with ;
- , for each with ;
- , for each with ;
3.3. Algorithmic Approaches
3.3.1. Gradient Descent
| Algorithm 1: Gradient Descent |
 |
3.3.2. Interior Point Methods
3.3.3. Geometric Programming
3.3.4. Exponential Cone Programming
4. Computational Results
4.1. Data
- (1)
- Gates. The instances of the type (1) are based on the “gates” (Rdn, Unq, Xor, And, RdnXor, RdnUnqXor, XorAnd) described Table 1 of [1]:
- Rdn uniformly distributed.
- Unq , independent, uniformly distributed in .
- Xor , independent, uniformly distributed in .
- And , independent, uniformly distributed in .
- RdnXor , , , independent, uniformly distributed in .
- RdnUnqXor , ; , independent, uniformly distributed in .
- XorAnd , independent, uniformly distributed in .
Each gate gives rise to two sets of instances: (1a) the “unadulterated” probability distribution computed from the definition of the gate (see Table A1); (1b) empirical distributions generated by randomly sampling from and computing . In creating the latter instances, we incorporate “noise” by perturbing the output randomly with a certain probability. We used 5 levels of noise, corresponding to increased probabilities of perturbing the output. For example, And 0 refers to the empirical distribution of the And gate without perturbation (probability ), And 4 refers to the empirical distribution of the And gate with output perturbed with probability . The perturbation probabilities are: 0, , , , . (See Table A2 and Table A3). - (2)
- Example-31 instances. In Appendix A.2 of their paper, Bertschinger et al. discuss the following input probability distribution: are independent uniformly random in . They present this as an example that the optimization problem can be “ill-conditioned”. We have derived a large number of instances based on that idea, by taking uniformly distributed on , with ranging in and in . These instances are referred to as “independent” in Table A4. We also created “noisy” versions of the probability distributions by perturbing the probabilities. In the results, we split the instances into two groups according to whether the fraction is at most 2 or greater than 2. (The rationale behind the choice of the sizes of , , is the fact mentioned in Section 3.2, that the Hessian has a kernel in the tangent space if the ratio is high.)
- (3)
- Discretized gaussians.We wanted to have a type of instances which was radically different from the somewhat “combinatorial” instances (1) and (2). We generated (randomly) twenty covariance matrices between standard Gaussian random variables , , and . We then discretized the resulting continuous 3-dimensional Gaussian probability distribution by integrating numerically (We used the software Cuba [16] in version 4.2 for that) over boxes , , , ; and all of their translates which held probability mass at least .
4.2. Convex Optimization Software We Used
- CVXOPT [18] is written and maintained by Andersen, Dahl, and Vandenberghe. It transforms the general Convex Problems with nonlinear objective function into an epigraph form (see Section 2.1), before it deploys an Interior Point method. We used version 1.1.9.
- Artelys Knitro [19] is an optimization suite which offers four algorithms for general Convex Programming, and we tested all of them on (CP). The software offers several different convex programming solvers: We refer by “Knitro_Ip” to their standard Interior Point Method [20]; by “Knitro_IpCG” to their IPM with conjugate gradient (uses projected cg to solve the linear system [21]); “Knitro_As” is their Active Set Method [22]; “Knitro_SQP” designates their Sequential Quadratic Programming Method [19]. We used version 10.2.
- Ipopt [20] is a software for nonlinear optimization which can also deal with non-convex objectives. At its heart is an Interior Point Method (as the name indicates), which is enhanced by approaches to ensure convergence even in the non-convex case. We used version 3.0.
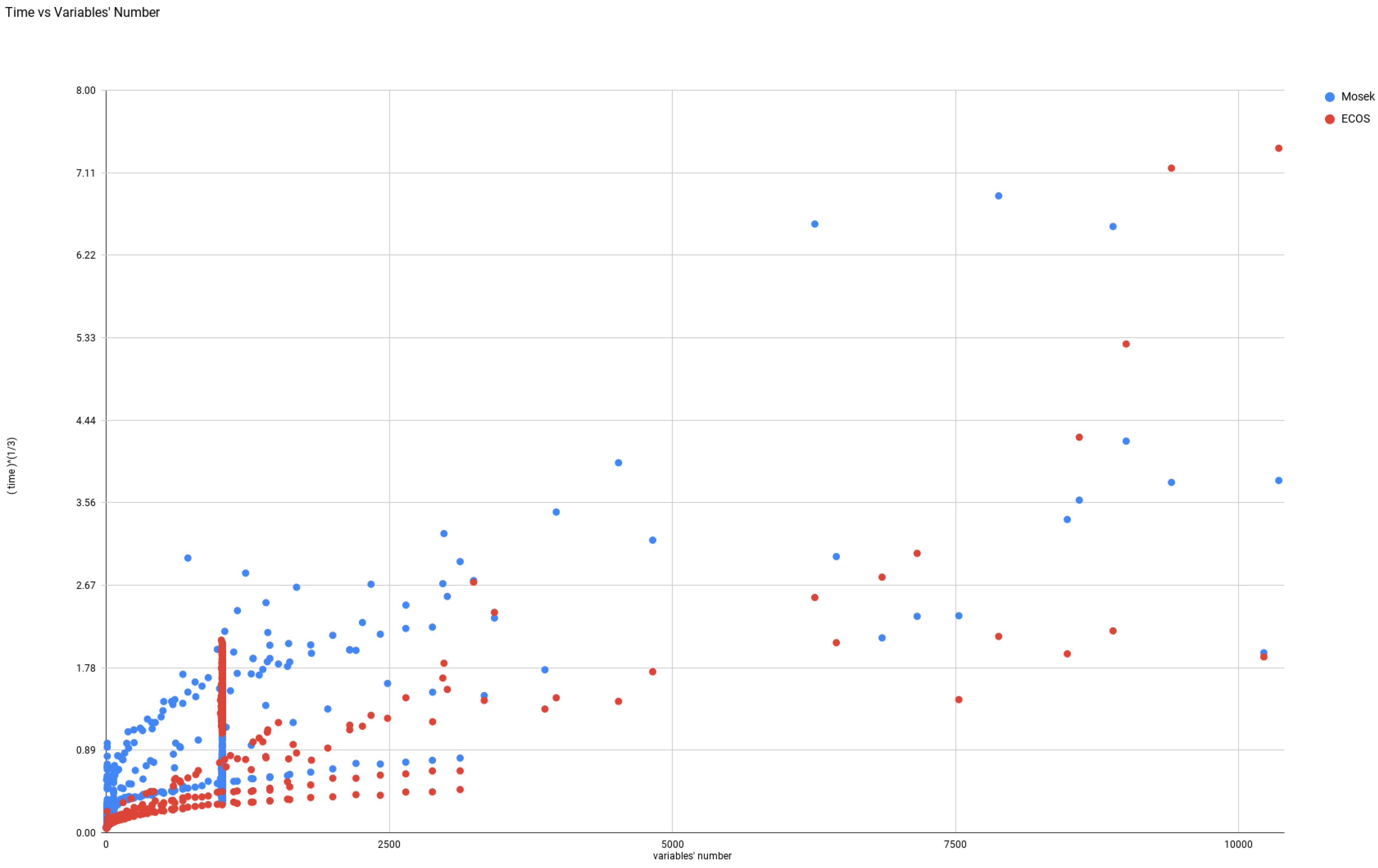
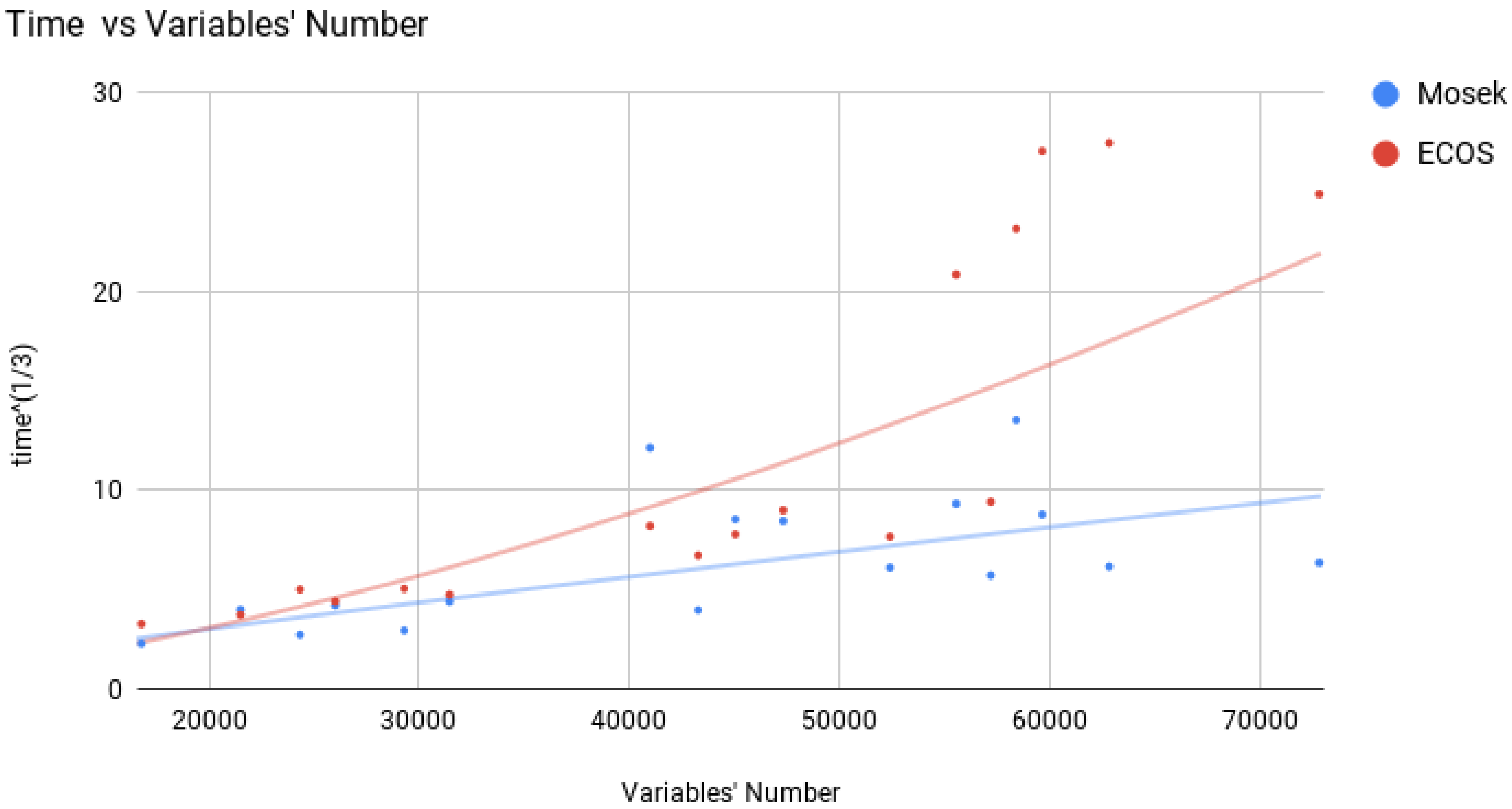
- ECOS. We are aware of only two Conic Optimization software toolboxes which allow to solve Exponential Cone Programs: ECOS and SCS.ECOS is a lightweigt numerical software for solving convex cone programs [26], using an Interior Point approach. We used the version from Nov 8, 2016.
4.3. Results
- the maximum amount by which any of the marginal equations is violated;
- the maximum amount by which any of the nonnegativity inequaities is violated;
- the maximum amount by which the inequality “” in Theorem 1 is violated;
- the maximum amount by which the complementarity is violated.
4.3.1. Gradient Descent
4.3.2. Interior Point algorithms
4.3.3. Geometric Programming: CVXOPT
4.3.4. Exponential Cone Programming: ECOS & SCS
4.3.5. Miscellaneous Approaches
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Tables of Instances and Computational Results
| Instance | CVXOPT | Knitro_Ip | Knitro_IpCG | Knitro_As | Knitro_SQP | Mosek | Ipopt | ECOS | GD | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | time () | |
| XOR | y | 1 | 0.06 | y | 0.7 | 0.31 | y | 98 | 0.8 | n | y | 2 | 0.63 | y | 0.18 | 0.28 | y | 0.15 | 1.5 | y | 0.03 | 0.001 | 25 | ||
| AND | y | 0.5 | 2 | y | 30 | 0.5 | y | 52 | 13 | n | n | y | 0.06 | 0.15 | y | 0.09 | 10 | y | 0.03 | 0.01 | 25 | ||||
| UNQ | y | 0.5 | 0.02 | y | 0.1 | 8 | y | 0.17 | 0.04 | n | y | 0.8 | 2 | n | 0.07 | n | y | 0.02 | 0.01 | 14 | |||||
| RDN | y | 0.4 | 0.007 | y | 0.07 | y | 0.09 | 0.38 | n | y | 0.1 | 4 | y | 0.03 | 0.025 | n | y | 0.02 | 0.002 | 15 | |||||
| XORAND | y | 0.6 | 2 | y | 0.2 | 0.53 | y | 0.9 | 0.14 | n | y | 0.6 | y | 0.09 | 0.2 | n | y | 0.03 | 0.005 | 14 | |||||
| RDNXOR | y | 3 | 0.12 | y | 0.2 | 0.06 | y | 271 | 0.3 | n | y | y | 0.2 | 2 | y | 0.2 | 2 | y | 0.05 | 0.002 | 24 | ||||
| RDNUNQXOR | y | 14 | 0.4 | y | 1.3 | 0.001 | y | 537 | 0.09 | n | n | y | 0.01 | 6 | y | 0.5 | 150 | y | 0.16 | 0.008 | 77 | ||||
| Instance | CVXOPT | Knitro_Ip | Knitro_IpCG | Knitro_As | Knitro_SQP | Mosek | Ipopt | ECOS | GD | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | avg. tm | |
| XOR 0 | 100 | 0.01 | 3 | 100 | 0.9 | 0.46 | 100 | 150 | 1.06 | 0 | 30 | 4 | 0.87 | 100 | 4 | 0.004 | 100 | 0.1 | 2 | 100 | 0.04 | 0.01 | 28 | ||
| XOR 1 | 100 | 2.2 | 3 | 100 | 1 | 0.98 | 89 | 254 | 2.02 | 0 | 17 | 4 | 0.67 | 100 | 1.9 | 0.0066 | 100 | 0.2 | 3 | 100 | 0.03 | 0.01 | 35 | ||
| XOR 2 | 100 | 2 | 3 | 100 | 1 | 0.92 | 63 | 259 | 1 | 0 | 26 | 9 | 0.91 | 100 | 12 | 0.0053 | 100 | 0.3 | 2 | 100 | 0.04 | 0.01 | 36 | ||
| XOR 3 | 99 | 2 | 4 | 100 | 1 | 0.96 | 70 | 363 | 1 | 0 | 27 | 7 | 0.99 | 100 | 7 | 0.0056 | 100 | 0.2 | 2 | 100 | 0.03 | 0.01 | 36 | ||
| XOR 4 | 100 | 1 | 4 | 100 | 1.3 | 1 | 98 | 40 | 1 | 0 | 20 | 13 | 0.98 | 100 | 8 | 0.0052 | 100 | 0.1 | 100 | 0.03 | 0.01 | 32 | |||
| AND 0 | 100 | 300 | 0.6 | 100 | 40 | 0.7 | 100 | 76 | 22.5 | 0 | 0 | 100 | 0.07 | 0.41 | 0 | 100 | 0.03 | 0.01 | 27 | ||||||
| AND 1 | 65 | 2 | 2 | 100 | 1 | 2.9 | 100 | 17 | 3.2 | 0 | 0 | 100 | 0.9 | 24 | 100 | 0.3 | 2 | 100 | 0.04 | 0.01 | 42 | ||||
| AND 2 | 67 | 3 | 1 | 100 | 2 | 1.7 | 100 | 4.9 | 4 | 0 | 0 | 100 | 1.2 | 0.11 | 100 | 0.3 | 100 | 0.04 | 0.01 | 40 | |||||
| AND 3 | 51 | 3 | 2 | 100 | 1.9 | 1.9 | 100 | 2 | 18 | 0 | 0 | 100 | 1.4 | 0.04 | 100 | 4 | 2 | 100 | 0.04 | 0.01 | 39 | ||||
| AND 4 | 54 | 2 | 2 | 100 | 1 | 5.4 | 100 | 2 | 9 | 0 | 0 | 100 | 0.5 | 41 | 100 | 0.5 | 4 | 100 | 0.04 | 0.01 | 40 | ||||
| UNQ 0 | 100 | 0.4 | 2 | 100 | 0.4 | 100 | 0.5 | 0.09 | 0 | 100 | 1.4 | 100 | 0.04 | 0 | 100 | 0.02 | 0.007 | 16 | |||||||
| UNQ 1 | 100 | 4 | 4 | 100 | 1 | 6 | 100 | 1.9 | 9 | 0 | 33 | 6 | 5 | 100 | 0.6 | 0.036 | 100 | 0.7 | 3 | 100 | 0.07 | 0.01 | 42 | ||
| UNQ 2 | 100 | 5 | 5 | 100 | 2 | 0.04 | 100 | 2 | 0.84 | 0 | 26 | 13 | 0.46 | 100 | 0.69 | 0.12 | 100 | 0.7 | 4 | 100 | 0.07 | 0.008 | 44 | ||
| UNQ 3 | 100 | 5 | 7 | 100 | 2 | 6 | 100 | 1 | 40 | 0 | 38 | 9 | 10 | 100 | 0.7 | 0.022 | 100 | 0.6 | 4 | 100 | 0.07 | 0.004 | 44 | ||
| UNQ 4 | 20 | 4 | 0.09 | 100 | 1.5 | 0.04 | 100 | 1 | 21 | 0 | 18 | 8 | 2.6 | 100 | 0.6 | 0.0019 | 100 | 0.7 | 3 | 100 | 0.08 | 0.005 | 42 | ||
| RDN 0 | – | 2 | 2 | 100 | 0.4 | 100 | 0.4 | 0.51 | 0 | 100 | 0.6 | 100 | 1 | 0.0029 | 30 | 0.5 | 100 | 0.02 | 0.01 | 16 | |||||
| RDN 1 | 0 | 100 | 1 | 2.8 | 100 | 1.2 | 2.8 | 0 | 8 | 2 | 100 | 0.3 | 0.005 | 100 | 0.3 | 2 | 100 | 0.04 | 0.01 | 41 | |||||
| RDN 2 | 0 | 100 | 1.9 | 6.7 | 100 | 1.9 | 6.2 | 0 | 14 | 4.5 | 100 | 1.1 | 0.01 | 100 | 0.5 | 2 | 100 | 0.04 | 0.01 | 40 | |||||
| RDN 3 | 0 | 100 | 1.7 | 4.1 | 100 | 1.8 | 9.8 | 0 | 35 | 4 | 2.7 | 100 | 0.4 | 2 | 100 | 0.6 | 4 | 100 | 0.05 | 0.01 | 41 | ||||
| RDN 4 | 1 | 12 | 2 | 100 | 0.9 | 0.07 | 100 | 0.8 | 1 | 0 | 3 | 3 | 100 | 0.2 | 100 | 0.4 | 4 | 100 | 0.04 | 0.008 | 41 | ||||
| Instance | CVXOPT | Knitro_Ip | Knitro_IpCG | Knitro_As | Knitro_SQP | Mosek | Ipopt | ECOS | GD | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | avg. tm | Opt meas. | % solved | time () | opt. meas. () | time () | |
| XORAND 0 | 100 | 0.6 | 20 | 100 | 0.6 | 0.74 | 100 | 0.9 | 0.2 | 0 | 100 | 2 | 100 | 0.1 | 0.4 | 0 | 100 | 0.03 | 0.01 | 27 | |||||
| XORAND 1 | 94 | 6 | 100 | 1.1 | 5 | 100 | 5 | 6.2 | 0 | 35 | 9 | 4.9 | 100 | 1 | 0.5 | 100 | 0.6 | 8 | 100 | 0.08 | 18 | 43 | |||
| XORAND 2 | 67 | 8 | 12.6 | 100 | 2 | 6.2 | 100 | 10 | 8.2 | 0 | 15 | 22 | 5.4 | 100 | 1.3 | 0.4 | 100 | 0.8 | 100 | 0.09 | 0.01 | 42 | |||
| XORAND 3 | 12 | 100 | 2 | 5.7 | 100 | 2 | 8.7 | 0 | 15 | 16 | 6.9 | 100 | 1.3 | 2.2 | 100 | 1 | 6 | 100 | 0.1 | 0.03 | 42 | ||||
| XORAND 4 | 0 | 100 | 2 | 7.2 | 100 | 3 | 8 | 0 | 93 | 2 | 100 | 0.7 | 40 | 100 | 0.8 | 4 | 100 | 0.1 | 0.04 | 43 | |||||
| RDNXOR 0 | 100 | 3 | 3.11 | 100 | 1 | 0.46 | 70 | 407 | 1 | 0 | 30 | 6 | 0.23 | 100 | 1 | 2 | 100 | 0.2 | 2 | 100 | 0.06 | 0.01 | 27 | ||
| RDNXOR 1 | 0 | 100 | 3.5 | 18.2 | 100 | 2 | 30 | 0 | 0 | 100 | 25 | 5 | 1 | 261 | 0.016 | 100 | 0.3 | 0.01 | 40 | ||||||
| RDNXOR 2 | 1 | 190 | 170 | 100 | 9 | 60 | 100 | 3 | 250 | 0 | 0 | 100 | 250 | 50 | 90 | 10 | 1.9 | 100 | 0.4 | 0.01 | 41 | ||||
| RDNXOR 3 | 0 | 100 | 8 | 93 | 100 | 3 | 30 | 0 | 1 | 100 | 15 | 0.01 | 99 | 4.7 | 0.02 | 100 | 0.3 | 0.01 | 40 | ||||||
| RDNXOR 4 | 1 | 145 | 2 | 100 | 6 | 90 | 100 | 5 | 31 | 0 | 0 | 100 | 15 | 0.01 | 100 | 5 | 0.02 | 100 | 0.4 | 0.01 | 43 | ||||
| RDNUNQXOR 0 | 90 | 25 | 3 | 100 | 2 | 0.34 | 100 | 636 | 1 | 0 | 0 | 100 | 6 | 0.2 | 100 | 0.7 | 234 | 100 | 0.3 | 0.008 | 75 | ||||
| RDNUNQXOR 1 | 0 | 100 | 57 | 297 | 100 | 34 | 107 | 0 | 0 | 100 | 269 | 0.4 | 0 | 100 | 200 | 0.01 | 1156 | ||||||||
| RDNUNQXOR 2 | 0 | 100 | 110 | 364 | 100 | 60 | 128 | 0 | 0 | 100 | 483 | 4 | 0 | 100 | 195 | 0.01 | 1170 | ||||||||
| RDNUNQXOR 3 | 0 | 100 | 130 | 561 | 100 | 91 | 597 | 0 | 0 | 100 | 307 | 20 | 0 | 100 | 224 | 0.01 | 1140 | ||||||||
| RDNUNQXOR 4 | 0 | 100 | 129 | 422 | 100 | 132 | 0 | 0 | 100 | 388 | 0.003 | 92 | 437 | 207 | 100 | 555 | 0.024 | 1160 | |||||||
| Instance | CVXOPT | Mosek | Ipopt | ECOS | GD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | time () | |
| Independent 1 | 100 | 28 | 1.15 | 100 | 4 | 9 | 100 | 18 | 3 | 100 | 0.5 | 0.01 | 100 |
| Independent 2 | 100 | 255 | 0.2 | 100 | 22 | 0.003 | 92 | 437 | 207 | 100 | 2 | 0.02 | 802 |
| Noisy 1 | 34 | 113 | 2 | 100 | 87 | 0.008 | 38 | 6.2 | 2 | 100 | 2.8 | 0.014 | 100 |
| Noisy 2 | 0 | 100 | 648 | 0.011 | 7 | 602 | 2 | 100 | 8 | 0.016 | 813 | ||
| Instance | CVXOPT | Knitro_Ip | Knitro_IpCG | Knitro_As | Knitro_SQP | Mosek | Ipopt | ECOS | GD | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | % solved | time () | opt. meas. () | time () | |
| Gauss-1 | 0 | 21 | 820 | 4 | 0 | 0 | 0 | 71 | 0.27 | 0.4 | 0 | 100 | 4.2 | 0.19 | 1940 | ||||||||||
| Gauss-2 | 0 | 2.7 | 950 | 10 | 5 | 1020 | 300 | 0 | 0 | 75 | 7.6 | 4 | 0 | 96 | 52 | 1.06 | 1890 | ||||||||
| Gauss-3 | 0 | 0 | 11 | 2170 | 900 | 0 | 0 | 65 | 551 | 2 | 0 | 96 | 632 | 6 | – | ||||||||||
| Gauss-4 | 0 | 0 | 7 | 2560 | 2000 | 0 | 0 | 57 | 4 | 60 | 0 | 75 | 3 | 400 | – | ||||||||||
References
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided Self-Organization: Inception; Springer: New York, NY, USA, 2014; pp. 159–190. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared information—New insights and problems in decomposing information in complex systems. In Proceedings of the European Conference on Complex Systems, Brussels, Belgium, 2–7 September 2012; Springer: Cham, Switzerland, 2013; pp. 251–269. [Google Scholar]
- Nemirovski, A. Efficient Methods in Convex Programming. Available online: http://www2.isye.gatech.edu/~nemirovs/Lect_EMCO.pdf (accessed on 6 October 2017).
- Wibral, M.; Priesemann, V.; Kay, J.W.; Lizier, J.T.; Phillips, W.A. Partial information decomposition as a unified approach to the specification of neural goal functions. Brain Cognit. 2017, 112, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Ruszczyński, A.P. Nonlinear Optimization; Princeton University Press: Princeton, NJ, USA, 2006; Volume 13. [Google Scholar]
- Bubeck, S.; Eldan, R. The entropic barrier: A simple and optimal universal self-concordant barrier. arXiv, 2014; arXiv:1412.1587. [Google Scholar]
- Bubeck, S.; Eldan, R. The entropic barrier: A simple and optimal universal self-concordant barrier. In Proceedings of the 28th Conference on Learning Theory, Paris, France, 3–6 July 2015. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Makkeh, A. Applications of Optimization in Some Complex Systems. Ph.D. Thesis, University of Tartu, Tartu, Estonia, 2017. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Boyd, S.; Kim, S.J.; Vandenberghe, L.; Hassibi, A. A tutorial on geometric programming. Optim. Eng. 2007, 8, 67–127. [Google Scholar] [CrossRef]
- Chares, R. Cones and interior-point algorithms for structured convex optimization involving powers and exponentials. Doctoral dissertation, UCL-Université Catholique de Louvain, Louvain-la-Neuve, Belgium, 2009. [Google Scholar]
- Hahn, T. CUBA—A library for multidimensional numerical integration. Comput. Phys. Commun. 2005, 168, 78–95, [hep-ph/0404043]. [Google Scholar] [CrossRef]
- Lubin, M.; Dunning, I. Computing in operations research using Julia. INFORMS J. Comput. 2015, 27, 238–248. [Google Scholar] [CrossRef]
- Sra, S.; Nowozin, S.; Wright, S.J. Optimization for Machine Learning; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Byrd, R.; Nocedal, J.; Waltz, R. KNITRO: An Integrated Package for Nonlinear Optimization. In Large-Scale Nonlinear Optimization; Springer: New York, NY, USA, 2006; pp. 35–59. [Google Scholar]
- Waltz, R.A.; Morales, J.L.; Nocedal, J.; Orban, D. An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Program. 2006, 107, 391–408. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Byrd, R.H.; Gould, N.I.; Nocedal, J.; Waltz, R.A. An algorithm for nonlinear optimization using linear programming and equality constrained subproblems. Math. Program. 2004, 100, 27–48. [Google Scholar] [CrossRef]
- ApS, M. Introducing the MOSEK Optimization Suite 8.0.0.94. Available online: http://docs.mosek.com/8.0/pythonfusion/intro_info.html (accessed on 6 October 2017).
- Andersen, E.D.; Ye, Y. A computational study of the homogeneous algorithm for large-scale convex optimization. Comput. Optim. Appl. 1998, 10, 243–269. [Google Scholar] [CrossRef]
- Andersen, E.D.; Ye, Y. On a homogeneous algorithm for the monotone complementarity problem. Math. Program. 1999, 84, 375–399. [Google Scholar] [CrossRef]
- Domahidi, A.; Chu, E.; Boyd, S. ECOS: An SOCP solver for embedded systems. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3071–3076. [Google Scholar]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. Conic Optimization via Operator Splitting and Homogeneous Self-Dual Embedding. J. Optim. Theory Appl. 2016, 169, 1042–1068. [Google Scholar]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. SCS: Splitting Conic Solver, Version 1.2.7. Available online: https://github.com/cvxgrp/scs (accessed on 6 October 2017).
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. Available online: http://cvxr.com/cvx (accessed on 6 October 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makkeh, A.; Theis, D.O.; Vicente, R. Bivariate Partial Information Decomposition: The Optimization Perspective. Entropy 2017, 19, 530. https://doi.org/10.3390/e19100530
Makkeh A, Theis DO, Vicente R. Bivariate Partial Information Decomposition: The Optimization Perspective. Entropy. 2017; 19(10):530. https://doi.org/10.3390/e19100530
Chicago/Turabian StyleMakkeh, Abdullah, Dirk Oliver Theis, and Raul Vicente. 2017. "Bivariate Partial Information Decomposition: The Optimization Perspective" Entropy 19, no. 10: 530. https://doi.org/10.3390/e19100530
APA StyleMakkeh, A., Theis, D. O., & Vicente, R. (2017). Bivariate Partial Information Decomposition: The Optimization Perspective. Entropy, 19(10), 530. https://doi.org/10.3390/e19100530





