Abstract
Accurately determining dependency structure is critical to understanding a complex system’s organization. We recently showed that the transfer entropy fails in a key aspect of this—measuring information flow—due to its conflation of dyadic and polyadic relationships. We extend this observation to demonstrate that Shannon information measures (entropy and mutual information, in their conditional and multivariate forms) can fail to accurately ascertain multivariate dependencies due to their conflation of qualitatively different relations among variables. This has broad implications, particularly when employing information to express the organization and mechanisms embedded in complex systems, including the burgeoning efforts to combine complex network theory with information theory. Here, we do not suggest that any aspect of information theory is wrong. Rather, the vast majority of its informational measures are simply inadequate for determining the meaningful relationships among variables within joint probability distributions. We close by demonstrating that such distributions exist across an arbitrary set of variables.
Keywords:
stochastic process; transfer entropy; causation entropy; partial information decomposition; network science PACS:
89.70.+c; 05.45.Tp; 02.50.Ey; 02.50.−r
1. Introduction
Information theory is a general, broadly applicable framework for understanding a system’s statistical properties [1]. Due to its focus on probability distributions, it allows one to compare dissimilar systems (e.g., species abundance to ground state configurations of a spin system) and has found many successes in the physical, biological and social sciences [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] far outside its original domain of communication. Often, the issue on which it is brought to bear is discovering and quantifying dependencies [20,21,22,23,24,25]. Here, we define a dependency to be any deviation from statistical independence. It is possible for a single multivariate distribution to consist of many, potentially overlapping, dependencies. Consider the simple case of three variables X, Y, Z, where X and Y are coin flips and Z is their concatenation. We would say here that there are two dependencies: an dependency and a dependency. It is important to note that, though there are some similarities, this notion of a dependency is distinct from that used within the Bayesian network community.
The past two decades, however, produced a small, but important body of results detailing how standard Shannon information measures are unsatisfactory for determining some aspects of dependency and shared information. Within information-theoretic cryptography, the conditional mutual information has proven to be a poor bound on secret key agreement [26,27]. The conditional mutual information has also been shown to be unable to accurately measure information flow ([28] and references therein). Finally, the inability of standard methods of decomposing the joint entropy to provide any semantic understanding of how information is shared has motivated entirely new methods of decomposing information [29,30]. Common to all these is the fact that conditional mutual information conflates intrinsic dependence with conditional dependence. To be clear, the conditional mutual information between X and Y given Z cannot distinguish the case where X and Y are related ignoring Z (intrinsic dependence) from the case where X and Y are related due to the influence of Z (conditional dependence).
Here, we demonstrate a related, but deeper issue: Shannon information measures—entropy, mutual information and their conditional and multivariate versions—can fail to distinguish joint distributions with vastly differing internal dependencies.
Concretely, we start by constructing two joint distributions, one with dyadic sub-dependencies and the other with strictly triadic sub-dependencies. From there, we demonstrate that no standard Shannon-like information measure, and exceedingly few nonstandard methods, can distinguish the two. Stated plainly: when viewed through Shannon’s lens, these two distributions are erroneously equivalent. While distinguishing these two (and their internal dependencies) may not be relevant to a mathematical theory of communication, it is absolutely critical to a mathematical theory of information storage, transfer and modification [31,32,33,34]. We then demonstrate two ways in which these failures generalize to the multivariate case. The first generalizes our two distributions to the multivariate and polyadic case via “dyadic camouflage”. The second details a method of embedding an arbitrary distribution into a larger variable space using hierarchical dependencies, a technique we term “dependency diffusion”. In this way, one sees that the initial concerns about information measures can arise in virtually any statistical multivariate analysis. In this short development, we assume a working knowledge of information theory, such as found in standard textbooks [35,36,37,38].
2. Development
We begin by considering the two joint distributions shown in Table 1. The first represents dyadic relationships among three random variables X, Y, and Z. Additionally, the second, the triadic relationships among them. (This distribution was first considered as RDNXOR in [39], though for other, but related reasons.) These appellations are used for reasons that will soon be apparent. How are these distributions structured? Are they structured identically or are they qualitatively distinct? It is clear from inspection that they are not identical, but a lack of isomorphism is less obvious.

Table 1.
The (a) dyadic and (b)triadic probability distributions over the three random variables X, Y and Z that take values in the four-letter alphabet . Though not directly apparent from their tables of joint probabilities, the dyadic distribution is built from dyadic (pairwise) sub-dependencies, while the triadic from triadic (three-way) sub-dependencies.
We can develop a direct picture of underlying dependency structure by casting the random variables’ four-symbol alphabet used in Table 1 into composite binary random variables, as displayed in Table 2. It can be readily verified that the dyadic distribution follows three simple rules: , and ; in particular, three dyadic rules. The triadic distribution similarly follows simple rules: (the xor relation [40], or equivalently, any one of them is the xor of the other two), and ; two triadic rules.

Table 2.
Expansion of the (a) dyadic and (b) triadic distributions. In both cases, the variables from Table 1 were interpreted as two binary random variables, translating, e.g., into . In this light, it becomes apparent that the dyadic distribution consists of the sub-dependencies , and , while the triadic distribution consists of and . These relationships are pictorially represented in Figure 1.
While this expansion to binary sub-variables is not unique, it is representative of the distributions. One could expand the dyadic distribution, for example, in such a way that some of the sub-variables would be related by xor. However, those same sub-variables would necessarily be involved in other relationships, limiting their expression in a manner similar to that explored in [41]. This differs from our triadic distribution in that its two sub-dependencies are independent. That these binary expansions are, in fact, representative and that the triadic distribution cannot be written in a way that relies only on dyadic relationships can be seen in the connected information explored later in the section. For the dyadic distribution, there is no difference between the maximum entropy distribution constraining pairwise interactions from the distribution itself. However, the maximum entropy distribution obtained by constraining the pairwise interactions in the triadic distribution has a larger entropy than the triadic distribution itself, implying that there is structure that exists beyond the pairwise interactions.
These dependency structures are represented pictorially in Figure 1. Our development from this point on will not use any knowledge of these structures, but rather, it will attempt to distinguish the structures using only information measures.
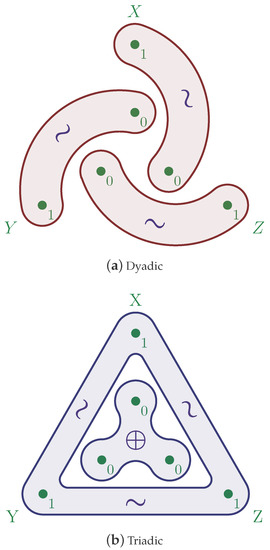
Figure 1.
Dependency structure for the (a) dyadic and (b) triadic distributions. Here, ∼ denotes that two or more variables are distributed identically, and ⊕ denotes the enclosed variables form the xor relation. Note that although these dependency structures are fundamentally distinct, their information diagrams (Figure 2) are identical.
What does an information-theoretic analysis say? Both the dyadic and triadic distributions describe events over three variables, each with an alphabet size of four. Each consists of eight joint events, each with a probability of 1/8. As such, each has a joint entropy of bit (The SI standard unit for time is the second, and its symbol is s; analogously, the standard (IEC 60027-2, ISO/IEC 80000-13) unit for information is the bit, and its symbol is bit. As such, it is inappropriate to write 3 bits, just as it would be inappropriate to write 3 ss). Our first observation is that any entropy—conditional or not—and any mutual information—conditional or not—will be identical for the two distributions. Specifically, the entropy of any variable conditioned on the other two vanishes: bit; the mutual information between any two variables conditioned on the third is unity: bit; and the three-way co-information also vanishes: bit. These conclusions are compactly summarized in the form of the information diagrams (I-diagrams) [42,43] shown in Figure 2. This diagrammatically represents all of the possible Shannon information measures (I-measures) [43] of the distribution: effectively, all the multivariate extensions of the standard Shannon measures, called atoms. It is important to note that the analogy between information theory and set theory should not be taken too far: while set cardinality is strictly nonnegative, information atoms need not be; see [38] for more details. The values of the information atoms are identical between the two distributions.
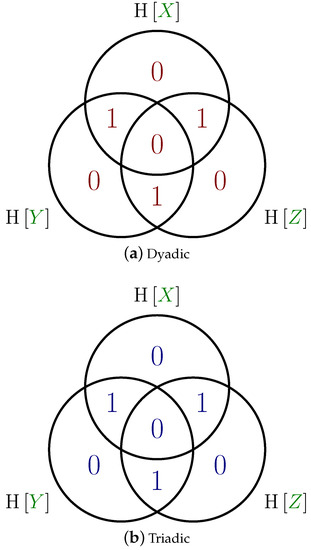
Figure 2.
Information diagrams for the (a) dyadic and (b) triadic distributions. For the three-variable distributions depicted here, the diagram consists of seven atoms: three conditional entropies (each with value 0 bit), three conditional mutual information (each with value 1 bit) and one co-information (0 bit). Note that the two diagrams are identical, meaning that although the two distributions are fundamentally distinct, no standard information-theoretic measure can differentiate the two.
As a brief aside, it is of interest to note that it has been suggested (e.g., in [44,45], among others) that zero co-information implies that at least one variable is independent of the others; that is, in this case, a lack of three-way interactions. Krippendorff [46] early on demonstrated that this is not the case, though these examples more clearly exemplify this fact.
We now turn to the implications of the two information diagrams, Figure 2a,b, being identical. There are measures [20,22,44,47,48,49,50,51,52,53] and expansions [54,55,56] purporting to measure or otherwise extract the complexity, magnitude or structure of dependencies within a multivariate distribution. Many of these techniques, including those just cited, are sums and differences of atoms in these information diagrams. As such, they are unable to differentiate these distributions.
To drive home the point that the concerns raised here are very broad, Table 3 enumerates the result of applying a great many information measures to this pair of distributions. It is organized from top to bottom into four sections: entropies, mutual information, common information and other measures.

Table 3.
Suite of information measures applied to the dyadic and triadic distributions, where: H [•] is the Shannon entropy [35], H2 [•] is the order-2 Rényi entropy [61], Sq [•] is the Tsallis entropy [62], I [•] is the co-information [44], T [•] is the total correlation [47], B [•] is the dual total correlation [48,63], J [•] is the CAEKL mutual information [49], II [•] is the interaction information [64], K [•] is the Gács–Körner common information [57], C [•] is the Wyner common information [65,66], G [•] is the exact common information [67], F [•] is the functional common information, M [•] is the MSS common information, I [• ↓ •] is the intrinsic mutual information [26], I [• ⇓ •] is the reduced intrinsic mutual information [27], X [•] is the extropy [68], R [•] is the residual entropy or erasure entropy [60,63], P [•] is the perplexity [69], D [•] is the disequilibrium [51], CLMRP [•] is the LMRP complexity [51] and TSE [•] is the TSE complexity [59]. Only the Gács–Körner common information and the intrinsic mutual information, highlighted, are able to distinguish the two distributions; the Gács–Körner common information via the construction of a sub-variable () common to X, Y and Z and the intrinsic mutual information via the relationship being independent of Z.
None of the entropies, dependent only on the probability mass function of the distribution, can distinguish the two distributions. Nor can any of the mutual information, as they are functions of the information atoms in the I-diagrams of Figure 2.
The common information, defined via auxiliary variables satisfying particular properties, can potentially isolate differences in the dependencies. Though only one of them—the Gács–Körner common information K [•] [57,58], involving the construction of the largest “subrandom variable” common to the variables—discerns that the two distributions are not equivalent because the triadic distribution contains the subrandom variable common to all three variables.
Finally, only two of the other measures identify any difference between the two. Some fail because they are functions of the probability mass function. Others, like the TSE complexity [59] and erasure entropy [60], fail since they are functions of the I-diagram atoms. Only the intrinsic mutual information I [• ↓ •] [26] and the reduced mutual information I [• ⇓ •] [27] distinguish the two since the dyadic distribution contains three dyadic sub-variables each of which is independent of the third variable, whereas in the triadic distribution, the conditional dependence of the xor relation can be destroyed.
Figure 3 demonstrates three different information expansions—that, roughly speaking, group variables into subsets of difference sizes or “scales”—applied to our distributions of interest. The first is the complexity profile [55]. At scale k, the complexity profile is the sum of all I-diagram atoms consisting of at least k variables conditioned on the others. Here, since the I-diagrams are identical, so are the complexity profiles. The second profile is the marginal utility of information [56], which is a derivative of a linear programming problem whose constraints are given by the I-diagram, so here, again, they are identical. Finally, we have Schneidman et al.’s connected information [70], which comprise the differences in entropies of the maximum entropy distributions whose k- and -way marginals are fixed to match those of the distribution of interest. Here, all dependencies are detected once pairwise marginals are fixed in the dyadic distribution, but it takes the full joint distribution to realize the xor sub-dependency in the triadic distribution.
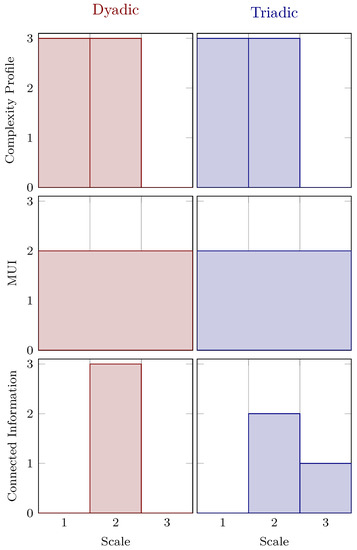
Figure 3.
Suite of information expansions applied to the dyadic and triadic distributions: the complexity profile [55], the marginal utility of information [56] and the connected information [70]. The complexity profile and marginal utility of information profiles are identical for the two distributions as a consequence of the information diagrams (Figure 2) being identical. The connected information, quantifying the amount of dependence realized by fixing k-way marginals, is able to distinguish the two distributions. Note that although each of the x-axes is a scale, exactly what that means depends on the measure. Furthermore, while the scale for both the complexity profile and the connected information is discrete, the scale for the marginal utility of information is continuous.
While it is well known that causality cannot be determined from probability distributions alone [71], here we point out a related, though different issue. While causality is, in some sense, the determination of the precedence within a dependency, the results above demonstrate that many measures of Granger-like causality are insensitive to the order (dyadic, triadic, etc.) of a dependency (Note that here we do not demonstrate that the order of a dependency cannot be determined from the probability distribution, as Pearl has done for causality [71]. Rather, our demonstration is limited to Shannon-like information measures.). Neither the transfer entropy [20], the transinformation [53], the directed information [52], the causation entropy [22], nor any of their generalizations based on conditional mutual information differentiate between intrinsic relationships and those induced by the variables they condition on (As discussed there, the failure of these measures stems from the possibility of conditional dependence, whereas the aim for these directed measures is to quantify the information flow from one time series to another excluding the influences of the second. In this light, we propose [26] as an incremental improvement over the transfer entropy). This limitation underlies prior criticisms of these functions as measures of information flow [28]. Furthermore, separating out these contributions to the transfer entropy has been discussed in the context of the partial information decomposition in [72].
A promising approach to understanding informational dependencies is the partial information decomposition (PID) [29]. This framework seeks to decompose a mutual information of the form I[(I0,I1):O] into four nonnegative components: the information R that both inputs and redundantly provide the output O, the information that uniquely provides O, the information that uniquely provides O and, finally, the information S that both and synergistically or collectively provide O.
Under this decomposition, our two distributions take on very different characteristics (Here, we quantified the partial information lattice using the best-in-class technique of [73], though calculations using three other techniques [74,75,76] match. There is a recent debate suggesting that the measure of Bertschinger et al. is not in fact correct, but it is likely, due to the agreement among these measures, that any “true” measure of redundancy would result in the same decomposition. The original PID measure , however, assigns both distributions: 1 bit of redundant information and 1 bit of synergistic information.). For both, the decomposition is invariant as far as which variables are selected as , and O. For the dyadic distribution, PID identifies both bits in I[(I0,I1):O] as unique, one from each input , corresponding to the dyadic sub-dependency shared by and O. Orthogonally, for the triadic distribution PID identifies one of the bits as redundant, stemming from , and the other as synergistic, resulting from the xor relation among , and . These decompositions are displayed pictorially in Figure 4.
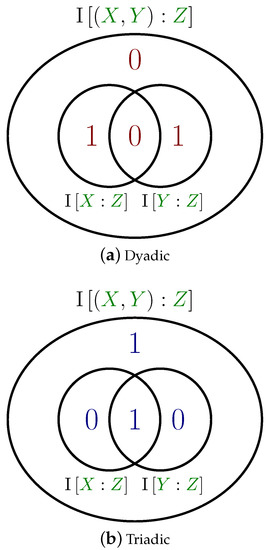
Figure 4.
Partial information decomposition diagrams for the (a) dyadic and (b) triadic distributions. Here, X and Y are treated as inputs and Z as output, but in both cases, the decomposition is invariant to permutations of the variables. In the dyadic case, the relationship is realized as 1 bit of unique information from X to Z and 1 bit of unique information from Y to Z. In the triadic case, the relationship is quantified as X and Y providing 1 bit of redundant information about Z while also supplying 1 bit of information synergistically about Z.
Another somewhat similar approach is that of integrated information theory [77]. However, this approach requires a known dynamic over the variables and is, in addition, highly sensitive to the dynamic. Here, in contrast, we considered only simple probability distributions without any assumptions as to how they might arise from the dynamics of interacting agents. That said, one might associate an integrated information measure with a distribution via the maximal information integration over all possible dynamics that give rise to the distribution. We leave this task for a later study.
3. Discussion
The broad failure of Shannon information measures to differentiate the dyadic and polyadic distributions has far-reaching consequences. Consider, for example, an experiment where a practitioner places three probes into a cluster of neurons, each probe touching two neurons and reporting zero when they are both quiescent, one when the first is excited but the second quiescent, two when the second is excited, but the first quiescent, and three when both are excited. Shannon-like measures—including the transfer entropy and related measures—would be unable to differentiate between the dyadic situation consisting of three pairs of synchronized neurons, the triadic situation consisting of a trio of synchronized neurons and a trio exhibiting the xor relation, a relation requiring nontrivial sensory integration. Such a situation might arise when probing the circuitry of the Drosophila melanogaster connectome [78], for instance.
Furthermore, while partitioning each variable into sub-variables made the dependency structure clear, we do not believe that such a refinement should be a necessary step in discovering such a structure. Consider that we demonstrated that refinement is not strictly needed, since the partial information decomposition (as quantified using current techniques) was able to discover the distribution’s internal structure without it.
These results, observations and the broad survey clearly highlight the need to extend Shannon’s theory. In particular, the extension must introduce a fundamentally new measure, not merely sums and differences of the standard Shannon information measures. While the partial information decomposition was initially proposed to overcome the interpretational difficulty of the (potentially negative valued) co-information, we see here that it actually overcomes a vastly more fundamental weakness with Shannon information measures. While negative information atoms can subjectively be seen as a flaw, the inability to distinguish dyadic from polyadic relations is a much deeper and objective issue.
This may lead one to consider the partial information decomposition as the needed extension to Shannon theory. As it currently stands, we do not. The partial information decomposition depends on interpreting some random variables as “inputs” and others as “outputs”. While this may be perfectly natural in some contexts, it is not satisfactory in general. It is possible that, were an agreeable multivariate partial information measure to be developed, the decomposition of, e.g., could lead to a satisfactory symmetric decomposition. In any case, there has been longstanding interest in creating a symmetric decomposition analogous to the partial information decomposition [46] with some recent progress [79,80,81].
4. Dyadic Camouflage and Dependency Diffusion
The dyadic and triadic distributions we analyzed thus far were deliberately chosen to have small dimensionality in an effort to make them and the failure of Shannon information measures as comprehensible and intuitive as possible. Since a given dataset may have exponentially many different three-variable subsets, even just the two distributions examined here represent hurdles that information-based methods of dependency assessment must overcome. However, this is simply a starting point. We will now demonstrate that there exist distributions of arbitrary size whose k-way dependencies are masked, meaning the k-way co-information () are all zero, and so, from the perspective of Shannon information theory, are indistinguishable from a distribution of the same size containing only dyadic relationships. Furthermore, we show how any such distribution may be obfuscated over any larger set of variables. This likely mandates a search over all partitions of all subsets of a system, making the problem of finding such distributions in the EXPTIME computational complexity class [82], meaning such a procedure will take time exponential in the size of the distribution.
Specifically, consider the four-variable parity distribution consisting of four binary variables such that . This is a straightforward generalization of the xor distribution used in constructing the triadic distribution. We next need a generalization of the “giant bit” [63], which we call dyadic camouflage, to mix with the parity, informationally “canceling out” the higher-order mutual information even though dependencies of such orders exist in the distribution. An example dyadic camouflage distribution for four variables is given in Figure 5.
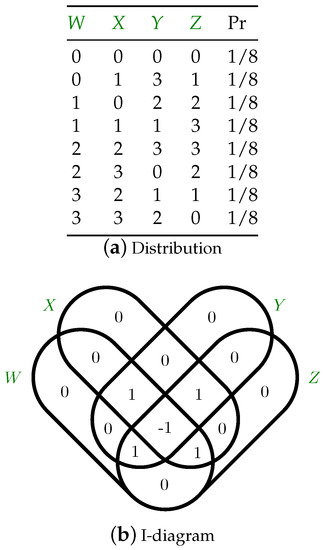
Figure 5.
Dyadic camouflage distribution: This distribution, when uniformly and independently mixed with the four-variable parity distribution (in which each variable is the parity of the other three), results in a distribution whose I-diagram incorrectly implies that the distribution contains only dyadic dependencies. The atoms of the camouflage distribution are constructed so that they cancel out the “interior” atoms of the parity distribution (whose and ), leaving just the parity distribution’s pairwise conditional atoms: , , , , , and , all equal to one, while all others are zero.
Generically, consider an n-variable parity distribution, that is a distribution where . It has an associated n-variable dyadic camouflage distribution with an alphabet size for each random variable of , and the entire joint distribution consists of equally likely outcomes, both numbers determined due to entropy considerations. Specifically, in a parity distribution, each variable has 1 bit of entropy, and when mixed with its camouflage, it should have bits. Therefore, each variable in the camouflage distribution needs bits of entropy and needs, with uniform probability over those outcomes, characters in the alphabet. Furthermore, since the parity distribution itself has bits total, while its camouflaged form will have n choose two (=) bits and, again with uniform probability, there must be outcomes. The distribution is constrained such that any two variables are completely determined by the remaining . Moreover, each m-variable () sub-distribution consists of m mutually independent random variables.
The goal, then, is to construct such a distribution. One method of doing so is to begin by writing down one variable in increasing lexicographic order such that it has the correct number of outcomes; e.g., column W in Figure 5a. Then, find permutations of this column such that any two columns are determined from the remaining . While such a search may be difficult, a distribution with these properties provably exists [83].
Finally, one can obfuscate any distribution by embedding it in a larger collection of random variables. Given a distribution D over n variables, associate each random variable i of D with a k-variable subset of a distribution in such a way that there is a mapping from the k-outcomes in the subset of to the outcome of the variable i in D. For example, one can embed the xor distribution over into six variables via , and . In other words, the parity of is equal to the xor of the parities of and . In this way, one must potentially search over all partitions of all subsets of in order to discover the distribution D hiding within. We refer to this method of obfuscation as dependency diffusion.
The first conclusion is that the challenges of conditional dependence can be found in joint distributions over arbitrarily large sets of random variables. The second conclusion, one that heightens the challenge to discovery, is that even finding which variables are implicated in polyadic dependencies can be exponentially difficult. Together, the camouflage and diffusion constructions demonstrate how challenging it is to discover, let alone work with, multivariate dependencies. This difficulty strongly implies that the current state of information-theoretic tools is vastly underpowered for the types of analyses required of our modern, data-rich sciences.
It is unlikely that the parity plus dyadic camouflage distribution discussed here is the only example of Shannon measures conflating the arity of dependencies and thus producing an information diagram identical to that of a qualitatively distinct distribution. This suggests an important challenge: find additional, perhaps simpler, joint distributions exhibiting this phenomenon.
5. Conclusions
To conclude, we constructed two distributions that cannot be distinguished using conventional (and many non-conventional) Shannon-like information measures. In fact, of the more than two dozen measures we surveyed, only five were able to separate the distributions: the Gács–Körner common information, the intrinsic mutual information, the reduced intrinsic mutual information, the connected information and the partial information decomposition.
The failure of the Shannon-type measures is perhaps not surprising: nothing in the standard mathematical theories of information and communication suggests that such measures should be able to distinguish these distributions [84]. However, distinguishing dependency structures such as dyadic from triadic relationships is of the utmost importance to the sciences; consider for example determining multi-drug interactions in medical treatments. Critically, since interpreting dependencies in random distributions is traditionally the domain of information theory, we propose that new extensions to information theory are needed.
These results may seem like a deal-breaking criticism of employing information theory to determine dependencies. Indeed, these results seem to indicate that much existing empirical work and many interpretations have simply been wrong and, worse even, that the associated methods are misleading while appearing quantitatively consistent. We think not, though. With the constructive and detailed problem diagnosis given here, at least we can see this issue. It is now a necessary step to address it. This leads us to close with a cautionary quote:
“The tools we use have a profound (and devious!) influence on our thinking habits, and, therefore, on our thinking abilities”.(Edsger W. Dijkstra [85])
Acknowledgments
We thank N. Barnett and D. P. Varn for helpful feedback. James P. Crutchfield thanks the Santa Fe Institute for its hospitality during visits as an External Faculty member. This material is based on work supported by, or in part by, the U. S. Army Research Laboratory and the U. S. Army Research Office under Contracts W911NF-13-1-0390 and W911NF-13-1-0340.
Author Contributions
Both authors contributed equally to the theoretical development of the work. R.G.J. carried out all numerical calculations. Both authors contributed equally to the writing of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. A Python Discrete Information Package
Hand calculating the information quantities used in the main text, while profitably done for a few basic examples, soon becomes tedious and error prone. We provide a Jupyter notebook [86] making use of dit (“Discrete Information Theory”) [87], an open source Python package that readily calculates these quantities.
References
- Kullback, S. Information Theory and Statistics; Dover: New York, NY, USA, 1968. [Google Scholar]
- Quastler, H. Information Theory in Biology; University of Illinois Press: Urbana-Champaign, IL, USA, 1953. [Google Scholar]
- Quastler, H. The status of information theory in biology—A roundtable discussion. In Symposium on Information Theory in Biology; Yockey, H.P., Ed.; Pergamon Press: New York, NY, USA, 1958; 399p. [Google Scholar]
- Kelly, J. A new interpretation of information rate. IRE Trans. Inf. Theory 1956, 2, 185–189. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory, 2nd ed.; Academic Press: New York, NY, USA, 1962. [Google Scholar]
- Bialek, W.; Rieke, F.; De Ruyter Van Steveninck, R.R.; Warland, D. Reading a neural code. Science 1991, 252, 1854–1857. [Google Scholar] [CrossRef] [PubMed]
- Strong, S.P.; Koberle, R.; de Ruyter van Steveninck, R.R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197. [Google Scholar] [CrossRef]
- Ulanowicz, R.E. The central role of information theory in ecology. In Towards an Information Theory of Complex Networks; Dehmer, M., Mehler, A., Emmert-Streib, F., Eds.; Springer: Berlin, Germany, 2011; pp. 153–167. [Google Scholar]
- Grandy, W.T., Jr. Entropy and the Time Evolution of Macroscopic Systems; Oxford University Press: Oxford, UK, 2008; Volume 141. [Google Scholar]
- Harte, J. Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics. Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Nalewajski, R.F. Information Theory of Molecular Systems; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Garland, J.; James, R.G.; Bradley, E. Model-free quantification of time-series predictability. Phys. Rev. E 2014, 90, 052910. [Google Scholar] [CrossRef] [PubMed]
- Kafri, O. Information theoretic approach to social networks. J. Econ. Soc. Thought 2017, 4, 77. [Google Scholar]
- Varn, D.P.; Crutchfield, J.P. Chaotic crystallography: How the physics of information reveals structural order in materials. Curr. Opin. Chem. Eng. 2015, 777, 47–56. [Google Scholar]
- Varn, D.P.; Crutchfield, J.P. What did Erwin mean? The physics of information from the materials genomics of aperiodic crystals and water to molecular information catalysts and life. Phil. Trans. R. Soc. A 2016, 374. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.-Y.; Rong, C.; Lu, T.; Zhou, P.; Liu, S. Information functional theory: Electronic properties as functionals of information for atoms and molecules. J. Phys. Chem. A 2016, 120, 3634–3642. [Google Scholar] [CrossRef] [PubMed]
- Kirst, C.; Timme, M.; Battaglia, D. Dynamic information routing in complex networks. Nat. Commun. 2016, 7, 11061. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo, E.J.; Williams, P.L.; Beer, R.D. Information flow through a model of the C. elegans klinotaxis circuit. PLoS ONE 2015, 10, e0140397. [Google Scholar]
- James, R.G.; Burke, K.; Crutchfield, J.P. Chaos forgets and remembers: Measuring information creation, destruction, and storage. Phys. Lett. A 2014, 378, 2124–2127. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Fiedor, P. Partial mutual information analysis of financial networks. Acta Phys. Pol. A 2015, 127, 863–867. [Google Scholar] [CrossRef]
- Sun, J.; Bollt, E.M. Causation entropy identifies indirect influences, dominance of neighbors and anticipatory couplings. Phys. D Nonlinear Phenom. 2014, 267, 49–57. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.I.; Kim, H.; Davies, P.C.W. The informational architecture of the cell. Phil. Trans. R. Soc. A 2016, 273. [Google Scholar] [CrossRef] [PubMed]
- Lee, U.; Blain-Moraes, S.; Mashour, G.A. Assessing levels of consciousness with symbolic analysis. Phil. Trans. R. Soc. Lond. A 2015, 373. [Google Scholar] [CrossRef] [PubMed]
- Maurer, U.; Wolf, S. The intrinsic conditional mutual information and perfect secrecy. In Proceedings of the 1997 IEEE International Symposium on Information Theory, Ulm, Germany, 29 June–4 July 1997; p. 8. [Google Scholar]
- Renner, R.; Skripsky, J.; Wolf, S. A new measure for conditional mutual information and its properties. In Proceedings of the 2003 IEEE International Symposium on Information Theory, Yokohama, Japan, 29 June–4 July 2003; p. 259. [Google Scholar]
- James, R.G.; Barnett, N.; Crutchfield, J.P. Information flows? A critique of transfer entropies. Phys. Rev. Lett. 2016, 116, 238701. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared information: New insights and problems in decomposing information in complex systems. In Proceedings of the European Conference on Complex Systems 2012; Springer: Berlin, Germany, 2013; pp. 251–269. [Google Scholar]
- Lizier, J.T. The Local Information Dynamics of Distributed Computation in Complex Systems. Ph.D. Thesis, University of Sydney, Sydney, Austrilia, 2010. [Google Scholar]
- Ay, N.; Polani, D. Information flows in causal networks. Adv. Complex Syst. 2008, 11, 17–41. [Google Scholar] [CrossRef]
- Chicharro, D.; Ledberg, A. When two become one: The limits of causality analysis of brain dynamics. PLoS ONE 2012, 7, e32466. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B Condens. Matter Complex Syst. 2010, 73, 605–615. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Yeung, R.W. A First Course in Information Theory; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Csiszar, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- MacKay, D.J.C. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided Self-Organization: Inception; Springer: Berlin, Germany, 2014; pp. 159–190. [Google Scholar]
- Cook, M. Networks of Relations. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2005. [Google Scholar]
- Merchan, L.; Nemenman, I. On the sufficiency of pairwise interactions in maximum entropy models of networks. J. Stat. Phys. 2016, 162, 1294–1308. [Google Scholar] [CrossRef]
- Reza, F.M. An Introduction to Information Theory; Courier Corporation: North Chelmsford, MA, USA, 1961. [Google Scholar]
- Yeung, R.W. A new outlook on Shannon’s information measures. IEEE Trans. Inf. Theory 1991, 37, 466–474. [Google Scholar] [CrossRef]
- Bell, A.J. The co-information lattice. In Proceedings of the 4th International Workshop on Independent Component Analysis and Blind Signal Separation, Nara, Japan, 1–4 April 2003; Amari, S.M.S., Cichocki, A., Murata, N., Eds.; Springer: New York, NY, USA, 2003; Volume ICA 2003, pp. 921–926. [Google Scholar]
- Bettencourt, L.M.A.; Stephens, G.J.; Ham, M.I.; Gross, G.W. Functional structure of cortical neuronal networks grown in vitro. Phys. Rev. E 2007, 75, 021915. [Google Scholar] [CrossRef] [PubMed]
- Krippendorff, K. Information of interactions in complex systems. Int. J. Gen. Syst. 2009, 38, 669–680. [Google Scholar] [CrossRef]
- Watanabe, S. Information theoretical analysis of multivariate correlation. IBM J. Res. Dev. 1960, 4, 66–82. [Google Scholar] [CrossRef]
- Han, T.S. Linear dependence structure of the entropy space. Inf. Control 1975, 29, 337–368. [Google Scholar] [CrossRef]
- Chan, C.; Al-Bashabsheh, A.; Ebrahimi, J.B.; Kaced, T.; Liu, T. Multivariate mutual information inspired by secret-key agreement. Proc. IEEE 2015, 103, 1883–1913. [Google Scholar] [CrossRef]
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Anatomy of a bit: Information in a time series observation. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 037109. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, P.W.; Martin, M.T.; Plastino, A.; Rosso, O.A. Intensive entropic non-triviality measure. Physica A 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Massey, J. Causality, feedback and directed information. In Proceedings of the International Symposium on Information Theory and Its Applications, Waikiki, HI, USA, 27–30 November 1990; Volume ISITA-90, pp. 303–305. [Google Scholar]
- Marko, H. The bidirectional communication theory: A generalization of information theory. IEEE Trans. Commun. 1973, 21, 1345–1351. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Gintautas, V.; Ham, M.I. Identification of functional information subgraphs in complex networks. Phys. Rev. Lett. 2008, 100, 238701. [Google Scholar] [CrossRef] [PubMed]
- Bar-Yam, Y. Multiscale complexity/entropy. Adv. Complex Syst. 2004, 7, 47–63. [Google Scholar] [CrossRef]
- Allen, B.; Stacey, B.C.; Bar-Yam, Y. Multiscale Information Theory and the Marginal Utility of Information. Entropy 2017, 19, 273. [Google Scholar] [CrossRef]
- Gács, P.; Körner, J. Common information is far less than mutual information. Probl. Control Inf. 1973, 2, 149–162. [Google Scholar]
- Tyagi, H.; Narayan, P.; Gupta, P. When is a function securely computable? IEEE Trans. Inf. Theory 2011, 57, 6337–6350. [Google Scholar] [CrossRef]
- Ay, N.; Olbrich, E.; Bertschinger, N.; Jost, J. A unifying framework for complexity measures of finite systems. In Proceedings of the European Conference on Complex Systems 2006 (ECCS06); European Complex Systems Society (ECSS): Paris, France, 2006. [Google Scholar]
- Verdu, S.; Weissman, T. The information lost in erasures. IEEE Trans. Inf. Theory 2008, 54, 5030–5058. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 20 June–30 July 1960; pp. 547–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Abdallah, S.A.; Plumbley, M.D. A measure of statistical complexity based on predictive information with application to finite spin systems. Phys. Lett. A 2012, 376, 275–281. [Google Scholar] [CrossRef]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Wyner, A.D. The common information of two dependent random variables. IEEE Trans. Inf. Theory 1975, 21, 163–179. [Google Scholar] [CrossRef]
- Liu, W.; Xu, G.; Chen, B. The common information of n dependent random variables. In Proceedings of the 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–1 October 2010; pp. 836–843. [Google Scholar]
- Kumar, G.R.; Li, C.T.; El Gamal, A. Exact common information. In Proceedings of the 2014 IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 161–165. [Google Scholar]
- Lad, F.; Sanfilippo, G.; Agrò, G. Extropy: Complementary dual of entropy. Stat. Sci. 2015, 30, 40–58. [Google Scholar] [CrossRef]
- Jelinek, F.; Mercer, R.L.; Bahl, L.R.; Baker, J.K. Perplexity—A measure of the difficulty of speech recognition tasks. J. Acoust. Soc. Am. 1977, 62, S63. [Google Scholar] [CrossRef]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef] [PubMed]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Williams, P.L.; Beer, R.D. Generalized measures of information transfer. arXiv, 2011; arXiv:1102.1507. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Chong, E.K.P.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection information based on common randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Ince, R.A.A. Measuring multivariate redundant information with pointwise common change in surprisal. arXiv, 2016; arXiv:1602.05063. [Google Scholar]
- Albantakis, L.; Oizumi, M.; Tononi, G. From the phenomenology to the mechanisms of consciousness: Integrated information theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar]
- Takemura, S.; Bharioke, A.; Lu, Z.; Nern, A.; Vitaladevuni, S.; Rivlin, P.K.; Katz, W.T.; Olbris, D.J.; Plaza, S.M.; Winston, P.; et al. A visual motion detection circuit suggested by Drosophila connectomics. Nature 2013, 500, 175–181. [Google Scholar] [CrossRef] [PubMed]
- Rosas, F.; Ntranos, V.; Ellison, C.J.; Pollin, S.; Verhelst, M. Understanding interdependency through complex information sharing. Entropy 2016, 18, 38. [Google Scholar] [CrossRef]
- Ince, R.A. The Partial Entropy Decomposition: Decomposing multivariate entropy and mutual information via pointwise common surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef]
- Pica, G.; Piasini, E.; Chicharro, D.; Panzeri, S. Invariant components of synergy, redundancy, and unique information among three variables. Entropy 2017, 19, 451. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman: New York, NY, USA, 1979. [Google Scholar]
- Chen, Q.; Cheng, F.; Lie, T.; Yeung, R.W. A marginal characterization of entropy functions for conditional mutually independent random variables (with application to Wyner’s common information). In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 974–978. [Google Scholar]
- Shannon, C.E. The bandwagon. IEEE Trans. Inf. Theory 1956, 2, 3. [Google Scholar] [CrossRef]
- Dijkstra, E.W. How do we tell truths that might hurt? In Selected Writings on Computing: A Personal Perspective; Springer: Berlin, Germany, 1982; pp. 129–131. [Google Scholar]
- Jupyter. Available online: https://github.com/jupyter/notebook (accessed on 7 October 2017).
- James, R.G.; Ellison, C.J.; Crutchfield, J.P. Dit: Discrete Information Theory in Python. Available online: https://github.com/dit/dit (accessed on 7 October 2017).
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).