1. Introduction
In the context of the sum of a large number of positive random variables, an interesting phenomenon occurs when a single variable carries a finite fraction of the sum [
1]. Such a phenomenon has been put forward for instance in the context of the glass transition [
2,
3]. In the framework of particle or mass transport models [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13], where the sum of the random variables is fixed to a constant value due to a conservation law of the underlying dynamics, this phenomenon has been called “condensation”. This condensation phenomenon has since then been reported in different contexts like in extreme value statistics [
14], and in the sample variance of exponentially distributed random variables as well as for conditioned random-walks [
1,
15,
16]. A similar mechanism is also at the basis of the condensation observed in the non-equilibrium dynamics of non-interacting field-theoretical models [
17,
18,
19,
20]. A more general type of condensation, induced by interaction, has also been put forward [
21], but in the following we shall focus on cases without interaction, apart from a possible constraint on the total mass.
As mentioned above, standard condensation results from the presence of a constraint fixing the sum of the random variables to a given value. However, the fact that a single random variable carries a finite fraction of the sum is also observed for fat-tailed random variables with infinite mean—a phenomenon sometimes called the Noah effect [
22,
23]. The goal of the present paper is to present a comparative study of these two scenarios, that we shall respectively denote as
constrained condensation and
unconstrained condensation. Note that the term “condensation” is commonly used in the literature to describe the constrained case, but we shall extend its use to the unconstrained case, to emphasize possible analogies between the two scenarios. Considering the set of
N random variables
with joint distribution
, unconstrained condensation takes place when the sum
, in the limit
, is dominated by few terms, i.e., a number of terms of order
. This happens for instance to the sum of
N independent and identically distributed (iid) Levy-type random variables, with probability density
decaying asymptotically as a power law,
, with an exponent
. This unconstrained condensation effect (sometimes also referred to as “localization” [
24] depending on the context) is often characterized by the participation ratio
[
3,
25], defined as
where
is a real number, and where the brackets indicate an average over the
’s. For broadly distributed random variables it can be shown, with the calculation presented in [
25] and briefly recalled here in
Section 2, that there is a critical value
for the exponent of the power-law distribution such that for
the asymptotic value of the participation ratio is zero,
, whereas for a broad enough tail,
, one has
for any value
. The average in Equation (
1) is computed with respect to the probability distribution
. The participation ratio is therefore the “order parameter” for condensation in the sum of random variables. It is in fact easy to see from Equation (
1) that when all the random variables contribute “democratically” to the sum, namely when each of them is of order
, then the asymptotic behaviour of the participation ratio is
, which goes to zero when
. In contrast, if the sum is dominated by few terms of order
, asymptotically one has
.
As a physical example, the relevance of participation ratios to unveil unconstrained condensation was also shown for the phase-space condensation taking place in the glass phase of the Random Energy Model (REM) [
3,
25]. The REM is a system with
configurations, where each configuration
i has the Boltzmann weight
, and the energies
are iid random variables, usually assumed to have a Gaussian distribution with a variance proportional to
N. The random variables with respect to which condensation takes place in the glass phase are the probabilities
of the different configurations. The corresponding participation ratio takes the same form as Equation (
1), simply replacing
by
. It has been shown [
3,
25] that for values of the inverse temperature
, where
is the critical value for the glass transition, the value of the sum
is dominated, in the limit
, by
terms: in this case the asymptotic value of
is finite. In particular one can prove that for an inverse temperature
the participation ratio of the REM has precisely the same form as for the sum of iid Levy random variables
with distribution
(the exponent
is thus proportional to temperature).
In the above cases unconstrained condensation occurs for
, that is when the first moment of the power-law distribution is infinite. The situation is different, though, when one considers power-law distributed random variables with a fixed total sum
, a case which we refer to as
constraint-driven condensation, or simply
constrained condensation. Such a phenomenon, which is also related to the large of heavy-tailed sums (see, e.g., [
26]), is found for instance in the stationary distribution of the discrete Zero Range Process and its continuous variables generalization [
7,
8,
10]. The latter is represented by a lattice with
N sites, each carrying a continuous mass
, endowed with some total-mass conserving dynamical rules. For this model the stationary distribution is:
where
is the average density fixed by the initial total mass
, and where
is a normalization constant (or partition function). In mass transport models the shape of the distribution
depends on the dynamical rules, and has typically a power-law tail,
In [
7,
8,
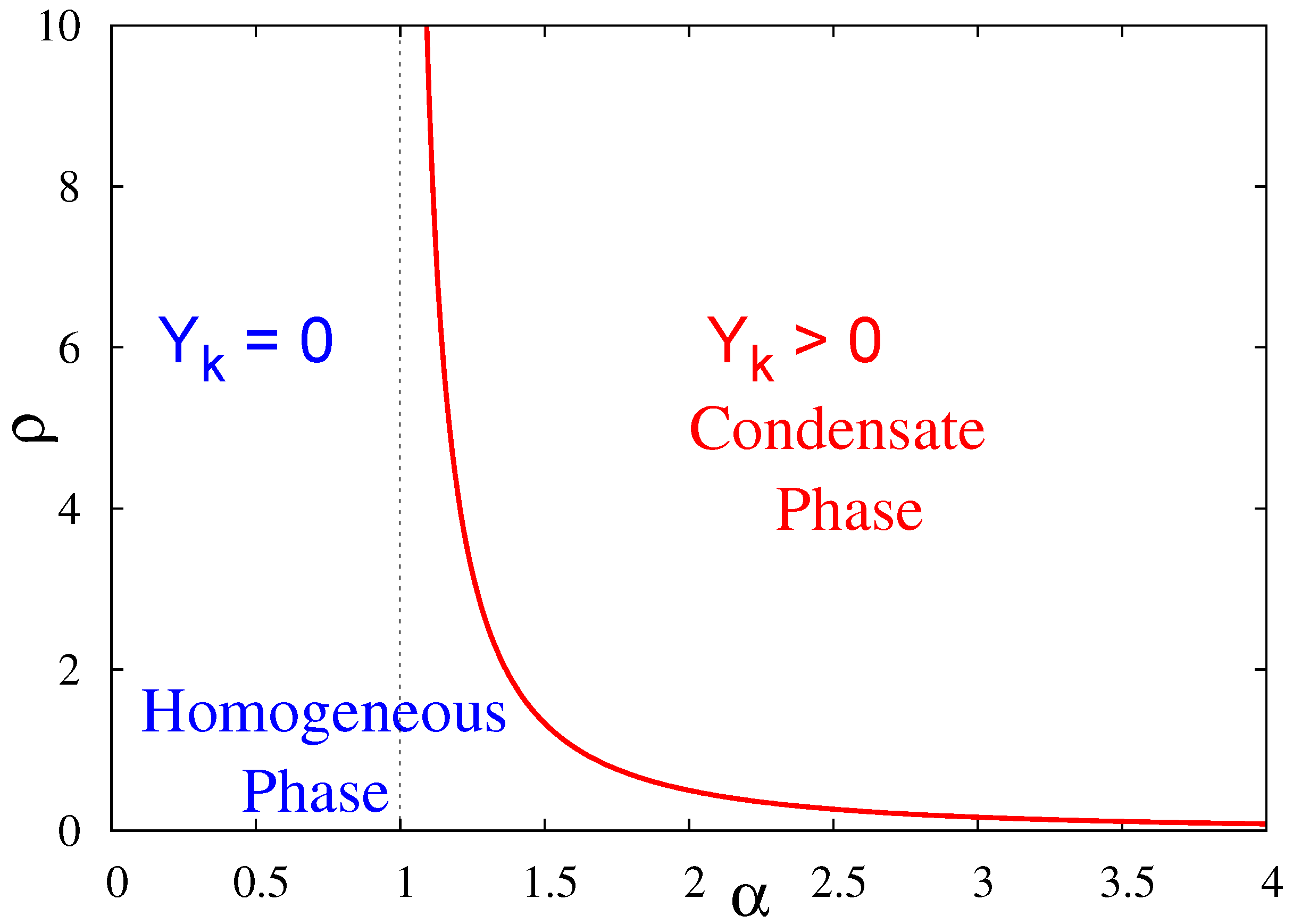
10] it has been shown that, in the presence of a constraint on the total value of the mass, constrained condensation never takes place for exponents of the local power-law distribution in the interval
, while on the contrary when
there exists a critical value
such that for
the system is in the condensed phase. It thus turns out that constraining the random variables to have a fixed sum deeply modifies their statistical properties in this case—while naive intuition based on elementary statistical physics, like the equivalence of ensembles, may suggest that fixing the sum may not make an important difference. It is also worth emphasizing that there is a significant difference between constrained and unconstrained condensation. In the unconstrained case, a few variables carry a finite fraction of the sum, while in the constrained case, only a single variable takes a macroscopic fraction of the sum (note that the situation may be different, though, in the presence of correlations between the variables [
21]). We thus see that the “condensation” phenomenon we define here as a non-vanishing value of the participation ratio in the infinite
N limit is a weak notion of condensation, which is more general than the standard condensation reported in the constrained case. In particular, this weak condensation effect does not imply the existence of a proper condensate, that is a “bump” in the tail of the marginal distribution
with a vanishing relative width. The bump may have a non-vanishing relative width, or may even not exist, the distribution
being monotonously decreasing in this case (see [
8] for an exactly solvable example). When relevant, we shall emphasize this specific character of the condensation by using the term “weak condensation”.
The goal of the present work is to understand the relation between these two cases, which differ only by the presence or absence of a constraint on the total mass, but yield opposite ranges of values of
for the existence of condensation. To better grasp the nature of this difference, we study here the case where the total mass is fixed to a superextensive value
, with
, thus extending some of the results presented in [
8]. The choice of a superextensive mass is motivated by the fact that in the unconstrained case, the total mass
, being the sum of iid broadly distributed variables, typically scales superextensively, as
, for
. This suggests that the case of a superextensive fixed mass may be closer to the unconstrained case, and that the value
may play a specific role. This will be confirmed by the detailed calculations presented in
Section 4. Yet, before dealing with the superextensive mass case, we will first recall in
Section 2 how to compute the participation ratios in the case of unconstrained condensation, and present in
Section 3 a simplified evaluation of the participation ratio in the case of constrained condensation with an extensive fixed mass.
2. Unconstrained Condensation
In the unconstrained case, where the masses are simply independent and identically distributed random variables with a broad distribution, the evaluation of the average participation ratio
is well-know and has been performed using different methods [
3,
25]. We sketch here the derivation of
using the auxiliary integral method put forward in [
25].
Noting that
one obtains, using the property that the random variables
are independent and identically distributed,
where the brackets
indicate an average over a single variable
m with distribution given in Equation (
4);
is the Euler Gamma function, defined as
. For large
N, the factor
in Equation (
6) takes very small values except if
t is small, in which case
is close to 1. Using a simple change of variable, one finds for
[
25]
with
, so that for
,
again for small
t. In a similar way, one also obtains for
[
25]
Using now the change of variable
, the last integral can be expressed in terms of the Gamma function, eventually leading, in the limit
, to [
3,
25],
The participation ratio is thus non-zero for , and goes to zero linearly when . A similar calculation in the case yields in the limit . Hence condensation occurs for in the unconstrained case. As we shall see below, the opposite situation occurs in the constrained case.
4. Constraint to a Superextensive Total Mass
As explained in the introduction, the unconstrained condensation occurs for
, while the constraint-driven condensation occurs at
(and at high enough density). Given that the typical total mass in the unconstrained case is superextensive for
, it is of interest to study condensation effects in the more general case of a fixed superextensive total mass
, with
and
a parameter which generalizes the usual notion of density. The joint probability distribution
reads in this case
where
is a normalization factor (see Equation (
3)). We wish to determine for which values of
and
condensation occurs in this case, using as an order parameter for condensation the participation ratio
, which reads in the present case as
The expression of the marginal distribution
in the case of the superextensive total mass is given below in Equation (
41).
In the following paragraphs, we first use in
Section 4.1 the integral representation of the partition function
in order to get indications on the phase diagram in the
plane. This preliminary analysis will suggest the existence of a transition line, that will be confirmed in
Section 4.2,
Section 4.3 and
Section 4.4 by an explicit determination of the marginal distribution
and the participation ratio
respectively below, above and on the transition line.
4.1. Preliminary Analysis of the Phase Diagram
We start by expressing the partition function
as an integral representation in terms of its inverse Laplace transform. The Laplace transform
of
is expressed as
where
is defined in Equation (
15). After a simple change of variable, the inverse Laplace representation of the partition function
reads
The value of
, although arbitrary, can be conveniently chosen to be the saddle-point value of the argument of the exponential in Equation (
29), when a saddle-point
exists (this is due to the presence of a branch-cut singularity on the negative real axis, as discussed in the previous section). When no saddle-point exists, the equivalence between canonical and grand-canonical ensemble breaks down, and condensation is expected to occur. A saddle-point solution of the integral in Equation (
29) should satisfy the following equation,
Note that this approach is heuristic, since the saddle-point should in principle not depend on N. However, the N-dependence is not a problem when testing the existence of a saddle-point. If it exists, the saddle-point evaluation of the integral then requires a change of variable for (some power of) N to appear only as a global prefactor in the argument of the exponential.
For
, we know from the results of
Section 3 that the saddle-point Equation (
30) has a solution only if
. This condition is never satisfied for
and
, so that no saddle-point exists and condensation occurs for any value of
when
.
The situation is thus quite similar to the extensive mass case: there is a homogeneous phase carrying a total mass which coexists with a superextensive condensate with a mass , so that the condensate carries a fraction of the total mass equal to one in the limit . It follows that the participation ratio in this limit.
In contrast, for
, the function
spans the whole positive real axis, and the saddle-point Equation (
30) always has a solution
, which goes to 0 when
. One then has to factor out the
N-dependence through an appropriate change of variable, and to check whether a saddle-point evaluation of the integral can be made. For
, one has
, so that
. Using the change of variable
in the integral appearing in Equation (
30), the argument of the exponential can be rewritten as
with
, and where we have used the small-
s expansion
, valid for
. The saddle-point evaluation of the integral is valid only if the
N-dependent prefactor diverges, meaning that
, or equivalently
Hence for
and
, a saddle-point evaluation of the partition function is possible, and the equivalence between canonical and grand-canonical ensembles holds: the system is in the homogeneous phase, and no condensation occurs. For
, the saddle-point evaluation of the partition function is no longer possible, which suggests that the equivalence of ensembles breaks down. This is an indication that condensation may occur. We show through explicit calculations in
Section 4.3 and
Section 4.4 that condensation occurs when
, in the sense that the participation ratio
takes a nonzero value in the infinite
N limit.
Before proceeding to a detailed characterization of this condensation, let us briefly comment on the value of
. For
, the total mass in the system scales as
, and this scaling precisely corresponds to the typical value of the total mass present in the unconstrained case (see
Section 2), as already noticed in [
8]. Hence
corresponds to imposing a total mass much smaller than the “natural” unconstrained mass, while for
one imposes a mass much larger than the typical unconstrained mass, leading to condensation. In this sense, the situation is similar to that of the extensive mass case for
, where condensation occurs when a mass
M larger that the unconstrained mass
is imposed,
. In
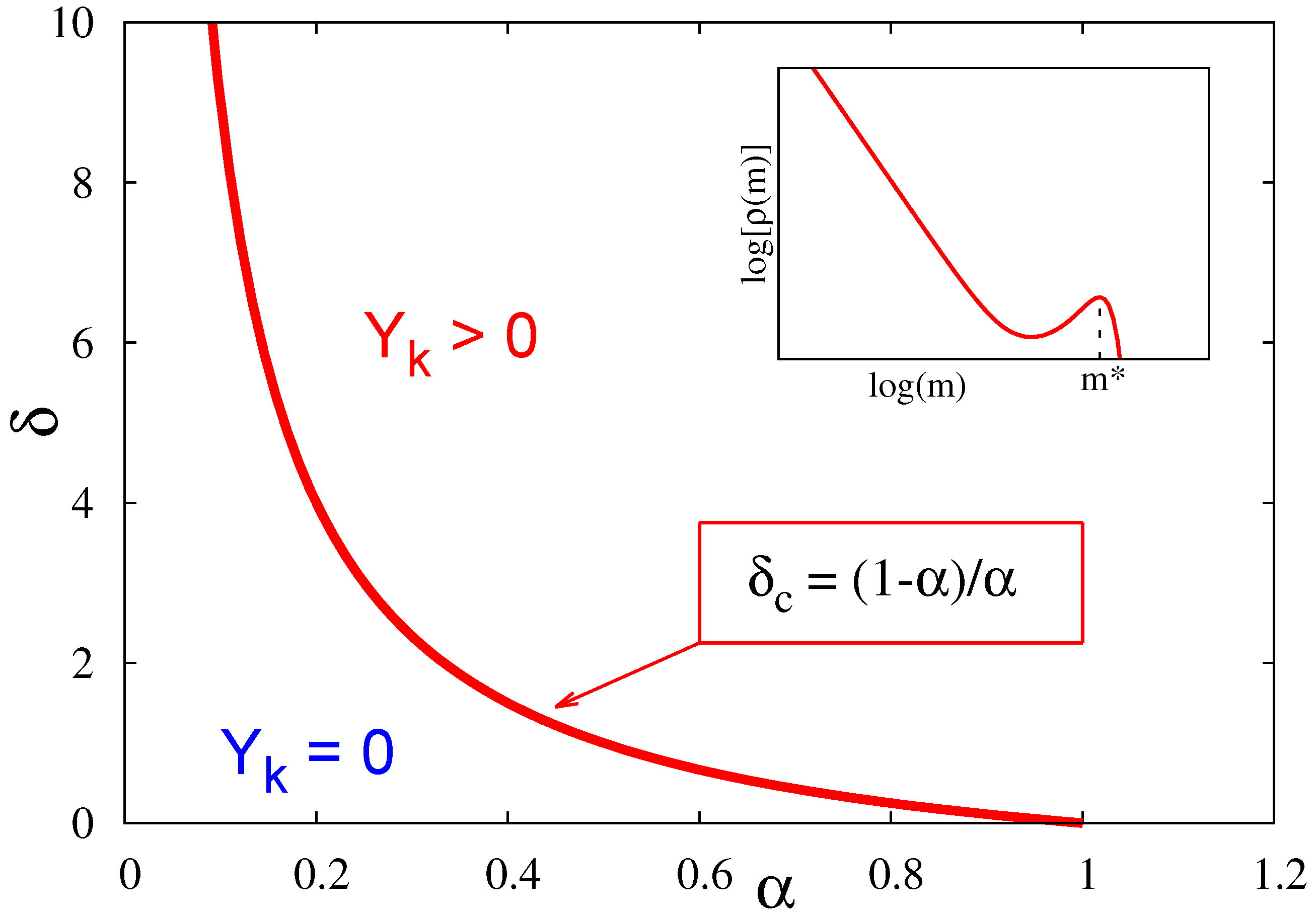
Figure 2 we present the phase diagram of the model for the case of a constraint to a superextensive total mass, which is a phase diagram in the plane
. Two observations are in order for this phase diagram. First, as will be explained in detail in in
Section 4.3 and
Section 4.4, the presence of a condensed phase never depends on the value of the parameter
, apart on the transition line
. Second, on the transition line
(see
Figure 2), the system is in the condensed phase (see
Section 4.4), at variance with the behaviour on the critical line
for the case of extensive mass (see the phase diagram in
Figure 1), in which case the system is
not in the condensed phase on the transition line.
In the forthcoming sections, we evaluate the distribution
and the participation ratio
for
in the three cases
(
Section 4.2),
(
Section 4.3) and
(
Section 4.4) respectively.
4.2. Case : Homogeneous Phase
As we have seen above, the system remains homogeneous for
and
, and the equivalence between canonical and grand-canonical ensembles holds. One can thus more conveniently perform calculations in the grand-canonical ensemble, with a chemical potential
which depends on
N, and which will be determined below as a function of the total mass. The single-mass distribution
simply reads
where we have neglected the correction to the normalization factor, as the latter remains very close to 1 since
is very small.
Note that the distribution
monotonously decays at large
m as
as is typical for a homogeneous phase. The
k-th moment of this distribution is obtained for
as
The value of
is then determined from the condition
, yielding
The participation ratio
is then given by
with
and where
is defined in Equation (
32). One thus obtains that
as it should, and that for
,
when
, which confirms the absence of condensation for
. Yet, it is interesting to note that the decay of
becomes slower when increasing
, and becomes approximately logarithmic in
N when
.
4.3. Case : Condensed Phase
When
(and
), the partition function
can no longer be evaluated by a saddle-point method, and equivalence of ensembles breaks down, so that one has to work in the canonical ensemble. From Equation (
28), the Laplace transform
reads in the large
N limit, using the small-
s behavior
,
with
.
By assuming a scaling function
which satisfies the normalization condition
and which has the asymptotic behaviour
for
, one can guess the following expression for the partition function
in direct space:
It is then not difficult to check that the expression in Equation (
40) is (asymptotically in
N) the correct one: the expansion for small
s of its Laplace transform corresponds precisely to the expression of
in Equation (
39).
From the knowledge of
one can then compute the distribution
, which reads as
and has a non-monotonous shape, as seen by evaluating
in the regime
with
, which leads to
Note that the divergences at
and
are regularized for values of
x such that
and
respectively. The non-monotonic shape of
, which is schematically represented in the inset of
Figure 2, is a strong similarity that the constrained condensation for
(and superextensive total mass) bears with the constrained condensation for
(and extensive total mass). At the same time such a non-monotonic shape of
is a remarkable qualitative difference with the case of unconstrained condensation found for the same range of the exponent,
, in which case the local mass distribution decays monotonously at large values as
. Interestingly, the expression Equation (
41) of
can be rewritten as
with
, which shows that the “bump” occuring for
has a width
. Hence its relative width scales as
and goes to zero when
for
. In this case it is therefore legitimate to call the bump a condensate, because it has a well-defined mass
.
To complete the analysis, let us compute the participation ratio
. In the large
N limit, the moment
can be computed as, using the change of variable
,
where we have used the asymptotic (large argument) behavior of
and
. It is then easy to show (see
Appendix A) that the integral in Equation (
44) tends to
when
. One thus simply gets
which, using
, immediately leads to the conclusion that
in the limit
. Hence, as anticipated above, a strong condensation occurs for
and
, in the sense that the condensate carries almost all the mass present in the system.
4.4. Case : Marginal Condensed Phase
For
and
, the Laplace transform of the partition function reads for large
N as
and from the expression in Equation (
46) the partition function is obtained as
where the function
is independent of
N and is defined by its Laplace transform,
(
H is actually a one-sided Lévy distribution). The small
s behavior
implies the large
behavior
where again
A is defined from the large
m behavior
.
The distribution
is given for large
N by
with
. It is interesting to evaluate
in the regime where
with
, which leads to
For large enough
, the shape of
is not monotonous, since the large
expansion of Equation (
51) yields
with a regularization of the divergence appearing at
for
, and of the divergence at
for
. So here again, a bump appears in the distribution, but its width scales as
as seen from Equation (
50), so that the relative width remains of the order of one. Following [
8], one may call this bump a “pseudo-condensate”.
The above argument on the existence of the bump in the distribution
was based on a large
limit. The explicit example studied in [
8] indeed shows that the bump may disappear below a certain value of
.
We now turn to the evaluation of the moment
. Using the change of variable
, as well as the asymptotic (large argument) behaviors of
and
, the moment
can be evaluated as
It follows that
is given by
which is one of the main results of this paper. Note that the convergence of the integral at the upper bound implies
. Note also that the integral in Equation (
54) is a convolution, which in some cases may be conveniently evaluated using a Laplace transform, given that
is known through its Laplace transform. For a numerical evaluation of
, one may thus compute analytically the Laplace transform of the integral in Equation (
54), yielding
and perform numerically the inverse Laplace transform.
The Laplace transform approach is also convenient to determine analytically the small
behavior of
, since the inverse Laplace transform can be evaluated through a saddle-point calculation in this limit. One finds
with parameters
,
c and
B given by
More detailed calculations on the derivation of Equation (
56) are reported in
Appendix A.
In the large
limit, it is easy to show that
goes to 1, following a procedure similar to the one used in the case
. It is of interest to compute the first correction in
(see
Appendix A), and one finds
with
Note in particular that if , the convergence of to 1 is very slow.
In summary, one has in the case
a non-standard, weak condensation effect, which does not correspond to the genuine condensation effect reported in the literature [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. Here, the weak condensation effect simply means that the participation ratio takes a nonzero value in the infinite size limit, indicating that a few random variables carry a finite fraction of the sum. However, as mentioned above, there is no well-defined condensate that would coexist with a fluid phase. Depending on the generalized density
, the marginal distribution
either decreases monotonously, or has a bump which corresponds only to a pseudo-condensate, since the relative width of the bump remains of the order of one, see Equation (
50). In addition, the line
does not correspond to a well-defined transition line in the
plane, in the sense that the state of the system continuously depends on the generalized density
, as shown by the expression of the participation ratio
given in Equation (
54).
5. Conclusions
The general motivation of this work was to better understand the connection between condensation in the unconstrained case and in the constrained case with extensive mass, because condensation occurs on opposite ranges of the exponent (which defines the power-law decay of the unconstrained probability distribution), respectively and . To this aim, we have studied condensation in the case where the total mass is constrained to a superextensive value , where , motivated by the fact that the typical scaling of the total mass is also superextensive, , when condensation takes place in the unconstrained case, which happens for .
We indeed found that the case of a fixed superextensive total mass interpolates in a sense between the case with a fixed extensive mass and the unconstrained case: condensation is found for values of the power law exponent in the interval , as in the case of unconstrained condensation, but with qualitative features more similar to the case of constrained condensation with extensive mass: for (and for at large enough ) the marginal distribution of the local mass has a secondary peak related to the condensate fraction, at variance with unconstrained case where decays monotonously for increasing values of m.
The inclusion in the problem of the new parameter
, which characterizes the superextensive scaling
of the total mass, allowed us to draw the two-dimensional (
,
) phase diagram shown in
Figure 2. At variance with the two models usually studied in the literature, where condensation takes place
either for
, without the constraint,
or for
, with constrained extensive mass, in the case of a constrained superextensive mass condensation is found
both for
(when
)
and for
(when
).
More in detail, we have shown that as soon as
, constrained condensation occurs for any
, irrespective of the value of the generalized density
, when the system is constrained to have a superextensive value of the mass. This case is qualitatively similar to the case of an extensive mass
with a large density
. For
, a weak form of condensation occurs if
, in the sense that the participation ratio takes a nonzero value in the infinite
N limit. Here,
is precisely the scaling exponent of the mass in the unconstrained case. When
, only a pseudo-condensate with non-vanishing relative fluctuations appears, or the distribution
may even decay monotonously. This is confirmed by the expression Equation (
54) of
(
and constraint to superextensive mass with
), which differs from Equation (
25) obtained in the case of
and a fixed extensive mass. The situation is thus different from standard condensation, but the nonzero asymptotic value of the participation ratio indicates that some non-trivial phenomenon (that we call weak condensation) takes place. On the contrary, when
condensation takes the form of a bump with vanishing relative width in the marginal distribution
. It thus shares similarities with the standard condensation phenomenon.
To conclude, we note that the qualitative idea that condensation occurs when one imposes a total mass larger than the “natural” mass the system would have in the unconstrained case remains valid: this is always the case for
(both for extensive and superextensive constraints), but it is also the case to some extent for
, where condensation is present for
. Yet, one has to be aware that the notion of “natural mass” is not firmly grounded in this case, and is just a heuristic concept associated to a typical scaling
with the system size
N. One further subtlety is whether condensation occurs or not on the transition line. For the constrained case with an extensive mass, condensation does not occur at the critical density
. In contrast, a weak form of condensation occurs at
(see
Section 4.4), which may suggest a discontinuous condensation transition as a function of
. However, for
the condensation properties actually depend on the generalized density
, see Equation (
54), so that this weak condensation is actually continuous (in the sense that
goes to zero when
) if one looks on a finer scale in terms of
.