Far-From-Equilibrium Time Evolution between Two Gamma Distributions
Abstract
:1. Introduction
2. Stochastic Logistic Model
3. Diagnostics
4. Results
4.1.
4.2.
4.3.
5. Conclusions
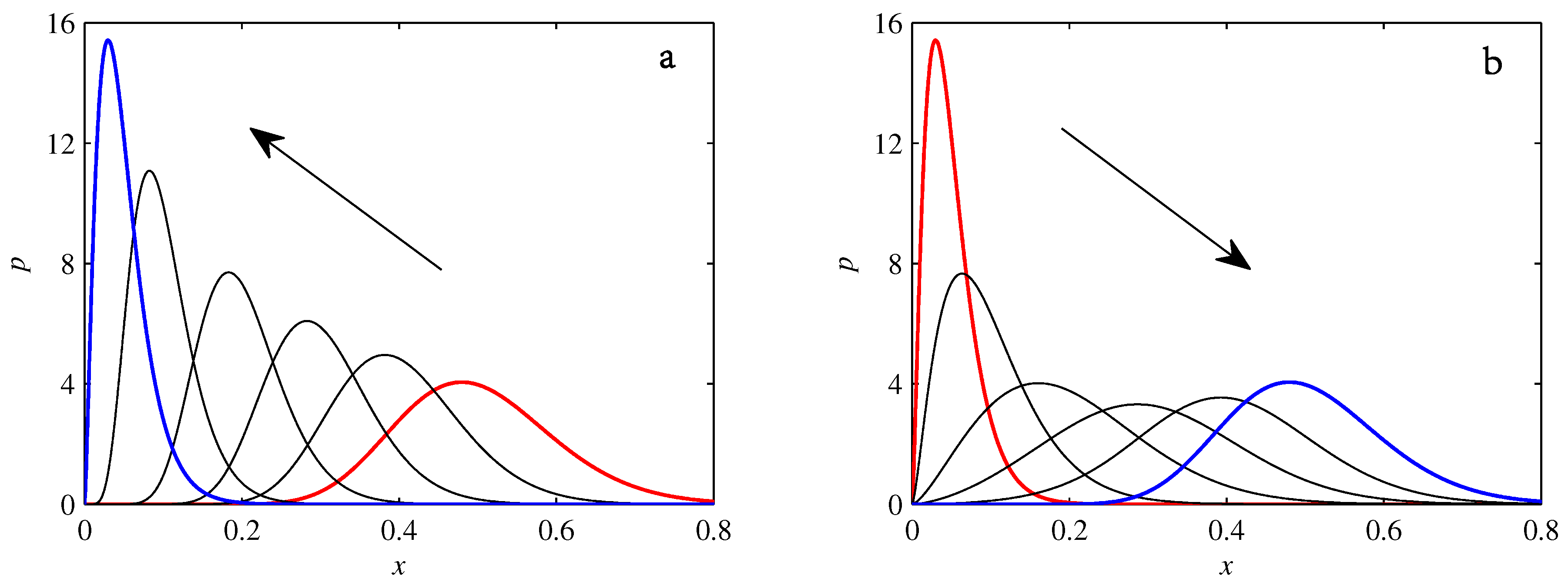
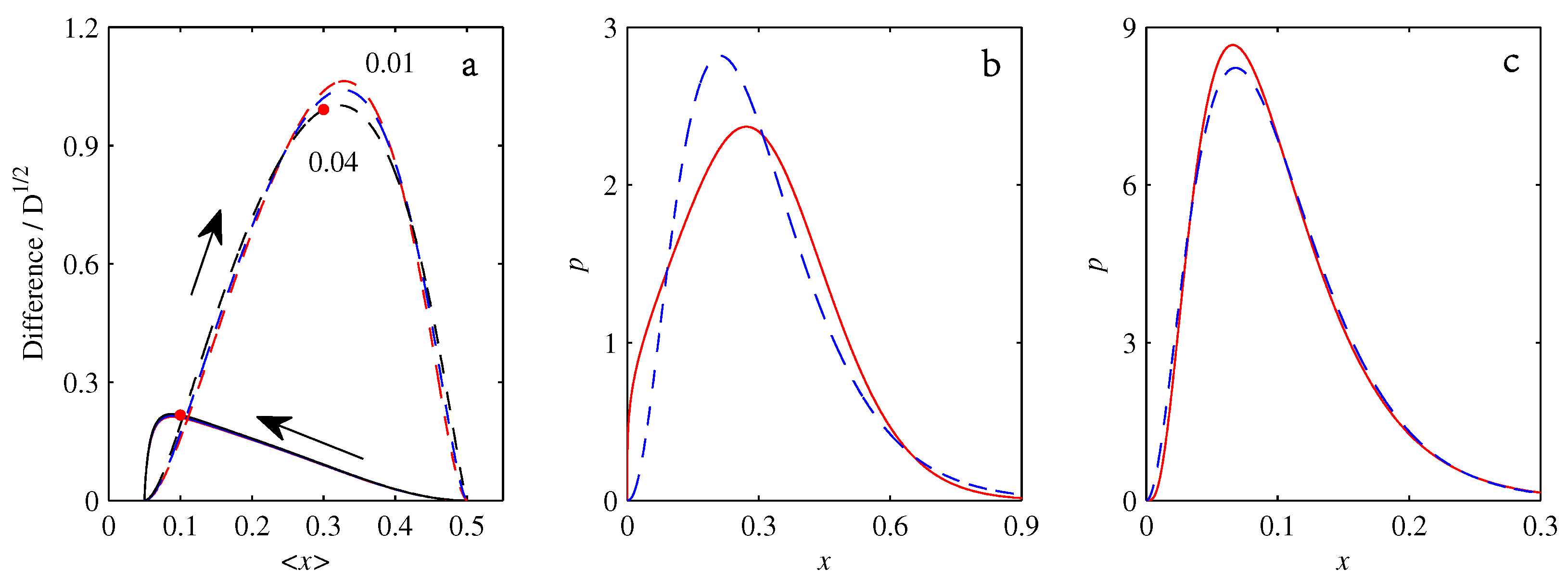
- If , so that stationary solutions exist, but D is also sufficiently close to that a gamma distribution differs significantly from a Gaussian, then the time-dependent PDFs will also differ significantly from gamma distributions.
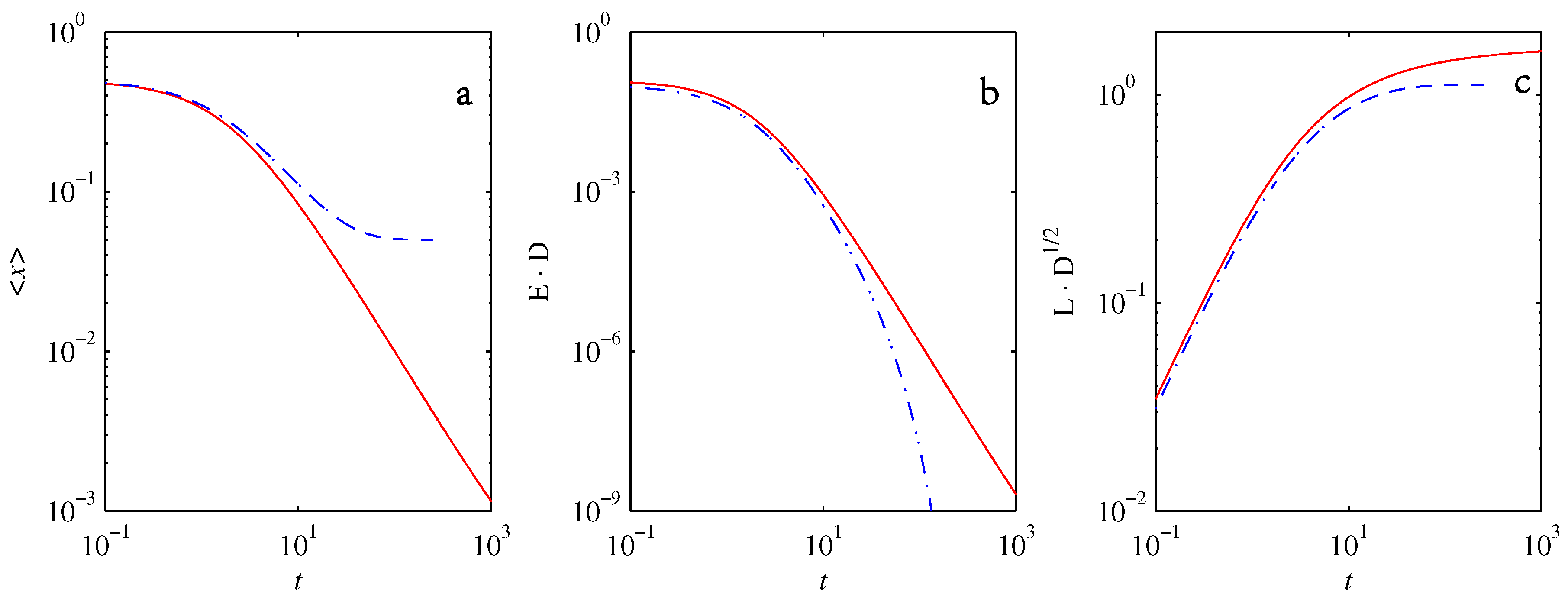
- If , stationary gamma distributions do not exist at all. Instead, peaks move ever closer to the origin and in the process increasingly differ from gamma distributions.
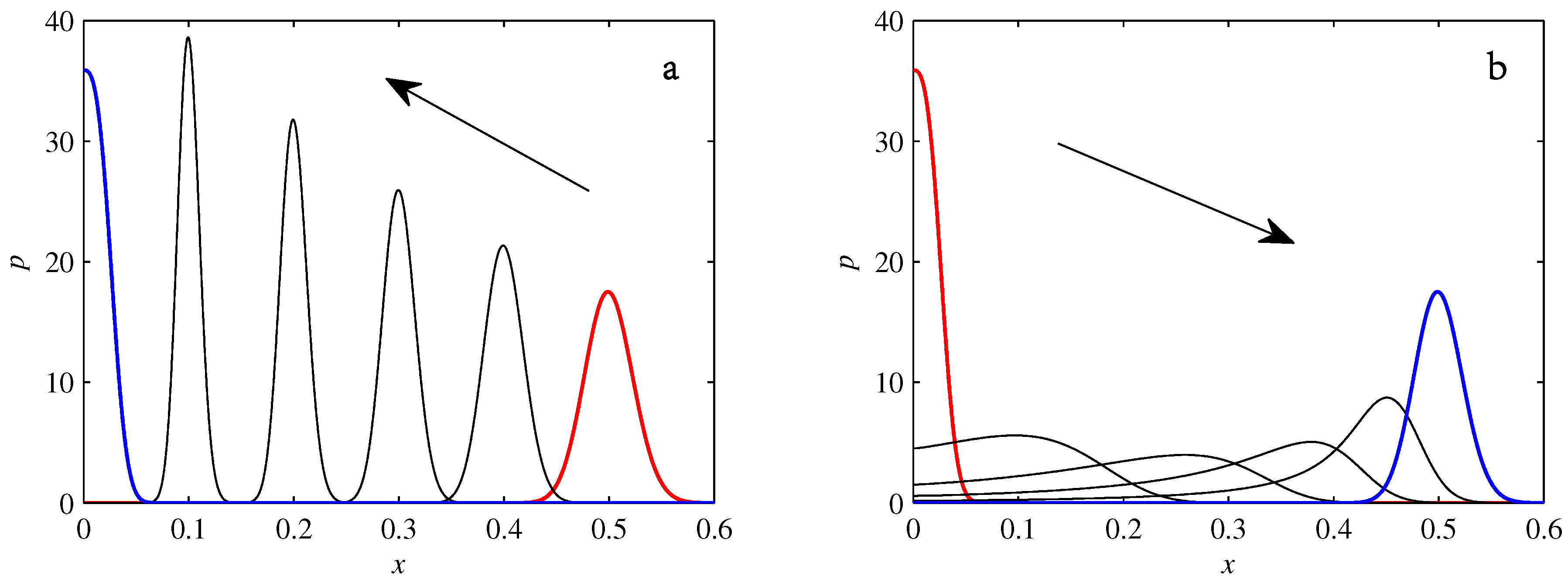
- If the initial condition is a peak right on the origin—either as a result of adding additive noise to produce stationary solutions even for , or simply as an arbitrary initial condition—then any evolution away from the origin will differ significantly from gamma distributions. Unlike the previous two items, which become more pronounced for larger D, this effect is most clearly visible for smaller D, where the mismatch between the naturally narrower peaks and the extreme broadening seen in Figure 11 becomes increasingly significant.
Author Contributions
Conflicts of Interest
Appendix A. Derivation of the Fokker–Planck Equations
Appendix B. Time-Dependent Analytical Solutions of Equation (3)
References
- Risken, H. The Fokker-Planck Equation: Methods of Solution and Applications; Springer: Berlin, Germany, 1996. [Google Scholar]
- Klebaner, F. Introduction to Stochastic Calculus with Applications; Imperial College Press: London, Britain, 2012. [Google Scholar]
- Gardiner, C. Stochastic Methods, 4th ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Saw, E.-W.; Kuzzay, D.; Faranda, D.; Guittonneau, A.; Daviaud, F.; Wiertel-Gasquet, C.; Padilla, V.; Dubrulle, B. Experimental characterization of extreme events of inertial dissipation in a turbulent swirling flow. Nat. Commun. 2016, 7, 12466. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Diamond, P.H. On intermittency in drift wave turbulence: Structure of the probability distribution function. Phys. Rev. Lett. 2002, 88, 225002. [Google Scholar] [PubMed]
- Kim, E.; Diamond, P.H. Zonal flows and transient dynamics of the L-H transition. Phys. Rev. Lett. 2003, 90, 185006. [Google Scholar] [PubMed]
- Kim, E. Consistent theory of turbulent transport in two dimensional magnetohydrodynamics. Phys. Rev. Lett. 2006, 96, 084504. [Google Scholar]
- Kim, E.; Anderson, J. Structure-based statistical theory of intermittency. Phys. Plasmas 2008, 15, 114506. [Google Scholar]
- Newton, A.P.L.; Kim, E.; Liu, H.-L. On the self-organizing process of large scale shear flows. Phys. Plasmas 2013, 20, 092306. [Google Scholar]
- Srinivasan, K.; Young, W.R. Zonostrophic instability. J. Atmos. Sci. 2012, 69, 1633–1656. [Google Scholar]
- Sayanagi, K.M.; Showman, A.P.; Dowling, T.E. The emergence of multiple robust zonal jets from freely evolving, three-dimensional stratified geostrophic turbulence with applications to Jupiter. J. Atmos. Sci. 2008, 65, 3947–3962. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Giuliani, A.; Hashimoto, M.; Erenpreisa, J.; Yoshikawa, K. Emergent self-organized criticality in gene expression dynamics: Temporal development of global phase transition revealed in a cancer cell line. PLoS ONE 2015, 10, e0128565. [Google Scholar]
- Tang, C.; Bak, P. Mean field theory of self-organized critical phenomena. J. Stat. Phys. 1988, 51, 797–802. [Google Scholar]
- Jensen, H.J. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Pruessner, G. Self-Organised Criticality; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Longo, G.; Montévil, M. From physics to biology by extending criticality and symmetry breaking. Prog. Biophys. Mol. Biol. 2011, 106, 340–347. [Google Scholar] [CrossRef] [PubMed]
- Flynn, S.W.; Zhao, H.C.; Green, J.R. Measuring disorder in irreversible decay processes. J. Chem. Phys. 2014, 141, 104107. [Google Scholar] [CrossRef] [PubMed]
- Nichols, J.W.; Flynn, S.W.; Green, J.R. Order and disorder in irreversible decay processes. J. Chem. Phys. 2015, 142, 064113. [Google Scholar] [CrossRef]
- Ferguson, M.L.; Le Coq, D.; Jules, M.; Aymerich, S.; Radulescu, O.; Declerck, N.; Royer, C.A. Reconciling molecular regulatory mechanisms with noise patterns of bacterial metabolic promoters in induced and repressed states. Proc. Natl. Acad. Sci. USA 2012, 109, 155–160. [Google Scholar]
- Shahrezaei, V.; Swain, P.S. Analytical distributions for stochastic gene expression. Proc. Natl. Acad. Sci. USA 2008, 105, 17256. [Google Scholar] [CrossRef]
- Thomas, R.; Torre, L.; Chang, X.; Mehrotra, S. Validation and characterization of DNA microarray gene expression data distribution and associated moments. BMC Bioinform. 2010, 11, 576. [Google Scholar] [CrossRef] [PubMed]
- Iyer-Biswas, S.; Hayot, F.; Jayaprakash, C. Stochasticity of gene products from transcriptional pulsing. Phys. Rev. E 2009, 79, 031911. [Google Scholar] [CrossRef] [PubMed]
- Elgart, V.; Jia, T.; Fenley, A.T.; Kulkarni, R. Connecting protein and mRNA burst distributions for stochastic models of gene expression. Phys. Biol. 2011, 8, 046001. [Google Scholar] [CrossRef]
- Delbrück, M. The burst size distribution in the growth of bacterial viruses (bacteriophages). J. Bacteriol. 1945, 50, 131. [Google Scholar]
- Delbrück, M. Statistical fluctuations in autocatalytic reactions. J. Chem. Phys. 1940, 8, 120–124. [Google Scholar] [CrossRef]
- Kim, E.; Liu, H.; Anderson, J. Probability distribution function for self-organization of shear flows. Phys. Plasmas 2009, 16, 052304. [Google Scholar] [CrossRef]
- Kim, E.; Hollerbach, R. Time-dependent probability density function in cubic stochastic processes. Phys. Rev. E 2016, 94, 052118. [Google Scholar] [CrossRef] [PubMed]
- De Jong, I.G.; Haccou, P.; Kuipers, O.P. Bet hedging or not? A guide to proper classification of microbial survival strategies. Bioessays 2011, 33, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Balaban, N.; Merrin, J.; Chait, R.; Kowalik, L.; Leibler, S. Bacterial persistence as a phenotypic switch. Science 2004, 305, 1622–1625. [Google Scholar] [PubMed]
- Glansdorff, P.; Prigogine, I. Thermodynamic theory of structure, stability and fluctuations. Am. J. Phys. 1973, 41, 147–148. [Google Scholar]
- Suzuki, M. Microscopic theory of formation of macroscopic order. Phys. Lett. A 1980, 75, 331–332. [Google Scholar]
- Suzuki, M. The variational theory and rate equation method with applications to relaxation near the instability point. Phys. A Stat. Mech. Appl. 1981, 105, 631–641. [Google Scholar] [CrossRef]
- Langer, J.S.; Baron, M.; Miller, H.D. New computational method in the theory of spinodal decomposition. Phys. Rev. A 1975, 11, 1417. [Google Scholar] [CrossRef]
- Saito, Y. Relaxation in a bistable system. J. Phys. Soc. Jpn. 1976, 61, 388–393. [Google Scholar] [CrossRef]
- Hasegawa, H. Variational approach in studies with Fokker-Planck equations. Prog. Theor. Phys. 1977, 58, 128–146. [Google Scholar] [CrossRef]
- Dennis, B.; Costantino, R.F. Analysis of steady-state populations with the gamma abundance model: Application to Tribolium. Ecology 1988, 69, 1200–1213. [Google Scholar] [CrossRef]
- Liao, H.-Y.; Ai, B.-Q.; Hu, L. Effects of multiplicative colored noise on bacteria growth. Braz. J. Phys. 2007, 37, 1125–1128. [Google Scholar] [CrossRef]
- Wong, E.; Zakai, M. On the convergence of ordinary integrals to stochastic integrals. Ann. Math. Stat. 1960, 36, 1560–1564. [Google Scholar] [CrossRef]
- Bagui, S.C.; Mehra, K.L. Convergence of binomial, Poisson, negative-binomial, and gamma to normal distribution: Moment generating functions technique. Am. J. Math. Stat. 2016, 6, 115–121. [Google Scholar]
- Kim, E.; Hollerbach, R. Geometric structure and information change in phase transitions. Phys. Rev. E 2017, 95, 062107. [Google Scholar] [CrossRef] [PubMed]
- Hollerbach, R.; Kim, E. Information geometry of non-equilibrium processes in a bistable system with a cubic damping. Entropy 2017, 19, 268. [Google Scholar] [CrossRef]
- Tenkès, L.-M.; Hollerbach, R.; Kim, E. Time-dependent probability density functions and information geometry in stochastic logistic and Gompertz models. arXiv, 2017; arXiv:1708.02789. [Google Scholar]
- Frieden, B.R. Physics from Fisher Information; Cambridge University Press: Cambridge, Britain, 2000. [Google Scholar]
- Wootters, W.K. Statistical distance and Hilbert space. Phys. Rev. D 1981, 23, 357. [Google Scholar] [CrossRef]
- Nicholson, S.B.; Kim, E. Investigation of the statistical distance to reach stationary distributions. Phys. Lett. A 2015, 379, 83–88. [Google Scholar] [CrossRef]
- Nicholson, S.B.; Kim, E. Structures in sound: Analysis of classical music using the information length. Entropy 2016, 18, 258. [Google Scholar] [CrossRef]
- Heseltine, J.; Kim, E. Novel mapping in a non-equilibrium stochastic process. J. Phys. A 2016, 49, 175002. [Google Scholar] [CrossRef]
- Kim, E.; Lee, U.; Heseltine, J.; Hollerbach, R. Geometric structure and geodesic motion in a solvable model of non-equilibrium stochastic process. Phys. Rev. E 2016, 93, 062127. [Google Scholar] [CrossRef] [PubMed]
- Bertoin, J.; Yor, M. Exponential functionals of Lévy processes. Prob. Surv. 2005, 2, 191–212. [Google Scholar] [CrossRef]
- Matsumoto, H.; Yor, M. Exponential functionals of Brownian motion, I: Probability laws at fixed time. Prob. Surv. 2005, 2, 312–347. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, E.-j.; Tenkès, L.-M.; Hollerbach, R.; Radulescu, O. Far-From-Equilibrium Time Evolution between Two Gamma Distributions. Entropy 2017, 19, 511. https://doi.org/10.3390/e19100511
Kim E-j, Tenkès L-M, Hollerbach R, Radulescu O. Far-From-Equilibrium Time Evolution between Two Gamma Distributions. Entropy. 2017; 19(10):511. https://doi.org/10.3390/e19100511
Chicago/Turabian StyleKim, Eun-jin, Lucille-Marie Tenkès, Rainer Hollerbach, and Ovidiu Radulescu. 2017. "Far-From-Equilibrium Time Evolution between Two Gamma Distributions" Entropy 19, no. 10: 511. https://doi.org/10.3390/e19100511
APA StyleKim, E.-j., Tenkès, L.-M., Hollerbach, R., & Radulescu, O. (2017). Far-From-Equilibrium Time Evolution between Two Gamma Distributions. Entropy, 19(10), 511. https://doi.org/10.3390/e19100511





