A Multivariate Multiscale Fuzzy Entropy Algorithm with Application to Uterine EMG Complexity Analysis
Abstract
:1. Introduction
2. Multivariate Multiscale Fuzzy Entropy (MMFE)
- For each delay vector, the baseline/local mean is first removed in the following way: where ;
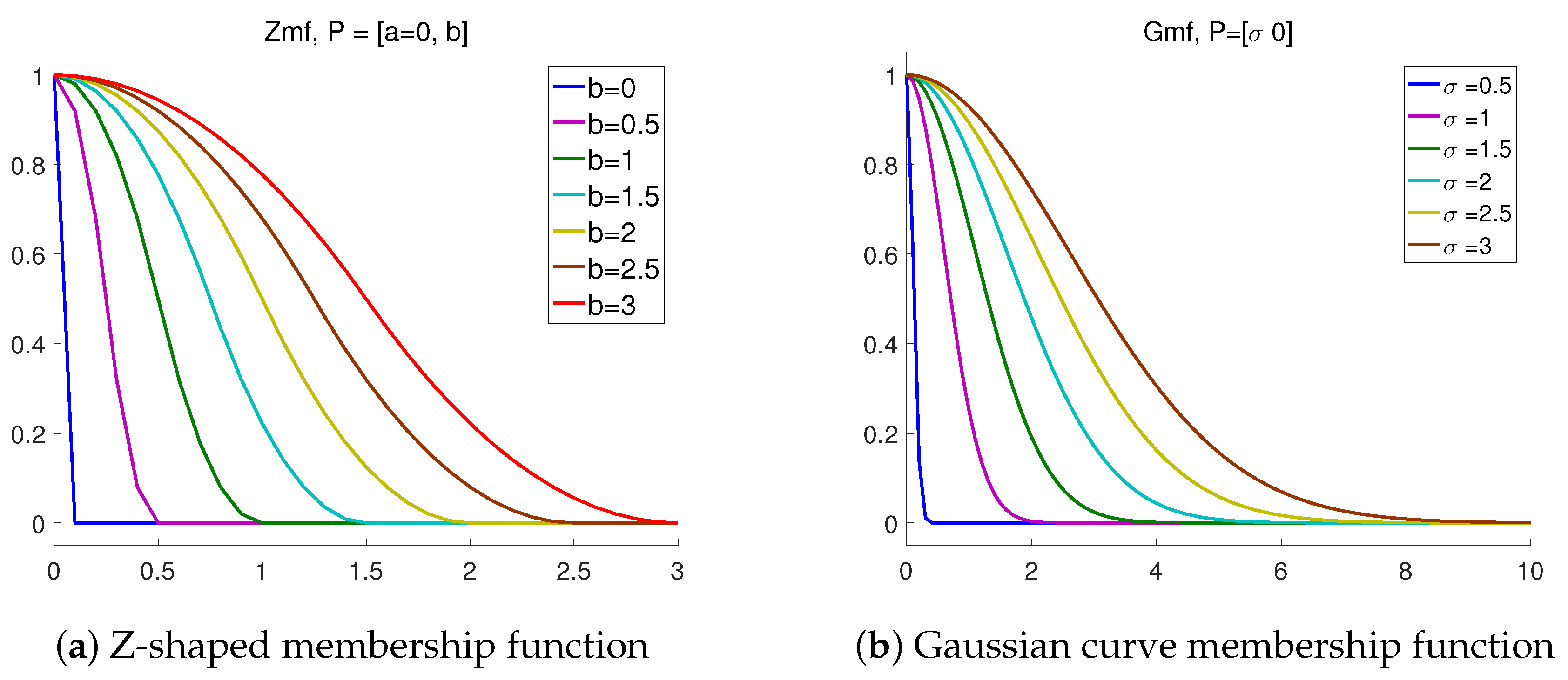
- Any fuzzy membership function (like the Gaussian one used in the following) can be used in calculating MFSampEn: .
2.1. The Multivariate Fuzzy Sample Entropy
- Form composite delay vectors ∈ , where and ;
- For each delay vector, remove the local mean: where ;
- Define the distance between any two composite delay vectors and as the maximum norm [27], that is, ;
- For a given composite delay vector and a tolerance r, calculate the similarity degree to other vector through a fuzzy membership function , i.e., . Then, define the function
- Extend the dimensionality of the multivariate delay vector in Step 1 from m to . This can be performed in p different ways, as from a space defined by the embedding vector the system can evolve to any space for which the embedding vector is (). Thus, a total of vectors in are obtained, where denotes any embedded vector upon increasing the embedding dimension from to for a specific variable k. In the process, the embedding dimension of the other data channels is kept unchanged, so that the overall embedding dimension of the system undergoes the change from m to ;
- For a given , calculate the similarity degree to another vector through a fuzzy membership function , i.e., . Then, define the function
- In this way, represents the probability that any two composite delay vectors are similar in the dimension m, whereas is the probability that any two composite delay vectors will be similar in the dimension .
- Finally, for a tolerance level r, MFSampEn is calculated as the negative of a natural logarithm of the conditional probability that two composite delay vectors close to each other in an m-dimensional space will also be close to each other when the dimensionality is increased by one, and can be estimated by the statistic
2.2. Fuzzy Membership Function
3. Validation on Synthetic Data
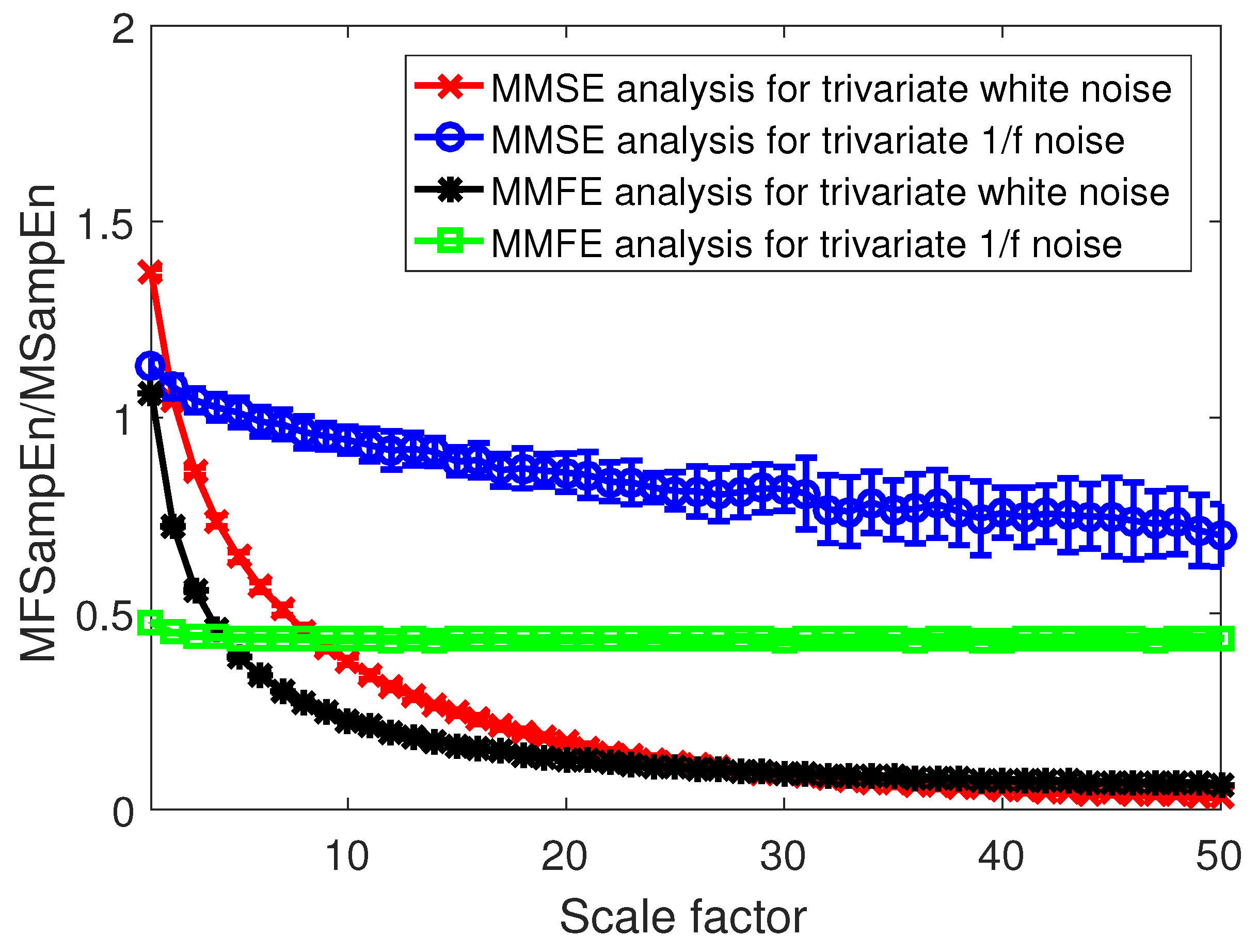
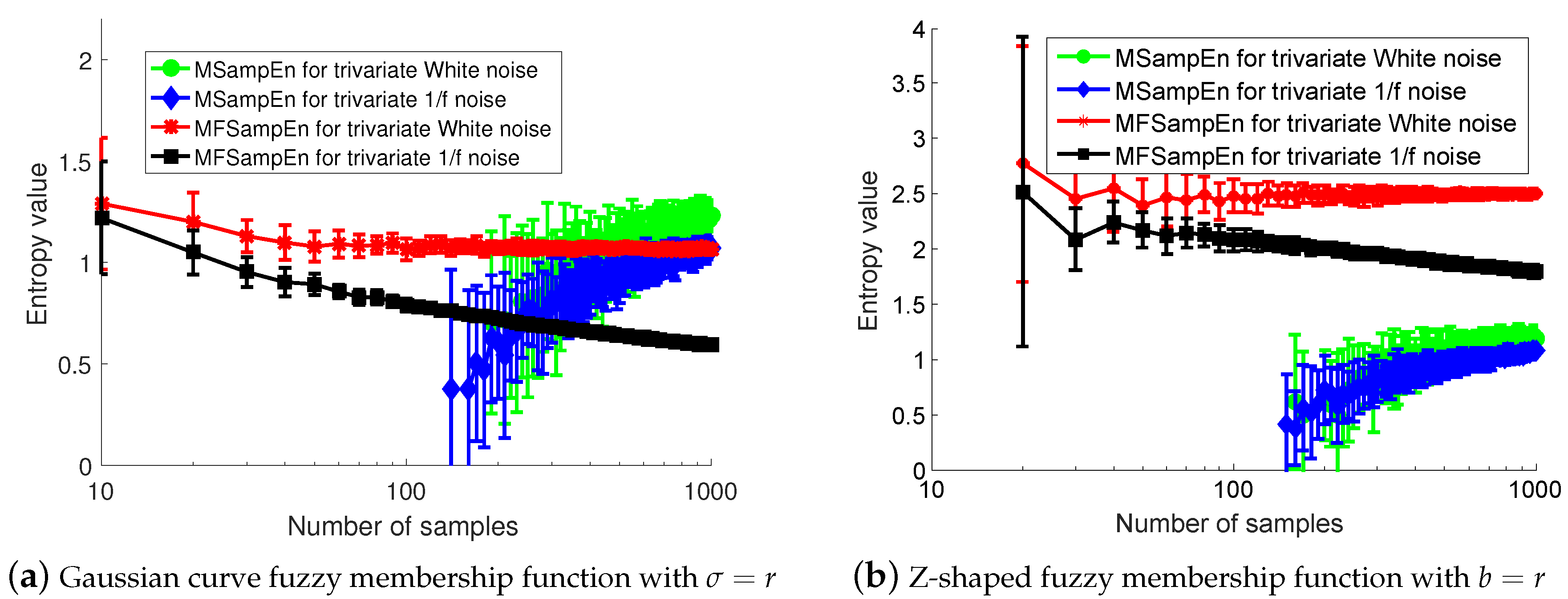
3.1. Effect of Data Length on Multivariate Fuzzy Sample Entropy
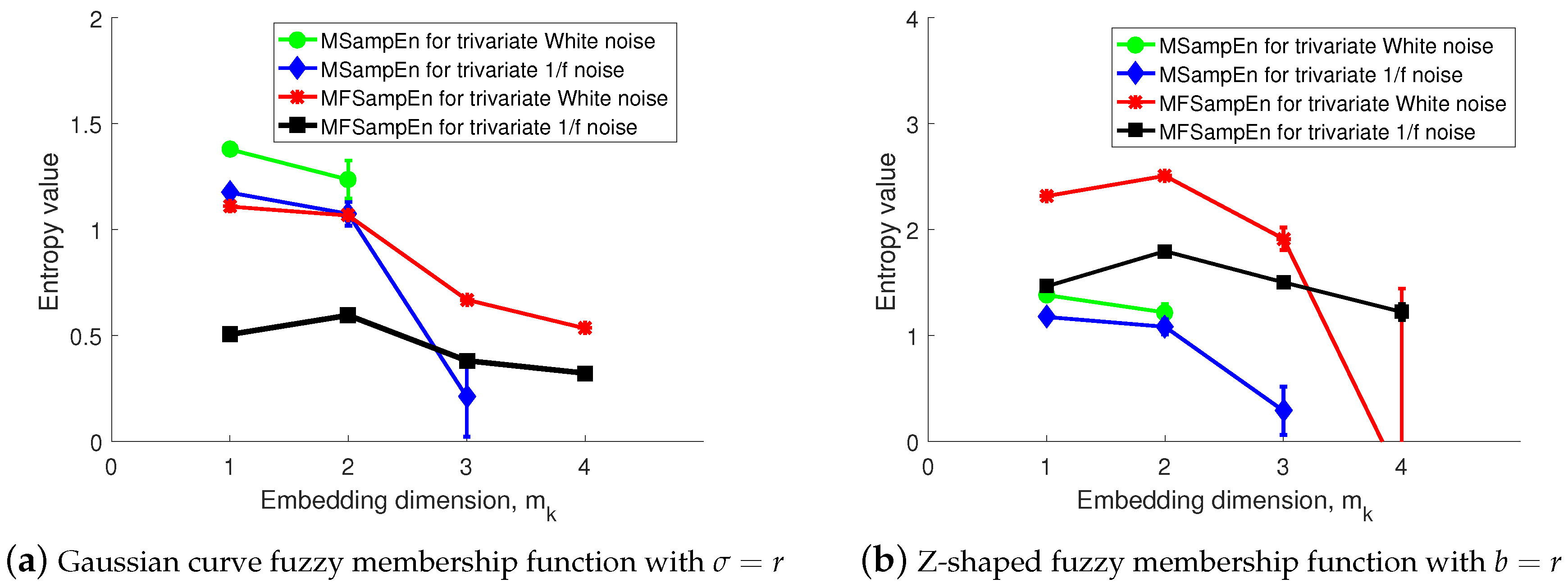
3.2. Sensitivity to the Embedding Dimension
4. Applications to Uterine EMG Signal Chracterization
4.1. TPEHG Database
- 262 records were obtained during pregnancies where delivery was on term (duration of gestation at delivery >37 weeks):
- –
- 143 records were obtained before the 26th week of gestation (Term-early);
- –
- 119 were obtained later during pregnancy, during or after the 26th week of gestation (Term-Late);
- 38 records were obtained during pregnancies which ended prematurely (pregnancy duration ≤37 weeks), of which:
- –
- 19 records were obtained before the 26th week of gestation (Preterm-early);
- –
- 19 records were obtained during or after the 26th week of gestation (Preterm-late).
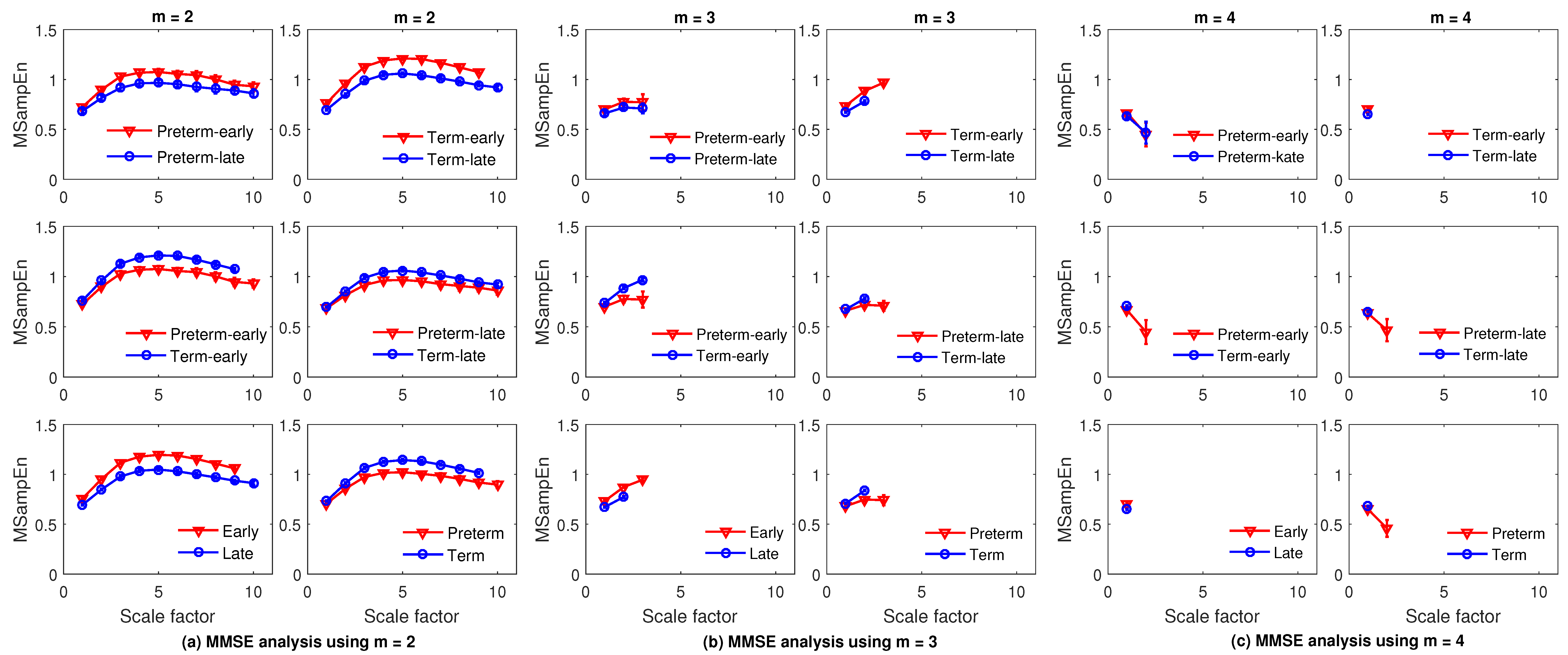
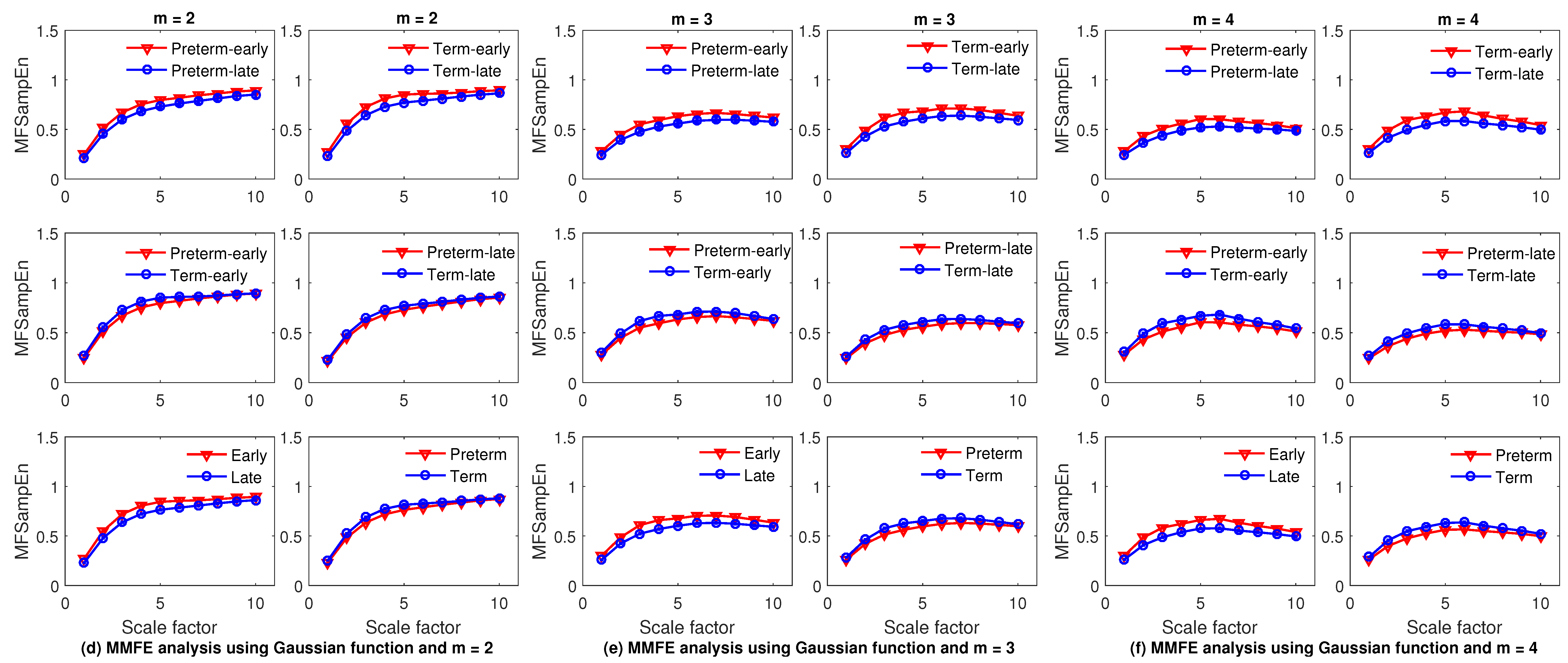
4.2. Feature Extraction Using MMFE and MMSE
4.3. Approach for Imbalanced Learning
4.4. Classifiers Used
4.5. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Gell-Mann, M. Let’s call it plectics. Complexity 1995, 1, 3. [Google Scholar] [CrossRef]
- Goldenfeld, N.; Kadanoff, L.P. Simple Lessons from Complexity. Science 1999, 284, 87–89. [Google Scholar] [CrossRef] [PubMed]
- Foote, R. Mathematics and Complex Systems. Science 2007, 318, 410–412. [Google Scholar] [CrossRef] [PubMed]
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Manson, S.M. Simplifying complexity: A review of complexity theory. Geoforum 2001, 32, 405–414. [Google Scholar] [CrossRef]
- Editorial. No man is an island. Nat. Phys. 2009, 5. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. AJP Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Hornero, R.; Abásolo, D.; Escudero, J.; Gomez, C. Nonlinear analysis of electroencephalogram and magnetoencephalogram recordings in patients with Alzheimer’s disease. Phil. Trans. R. Soc. A 2009, 367, 317–336. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Physica A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Takahashi, T.; Cho, R.Y.; Murata, T.; Mizuno, T.; Kikuchi, M.; Mizukami, K.; Kosaka, H.; Takahashi, K.; Wada, Y. Age-related variation in EEG complexity to photic stimulation: A multiscale entropy analysis. Clin. Neurophysiol. 2009, 120, 476–483. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Ghiran, I.; Peng, C.K.; Nicholson-Weller, A.; Goldberger, A.L. Complex dynamics of human red blood cell flickering: Alterations with in vivo aging. Phys. Rev. E 2008, 78, 020901. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Valencia, J.; Porta, A.; Vallverdu, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined Multiscale Entropy: Application to 24-h Holter Recordings of Heart Period Variability in Healthy and Aortic Stenosis Subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Rehman, N.; Looney, D.; Rutkowski, T.; Mandic, D. Dynamical complexity of human responses: a multivariate data-adaptive framework. Bull. Pol. Acad. Sci. Tech. Sci. 2012, 60, 433–445. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.U.; Mandic, D.P. Multivariate Multiscale Entropy Analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. Multivariate refined composite multiscale entropy analysis. Phys. Lett. A 2016, 380, 1426–1431. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Physica D 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Grassberger, P.; Schreiber, T.; Schaffrath, C. Nonlinear time sequence analysis. Int. J. Bifurc. Chaos 1991, 1, 521–547. [Google Scholar] [CrossRef]
- Vinken, M.P.G.C.; Rabotti, C.; Mischi, M.; Oei, S.G. Accuracy of Frequency-Related Parameters of the Electrohysterogram for Predicting Preterm Delivery: A Review of the Literature. Obstet. Gynecol. Surv. 2009, 64, 529–541. [Google Scholar] [CrossRef] [PubMed]
- Garfield, R.E.; Maner, W.L. Physiology and electrical activity of uterine contractions. Semin. Cell Dev. Biol. 2007, 18, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Lucovnik, M.; Kuon, R.J.; Chambliss, L.R.; Maner, W.L.; Shi, S.Q.; Shi, L.; Balducci, J.; Garfield, R.E. Use of uterine electromyography to diagnose term and preterm labor. Acta Obstet. Gynecol. Scand. 2011, 90, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Steer, P. The epidemiology of preterm labour. Int J. Obstet. Gynaecol. 2005, 112, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Born Too Soon: The Global Action Report on Preterm Birth. Available online: http://www.who.int/pmnch/media/news/2012/201204_borntoosoon-report.pdf (accessed on 20 December 2016).
- Rogers, L.K.; Velten, M. Maternal inflammation, growth retardation, and preterm birth: Insights into adult cardiovascular disease. Life Sci. 2011, 89, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Harrison, M.S.; Goldenberg, R.L. Global burden of prematurity. Semin. Fetal Neonatal Med. 2016, 21, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Ren, P.; Yao, S.; Li, J.; Valdes-Sosa, P.A.; Kendrick, K.M. Improved Prediction of Preterm Delivery Using Empirical Mode Decomposition Analysis of Uterine Electromyography Signals. PLoS ONE 2015, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Fergus, P.; Cheung, P.; Hussain, A.; Al-Jumeily, D.; Dobbins, C.; Iram, S. Prediction of Preterm Deliveries from EHG Signals Using Machine Learning. PLoS ONE 2013, 10, e77154. [Google Scholar] [CrossRef] [PubMed]
- Smrdel, A.; Jager, F. Separating sets of term and pre-term uterine EMG records. Physiol. Meas. 2015, 36, 341–355. [Google Scholar] [CrossRef] [PubMed]
- Fele-Žorž, G.; Kavšek, G.; Novak-Antolič, Ž.; Jager, F. A comparison of various linear and non-linear signal processing techniques to separate uterine EMG records of term and pre-term delivery groups. Med. Biol. Eng. Comput. 2008, 46, 911–922. [Google Scholar] [CrossRef] [PubMed]
- Akay, M. Nonlinear Biomedical Signal Processing Vol. II: Dynamic Analysis and Modeling, 1st ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Small, M. Dynamics of Biological Systems, 1st ed.; CRC Press: London, UK, 2011. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed.; Westview Press: Cambridge, UK, 2014. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet : Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Di Marco, L.Y.; Di Maria, C.; Tong, W.C.; Taggart, M.J.; Robson, S.C.; Langley, P. Recurring patterns in stationary intervals of abdominal uterine electromyograms during gestation. Med. Biol. Eng. Comput. 2014, 52, 707–716. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceddings of the 2008 IEEE International Joint Conference on Neural Networks, Hong Kong, China, 1–8 June 2008; pp. 1322–1328.
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Int. Res. 2002, 16, 321–357. [Google Scholar]

| Different Parameters | Best Classifier | Sensitivity | Specificity | CA | AUC | |
|---|---|---|---|---|---|---|
| Early | , MMSE | Bagged tree | 97 | 90 | 93 | 0.98 |
| , MMFE with Gaussian function | Fine Gaussian SVM | 90 | 100 | 95 | 1 | |
| , MMFE with Z function | Fine Gaussian SVM | 91 | 100 | 95.4 | 0.99 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 90 | 99 | 94.1 | 0.99 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 87 | 100 | 93.6 | 0.99 | |
| Late | , MMSE | Fine Gaussian SVM | 78 | 99 | 88.5 | 0.99 |
| , MMFE with Gaussian function | Fine Gaussian SVM | 90 | 99 | 94.4 | 1 | |
| , MMFE with Z function | Fine Gaussian SVM | 84 | 99 | 91.7 | 0.99 | |
| , MMFE with Gaussian function | Quadratic SVM | 98 | 89 | 93.7 | 0.98 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 84 | 98 | 91.1 | 0.98 | |
| Early and Late combined | , MMSE | Fine Gaussian SVM | 84 | 99 | 91.9 | 0.99 |
| , MMFE with Gaussian function | Fine Gaussian SVM | 92 | 98 | 94.9 | 0.99 | |
| , MMFE with Z function | Fine Gaussian SVM | 90 | 99 | 94.3 | 0.99 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 87 | 97 | 92.1 | 0.98 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 91 | 98 | 94.3 | 0.98 | |
| Different Parameters | Best Classifier | Sensitivity | Specificity | CA | AUC | |
|---|---|---|---|---|---|---|
| Early | , MMSE | Fine Gaussian SVM | 88 | 95 | 91.3 | 0.98 |
| , MMFE with Gaussian function | Fine Gaussian SVM | 91 | 92 | 91.5 | 0.98 | |
| , MMFE with Z function | Fine Gaussian SVM | 89 | 94 | 91.8 | 0.97 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 94 | 99 | 96.5 | 0.99 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 81 | 97 | 89.4 | 0.98 | |
| Late | , MMSE | Fine Gaussian SVM | 76 | 97 | 86.4 | 0.94 |
| , MMFE with Gaussian function | Fine Gaussian SVM | 91 | 93 | 92.3 | 0.98 | |
| , MMFE with Z function | Fine Gaussian SVM | 88 | 97 | 92.5 | 0.98 | |
| , MMFE with Gaussian function | Bagged tree | 94 | 87 | 90.4 | 0.96 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 88 | 95 | 91.6 | 0.96 | |
| Early and Late combined | , MMSE | Fine Gaussian SVM | 83 | 95 | 88.7 | 0.95 |
| , MMFE with Gaussian function | Fine Gaussian SVM | 91 | 91 | 90.9 | 0.97 | |
| , MMFE with Z function | Fine Gaussian SVM | 94 | 92 | 92.6 | 0.97 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 92 | 93 | 92.7 | 0.98 | |
| , MMFE with Gaussian function | Fine Gaussian SVM | 93 | 94 | 93.5 | 0.97 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.U.; Chanwimalueang, T.; Thayyil, S.; Mandic, D.P. A Multivariate Multiscale Fuzzy Entropy Algorithm with Application to Uterine EMG Complexity Analysis. Entropy 2017, 19, 2. https://doi.org/10.3390/e19010002
Ahmed MU, Chanwimalueang T, Thayyil S, Mandic DP. A Multivariate Multiscale Fuzzy Entropy Algorithm with Application to Uterine EMG Complexity Analysis. Entropy. 2017; 19(1):2. https://doi.org/10.3390/e19010002
Chicago/Turabian StyleAhmed, Mosabber U., Theerasak Chanwimalueang, Sudhin Thayyil, and Danilo P. Mandic. 2017. "A Multivariate Multiscale Fuzzy Entropy Algorithm with Application to Uterine EMG Complexity Analysis" Entropy 19, no. 1: 2. https://doi.org/10.3390/e19010002
APA StyleAhmed, M. U., Chanwimalueang, T., Thayyil, S., & Mandic, D. P. (2017). A Multivariate Multiscale Fuzzy Entropy Algorithm with Application to Uterine EMG Complexity Analysis. Entropy, 19(1), 2. https://doi.org/10.3390/e19010002






