Radiative Entropy Production along the Paludification Gradient in the Southern Taiga
Abstract
:1. Introduction
2. Theory, Methods, and Data
2.1. Theory
2.2. Methods
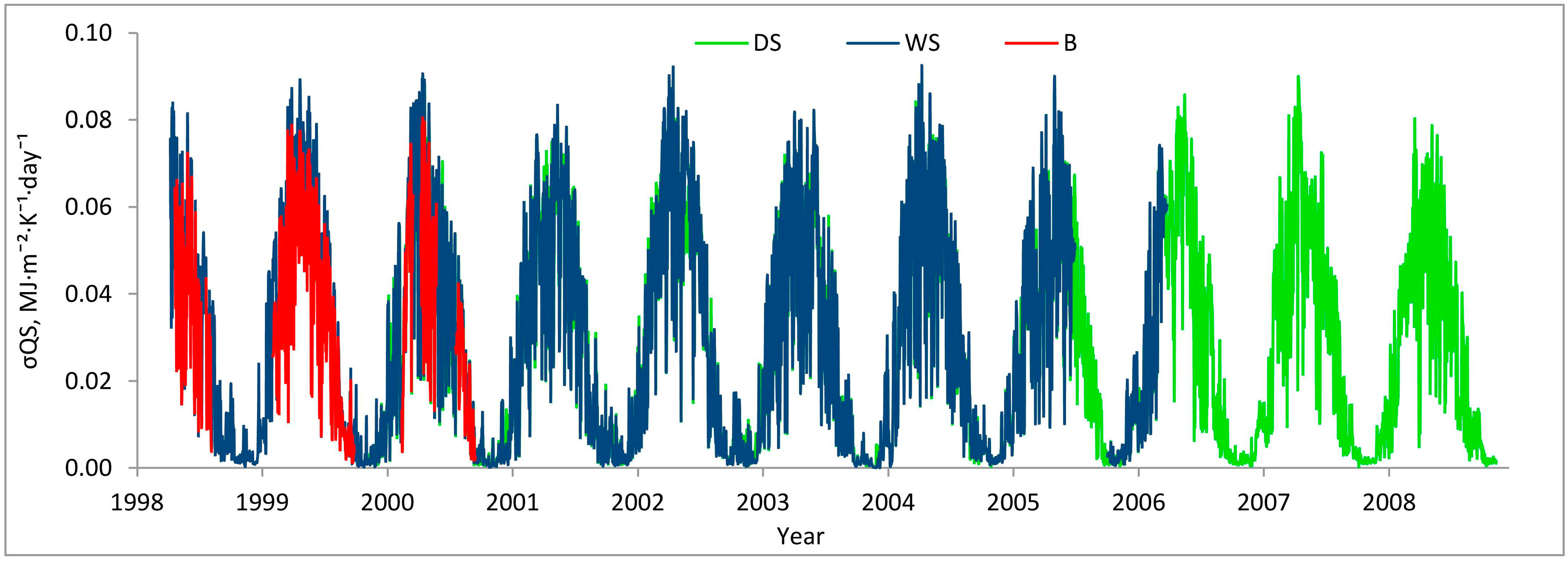
2.3. Sites and Data
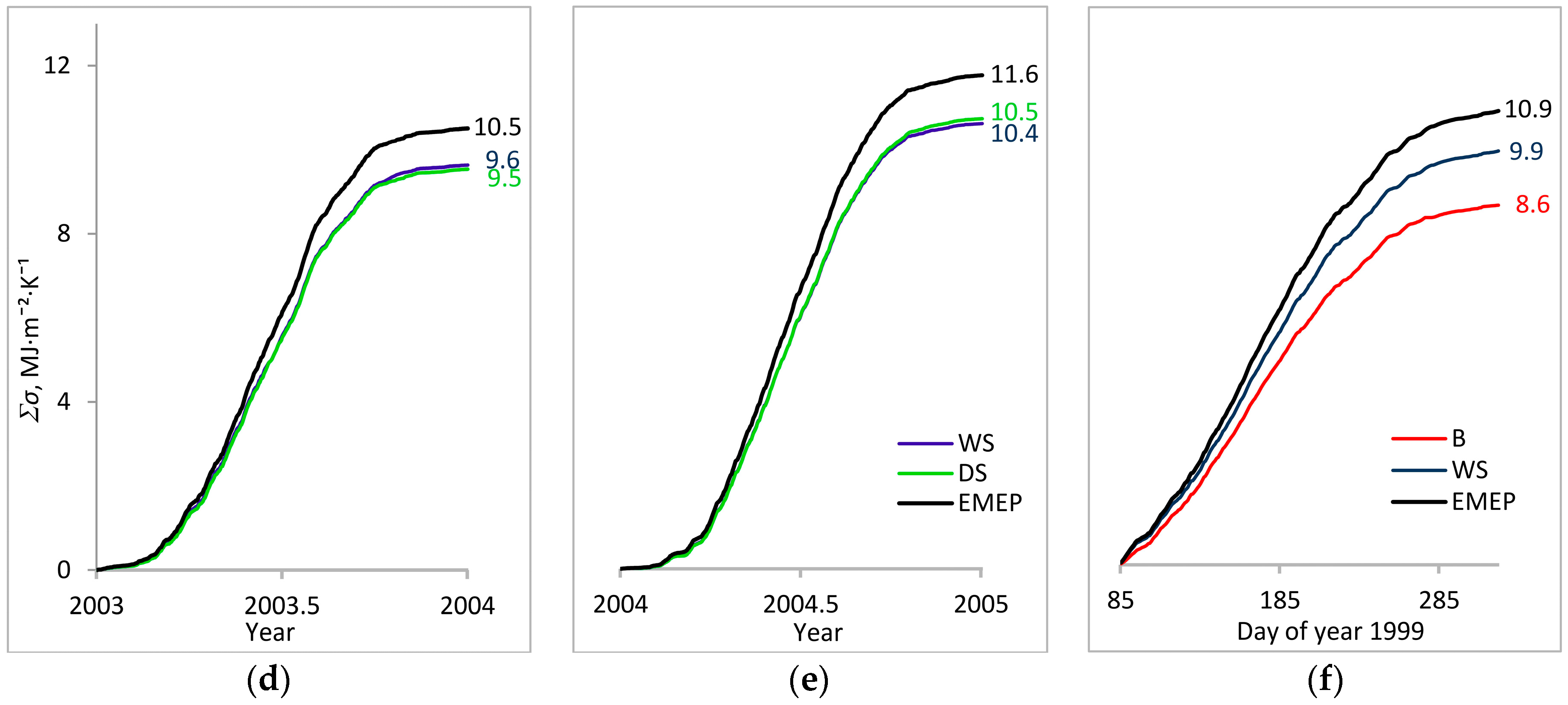
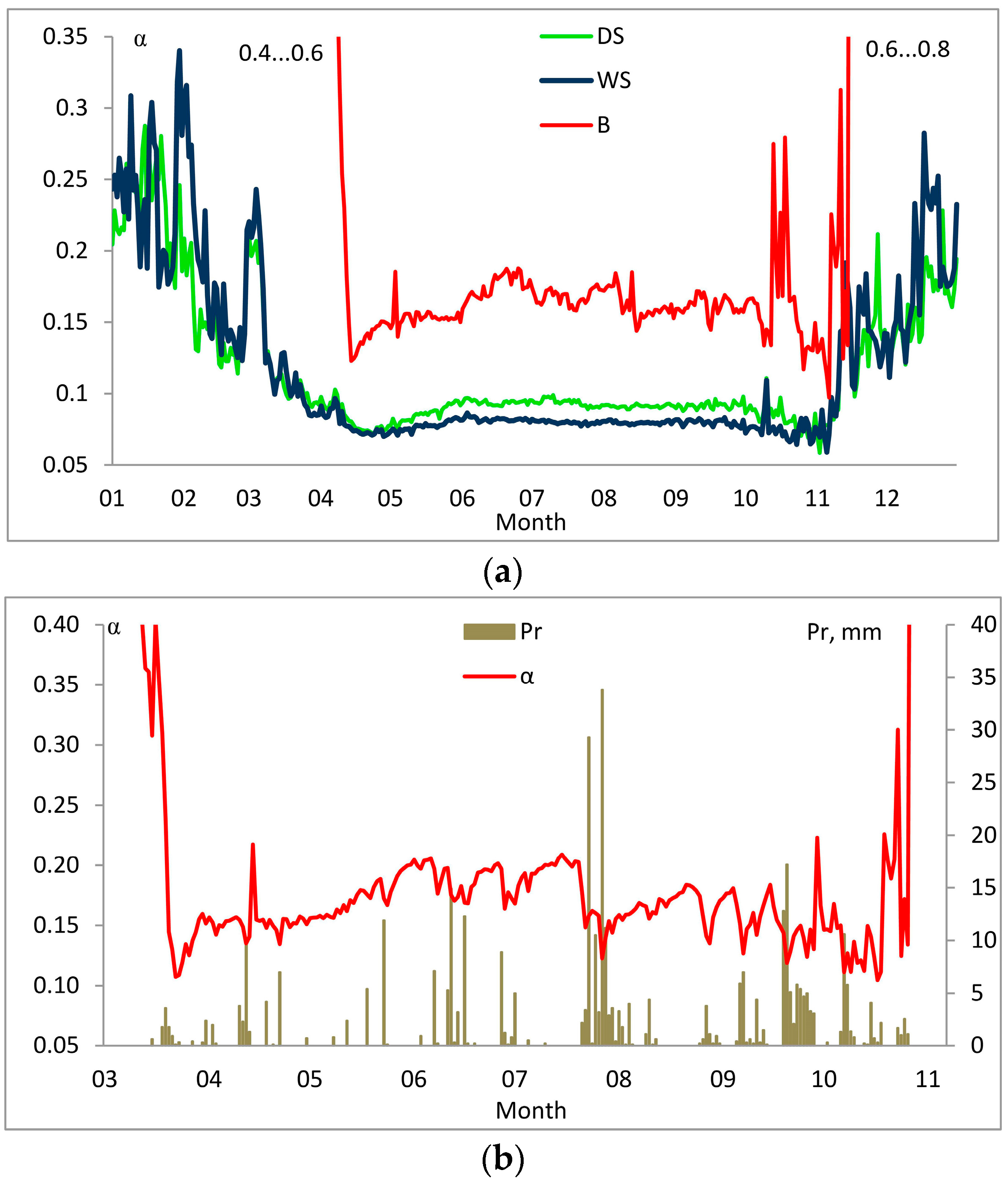
3. Results
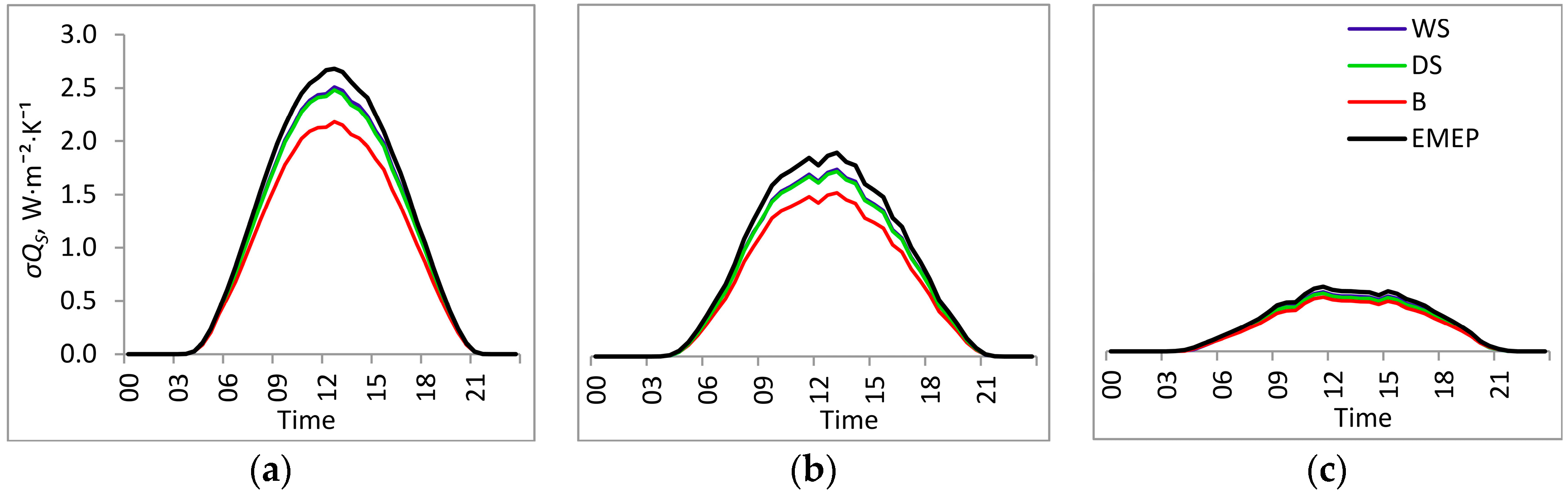
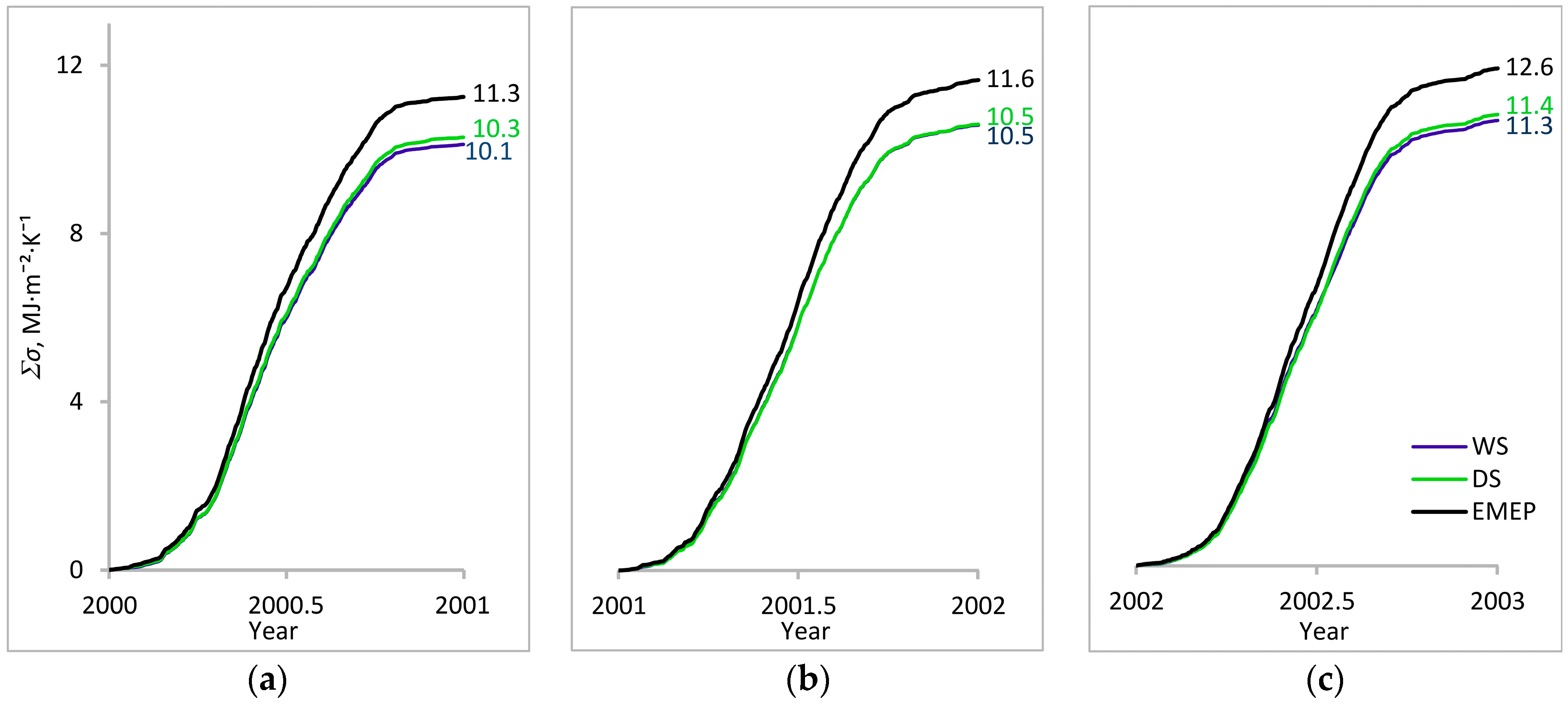
3.1. Entropy Production in Ecosystems of the Southern Taiga
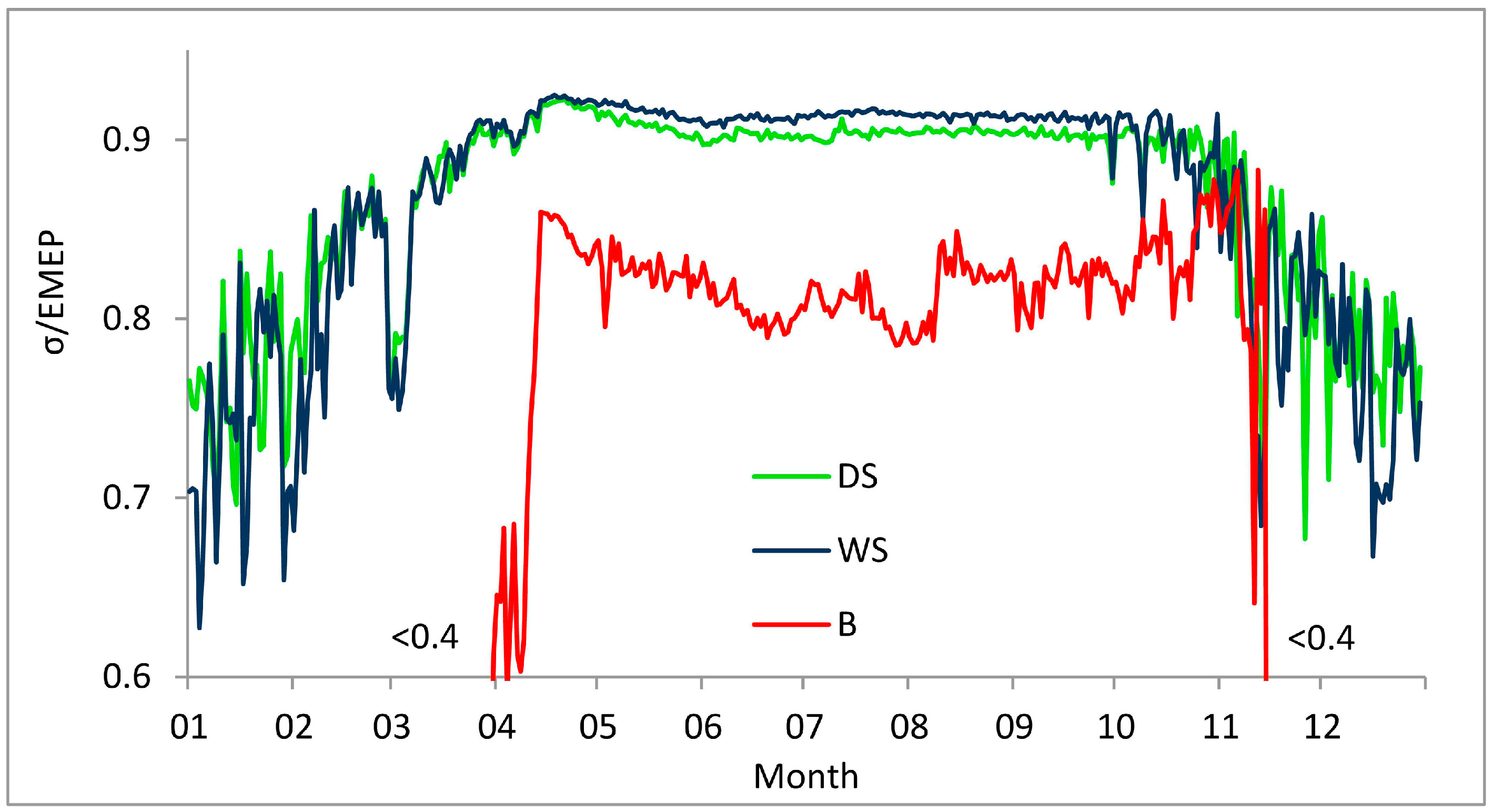
3.2. Factors Affecting Entropy Production
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kleidon, A.; Lorenz, R. Entropy Production by Earth System Processes. In Non-Equilibrium Thermodynamics and the Production of Entropy: Life, Earth, and Beyond; Kleidon, A., Lorenz, R.D., Eds.; Springer: Berlin/Heigelberg, Germany, 2005; Chapter 1; pp. 1–20. [Google Scholar]
- Chen, G.Q. Exergy consumption of the earth. Ecol. Model. 2005, 184, 363–380. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Fath, B.D.; Bastianoni, S.; Marques, J.C.; Müller, F.; Nielsen, S.N.; Patten, B.C.; Tiezzi, E.; Ulanowicz, R.E. A New Ecology: Systems Perspective; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Aoki, I. Entropy production in living systems: From organisms to ecosystems. Thermochim. Acta 1995, 250, 359–370. [Google Scholar] [CrossRef]
- Jorgensen, S.E.; Svirezhev, Y.M. Towards a Thermodynamic Theory for Ecological Systems; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Kirwan, A.D. Quantum and ecosystem entropies. Entropy 2008, 10, 58–70. [Google Scholar] [CrossRef]
- Baldwin, R.A. Use of maximum entropy modeling in wildlife research. Entropy 2009, 11, 854–866. [Google Scholar] [CrossRef]
- Kleidon, A.; Malhi, Y.; Cox, P.M. Maximum entropy production in environmental and ecological systems. Philos. Trans. R. Soc. Lond. Ser. B 2010, 365, 1297–1302. [Google Scholar] [CrossRef] [PubMed]
- Silow, E.A.; Mokry, A.V.; Jørgensen, S.E. Some applications of thermodynamics for ecological systems. In Thermodynamics—Interaction Studies—Solids, Liquids and Gases; Moreno-Pirajan, J.C., Ed.; InTech: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef]
- Lin, H.; Cao, M.; Stoy, P.C.; Zhang, Y. Assessing self-organization of plant communities—A thermodynamic approach. Ecol. Model. 2009, 220, 784–790. [Google Scholar] [CrossRef]
- Maes, W.H.; Pashuysen, T.; Trabucco, A.; Veroustraete, F.; Muys, B. Does energy dissipation increase with ecosystem succession? Testing the ecosystem exergy theory combining theoretical simulations and thermal remote sensing observations. Ecol. Model. 2011, 222, 3917–3941. [Google Scholar] [CrossRef]
- Norris, C.; Hobson, P.; Ibisch, P.L. Microclimate and vegetation function as indicators of forest thermodynamic efficiency. J. Appl. Ecol. 2012, 49, 562–570. [Google Scholar] [CrossRef]
- Stoy, P.C.; Lin, H.; Novick, K.A.; Siqueira, M.; Juang, J.Y. The role of vegetation on the ecosystem radiative entropy budget and trends along ecological succession. Entropy 2014, 16, 3710–3731. [Google Scholar] [CrossRef]
- Miedziejko, E.M.; Kędziora, A. Impact of plant canopy structure on the transport of ecosystem entropy. Ecol. Model. 2014, 289, 15–25. [Google Scholar] [CrossRef]
- Lin, H.; Cao, M.; Zhang, Y. Self-organization of tropical seasonal rain forest in southwest China. Ecol. Model. 2011, 222, 2812–2816. [Google Scholar] [CrossRef]
- Song, Q.; Lin, H.; Zhang, Y.; Tan, Z.; Zhao, J.; Zhao, J.; Zhang, X.; Zhou, W.; Yu, L.; Yang, L.; et al. The effect of drought stress on self-organization in seasonal tropical rainforest. Ecol. Model. 2013, 265, 136–139. [Google Scholar] [CrossRef]
- Svirezhev, Y.M. Thermodynamics and ecology. Ecol. Model. 2000, 132, 11–22. [Google Scholar] [CrossRef]
- Lin, H. Thermodynamic entropy fluxes reflect ecosystem characteristics and succession. Ecol. Modell. 2015, 298, 75–86. [Google Scholar] [CrossRef]
- Lin, H.; Fan, Z.; Shi, L.; Arain, A.; McCaughey, H.; Billesbach, D.; Siqueira, M.; Bracho, R.; Oechel, W. The Cooling Trend of Canopy Temperature during the Maturation, Succession, and Recovery of Ecosystems. Ecosystems 2016, 1–10. [Google Scholar] [CrossRef]
- Skene, K.R. The energetics of ecological succession: A logistic model of entropic output. Ecol. Model. 2013, 250, 287–293. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Schymanski, S.J.; Kleidon, A. Quantifying the thermodynamic entropy budget of the land surface: Is this useful? Earth Syst. Dyn. 2011, 2, 87–103. [Google Scholar] [CrossRef]
- Vompersky, S.E.; Sirin, A.A.; Sal’nikov, A.A.; Tsyganova, O.P.; Valyaeva, N.A. Estimation of forest cover extent over peatlands and paludified shallow-peat lands in Russia. Contemp. Probl. Ecol. 2011, 4, 734–741. [Google Scholar] [CrossRef]
- Puzachenko, Yu.G.; Kotlov, L.P.; Sandlerskiy, R.B. Analysis of changes of land cover using multispectral remote sensing information in the central forest reserve. Izv. Geogr. 2014, 3, 5–18. [Google Scholar] [CrossRef]
- Glushkov, I.V. Current State and History of Development of Watershed Swamps and Paludified Forests of Central Forest Reserve. Ph.D. Dissertation, Institute of Forest Science, Russian Academy of Sciences (ILAN), Moscow, Russian, 2012. [Google Scholar]
- Puzachenko, Y.; Sandlersky, R.; Sankovski, A. Methods of evaluating thermodynamic properties of landscape cover using multispectral reflected radiation measurements by the Landsat satellite. Entropy 2013, 15, 3970–3982. [Google Scholar] [CrossRef]
- Hollinger, D.Y.; Ollinger, S.V.; Richardson, A.D.; Meyers, T.; Dail, D.B.; Martin, M.E.; Scott, N.A.; Arkebauer, T.J.; Baldocchi, D.D.; Clark, K.L.; et al. Albedo estimates for land surface models and support for a new paradigm based on foliage nitrogen concentration. Glob. Chang. Biol. 2009, 16, 696–710. [Google Scholar] [CrossRef]
- Berglund, E.R.; Mace, A.C., Jr. Seasonal Albedo Variation of Black Spruce and Sphagnum-Sedge Bog Cover Types. J. Appl. Meteorol. 1972, 11, 806–812. [Google Scholar] [CrossRef]
- Kurbatova, J.; Arneth, A.; Vygodskaya, N.N.; Kolle, O.; Varlargin, A.V.; Milyukova, I.M.; Tchebakova, N.M.; Schulze, E.; Lloyd, J. Comparitive ecosystem-atmosphere exchange of energy and mass in European Russian and central Siberian bog. I. Interseasonal and interannual variability of energy and latent heat fluxes during the snowfree period. Tellus B 2002, 54, 497–513. [Google Scholar] [CrossRef]
- Lohila, A.; Minkkinen, K.; Laine, J.; Savolainen, I.; Tuovinen, J.P.; Korhonen, L.; Laurila, T.; Tietäväinen, H.; Laaksonen, A. Forestation of boreal peatlands: Impacts of changing albedo and greenhouse gas fluxes on radiative forcing. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Holdaway, R.J.; Sparrow, A.D.; Coomes, D.A. Trends in entropy production during ecosystem development in the Amazon Basin. Philos. Trans. R. Soc. Lond. Ser. B 2010, 365, 1437–1447. [Google Scholar] [CrossRef] [PubMed]
- Jones, H.G. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Desherevskii, A.V.; Zhuravlev, V.I.; Nikolsky, A.N.; Sidorin, A.Ya. Technologies for analysis of geophysical time series. Part 1. Requirements for software. Seism. Instrum. 2016, 52, 61–82. [Google Scholar]
- Desherevskii, A.V.; Zhuravlev, V.I.; Nikolsky, A.N.; Sidorin, A.Ya. Technologies for analysis of geophysical time series. Part 2. WinABD—A software package for maintenance and data analysis of geophysical monitoring. Seism. Instrum. 2016, 52, 50–80. [Google Scholar]
- Desherevskii, A.V.; Zhuravlev, V.I.; Nikolsky, A.N.; Sidorin, A.Ya. Problems in analysis of time series with gaps and their solutions in WinABD software package. Geophys. Process. Biosph. 2016, 15, 5–34. [Google Scholar]
- Vygodskaya, N.N.; Schulze, E.D.; Tchebakova, N.M.; Karpachevskii, L.O.; Kozlov, D.; Sidorov, K.N.; Panfyorov, M.I.; Abrazko, M.A.; Shaposhnikov, E.S.; Solnzeva, O.N.; et al. Climatic control of stand thinning in unmanaged spruce forests of the southern taiga in European Russia. Tellus B 2002, 54, 443–461. [Google Scholar] [CrossRef]
- Schulze, E.D.; Vygodskaya, N.N.; Tchebakova, N.M.; Czimczik, C.I.; Kozlov, D.N.; Lloyd, J.; Mollicone, D.; Parfenova, E.; Sidorov, K.N.; Varlagin, A.V.; et al. The Eurosiberian transect: An introduction to the experimental region. Tellus B 2002, 54, 421–428. [Google Scholar] [CrossRef]
- Desherevskaya, O.; Kurbatova, J.; Oltchev, A. Climatic conditions of the south part of Valday hills, Russia, and their projected changes during the 21st century. Open Geogr. J. 2010, 3, 73–79. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth. Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Minaeva, T.J.; Glushkov, I.V.; Nosova, M.B.; Starodubceva, O.A.; Kuraeva, E.N.; Volkova, E.M. Survey of bogs of Central Forest Reserve. Trudy Central’no-Lesnogo Zapovednika 2007, 4, 267–296. (In Russian) [Google Scholar]
- Kurbatova, J.; Li, C.; Varlagin, A.; Xiao, X.; Vygodskaya, N. Modeling carbon dynamics in two adjacent spruce forests with different soil conditions in Russia. Biogeosciences 2008, 5, 969–980. [Google Scholar] [CrossRef]
- Kurbatova, J.; Tatarinov, F.; Molchanov, A.; Varlagin, A.; Avilov, V.; Kozlov, D.; Ivanov, D.; Valentini, R. Partitioning of ecosystem respiration in a paludified shallow-peat spruce forest in the southern taiga of European Russia. Environ. Res. Lett. 2013, 8, 045028. [Google Scholar] [CrossRef]
- Šantrůčková, H.; Kaštovská, E.; Kozlov, D.; Kurbatova, J.; Livečková, M.; Shibistova, O.; Tatarinov, F.; Lloyd, J. Vertical and horizontal variation of carbon pools and fluxes in soil profile of wet southern taiga in European Russia. Boreal Environ. Res. 2010, 15, 357–369. [Google Scholar]
- Arneth, A.; Kurbatova, J.; Lloyd, D.; Kolle, O.; Schibistova, O.; Vygodskaya, N.N.; Schulze, E.-D.; Lloyd, J. Ecosystem-atmosphere exchange of energy and mass in a European Russia and a central Siberia bog. II. Internseasonal and interannual variability of CO2 fluxes. Tellus B 2002, 54, 514–530. [Google Scholar] [CrossRef]
- Vygodskaya, N.N.; Abrazhko, V.I.; Varlagin, A.V.; Kurbatova, Ju.A.; Sidorov, K.N.; Milyukova, I.M.; Sogachev, A.F.; Sogacheva, L.M.; Shaposhnikov, E.S.; Nepomnyashii, G.I.; et al. Long-Term Dynamics of Soil Moisture and Drying of Spruce Trees in Spruce Forests of the Southern Taiga. Lesovedenie 2004, 1, 3–22. [Google Scholar]
- Vygodskaya, N.N.; Oltchev, A.V.; Kurbatova, J.A.; Varlargin, A.V. Gross primary production (GPP) of unmanaged over-mature spruce forests at southern European taiga: Eddy covariance measurements and modeling approach. In Modeling Forest Production, Scientific Tools—Data Needs and Sources, Validation and Application; Hasenauer, H., Makela, A., Eds.; BOKU University of Natural Resources and Applied Life Sciences: Vienna, Austria, 2004; pp. 421–430. [Google Scholar]
- FLUXNET. Available online: https://fluxnet.ornl.gov/ (accessed on 13 January 2017).
- Kitaev, L.M.; Titkova, T.B. Variability of snow cover albedo—The analysis of the satellite data. Curr. Probl. Remote Sens. Earth Space 2011, 8, 47–57. [Google Scholar]
- Moore, P.D. The future of cool temperate bogs. Environ. Conserv. 2002, 29, 3–20. [Google Scholar] [CrossRef]
- Minayeva, T.Y.; Trofimov, S.Y.; Chichagova, O.A.; Dorofeyeva, E.I.; Sirin, A.A.; Glushkov, I.V.; Mikhailov, N.D.; Kromer, B. Carbon accumulation in soils of forest and bog ecosystems of southern Valdai in the Holocene. Biol. Bull. 2008, 35, 524–532. [Google Scholar] [CrossRef]
- Novenko, E.; Olchev, A.; Desherevskaya, O.; Zuganova, I. Paleoclimatic reconstructions for the south of Valdai Hills (European Russia) as paleo-analogues of possible regional vegetation changes under global warming. Environ. Res. Lett. 2009, 4, 045016. [Google Scholar] [CrossRef]

| Dry Spruce Forest (DS) | Wet Spruce Forest (WS) | Bog (B) | |
|---|---|---|---|
| Site coordinates | 32.9239° N, 56.4617° E | 32.9039° N, 56.4476° E | 33.0325° N, 56.4750° E |
| Site altitude, m a.s.l. | 265.00 | 262.50 | 253.75 |
| Vegetation type | Mature nemorose spruce forest with broad-leaved species | Mature paludified shallow-peat spruce forest with birch | Oligotrophic peat bog |
| Measurement period | 2000–2008, second half of 2015 | 1998–2005, 2nd halves of 2006 and 2014, 2015 | Warm periods of 1998–2000 |
| Site (Period) | σQS | σQL | EMEP | σ/EMEP | Qs,net | α | Tsurf |
|---|---|---|---|---|---|---|---|
| W·m−2·K−1 | W·m−2 | K | |||||
| WS (2000–2005) | 0.3316 | 0.0026 2 | 0.3642 | 0.919 | 100.25 | 0.114 | 279.28 |
| DS (2000–2005) | 0.3277 | 0.0033 2 | 0.3653 | 0.901 | 99.55 | 0.117 | 279.19 |
| WS (Apr–Oct 1999) | 0.5164 | 0.0041 | 0.5662 | 0.912 | 159.15 | 0.076 | 286.73 |
| B (Apr–Oct 1999) | 0.4563 | 0.0057 | 0.5686 | 0.802 | 143.01 | 0.166 | 287.35 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuricheva, O.; Mamkin, V.; Sandlersky, R.; Puzachenko, J.; Varlagin, A.; Kurbatova, J. Radiative Entropy Production along the Paludification Gradient in the Southern Taiga. Entropy 2017, 19, 43. https://doi.org/10.3390/e19010043
Kuricheva O, Mamkin V, Sandlersky R, Puzachenko J, Varlagin A, Kurbatova J. Radiative Entropy Production along the Paludification Gradient in the Southern Taiga. Entropy. 2017; 19(1):43. https://doi.org/10.3390/e19010043
Chicago/Turabian StyleKuricheva, Olga, Vadim Mamkin, Robert Sandlersky, Juriy Puzachenko, Andrej Varlagin, and Juliya Kurbatova. 2017. "Radiative Entropy Production along the Paludification Gradient in the Southern Taiga" Entropy 19, no. 1: 43. https://doi.org/10.3390/e19010043
APA StyleKuricheva, O., Mamkin, V., Sandlersky, R., Puzachenko, J., Varlagin, A., & Kurbatova, J. (2017). Radiative Entropy Production along the Paludification Gradient in the Southern Taiga. Entropy, 19(1), 43. https://doi.org/10.3390/e19010043





