Abstract
Entropy production (σ) is a measure of ecosystem and landscape stability in a changing environment. We calculated the σ in the radiation balance for a well-drained spruce forest, a paludified spruce forest, and a bog in the southern taiga of the European part of Russia using long-term meteorological data. Though radiative σ depends both on surface temperature and absorbed radiation, the radiation effect in boreal ecosystems is much more important than the temperature effect. The dynamic of the incoming solar radiation was the main driver of the diurnal, seasonal, and intra-annual courses of σ for all ecosystems; the difference in ecosystem albedo was the second most important factor, responsible for seven-eighths of the difference in σ between the bog and forest in a warm period. Despite the higher productivity and the complex structure of the well-drained forest, the dynamics and sums of σ in two forests were very similar. Summer droughts had no influence on the albedo and σ efficiency of forests, demonstrating high self-regulation of the taiga forest ecosystems. On the contrary, a decreasing water supply significantly elevated the albedo and lowered the σ in bog. Bogs, being non-steady ecosystems, demonstrate unique thermodynamic behavior, which is fluctuant and strongly dependent on the moisture supply. Paludification of territories may result in increasing instability of the energy balance and entropy production in the landscape of the southern taiga.
1. Introduction
Self-organizing open systems, which create “order out of chaos”, must discharge entropy outside, supporting their low-entropy inner structure. For example, a natural ecosystem supports its complex structure through converting low-entropy solar radiation into other high-entropy forms of energy, mainly long-wave radiation, latent and sensible heat energy, etc. [1]. Since the same amount of energy in the form of solar radiation contains more photons than this energy in the form of long-wave radiation, “…the entering solar radiation is more organized than the leaving backscattered and terrestrial radiation” [2]. For a given open system, thermodynamic entropy associated with incoming/outgoing fluxes of energy is somehow connected with informational or structural entropy reflecting the complexity of the system structure.
Entropy in thermodynamics is a measure of “to what extent work has been degraded to heat” [3]. Entropy production is proportional to the degree of the conversion of energy from high-quality forms (energy able to make some work) to low-quality forms (dissipated energy). This process of energy degradation is common for Earth systems [1]. Patterns of energy degradation in different natural systems may be regarded as an indication of their current condition, tolerance, the level of their disturbance, etc. [4,5,6,7,8,9,10]. For such indications, structural and thermodynamic entropy in different types of ecosystems should be estimated and linked to ecological parameters (biomass, primary production, and others) and meteorological parameters (incident radiation, temperature, soil wetness, and others).
Recent investigations found that energy dissipation (closely related to entropy production) in ecosystems depends on the type of plant community [11,12,13,14], canopy architecture [15], weather conditions, seasonality [11,13,16,17], level of disturbance [18,19,20], and stage of succession [14,20,21]. In most of these studies, eco-climatic all-year measurements for the study of biosphere-atmosphere exchange were used; they provide various and detailed data for the evaluation of thermodynamic entropy fluxes in an ecosystem [22]. Based on the set of the thermodynamic indicators, Lin et al. [11] demonstrated that the tropical rainforest of Xishuangbanna, China, was highly self-organized and played an important role in local environmental stability via thermal regulation of the land surface in comparison with rubber plantation and grass communities. Higher energy dissipation was obtained through increased evapotranspiration or increased surface roughness, generally related to succession in terrestrial ecosystems, from non-vegetated land to forest in Flandres, Belgium [12]. Old-growth woodlands in the UK, Germany, and Ukraine attenuated surface temperature and dissipated energy more efficiently than the nearby native species plantations, particularly at higher temperatures [13]. Xishuangbanna forest was the least self-organized and the least able to capture energy during the dry season [17]. It was found that the entropy production was significantly distinguished for different types of ecosystems in the FLUXNET database [14], although the calculations were based on the indirect data on outgoing radiation. Stoy et al. [14] also corroborated that entropy production increased, then decreased, through successional stages of ecosystems of the Duke Forest, NC, USA; however, the authors considered planted pine as a stage of natural succession. The dependencies between the leaf area index and entropy production were found for west Polish lowland ecosystems [15]. Forest islands in Poland had higher fractal dimensions and higher dissipation of energy than crop fields; therefore, the hypothesis was made that the architecture of the plant canopy, due to its role in entropy removal into the environment, might be one of the parameters controlling the functioning of ecosystem [15]. Deforested sites had lower entropy production than nearby forested sites in different parts of North America [19]. Trends of cooling and increasing energy dissipation, as well as higher self-regulation of ecosystems during maturation, succession, and recovery after the disturbance were distinguished using data of 12 chronosequences from the FLUXNET database [20].
Different types of ecosystems in the same radiation environment have their own patterns of energy flux partitioning, and so their own pattern of thermodynamic entropy production. The assessment of thermodynamic entropy fluxes in a mosaic of ecosystems of a landscape, coupled with data for land use, land-use change, and forestry, will allow one to give the overall picture of land surface functions in terms of entropy production [12]. Revealing the year-to-year variation of entropy fluxes due to changing radiation and precipitation regimes of a territory may give the limits of natural variability of entropy production in the whole landscape. Spatiotemporal changes in the entropy production of ecosystems in a given region may be considered as a measure of climate and anthropogenic impact on a landscape [21].
Entropy production along some ecological gradients, such as soil fertility and moistening, has not been under detailed investigation before. For instance, less attention was given to the entropy production of bogs and paludified forests, occupying vast areas in humid climates. In Russia, bogs and paludified shallow-peat lands (the peat layer is less than 30 cm) cover over one-fifth of the territory, and bogs, particularly, cover over 8% of the territory [23]. These areas may significantly change due to labile forest-bog boundaries, which may shift by up to 30 m within a five-year period (in the southern taiga) [24]. Some bogs had no response to climatic changes and are characterized by very slow growth, while others quickly expanded toward surrounding forests after an increase in precipitation [25]. According to a study by Puzachenko et al. [26] based on multispectral remote sensing, the thermodynamic behavior of bogs was distinctive from neighboring forests and meadows. The reflection of radiation in different spectral channels in bogs was unstable, but entropy production and the information increment during the entire vegetative season was relatively stable [26]. While northern coniferous forests usually reflect 6%–9% of the incoming solar radiation [27], bogs reflect 11%–20% [28,29,30]. Changing the proportion of forest and bog areas may exert great influence on the radiation balance and thermodynamics of landscapes.
In this study we used long-term experimental data to assess thermodynamic entropy production in three southern taiga ecosystems along the paludification gradient. The sites use approximately the same amount of incoming solar radiation; therefore, the difference in entropy production was determined by ecosystem characteristics. We reveal how drought conditions affect entropy production in the studied ecosystems and provide an analysis of the parameters affecting the ecosystem entropy production and the efficiency of ecosystem entropy production along the ecosystem moistening gradient in the southern taiga.
2. Theory, Methods, and Data
2.1. Theory
Our calculation is based on the concept of the transformation of high-quality (low-entropy) energy into low-quality (high-entropy) energy with the production of some entropy. To calculate entropy production and the empirical maximum of entropy production (EMEP), we used the technique from Stoy et al. [14]. This method is based on quantifying entropy production following Brunsell et al. [22] and using the approach of Holdaway et al. [31]. It requires data on the air temperature and on short-wave incoming (QS,in), short-wave outgoing (QS,out), long-wave incoming (QL,in), and long-wave outgoing (QL,out) radiation.
Following the chosen technique, we did not assess the entropy production associated with all terms of the full energy budget equation due to some difficulties of its estimation, described in [14] in detail. Therefore, we investigated only the entropy production associated with radiation conversion at the land surface, predominantly absorbing the low-entropy solar radiation.
The net radiation at the Earth’s surface Rn is formed as the difference of the incoming and outgoing radiation fluxes:
where QS,in and QS,out are the incoming and outgoing short-wave radiation, respectively; QL,in and QL,out are the incoming and outgoing long-wave radiation, respectively; net short-wave radiation QS,net = QS,in − QS,out; and net long-wave radiation QL,net = QL,in − QL,out. All terms are in W·m−2.
The entropy production of ecosystems associated with short-wave radiation conversion equals:
where Tsun is the sun’s surface temperature, which approximately equals 5780 K; Tsurf is the radiometric surface temperature, calculated from QL,out using the Stefan-Boltzmann equation:
where C is the Stefan-Boltzmann constant; A is the view factor assumed to be one; and εsurf is the surface emissivity calculated as:
where α is the short-wave albedo, calculated here as the daily average of noontime (average from 11 a.m. to 2 p.m. LST), QS,out divided by QS,in. Note that in Equation (2), QS,net depends on full-day, rather than noontime, albedo.
Entropy production associated with long-wave radiation is equal to:
where Tsky is the temperature of the sky and it also can be accessed from QL,in using the Stefan-Boltzmann equation:
The emissivity of the sky, εsky, was assumed to be 0.85 and A was again assumed to be one.
The total radiative entropy production σ is the sum of σQS and σQL:
The empirical maximum entropy production (EMEP) in short-wave balance reflects the highest possible amount of entropy that the terrestrial surface could produce if it absorbed all of the real incoming radiation, but its temperature did not increase to produce H (if it was a cold black body), i.e., in calculations of EMEP short-wave radiation, QS,net is assumed to be equal to QS,in and Tsurf is replaced by Tair:
EMEP in the long-wave radiation conversion σQL,max is often two orders of magnitude less than [22], so the total EMEP is approximately equal to :
The efficiency of entropy production σ/EMEP is the useful parameter for the comparison of ecosystem functioning at the different time-scales and for comparison of different ecosystems [14].
Let us make an estimation of orders of terms in Equation (2) using real data. If Tsurf ranges from –80 °C to +80 °C (approximate temperature limits on Earth’s surface), 1/Tsurf ranges from 0.05177 to 0.02832 K−1, while 1/Tsun = 0.000173 K−1, i.e., 1/Tsun amounts to 3.3%–6.1% of 1/Tsurf. If we suppose (1) the diurnal temperature ranges from 0 to 40 °C; (2) consequent day-to-day temperature changes from 10 to 20 °C; and (3) inter-annual temperature changes from 20 to 25 °C (in most real ecosystems the range is usually smaller), the temperature term will vary by about 14.4% around the average value in the first case, by about 3.7% in the second case, and by about 1.8% in the third case. By contrast, the radiative term QS,net may range from 0 to more than 1000 W·m−2 during the day, three-fold (hundreds W·m−2) from an overcast day to a clear day, and by 10%–20% from year to year. Consequently, using real data, QS,net usually shows much greater variation at different time-scales than .
According to the Equation (2) the greatest entropy production under a given radiation input would be associated with dark, but cold, ecosystems, i.e., ecosystems that absorb more solar energy, but maintain a low temperature (for example, via enhanced evapotranspiration). However, what is the relative significance of these two factors (radiative effect through ecosystem albedo versus temperature effect)? A 10 °C difference between ecosystems in temperature will result in 3.5%–3.7% difference in σ, whereas we may hardly find adjacent ecosystems with so large a simultaneous difference in surface temperature (we may except snow versus snow-less surfaces), neighboring ecosystems with 5%–10% difference in albedo are common (i.e., old forest or water surface versus grassland or bog [32]). The radiative term again plays the major role in radiative entropy production differences at the landscape scale, but the temperature term may also be important in cases of ecosystems having similar albedo, but distinguished temperature (for example, forest versus lake).
2.2. Methods
To calculate σ and EMEP we used in situ data on air temperature, short-wave incoming (QS,in), short-wave outgoing (QS,out), long-wave incoming (QL,in), and long-wave outgoing (QL,out) radiation, collected at eddy covariance sites with a native half-hourly time-step (see Section 2.3). Quality control of the used data included spike removal, the exclusion of non-physical values, like non-zero short-wave radiation at night (which sometimes takes place due to instrument biases), examination of congruence of in- and outgoing short-wave radiation using albedo values, excluding days in December–February with too low short-wave radiation for albedo calculations, etc. WinABD software (Deshcherevskii, IPE RAS, Moscow, Russia [33,34,35]) was used for the analysis of long-term data with unavoidable gaps. For the calculation of daily, monthly, and annual entropy sums, missed data on radiation were filled. However, missed data rates in the key parameters for our calculation, i.e. fluxes of short-wave radiation, did not exceed 4% of all data for the studied periods (see Section 2.3). Incoming short-wave radiation was filled using data on photosynthetically active radiation at the same site (correlation coefficients for available quaility-controlled data were 0.99), or extrapolation from neighboring site (correlation coefficients were more than 0.96). Reflected radiation was filled using the average duirnal course of the albedo in the same season multiplied by QS,in after filling of QS,in. Long-wave outgoing radiation was filled using air temperature above the canopy, because these parameters demonstrated an excellent correlation (>0.99). If such information was absent, we used a running mean (in case of 30 min–2 h gaps), running average diurnal course, or mean diurnal course for the same month in other years (for gaps from a few days to few weeks). To analyze how entropy production and σ/EMEP change under varying weather conditions in the mid-growing-season, only data from 15 May to 31 July were chosen. Sunny, variable clouds, and overcast days were selected using the following rough approximation: for each site, separately, 10% of days with the highest QS,in sums were determined as “sunny”, 10% of days with the lowest QS,in sums were determined as “overcast”, and days from the 45th percentile to the 55th percentile of QS,in sums were considered as “variable cloud” days. The first sample was in a good agreement with sunny days distinguished by the regular diurnal course, though a few days with low cloud amounts were also regarded as “sunny”.
2.3. Sites and Data
Studied sites are located in the Central Forest Biosphere Reserve (CFBR) (56.5° N, −33.0° E, 200–240 m above sea level) in the southern part of Valdai Hills, Tver region. The vegetation of the reserve is typical for southern and middle taiga of the European part of Russia [36,37]. The reserve has a core area of 24,447 ha surrounded by a buffer zone of 46,061 ha. The core is situated far enough from industrial and residential areas and is not affected by serious anthropogenic activity or air pollution, but in the last decades significant climate and vegetation changes have been taking place within the territory.
The most wide-spread ecosystems in CFBR (Figure 1) are old spruce forests with a mixture of broad-leaved or small-leaved trees (59% of the core reserve area in 1986 and 49% in 2010), birch or aspen stands and fellings (32% in 1986 and 30% in 2010), restoring spruce forests at windfalls and burnt areas (12% in 2010), and bogs (9% of the core reserve area in 1986 and 11% in 2010) [24]. Puzachenko et al. [24] reported that the bog area in the CFBR had increased by 20% in 1986–2010 due to the propagating of bogs toward surrounding forests and the destruction of swampy pine forests. This may be connected with a significant increase in winter temperature (by 4.0 °C in January) and annual precipitation in 1963–1999 [38], resulting in an increase of duration of mid-seasons.
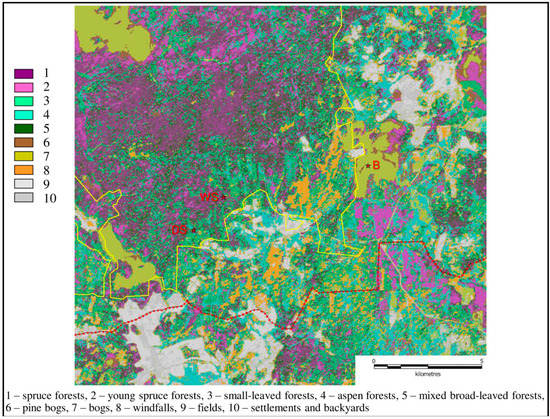
Figure 1.
Vegetation cover in the southeastern part of the Central Forest Biosphere Reserve. Wet Spruce (WS), Dry Spruce (DS), and Bog (B) are the studied sites (see below). The yellow line is the boundary of the core of the reserve and red points mark the boundary of the buffer zone.
The territory belongs to the humid continental climate (Dfb type in the Köppen-Geiger classification system [39]). According to the data of the adjacent Fyodorovskoye weather station, the mean annual temperature at 2 m height for the period of 1981–1999 was 4.1 °C with −7.2 °C in January and 16.5 °C in July; average annual precipitation was 752 mm [38]. Snowmelt generally occurs in late March or early April, while snow cover usually forms in mid-November; the number of days with snow cover in the 1990s varied from 122 to 176 (on average, 148) [29]. Annual precipitation significantly exceeds evapotranspiration, which determines the positive moisture balance of the region. Thirty percent of the territory of the reserve is subjected to paludification due to shallow river valleys and glacial clay soils [40].
The data on short-wave and long-wave radiation were collected at three eddy covariance sites in the CFBR (Table 1), established in 1998 and 2000 as part of the EUROSIBERIAN CARBONFLUX project.

Table 1.
Site descriptions.
The towers are located in three adjacent ecosystems [29,41,42,43,44]: dry spruce forest (DS), wet spruce forest (WS) and bog (B). DS site (32.9239° N, 56.4617° E, 265.00 m a.s.l.) represents the mature (up to 200 years old) nemorose spruce forest with Picea abies (53%), Acer platanoides (18%), Ulmus glabra (6.4%), Populus tremula (6%), and Betula pubescens (5%) trees and undergrowth with Dryopteris filix-mas, Oxalis acetosella, and others, growing on a well-drained slope. The height of trees reach 30–35 m. DS forest has the highest productivity among the all adjacent forest types in the CFBR and represents a typical undisturbed vegetation of the European southern taiga. The average ground water depth is about 1.5 m [41,45,46]. We analyzed the data of the DS station for 2000–2008 and May–December of 2015. The WS site (32.9039° N, 56.4476° E, 262.50 m a.s.l.) is located on a homogenous flat surface covered by the mature (up to 200 years old) paludified shallow-peat forest with Picea abies (86%) and Betula pubesenes (14%), with a small admixture of Pinus Sylvestris, and undergrowth dominated by Vaccinium myrtillus, Sphagnum girgensohnii, and S. magellanicum in peaty soils. Peat depth is 50 cm–1 m. The average tree height is about 23 m with maximum values of 27 m. The forest is low-productive; its habitus is similar to undisturbed vegetation of middle-northern taiga. Ground waters well up to the moss surface and above it after snow-melting [42], whereas in summer the ground water level sinks to 10–50 cm under the surface. In some very dry summers (2010, 2015) the ground water level at WS dropped lower than 120 cm. The WS tower has been working since June 1998, but data on the reflected radiation were available only for 1998–2005, January–May 2006, and June–December 2014 and 2015. The distance between towers in the two forests is about 2 km. The bog site (33.0325° N, 56.4750° E, 253.75 m a.s.l.) is established at bog Starosel’skiy Mokh, having an area of 988.4 ha. The bog consists of a mosaic of small (0.1–0.4 m) ridges dominated by Sphagnum magellanicum and hollows dominated by S. balticum or S. majus. After the snow melts, the entire surface of the bog is flooded [29], in summer the water level is 5–20 cm under the moss surface, and after rains the total area of water in the hollows increases. In droughts, the water level may drop to 60 cm under the moss surface [40]. The tower at the bog was in operation only during warm periods of 1998–2000 (from March–April to October–November).
The eddy covariance towers were equipped with instruments usual to FLUXNET [47] sites. At all sites the short-wave incoming and outgoing radiation was measured by a CM14 pyranometer (Kipp and Zonen, Delft, The Netherlands) and net all-wave radiation was measured by a LXG055 net-radiometer (Schulze-Däke, Dr. Bruno Lange GmbH, Berlin, Germany). Temperature was measured by an HMP35D sensor (Vaisala, Helsinki, Finland). At DS, WS, and B sites sensors were levelled at a height of 42, 29, and 6 m, respectively. Datasets were collected via data loggers with 10 s–1 min frequency and stored in 30 min tables.
Missed data on solar and reflected radiation at the WS site for in 1999–2004 made up 1% and 3% of all data, respectively. For reflected radiation, these were mainly two gaps of 15 day and 10 day length, and for solar radiation, it was mainly one gap of a 10 day length. Missed data on short-wave radiation at the DS site in 2000–2004 made up 4% of all data, mainly two gaps of 25 day length and 17 day length.
3. Results
3.1. Entropy Production in Ecosystems of the Southern Taiga
Figures of the diurnal course of the entropy production and EMEP at the studied sites in different weather conditions (Figure 2) show that the WS and DS forests were very similar, but entropy production in the bog was much lower than in the forests. The most significant difference of σ values between the forests and the bog was associated with sunny conditions. The σ/EMEP at forest sites increased slightly (insignificant in comparison to the standard deviation) with increasing cloudiness. The σ/EMEP rose significantly only at the bog site and on overcast days (σ/EMEP = 0.842 ± 0.015) compared to clear days (σ/EMEP = 0.801 ± 0.019).
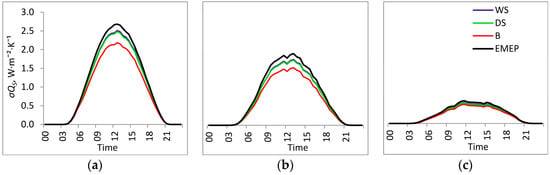
Figure 2.
Diurnal course of entropy production (σQS) and EMEP at the wet spruce (WS), dry spruce (DS), and bog (B) sites in the Central Forest Biosphere Reserve in sunny conditions (a); variable clouds (b); and overcast conditions (c). See Section 2.1 and Section 2.2 for details of the data sample method and period.
Entropy production has a distinctive seasonal pattern (Figure 3), which is typical for a boreal climate. The efficiency of entropy production (Figure 4) in the forests varied from 0.78 (WS) and 0.81 (DS) in winter to 0.91 (WS) and 0.90 (DS) in summer. In some winter months, the σ/EMEP in forests dropped to 0.5–0.6, but on average it was relatively high. The wet spruce forest in summer had a slightly higher efficiency than the dry one. The maximal efficiency in forests was formed in April, just after the snow melted; it then decreased during May and remained constant for the rest of the growing season. The June–October levels of the σ/EMEP in forests were quite stable and consistent between forests in different years.
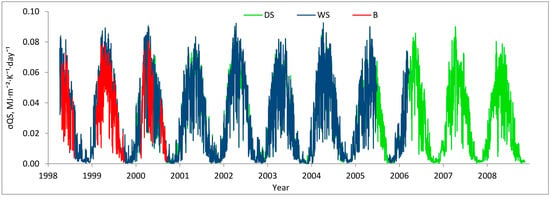
Figure 3.
Daily entropy production (σQS) in short-wave radiation balance at bog (B), wet spruce (WS), and dry spruce (DS) sites in the Central Forest Biosphere Reserve.
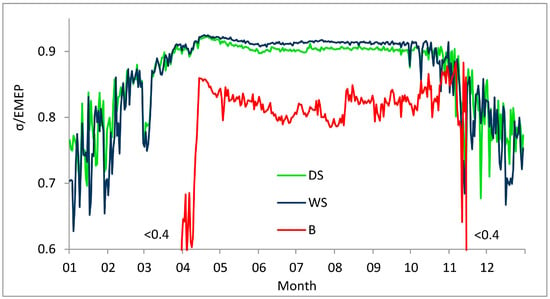
Figure 4.
Efficiency of entropy production in radiation balance (σ/EMEP) at bog (B), wet spruce (WS), and dry spruce (DS) sites (mean for all years, B data with 10 day smoothing). σ/EMEP at B in March and mid-November was 0.5–0.8.
The efficiency of entropy production at the bog site had significant day-to-day and month-to-month variations during the growing season (Figure 4). The bog station was in operation only during spring-autumn periods of 1998–2000, so we had only 27 days of radiation data while the bog was covered with snow. These data show that the bog under snow had a very low entropy production efficiency of about 0.4. With the snow melting, the σ/EMEP at the bog site rose rapidly, reaching the spring peak, and then gradually decreased during the first half of summer, and increased again to the autumn peak. In November, the entropy production efficiency of the bog reached the level of the forest sites. Fluctuations of the σ/EMEP in the warm periods at the bog site were much greater than at the WS site.
Though in warm periods the monthly entropy production in the long-wave radiation balance in the spruce forests rarely exceeded 2% of σQS, in late autumn and in winter σQL sometimes reached 5%–7% of σQS. Entropy production in the long-wave radiation balance at site B during April–October was higher than at the WS site by a factor of 1.4.
Annual σQS sums for 2000–2005 in wet and dry spruce forests were almost identical, i.e., 10.6 ± 0.7 and 10.4 ± 0.5 W·m−2·K−1·year−1 (Table 2) in WS and DS, respectively (Figure 5). The bog monthly σQS sums in the growing season of 1999 were lower by 8%–18% than in the WS forest, and the cumulative sum of σQS for April–October at B was 11.6% lower than in the WS forest. Annual σQL at WS and DS sites reached 0.8 and 1.0% of σQS, respectively.

Table 2.
Average entropy production and meteorological parameters 1 at the bog (B), wet spruce (WS), and dry spruce (DS) sites in the CFBR.

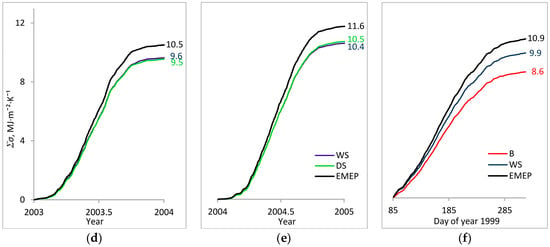
Figure 5.
Cumulative sums of observed entropy production (Σσ) and EMEP at the wet spruce (WS), dry spruce (DS), and bog (B) sites in the Central Forest Biosphere Reserve in 2000 (a); 2001 (b); 2002 (c); 2003 (d); 2004 (e); and April–October of 1999 (f).
Radiative entropy production in the studied ecosystems had strong diurnal and seasonal courses and inter-annual variation at a level of 10%. Most (90%) of the annual entropy production in spruce forests was associated with the snow-free period determined by the level of albedo. According to tower measurements, the 2000–2008 snow-free period lasted from 27 March to 4 November (222 days). Wet and dry spruce forests were very close in terms of entropy production, but entropy production at the bog in April–October of 1999 was 11.6% lower than in the wet spruce forest. The efficiency of entropy production in spruce forests during the growing season was stable and exceeded 90%, but it strongly fluctuated in winter and decreased by 10%–20% in comparison with the summer level. The efficiency of entropy production at the bog during the growing season significantly increased after rains, as well as in April and November, in comparison with mid-summer, and dropped sharply when the bog was snow-blanketed.
3.2. Factors Affecting Entropy Production
According to Equation (2), there are two groups of factors affecting entropy production: radiation (changes in Qs,in and albedo) and surface temperature. We will estimate the importance of these two groups on different time-scales for the studied sites.
The monthly sums of incident radiation (Qs,in) at all three sites were very close, suggesting that the studied ecosystems receive approximately the same amount of solar energy. Net short-wave radiation, Qs,net, in the boreal climate of the CFBR was 3183 ± 167 (1999–2006) and 3110 ± 170 (2000–2008) MJ·m−2·year−1 at WS and DS, respectively. For comparison, two-year means of Qs,net in temperate-climate ecosystems of the Duke Forest (Durham, NC, USA) were 4395 (Old Field), 4912 (Planted Pine) and 4736 (Hardwood) MJ·m−2·year−1 [14]. The albedo of the bog in April–October was significantly higher and Qs,net was about 10.1% lower than that of spruce forests.
The low-productive paludified forest has a slightly lower short-wave daily albedo (α), calculated as the daily sums of Qs,in/Qs,out, during the summer months than the highly productive nemorose forest, namely 0.080 versus 0.094, but in other seasons the α of WS was slightly higher (Figure 6). From June to September α was quite stable in the two spruce forests. On the contrary, the bog α varied over a wide range, from 0.15 to 0.20, and dropped by 0.025–0.05 after each rain event. The albedo did not depend on cloudiness for the spruce forests, but α at the bog was significantly lower on “overcast” days (under our criteria, see Section 2.2). It is explained by the fact that, on these days, precipitation events usually took place and the water level, water area, and peat moistening of the bog increased, whereas water has a lower α than the bog plant cover. The highest difference in α between the bog and forests was recorded at the end of periods without rain. Twice a year, just after the snow melted and just before the formation of snow cover, a distinctive decrease in α at all sites took place, which is probably linked with phenological changes of herbs and mosses and/or the flooding of soil and mosses with water. In these few spring and autumn days, the ecosystem α came to its annual low, i.e., 0.07 at the spruce sites and 0.10–0.12 at the bog site. The considerable difference between the bog and spruce sites was also found in the winter level of α: while the snow-blanketed bog reflected 40%–80% of the incident solar radiation, the evergreen spruce forests sent back only 15%–30%. The low α of the bog under snow was also the cause of the low entropy production efficiency.
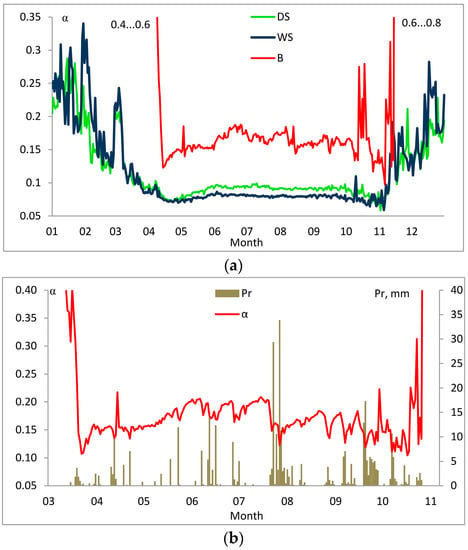
Figure 6.
(a) Seasonal course of albedo (α) at the dry spruce (DS), wet spruce (WS), and bog (B) sites; (b) Albedo (α) and daily precipitation sums (Pr) at the bog site in 1999; α of B in March and mid-November was 0.4–0.6 and 0.6–0.8, respectively.
According to Equation (2), the seasonal variation of entropy production in the boreal climate followed the dynamics of the net short-wave radiation (see Figure 3). Averaged for all given years, QS,net in December at WS (25.5 MJ·m−2·month−1) was 22 times lower than in July (563.6 MJ·m−2·month−1), while (1/Tsurf − 1/Tsun) ranged only from 0.003746 (with an average temperature of −6.2 °C) to 0.003416 (with a temperature of +19.6 °C), which makes up a difference of 9.2% between the minimal and the maximal values. At DS, QS,net in December (on average for all measurement periods) was 23 times lower than in July, while (1/Tsurf − 1/Tsun) differed by 8.9%. So, in CFBR, QS,net variations were 240–260 times greater than variations of (1/Tsurf − 1/Tsun), which allows us to conclude that temperature plays a minimal role in the seasonal variation of radiative entropy production.
The inter-annual variation of entropy production also was driven by variations in short-wave radiation. In “sunny” 2002, QS,net as well as QS,in were maximal among all years of measurements, and the σ sum also reached its highest level, whereas in “cloudy” 2003, both QS,net and σ were minimal. The coefficient of variation (CV) of the temperature term (1/Tsurf − 1/Tsun) between different years at WS was 0.19% and at DS it was 0.21%, while the CV of QS,net was at 6.13% at WS and at 5.47% at DS. In other words, the inter-annual variation of QS,net was 32-fold (at WS) or 26-fold (at DS) larger than the inter-annual variation of (1/Tsurf − 1/Tsun). Inter-annual changes in solar radiation were much more important for entropy production in comparison to changes in temperature. Annual entropy production was at its highest in 2002 and 2015 with dry and sunny summers. Therefore, in southern taiga forests, drought had a positive role in entropy production.
For CFBR spruce forests, the full-year albedo of WS was slightly lower (by 0.3%) and Qs,net was a bit higher than that of DS, but this difference was of the same order for the final value of σ as the random fluctuation of the simultaneous incoming radiation (due to changing cloudiness) between the sites. The surface temperature was almost equal for the two spruce forests. The bog site was characterized by both lower Qs,net and 1/Tsurf than the WS forest. The bog was usually warmer than the forest: the average radiative surface temperature at B in April–October was 0.63 °C higher than at WS, but on some summer days it was 2–4 °C higher. On some November days the difference between the daily-averaged temperature at B and WS reached 6 °C because the bog was still left snow-free due to the high heat storage capacity of the incorporated water. However, even this 6 °C difference resulted only in a 2.3% difference in the daily entropy production, whereas the November albedo difference resulted in a 4% difference in σ. During daytime in the warm period of 1999, the temperature term of Equation (2) varied only from 0.0030 to 0.0036 K−1 both at the WS and B sites, while the radiation term varied from 0 to more than 900 Wt·m−2. Therefore, for analysis of the significance of the two terms for the integral σ, we may regard the temperature term as almost constant. Through the rates of the averaged temperature terms at the two sites, the integral radiation terms at the two sites, and the integral entropy production at the two sites, we may evaluate the relative importance of the two terms for the increased σ of the WS forest in comparison to the bog. The temperature effect on the larger value of σ at WS than at B was only about one-eighth, and seven-eighths of the entropy increment was associated with higher radiation absorption by the forest.
The tentative calculations for the entropy production in the WS forest under higher temperatures, but the same radiation, showed that if the surface temperature increased by 2, 4, and 6 °C, respectively, the annual sum of σ, averaged for 2000–2005, would decrease only by 0.8%, 1.6%, and 2.3%.
The above-given calculations demonstrate that changes in the incoming solar radiation (linked with changes in cloudiness) had a much larger effect on the daily, seasonal, and inter-annual variability of entropy production than changes in the surface temperature. Changes in temperature became more significant if the annual sums of entropy production were compared at different sites. The entropy production efficiency in spruce forests during all of the growing seasons was high and very stable due to the stable albedo. Temperature changes in warm periods had a minor effect on the entropy production. When moistening of the bog increased (after rains and in mid-seasons), the albedo significantly decreased and the efficiently of the entropy production increased.
4. Discussion
In general, radiative entropy production in forest and bog ecosystems of the Central Forest Biosphere Reserve followed the dynamics of incoming solar radiation and had clear diurnal and seasonal courses, as well as 10% variation from year to year. Ninety percent of the annual entropy in spruce forests was produced during a warm period, both because of the dramatic decrease in incoming radiation and the increase of albedo. Snow-covered land surface, measured using satellite data, usually has an albedo of 40%–80%, depending on the snow depth, structure, and wetness, and tall vegetation significantly decreases the winter albedo [48]. Though paludified spruce forest had a much simpler canopy structure and lower bioproductivity and biodiversity than nemorose spruce forest, the entropy production dynamics and sums in the two spruce forests were very similar. Entropy production at the bog in April–October of 1999 made up only 88.4% of that of the WS site, because the bog had both a higher albedo and an elevated surface temperature in comparison with the forest sites. Much of this difference in entropy production (seven-eighths) was due to a much higher albedo of the bog, and only one-eighth of the difference came from the higher temperature.
We may conclude that though the entropy production in the ecosystem radiation balance depends both on the temperature and absorbed radiation, in boreal ecosystems the difference between these two terms is so great that the temperature effect may be regarded as only a small correction to the radiation effect. Under the given incoming radiation, the shape of the seasonal course of entropy production would depend only on seasonal changes of the ecosystem albedo. However, the influence of the temperature term is appreciable for annual entropy sums and for a comparison of neighboring ecosystems that differ significantly in temperature.
In warm periods, when the major part of the annual entropy is produced, the efficiency of the entropy production in the studied spruce forests was stable and exceeded 90%, but in winter it decreased by 10%–20%, in comparison with the summer level, and fluctuated strongly. Snow-covered bog had the maximal albedo and minimal entropy production among all of the studied ecosystems in all seasons. The bog site was characterized by a significant increase in the entropy production efficiency in mid-seasons and after rain events, following the trend of decreasing albedo with the elevated moistening of the bog. We suggest that annual entropy production sums at the bog ecosystems, unlike forests, would depend on the precipitation in snow-free periods. It probably increases in wet periods and decreases in droughts, but we need more data for testing this hypothesis.
Vegetating forest ecosystems have a strong tendency to support entropy production on the same level, whereas beyond the bounds of the growing season the entropy production significantly fluctuates. In spite of the large difference in soil and hydrological conditions, paludified peat and dry nemorose spruce forests produce very similar amounts of entropy. The studied taiga forests support a relatively stable albedo and, thus, entropy production during droughts, taking advantage of increased solar radiation input. The stable radiation balance of forests of the southern taiga, regardless of the moisture supply, demonstrates the buffer and climate-regulative role of forests.
On the contrary, entropy production in the bog was very unstable and strongly depended on the moisture supply in the growing season. Radiation absorption and entropy production in the bog significantly increased after precipitation, demonstrating that elevated water nutrition was favorable for the bog. In general, the bog-regulated entropy production was significantly weaker than that of the forests, both during the growing season and in winter. The particular thermodynamic behavior of bogs may be connected with the fact that bogs, unlike forests, are inherently non-equilibrium systems, persistently thickening and fixing carbon from the atmosphere at long time-scales [49,50]. Note that the albedo and surface temperature typically increase along serial stages, such as the “lake-overgrown lake-bog”; therefore, the statement of Lin et al. [20] regarding the cooling and darkening of ecosystems during maturation and succession is not valid for bogs. Counter to the fact that there is a fair connection between the mass balance and thermodynamic behavior of ecosystems is the similar entropy production of the two studied spruce forests, though DS was a carbon sink of 2200 kg·C·ha−1·year−1 and WS was a carbon source of 1800 kg·C·ha−1·year−1 in 1999–2004 [41].
Pollen analysis for central European Russia showed that in the second half of the Holocene (4500–0 14C year BP), the increasing winter temperature resulted in the expansion of mixed coniferous broad-leaved forests, while cooling and moistening of the area resulted in an increasing area of pure spruce forests and the development of oligotrophic sphagnum bogs [51]. Under excessive moistening, some types of bogs exhibit intensive vertical growth, carbon accumulation, and may expand rapidly toward surrounding forests [25]. Modern investigations of [24] using remote sensing data showed that in 1986–2010, in the Central Forest Biosphere Reserve, the total bog area increased from 8% to 10% of the territory. Swamping of territories may result in the increasing instability of the energy balance and entropy production in the landscape of the southern taiga.
Acknowledgments
This work was supported by the Russian Science Foundation, project 14-27-00065.
Author Contributions
Juriy Puzachenko organized the work on the paper, made substantial contributions to Section 2.3 and interpreted of the results; Olga Kuricheva analyzed the data, prepared Figure 2, Figure 3, Figure 4 and Figure 6, and wrote the manuscript with all coauthors; Vadim Mamkin made Figure 5 and wrote the manuscript with all coauthors; Robert Sandlersky prepared Figure 1 and made substantial contributions to Section 2.3; Andrej Varlagin and Juliya Kurbatova performed the experiments and contributed data, and made substantial contributions to Section 2.3. All authors have read and corrected the text and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kleidon, A.; Lorenz, R. Entropy Production by Earth System Processes. In Non-Equilibrium Thermodynamics and the Production of Entropy: Life, Earth, and Beyond; Kleidon, A., Lorenz, R.D., Eds.; Springer: Berlin/Heigelberg, Germany, 2005; Chapter 1; pp. 1–20. [Google Scholar]
- Chen, G.Q. Exergy consumption of the earth. Ecol. Model. 2005, 184, 363–380. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Fath, B.D.; Bastianoni, S.; Marques, J.C.; Müller, F.; Nielsen, S.N.; Patten, B.C.; Tiezzi, E.; Ulanowicz, R.E. A New Ecology: Systems Perspective; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Aoki, I. Entropy production in living systems: From organisms to ecosystems. Thermochim. Acta 1995, 250, 359–370. [Google Scholar] [CrossRef]
- Jorgensen, S.E.; Svirezhev, Y.M. Towards a Thermodynamic Theory for Ecological Systems; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Kirwan, A.D. Quantum and ecosystem entropies. Entropy 2008, 10, 58–70. [Google Scholar] [CrossRef]
- Baldwin, R.A. Use of maximum entropy modeling in wildlife research. Entropy 2009, 11, 854–866. [Google Scholar] [CrossRef]
- Kleidon, A.; Malhi, Y.; Cox, P.M. Maximum entropy production in environmental and ecological systems. Philos. Trans. R. Soc. Lond. Ser. B 2010, 365, 1297–1302. [Google Scholar] [CrossRef] [PubMed]
- Silow, E.A.; Mokry, A.V.; Jørgensen, S.E. Some applications of thermodynamics for ecological systems. In Thermodynamics—Interaction Studies—Solids, Liquids and Gases; Moreno-Pirajan, J.C., Ed.; InTech: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef]
- Lin, H.; Cao, M.; Stoy, P.C.; Zhang, Y. Assessing self-organization of plant communities—A thermodynamic approach. Ecol. Model. 2009, 220, 784–790. [Google Scholar] [CrossRef]
- Maes, W.H.; Pashuysen, T.; Trabucco, A.; Veroustraete, F.; Muys, B. Does energy dissipation increase with ecosystem succession? Testing the ecosystem exergy theory combining theoretical simulations and thermal remote sensing observations. Ecol. Model. 2011, 222, 3917–3941. [Google Scholar] [CrossRef]
- Norris, C.; Hobson, P.; Ibisch, P.L. Microclimate and vegetation function as indicators of forest thermodynamic efficiency. J. Appl. Ecol. 2012, 49, 562–570. [Google Scholar] [CrossRef]
- Stoy, P.C.; Lin, H.; Novick, K.A.; Siqueira, M.; Juang, J.Y. The role of vegetation on the ecosystem radiative entropy budget and trends along ecological succession. Entropy 2014, 16, 3710–3731. [Google Scholar] [CrossRef]
- Miedziejko, E.M.; Kędziora, A. Impact of plant canopy structure on the transport of ecosystem entropy. Ecol. Model. 2014, 289, 15–25. [Google Scholar] [CrossRef]
- Lin, H.; Cao, M.; Zhang, Y. Self-organization of tropical seasonal rain forest in southwest China. Ecol. Model. 2011, 222, 2812–2816. [Google Scholar] [CrossRef]
- Song, Q.; Lin, H.; Zhang, Y.; Tan, Z.; Zhao, J.; Zhao, J.; Zhang, X.; Zhou, W.; Yu, L.; Yang, L.; et al. The effect of drought stress on self-organization in seasonal tropical rainforest. Ecol. Model. 2013, 265, 136–139. [Google Scholar] [CrossRef]
- Svirezhev, Y.M. Thermodynamics and ecology. Ecol. Model. 2000, 132, 11–22. [Google Scholar] [CrossRef]
- Lin, H. Thermodynamic entropy fluxes reflect ecosystem characteristics and succession. Ecol. Modell. 2015, 298, 75–86. [Google Scholar] [CrossRef]
- Lin, H.; Fan, Z.; Shi, L.; Arain, A.; McCaughey, H.; Billesbach, D.; Siqueira, M.; Bracho, R.; Oechel, W. The Cooling Trend of Canopy Temperature during the Maturation, Succession, and Recovery of Ecosystems. Ecosystems 2016, 1–10. [Google Scholar] [CrossRef]
- Skene, K.R. The energetics of ecological succession: A logistic model of entropic output. Ecol. Model. 2013, 250, 287–293. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Schymanski, S.J.; Kleidon, A. Quantifying the thermodynamic entropy budget of the land surface: Is this useful? Earth Syst. Dyn. 2011, 2, 87–103. [Google Scholar] [CrossRef]
- Vompersky, S.E.; Sirin, A.A.; Sal’nikov, A.A.; Tsyganova, O.P.; Valyaeva, N.A. Estimation of forest cover extent over peatlands and paludified shallow-peat lands in Russia. Contemp. Probl. Ecol. 2011, 4, 734–741. [Google Scholar] [CrossRef]
- Puzachenko, Yu.G.; Kotlov, L.P.; Sandlerskiy, R.B. Analysis of changes of land cover using multispectral remote sensing information in the central forest reserve. Izv. Geogr. 2014, 3, 5–18. [Google Scholar] [CrossRef]
- Glushkov, I.V. Current State and History of Development of Watershed Swamps and Paludified Forests of Central Forest Reserve. Ph.D. Dissertation, Institute of Forest Science, Russian Academy of Sciences (ILAN), Moscow, Russian, 2012. [Google Scholar]
- Puzachenko, Y.; Sandlersky, R.; Sankovski, A. Methods of evaluating thermodynamic properties of landscape cover using multispectral reflected radiation measurements by the Landsat satellite. Entropy 2013, 15, 3970–3982. [Google Scholar] [CrossRef]
- Hollinger, D.Y.; Ollinger, S.V.; Richardson, A.D.; Meyers, T.; Dail, D.B.; Martin, M.E.; Scott, N.A.; Arkebauer, T.J.; Baldocchi, D.D.; Clark, K.L.; et al. Albedo estimates for land surface models and support for a new paradigm based on foliage nitrogen concentration. Glob. Chang. Biol. 2009, 16, 696–710. [Google Scholar] [CrossRef]
- Berglund, E.R.; Mace, A.C., Jr. Seasonal Albedo Variation of Black Spruce and Sphagnum-Sedge Bog Cover Types. J. Appl. Meteorol. 1972, 11, 806–812. [Google Scholar] [CrossRef]
- Kurbatova, J.; Arneth, A.; Vygodskaya, N.N.; Kolle, O.; Varlargin, A.V.; Milyukova, I.M.; Tchebakova, N.M.; Schulze, E.; Lloyd, J. Comparitive ecosystem-atmosphere exchange of energy and mass in European Russian and central Siberian bog. I. Interseasonal and interannual variability of energy and latent heat fluxes during the snowfree period. Tellus B 2002, 54, 497–513. [Google Scholar] [CrossRef]
- Lohila, A.; Minkkinen, K.; Laine, J.; Savolainen, I.; Tuovinen, J.P.; Korhonen, L.; Laurila, T.; Tietäväinen, H.; Laaksonen, A. Forestation of boreal peatlands: Impacts of changing albedo and greenhouse gas fluxes on radiative forcing. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Holdaway, R.J.; Sparrow, A.D.; Coomes, D.A. Trends in entropy production during ecosystem development in the Amazon Basin. Philos. Trans. R. Soc. Lond. Ser. B 2010, 365, 1437–1447. [Google Scholar] [CrossRef] [PubMed]
- Jones, H.G. Plants and Microclimate: A Quantitative Approach to Environmental Plant Physiology; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Desherevskii, A.V.; Zhuravlev, V.I.; Nikolsky, A.N.; Sidorin, A.Ya. Technologies for analysis of geophysical time series. Part 1. Requirements for software. Seism. Instrum. 2016, 52, 61–82. [Google Scholar]
- Desherevskii, A.V.; Zhuravlev, V.I.; Nikolsky, A.N.; Sidorin, A.Ya. Technologies for analysis of geophysical time series. Part 2. WinABD—A software package for maintenance and data analysis of geophysical monitoring. Seism. Instrum. 2016, 52, 50–80. [Google Scholar]
- Desherevskii, A.V.; Zhuravlev, V.I.; Nikolsky, A.N.; Sidorin, A.Ya. Problems in analysis of time series with gaps and their solutions in WinABD software package. Geophys. Process. Biosph. 2016, 15, 5–34. [Google Scholar]
- Vygodskaya, N.N.; Schulze, E.D.; Tchebakova, N.M.; Karpachevskii, L.O.; Kozlov, D.; Sidorov, K.N.; Panfyorov, M.I.; Abrazko, M.A.; Shaposhnikov, E.S.; Solnzeva, O.N.; et al. Climatic control of stand thinning in unmanaged spruce forests of the southern taiga in European Russia. Tellus B 2002, 54, 443–461. [Google Scholar] [CrossRef]
- Schulze, E.D.; Vygodskaya, N.N.; Tchebakova, N.M.; Czimczik, C.I.; Kozlov, D.N.; Lloyd, J.; Mollicone, D.; Parfenova, E.; Sidorov, K.N.; Varlagin, A.V.; et al. The Eurosiberian transect: An introduction to the experimental region. Tellus B 2002, 54, 421–428. [Google Scholar] [CrossRef]
- Desherevskaya, O.; Kurbatova, J.; Oltchev, A. Climatic conditions of the south part of Valday hills, Russia, and their projected changes during the 21st century. Open Geogr. J. 2010, 3, 73–79. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth. Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Minaeva, T.J.; Glushkov, I.V.; Nosova, M.B.; Starodubceva, O.A.; Kuraeva, E.N.; Volkova, E.M. Survey of bogs of Central Forest Reserve. Trudy Central’no-Lesnogo Zapovednika 2007, 4, 267–296. (In Russian) [Google Scholar]
- Kurbatova, J.; Li, C.; Varlagin, A.; Xiao, X.; Vygodskaya, N. Modeling carbon dynamics in two adjacent spruce forests with different soil conditions in Russia. Biogeosciences 2008, 5, 969–980. [Google Scholar] [CrossRef]
- Kurbatova, J.; Tatarinov, F.; Molchanov, A.; Varlagin, A.; Avilov, V.; Kozlov, D.; Ivanov, D.; Valentini, R. Partitioning of ecosystem respiration in a paludified shallow-peat spruce forest in the southern taiga of European Russia. Environ. Res. Lett. 2013, 8, 045028. [Google Scholar] [CrossRef]
- Šantrůčková, H.; Kaštovská, E.; Kozlov, D.; Kurbatova, J.; Livečková, M.; Shibistova, O.; Tatarinov, F.; Lloyd, J. Vertical and horizontal variation of carbon pools and fluxes in soil profile of wet southern taiga in European Russia. Boreal Environ. Res. 2010, 15, 357–369. [Google Scholar]
- Arneth, A.; Kurbatova, J.; Lloyd, D.; Kolle, O.; Schibistova, O.; Vygodskaya, N.N.; Schulze, E.-D.; Lloyd, J. Ecosystem-atmosphere exchange of energy and mass in a European Russia and a central Siberia bog. II. Internseasonal and interannual variability of CO2 fluxes. Tellus B 2002, 54, 514–530. [Google Scholar] [CrossRef]
- Vygodskaya, N.N.; Abrazhko, V.I.; Varlagin, A.V.; Kurbatova, Ju.A.; Sidorov, K.N.; Milyukova, I.M.; Sogachev, A.F.; Sogacheva, L.M.; Shaposhnikov, E.S.; Nepomnyashii, G.I.; et al. Long-Term Dynamics of Soil Moisture and Drying of Spruce Trees in Spruce Forests of the Southern Taiga. Lesovedenie 2004, 1, 3–22. [Google Scholar]
- Vygodskaya, N.N.; Oltchev, A.V.; Kurbatova, J.A.; Varlargin, A.V. Gross primary production (GPP) of unmanaged over-mature spruce forests at southern European taiga: Eddy covariance measurements and modeling approach. In Modeling Forest Production, Scientific Tools—Data Needs and Sources, Validation and Application; Hasenauer, H., Makela, A., Eds.; BOKU University of Natural Resources and Applied Life Sciences: Vienna, Austria, 2004; pp. 421–430. [Google Scholar]
- FLUXNET. Available online: https://fluxnet.ornl.gov/ (accessed on 13 January 2017).
- Kitaev, L.M.; Titkova, T.B. Variability of snow cover albedo—The analysis of the satellite data. Curr. Probl. Remote Sens. Earth Space 2011, 8, 47–57. [Google Scholar]
- Moore, P.D. The future of cool temperate bogs. Environ. Conserv. 2002, 29, 3–20. [Google Scholar] [CrossRef]
- Minayeva, T.Y.; Trofimov, S.Y.; Chichagova, O.A.; Dorofeyeva, E.I.; Sirin, A.A.; Glushkov, I.V.; Mikhailov, N.D.; Kromer, B. Carbon accumulation in soils of forest and bog ecosystems of southern Valdai in the Holocene. Biol. Bull. 2008, 35, 524–532. [Google Scholar] [CrossRef]
- Novenko, E.; Olchev, A.; Desherevskaya, O.; Zuganova, I. Paleoclimatic reconstructions for the south of Valdai Hills (European Russia) as paleo-analogues of possible regional vegetation changes under global warming. Environ. Res. Lett. 2009, 4, 045016. [Google Scholar] [CrossRef]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).