2.1. Entropy Production Due to the Ion Flux across the Membrane in a Two-Compartment System
The change in entropy of an open system is composed of two parts:
dSe is the entropy change due to the exchange of matter and energy with the surroundings; and
dSi is the entropy change due to the irreversible processes in the interior of the system [
8,
9]. The change in entropy can be written as
For an isolated system,
dSe = 0. According to the second law of thermodynamics,
The entropy production rate or the change of entropy with time is
A form of the Gibbs equation, the fundamental equation for small changes in entropy, is
or the differential form,
Here,
T is the temperature;
is the internal energy;
p is the pressure;
is the volume;
n is the number of molecules; and
μ is the chemical potential of the uncharged diffusing species. For ion diffusion or electrodiffusion, the electrochemical potential,
, should be treated as a primary thermodynamic quantity because the chemical potential and the electrical potential cannot be separated experimentally [
8,
13]. Here,
k is the Boltzmann constant;
c is the concentration;
z is the valence of the ion;
e is the elementary charge; and
V is the electrical potential. The entropy change can be expressed as
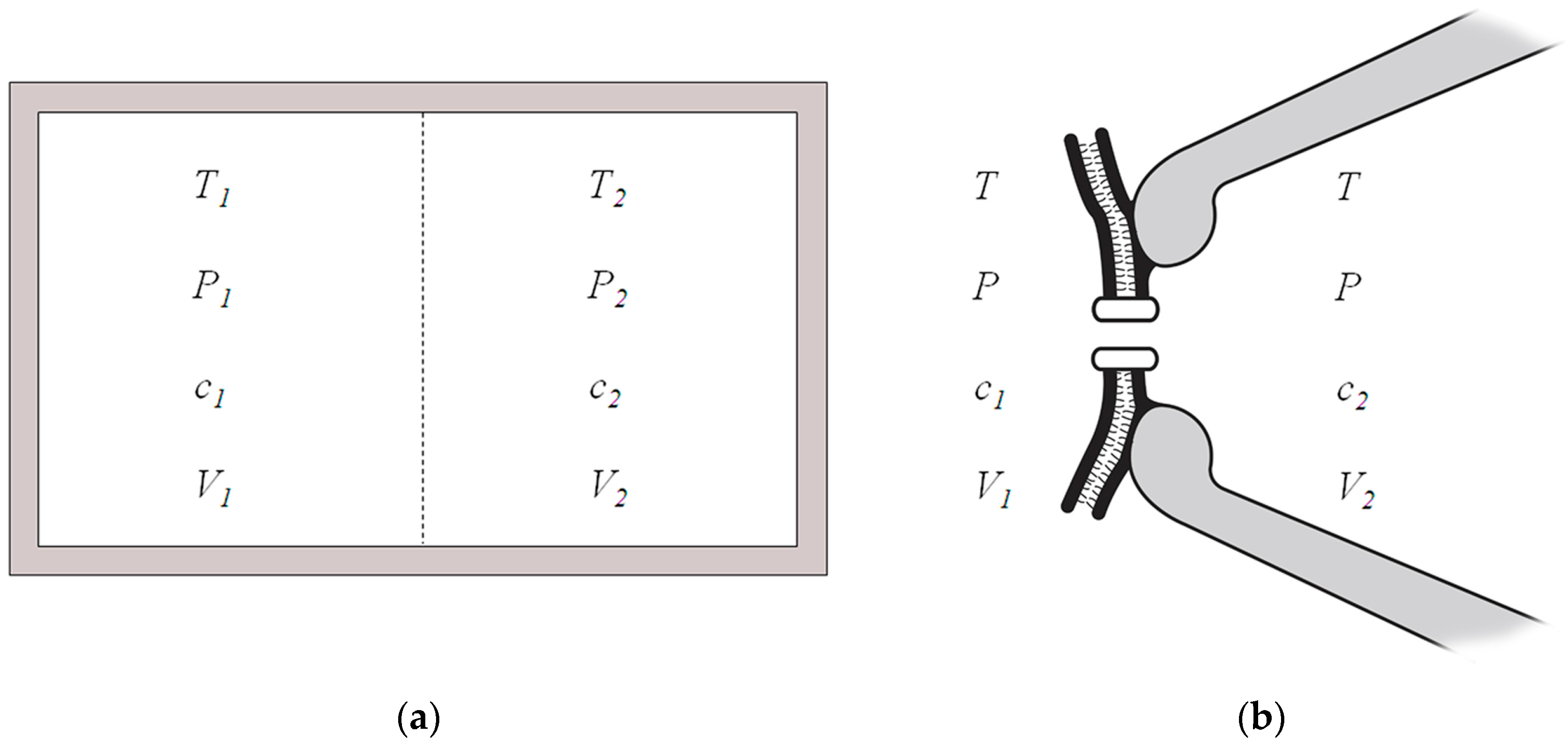
In a two-compartment isolated system, enclosed by rigid adiabatic walls, separated by a diathermal, elastic, ion-permeable membrane (
Figure 1a), the sum of the entropy change of the system given by the irreversible processes is [
8]:
The physical meanings of Equation (7) are the thermodynamic driving forces for fluxes: temperature difference for heat transfer, pressure difference for volume flow, and electrochemical potential difference for ion transport across the membrane.
Let us consider a system in the voltage-clamp patch-clamp recording [
14] consisting of a cell membrane and an ion channel with the adjacent contacting intracellular and extracellular solutions at both sides as illustrated in
Figure 1b. In this circumstance, the temperature and pressure of both sides are the same and are in equilibrium with the surroundings,
T1 =
T2 =
T,
P1 =
P2 =
P. The intracellular and extracellular electrical potentials are clamped at fixed voltages in the voltage-clamp study. The ion concentrations at both sides are also fixed because the number of ions transported is several orders far less than the reservoirs of ion solutions. The highly selective ion channel is permeable to a certain species of ion. Therefore, the entropy production due to the ion transport across the cell membrane in the two-compartment patch clamp recording system, although not truly enclosed by rigid adiabatic walls, can be estimated as in the isolated system shown in
Figure 1a. The entropy change in the patch-clamp recording system due to the electrodiffusion or diffusion of a certain species of ion across the membrane is
Hence, the entropy production in a unit time, or the entropy production rate is
here
J is the net flux across the membrane.
2.2. The Empirical Linear Relationship between the Ion Flux and the Driving Force across the Membrane
It is often convenient to describe the ion flux across the membrane as having a linearly proportional relationship with the driving force. The empirical linear formula can be expressed as
where
L is the phenomenological linear coefficient.
The electrochemical potential difference across the cell membrane is
Here,
Vm is the membrane potential; by definition,
Vm =
.
Veq =
is the equilibrium potential determined by the Nernst equation. Thus,
Electrophysiologists usually express the empirical ohmic formula between the current (
I) and the driving force (
Vm −
Veq) as [
15]:
Here,
G is the conductance. Equations (13) and (12) are comparable, and (
Vm −
Veq) has the same thermodynamic meaning as the electrochemical potential difference across the membrane, that is, the driving force for the ion flux.
It should be noted that the empirical linear relationship between the driving force and the ion flux or current in Equations (10) and (13) is merely approximations. Experimental tests are required in each ion and voltage conditions in recordings on different ion channels. Theoretically, the linear relationships between the thermodynamic driving forces and the fluxes are near-equilibrium approximations [
8,
9]. In electrophysiology, voltage-clamp experimental recordings have shown a fairly linear relationship between the driving force and the ion current in the physiological voltage range in many ion channels under symmetric ionic concentrations [
15]. However, some ion channels are known to have a nonlinear current–“driving force” relationship because the structure or the permeation barrier of the channel is asymmetrical. The difference of the concentrations of permeant ion on both sides also affects the magnitude of the ion currents. Nevertheless, the entropy change and the entropy production rate as expressed in Equations (8) and (9) still hold true regardless of whether the relationship between the driving force and the ion flux is linear or not linear.
2.3. Electrodiffusion in the Continuous Ion Solution by the Electrochemical Potential Gradient
In a continuous solution, the ion is surrounded by water molecules. At the molecular level, each ion just moves randomly without specific direction until it collides with the background water molecules and loses its forward momentum. Macroscopically, the ions diffuse from high concentration areas to low concentration areas. The diffusion flux can be expressed by Fick’s Law:
Here,
D is the diffusion coefficient,
D =
.
is the mobility coefficient.
When an electrical field is applied through the solution, the electrical force on the ions causes them to drift along the direction of the gradient of the electrical potential. In addition, the ions will also collide with the background water molecules and become damped by the surrounding water molecules. The resulting average drifting velocity is proportional to the electrical force [
16]:
The drift flux will be
The ion flux of electrodiffusion (
Jed) in the continuous solution can be written as the Nernst–Planck equation:
It is interesting that from nonequilibrium thermodynamics, the flux of electrodiffusion can be expressed from the gradient of the electrochemical potential [
8,
9]:
Letting the linear coefficient
Lk =
and then substituting this into Equation (18) also gives the Nernst–Planck equation for electrodiffusion:
2.4. Nonequilibrium Thermodynamics in Small Systems: Fluctuation Theorem and the Ussing Flux Ratio
In small nonequilibrium systems, thermal fluctuations make it possible for transient events to occur in a direction that is opposed to the overall positive entropy production. The fluctuation theorem, which was formulated in 1993, quantified the ratio of the probability of entropy-producing events (forward runs),
P(+
σ), to the probability of entropy-consuming events (backward runs),
P(−
σ), over a short time in small dissipative nonequilibrium systems [
17,
18,
19]. The fluctuation theorem is valid far from equilibrium in linear or nonlinear regime according to the nonequilibrium statistical mechanics. The general form of the fluctuation theorem is
where
or
is the positive or negative entropy production rate,
. If we view the nanometer-sized biological molecules as Brownian ratchets, the fluctuation theorem can quantify the ratio of forward steps to the backward steps in a short period of time. The direct experimental verification of the theorem is a difficult task because of the tiny scales involved in the experiment. In 2002, a satisfactory experimental test was carried out by measuring the position trajectory of a colloid particle captured in an optical trap [
20].
When an ion channel and its adjacent solutions are regarded as a small nonequilibrium system, the ratio of the probability of the forward transport event (down the direction of electrochemical potential gradient) to the backward transport event (against the direction of electrochemical potential gradient) can be derived based on the fluctuation theorem [
12,
21]. This probability ratio is equal to the Ussing flux ratio, which is the ratio of unidirectional outward flux to unidirectional inward flux, as determined by radioisotope experimental studies in squid axon systems in the 1950s [
22,
23], and later in the cloned expression systems of ion channels [
24,
25].
The entropy produced when an ion is transported across the membrane from the intracellular to extracellular solution can be obtained from Equations (8) and (11):
Thus, the ratio of forward transport runs to backward transport runs can be estimated by substituting Equation (21) into Equation (20):
This probability ratio of forward to backward transfer steps in a single channel molecule is equal to the Ussing flux ratio determined from radioisotope transfer events carried by macroscopic ion currents over a time. The ratio of the outward flux (
Jio) and the inward flux (
Joi) is
As Hodgkin and Keynes proposed in 1955, for a multi-ion, single-file, long pore, the flux ratio equation is raised to the nth power [
22]. From the view of the fluctuation theorem, the entropy change for a radioisotope tracer transfer event from the intracellular to extracellular solution will be
nS [
12]. Therefore,
The flux-ratio exponent,
n, was measured to be 2.5 to 3.5 in different K
+ channels [
22,
24,
25], which suggested that there might be 2 to 3 K
+ ions simultaneously occupying the multi-ion single file K
+ channel pore. The first X-ray crystal structure of the K
+ channel pore was determined by MacKinnon’s group in 1998 [
26], which confirmed the prediction by Hodgkin and Keynes. The flux ratio was also estimated by a Brownian dynamics study which simulated the ion flux trajectory in nanosecond scale [
27].
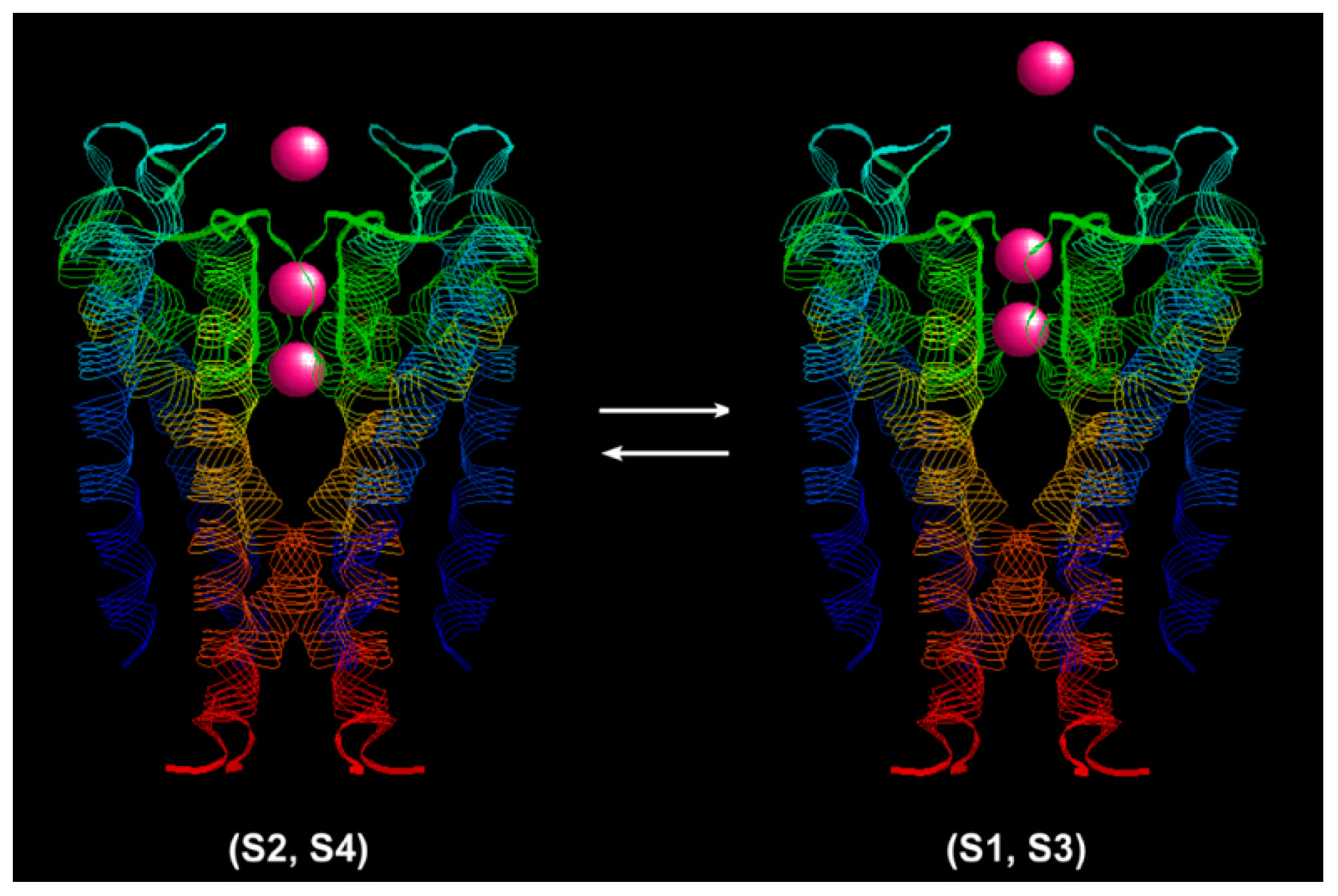
The K
+ ion conduction process is shown in
Figure 2 with a structure model of the KcsA channel (PDB: 1j95) [
28]. The narrow selectivity filter is 12 Å long. The coordinating ligands of the single-file pore just fit with a dehydrated K
+ ion. There are four K
+ binding sites in the selectivity filter. The selectivity filter contains two K
+ ions about 7.5 Å apart at a time [
26]. The ions jiggle rapidly in the Brownian environment between the (S1, S3) configuration (K
+-water-K
+-water) and the (S2, S4) configuration (water-K
+-water-K
+) [
29]. An event of outward ion conduction occurs when a K
+ ion from the intracellular cavity binds to the S4 site and electrostatically repulses one ion into the extracellular solution. Conversely, inward ion conduction occurs when a K
+ ion binds to the extracellular mouth, dehydrates, and knocks off the inner most K
+ ion. The direction of the net transport is determined by the driving force,
. The ratio of the forward transition step to the backward step can be estimated from the fluctuation theorem.
The interpretation of the Ussing flux ratio from the fluctuation theorem is an example of applying the nonequilibrium thermodynamics of small systems to the classic empirical flux ratio formulated by the early pioneer studies in electrophysiology. It is interesting that the flux ratio is determined by the electrochemical potential difference across the membrane, and is not dependent on the internal structural parameters of the ion channel in the nonequilibrium condition.
2.5. The Magnitude of the Unidirectional Outward Flux and Inward Flux in Nonequilibirium and Equilibrium Conditions
At the equilibrium potential, when , the unidirectional outward flux (Jio) equals the unidirectional inward flux (Joi), and the net ion flux is zero. The probability of the forward transport event equals the probability of the backward transport event in the equilibrium circumstance, regardless of the symmetry or asymmetry of the internal structure or energy profiles within the channel pore. However, the magnitude of the unidirectional flux can be related to the internal parameters within the channel.
We can estimate the magnitude of the unidirectional outward and inward fluxes. The net flux (
Jnet) is the difference of the outward flux from the inward flux:
By solving Equations (24) and (25) analytically, one obtains:
and
The magnitudes of the outward flux and the inward flux must be the same at the equilibrium potential. If we substitute
Jnet =
g into Equations (26) and (27), (here
g is the slope conductance around the linear region near the equilibrium potential), then when
→ 0, we can use the derivatives of the numerator and denominator by the l’Hôpital’s rule to evaluate the limit from either Equation (26) or Equation (27). Thus, one obtains the magnitude of the unidirectional flux at equilibrium potential as Hodgkin formulated in 1951 [
30]:
The conductance is a measure of the ease with which the ions flow through the channel in response to the driving force under nonequilibrium conditions. As shown in Equation (28), the conductance near the equilibrium potential is proportional to the magnitude of the inward or outward unidirectional flux. Thus, the conductance also reflects the ease of the forward or backward transport in the equilibrium circumstance, which can be viewed as the overall barrier determined by the internal structure, energy profiles, and the adjacent ionic and electrochemical conditions of the ion channel. This overall barrier thus determines the basal transport frequency at the equilibrium potential.
2.6. The Roles of the Multi-Ion Single-File Pores in “Driving Force”-Dependent Processes in the Membrane
The ion channel has an implicit multi-ion, single-file feature, which means at least two ions occupying the narrow long pore at a time. The ions have to line up in a row and move concertedly along the one-atom width long pore [
15,
22]. Hence, the diffusion or electrodiffusion within the ion channel is anisotropic or directional, which makes it capable of utilizing the electrochemical driving force across the membrane to couple the movement of other specific ions in the pore. Flux coupling does not occur in the bulk ion solution, where each ion just walks randomly without a specific direction with a correlation time of 10
−13 s, and forgets its initial momentum within 0.5 Å, a mean free path less than the radius of the atom. For comparison, the average distance between two K
+ ions is 25 Å in a 100 mM K
+ solution, so each ion will not collide or interact with each other. The electrochemical driving force for ion flux has no directional effect on other specific ion or molecular species in the bulk solution, even when there is electrochemical potential gradient across different regions in the continuous solution. However, the driving force predicts the direction of the macroscopic net ion flux. Flux coupling cannot take place in a single-ion channel because the pore cannot tell from which side the ion binds onto the sole binding site, and thus cannot distinguish the direction of the ion flux. However, in a multi-ion single-file pore, the electrochemical driving force for the ion flux can exert its directional impact on the movement of other specific ions or on the configuration of certain molecules. Examples of how molecular machines in the membrane utilize the electrochemical driving force of ion fluxes are introduced in the following.
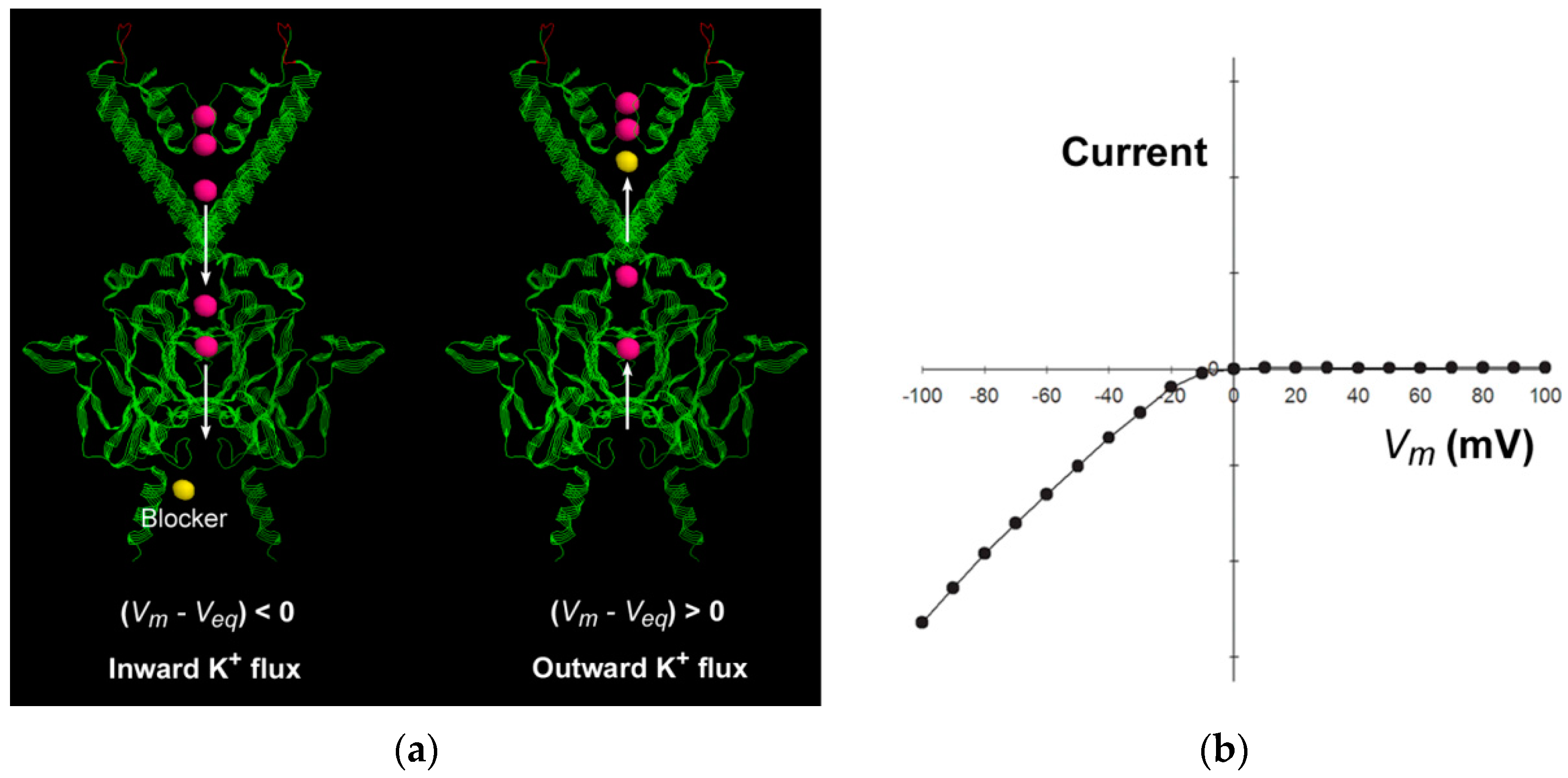
The inward-rectifier K
+ (Kir) channels are featured by strong inward rectification in the current–voltage relationship in the presence of intracellular polyamines or Mg
2+ [
15,
31], which means that the inward current is much larger than the outward current (
Figure 3). The current–voltage relationship shifts parallel to the same amount as the equilibrium potential shifts, as the extracellular or intracellular K
+ concentration changes. The inward rectification has been attributed to the “driving force”-dependent or flux-coupled block, which means that the movement and thus the apparent binding rate of the blocker is coupled by the direction of K
+ flux, so the apparent affinity of the intracellular blocker is influenced by the driving force for K
+ ion conduction [
1,
2]. The elongated narrow long cytoplasmic pore in the Kir channel extends the single-file pathway to 60 Å [
32,
33], and thus facilitates the flux-coupling between the conducting K
+ ion flux and the blocker in the multi-ion cytoplasmic pore. When
, the intracellular blocker would be coupled by the outward conducting K
+ ion flux to encounter the deeper binding site to block the pore. When
, the K
+ flux is predominantly inward, and the inner K
+ ions in the cytoplasmic pore always preclude the intracellular blocker from entering to the pore, so no blockage occurs. The strong inward rectification results from the steep changes in the direction and flux ratio of the K
+ ion flux near the equilibrium potential [
1,
2].
The electrochemical driving force can affect the intrinsic gating for K
+ permeation in the absence of blockers in certain ion channels. In K2P K
+ channels, the permeation barrier is greatly affected by the direction of the K
+ flux driven by the electrochemical gradient. A model of flux-coupled gating in the multi-ion selectivity filter in the K2P K
+ channel has been proposed to explain the intrinsic strongly outward rectifying current–voltage relationship without extracellular or intracellular blockers [
35]. The gating barrier to ion permeation within the channel pore is “driving force”-dependent because the barrier is significantly affected by the direction of the K
+ ion flux. In K2P channels, when
, the outward K
+ flux activates the channel by promoting the ion-occupied permeating state; the electrostatic repulsion between the ions in the selectivity filter elevates the electrical potential energy and lowers the activation barrier for outward ion conduction. When
, the channel reverts to an ion-depleted inactive state with low conductance. The barrier in one flux direction is significantly lower than the barrier in the opposite flux direction. The “driving force”-dependent gating in K2P channels shares some common physical principles with the current–voltage relationship in the diode in the electrical circuit [
36], and with the rectified rotations in the Feynman’s imaginary Brownian ratchet [
16]. Strong rectification occurs when the energy barrier to transport is significantly coupled by the direction of the thermodynamic driving force in these specially designed molecular machines or gadgets.
The channel structure is also crucial to flux-coupled biochemical reactions, such as the role of the proton channel on the F
O portion of ATP synthase on the inner mitochondrial membrane [
3,
4,
5,
6]. The ATP synthase transduces the electrochemical gradient of the proton to energize the production of ATP. Models of rotary single-file ion transport by the F
O portion of the ATP synthase have been proposed [
37,
38]. F
O may function as a torque-generating, single-file ion channel. The rotary of the c-ring against the a-subunit may be controlled by the occupancy of an ion pair between adjacent residues on the c-subunit and a-subunit. The two-staggered noncontiguous half-channels—the P channel and the N channel—placed left and right to the positively charged arginine residue on the a-subunit, provide the access or exit pathway for proton ions facing outside or inside the membrane. The c-ring can rotate clockwise or counterclockwise by stochastic fluctuation force. The net direction of rotation depends on the electrochemical driving force for proton transport across the membrane [
38]. Although the two half-channels are noncontiguous, a hydrogen ion that binds the c-ring via the P channel can induce the release of another hydrogen ion from the N channel by promoting an elementary rotational step of the c-ring [
39,
40], so the transport of the ions in the two half-channels and on the c-ring is energetically coupled.
The Curie–Prigogine principle states that simultaneous diffusion and chemical reaction cannot be coupled in an isotropic system such as in a bulk ion solution [
8,
10]. Hence, a membrane channel is needed for utilizing the electrochemical potential difference across the membrane to couple other molecular events or reactions. The multi-ion alignment, either by direct coupling between the ions in a single-file channel pore, or by rotary single-file ion transport by the F
O portion of the ATP synthase, makes it possible for the molecular machine to distinguish the direction of the ion flux driven by the electrochemical potential gradient across the membrane, and thus harness the natural tendency of entropy production to couple a specific physical process or chemical reaction in biological systems.