Abstract
We investigate an intermittent process obtained from the combination of a nonlinear diffusion equation and pauses. We consider the porous media equation with reaction terms related to the rate of switching the particles from the diffusive mode to the resting mode or switching them from the resting to the movement. The results show that in the asymptotic limit of small and long times, the spreading of the system is essentially governed by the diffusive term. The behavior exhibited for intermediate times depends on the rates present in the reaction terms. In this scenario, we show that, in the asymptotic limits, the distributions for this process are given by in terms of power laws which may be related to the q-exponential present in the Tsallis statistics. Furthermore, we also analyze a situation characterized by different diffusive regimes, which emerges when the diffusive term is a mixing of linear and nonlinear terms.
1. Introduction
Nowadays, anomalous diffusion plays an important role in the understanding of several phenomena, e.g., in biology [1,2,3,4], engineering [5,6], and physics [7,8,9]. Among them, we have the transport through the porous media [10,11], dynamic processes in protein folding [12], infiltration [13], single particle tracking [14], electrical response [15,16], and diffusion on fractals [17]. One of the main features present in these contexts is the nonlinear time dependence manifested by the second moment, e.g., (where and are related to subdiffusion and superdiffusion, respectively) usually related to non-Markovian processes. It is also interesting to point out that systems characterized by long tailed distributions, i.e., Lévy distributions [8,9], also exhibit anomalous diffusion.
These situations related to anomalous diffusion have been investigated by taking into account, for example, fractional diffusion equations [18,19,20,21], generalized Langevin equations [22,23], master equations [24,25], random walks [26], and nonlinear diffusion equations [27,28,29,30,31,32,33,34,35,36,37]. It is worth emphasizing that the nonlinear diffusion equations may be related to a thermodynamic [38] characterized by power–law distributions with a compact or a long-tailed behavior, which, in a suitable limit, can be connected with the Lévy distributions. They can also be related with other approaches such as Langevin equations [22,23] and random walks, and have also been analyzed by considering the presence of reaction terms [34]. Towards this, they lead us to an extension of the Fisher equation widely used to model population biology [39] and provide a simple generalization of the Verhulst logistic equation [40]. Thus, the comprehension of the formal aspects present in these approaches are an important point to establish a suitable link between the models and the experimental results. In a sense, our goal is to investigate an intermittent process resulting from the combination of the diffusion (motion) and pauses. For this, we consider the porous media equation with reaction terms related to the rate of switching the particles from the diffusive mode to the resting mode or switching them from the resting to the movement. The results show that, in the asymptotic limit of small and long times, the spreading of the system is essentially governed by a porous media equation. The behavior exhibited for intermediate times depends on the reaction terms related to the motion and pauses. For this process, we also show that, in the asymptotic limits, the distributions can be expressed in terms of power laws, which may be related to the q – exponential present in the Tsallis statistics. This analysis is performed in Section 2. Section 3 includes our discussion and conclusions.
2. Diffusion and Pauses
Let us start our discussion regarding the processes characterized by diffusion with pauses by considering first the standard case, i.e., the usual diffusion for the particles in motion. In this scenario, we may assume that the diffusion is essentially governed by the Einstein equation [41]:
in the absence of pauses. Following the development reported in [41], in order to introduce the reaction terms related to the motion and pauses, we may consider that, during the period τ, the probability of not switching from the diffusive to the resting is and for the reverse is . The transition between these states (diffusion ⇌ rest) is typical of a two-level continuous-time discrete Markov process. Furthermore, we introduce and for describing the density of particle in moving and in resting, respectively. Thus, Einstein’s equation turns into the system of equations
Equations (2) and (3) in the limit of and ( with , where ) yields
with . In Equations (4) and (5), and represent two different states. The first one represents the particles (species, or substance) diffusing, i.e., in motion, and the second corresponds to the particles (species, or substance) that are immobilized. Note that Equation (4) of the previous set of equations has the diffusive term, i.e., , which promotes the spreading of the system. Equation (5) has no diffusive term and leads the particles to the rest, in contrast to Equation (4). Consequently, this system of equations can be related to the following process: diffusion ⇌ pauses as expected.
For these equations, it is possible to obtain exact solutions by using the standard calculus techniques. In particular, for the boundary conditions and and the initial conditions and , they are given by
with
and
Figure 1 shows, for this case, the behavior of the mean square displacement . One can observe that, for small times, i.e., , the influence of the reaction terms is not pronounced and the spreading of essentially behaves as in the usual diffusion. A similar feature is verified for the long times, i.e., as shown in Figure 1; however, this case is characterized by an effective diffusion coefficient. For intermediate times, , the reaction terms play an important role, and we have a pronounced effect of an intermittent process characterized by an interchange between motion and pauses. This fact is manifested by the mean square displacement, which, in this time interval, exhibits a subdiffusion instead of the usual one.

Figure 1.
Behavior of the mean square displacement obtained from Equations (6) and (7). For simplicity, we consider and , where and represent arbitrary unities of length and time.
The nonlinear case related to the anomalous diffusion and the Tsallis statistics may be obtained from the previous approach by incorporating, in the dispersal term, a nonlinear dependence on the distribution, e.g., , and modifying the additional terms related to the probability of diffusing or resting in order to preserve the linearity of the reaction terms. Thus, the nonlinearity present in the dispersal term will only appear in the diffusive term, which promotes the spreading of the particles. This nonlinear dependence on the dispersal term is connected to the feature that the jumping probability depends explicitly on the distribution . In this case, it may describe situations characterized by distributions with a compact form or a long-tailed distribution that asymptotically may be connected to the Lévy distributions [42], implying that the diffusion coefficient in any element of the system depends on the history of the element. For this case, we have that
By taking into account the limit and in the previous set of equations, we obtain
with
Notice that it is also possible to assume that the kernel may depend explicitly on ; however, for this case, the definition of diffusion coefficient will be different from the previous one. Equation (13) is equal to Equation (4) for , and, consequently, the diffusion process is usual. For , we obtain the cases described by the following differential equations:
The diffusive term present in Equation (16) has a nonlinear dependence on the distribution , characteristic of an anomalous correlated diffusion [38] and enables us a connection with the Tsallis statistics that is based on the following entropy [38]:
where the index q represents a degree of nonextensivity of the system [38] and recovers the Boltzmann–Gibbs entropy. It is worth mentioning that Equation (16) in the absence of reaction terms has been applied in several situations such as percolation of gases through porous media ( [43]), thin saturated regions in porous media ( [44]), thin liquid films spreading under gravity ( [45]), and solid-on-solid model for surface growth ( [46]). The solutions for Equation (16) may have a compact or a long-tailed behavior depending on the choice of ν and, similar to the linear case, the additional terms promote the transition between the motion and pauses during the diffusive process.
For the particular case , i.e., the particles are only switched from the diffusive mode to the resting mode, and we may obtain a formal solution for the previous set of equations by considering the boundary conditions and , and the initial conditions and . In particular, for this case, it is possible to show that
with , ,
where , and are the q-exponential functions present in the Tsallis statistics, defined as follows:
The presence of the q-exponential in Equations (19) and (20) enables us to obtain a short () or a long () tailed behavior for the solution depending on the choice of the parameter q. In fact, Equation (19) has a compact behavior for q less than one due to the “cut-off” manifested by the q-exponential to retain the probabilistic interpretation associated to . Consequently, exhibits a similar behavior for q less than one. On the other hand, for q greater than one, Equation (19) has the asymptotic limit governed by a power–law behavior, which may also related to a Lévy distribution, as shown in [42]. In this case, the solutions obtained for the previous set of equations may be asymptotically related to the solutions obtained in [47] for fractional diffusion equations, which asymptotically are governed by power laws. The mean square displacement related to the distribution is given by
which, for small times, i.e., , and, for long times, i.e., , yields . For , we have that
with for small times and for long times, characterizing that, for long times, all the particles are switched from the diffusive mode to the resting mode.
For the case , we have an interplay between diffusion and pauses. In this case, it is possible to show that and that the survival probabilities () related to and for this case satisfy the following set of equations:
and, consequently, the solution is given by
with . The previous equations show that, for long times, the equilibrium between particles switched from the motion to the rest (or to the rest to the motion) is reached for and . An important point about these solutions is the absence of the parameter ν and only the presence of the rates and . In this case, this feature implies that the interchange between the states of motion and pauses is independent of the diffusion process. Performing some numerical calculations, it is possible to obtain more information about the behavior of the mean square displacement and the distributions and . In fact, by using the numerical algorithms based on central differences [48], it is possible to numerically solve Equations (16) and (17) that are coupled by the reaction terms. Figure 2 and Figure 3 show the behavior of the mean square displacement for and obtained by solving numerically Equations (16) and (17). The system was defined in the interval and discretized in increments of with to perform numerically the time evolution and obtain the results presented in these figures. These choices for and verify the condition required for the stability of the solutions during the time evolution of the initial condition in order to satisfy the boundary conditions. These considerations were also applied in the numerical calculations performed to obtain the other figures. The initial behavior, i.e., , manifested by is characterized by the porous media equation in the absence of reaction terms. It may be subdiffusive or superdiffusive depending on the choice of ν, i.e., or . In Figure 2, we have a subdiffusive () behavior for small times, in contrast to Figure 3, where the superdiffusive is obtained. For long times, we also observe that the system is essentially governed by the porous media equation with an effective diffusion coefficient as a result of the intermittent motion of the particles which are constantly switching from the diffusive mode to the resting mode or switching from the resting to the movement. For intermediate times, we have a different behavior from the one obtained from the porous media equation due to the interchanges between motion and pauses.
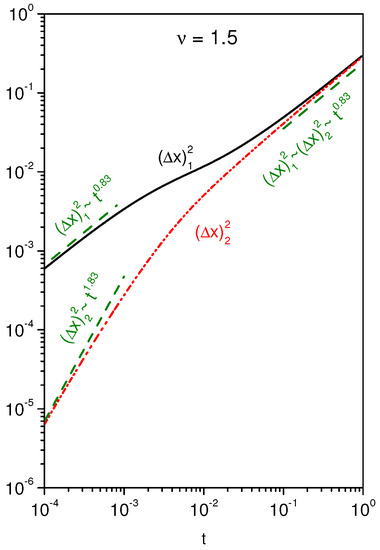
Figure 2.
Behavior of the mean square displacement obtained from Equations (16) and (17) for . For simplicity, we consider , , and , where and represent arbitrary units of length and time.
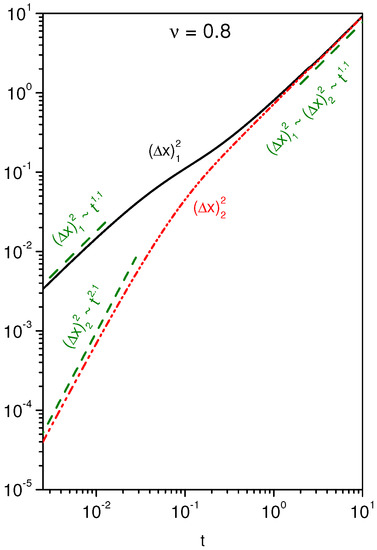
Figure 3.
Behavior of the mean square displacement obtained from Equations (16) and (17) for . For simplicity, we consider and , where and represent arbitrary units of length and time.
In order to investigate the behavior of the solutions, in the asymptotic limit of long times, we may analyze the following equation:
which can obtained from the previous set of equations. For , by taking into account , this equation can be approximated to
which also has the solutions given in terms of the q-exponential functions.
In fact, after performing some calculations, it is possible to show that
with , ,
Figure 4 illustrates the solution obtained numerically and the approximated one obtained above for long times in order to show that, for long times, we have a complete agreement between them.
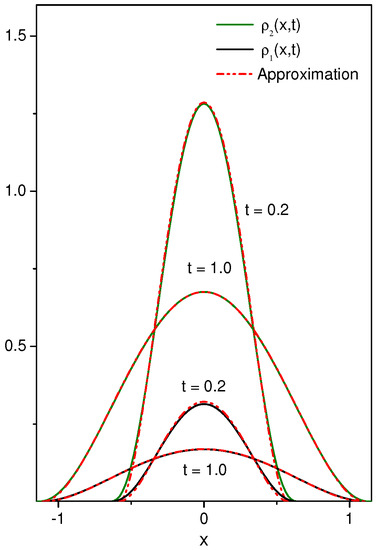
Figure 4.
This figure illustrates the behavior of and obtained numerically from the Equations (16) and (17) and approximated ones obtained from Equation (31) and by considering without loss of generality . For simplicity, we also consider , , , and , where and represent arbitrary units of length and time.
Other choices for are also possible—in particular, , which may be related to different diffusive behavior, one characterized by an usual diffusion and the other by an anomalous one. A particular application of this choice is found in the spatial distribution of dispersing animals [49]. Figure 5 and Figure 6 illustrate the behavior of the mean square displacement for this case by considering the boundary conditions and and the initial conditions and .
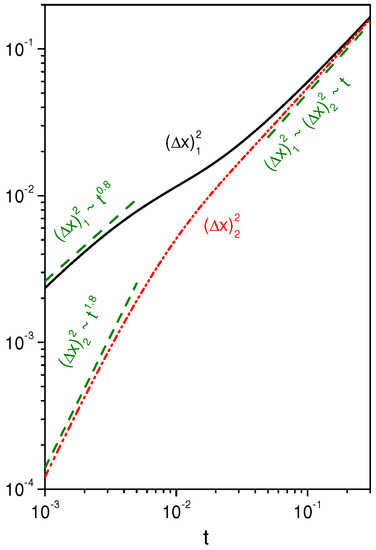
Figure 5.
Behavior of the mean square displacement obtained from Equations (13) and (14) for with . For simplicity, we consider , , and , where and represent arbitrary units of length and time.
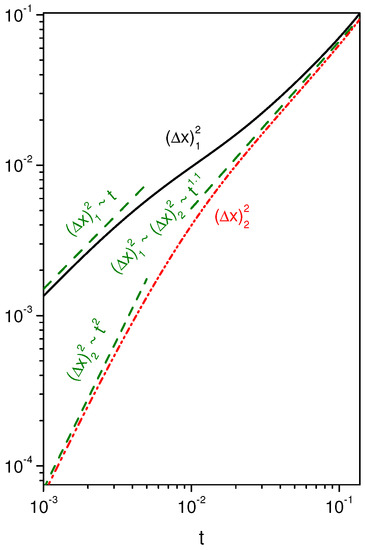
Figure 6.
Behavior of the mean square displacement obtained from Equations (13) and (14) for with . For simplicity, we consider , , and , and , where and represent arbitrary units of length and time.
One can observe that the behavior for small times is governed by a subdiffusion if and by the usual one if . For long times, we have an usual diffusion if and a superdiffusion if . It is important to note that, for these cases, we have different diffusive regimes present in these systems due to the mixing between the linear and nonlinear diffusive terms, and, as pointed out in [50], they are characterized by crossover times.
3. Discussion and Conclusions
We have analyzed an intermittent process governed by a nonlinear diffusion equation. We have first considered the case with , for which the particles are switched to the motion state to the rest. For this case, we have obtained exact solutions in terms of the q-exponentials of the Tsallis statistics. We have also verified for this case that, depending on the choice of the parameter ν, the solution may exhibit a compact or a long-tailed behavior, which may be connected to a subdiffusion or superdiffusion process. For the case with , which implies in an interchange between two states, motion and rest, we have performed a numerical analysis and verified that, for small and long times, the behavior of is essentially characterized by a diffusive behavior. For intermediate times, i.e., , the reaction terms that characterize the motion and pauses play an important role, and the system exhibits a different diffusive regime from the initial. For , we observe an initial behavior characterized by a fast diffusion and asymptotically governed by a behavior of the diffusive term present in Equation (16). In this case, the distributions are given in terms of q-exponentials and the asymptotic behavior, compact or long-tailed, depending on the value of ν. Furthermore, we have considered a situation characterized by the presence of different regimes, and it showed that the asymptotic regime is faster than the first one exhibited by the system.
Acknowledgments
The authors are thankful to CNPq (Brazilian agency) for partial financial support.
Author Contributions
All the authors have approved the final manuscript. E.K.L., L.R.S., and L.R.E. formulated the problem and performed the analytical calculations and some numerical simulations; H.V.R. and M.K.L. performed part of the numerical calculations, analyzed results and wrote the paper; M.A.F.S. drew the figures, read and checked the whole manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cherstvy, A.G.; Chechkin, A.V.; Metzler, R. 2014 Particle invasion, survival, and non-ergodicity in 2D diffusion processes with space-dependent diffusivity. Soft Matter 2014, 10, 1591–1601. [Google Scholar] [CrossRef] [PubMed]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [PubMed]
- Bressloff, P.C. Stochastic Processes in Cell Biology; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Snopok, B.A. Nonexponential Kinetics of Surface Chemical Reactions. Theor. Exp. Chem. 2014, 50, 67–95. [Google Scholar] [CrossRef]
- Strizhak, P.E. Macrokinetics of Chemical Processes on Porous Catalysts having regard to Anomalous Diffusion. Theor. Exp. Chem. 2004, 40, 203–208. [Google Scholar] [CrossRef]
- Avnir, D. The Fractal Approach to Heterogeneous Chemistry; Wiley-Interscience: New York, NY, USA, 1990. [Google Scholar]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Lévy walks. Rev. Mod. Phys. 2015, 87, 483–530. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport: Foundations and Applications; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- McDowell-Boyer, L.M.; Hunt, J.M.; Sitar, N. Particle Transport Through Porous Media. Water Resour. Res. 1986, 22, 1901–1921. [Google Scholar] [CrossRef]
- De Smedt, F.; Wierenga, P.J. A generalized solution for solute flow in soils with mobile and immobile water. Water Resour. Res. 1979, 15, 1137–1141. [Google Scholar] [CrossRef]
- McGuffee, S.R.; Elcock, A.H. Diffusion, Crowding & Protein Stability in a Dynamic Molecular Model of the Bacterial Cytoplasm. PLoS Comput. Biol. 2010, 6, e1000694. [Google Scholar]
- Filipovitch, N.; Hill, K.M.; Longjas, A.; Voller, V.R. Infiltration experiments demonstrate an explicit connection between heterogeneity and anomalous diffusion behavior. Water Resour. Res. 2016, 52, 5167–5178. [Google Scholar] [CrossRef]
- Gmachowski, L. Fractal model of anomalous diffusion. Eur. Biophys. J. 2015, 44, 613–621. [Google Scholar] [CrossRef] [PubMed]
- Santoro, P.A.; de Paula, J.L.; Lenzi, E.K.; Evangelista, L.R. Anomalous diffusion governed by a fractional diffusion equation and the electrical response of an electrolytic cell. J. Chem. Phys. 2011, 135, 114704. [Google Scholar] [CrossRef] [PubMed]
- Lenzi, E.K.; Fernandes, P.R.G.; Petrucci, T.; Mukai, H.; Ribeiro, H.V. Anomalous-diffusion approach applied to the electrical response of water. Phys. Rev. E 2011, 84, 041128. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, I.M. Anomalous Diffusion on Fractal Networks. In Mathematics of Complexity and Dynamical Systems; Robert, A.M., Ed.; Springer: New York, NY, USA, 2011; pp. 13–25. [Google Scholar]
- Barkai, E. Fractional Fokker-Planck equation, solution, and application. Phys. Rev. E 2001, 63, 046118. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Lenzi, M.K.; Zola, R.S.; Ribeiro, H.V.; Zola, F.C.; Evangelista, L.R.; Gonçalves, G. Reaction on a solid surface supplied by an anomalous mass transfer source. Physica A 2014, 410, 399–406. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Borland, L. Microscopic dynamics of the nonlinear Fokker-Planck equation: A phenomenological model. Phys. Rev. E 1998, 57, 6634–6642. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Lenzi, E.K.; da Silva, L.R.; Ribeiro, H.V.; Picoli, S., Jr.; Mendes, R.S. Different diffusive regimes, generalized Langevin and diffusion equations. Phys. Rev. E 2012, 85, 011147. [Google Scholar] [CrossRef] [PubMed]
- Kenkre, V.M.; Montroll, E.W.; Shlesinger, M.F. Generalized master equations for continuous-time random walks. J. Stat. Phys. 1973, 9, 45–50. [Google Scholar] [CrossRef]
- Pagnini, G.; Mura, A.; Mainardi, F. Generalized Fractional Master Equation for Self-Similar Stochastic Processes Modelling Anomalous Diffusion. Int. J. Stoch. Anal. 2012, 2012, 427383. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Silva, A.T.; Lenzi, E.K.; Evangelista, L.R.; Lenzi, M.K.; da Silva, L.R. Fractional nonlinear diffusion equation, solutions and anomalous diffusion. Physica A 2007, 375, 65–71. [Google Scholar] [CrossRef]
- Alibaud, N.; Cifani, S.; Jakobsen, E.R. Continuous dependence estimates for nonlinear fractional convection-diffusion equations. SIAM J. Math. Anal. 2012, 44, 603–632. [Google Scholar] [CrossRef]
- Pascal, H. A nonlinear model of heat conduction. J. Phys. A 1992, 25, 939–948. [Google Scholar] [CrossRef]
- Daly, E.; Porporato, A. Similarity solutions of nonlinear diffusion problems related to mathematical hydraulics and the Fokker-Planck equation. Phys. Rev. E 2004, 70, 056303. [Google Scholar] [CrossRef] [PubMed]
- Troncoso, P.; Fierro, O.; Curilef, S.; Plastino, A.R. A family of evolution equations with nonlinear diffusion, Verhulst growth, and global regulation: Exact time-dependent solutions. Physica A 2007, 375, 457–466. [Google Scholar] [CrossRef]
- Plastino, A.R.; Plastino, A. Non-Extensive Statistical Mechanics and Generalized Fokker-Planck Equation. Physica A 1995, 222, 347–354. [Google Scholar] [CrossRef]
- Silva, P.C.; da Silva, L.R.; Lenzi, E.K.; Mendes, R.S.; Malacarne, L.C. Nonlinear diffusion equation, Tsallis formalism and exact solutions. Physica A 2004, 342, 16–19. [Google Scholar]
- Plastino, A.R.; Casas, M.; Plastino, A. A nonextensive maximum entropy approach to a family of nonlinear reaction-diffusion equations. Physica A 2000, 280, 289–303. [Google Scholar] [CrossRef]
- Wada, T.; Scarfone, A.M. On the non-linear Fokker-Planck equation associated with κ-entropy. AIP Conf. Proc. 2007, 965, 177–180. [Google Scholar]
- Wada, T.; Scarfone, A.M. Asymptotic solutions of a nonlinear diffusive equation in the framework of κ-generalized statistical mechanics. Eur. Phys. J. B 2009, 70, 65–71. [Google Scholar] [CrossRef]
- Frank, T.D. Nonlinear Fokker-Planck Equations; Springer-Verlag: Heidelberg, Germany, 2005. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer-Verlag: New York, NY, USA, 2009. [Google Scholar]
- Murray, J. Mathematical Biology; Springer: Berlin, Germany, 1989. [Google Scholar]
- Rigo, A.; Plastino, A.R.; Casas, M.; Plastino, A. Anomalous diffusion coupled with Verhulst-like growth dynamics: Exact time-dependent solutions. Phys. Lett. A 2000, 276, 97–102. [Google Scholar] [CrossRef]
- Mendez, V.; Campos, D.; Bartumeus, F. Stochastic Foundations in Movement Ecology; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Tsallis, C.; Levy, S.V.F.; Souza, A.M.C.; Maynard, R. Statistical-Mechanical Foundation of the Ubiquity of Lévy Distributions in Nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar] [CrossRef] [PubMed]
- Muskat, M. The Flow of Homogeneous Fluids Through Porous Media; McGraw-Hill: New York, NY, USA, 1937. [Google Scholar]
- Polubarinova-Kochina, P.Y. Theory of Ground Water Movement; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Buckmaster, J. Viscous sheets advancing over dry beds. J. Fluid Mech. 1977, 81, 735–756. [Google Scholar] [CrossRef]
- Spohn, H. Surface dynamics below the roughening transition. J. Phys. France I 1993, 3, 69–81. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Menechini, N.R.; Tateishi, A.A.; Lenzi, M.K.; Ribeiro, H.V. Fractional diffusion equations coupled by reaction terms. Physica A 2016, 458, 9–16. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A. Numerical Recipes in Fortran: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Shigesada, N. Spatial Distribution of Dispersing Animals. J. Math. Biology 1980, 9, 85–96. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Mendes, R.S.; Tsallis, C. Crossover in diffusion equation: Anomalous and normal behaviors. Phys. Rev. E 2003, 67, 031104. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).