1. Introduction
In recent years, automobile industry has made great progress in improving internal combustion engine thermal efficiencies. Current manufactured gasoline engines are working with maximum thermal efficiencies of 30%–36%, while diesel engines already reach 40%–47% [
1]. Nowadays, the engine thermal efficiency is close to its technical limits but still not sufficient to meet future fuel economy targets without additional technologies. More than half of the fuel energy in the internal combustion engines is discharged in the form of heat to the environment. Waste heat recovery is considered as one of the most promising technologies to improve the engine thermal efficiency [
2].
Several technologies can be applied to recover the waste heat of an internal combustion engine, including turbocompounding, organic Rankine cycle (ORC), and thermoelectric generators [
3,
4,
5,
6]. When comparing these technologies, two key factors should be taken into consideration. One is the utilization of the waste heat temperature range, the other is the efficiency improvement potentials. ORC can utilize all kinds of engine waste heat, and the engine BSFC saving potentials are very promising, around 5%–15% [
7]. Hence, ORC is considered as the most appropriate waste heat recovery technology in the current conditions.
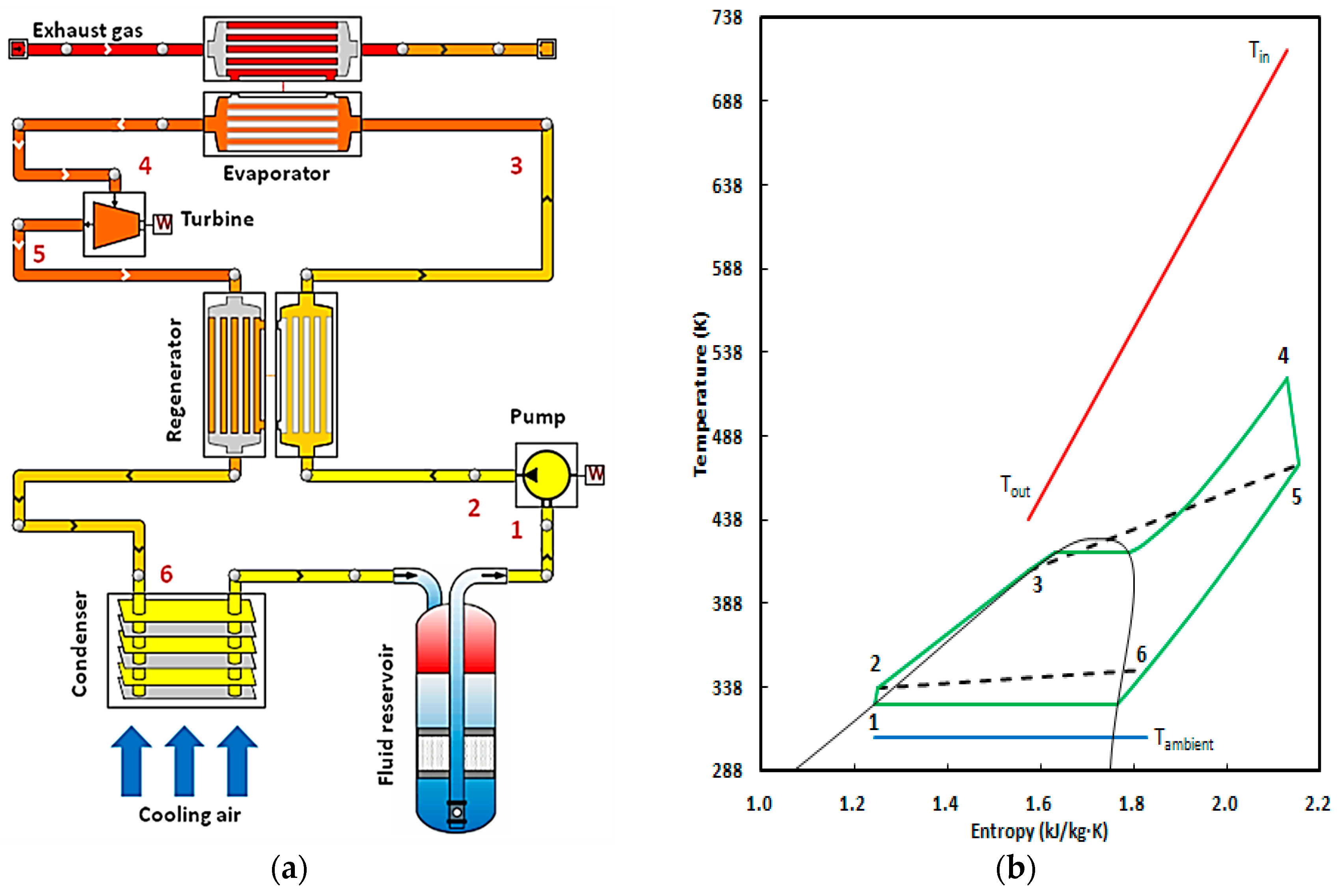
Figure 1 shows the demonstration of a regenerative organic Rankine cycle utilized for heavy-duty diesel engine exhaust gas recovery. The working fluid from the fluid reservoir is firstly pressurized by the working fluid pump, and then preheated in the regenerator by the high temperature working fluid out of the turbine. Secondly, the working fluid continues to be heated to the overheating state by the diesel engine high temperature exhaust gas, and then the superheating vapor enters into the turbine where it expands to the condensation pressure, during which mechanical work is transmitted to the application device through the shaft of the turbine. Finally, the working fluid is cooled sequentially in the regenerator and condenser to come back to the liquid state flowing into the fluid reservoir to complete the cycle.
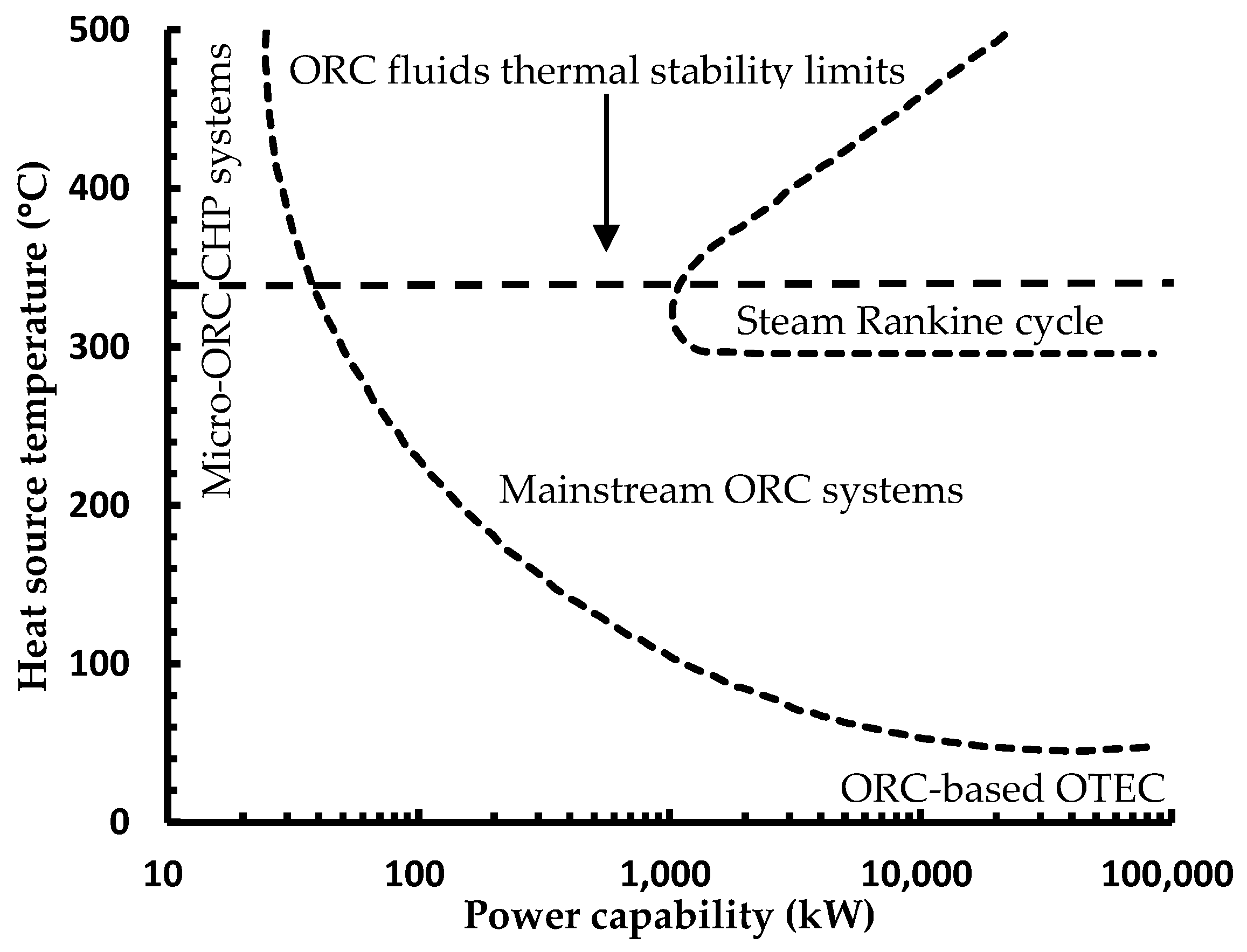
The use of organic fluids instead of water largely extends the application fields of Rankine cycle, making it promising especially in the low heat source temperature and small power size applications [
8]. The Current and future ORC application fields versus steam Rankine cycle systems in terms of average temperature of the energy source and power capacity is shown in
Figure 2. The steam Rankine cycle can be efficient only when the heat source temperature is above 300 °C and the system power capacity is above 1 MW. However, for ORC systems, the current application fields have extended to about 30 kW power capacities and 60 °C heat source temperatures. Two extreme applications are ORC based ocean thermal energy conversion (OTEC) for very low heat source temperatures and very large power capabilities, and micro-ORC combined heat and power (CHP) systems for very high heat source temperatures and very small power capabilities. The main advantages of ORC consist of two aspects [
9]: (1) the working fluid can be an additional degree of freedom for a better design of the thermodynamic cycle for a specific heat source temperature, especially some of which are very efficient for low temperature applications; and (2) for the small power size applications, it is possible to design an efficient, reliable and cost-effective organic vapor expander. As for the heavy-duty diesel engine organic Rankine cycles, the power capacities are commonly within 30 kW, and heat source temperatures are either below 100 °C for engine coolant or above 400 °C for exhaust gases. As the core component of ORC systems, no efficient, reliable and cost-effective expanders can be found in the market until now for this specific application.
Radial turbines are good candidates because of the advantages of small size, light weight, high design efficiencies, high reliability [
10,
11] and cost-effectiveness in mass productions. Many researchers have carried out studies related to the radial turbine design. As the organic fluid properties are totally different from air, these researches are mainly divided into two technical routes. One route focuses on forward design, including preliminary design of geometry parameters and aerodynamic design of blade profiles [
12,
13,
14,
15,
16,
17,
18,
19,
20,
21]. Dolz et al. [
13] propose that the pre-design of turbomachinery must take real gas equations of state into consideration, because the specific energy deviation between real gas and perfect gas can be as large as 100%, which may lead to total wrong turbine preliminary design result. Fiaschi et al. [
19,
20] propose an accurate 0-D model to design low size radial ORC turbines. Different methods for the design of radial turbines were screened, with special attention paid to the estimation of losses. The results indicated that the total-to-total efficiencies of the designed turbines ranged from 72% to 80%. Costall et al. [
21] also propose a detailed design methodology for ORC radial turbines. They used the methodology to design a radial turbine for the heavy-duty off-road diesel engine application. After three times of optimization, the best turbine produced 45.6 kW at 56.1% efficiency. Colonna et al. [
16,
17] made the fluid-dynamic design of ORC turbine using CFD tools. The authors numerically investigated the real gas effects occurring in the supersonic ORC stator nozzles. The results showed that a nozzle geometry with much higher exit-to-throat area ratio was required to obtain an efficient expansion. Wheeler and Ong [
14,
15] mainly focus on the radial turbine rotor flow mechanisms and geometry optimizations by the CFD tools. They suggested that small changes in the inducer shape had a significant effect on turbine efficiency due to the development of supersonic flows in the rotor. The strong interaction between the vane trailing-edge shocks and rotor leading-edge lead to a significant drop in efficiency, which should be specially considered.
The design and development of a turbine, which can be finally sold in the market, is a complex engineering problem involving turbine preliminary design, aerodynamic design of the blades, CFD analysis on the aerodynamic performance, rotor-dynamic analysis and system integration of turbine and auxiliary components [
22]. In order to reduce the developmental effort involved in turbine preliminary design aspect, the other technical route is proposed to adapt an existing turbine using air as working fluid for ORC applications, namely similarity design [
23,
24,
25,
26]. Zhang et al. [
24] established a performance prediction method from air to refrigerants taking compressibility factor into consideration. The results indicated that the relative deviation of main performance parameters at the design point working condition was no more than 5%, and under all working conditions were no more than 10%. White and Sayma [
25] applied the similarity theory to predict turbine off-design performance over a range of different operating conditions while utilizing different working fluids. The original similitude theory using turbine total inlet conditions was found to only apply within a small range of operating conditions, so a modified similitude theory was suggested that using the choked flow conditions instead. The results agreed with the CFD predictions within 2% for three organic fluids R245fa, R123 and R1234yf, right up until the choked mass flow rate. Wong and Krumdieck [
26] scaled an industrial gas turbine to two refrigerants: R134a and R245fa. Three different approaches using the similarity theory were applied to scale the turbine performance map using air and generated the performance map for the two refrigerants. The results showed that the complete similarity could not be achieved for the same turbomachinery with two different working fluids, even at the best efficiency point. The authors indicated that the constant ratio of change of enthalpy to the squared of speed of sound in the turbine inlet approach would provide the highest accuracy in the performance estimation. The average errors of R134a and R245fa compared with air were 7.2% and 8.7%, respectively.
Until now, for the second technical route of turbine design, nearly all the literature focuses on the issue that finding an air turbine as the preliminary design result of organic fluids, but the issue of whether the aerodynamic design of blade profiles can adapt the new kind of working fluid has not been analyzed yet. That is to say, when a turbine using air as working fluid turns into using refrigerants as working fluids, how the turbine efficiency will change, and what loss mechanism differences lead to the efficiency change. It is very meaningful to answer this question, because the radial turbines using air as the working fluid in turbocharging applications have been very mature, and many technologies have been developed to improve the turbine efficiencies. It may largely shorten the time of aerodynamic design process of blade profiles of an ORC turbine when referring to the existing efficiency improving technologies.
In this paper, a radial turbine, for the heavy-duty diesel engine ORC application, is numerically simulated using R245fa and air as the working fluid to compare the differences of their performance and loss mechanism. R245fa, a typical organic fluid, is chosen as the working fluid because of its environmental friendly properties [
27], good thermodynamic performance in the heavy-duty diesel engine applications [
28] and high turbine nominal efficiency for small power size applications [
20]. Firstly, the similarity criteria are deduced to obtain the similar operating condition between air and R245fa, and kinematic and dynamic similarities are verified. Then, the turbine performance maps are compared to find out the quantitative differences of total-to-static pressure ratio, reduced mass flow rate, reduced rotating speed and total-to-static isentropic efficiency. Finally, the similarities and differences of turbine entropy generation and loss mechanisms are discussed to explain the total-to-static isentropic efficiency difference.
2. Similarity Criteria
The general similarity criteria of turbines are summarized below, which can be found in the standard turbomachinery textbook [
29].
Besides, the compressibility effect was proven to have large influence on the turbine efficiency. Usually, for the perfect gas the compressibility effect can be determined by the pressure ratio. However, based on the analysis of Macchi and Perdichizzi [
30], for nonconventional fluids the associated similarity criterion of compressibility effect is volume expansion ratio, defined as the specific volume variation across the turbine in an isentropic process, which is applied instead of common characteristic parameter pressure ratio in this analysis.
Compressibility coefficient
Air, which behaves like the perfect gas, obeys the perfect gas EoS like Equation (7), and the isentropic process obeys the following relationships (Equations (8) and (9)).
The operating conditions of R245fa, including inlet pressure and temperature, rotating speed and outlet pressure, are obtained according to the thermodynamic analysis, and used as the input parameters to calculate all six similarity criteria (Equations (1)–(6)). Then, the similar operating conditions of air, including pressure ratio, rotating speed and inlet temperature, can be calculated in the following three steps.
Pressure ratios in the air operating conditions can be obtained by Equations (6) and (8):
Rotating speeds in the air operating conditions can be obtained by Equations (5), (9) and (10):
Fluid dynamic viscosities are determined by the inlet operating conditions and associate similarity criteria, according to Equations (4), (7) and (11):
Given the turbine outlet pressure, on the one hand, the dynamic viscosity can be calculated by Equation (12), using inlet temperature as the only input variable; on the other hand, the dynamic viscosity can be obtained based on the air thermodynamic property tables when temperature and pressure are known. The result is that a unique inlet temperature can be solved to satisfy both Equation (12) and air thermodynamic property tables. Then, rotating speeds can be calculated based on Equation (11).
3. Numerical Method
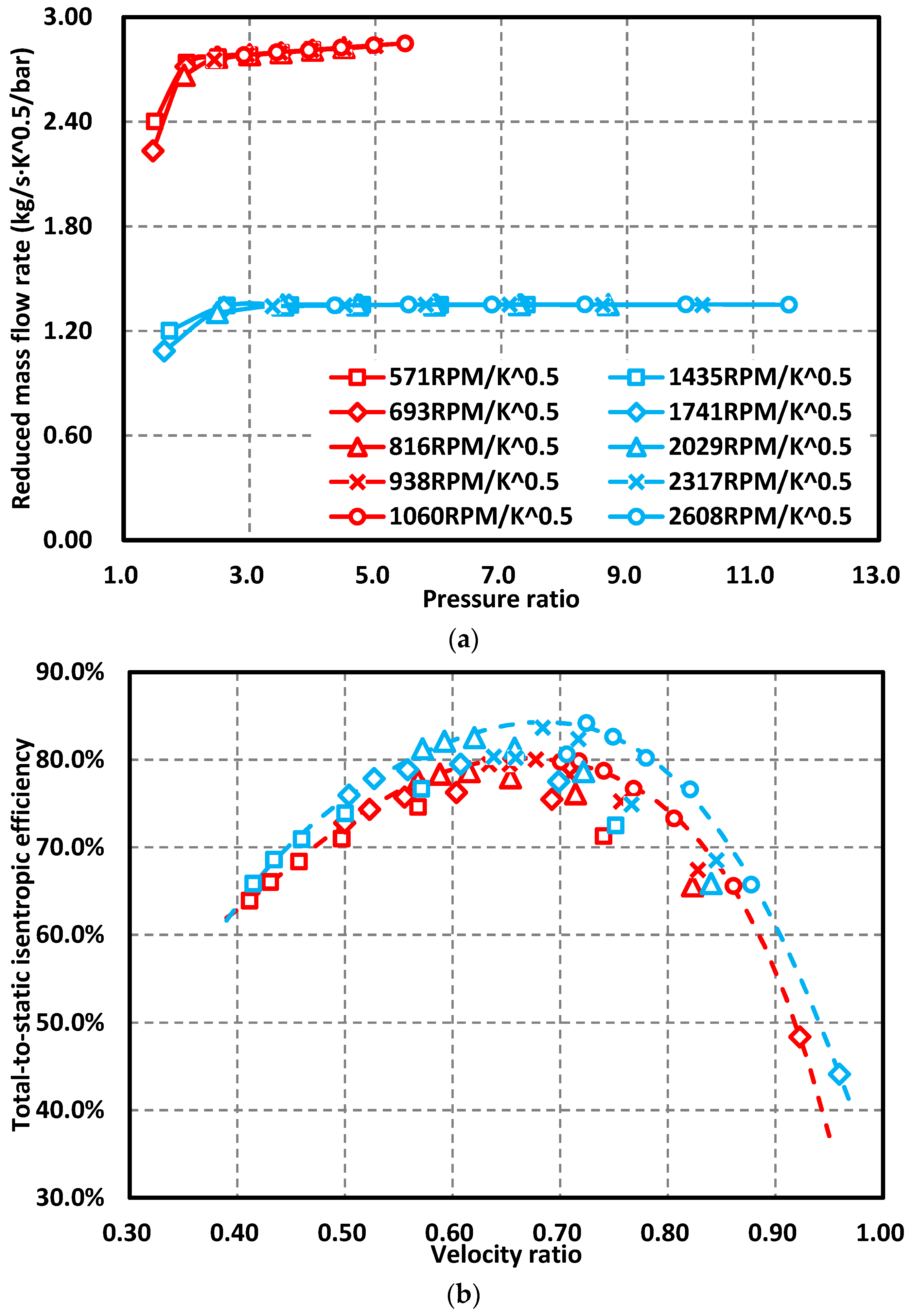
The radial turbine in this study was applied for the heavy-duty diesel engine coolant heat recovery. The waste heat temperature is only 90 °C, and the quantity of heat in the design point is about 164 kW. The design operating pressure ratio is 2.5, and the associated output power is 10 kW. The turbine design parameters and geometry parameters are shown in
Table 1 and
Table 2.
Three-dimensional steady computational fluid dynamics (CFD) simulations were carried out using the commercial code FINE
TM/Open. FINE
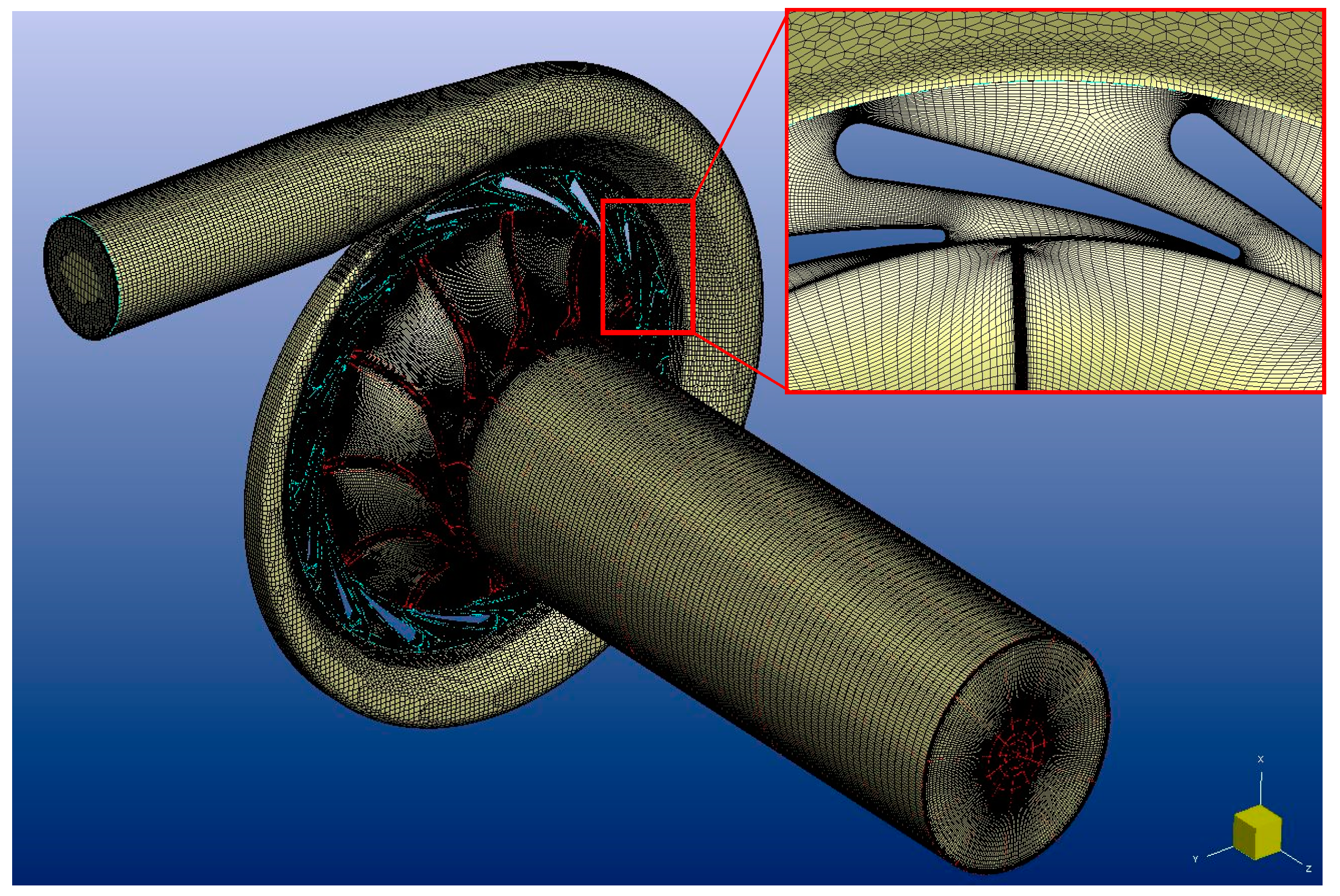
TM/Open is a Reynolds-average Navier-Stokes equation solver, which is based on the finite volume method, uses five stage explicit Runge-Kutta scheme and full hexahedra unstructured meshing strategy. The CFD domain consists of three components: the volute, full channels of nozzle ring and rotor wheel, which includes the exhaust pipe, as shown in
Figure 3. A fine mesh of 13,782,018 grid points was generated. The mesh distribution was 1,274,890 grid points within the volute, 233,472 grid points per single channel nozzle ring passage, and 818,368 grid points per single channel rotor wheel and exhaust pipe passage. The grid independency study showed that the increase of grid points by 100% only made a 0.1% difference in the simulated total pressure loss through the volute and 0.08% difference in the simulated turbine total-to-static isentropic efficiency. It indicates that the discretization error is reduced to an acceptable error in the current grid point number.
The Helmholtz free energy equation of state fitted for organic fluid R245fa is utilized to calculate the gas properties. The estimated uncertainty for density is 0.1% in the liquid phase below 400 K with pressures up to 30 MPa. In the vapor phase and at temperatures above 400 K, the uncertainty is 1% in density, with higher uncertainties in the critical region. The uncertainty in vapor pressure is 0.2% above 250 K, and rises to 0.35% above 370 K [
31]. The calculated thermodynamic properties were stored in the dedicated tables for the CFD code interpolation. The advantage of this approach is that no iterative inversion of the tables is done in the solver, therefore only a very small additional CPU time is needed. The bicubic interpolation approach was adopted to calculate values within the numerical interval.
Total pressure and temperature with velocity normal to the volute inlet was used as the inlet boundary condition. The averaged static pressure was used as the outlet boundary condition. The non-matching frozen rotor method was adopted to deal with the interface between the stationary and rotating domain. All the walls were treated as smooth and adiabatic. Surface roughness can have influence on boundary layer growth and loss at high Reynolds numbers, and this assumption can be reasonable for new blades especially at low Reynolds numbers, the roughness of which is unknown [
32]. Wall heat transfer is an important issue in the gas turbine airfoils simulations because of its extreme high temperature operating conditions and the adoption of blade cooling technology [
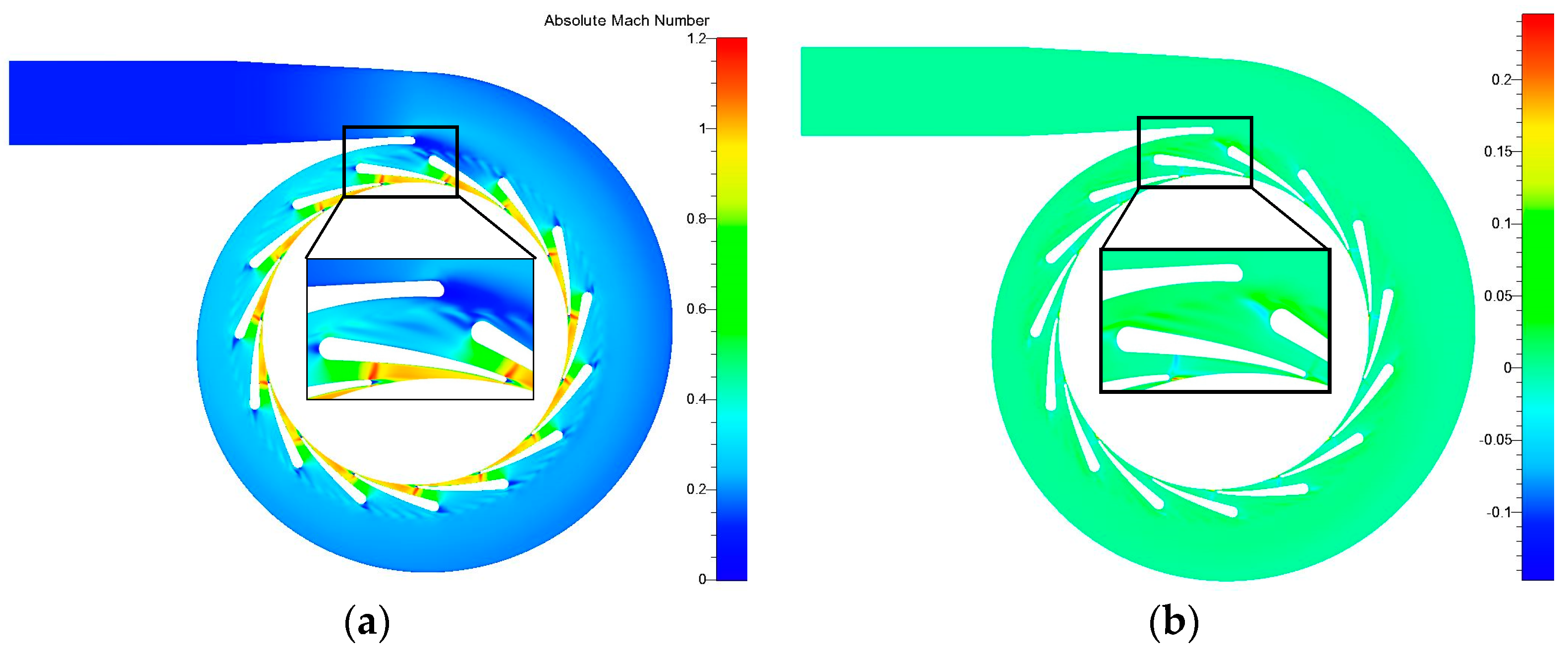
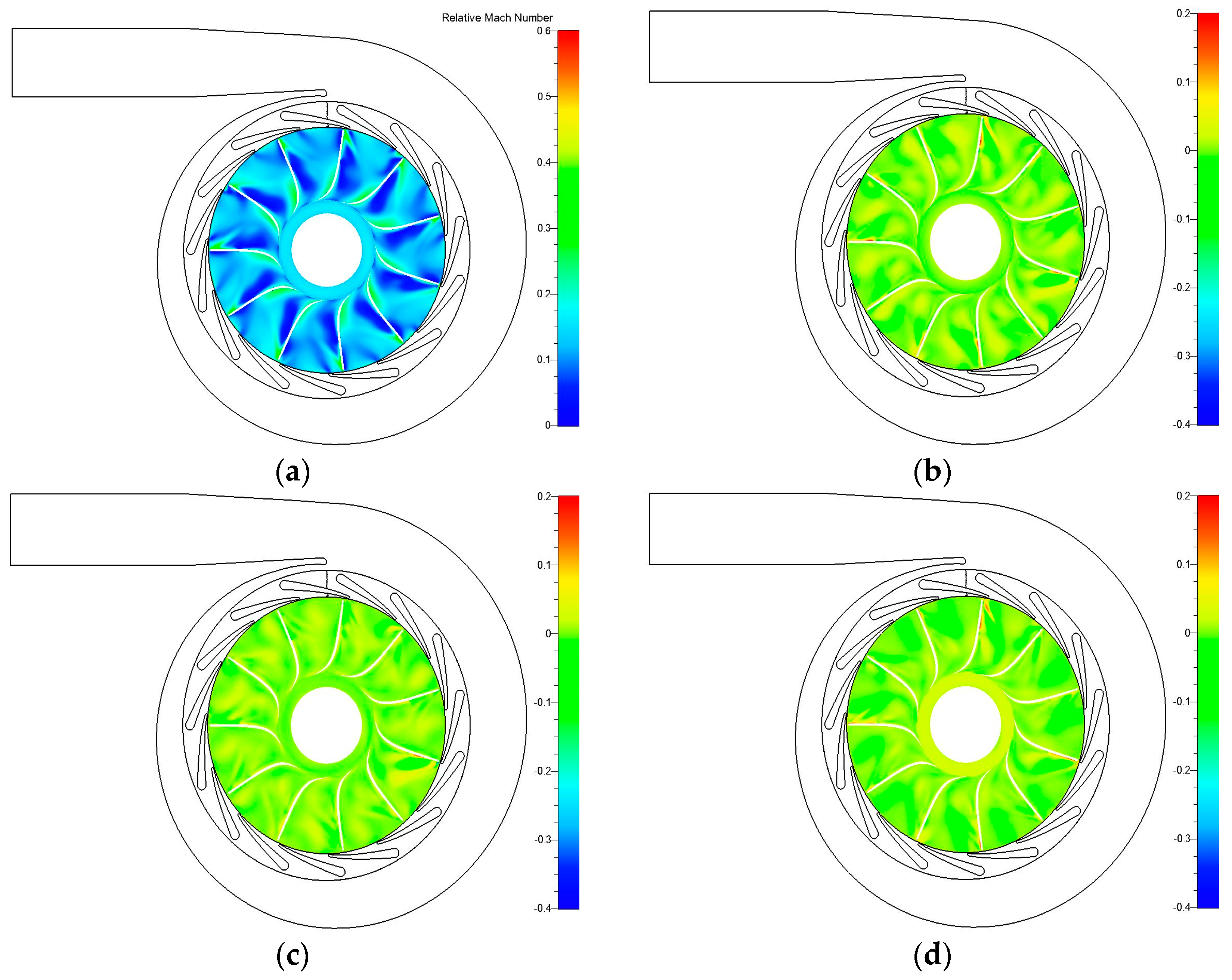
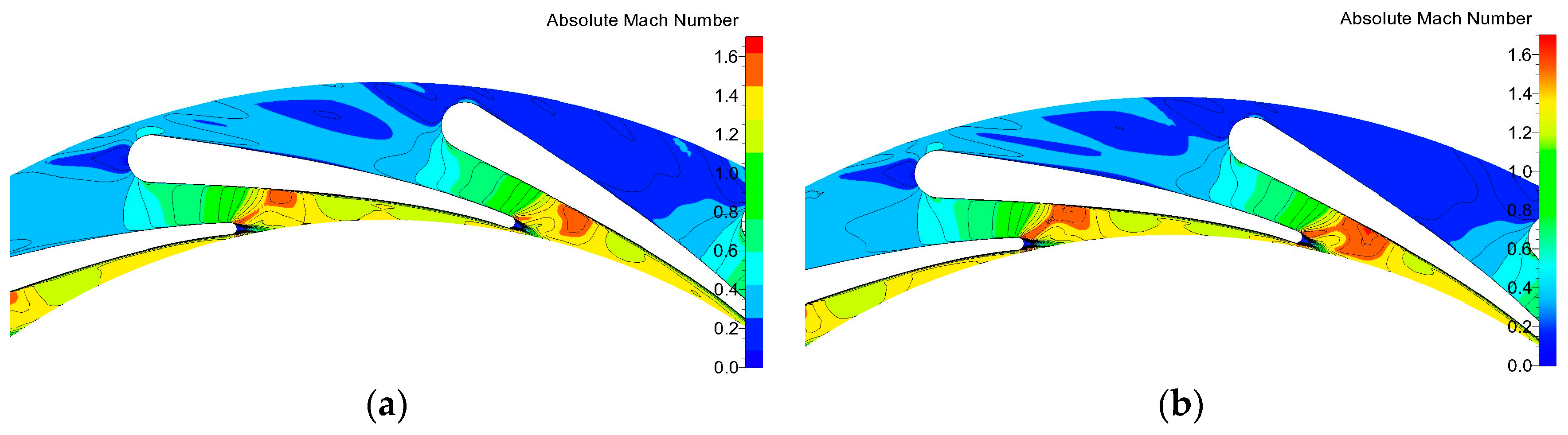
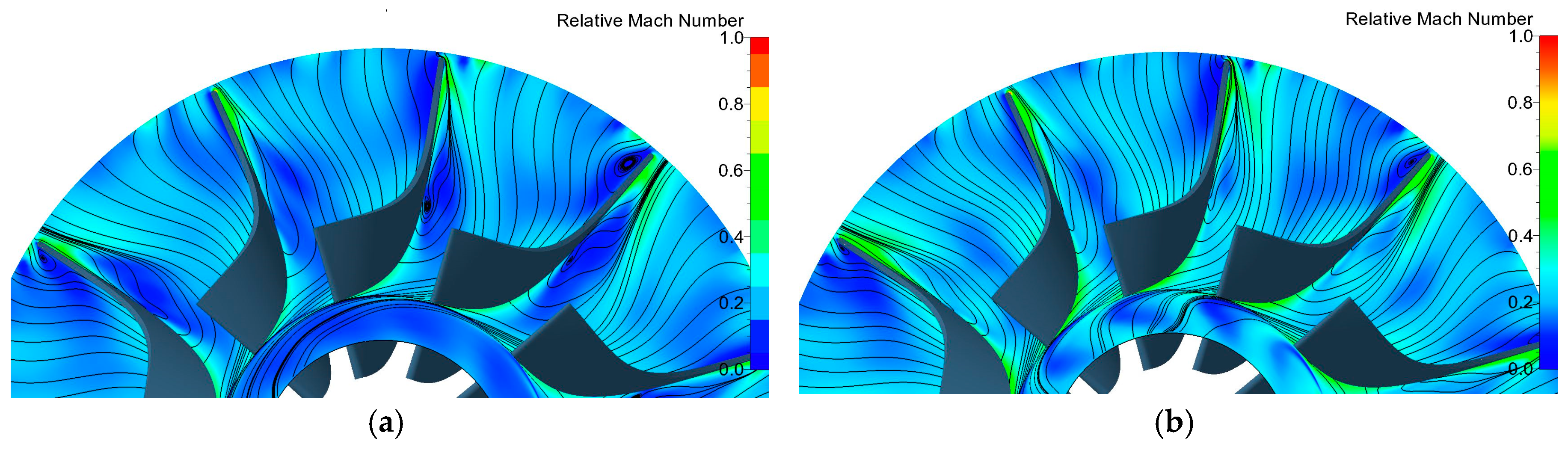
33]. As for the ORC radial turbine, the operating temperature is low and no blade cooling technology is adopted, so the heat transfer through the wall should be very limited. When fixing all these settings, the selection of appropriate turbulence model was discussed. Four turbulence models were compared, which were Spalart-Allmaras (S-A), low Reynolds number k-ε, k-ω shear stress transport (SST), and explicit algebraic Reynolds stress model (EARSM) turbulence models. The 50% span blade-to-blade flow fields of absolute Mach number in the stationary domain (shown in
Figure 4) and relative Mach number in the rotating domain (shown in
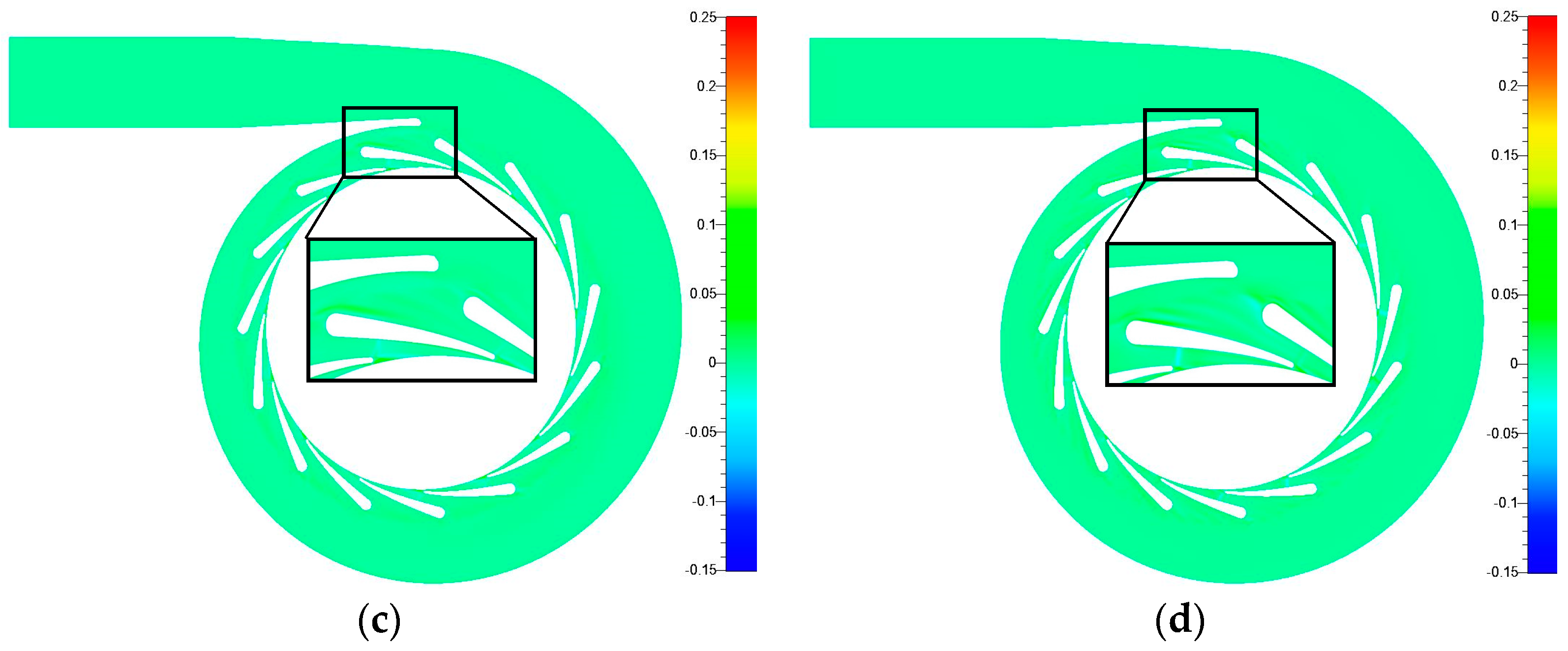
Figure 5) are compared, respectively. The shock wave positions are almost the same for the four turbulence models, the main difference is value evaluation of absolute Mach number. When the result of k-ω SST model is selected as the baseline, the difference of low Re k-ε model is almost zero. Spalart-Allmaras and EARSM models show smaller absolute Mach numbers in the shock wave position, but larger values near the leading edge of nozzle vanes. The difference values of EARSM model are generally smaller than those of Spalart-Allmaras model. As for the rotor separation flow simulation, using relative Mach number as the indicator, the separation flow in the suction side started earlier in most rotor wheel channels for Spalart-Allmaras model results. However, the phenomenon of separation flow starting earlier only happened in two or three rotor wheel channels in the low Re k-ε and EARSM models. In general, Spalart-Allmaras model shows the biggest difference compared with the other three models. For the other three turbulence models, k-ω SST and EARSM turbulence models have almost the same isentropic efficiency simulation results, the difference of which is only 0.03%, 1% higher than low Re k-ε model result and 3% higher than Spalart-Allmaras model result. Based on the flow field and isentropic efficiency comparison results, the turbulence model used in this simulation is k-ω SST model, which is also the commonly used two-equation turbulence model in the turbomachinery CFD simulation. The reasonability of these settings will be verified by the efficiency comparison between CFD simulations and experimental data.
The numerical method in this study is verified using the available experimental data of Kang [
34].
Table 3 shows CFD simulation results compared with literature experimental results. In this comparison, as the total parameters are used as inlet boundary conditions, so the static parameters have a little difference compared with the measured values. The efficiency comparison shows that the differences between simulation and experimental results for all the three operating conditions in the literature are within ±2.5%. The simulation results based on the numerical method introduced above show acceptable agreements with the experimental results, and can be used for further discussions.
5. Conclusions
In this paper, the performances of a radial turbine applied for heavy-duty diesel engine ORC systems are numerically simulated using R245fa and air as working fluid based on the similarity theory, and the turbine performance and loss mechanism differences are compared between these two working fluids. The results indicate the following conclusions.
Based on the built similarity criteria, the working fluid properties of specific heat ratio and gas constant have clear relationships with the turbine performance parameters, including total-to-static pressure ratio, reduced rotating speed and mass flow rate. As both specific heat ratio and gas constant of R245fa are smaller, the total-to-static pressure ratios for R245fa operating conditions are smaller than those for air conditions: the reduced rotating speeds of R245fa are 0.4-fold of those of air, and the reduced mass flow rates of R245fa are twice as many as those of air.
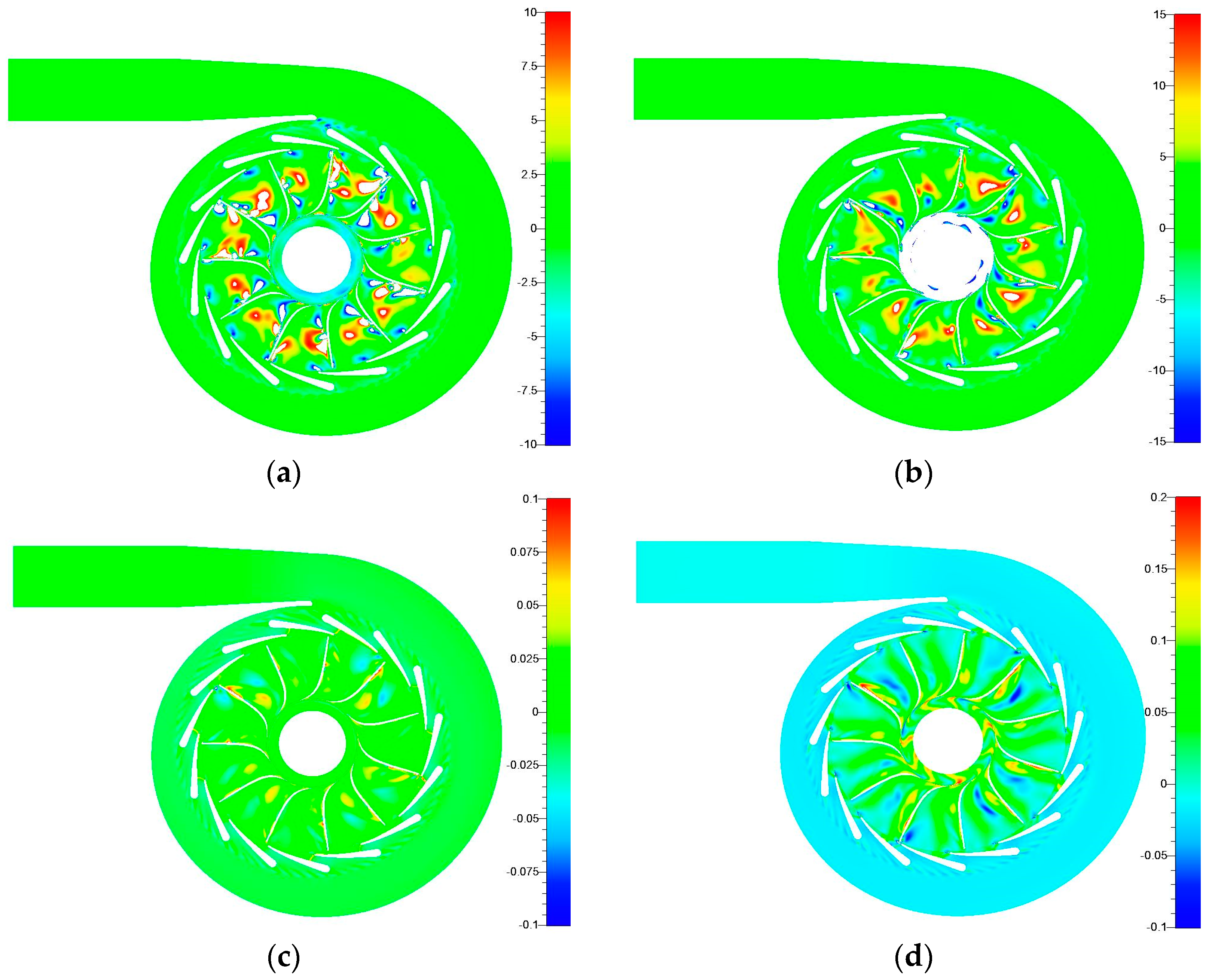
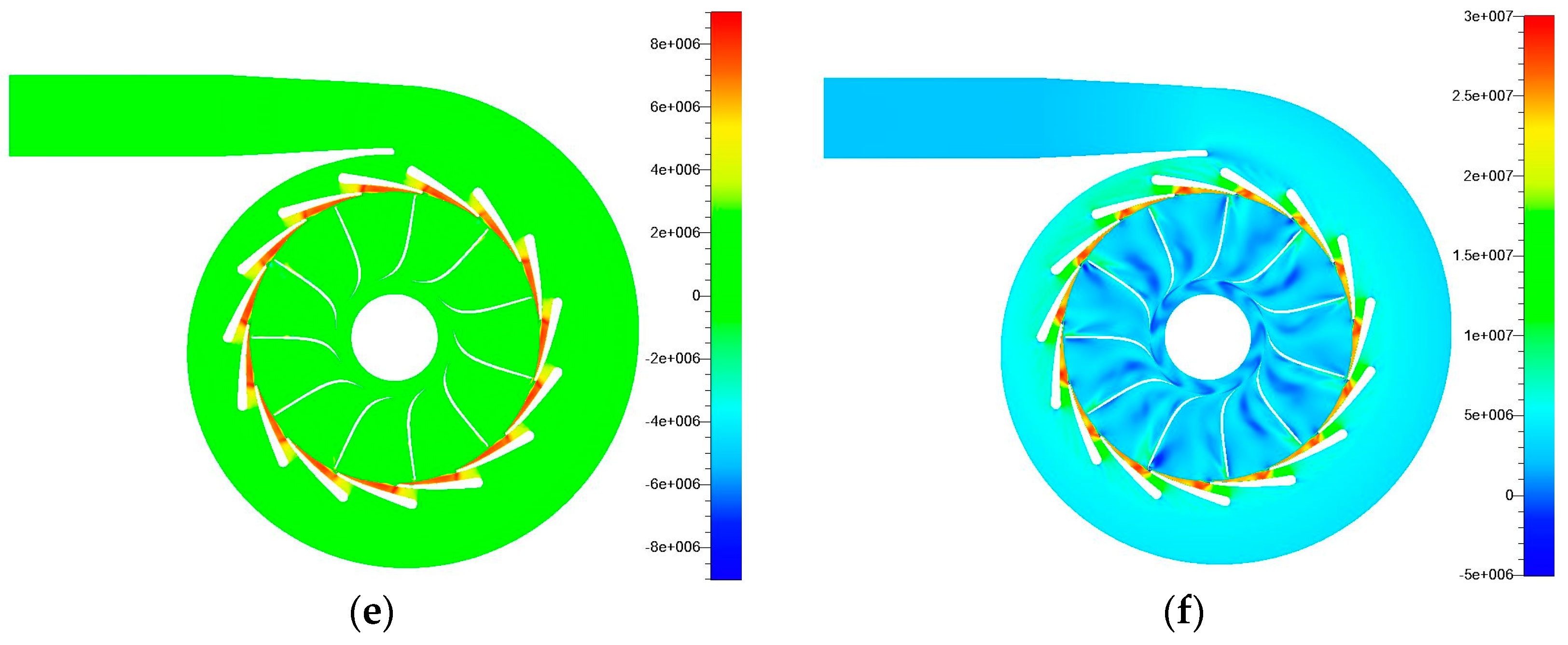
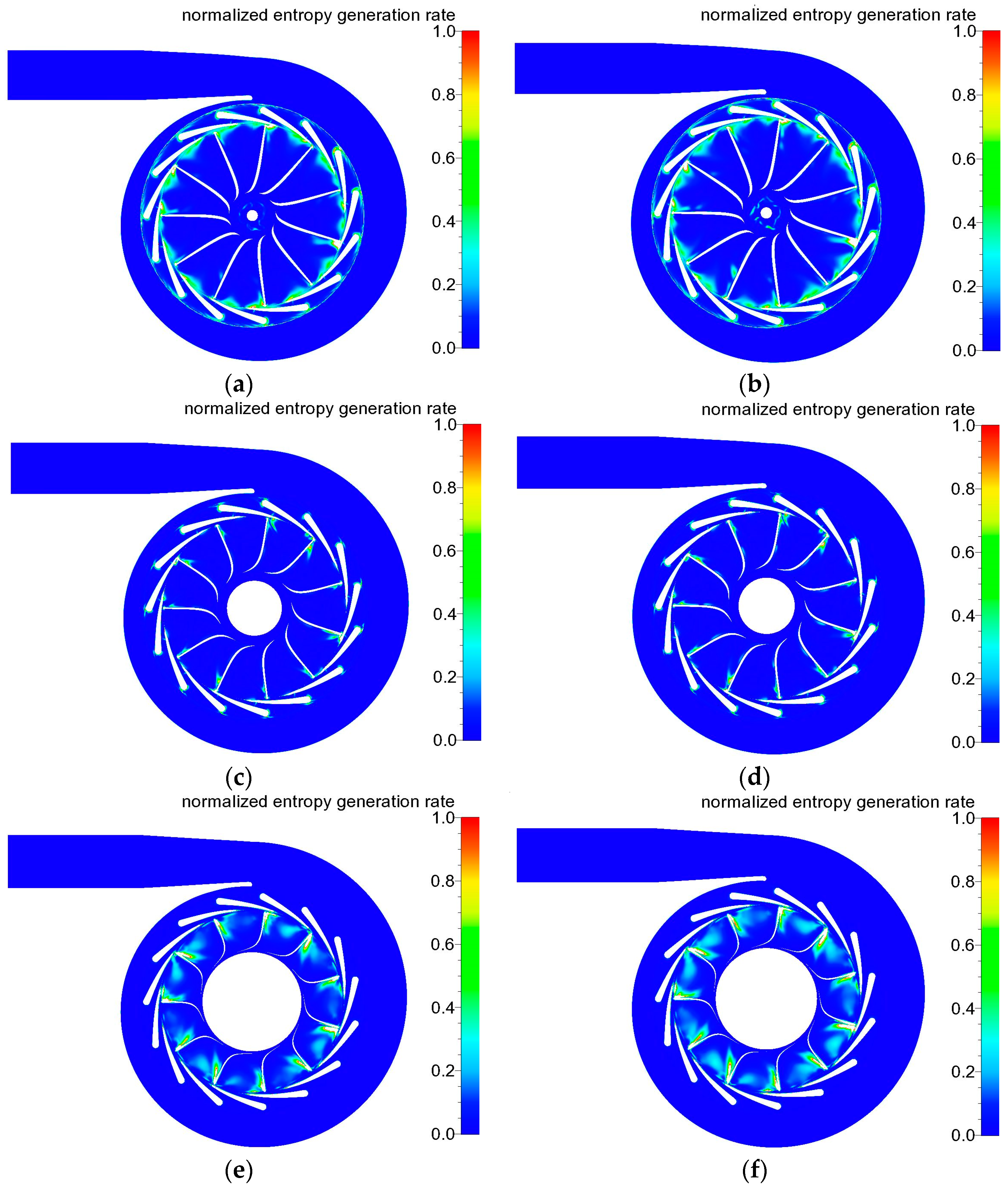
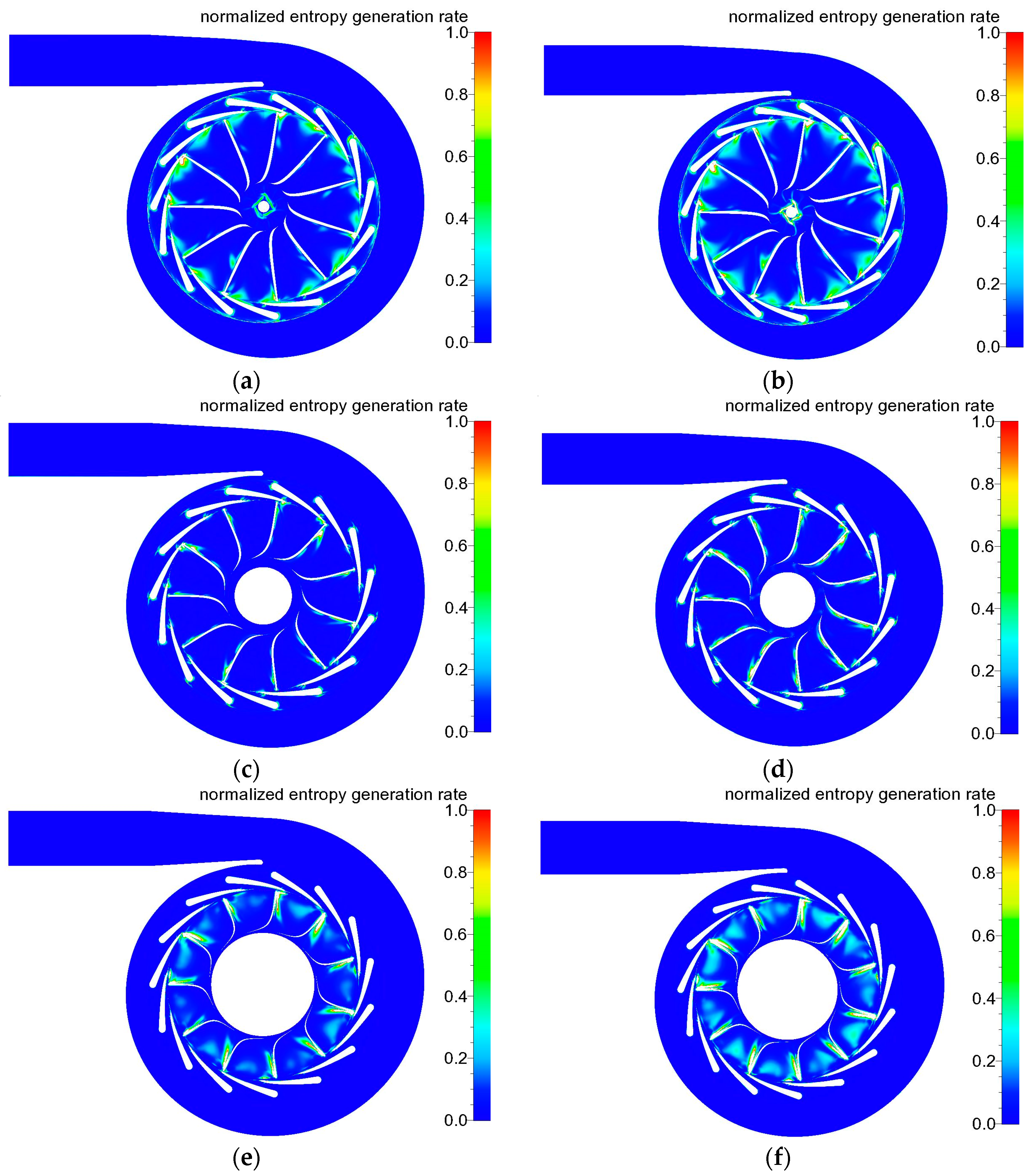
Turbine total-to-static isentropic efficiencies in the velocity ratio from 0.5 to 0.9 are more than 70% no matter using R245fa or air as the working fluid. Entropy generation rate per unit volume is introduced as the indicator to analysis the loss mechanisms. Six losses dominate the turbine efficiency decreasing: flow separation on the nozzle vane suction surface near the leading edge, shock wave loss in the throat of nozzle passage, symmetric detached vortex loss after the nozzle vane trailing edge, local incidence loss near the rotor hub surface, boundary layer separation vortex loss on the blade suction surface in the rotor passage, and tip leakage loss near the rotor shroud surface.
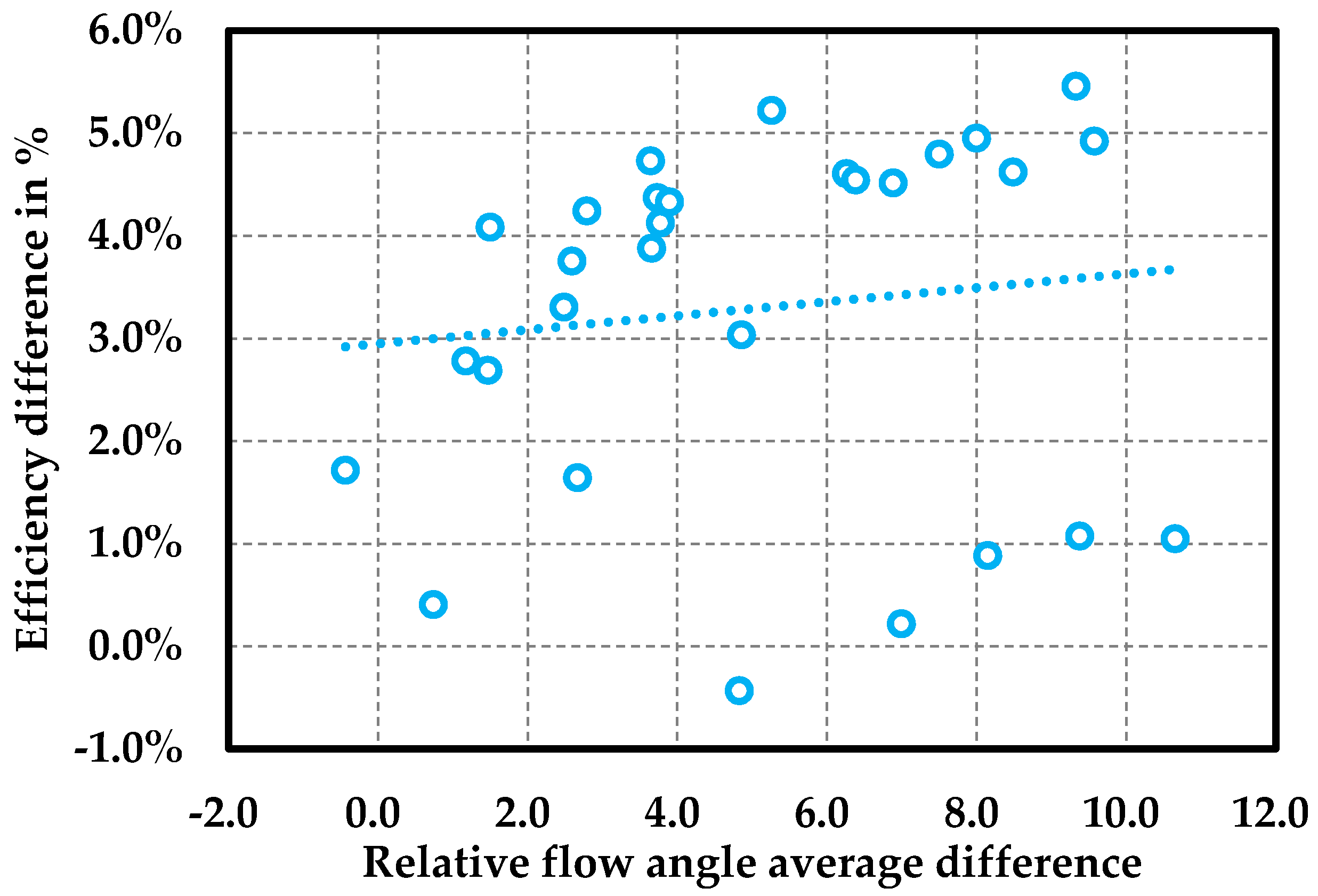
The nozzle throat shock wave and rotor passage separation vortex loss comparison between R245fa and air are analyzed deeply. The maximum absolute Mach numbers in the nozzle for R245fa are smaller than those for air, leading to about 1% of total pressure loss coefficient decrease. However, the rotor passage separation vortex for R245fa is larger, which eventually decreases the turbine isentropic efficiency. In general, the air turbine efficiencies are 3%–4% larger than those of the R245fa turbine in the velocity ratio between 0.5 and 0.9.
In the future, turbine rotor blades optimization based on the organic working fluid properties will be discussed in detail to decrease the rotor passage separation vortex and improve the organic fluid radial turbine efficiencies.