Abstract
This research focuses on entropy generation rate per unit volume in magneto-hydrodynamic (MHD) mixed convection boundary layer flow of a viscous fluid over an inclined stretching sheet. Analysis has been performed in the presence of viscous dissipation and non-isothermal boundary conditions. The governing boundary layer equations are transformed into ordinary differential equations by an appropriate similarity transformation. The transformed coupled nonlinear ordinary differential equations are then solved numerically by a shooting technique along with the Runge-Kutta method. Expressions for entropy generation (Ns) and Bejan number (Be) in the form of dimensionless variables are also obtained. Impact of various physical parameters on the quantities of interest is seen.
1. Introduction
Hydromagnetic (MHD) boundary layer flow over a stretching surface has vital importance because of its ever-increasing usage in industrial applications such as the production of paper, glassware, cable coatings, fabrication of adhesive tapes, artificial fibers, metal spinning, roofing shingles, fine-fiber mats, and metallic plates to mention a few among others. In all such technological processes, the kinematics of stretching and heat transfer have a significant impact in the improvement of final product quality through control of the rate of cooling. Boundary layer flow over a moving continuous flat surface was studied for the first time by Sakiadis [1]. Crane [2] obtained the closed form similarity solution of the boundary layer flow over a linear stretching sheet. After the work of Crane [2], several researchers revisited this problem addressing different aspects. Here we mention some very recent studies [3,4,5,6,7,8,9,10,11,12,13,14,15] for the convenience of readers. All these studies have been restricted to the situations in which flow is induced by horizontally/vertically stretching sheet. Haung et al. [16] investigated the heat transfer analysis in the boundary layer flow of a viscous fluid caused by an inclined stretching sheet. Qasim et al. [17] studied the effects of thermal radiation on mixed convection flow of viscoelastic fluid along an inclined sheet. Sravanthi [18] studied the MHD slip flow over an exponentially stretching inclined sheet by taking into account the Soret-Dufour effects. MHD boundary layer flow over an inclined stretching sheet under the effects of mixed convection, heat generation/absorption and blowing/suction was reported by Eldahad and Aziz [19].
In all the above investigations, the objective was to understand the flow behavior, i.e., to find the velocity profile and temperature distribution (first law analysis) in the boundary layer region. Moreover, to understand the energy losses during the boundary layer flow, it makes sense to perform a second law analysis. The losses of energy in the system during the process are proportional to the entropy generation. Entropy production is the measure of irreversibility in the heat transfer problems. The study of entropy generation within the system is important as it helps to trace the sources which destroy available energy. Therefore, by knowing these factors or sources one can minimize the entropy in order to retain the quality of energy, which is commonly referred to as entropy generation minimization (EMG). At present the research topic of entropy generation minimization has acquired special status amongst scientists worldwide who are re-examining all energy consuming, converting and producing systems and developing new techniques in order to remove all sources that destroy the available work. Bejan [20,21,22] calculated for the first time the volumetric entropy generation rate in a fluid flow process. After the seminal work of Bejan, many researchers have performed thermodynamic analysis of flows and heat transfers in order to minimize entropy production [23,24,25,26,27,28,29,30].
Despite the many studies on the second law analysis of boundary layer flows, the entropy generation analysis of a boundary layer flow over an inclined impermeable stretching sheet under the effects of magnetic field and viscous dissipation has not been reported in the literature. Motivated by the abovementioned facts, the present research has been undertaken to perform an irreversibility analysis of MHD mixed convection flow over an inclined stretching sheet.
2. Mathematical Formulation of the Problem
Consider the steady two dimensional boundary layer flow induced by the inclined stretching sheet having the linear stretching velocity uw(x) = cx. A magnetic field Bo is applied normally to the stretching sheet. Figure 1 shows the physical model and coordinates system. For boundary layer flow the continuity, momentum and energy equations take the following forms:
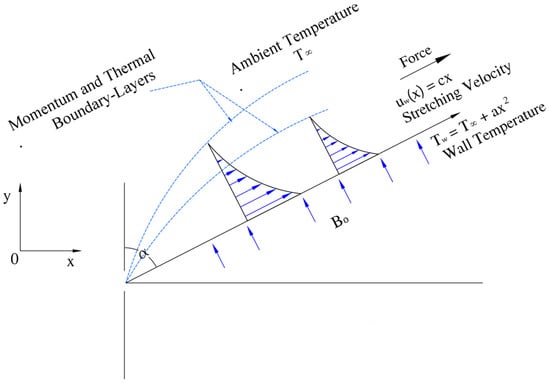
Figure 1.
Physical flow model and coordinatate system.
In the above equations, u and v represent velocity components in the directions of the x and y axes, T∞ shows the free stream temperature, g denotes gravitational acceleration, α* is the thermal diffusivity, ρ is the density of the fluid, v is the kinematic viscosity of the fluid, Bo depicts the imposed magnetic field, Cp represents the specific heat of the fluid at constant pressure, α is the inclination of the stretching sheet and β represents the thermal coefficient. Here we consider the thermal expansion coefficient β = mx–1 [31,32] and the surface temperature of the stretching sheet of the form Tw(x) = T∞ + ax2 [33,34,35] in order to have a self-similarity equation.
The relevant boundary conditions are:
in which Tw and uw respectively represent the temperature and velocity of the stretching boundary.
We look for a solution through the following transformation:
Incompressibility condition (1) is now automatically satisfied, whereas the other equations lead to the following expressions:
The dimensionless numbers appearing in Equations (7) and (8) are:
While the boundary conditions, Equations (4) and (5) take the following form:
The skin friction coefficient Cf and the Nusselt number Nux which are defined as:
where τw is the shear stress and qw is the heat flux and k is the thermal conductivity. Using variables (6), we obtain:
3. Irreversibility Analysis
In the presence of magnetic field, the entropy generation rate per unit volume is given by:
In the above equation Φ represents the viscous dissipation function, J is the current density and is the Del operator. In the present article it is supposed that the magnitude of QV is negligible compared to the electric current density J and the electric force E has no significant effects as compared to the magnetic force V × B. By taking these approximations and the Prandtl boundary layer approximation as well Equation (14) reduces to:
It is clearly seen from the above equation that there are three sources of entropy generation. The first source is the heat transfer which is due the presence of a temperature gradient in the problem, the second source is the viscous dissipation, which is due to the fluid friction, and the last source is the magnetic field which cause Joule dissipation irreversibility. The entropy generation number is the dimensionless form of volumetric entropy generation rate, which represent the ratio between volumetric entropy generation rate ( and characteristic entropy generation ( Using Equation (6) the entropy generation given in Equation (15) reduces to:
where and represent the characteristic entropy generation and dimensionless temperature parameter, respectively.
In many engineering problems engineers need to measure the relative importance of the sources of entropy generation, and for this important measurement the Bejan number is defined as:
By using similarity variables Be takes the following form:
4. Results and Discussion
In this section our concern is to analyse the effects of important physical parameters on the quantities of interest. Therefore Figure 2, Figure 3, Figure 4 and Figure 5 have been plotted.
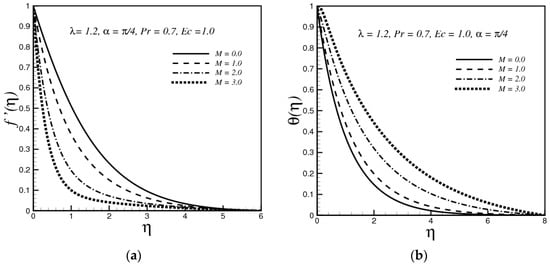
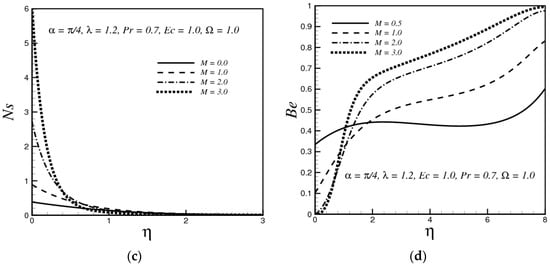
Figure 2.
(a) Variation of f’(η) with M; (b) variation of θ(η) with M; (c) variation of Ns with M; (d) variation of Be with M.
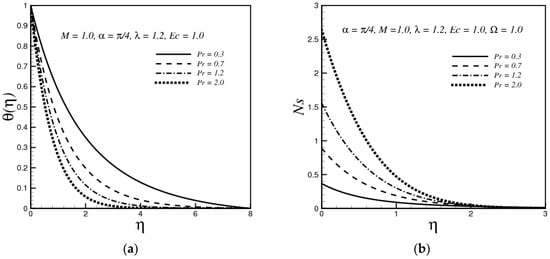
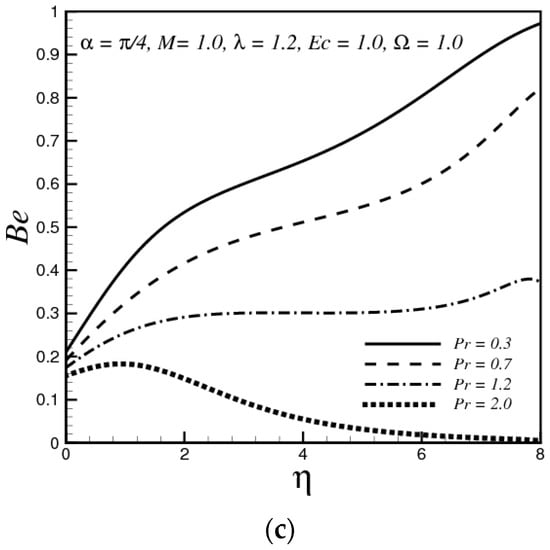
Figure 3.
(a) Variation of θ(η) with Pr; (b) Variation of Ns with Pr; (c) Variation of Be with Pr.
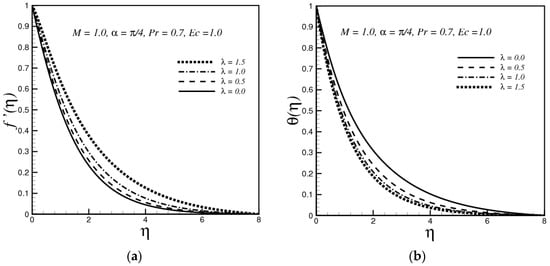
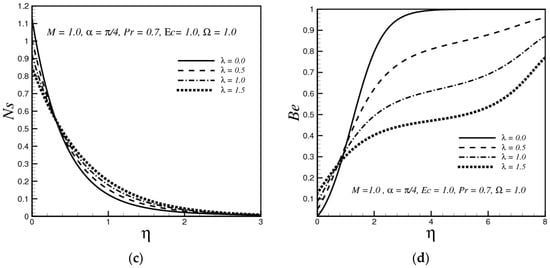
Figure 4.
(a) Variation of f’(η) with λ; (b) Variation of θ(η) with λ; (c) Variation of Ns with λ; (d) Variation of Be with λ.
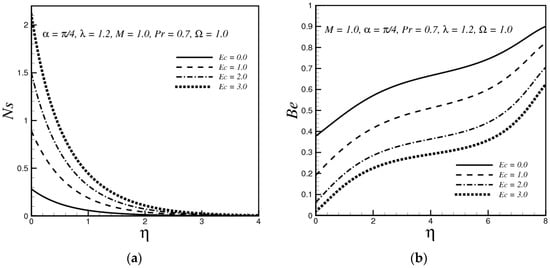
Figure 5.
(a) Variation of Ns with Ec; (b) Variation of Be with Ec.
4.1. Effects of the Magnetic Field Parameter
Figure 2a displays the impact of the magnetic field parameter M on the velocity profile. It is seen that the velocity decreases by increasing M. This is happening because the applied transverse magnetic field generates a Lorentz force, which decelerates the fluid velocity. Figure 2b displays the effect of M on the fluid temperature. It is seen that temperature rises with rising values of M. Physically, the presence of M sets up a retarding force (Lorentz force), which boosts the fluid friction and this fluid friction is responsible for the rise of temperature. Figure 2c presents the variation of entropy generation number for changing values of M. It is observed that Ns is increasing as a function of M which is due to the resistive nature of the magnetic force, so we can achieve the main goal of the second law of thermodynamics that is the minimization of entropy generation by reducing the magnetic field. Figure 2d demonstrates the variation of Bejan number Be with an increase in M, where it is observed that Be decreases as M increases. The graph depicts that with an increasing value of M, viscosity and magnetic irreversibility dominate the heat transfer irreversibility at the surface of the stretching sheet. The magnetic and viscosity irreversibility completely rule the thermal irreversibility for large values of M (M > 2) at the surface. However, far away from the stretching sheet the dominancy effects are reversed.
4.2. Effects of the Prandtl Number
The impact of Prandtl number Pr on the fluid temperature is depicted in Figure 3a. The graph depicts that the temperature decreases with large values of the Pr number. Physically, a fluid with high Pr has low thermal diffusivity, which in turn reduces the temperature of the fluid. Figure 3b reveals that the dimensionless entropy generation Ns increases with the increasing value of Pr. This happens because with an increase in Pr increases the temperature gradients in the boundary layer, which in turn increases the Ns. Figure 3c demonstrates the influence of Pr on the Bejan number. The plot shows that for a fixed value of η the Bejan number decreases when Pr increases. It is also clear that near the surface of the stretching sheet, Be is close to zero, which means that the magnetic field intensity and fluid friction both play more important roles in the total entropy generation. Further, it is observed that far away from the stretching surface, the heat transfer contribution in the total entropy plays a substantial part.
4.3. Effects of the Mixed Convective Parameter
Figure 4a illustrates the effect of the mixed convection parameter λ on velocity. It is anticipated that velocity increases by increasing the mixed convection parameter λ. Physically with an increase in λ the buoyancy force increases, which results in an enhancement of the velocity profile. Figure 4b shows the effect of the buoyancy parameter on the temperature profile. It is seen that the thermal convective parameter decreases the temperature of the fluid. Figure 4c represents the variation of entropy generation number Ns versus different values of λ. Ns decreases near the boundary when λ increases and goes to zero asymptotically as we move away from the boundary. Figure 4d displays the effect of buoyancy parameter on the Bejan number. Be increases with the increasing value of λ. Also, the contribution of fluid friction and magnetic field in the entropy generation dominate the heat transfer effect at the surface. Further, it is perceived that far away from the boundary the effective source of the production of entropy is the conductive irreversibility.
4.4. Effects of Eckert Number
Figure 5a shows that Ns increases with the increasing value of Ec, so by decreasing the Eckert number Ec one can achieve the main objective of the second law of thermodynamics, the minimization of entropy production rate per unit volume. The effect of increasing the Ec on the entropy production is prominent near the surface of the stretching sheet, while it has no significant effect in the main flow region. The effect of Ec on Be is plotted in Figure 5b. It is observed that an increase in Ec decreases the Bejan number Be. On the surface of the stretching sheet the effects of magnetic and viscous irreversibility dominate the conductive irreversibility, whereas far away from the stretching sheet the contribution of heat transfer in the generation of entropy is prominent.
4.5. Effects of the Dimensionless Temperature Parameter
The variation of Ns with the increasing value of the dimensionless temperature parameter is portrayed in Figure 6a. This figure shows that Ns increases with the increasing value of Ω. It is verified that Ns asymptotically goes to zero as we move away from the boundary. Figure 6b shows the variation of Be with different values of Ω. It is clearly seen that near the stretching sheet the fluid friction and magnetic field irreversibility dominate. It is also observed that with increasing value of Ω the Be decreases and for small values of Ω the effect due to heat transfer dominates far away from the stretching sheet.
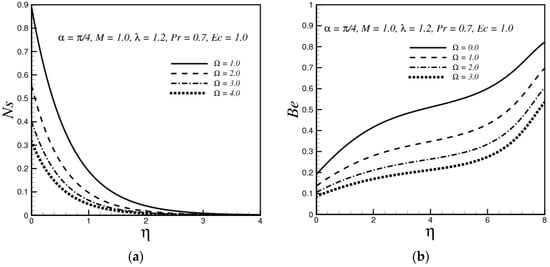
Figure 6.
(a) Variation of Ns with Ω; (b) Variation of Be with Ω.
5. Conclusions
The main conclusions of the present study are:
- (1)
- It is observed that the velocity magnetic parameter M has a decreasing effect on the velocity while the thermal convective parameter λ has an increasing effect on it.
- (2)
- The thickness of the thermal boundary layer increases as the values of magnetic parameter and Eckert number increase, while a decreasing effect has been observed with the variation of thermal convective parameter and Prandtl number.
- (3)
- Increasing in magnetic parameter and Eckert number enhance the entropy generation while entropy generation decreases with the increasing values of the thermal convective parameter and dimensionless temperature function.
- (4)
- The Bejan number decreases by increasing the magnetic parameter, thermal convective parameter and it is decreased by increasing the Prandtl number and Eckert number.
- (5)
- The values of skin friction coefficient and local Nusselt number increases with the increase of Pr. There is a decrease in local Nusselt number for large values of M and Ec (see Table 1).
 Table 1. Numerical values for skin friction coefficient and local Nusselt number.
Table 1. Numerical values for skin friction coefficient and local Nusselt number.
Acknowledgments
The authors, acknowledge with thanks the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah for technical and financial support.
Author Contributions
Muhammad Idrees Afridi and Muhammad Qasim formulated the problem. Muhammad Idrees Afridi, Muhammad Qasim, Ilyas Khan and Sharidan Shafie solved the problem. Ali Saleh Alshomrani computed the results. All the authors equally contributed in writing and proof reading the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | positive constant |
| Bo | applied constant magnetic field |
| Be | Bejan number |
| c | stretching velocity rate |
| Cp | specific heat at constant pressure |
| Ec | Eckert number |
| g | acceleration due to gravity |
| Grx | local Grashof number |
| J | electric current density |
| k | thermal conductivity of the fluid |
| M | magnetic field parameter |
| Ns | entropy generation number |
| Pr | Prandtl number |
| Rex | local Reynolds number |
| Ṡgen''' | volumetric entropy generation rate |
| Ṡo''' | characteristic volumetric entropy generation rate |
| T | temperature of the fluid |
| Tw(x) | wall temperature |
| T∞ | ambient temperature |
| u | velocity component in x direction |
| uw(x) | velocity of the stretching surface |
| v | velocity component in y direction |
| x, y | Cartessian coordinates along the surface and normal to it respectively |
Greeks Symbols
| α | inclination of the stretching sheet with y-axis |
| α* | thermal diffusitivity |
| β | coefficient of thermal expansion |
| η | similarity variable |
| θ | dimensionless temperature |
| μ | dynamic viscosity |
| ν | kinematic viscosity |
| ρ | density of the fluid |
| σ | electric conductivity |
| λ | mixed convection parameter/buoyancy parameter |
| Ω | dimensionless temperature parameter |
References
- Sakiadis, B.C. Boundary-layer behaviour on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Salleh, M.Z.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. J. Taiwan Inst. Chem. E. 2010, 41, 651–655. [Google Scholar] [CrossRef]
- Hsiao, K.L. MHD mixed convection of viscoelastic fluid over a stretching sheet with ohmic dissipation. J. Mech. 2008, 24, 29–34. [Google Scholar] [CrossRef]
- Hsiao, K.L. MHD stagnation point viscoelastic fluid flow and heat transfer on a thermal forming stretching sheet with viscous dissipation. Can. J. Chem. Eng. 2011, 89, 1228–1235. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 2013, 62, 526–533. [Google Scholar] [CrossRef]
- Qasim, M.; Noreen, S. Heat transfer in the boundary layer flow of a Casson fluid over a permeable shrinking sheet with viscous dissipation. Eur. Phys. J. Plus 2014, 129, 1–7. [Google Scholar] [CrossRef]
- Hsiao, K.L. Heat and mass mixed convection for MHD viscoelastic fluid past a stretching sheet with ohmic dissipation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1803–1812. [Google Scholar] [CrossRef]
- Mehmood, R.; Nadeem, S.; Akbar, N.S. Oblique stagnation flow of Jeffery fluid over a stretching convective surface: Optimal solution. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 454–471. [Google Scholar] [CrossRef]
- Makinde, O.D.; Mabood, F.; Khan, W.A.; Tshehla, M.S. MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J. Mol. Liq. 2016, 219, 624–630. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Mohamed, M.K.A.; Salleh, M.Z.; Ishak, A.; Pop, I. Stagnation point flow and heat transfer over a stretching/shrinking sheet in a viscoelastic fluid with convective boundary condition and partial slip velocity. Eur. Phys. J. Plus 2015, 130, 1–9. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. J. Magn. Magn. Mater. 2016, 407, 235–240. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Lee, C. MHD boundary layer flow over an unsteady shrinking sheet: Analytical and numerical approach. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 1339–1346. [Google Scholar] [CrossRef]
- Qasim, M.; Hayat, T.; Hendi, A.A. Effects of slip conditions on stretching flow with ohmic dissipation and thermal radiation. Heat Tran. Asian Res. 2011, 40, 641–654. [Google Scholar] [CrossRef]
- Huang, J.S.; Tsai, R.; Haung, K.H.; Haung, C.H. Thermal-diffusion and diffusion-thermo effects on natural convection along an inclined stretching surface in a porous medium with chemical reaction. Chem. Eng. Commun. 2011, 198, 453–461. [Google Scholar] [CrossRef]
- Qasim, M.; Hayat, T.; Obaidat, S. Radiation effect on the mixed convection flow of a viscoelastic fluid along an inclined stretching sheet. Z. Naturforsch. A 2012, 67, 195–202. [Google Scholar] [CrossRef]
- Sravanthi, C.S. Homotopy analysis solution of MHD slip flow past an exponentially stretching inclined sheet with Soret-Dufour effects. J. Niger. Math. Soc. 2016, 35, 208–266. [Google Scholar] [CrossRef]
- Eldahab, E.M.A.; Aziz, M.A.E. Blowing/Suction effect on hydromagnetic heat transfer by mixed convection from an inclined continuously stretching surface with internal heat generation/absorption. Int. J. Therm. Sci. 2004, 43, 709–719. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Bejan, A.; Kestin, J. Entropy generation through heat and fluid flow. J. Appl. Mech. 1983, 50, 475. [Google Scholar] [CrossRef]
- Makinde, O.D. Entropy generation in a liquid film falling along an inclined porous heated plate. Mech. Res. Commun. 2006, 33, 692–698. [Google Scholar] [CrossRef]
- Arikodlu, A.; Ozkol, I.; Komurgoz, G. Effects of slip on entropy generation in a single rotating disk in MHD flow. Appl. Energy 2008, 85, 1225–1236. [Google Scholar] [CrossRef]
- Tamayol, A.; Hooman, K.; Bahrami, M. Thermal analysis of flow in a porous medium over a permeable stretching wall. Transp. Porous Med. 2010, 85, 661–676. [Google Scholar] [CrossRef]
- Reveillere, A.; Baytas, A.C. Minimum entropy generation for laminar boundary layer flow over a permeable plate. Int. J. Exergy 2010, 7, 164–177. [Google Scholar] [CrossRef]
- Makinde, O.D.; Eegunjobi, A.S.; Tshehla, M.S. Thermodynamics analysis of variable viscosity hydromagnetic Couette flow in a rotating system with Hall effects. Entropy 2015, 17, 7811–7826. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Entropy analysis of nanofluid flow over a convectively heated radially stretching disk embedded in a porous medium. J. Nanofluids 2016, 5, 48–58. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy effects in hydromagnetic free convection flow past a vertical plate embedded in a porous medium in the presence of thermal radiation. Eur. J. Phys. Plus 2013, 128, 1–15. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy analysis of magneto hydrodynamic flow and heat transfer due to a stretching cylinder. J. Taiwan Inst. Chem. Eng. 2014, 45, 780–786. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Analysis of entropy generation effects in flow and heat transfer of viscous fluid through a porous medium between two radially stretching surfaces. Int. J. Exergy 2015, 18, 501–520. [Google Scholar] [CrossRef]
- Makinde, O.D.; Olanrewaju, P.O. Buoyancy effects on thermal boundary layer over a vertical late with a convective surface boundary conditions. J. Fluids Eng. 2010, 132, 1–4. [Google Scholar] [CrossRef]
- Makinde, O.D. Similarity solution for natural convection from a moving vertical plate with internal heat generation and a convective boundary condition. Therm. Sci. 2011, 15, 137–143. [Google Scholar]
- Mushtaq, M.; Asghar, S.; Hossain, M.A. Mixed convection flow of second grade fluid along a vertical stretching flat surface with variable surface temperature. Heat Mass Transf. 2007, 43, 1049–1061. [Google Scholar] [CrossRef]
- Vyas, P.; Srivastava, N. On dissipative radiactive MHD boundary layer flow in a porous medium over a non-isothermal stretching sheet. J. Appl. Fluid Mech. 2012, 5, 23–31. [Google Scholar]
- Abel, M.S.; Begum, G. Heat transfer in MHD viscoelastic fluid flow on stretching sheet with heat source/sink, viscous dissipation, stress work, and radiation for the case of large Prandtl number. Chem. Eng. Commun. 2008, 195, 1503–1523. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).