Perturbative Treatment of the Non-Linear q-Schrödinger and q-Klein–Gordon Equations
Abstract
:1. Introduction
Motivation
2. First Order Expansion of the q Exponential as a Solution of the Non-Linear NRT q-Schrödinger Equation
2.1. First Order Expansion of
2.2. Solution to the Non-Linear q-Schrödinger Equation
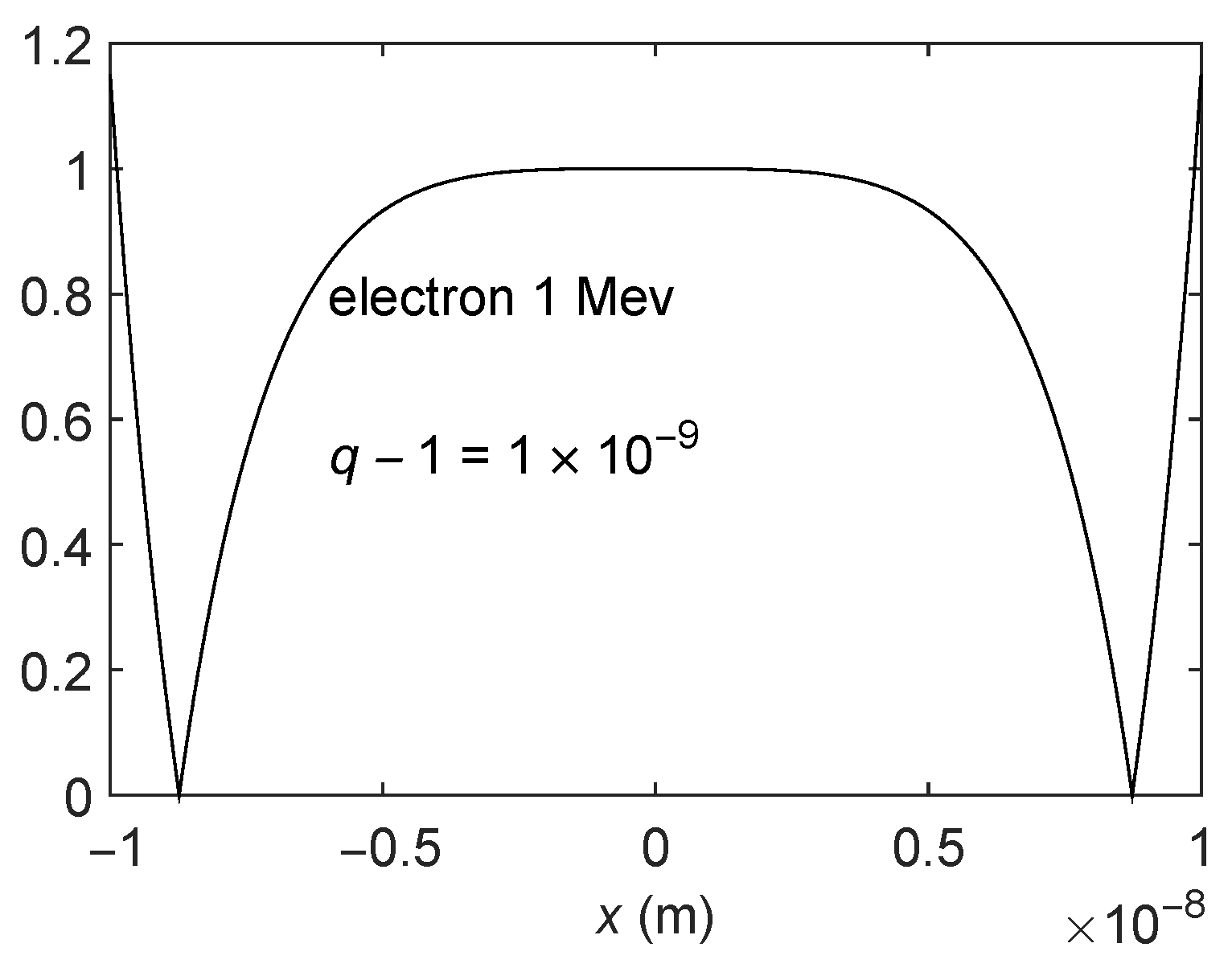
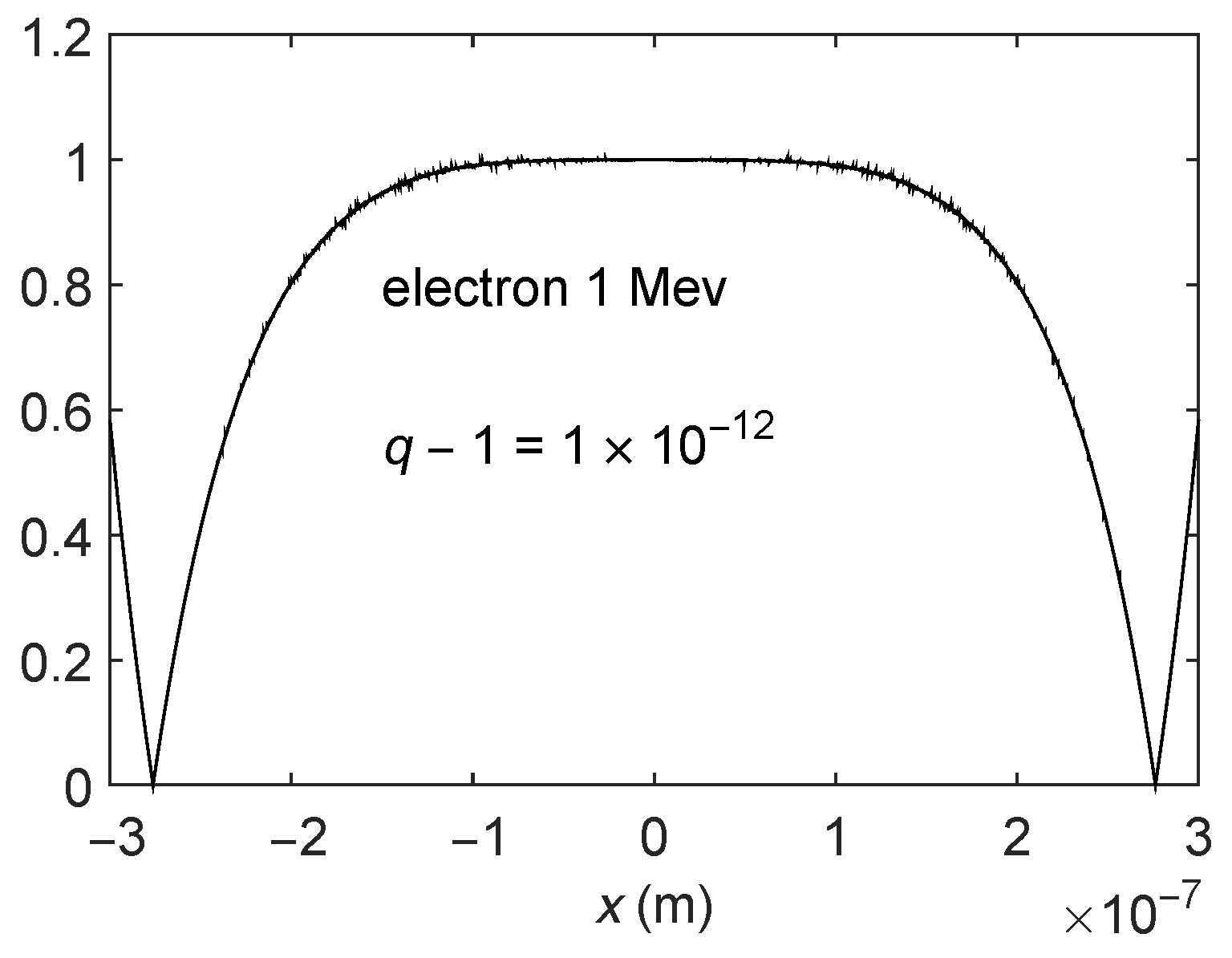
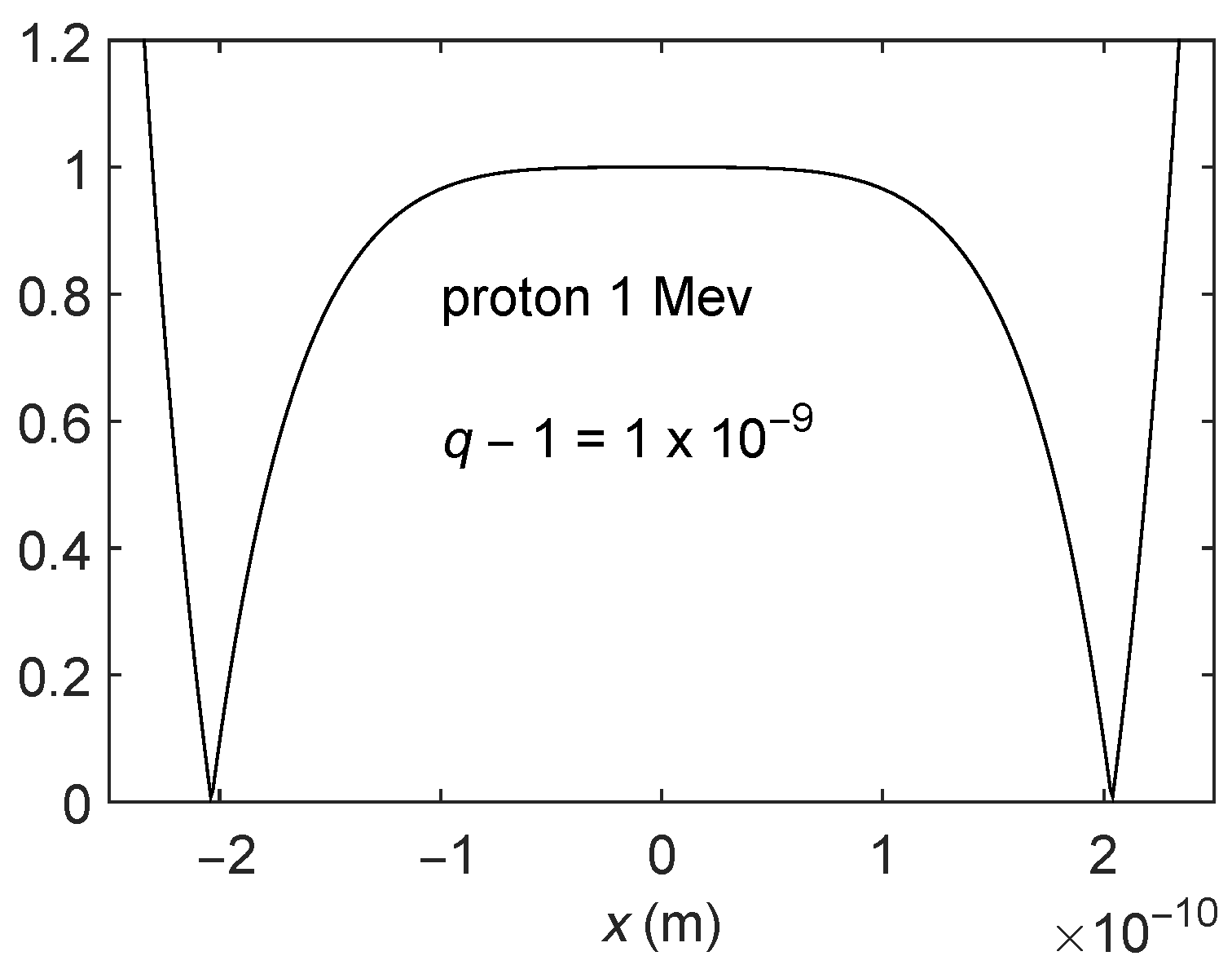
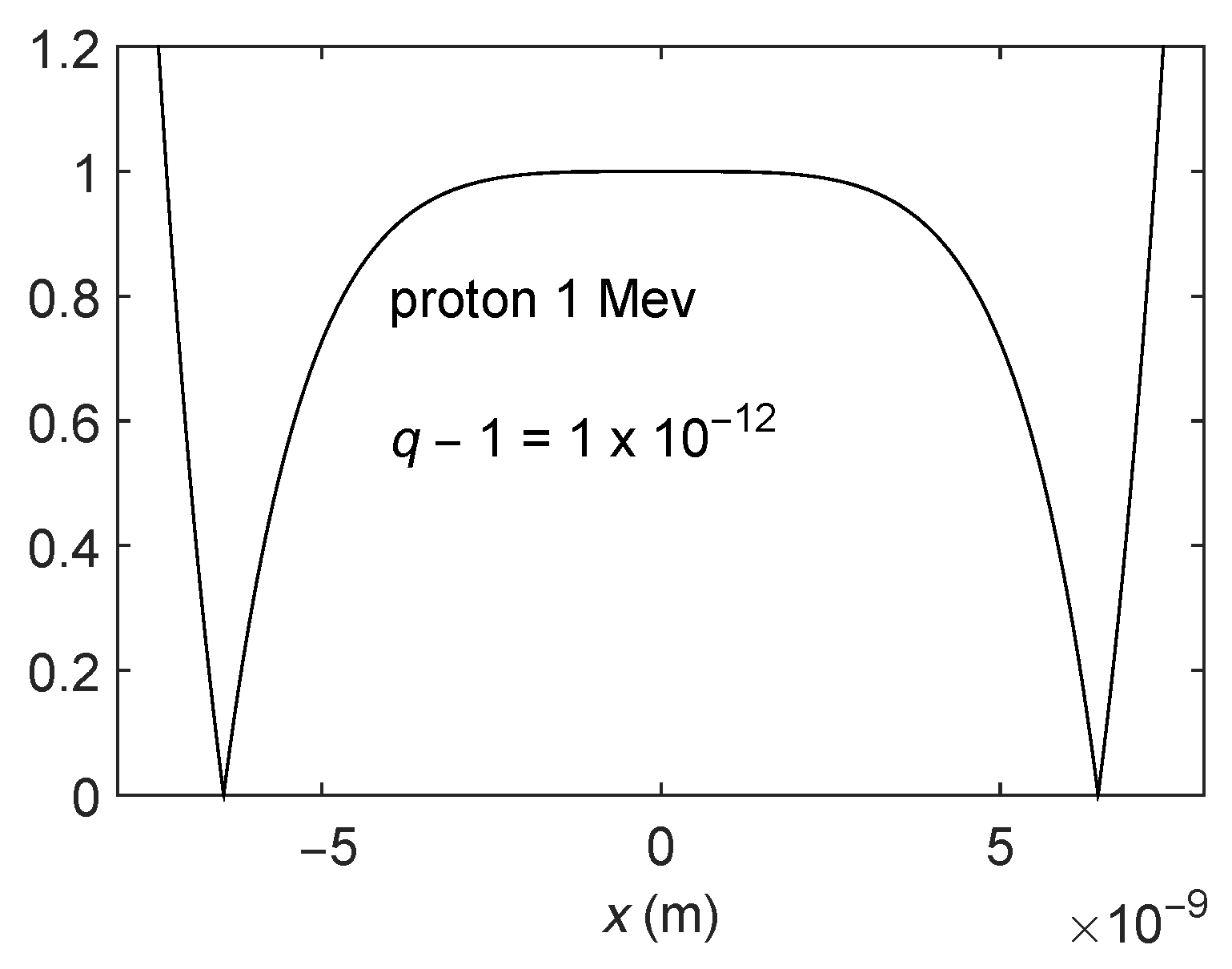
2.3. Comparison between the Exact and Approximate Solutions
3. First Order Treatment of a q-Gaussian
Comparison between the Exact and Approximate Solutions
4. Non-Linear q-Klein–Gordon Equation
Solution to the Klein–Gordon Equation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. First Order Expansion of ψ = eq
Appendix A.2. Second Derivative with Respect to x
Appendix B
Appendix B.1. Second Derivative with Respect to t
Appendix B.2. First Order Expansion of qF2q-1
References
- Boccara, N. Modeling Complex Systems; Springer: Berlin, Germany, 2004. [Google Scholar]
- Vignat, C.; Plastino, A. Why is the detection of q-Gaussian behavior such a common occurrence? Physica A 2009, 388, 601–608. [Google Scholar] [CrossRef]
- Plastino, A.; Rocca, M.C. From the hypergeometric differential equation to a non-linear Schroedinger one. Phys. Lett. A 2015, 379, 2690. [Google Scholar] [CrossRef]
- Nobre, F.D.; Rego-Monteiro, M.A.; Tsallis, C. Nonlinear generalizations of relativistic and quantum equations with a common type of solution. Phys. Rev. Lett. 2011, 106, 140601. [Google Scholar] [CrossRef] [PubMed]
- Plastino, A.R.; Souza, A.M.C.; Nobre, F.D.; Tsallis, C. Stationary and uniformly accelerated states in non-linear quantum mechanics. Phys. Rev. A 2014, 90, 062134. [Google Scholar] [CrossRef]
- Plastino, A.R.; Tsallis, C. Nonlinear Schroedinger equation in the presence of uniform acceleration. J. Math. Phys. 2013, 54, 041505. [Google Scholar] [CrossRef]
- Bountis, T.; Nobre, F.D. Travelling-wave and separated variable solutions of a nonlinear Schroedinger equation. J. Math. Phys. 2016, 57, 082106. [Google Scholar] [CrossRef]
- Plastino, A.; Rocca, M.C. q-Gamow States as continuous linear functionals on analytical test functions. Nucl. Phys. A 2016, 948, 19–27. [Google Scholar] [CrossRef]
- Plastino, A.; Rocca, M.C.; Ferri, G.L.; Zamora, D.J. q-Gamow States for intermediate energies. Nuc. Phys. A 2016, 955, 16–26. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Plastino, A.; Rocca, M.C. Hypergeometric connotations of quantum equations. Physica A 2016, 450, 435–443. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamora, J.; Rocca, M.C.; Plastino, A.; Ferri, G.L. Perturbative Treatment of the Non-Linear q-Schrödinger and q-Klein–Gordon Equations. Entropy 2017, 19, 21. https://doi.org/10.3390/e19010021
Zamora J, Rocca MC, Plastino A, Ferri GL. Perturbative Treatment of the Non-Linear q-Schrödinger and q-Klein–Gordon Equations. Entropy. 2017; 19(1):21. https://doi.org/10.3390/e19010021
Chicago/Turabian StyleZamora, Javier, Mario C. Rocca, Angelo Plastino, and Gustavo L. Ferri. 2017. "Perturbative Treatment of the Non-Linear q-Schrödinger and q-Klein–Gordon Equations" Entropy 19, no. 1: 21. https://doi.org/10.3390/e19010021
APA StyleZamora, J., Rocca, M. C., Plastino, A., & Ferri, G. L. (2017). Perturbative Treatment of the Non-Linear q-Schrödinger and q-Klein–Gordon Equations. Entropy, 19(1), 21. https://doi.org/10.3390/e19010021






