One-Parameter Fisher–Rényi Complexity: Notion and Hydrogenic Applications
Abstract
:1. Introduction
2. One-Parameter Fisher–Rényi Complexity Measure
2.1. The Notion
2.2. The Properties
2.2.1. Lower Bound
2.2.2. Invariance under Scaling and Translation Transformations
2.2.3. Monotonicity
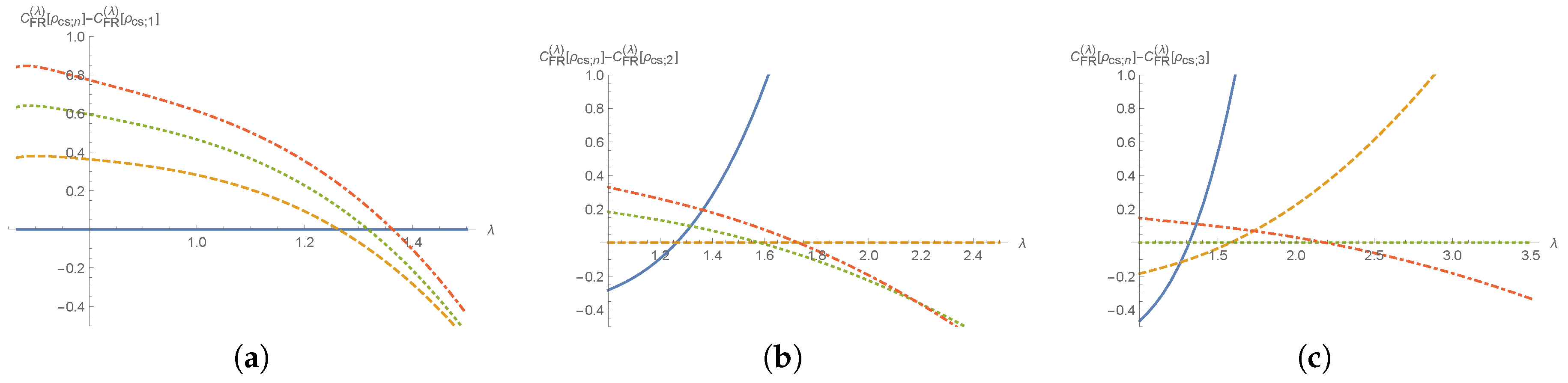
2.2.4. Behavior under Replications
2.2.5. Near-Continuity Behavior
3. The Hydrogenic Application
3.1. Generalized Fisher–Rényi Complexity of Hydrogenic States
3.2. Generalized Fisher–Rényi Complexity of Hydrogenic Circular States
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Calculation of the Fisher and Rényi-like Hydrogenic Integrals
Appendix B. Calculation of
References
- Gell-Mann, M. What is complexity? Complexity 1995, 1, 1–9. [Google Scholar]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Badii, R.; Politi, A. Complexity: Hierarchical Structure and Scaling in Physics; Henry Holt & CO.: New York, NY, USA, 1997. [Google Scholar]
- Gregersen, N.H. From Complexity to Life: On the Emergence of Life and Meaning; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Gell-Mann, M.; Lloyd, S. Effective complexity. In Nonextensive Entropy: Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: Oxford, UK, 2004; pp. 387–398. [Google Scholar]
- Frieden, B.R. Science from Fisher Information; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zuchowski, L.C. Disentangling Complexity from Randomness and Chaos. Entropy 2012, 14, 177–212. [Google Scholar] [CrossRef]
- Sen, K.D. (Ed.) Statistical Complexity; Springer: Berlin, Germany, 2012.
- Seitz, W.; Kirwan, A.D., Jr. Entropy vs. Majorization: What Determines Complexity? Entropy 2014, 16, 3793–3807. [Google Scholar] [CrossRef]
- Bawden, D.; Robinson, L. Waiting for Carnot: Information and complexity. J. Assoc. Inf. Sci. Technol. 2015, 66, 2177–2186. [Google Scholar] [CrossRef]
- Rudnicki, Ł.; Toranzo, I.V.; Sánchez-Moreno, P.; Dehesa, J.S. Monotone measures of statistical complexity. Phys. Lett. A 2016, 380, 377–380. [Google Scholar] [CrossRef]
- Lopez-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Pipek, J.; Varga, I. Statistical electron densities. Int. J. Quant. Chem. 1997, 64, 85. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Simple measure for complexity. Phys. Rev. E 1999, 59, 1459. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On tables of random numbers. Theor. Comput. Sci. 1998, 207, 387. [Google Scholar] [CrossRef]
- Lloyd, S. Measures of complexity: A Nonexhaustive List. IEEE Control Syst. Mag. 2001, 21, 7–8. [Google Scholar] [CrossRef]
- Catalan, R.G.; Garay, J.; López-Ruiz, R. Features of the extension of a statistical measure of complexity to continuous systems. Phys. Rev. E 2002, 66, 011102. [Google Scholar] [CrossRef] [PubMed]
- Vignat, C.; Bercher, J.-F. Analysis of signals in the Fisher–Shannon information plane. Phys. Lett. A 2003, 312, 27. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Yamano, T. A statistical measure of complexity with nonextensive entropy. Phys. A 2004, 340, 131–137. [Google Scholar] [CrossRef]
- Romera, E.; Dehesa, J.S. The Fisher–Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- López-Ruiz, R. Shannon information, LMC complexity and Rényi entropies: a straightforward approach. Biophys. Chem. 2005, 115, 215. [Google Scholar] [CrossRef] [PubMed]
- Dehesa, J.S.; Sánchez-Moreno, P.; Yáñez, R.J. Cramér-Rao information plane of orthogonal hypergeometric polynomials. J. Comput. Appl. Math. 2006, 186, 523–541. [Google Scholar] [CrossRef]
- Angulo, J.C.; Antolín, J.; Sen, K.D. Fisher–Shannon plane and statistical complexity of atoms. Phys. Lett. A 2008, 372, 670. [Google Scholar] [CrossRef]
- Romera, E.; Nagy, A. Fisher–Rényi entropy product and information plane. Phys. Lett. A 2008, 372, 6823. [Google Scholar] [CrossRef]
- Antolín, J.; Angulo, J.C. Complexity analysis of ionization processes and isoelectronic series. Int. J. Quant. Chem. 2009, 109, 586–593. [Google Scholar] [CrossRef]
- Romera, E.; López-Ruiz, R.; Sañudo, J.; Nagy, A. Generalized Statistical Complexity and Fisher–Rényi Entropy Product in the H-Atom. Int. Rev. Phys. 2009, 3, 207–211. [Google Scholar]
- López-Ruiz, R.; Nagy, Á.; Romera, E.; Sañudo, J. A generalized statistical complexity measure: Applications to quantum systems. J. Math. Phys. 2009, 50, 123528. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Angulo, J.C.; Dehesa, J.S. A generalized complexity measure based on Rényi entropy. Eur. Phys. J. D 2014, 68, 212. [Google Scholar] [CrossRef]
- Tan, R.; Terno, D.R.; Thompson, J.; Vedral, V.; Gu, M. Towards quantifying complexity with quantum mechanics. Eur. Phys. J. Plus 2014, 129, 191. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Fisher, R.A. Theory of statistical estimation. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Rényi, A. Probability Theory; North Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Antolin, J.; Lopez-Rosa, S.; Angulo, J.C. Renyi complexities and information planes: Atomic structure in conjugated spaces. Chem. Phys. Lett. 2009, 474, 233–237. [Google Scholar] [CrossRef]
- Johnson, O.; Vignat, C. Some results concerning maximum Rényi entropy distributions. Ann. I. H. Poincaré 2007, 43, 339–351. [Google Scholar] [CrossRef]
- Savaré, G.; Toscani, G. The concavity of Rényi entropy power. IEEE Trans. Inf. Theory 2014, 60, 2687. [Google Scholar] [CrossRef]
- Wang, L.; Madiman, M. Beyond the Entropy Power Inequality, via Rearrangements. IEEE Trans. Inf. Theory 2014, 60, 9. [Google Scholar] [CrossRef]
- Bercher, J.F. On a (β,q)-generalized Fisher information and inequalities involving q-Gaussian distributions. J. Math. Phys. 2012, 53, 063303. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Sánchez-Moreno, P.; Manzano, D.; Dehesa, J.S. Direct spreading measures of Laguerre polynomials. J. Comput. Appl. Math. 2011, 235, 1129–1140. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Niukkanen, A.W. Some Clebsch-Gordan type linearization relations and associated families of Dirichlet integrals. Math. Comput. Model. 2003, 37, 245–250. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toranzo, I.V.; Sánchez-Moreno, P.; Rudnicki, Ł.; Dehesa, J.S. One-Parameter Fisher–Rényi Complexity: Notion and Hydrogenic Applications. Entropy 2017, 19, 16. https://doi.org/10.3390/e19010016
Toranzo IV, Sánchez-Moreno P, Rudnicki Ł, Dehesa JS. One-Parameter Fisher–Rényi Complexity: Notion and Hydrogenic Applications. Entropy. 2017; 19(1):16. https://doi.org/10.3390/e19010016
Chicago/Turabian StyleToranzo, Irene V., Pablo Sánchez-Moreno, Łukasz Rudnicki, and Jesús S. Dehesa. 2017. "One-Parameter Fisher–Rényi Complexity: Notion and Hydrogenic Applications" Entropy 19, no. 1: 16. https://doi.org/10.3390/e19010016
APA StyleToranzo, I. V., Sánchez-Moreno, P., Rudnicki, Ł., & Dehesa, J. S. (2017). One-Parameter Fisher–Rényi Complexity: Notion and Hydrogenic Applications. Entropy, 19(1), 16. https://doi.org/10.3390/e19010016





