1. Introduction
Zoph et al. [
1] ask the question “How much information does a human translator add to the original? ” That is, once a source text has been compressed, how many additional bits are required to encode its human translation? If translation were a deterministic process, the answer would be close to zero. However, in reality, we observe an amount of free variation in target texts. We might guess, therefore, that human translators add something like 10% or 20% extra information, as they work.
To get an upper bound on this figure, Zoph et al. [
1] devise and implement an algorithm to actually compress target English in the presence of source Spanish. The size of their compressed English is 68% of the size of compressed Spanish. This bound seems rather generous. In setting up a common task, Zoph et al. [
1] encourage researchers to develop improved bilingual compression technology [
2].
In this paper, we investigate how good such algorithms might get. We do not do this by building better compression algorithms, but by seeing how well human beings can predict the behavior of human translators. Because human beings can predict fairly well, we may imagine that bilingual compression algorithms may one day do as well.
Shannon [
3] explores this exactly question for the simpler case of estimating the entropy of free text (not translation). If a human subject were able to write a probability distribution for each subsequent character in a text (given prior context), these distributions could be converted directly into entropy. However, it is hard to get these from human subjects. Shannon instead asks a subject to simply guess the next character until she gets it right, and he records how many guesses are needed to correctly identify it. The character sequence thus becomes a
guess sequence, e.g.:
The subject’s identical twin would be able to reconstruct the original text from the guess sequence, so in that sense, it contains the same amount of information.
Let
represent the character sequence, let
represent the guess sequence, and let
j range over guess numbers from 1 to 95, the number of printable English characters plus newline. Shannon [
3] provides two results.
(
Upper Bound). The entropy of
is no greater than the unigram entropy of the guess sequence:
| log( P()) = log(P()) = P(j) log(P(j)) |
This is because this unigram entropy is an upper bound on the entropy of , which equals the entropy of . In human experiments, Shannon obtains an upper bound of 1.3 bits per character (bpc) for English, significantly better than the character n-gram models of his time (e.g., 3.3 bpc for trigram).
(
Lower Bound). The entropy of
is no less than:
| j · [P(j) − P()] · log(j) |
with the proof given in his paper. Shannon reported a lower bound of 0.6 bpc.
1.1. Contributions of This Paper
Table 1 gives the context for our work, drawing prior numbers from Zoph et al. [
1]. By introducing results from a Bilingual Shannon Game, we show that there is significant room for improving bilingual compression algorithms, meaning there is significant unexploited redundancy in translated texts. Our contributions are:
A web-based bilingual Shannon Game tool.
A collection of guess sequences from human subjects, in both monolingual and bilingual conditions.
An analysis of machine guess sequences and their relation to machine compression rates.
An upper bound on the amount of information in human translations. For English given Spanish, we obtain an upper bound of 0.48 bpc, which is tighter than Shannon’s method, and significantly better than the current best bilingual compression algorithm (0.89 bpc).
2. Materials and Methods
2.1. Shannon Game Data Collection
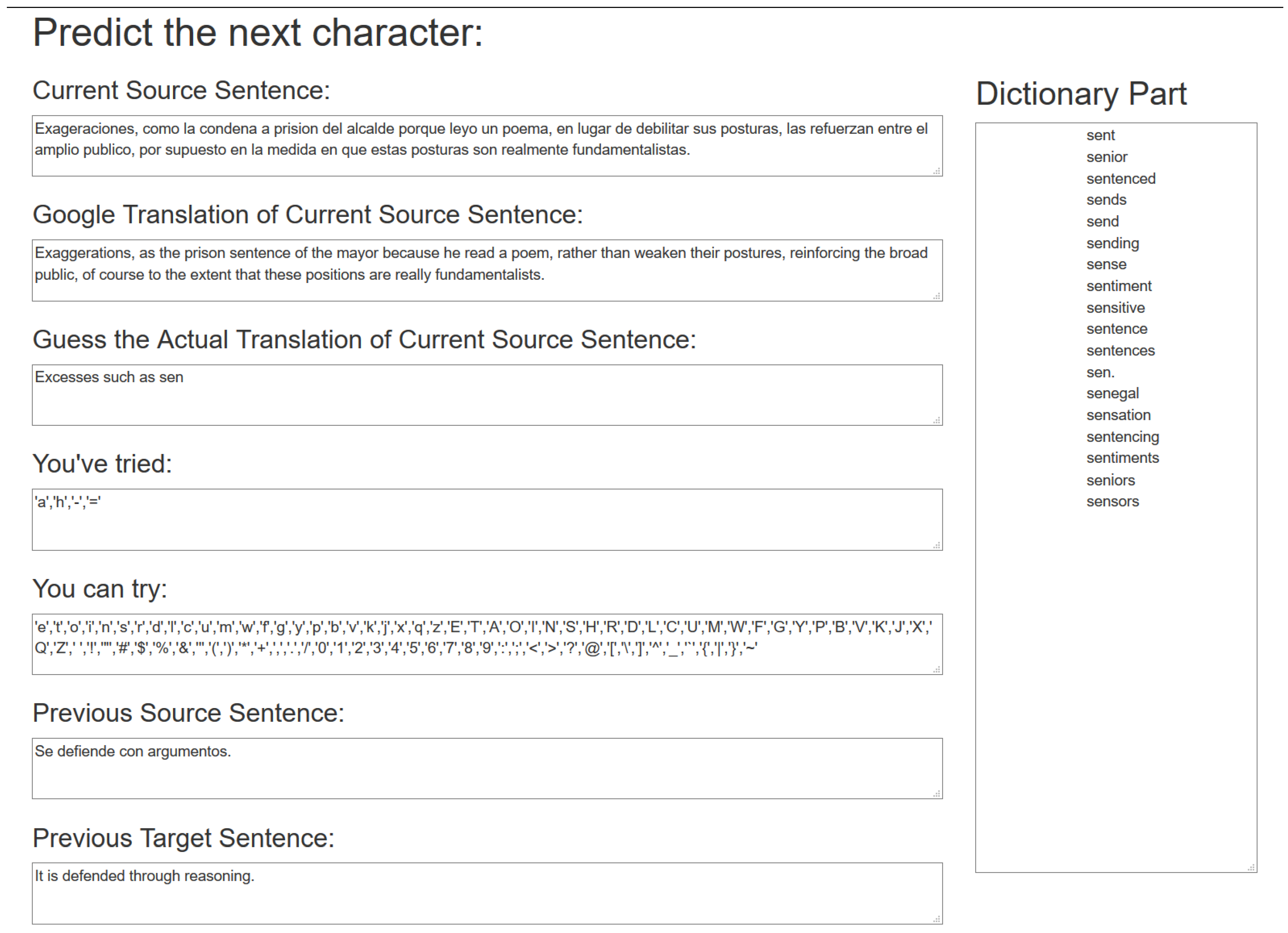
Figure 1 shows our bilingual Shannon Game interface. It displays the current (and previous) source sentence, an automatic Google translation (for assistance only), and the target sentence as guessed so far by the subject. The tool also suggests (for further assistance) word completions in the right panel. Our monolingual Shannon Game is the same, but with source sentences suppressed.
To gather data, we asked 3 English-speaking subjects plus a team of 4 bilingual people to play the bilingual Shannon game. For each subject/team, we assigned a distinct 3–5 sentence text from the Spanish/English Europarl corpus v7 [
30] and asked them to guess the English characters of the text one by one. We gathered a guess sequence with 684 guesses from our team and a guess sequence with 1694 guesses from our individuals (2378 guesses in total). We also asked 3 individuals and a team of 3 people to play the monolingual Shannon game. We gathered a guess sequence with 514 guesses from our team and a guess sequence with 1769 guesses from our individuals (2283 guesses in total).
Figure 2 shows examples of running the monolingual and bilingual Shannon Game on the same sentence.
2.2. An Estimation Problem
Our overall task is now to estimate the (per-guess) entropy of the guess sequences we collect from human subjects, to bound the entropy of the translator’s text. To accomplish this, we build an actual predictor for guess sequences. Shannon [
3] and Zoph et al. [
1] both use a unigram distribution over the guess numbers (in our case 1 to 95). However, we are free to use more context to obtain a tighter bound.
For example, we may collect 2-gram or 3-gram distributions over our observed guess sequence and use those to estimate entropy. In this case, it becomes important to divide our guess sequences into training and test portions—otherwise, a 10-gram model would be able to memorize large chunks of the guess sequences and deliver an unreasonably low entropy. Shannon [
3] applies some ad hoc smoothing to his guess counts before computing unigram entropy, but he does not split his data into test and train to assess the merits of that smoothing.
We set aside 1000 human guesses for testing and use the rest for training—1378 in the bilingual case, and 1283 in the monolingual case. We are now faced with how to do effective modeling with limited training data. However, before we turn to that problem, let us first work in a less limited playground, that of machine guess sequences rather human ones. This gives us more data to work with, and furthermore, because we know the machine’s actual compression rate, we can measure how tight our upper bound is.
2.3. Machine Plays the Monolingual Shannon Game
In this section, we force the state-of-the art text compressor PPMC [
6] to play the
monolingual Shannon Game. PPMC builds a context-dependent probability distribution over the 95 possible character types. We describe the PPMC estimator in detail in
Appendix A. For the Shannon Game, we sort PPMC’s distribution by probability, and continue to guess from the top down until we correctly identify the current character.
We let PPMC warm up on 50 m characters, then collect its guesses on the next 100 m characters (for training data), plus an additional 1000 characters (our test data). For the text corresponding to this test data, PPMC’s actual compression rate is 1.37 bpc.
The simplest model of the training guess sequence is a unigram model.
Table 2 shows the unigram distribution over 100 m characters of training, for both machine and human guess data (These numbers combine data collected from individuals and from teams. In the bilingual case, teams outperformed individuals, guessing correctly on the first try 94.3% of the time, versus 90.5% for individuals. In the monolingual case, individuals and teams performed equally well).
We consider two types of context—the
g guess numbers preceding the current guess, and the
c characters preceding the current guess. For example, if
and
, we estimate the probability of the next guess number from previous 3 characters and previous 2 guess numbers. In:
T h e _ c h a p
2 1 1 1 7 2 4 ?
we calculate P(? | character context =
; guess context =
).
The context gives us more accurate estimates. For example, if and the previous character is ‘q’, then we find the machine able to correctly guess the next character on its first try with probability 0.981, versus 0.732 if we ignore that context. Likewise, having g previous guesses allows us to model “streaks” on the part of the Shannon Game player.
As g and c grow, it becomes necessary to smooth, as test guess sequences begin to contain novel contexts. PPMC itself makes character predictions using c = 8 and g = 0, and it smooths with Witten-Bell, backing off to shorter n-gram contexts . We also use Witten-Bell, but with a more complex backoff scheme to accommodate the two context streams g and c. If we back off to the model with previous guesses and c previous characters, and if we back off to the model with g previous guesses and previous characters.
Table 3 shows test-set entropies obtained from differing amounts of training data, and differing amounts of context. We draw several conclusions from this data:
Character context (c) is generally more valuable than guess context (g).
With large amounts of training data, modest context (g = 1, c = 2) allows us to develop a fairly tight upper bound (1.44 bpc) on PPMC’s actual compression rate (1.37 bpc).
With small amounts of training data, Witten-Bell does not make effective use of context. In fact, adding more context can result in worse test-set entropy!
The last column of
Table 3 shows entropies for necessarily-limited human guess data, computed with the same methods used for machine guess data. We see that human guessing is only a bit more predictable than PPMC’s. Indeed, PPMC’s guesses are fairly good—its massive 8-gram database is a powerful counter to human knowledge of grammar and meaning.
2.4. Modeling Human Guess Sequences
How can we make better use of limited training data? Clearly, we do not observe enough instances of a particular context to robustly estimate the probabilities of the 95 possible guess numbers that may follow. Rather than estimating the multinomial directly, we instead opt for a parametric distribution. Our first choice is the geometric distribution, with one free parameter p, the chance of a successful guess at any point. For each context in the training data, we fit p to best explain the observations of which guesses follow. This one parameter can be estimated more robustly than the 94 free parameters of a multinomial.
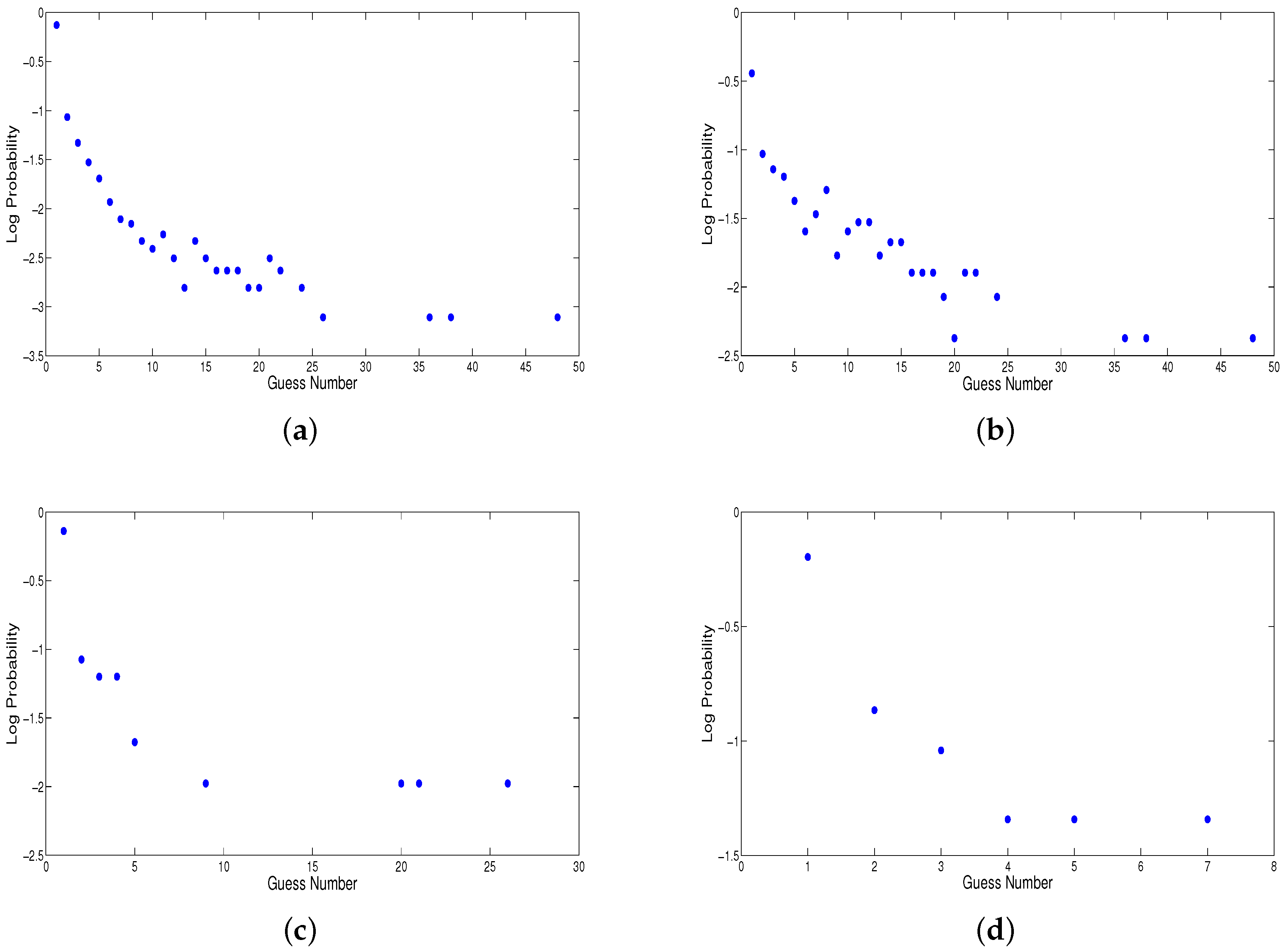
Figure 3 shows that the geometric distribution is a decent fit for our observed guess data, but it does not model the head of the distribution well—the probability of a correct guess on the first try is consistently greater than
p.
Therefore, we introduce a smoothing method (“Frequency and Geometric Smoothing”) that only applies geometric modeling to guess numbers greater than
i, where data is sparse. For each context, we choose
i such that we have seen all guess numbers
at least
k times each, where
Table 4 (left half) demonstrates the effect of different smoothing methods on estimated entropies for human guess data. The monolingual Witten-Bell smoothing column in this figure is the same of last column of
Table 3.
The right half of
Table 4 shows the bilingual case. For the machine case, we use the algorithm of Zoph et al. [
1]. Note that the machine and human subjects both make use of source-sentence context when predicting. However, we do not use source context when modeling guess sequences, only target context.
3. Results
For calculating final entropy bounds, we first divide our guess sequence into 1000 for training data, 100 for development, and remainder for test (1183 for the monolingual case and 1278 for the bilingual case). We use the development set to find the best context model and smoothing model. In all experiments, using previous characters, previous guesses, and Frequency and Geometric Smoothing works best.
Table 5 summarizes our results. As shown in the figure, we also computed Shannon lower bounds (see
Section 1) on all our guess sequences.
For the bilingual case of English-given-Spanish, we give a 0.48 bpc upper bound and a 0.21 bpc lower bound. In the case of machine predictors, we find that our upper bound is loose by about 13%, making it reasonable to guess that true translation entropy might be near 0.42 bpc.
4. Information Loss
So far, we estimate how much information a human translator adds to the source text when they translate. We use H
to represent the conditional entropy of an English text
E given Spanish text
S, i.e., how many bits are required to reconstruct
E from
S. A related question is how much information from the original text is
lost in the process of translation. In other words, how much of the precise wording of
S is no longer obvious when we only have the translation
E? We measure the number of bits needed to reconstruct the
S from
E, denoted H
. We could estimate
by running another (reversed) bilingual Shannon game in which subjects predict Spanish from English. However, fortunately we can skip this time-consuming process and calculate H
based on the definition of joint entropy [
31]:
where H
and H
are the monolingual entropies of
E and
S.
We can estimate H
using the monolingual Spanish Shannon game like what we did for estimating H
. However, as we show in this paper, PPMC compression is close to what we get from the monolingual human Shannon game (1.39 vs. 1.25). So we can estimate H
, using PPMC on Spanish Europarl data, as reported by [
1]. Using this estimate, we obtain the amount of information lost in translation as
.
We see that in the case Spanish and English, the translation process both adds and subtracts information. Other translation scenarios are asymmetric. For example, when translating the word “uncle” into Persian, we must add information (maternal or paternal uncle), but we do not lose information, as “uncle” can be reconstructed perfectly from the Persian word.
5. Conclusions
We have presented new bounds for the amount of information contained in a translation, relative to the original text. We conclude:
Bilingual compression algorithms have plenty of room to improve. There is substantial distance between the 0.95 bpc obtained by [
1] and our upper bound of 0.48 and lower bound of 0.21.
Zoph et al. [
1] estimate that a translator adds 68% more information on top an original text. This is because their English-given-Spanish bilingual compressor produces a text that is 68% as big as that produced by a monolingual Spanish compressor. Using monolingual and bilingual Shannon Game results, we obtain a revised estimate of 0.42/1.25 = 34% (Here, the denominator is monolingual English entropy, rather than Spanish, but we assume these are close under human-level compression).
Meanwhile, it should be possible to reduce our 0.48 upper bound by better modeling of guess sequence data, and by use of source-language context. We also conjecture that the bilingual Shannon Game can be used for machine translation evaluation, on the theory that good human translators exhibit more predictable behavior than bad machine translators.
Acknowledgments
This work was supported by ARO grant W911NF-10-1-0533.
Author Contributions
Marjan Ghazvininejad and Kevin Knight contributed equally to the conception, experiments, and write up. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. PPMC Compression
This description is based on our previous work [
1].
Prediction by partial matching (PPM) is the most well-known adaptive, predictive compression technique [
5]. It predicts by producing a complete probability distribution for the next character P(X|context), based on the previous
characters. It adaptively constructs empirical character n-gram tables (usually
) as it compresses. In a given context, a n-gram table may predict only a subset of characters, so PPM reserves some probability mass for an escape (ESC), after which it executes a hard backoff to the
-gram table. PPM models are different in assigning probabilities to ESC.
In PPMA, P(ESC) is , where D is the number of times the context has been seen. PPMB uses , where q is the number of distinct character types seen in the context. PPMC uses , also known as Witten-Bell smoothing. PPMD uses .
For compression, after the model calculates the probability of the next character given the context, it sends it to the
arithmetic coder [
4,
6].
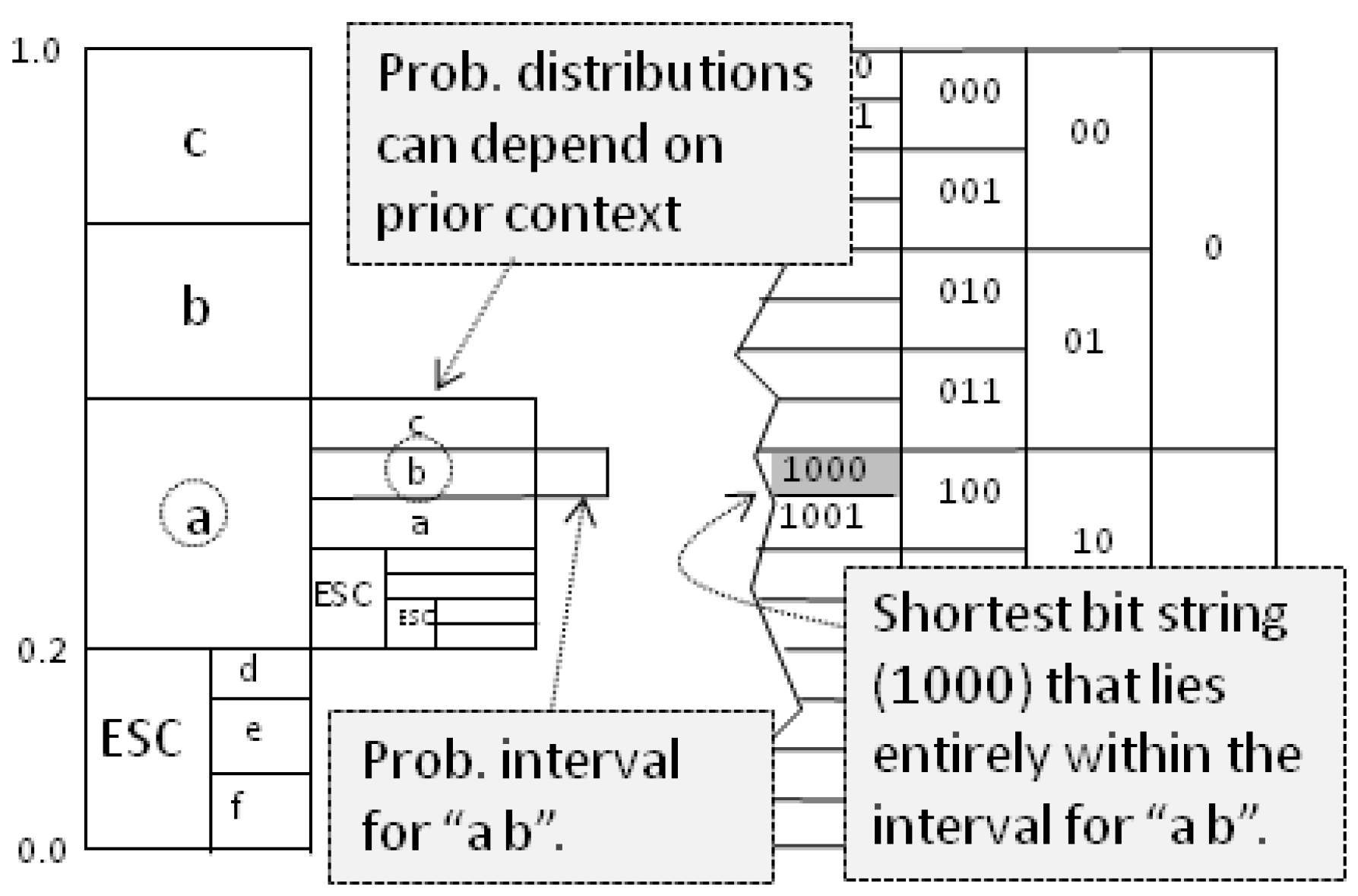
Figure A1 sketches the technique. We produce context-dependent probability intervals, and each time we observe a character, we move to its interval. Our working interval becomes smaller and smaller, but the better our predictions, the wider it stays. A document’s compression is the shortest bit string that fits inside the final interval. In practice, we do the bit-coding as we navigate probability intervals. In this paper, when we force the machine to play the Shannon game, we are only interested in the probability distribution of the next character, so we skip the arithmetic coding of the probabilities.
Figure A1.
Arithmetic coding.
Figure A1.
Arithmetic coding.
References
- Zoph, B.; Ghazvininejad, M.; Knight, K. How Much Information Does a Human Translator Add to the Original? In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015.
- Bilingual Compression Challenge. Available online: http://www.isi.edu/natural-language/compression (accessed on 28 December 2016).
- Shannon, C. Prediction and Entropy of Printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Rissanen, J.; Langdon, G. Universal modeling and coding. IEEE Trans. Inf. Theory 1981, 27, 12–23. [Google Scholar] [CrossRef]
- Cleary, J.; Witten, I. Data compression using adaptive coding and partial string matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef]
- Witten, I.; Neal, R.; Cleary, J. Arithmetic coding for data compression. Commun. ACM 1987, 30, 520–540. [Google Scholar] [CrossRef]
- Brown, P.F.; Della Pietra, V.J.; Mercer, R.L.; Della Pietra, S.A.; Lai, J.C. An estimate of an upper bound for the entropy of English. Comput. Linguist. 1992, 18, 31–40. [Google Scholar]
- Zobel, J.; Moffat, A. Adding compression to a full-text retrieval system. Softw. Pract. Exp. 1995, 25, 891–903. [Google Scholar] [CrossRef]
- Teahan, W.J.; Cleary, J.G. The entropy of English using PPM-based models. In Proceedings of the IEEE Data Compression Conference (DCC ’96), Snowbird, UT, USA, 31 March–3 April 1996; pp. 53–62.
- Witten, I.; Moffat, A.; Bell, T. Managing Gigabytes: Compressing and Indexing Documents And Images; Morgan Kaufmann: San Francisco, CA, USA, 1999. [Google Scholar]
- Mahoney, M. Adaptive Weighting of Context Models for Lossless Data Compression; Technical Report CS-2005-16; Florida Institute of Technology: Melbourne, FL, USA, 2005. [Google Scholar]
- Hutter, M. 50,000 Euro Prize for Compressing Human Knowledge. Available online: http://prize.hutter1.net (accessed on 29 September 2016).
- Conley, E.; Klein, S. Using alignment for multilingual text compression. Int. J. Found. Comput. Sci. 2008, 19, 89–101. [Google Scholar] [CrossRef]
- Martínez-Prieto, M.; Adiego, J.; Sánchez-Martínez, F.; de la Fuente, P.; Carrasco, R.C. On the use of word alignments to enhance bitext compression. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 30 March–1 April 2009; p. 459.
- Adiego, J.; Brisaboa, N.; Martínez-Prieto, M.; Sánchez-Martínez, F. A two-level structure for compressing aligned bitexts. In Proceedings of the 16th International Symposium on String Processing and Information Retrieval, Saariselka, Finland, 25–27 August 2009; pp. 114–121.
- Adiego, J.; Martínez-Prieto, M.; Hoyos-Torío, J.; Sánchez-Martínez, F. Modelling parallel texts for boosting compression. In Proceedings of the Data Compression Conference, Snowbird, UT, USA, 24–26 March 2010; p. 517.
- Sánchez-Martínez, F.; Carrasco, R.; Martínez-Prieto, M.; Adiego, J. Generalized biwords for bitext compression and translation spotting. J. Artif. Intell. Res. 2012, 43, 389–418. [Google Scholar]
- Conley, E.; Klein, S. Improved Alignment-Based Algorithm for Multilingual Text Compression. Math. Comput. Sci. 2013, 7, 137–153. [Google Scholar] [CrossRef]
- Grignetti, M. A note on the entropy of words in printed English. Inf. Control 1964, 7, 304–306. [Google Scholar] [CrossRef]
- Burton, N.; Licklider, J. Long-range constraints in the statistical structure of printed English. Am. J. Psychol. 1955, 68, 650–653. [Google Scholar] [CrossRef] [PubMed]
- Paisley, W. The effects of authorship, topic, structure, and time of composition on letter redundancy in English texts. J. Verbal Learn. Verbal Behav. 1966, 5, 28–34. [Google Scholar] [CrossRef]
- Guerrero, F. A New Look at the Classical Entropy of Written English. arXiv 2009. [Google Scholar]
- Jamison, D.; Jamison, K. A note on the entropy of partially-known languages. Inf. Control 1968, 12, 164–167. [Google Scholar] [CrossRef]
- Rajagopalan, K. A note on entropy of Kannada prose. Inf. Control 1965, 8, 640–644. [Google Scholar] [CrossRef]
- Newman, E.; Waugh, N. The redundancy of texts in three languages. Inf. Control 1960, 3, 141–153. [Google Scholar] [CrossRef]
- Siromoney, G. Entropy of Tamil prose. Inf. Control 1963, 6, 297–300. [Google Scholar] [CrossRef]
- Wanas, M.; Zayed, A.; Shaker, M.; Taha, E. First second-and third-order entropies of Arabic text (Corresp.). IEEE Trans. Inf. Theory 1976, 22, 123. [Google Scholar] [CrossRef]
- Cover, T.; King, R. A convergent gambling estimate of the entropy of English. IEEE Trans. Inf. Theory 1978, 24, 413–421. [Google Scholar] [CrossRef]
- Nevill, C.; Bell, T. Compression of parallel texts. Inf. Process. Manag. 1992, 28, 781–793. [Google Scholar] [CrossRef]
- Koehn, P. Europarl: A parallel corpus for statistical machine translation. In Proceedings of the Machine Translation Summit X, Phuket, Thailand, 12–16 September 2005; pp. 79–86.
- Cover, T.; Thomas, J. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006; pp. 16–18. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).