Abstract
In this work, the one-parameter Fisher–Rényi measure of complexity for general d-dimensional probability distributions is introduced and its main analytic properties are discussed. Then, this quantity is determined for the hydrogenic systems in terms of the quantum numbers of the quantum states and the nuclear charge.
1. Introduction
We all have an intuitive sense of what complexity means. In the last two decades, an increasing number of efforts have been published [1,2,3,4,5,6,7,8,9,10,11,12] to refine our intuitions about complexity into precise, scientific concepts, pointing out a large amount of open problems. Nevertheless, there is neither a consensus on the term complexity nor whether there is a simple core to complexity. Contrary to the Boltzmann–Shannon entropy, which is ever increasing according to the second law of thermodynamics, the complexity seems to behave very differently. Various precise, widely applicable, numerical and analytical proposals (see e.g., [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] and the monograph [8]) have been done, but they are yet very far to appropriately formalize the intuitive notion of complexity [11,29]. The latter suggests that complexity should be minimal at either end of the scale. However, a complexity quantifier to take into account the completely ordered and completely disordered limits (i.e., perfect order and maximal randomness, respectively) and to describe/explain the maximum between them is not known up until now.
Recently, keeping in mind the fundamental principles of the density functional theory, some statistical measures of complexity have been proposed to quantify the degree of structure or pattern of finite many-particle systems in terms of their single-particle density, such as the Crámer–Rao [23,26], Fisher–Shannon [18,21,24] and LMC (López-ruiz, Mancini and Calvet) [12,17] complexities and some modifications of them [13,22,25,27,28,29]. They are composed by a two-factor product of entropic measures of Shannon [31], Fisher [6,32] and Rényi [33] types. Most interesting for quantum systems are those which involve the Fisher information (namely, the Crámer–Rao and the Fisher–Shannon complexities, and their modifications [25,27,34]), mainly because this is by far the best entropy-like quantity to take into account the inherent fluctuations of the quantum wave functions by quantifying the gradient content of the single-particle density of the systems.
The objective of this article is to extend and generalize these Fisher-information-based measures of complexity by introducing a new complexity quantifier, the one-parameter Fisher–Rényi complexity, to discuss its properties and to apply it to the main prototype of Coulombian systems, the hydrogenic system. This notion is composed by two factors: a λ-dependent Fisher information (which quantifies various aspects of the quantum fluctuations of the physical wave functions beyond the density gradient, since it reduces to the standard Fisher information for ) and the Rényi entropy of order λ (which measures various facets of the spreading or spatial extension of the density beyond the celebrated Shannon entropy, which corresponds to the limiting case ).
The article is structured as follows. In Section 1, we introduce the notion of one-parameter Fisher–Rényi measure of complexity. In Section 2, we discuss the main analytical properties of this complexity, showing that it is bounded from below, invariant under scaling transformations and monotone. In addition, the near-continuity and the invariance under replications are also discussed. In Section 3, we apply the new complexity measure to the hydrogenic systems. Finally, some concluding remarks are given.
2. One-Parameter Fisher–Rényi Complexity Measure
In this section, the notion of one-parameter Fisher–Rényi complexity of a d-dimensional probability density is introduced, and its main analytic properties are discussed. This quantity is composed of two entropy-like factors of local (the one-parameter Fisher information of Johnson and Vignat [35], ) and global (the λ-order Rényi entropy power [36], ) characters.
2.1. The Notion
The one-parameter Fisher–Rényi complexity measure of the probability density , is defined by
where is the normalization factor given as
This purely numerical factor is necessary to let the minimal value of the complexity be equal to unity, as explained below in Section 2.2.1. The denotes the (scarcely known) λ-weighted Fisher information [35] defined by
(which, for , reduces to the standard Fisher information ), being the d-dimensional volume element. Finally, the symbol denotes the λ-Rényi entropy power (see e.g., [36]) given as
where and is the Shannon entropy [31].
The complexity measure has a number of conceptual advantages with respect to the Fisher-information-based measures of complexity previously defined; namely, the Crámer–Rao and Fisher–Shannon complexity and their modifications. Indeed, it quantifies the combined balance of different (λ-dependent) aspects of both the fluctuations and the spreading or spatial extension of the single-particle density ρ, in such a way that there is no dependence on any specific point of the system’s region. The Crámer–Rao complexity [23,26] (which is the product of the standard Fisher information mentioned above and the variance ) measures a single aspect of the fluctuations (namely, the density gradient) together with the concentration of the probability density around the centroid . The Fisher–Shannon complexity [18,21,24], defined by , quantifies the density gradient jointly with a single aspect of the spreading given by the Shannon entropy mentioned above. A modification of the previous measure by use of the Rényi entropy instead of the Shannon entropy, the Fisher–Rényi product of complexity-type, has been recently introduced [25,27,34]; it measures the gradient together with various aspects of the spreading of the density.
2.2. The Properties
Let us now discuss some properties of this notion: bounding from below, invariance under scaling transformations, monotonicity, behavior under replications and near continuity.
2.2.1. Lower Bound
The Fisher–Rényi complexity measure fulfills the inequality
(for , with ), and the minimal complexity occurs, as implicitly proved by Savaré and Toscani [36], if and only if the density has the following generalized Gaussian form
where and is the normalization constant given by
with
Thus, the complexity measure has a universal lower bound of minimal complexity, which is achieved for the family of densities .
2.2.2. Invariance under Scaling and Translation Transformations
The complexity measure is scaling and translation invariant in the sense that
where , with and . To prove this property, we follow the lines of Savaré and Toscani [36]. First, we calculate the generalized Fisher information of the transformed density, obtaining
Note that, in writing the first equality, we have used
Then, we determine the value of the λ-entropy power of the density , which turns out to be equal to
In particular, we have
2.2.3. Monotonicity
The existence of a non-trivial operation with interesting properties under which a complexity measure is monotone [11] is a valuable property of the measure in question from the axiomatic point of view. To show the monotone behavior of the Fisher–Rényi complexity we make use of the so-called rearrangements, which represent a useful tool in the theory of functional analysis, and, among other applications, have been used to prove relevant inequalities such as Young’s inequality with sharp constant.
Two of the main properties of rearrangements is that they preserve the norms, which implies that the rearrangements of a probability density give rise to another probability density, and that they make everything spherically symmetric. The second feature makes the rearrangement operation relevant for quantification of statistical complexity [11], since a spherically symmetric variant of a probability density can in an atomic context be viewed as less complex. Then, we introduce the definition of this operation as well as its effects over the entropic quantities that make up our complexity measure. Let f be a real-valued function, and . The symmetric decreasing rearrangement of f is defined as
with if and 0, otherwise. represents the super-level set of the function f, and (which denotes the symmetric rearrangement of a set ) is the Euclidean ball centered at 0 such as .
The central idea of this transformation is to build up from the rearranged super-level sets in the same manner that f is built from its super-level sets. As a by-product from its construction, turns out to be a spherically symmetric decreasing function (i.e., and moreover , where ), which means that, for any function and all
or, in other words, for any measurable subset , the volume of the sets and are the same.
It is known [37] that under this transformation and for any the Rényi and Shannon entropies remain unchanged, i.e.,
if both and are well defined, where . The invariance of the Rényi entropy follows from the preservation of the norms via rearrangements and the proof of the invariance of the Shannon entropy is done in [37]. Moreover, Wang and Madiman [37] consider the Fisher information, finding that the standard Fisher information decreases monotonically under rearrangements, i.e.,
Let us now consider the biparametric Fisher-like information, , of a probability density function , which is defined [38] by
with . Then, one notes that the one-parameter Fisher information, , given by (3), can be expressed in terms of the previous quantity with and as
On the other hand, considering the transformation with , the biparametric Fisher information becomes
also known as the β-Dirichlet energy of . If , note that the function corresponds to a quantum-mechanical wave function. By using the symmetric decreasing rearrangement to the density function ρ, the well-known Pólya–Szegö inequality states that
which implies that the minimizer of the left side is necessarily radially symmetric and decreasing, so the extremal function belongs to the subset of radially symmetric probability densities, and is represented by the generalized Gaussian given in (6). Now, by taking into account (14) and the invariance of the Rényi entropy (and, therefore, the Rényi entropy power, ), upon rearrangements, one obtains the monotone behavior of as
Finally, this observation together with (1) allows us to obtain the monotone behavior of this complexity measure proved by rearrangements, i.e.,
where the inequality is saturated for the generalized Gaussian, , which also means that the symmetric rearrangement of a generalized Gaussian gives another generalized Gaussian, i.e., rearrangements preserve this subset of radially symmetric probability densities .
2.2.4. Behavior under Replications
Here we study the behavior of the Fisher–Rényi complexity under n replications. We have found that, for one-dimensional densities with bounded support, this complexity measure behaves as follows:
where the density representing n replications of ρ is given by
where the points are chosen such that the supports of each density are disjoints. Then, the integrals
and
where the change of variable has been performed.
Thus, the two entropy factors (the generalized Fisher information and the Rényi entropy power) of the Fisher–Rényi measure gets modified as
so that from these two values and (1), we finally have the wanted behavior (19) of the Fisher–Rényi complexity under n replications. Although this has been proved in the one-dimensional case, similar arguments hold for general dimensional densities.
2.2.5. Near-Continuity Behavior
Here we illustrate that the Fisher–Rényi complexity is not near continuous by means of a one-dimensional counter-example. Recall first that a functional G is near continuous if for any , there exists , such that, if two densities ρ and are δ-neighboring (i.e., the Lebesgue measure of the points satisfying is zero), then . Now, let us consider the δ-neighboring densities
and
Due to the increasing oscillatory behaviour of for as δ tends to zero, the generalized Fisher information grows rapidly as δ decreases, while the Rényi entropy power tends to a constant value. Then, the more similar ρ and are, the more different are their values of . Therefore, the Fisher–Rényi complexity measure is not near continuous.
3. The Hydrogenic Application
In this section, we determine the one-parameter Fisher–Rényi complexity measure , given by (1), for the probability density of hydrogenic atoms consisting of an electron bound by the Coulomb potential, , where Z denotes the nuclear charge, and the position vector is given in spherical polar coordinates as , . Atomic units are used. The hydrogenic states are well known to be characterized by the three quantum numbers {}, with , and . They have the energies , and the corresponding quantum probability densities are given by
where , and the symbols and are the radial and angular parts of the density, which are given by
and
respectively. In addition, denotes the orthonormal Laguerre polynomials [39] with respect to the weight function on the interval , and are the well-known spherical harmonics, which can be expressed in terms of the Gegenbauer polynomials, via
where and . Let us now compute the complexity measure of the hydrogenic probability density, which, according to (1), is given by
where is the normalization constant given by (2) and the symbols and denote the integrals
which can be solved by following the lines indicated in Appendix A.
In the following, for simplicity and illustration purposes, we focus our attention on the computation of the complexity measure for two large, relevant classes of hydrogenic states: the and the circular states.
3.1. Generalized Fisher–Rényi Complexity of Hydrogenic States
For states one has so that the three angular integrals can be trivially determined, and the radial integrals simplify as
with
Thus, finally, the one-parameter (λ) Fisher–Rényi complexity measure for the -like hydrogenic states is given by
where
In particular, for the ground state (i.e., when ), we have shown in Appendix B that
which allows us to find the following value
for the one-parameter Fisher–Rényi complexity measure of the hydrogenic ground state, keeping in mind the value (2) for the normalization factor . We have done this calculation in detail to check our methodology; we are aware that, in this concrete example, it would have been simpler to start directly from the explicit expression of the wave function of the orbital . Operating in a similar way, we can obtain the complexity values for the rest of the -orbitals.
3.2. Generalized Fisher–Rényi Complexity of Hydrogenic Circular States
For circular states the degree and parameter, and , of the orthonormal Laguerre polynomials, become 0 and , respectively, so that the corresponding polynomials simplify as , and then the involved radial integrals follow as
On the other hand, the angular part of the wavefunction for the circular states reduces as
which allows us to readily compute the angular integrals , and as
Gathering the last six numbered expressions together with Equations (A2) and (A5), one finally obtains, according to (25), the following value
for the one-parameter Fisher–Rényi complexity measure of the hydrogenic circular states. This expression gives for the ground state (which is also a particular circular state with ) the same previously obtained value (34), which is a further checking of our results. To better understand this complicated formula, we depict in Figure 1 the behavior of the complexity measure of circular states, , as a function of λ. This figure contains three graphs which correspond to the complexity differences for , , and with fixed (Figure 1a), 2 (Figure 1b) and 3 (Figure 1c).
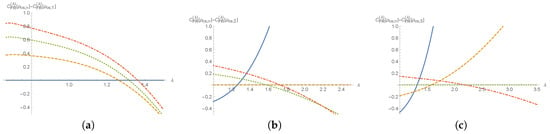
Figure 1.
Dependence of the complexity difference on λ for (solid blue), 2 (dashed yellow), 3 (dotted green) and 4 (dot dashed red), and with fixed (a), 2 (b) and 3 (c).
We observe that there exists a λ-dependence behavior for every couple of states in the following sense
Physically, this means that for small λ (i.e., close to its lowest value), the circular states become more complex as n increases (as one can intuitively think). However, for every couple of quantum numbers , we conjecture existence of a critical value for which the complexity of both states is the same, while for larger values of λ, the complexity dominance becomes swapped. This phenomenon would imply that, for very large values of λ, the complexity ordering of the set of circular states becomes completely reversed. The conjectured effect shows the existence of two -dependent regimes of complexity and provides a novel complexity-related insight into the internal structure of the states of the system under study.
4. Conclusions
In this article, we first explored the notion of a complexity quantifier for the finite quantum many-particle systems, the one-parameter Fisher–Rényi complexity, and also examined its main analytical properties. This notion extends all the previously known measures of complexity which are sensitive to the quantum fluctuations of the physical wavefunctions of the systems (Crámer–Rao, Fisher–Shannon, Fisher–Rényi-type) in the following sense: it does not depend on any specific point of the system’s region (opposite to the Crámer–Rao measure) and it quantifies the combined balance of various aspects of the fluctuations of the single-particle density beyond the gradient content (opposite to the Fisher–Shannon complexity and the Fisher–Rényi product, which only take into account a single aspect given by the density gradient content) and different facets of the spreading of this density function.
Then, we illustrated the applicability of this novel measure of complexity in the main prototype of electronic systems, the hydrogenic atom. We have obtained an analytically, algorithmic way to calculate its values for all quantum hydrogenic states, and we have given the explicit values for all the states and the circular states, which are specially relevant per se because they can be used as reference values for the complexity of Coulombian systems as reflected by the rich three-dimensional geometries of the electron density corresponding to their quantum states.
Acknowledgments
This work was partially supported by the Projects P11-FQM-7276 and FQM-207 of the Junta de Andalucia, and by the MINECO (Ministerio de Economía y Competitividad) and FEDER (European regional development fund) grants FIS2014- 54497P and FIS2014-59311P. Ł.R. acknowledges financial support by the grant number 2014/13/D/ST2/01886 of the National Science Center, Warsaw, Poland. Research in Cologne is supported by the Excellence Initiative of the German Federal and State Governments (Grant ZUK 81) and the DFG (GRO 4334/2-1). Ł.R. also acknowledges the support by the Foundation for Polish Science (FNP) and hospitality of the Freiburg Center for Data Analysis and Modeling. I.V.T. acknowledges the support of the Spanish Ministerio de Educación under the program FPU 2014.
Author Contributions
All authors have contributed equally to the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Calculation of the Fisher and Rényi-like Hydrogenic Integrals
Let us here show the methodology to solve the integrals
with
and
encountered in Section 3. Since the gradient operator is and the probability density does not depend on the azimuthal angle, ϕ, the integral can be written as
where one has used , and
and
Then, the complexity measure (25) can be rewritten as
It remains to calculate the radial integrals , and and the angular integrals , and . Let us start with the analytical determination of the radial integrals and . To do this, we use the differential relation of the Laguerre polynomials [39]
and the linearization-like formula of Srivastava–Niukkanen [40,41] for the product of several Laguerre polynomials given by
where the -linearization coeffients are
with the Pochhammer symbol [39] , the binomial number , and the Lauricella hypergeometric function of variables [40,41].
Then, we obtain the following analytical expressions for the radial integrals in terms of the parameters of the system:
where is
where one should keep in mind that the functions are given as in (A13).
Similarly, we can obtain the angular integrals by means of linerization-like formulas of the Gegenbauer polynomials or the associated Legendre polynomials of the first kind.
Appendix B. Calculation of
Here, we will determine the value of
where
and
since
Then, we obtain that
References
- Gell-Mann, M. What is complexity? Complexity 1995, 1, 1–9. [Google Scholar]
- Gell-Mann, M.; Lloyd, S. Information measures, effective complexity, and total information. Complexity 1996, 2, 44–52. [Google Scholar] [CrossRef]
- Badii, R.; Politi, A. Complexity: Hierarchical Structure and Scaling in Physics; Henry Holt & CO.: New York, NY, USA, 1997. [Google Scholar]
- Gregersen, N.H. From Complexity to Life: On the Emergence of Life and Meaning; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Gell-Mann, M.; Lloyd, S. Effective complexity. In Nonextensive Entropy: Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: Oxford, UK, 2004; pp. 387–398. [Google Scholar]
- Frieden, B.R. Science from Fisher Information; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zuchowski, L.C. Disentangling Complexity from Randomness and Chaos. Entropy 2012, 14, 177–212. [Google Scholar] [CrossRef]
- Sen, K.D. (Ed.) Statistical Complexity; Springer: Berlin, Germany, 2012.
- Seitz, W.; Kirwan, A.D., Jr. Entropy vs. Majorization: What Determines Complexity? Entropy 2014, 16, 3793–3807. [Google Scholar] [CrossRef]
- Bawden, D.; Robinson, L. Waiting for Carnot: Information and complexity. J. Assoc. Inf. Sci. Technol. 2015, 66, 2177–2186. [Google Scholar] [CrossRef]
- Rudnicki, Ł.; Toranzo, I.V.; Sánchez-Moreno, P.; Dehesa, J.S. Monotone measures of statistical complexity. Phys. Lett. A 2016, 380, 377–380. [Google Scholar] [CrossRef]
- Lopez-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Pipek, J.; Varga, I. Statistical electron densities. Int. J. Quant. Chem. 1997, 64, 85. [Google Scholar] [CrossRef]
- Shiner, J.S.; Davison, M.; Landsberg, P.T. Simple measure for complexity. Phys. Rev. E 1999, 59, 1459. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On tables of random numbers. Theor. Comput. Sci. 1998, 207, 387. [Google Scholar] [CrossRef]
- Lloyd, S. Measures of complexity: A Nonexhaustive List. IEEE Control Syst. Mag. 2001, 21, 7–8. [Google Scholar] [CrossRef]
- Catalan, R.G.; Garay, J.; López-Ruiz, R. Features of the extension of a statistical measure of complexity to continuous systems. Phys. Rev. E 2002, 66, 011102. [Google Scholar] [CrossRef] [PubMed]
- Vignat, C.; Bercher, J.-F. Analysis of signals in the Fisher–Shannon information plane. Phys. Lett. A 2003, 312, 27. [Google Scholar] [CrossRef]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Statistical complexity and disequilibrium. Phys. Lett. A 2003, 311, 126–132. [Google Scholar] [CrossRef]
- Yamano, T. A statistical measure of complexity with nonextensive entropy. Phys. A 2004, 340, 131–137. [Google Scholar] [CrossRef]
- Romera, E.; Dehesa, J.S. The Fisher–Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef] [PubMed]
- López-Ruiz, R. Shannon information, LMC complexity and Rényi entropies: a straightforward approach. Biophys. Chem. 2005, 115, 215. [Google Scholar] [CrossRef] [PubMed]
- Dehesa, J.S.; Sánchez-Moreno, P.; Yáñez, R.J. Cramér-Rao information plane of orthogonal hypergeometric polynomials. J. Comput. Appl. Math. 2006, 186, 523–541. [Google Scholar] [CrossRef]
- Angulo, J.C.; Antolín, J.; Sen, K.D. Fisher–Shannon plane and statistical complexity of atoms. Phys. Lett. A 2008, 372, 670. [Google Scholar] [CrossRef]
- Romera, E.; Nagy, A. Fisher–Rényi entropy product and information plane. Phys. Lett. A 2008, 372, 6823. [Google Scholar] [CrossRef]
- Antolín, J.; Angulo, J.C. Complexity analysis of ionization processes and isoelectronic series. Int. J. Quant. Chem. 2009, 109, 586–593. [Google Scholar] [CrossRef]
- Romera, E.; López-Ruiz, R.; Sañudo, J.; Nagy, A. Generalized Statistical Complexity and Fisher–Rényi Entropy Product in the H-Atom. Int. Rev. Phys. 2009, 3, 207–211. [Google Scholar]
- López-Ruiz, R.; Nagy, Á.; Romera, E.; Sañudo, J. A generalized statistical complexity measure: Applications to quantum systems. J. Math. Phys. 2009, 50, 123528. [Google Scholar] [CrossRef]
- Sánchez-Moreno, P.; Angulo, J.C.; Dehesa, J.S. A generalized complexity measure based on Rényi entropy. Eur. Phys. J. D 2014, 68, 212. [Google Scholar] [CrossRef]
- Tan, R.; Terno, D.R.; Thompson, J.; Vedral, V.; Gu, M. Towards quantifying complexity with quantum mechanics. Eur. Phys. J. Plus 2014, 129, 191. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Fisher, R.A. Theory of statistical estimation. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Rényi, A. Probability Theory; North Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Antolin, J.; Lopez-Rosa, S.; Angulo, J.C. Renyi complexities and information planes: Atomic structure in conjugated spaces. Chem. Phys. Lett. 2009, 474, 233–237. [Google Scholar] [CrossRef]
- Johnson, O.; Vignat, C. Some results concerning maximum Rényi entropy distributions. Ann. I. H. Poincaré 2007, 43, 339–351. [Google Scholar] [CrossRef]
- Savaré, G.; Toscani, G. The concavity of Rényi entropy power. IEEE Trans. Inf. Theory 2014, 60, 2687. [Google Scholar] [CrossRef]
- Wang, L.; Madiman, M. Beyond the Entropy Power Inequality, via Rearrangements. IEEE Trans. Inf. Theory 2014, 60, 9. [Google Scholar] [CrossRef]
- Bercher, J.F. On a (β,q)-generalized Fisher information and inequalities involving q-Gaussian distributions. J. Math. Phys. 2012, 53, 063303. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Sánchez-Moreno, P.; Manzano, D.; Dehesa, J.S. Direct spreading measures of Laguerre polynomials. J. Comput. Appl. Math. 2011, 235, 1129–1140. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Niukkanen, A.W. Some Clebsch-Gordan type linearization relations and associated families of Dirichlet integrals. Math. Comput. Model. 2003, 37, 245–250. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).