A Comparative Study of Empirical Mode Decomposition-Based Filtering for Impact Signal
Abstract
:1. Introduction
2. Related Works
2.1. Improved Empirical Mode Decomposition
- (1)
- Decompose signal to obtain the first mode by using EMD algorithm.where is the ratio of the standard deviation of the added white noise, is the white noise with unit variance under condition of the i-th ensemble number, is the total ensemble number, and is the first mode obtained EMD decomposition under the condition of i-th signal: .
- (2)
- Compute the difference signal
- (3)
- Decompose to obtain the first mode and define the second mode byHere, and stand for a function to extract the first IMF decomposed by EMD and the white noise with unit variance, respectively.
- (4)
- For k = 2, …, K, calculate the k-th residue and obtain the first mode. Define the (k + 1)-th mode as follows:where is a function to extract the k-th IMF decomposed by EMD.
- (5)
- Repeat step (4) until the residue contains no more than two extremes. The residual mode is then defined as:Therefore, the signal can be expressed as follows:
2.2. Fuzzy Entropy
- (1)
- Given a time sequence ( is the sample size) to form a sequence segment by choosing consecutive values in time sequenceThe vector represents consecutive values but removing the baseline .The expression is shown as follows:
- (2)
- The distance between the vector and is definedHere, .
- (3)
- The similarity degree between and is expressed by the fuzzy function . The expression of similarity is as follows:
- (4)
- Definition function
- (5)
- For dimension function, repeat steps (1) to (4), and obtain
- (6)
- The fuzzy entropy is defined by:Here, is the embedding dimension, is the similarity weight, is the tolerance threshold, and is the segment length.
3. Filtering Method
3.1. Identifying the Relevant Mode
- (1)
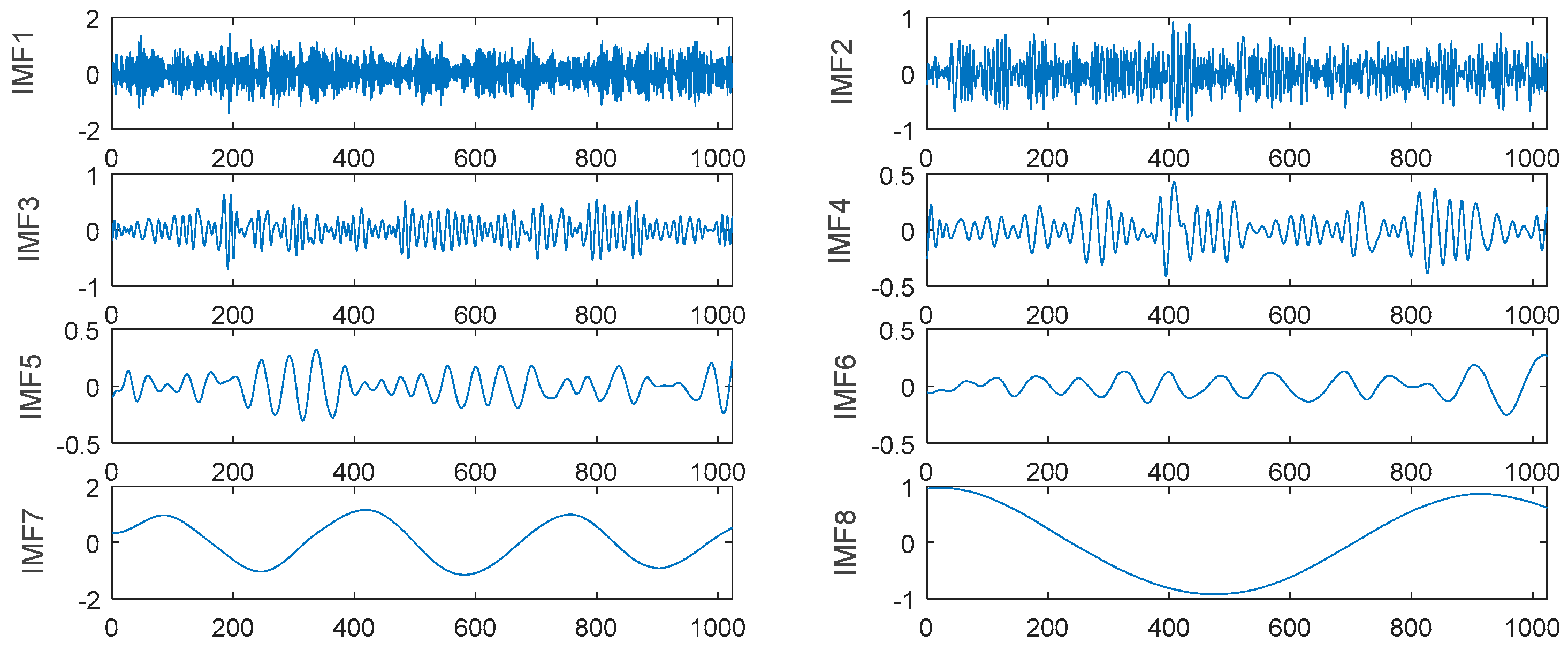
- The noisy signal x(t) is decomposed to obtain IMFi (i = 1, …, N) by EMD or the improved version.
- (2)
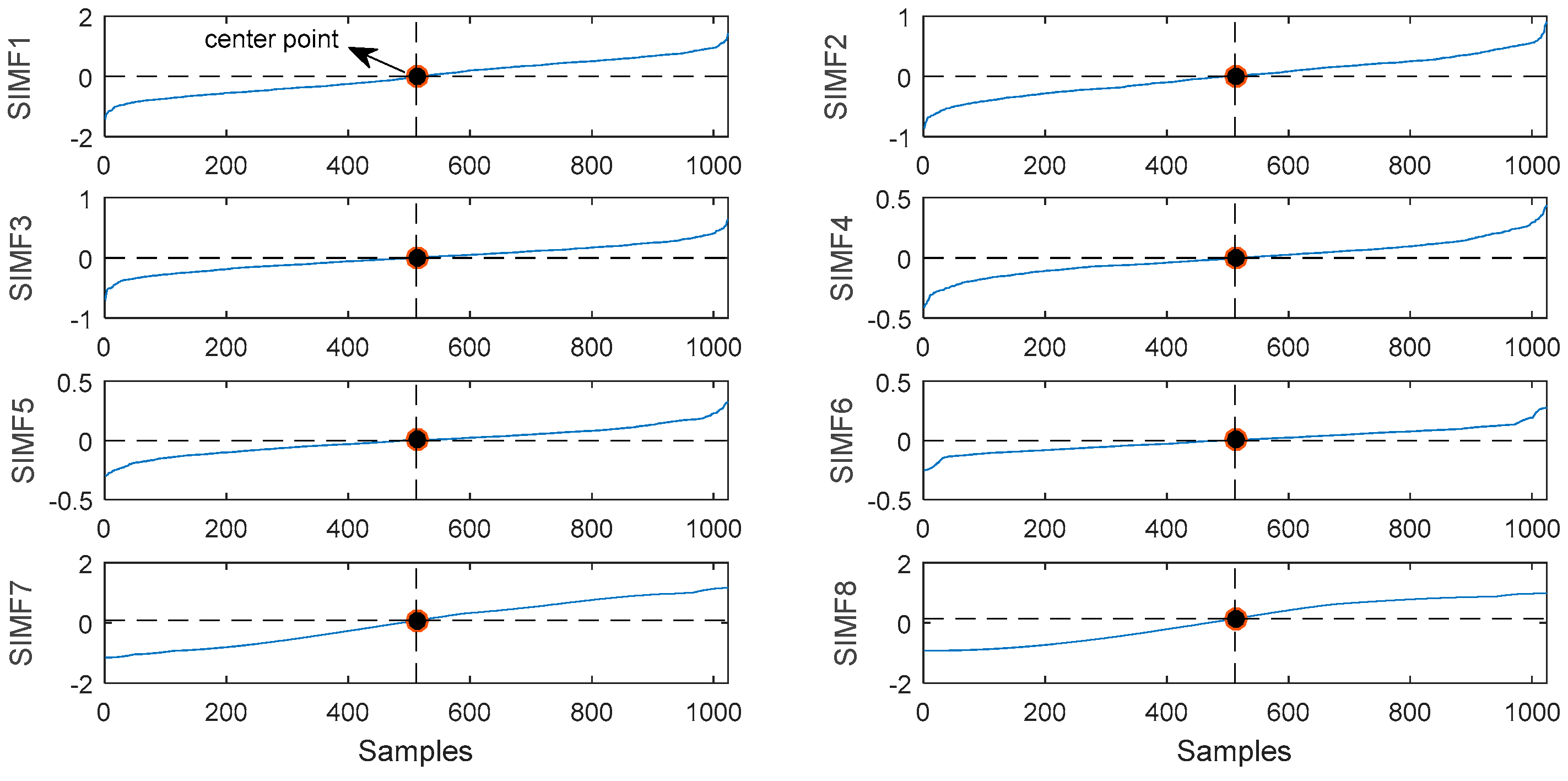
- Each IMF is sorted in ascending order, and the energy of the sorted data is calculated and then normalized to obtain a new waveform (the normalized new waveform is defined as NNW).
- (3)
- The complexity of each NNWi (except residue) is calculated by fuzzy entropy, and the value of fuzzy entropy is marked as Ei (i = 1, …, M − 1). Here, M is the number of modes by EMD or the improved version.
- (4)
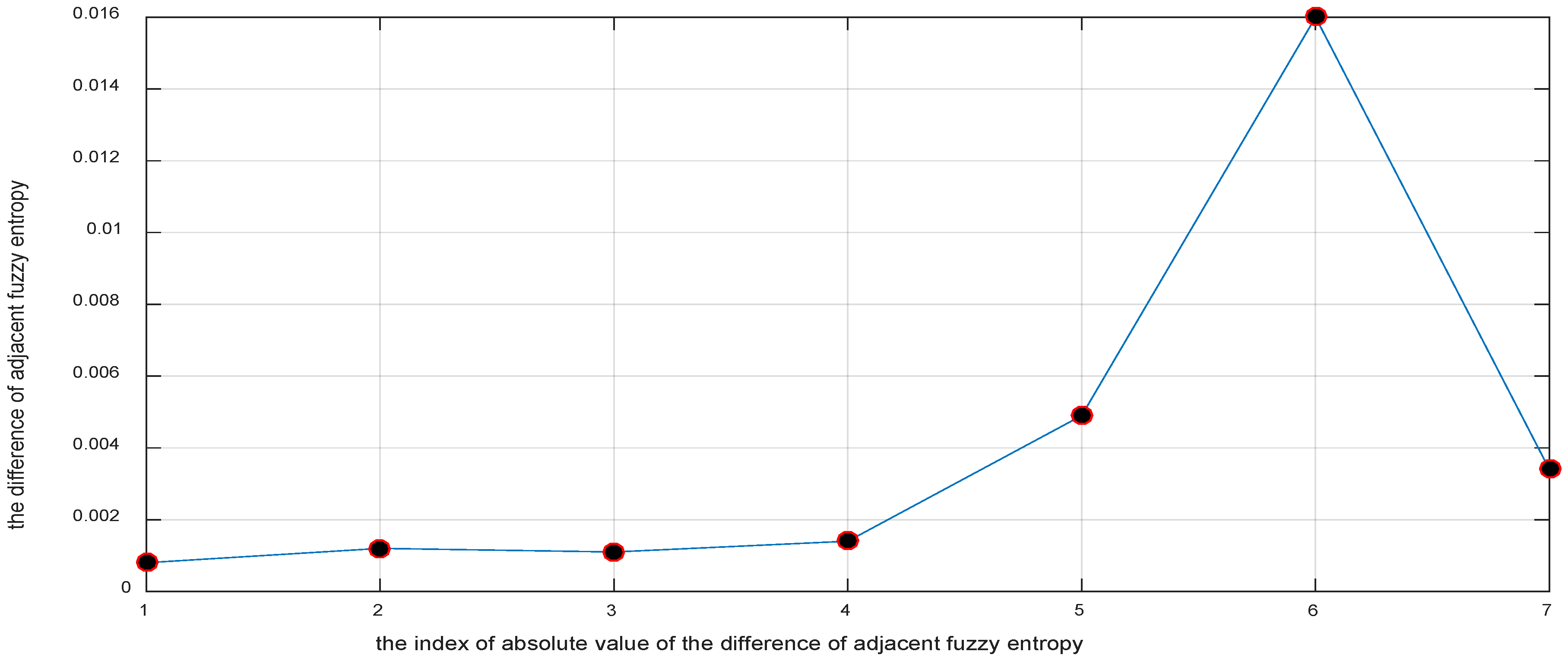
- The difference of adjacent Ei is obtained, and the absolute value of the difference is calculated.
- (5)
- The relevant mode is identified.
- (6)
- The filtered signal is obtained.
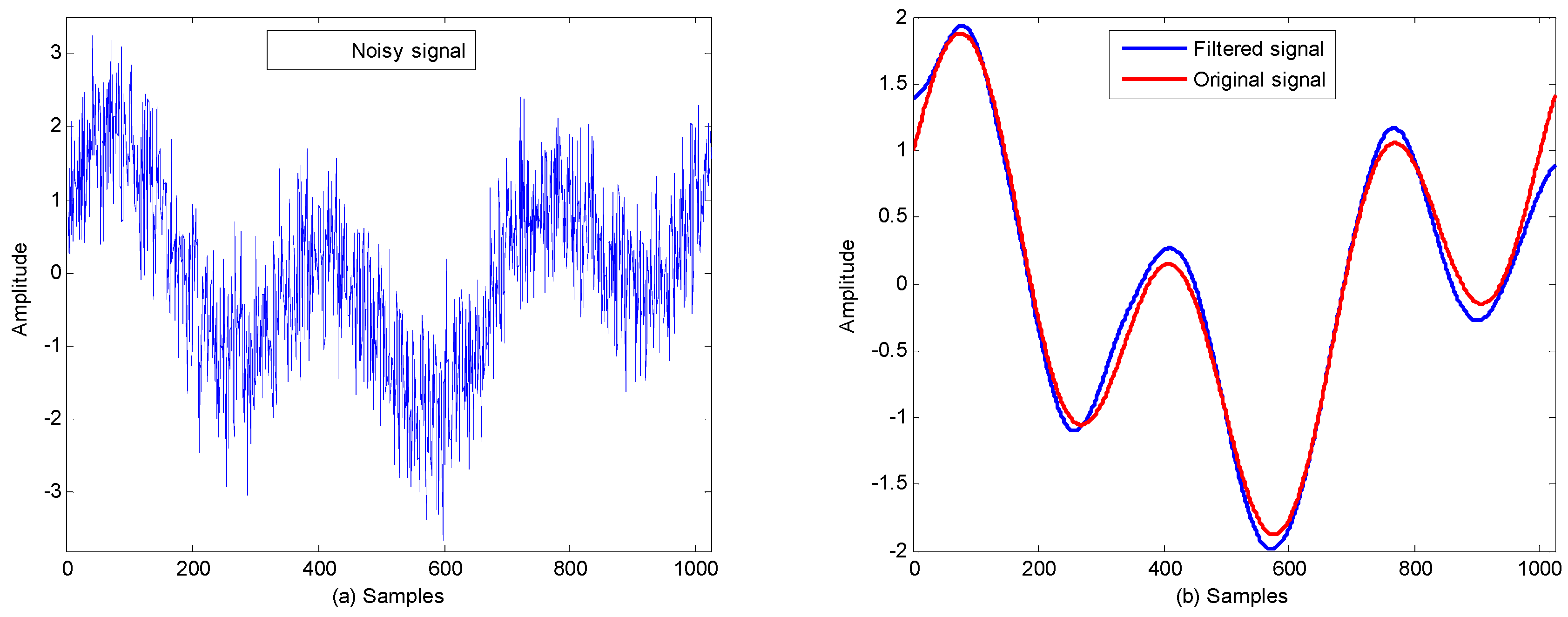
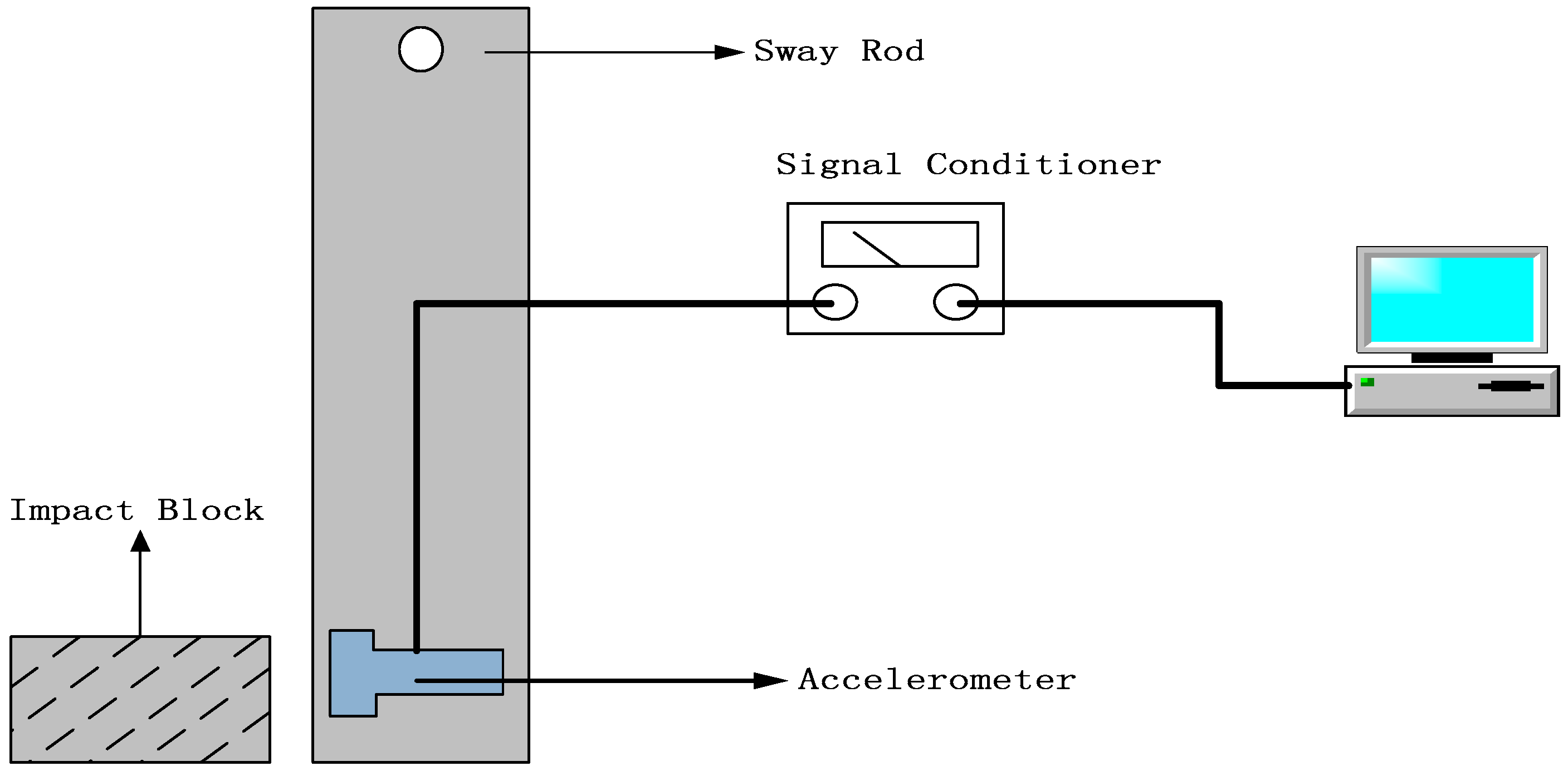
3.2. Application
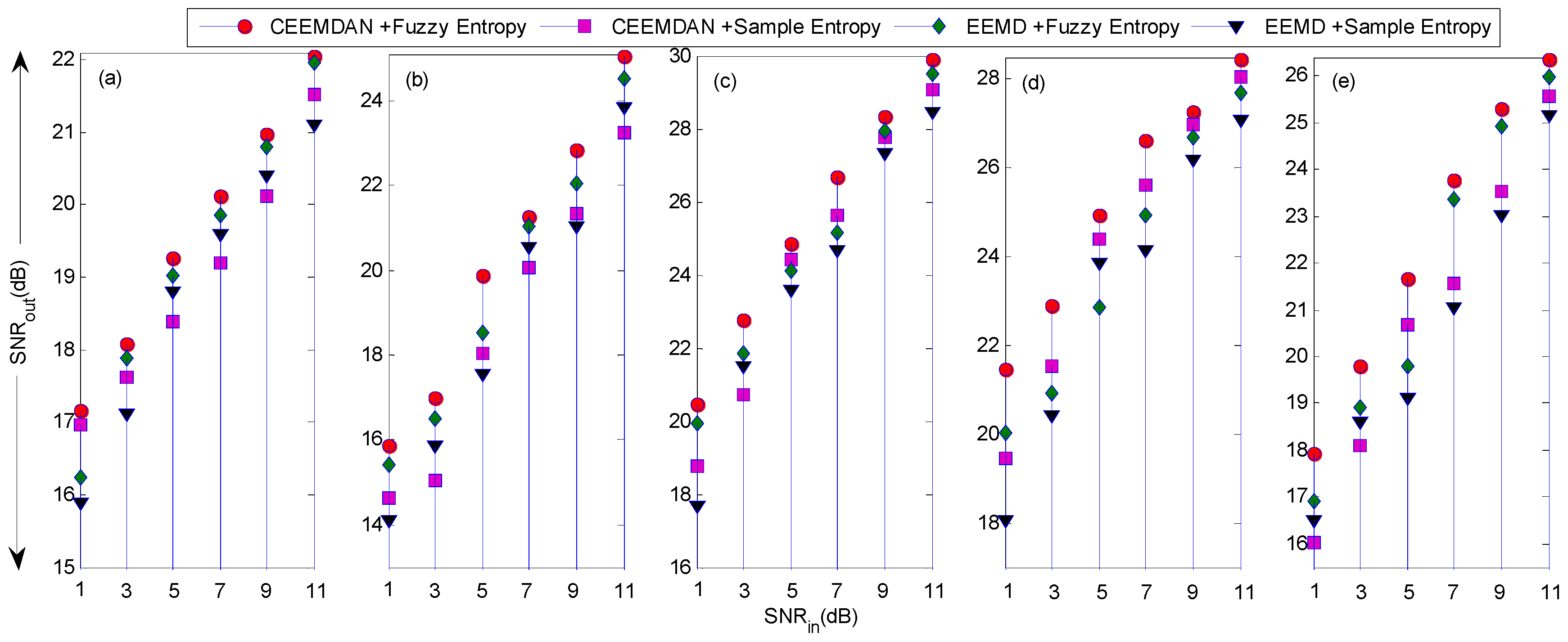
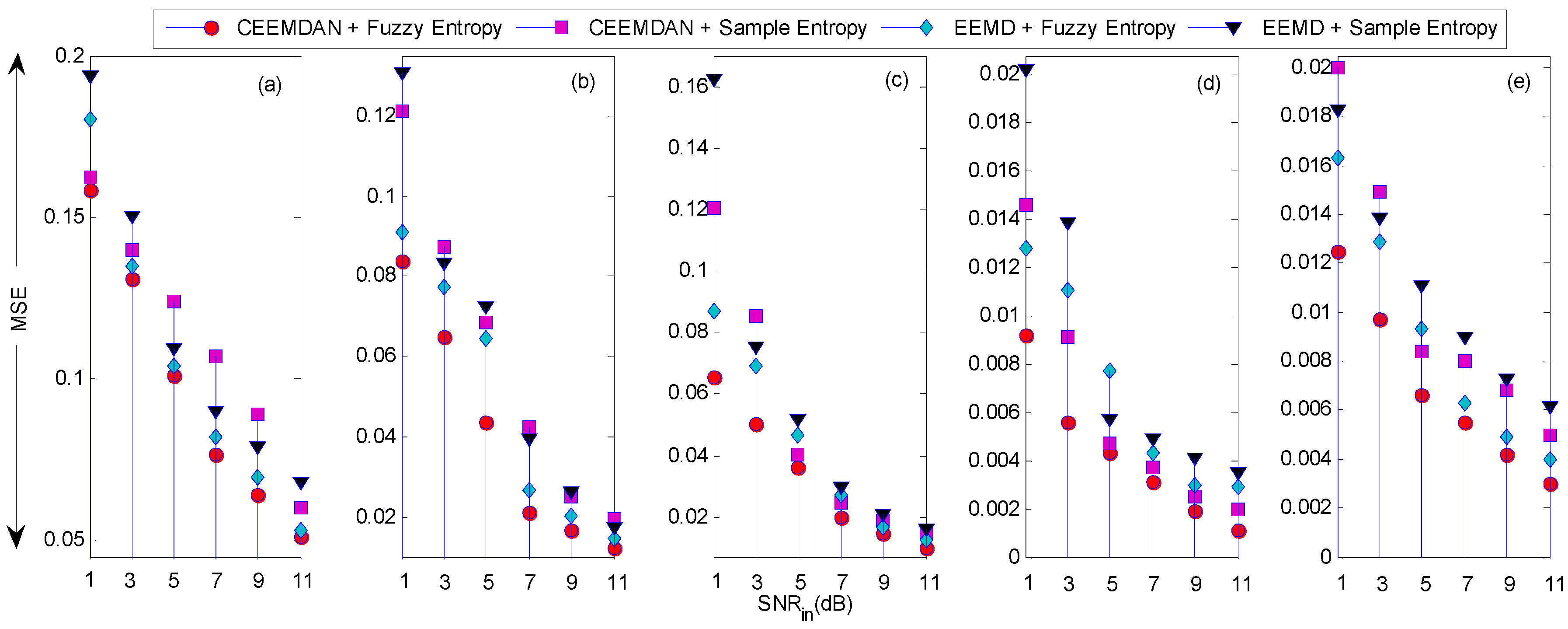
4. Results and Discussion
4.1. Simulated Signal Filtering
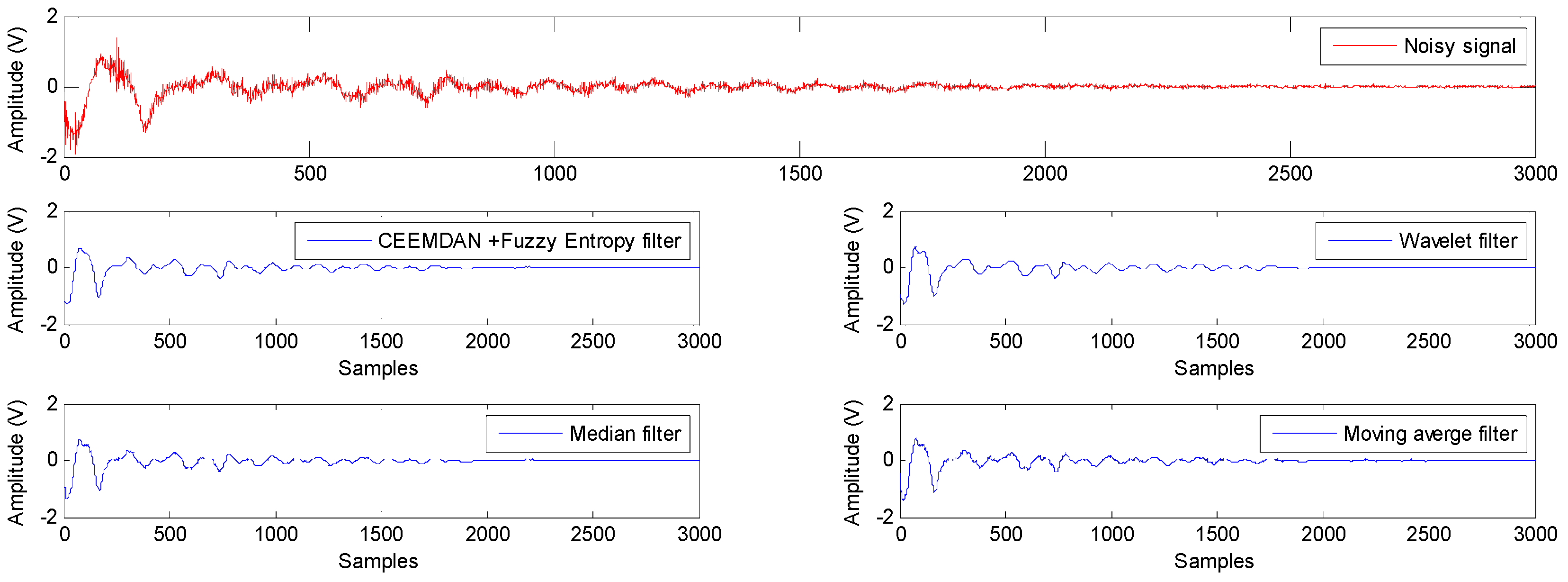
4.2. Impact Signal Filtering
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitooring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 310–314. [Google Scholar] [CrossRef]
- Feraboli, P.; Ireland, D.; Kedward, K. The Role of Force and Energy in Low Velocity Impact Events. In Proceedings of the 45th AIAA/AMSE/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Spring, CA, USA, 19–22 April 2004.
- Savadori, A. Impact testing of plastics: Present knowledge. Polym. Test. 1985, 5, 209–241. [Google Scholar] [CrossRef]
- Vandergheynst, P.; Antoine, J.P.; Vyve, E.V.; Goldberg, A.; Doghri, I. Modeling and simulation of an impact test using wavelets, analytical solutions and finite elements. Int. J. Solids Struct. 2001, 38, 5481–5508. [Google Scholar] [CrossRef]
- Liu, Y.; Liaw, B. Drop-weight impact tests and finite element modeling of cast acrylic/aluminum plates. Polym. Test. 2009, 28, 808–823. [Google Scholar] [CrossRef]
- Hazizan, M.A.; Cantwell, W.J. The low velocity impact response of an aluminium honeycomb sandwich structure. Compos. B Eng. 2003, 34, 679–687. [Google Scholar] [CrossRef]
- Proakis, J.G.; Mnaolakis, D.G. Digital Signal Processing: Principles, Algorithms, and Applications; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996; pp. 223–229. [Google Scholar]
- Goldstein, J.S.; Reed, I.S.; Scharf, L.L. A multistage representation of the Wiener filter based on orthogonal projections. IEEE Trans. Inf. Theory 1998, 44, 2943–2959. [Google Scholar] [CrossRef]
- Strela, V.; Heller, P.N.; Strang, G.; Topiwala, P.; Heil, C. The application of multiwavelet filterbanks to image processing. IEEE Trans. Image Process. 1999, 8, 548–563. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Huang, N.E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–905. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Emperical Mode Decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Ayenu-Prah, A.; Attohokine, N. A criterion for selecting relevant intrinsic mode functions in empirical mode decomposition. Adv. Adapt. Data Anal. 2010, 2, 1–24. [Google Scholar] [CrossRef]
- Peng, Z.K.; Tse, P.W.; Chu, F.L. A comparison study of improved Hilbert–Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Process. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Cexus, J.C. EMD-Based signal filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Komaty, A.; Boudraa, A.O.; Augier, B.; Daré-Emzivat, D. EMD-based filtering using similarity measure between probability density functions of IMFs. IEEE Trans. Instrum. Meas. 2014, 63, 27–34. [Google Scholar] [CrossRef]
- Yang, G.; Liu, Y.; Wang, Y.; Zhu, Z. EMD interval thresholding denoising based on similarity measure to select relevant modes. Signal Process. 2015, 109, 95–109. [Google Scholar] [CrossRef]
- Kopsinis, Y.; Mclaughlin, S. Development of EMD-Based Denoising Methods Inspired by Wavelet Thresholding. IEEE Trans. Signal Process. 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Mert, A.; Akan, A. Detrended fluctuation thresholding for empirical mode decomposition based denoising. Digit. Signal Process. 2014, 32, 48–56. [Google Scholar] [CrossRef]
- Siwal, D.; Suyal, V.; Prasad, A.; Mandal, S.; Singh, R. A new approach of denoising the regular and chaotic signals using Empirical Mode Decomposition: Comparison and application. Rev. Sci. Instrum. 2013, 84, 075117. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Chan, J.C.; Ma, H.; Saha, T.K.; Ekanayake, C. Self-adaptive partial discharge signal de-noising based on ensemble empirical mode decomposition and automatic morphological thresholding. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 294–303. [Google Scholar] [CrossRef]
- Fang, Y.-M.; Feng, H.-L.; Li, J.; Li, G.-H. Stress Wave Signal Denoising Using Ensemble Empirical Mode Decomposition and an Instantaneous Half Period Model. Sensors 2011, 11, 7554–7567. [Google Scholar] [CrossRef] [PubMed]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Process, Prague, Czech Republic, 22–27 May 2011.
- Humeau-Heurtier, A.; Abraham, P.; Mahe, G. Analysis of laser speckle contrast images variability using a novel empirical mode decomposition: Comparison of results with laser doppler flowmetry signals variability. IEEE Trans. Med. Imaging 2015, 34, 618–627. [Google Scholar] [CrossRef] [PubMed]
- Ye, R.; Suganthan, P.N.; Srikanth, N. A Comparative Study of Empirical Mode Decomposition-Based Short-Term Wind Speed Forecasting Methods. IEEE Trans. Sustain. Energy 2015, 6, 236–244. [Google Scholar]
- Li, C.; Zhan, L. A hybrid filtering method based on a novel empirical mode decomposition for friction signals. Meas. Sci. Technol. 2015, 26, 125003. [Google Scholar] [CrossRef]
- Li, C.; Zhan, L.; Shen, L. Friction Signal Denoising Using Complete Ensemble EMD with Adaptive Noise and Mutual Information. Entropy 2015, 17, 5965–5979. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wei, S.; Zhang, C.; Zhang, Y.; Jiang, X.; Liu, F.; Liu, C. Determination of Sample Entropy and Fuzzy Measure Entropy Parameters for Distinguishing Congestive Heart Failure from Normal Sinus Rhythm Subjects. Entropy 2015, 17, 6270–6288. [Google Scholar] [CrossRef]
- Leistedt, S.; Dumont, M.; Lanquart, J.P.; Jurysta, F.; Linkowski, P. Characterization of the sleep EEG in acutely depressed men using detrended fluctuation analysis. Clin. Neurophysiol. 2007, 118, 940–950. [Google Scholar] [CrossRef] [PubMed]
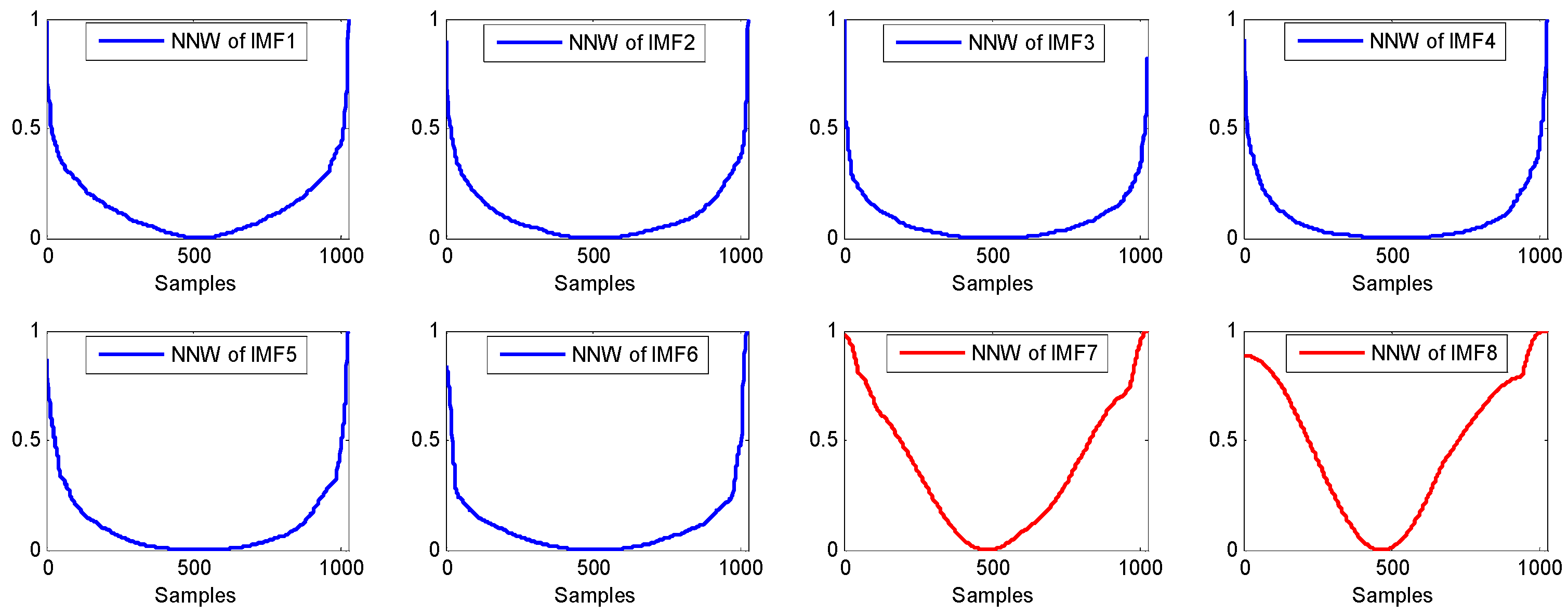
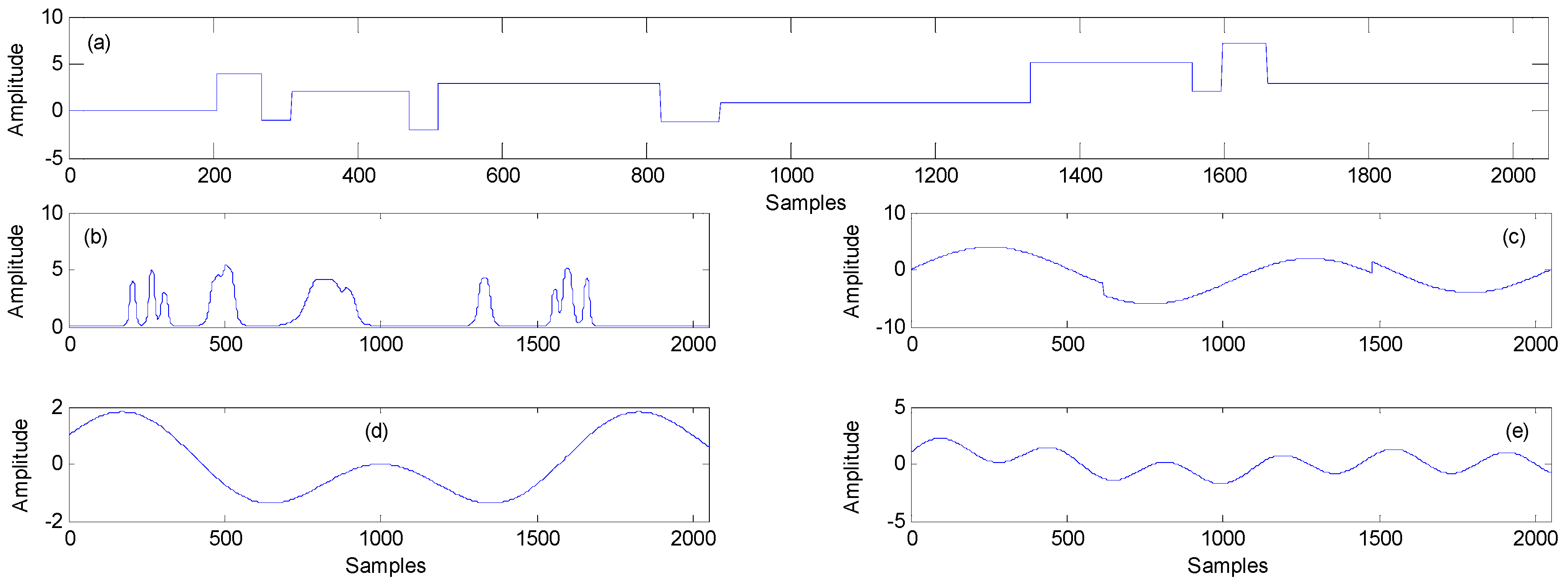
| Changed Waveform | NNW1 | NNW2 | NNW3 | NNW4 | NNW5 | NNW6 | NNW7 | NNW8 |
| Fuzzy Entropy | 0.0438 | 0.0446 | 0.0458 | 0.0469 | 0.0455 | 0.0406 | 0.0246 | 0.0212 |
| Order | Signal | Length of Data |
|---|---|---|
| a | Blocks | 2048 |
| b | Bumps | 2048 |
| c | Heavysine | 2048 |
| d | 2048 | |
| e | 2048 |
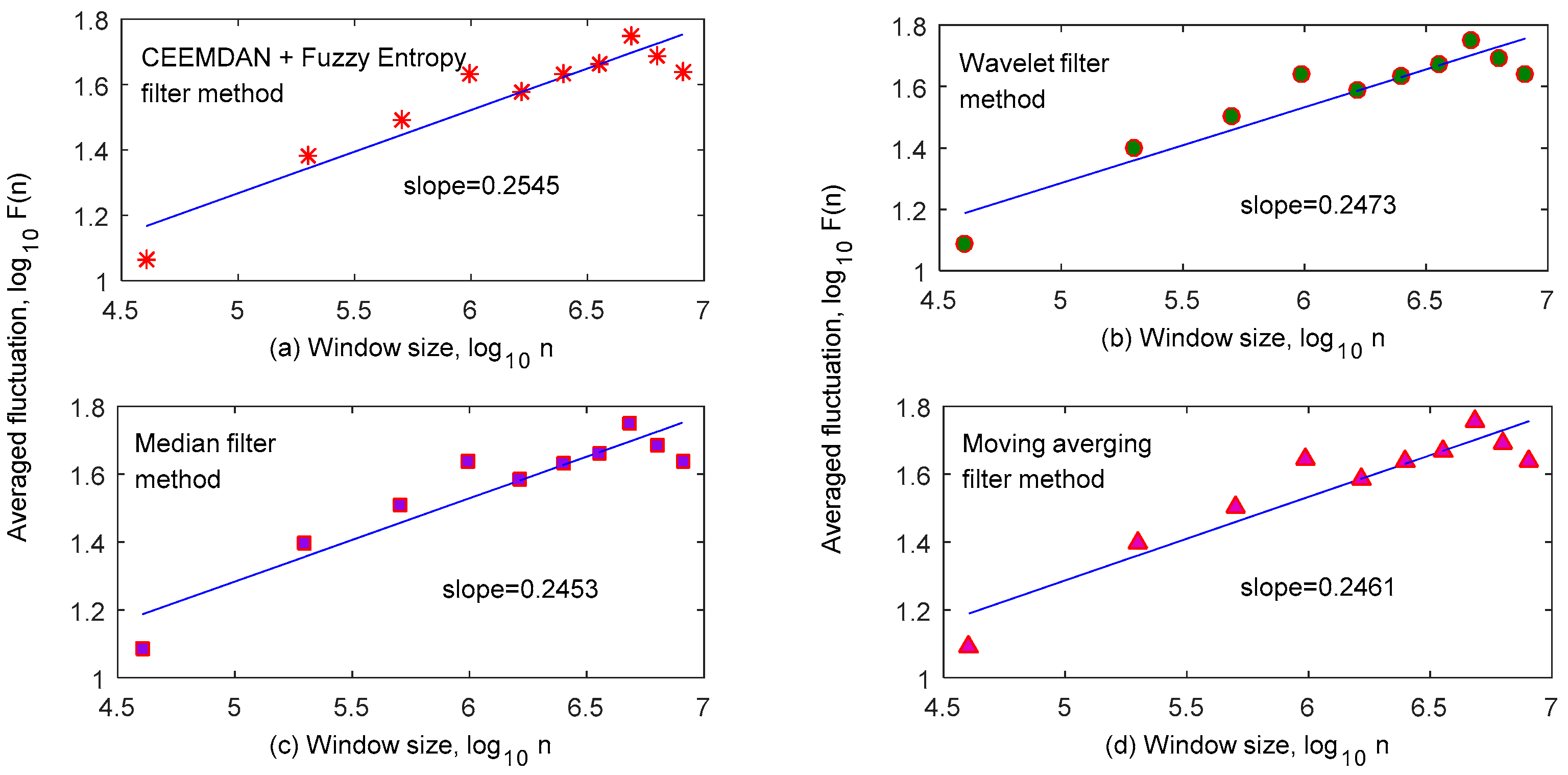
| Filter Method | RSNRout | RMSE | Fractal Scaling Index (α) |
|---|---|---|---|
| CEEMDAN | 7.5352 | 0.0086 | 0.2578 |
| Wavelet | 7.9124 | 0.0082 | 0.2473 |
| Median | 8.5065 | 0.0075 | 0.2453 |
| Moving Averaging | 8.2266 | 0.0080 | 0.2461 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, L.; Li, C. A Comparative Study of Empirical Mode Decomposition-Based Filtering for Impact Signal. Entropy 2017, 19, 13. https://doi.org/10.3390/e19010013
Zhan L, Li C. A Comparative Study of Empirical Mode Decomposition-Based Filtering for Impact Signal. Entropy. 2017; 19(1):13. https://doi.org/10.3390/e19010013
Chicago/Turabian StyleZhan, Liwei, and Chengwei Li. 2017. "A Comparative Study of Empirical Mode Decomposition-Based Filtering for Impact Signal" Entropy 19, no. 1: 13. https://doi.org/10.3390/e19010013
APA StyleZhan, L., & Li, C. (2017). A Comparative Study of Empirical Mode Decomposition-Based Filtering for Impact Signal. Entropy, 19(1), 13. https://doi.org/10.3390/e19010013





