Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet
Abstract
:1. Introduction
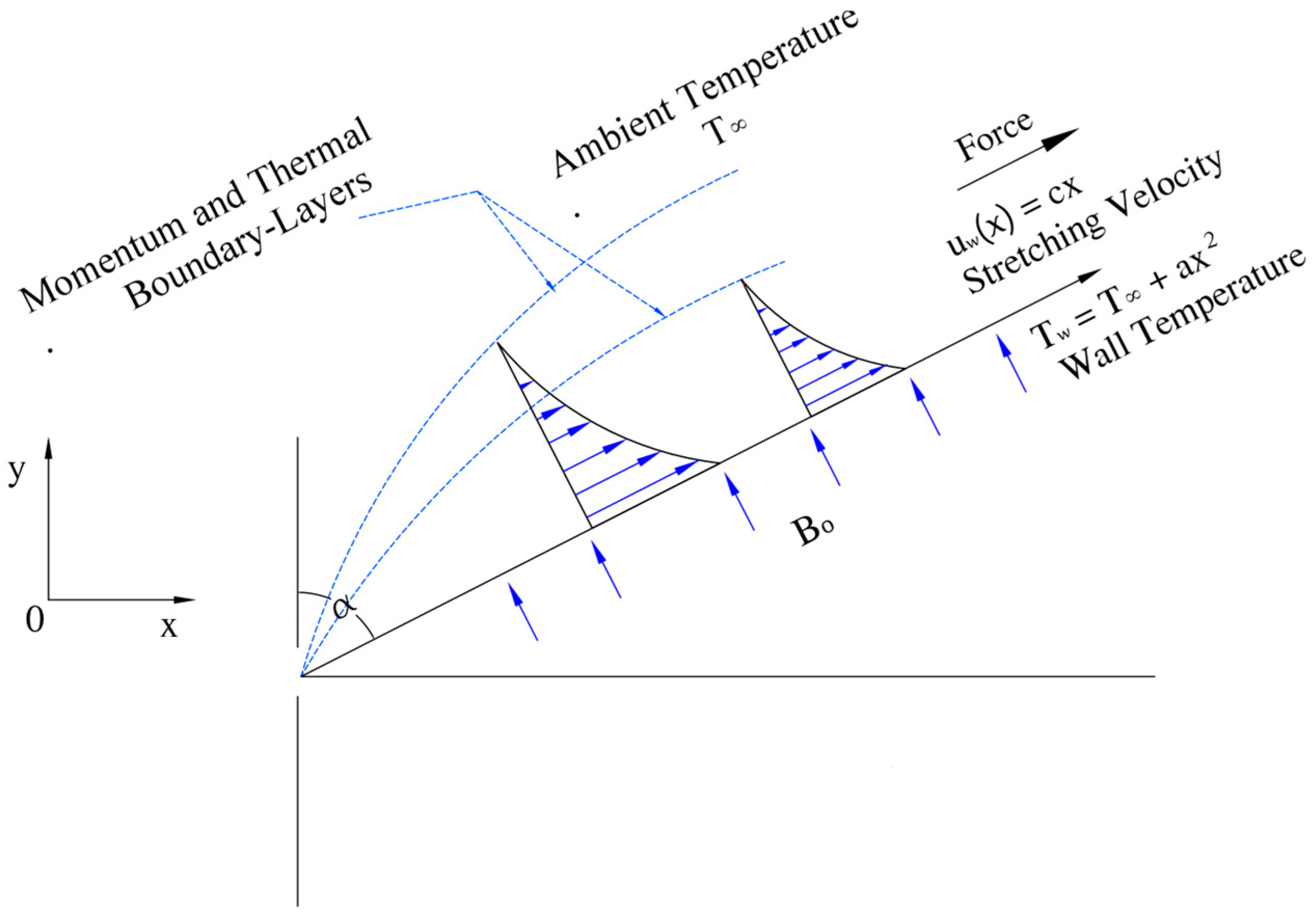
2. Mathematical Formulation of the Problem
3. Irreversibility Analysis
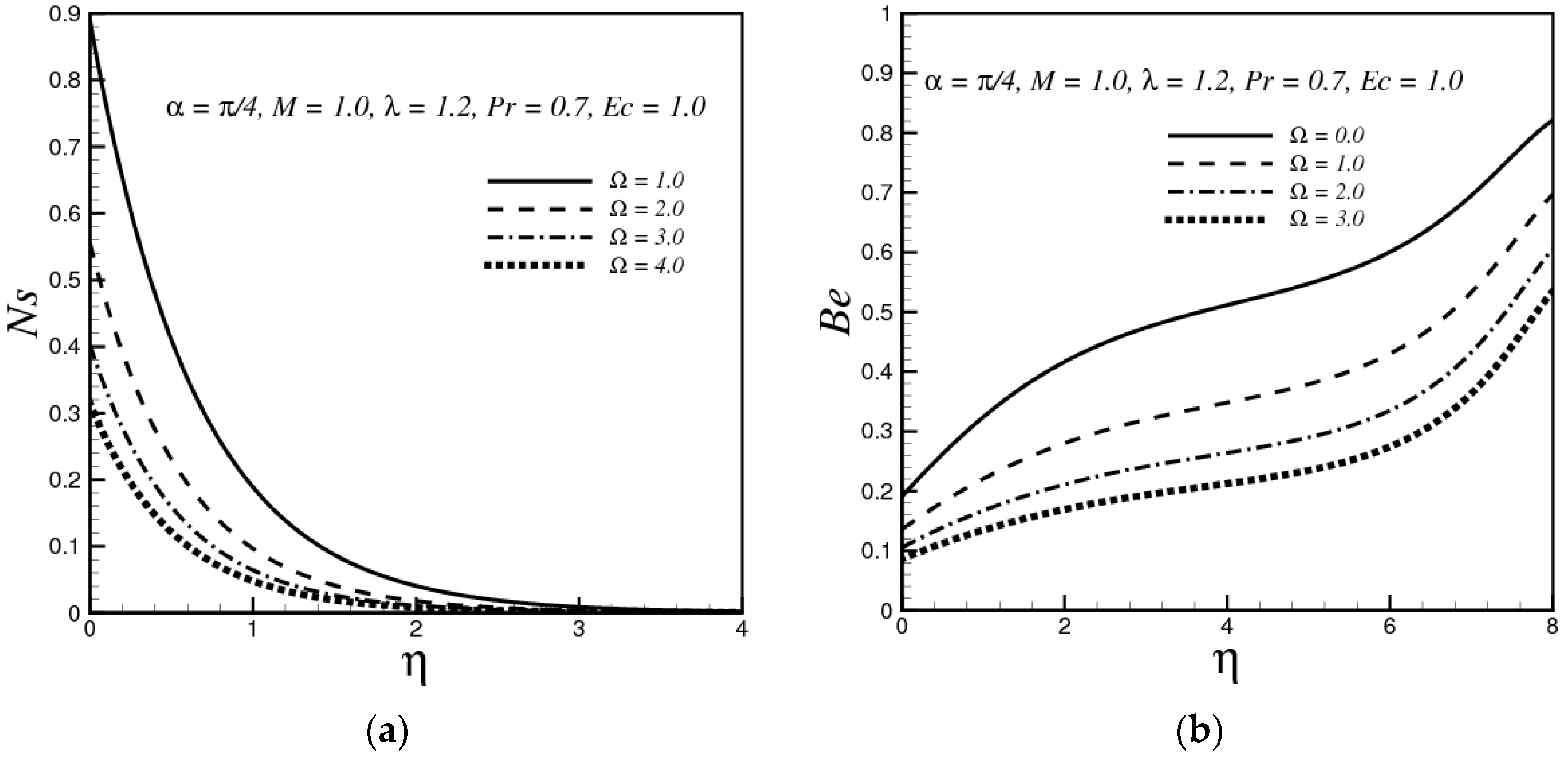
4. Results and Discussion
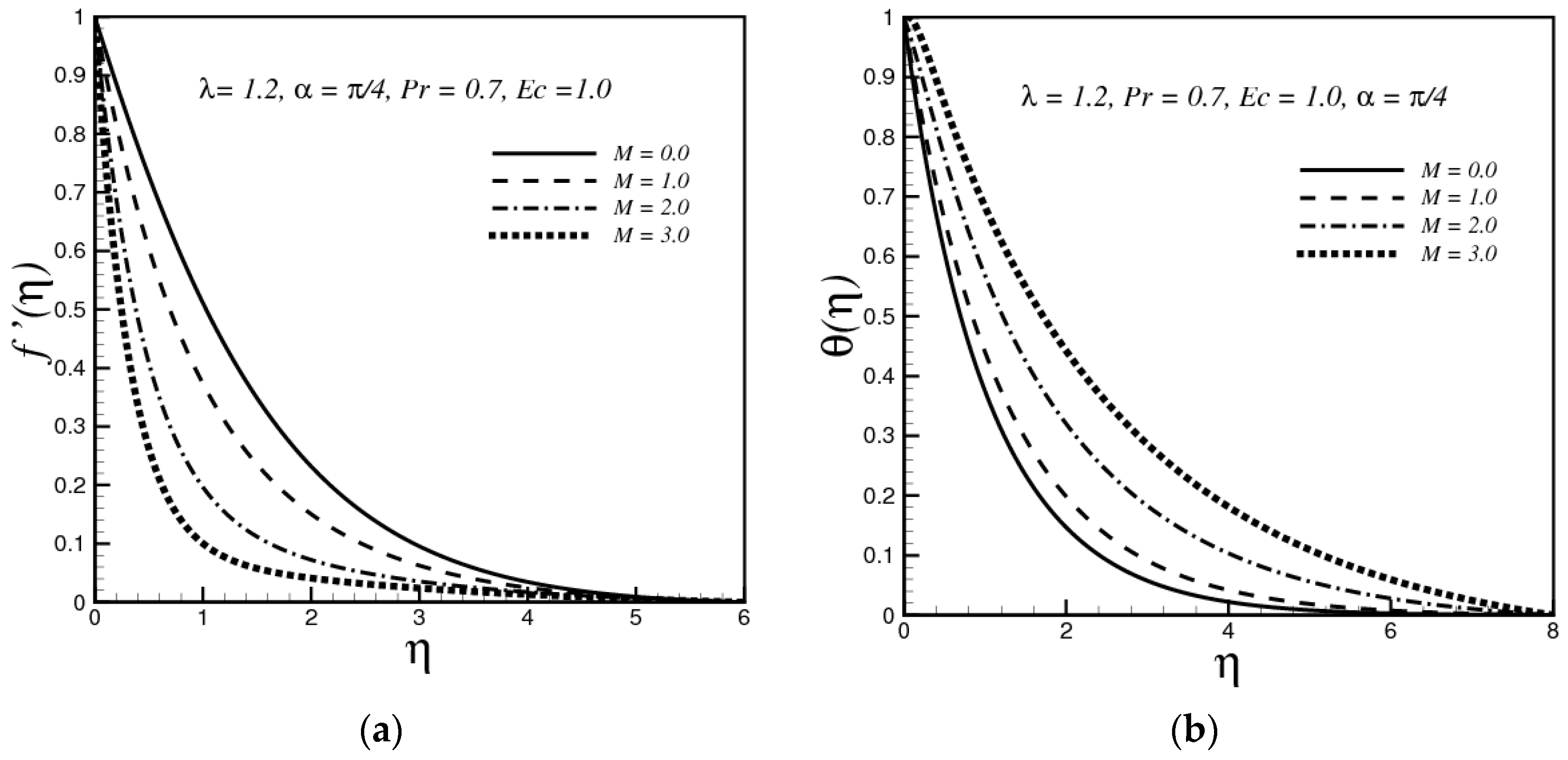
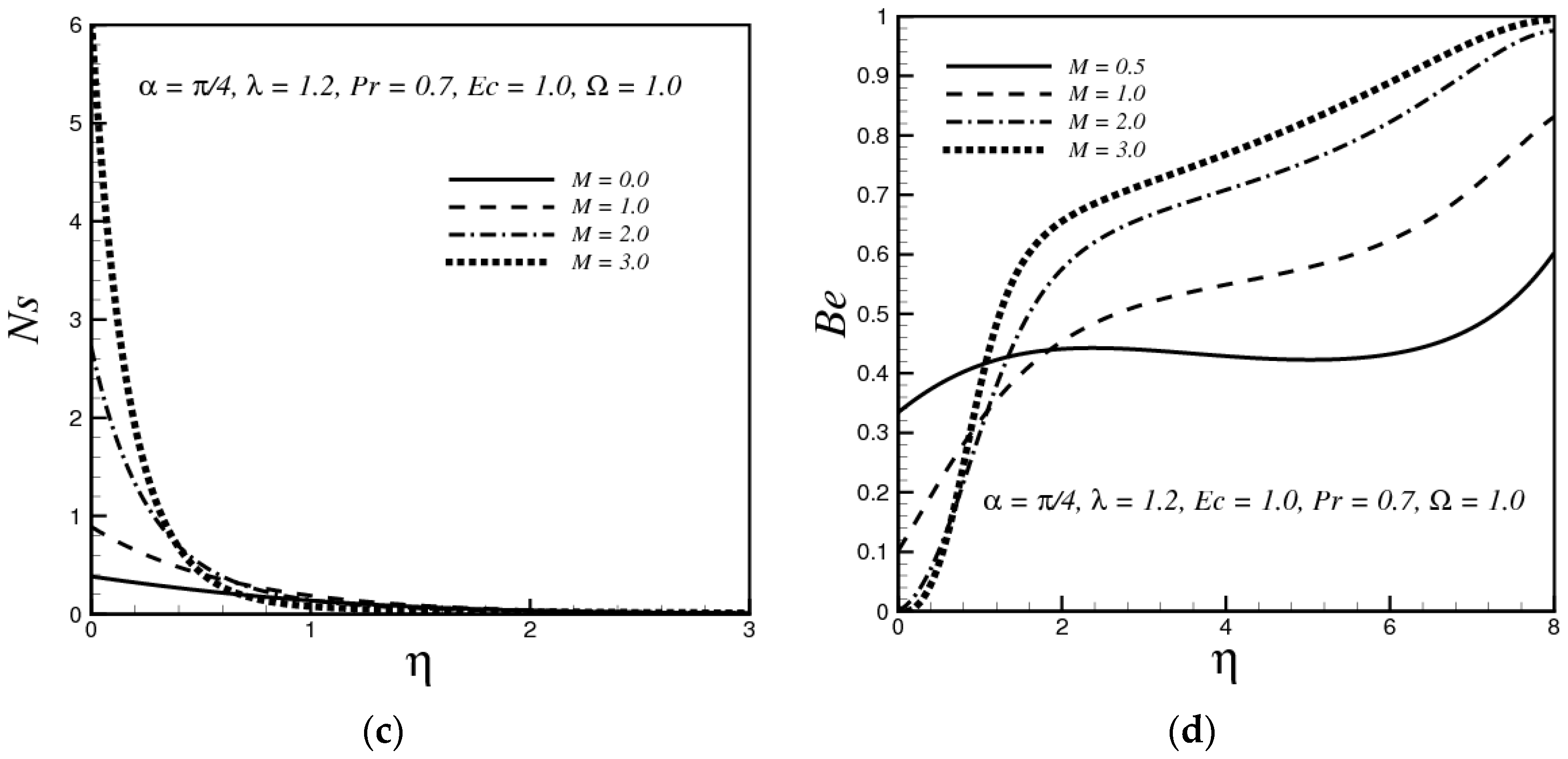
4.1. Effects of the Magnetic Field Parameter
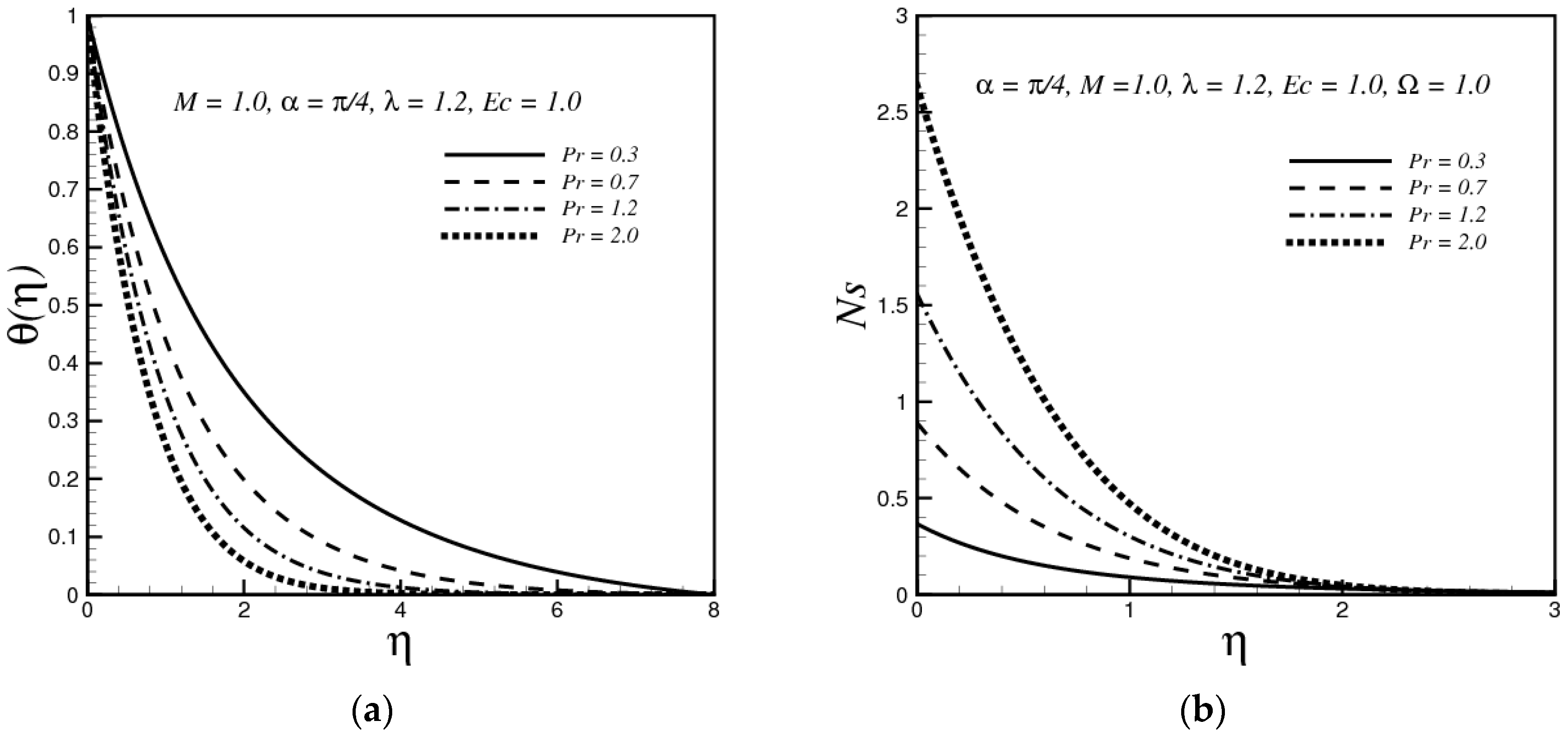
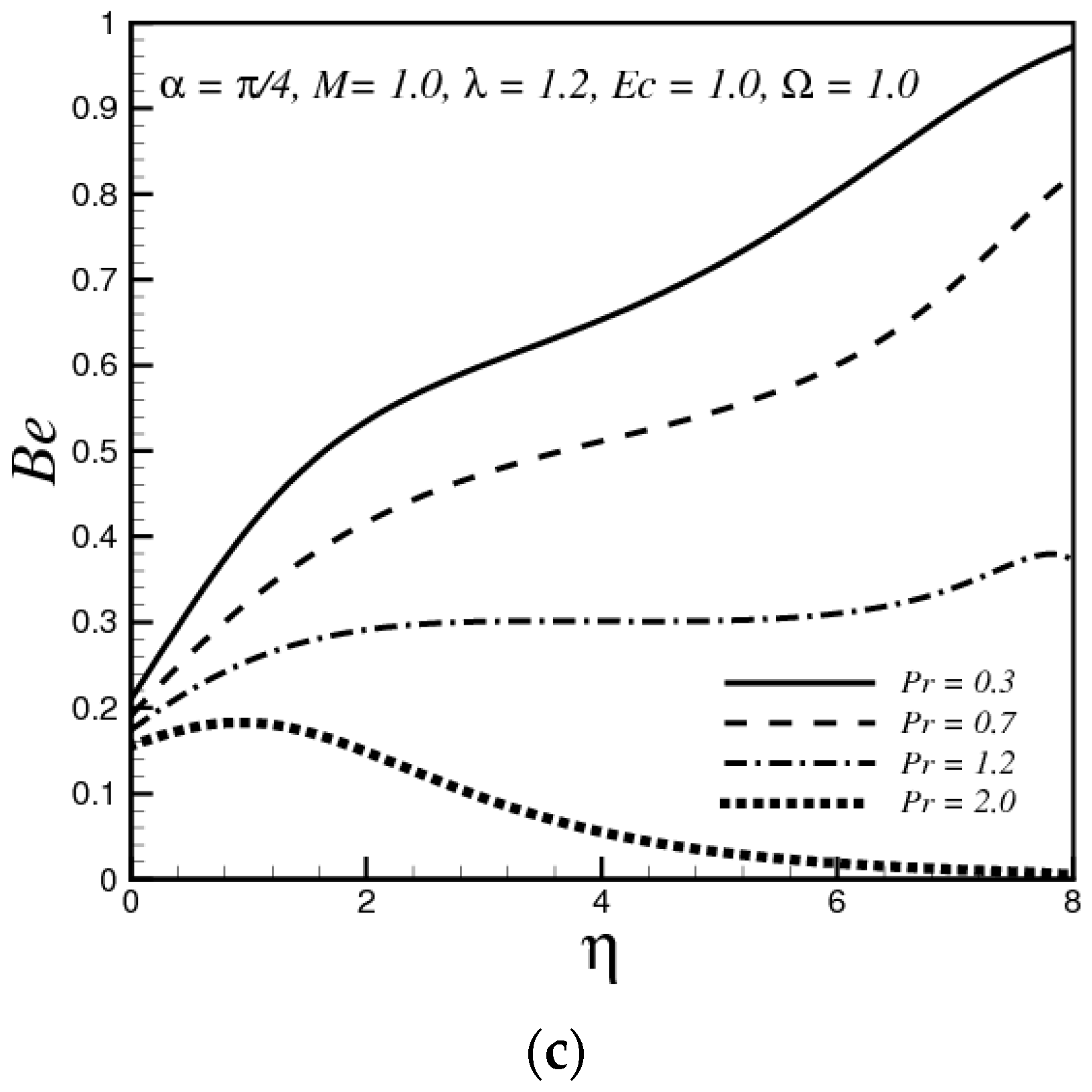
4.2. Effects of the Prandtl Number
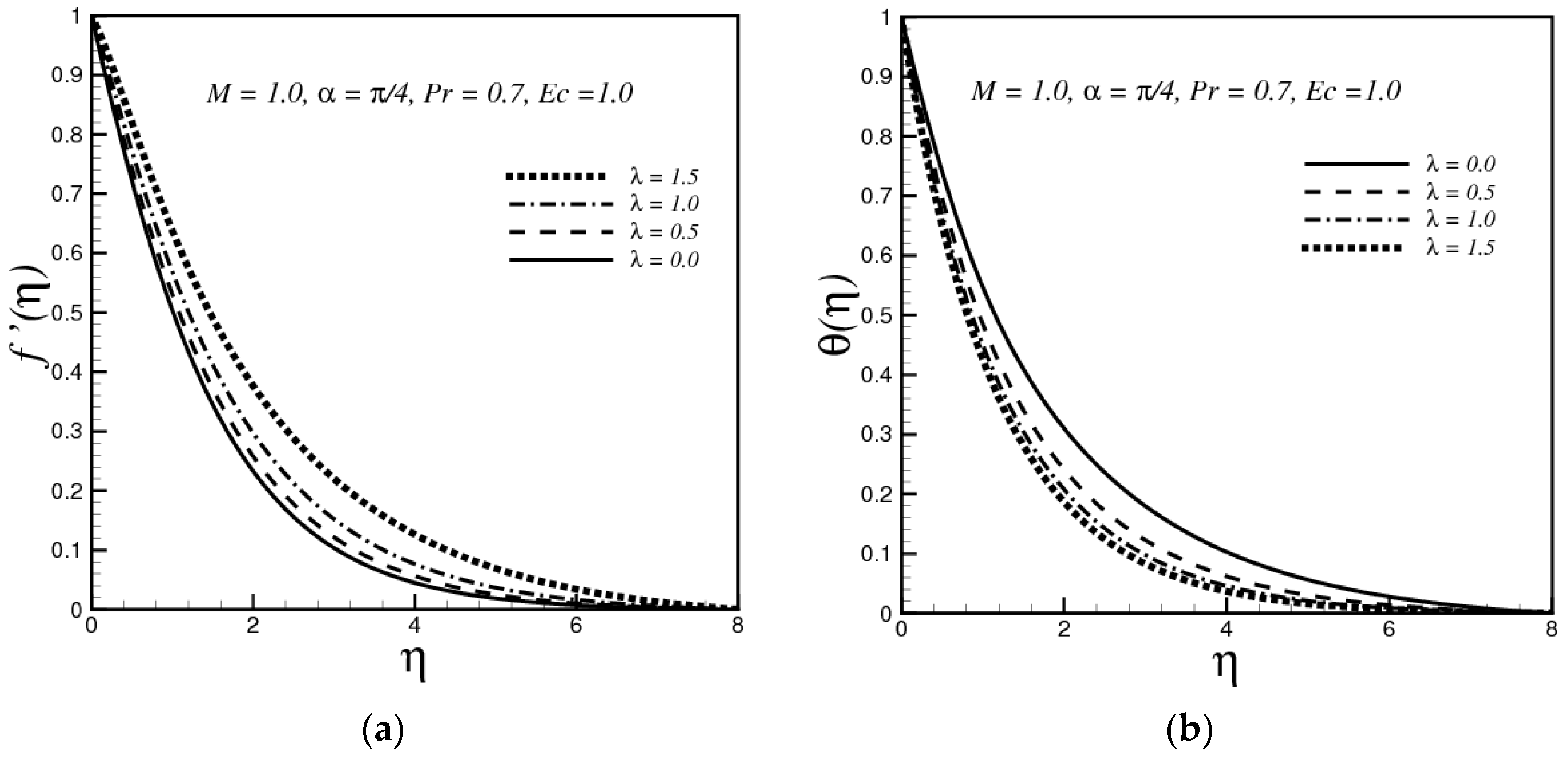
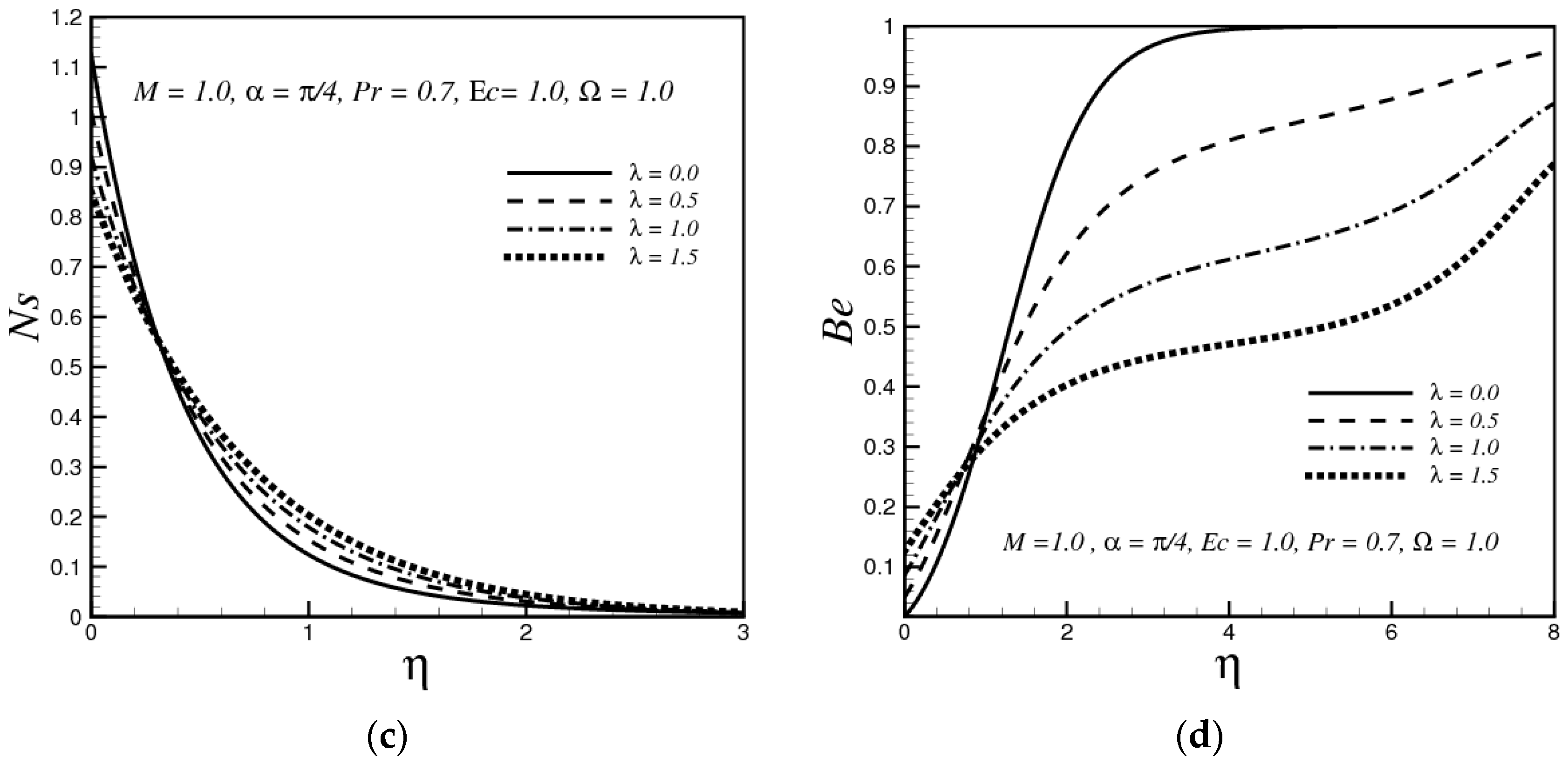
4.3. Effects of the Mixed Convective Parameter
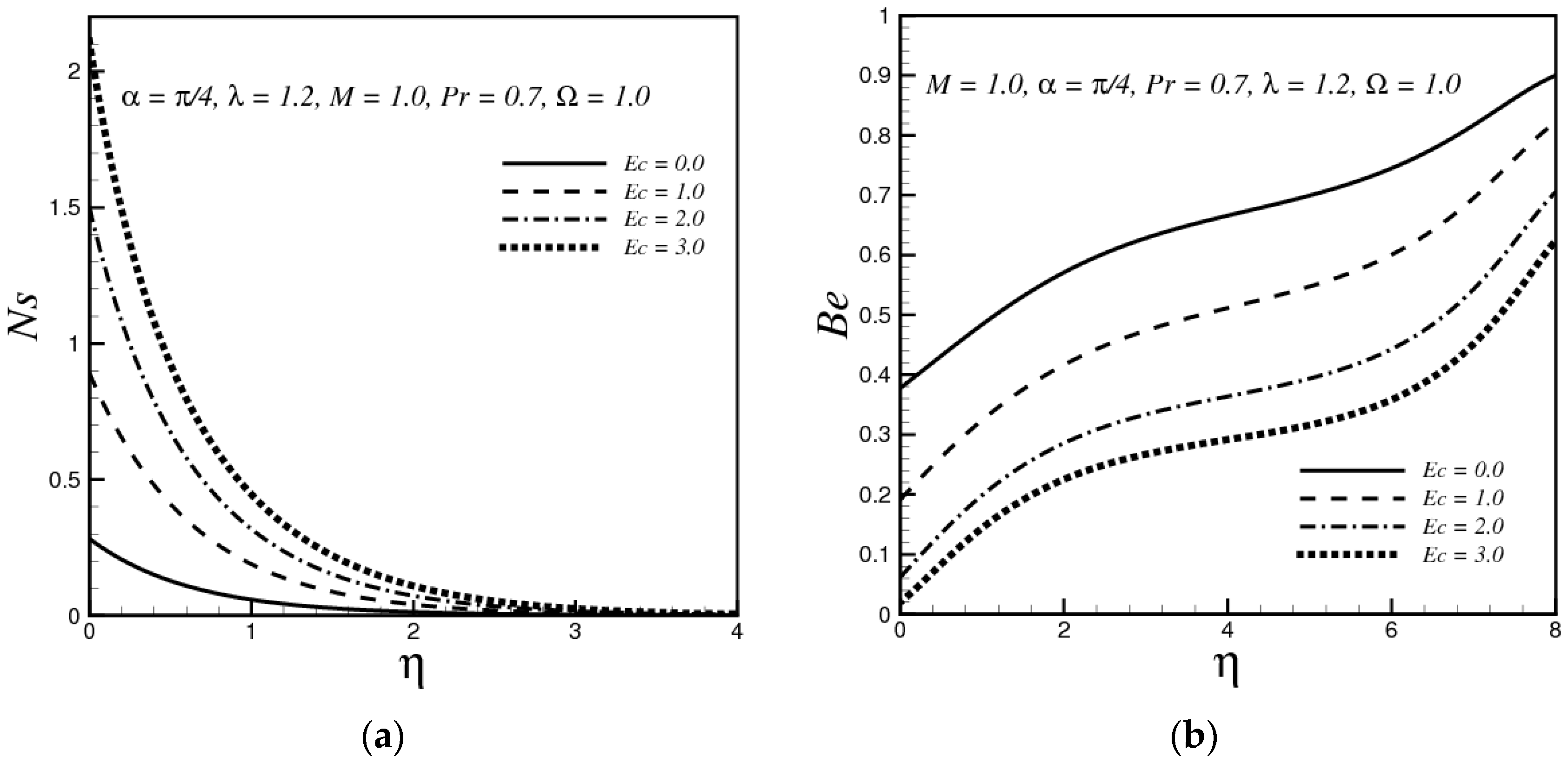
4.4. Effects of Eckert Number
4.5. Effects of the Dimensionless Temperature Parameter
5. Conclusions
- (1)
- It is observed that the velocity magnetic parameter M has a decreasing effect on the velocity while the thermal convective parameter λ has an increasing effect on it.
- (2)
- The thickness of the thermal boundary layer increases as the values of magnetic parameter and Eckert number increase, while a decreasing effect has been observed with the variation of thermal convective parameter and Prandtl number.
- (3)
- Increasing in magnetic parameter and Eckert number enhance the entropy generation while entropy generation decreases with the increasing values of the thermal convective parameter and dimensionless temperature function.
- (4)
- The Bejan number decreases by increasing the magnetic parameter, thermal convective parameter and it is decreased by increasing the Prandtl number and Eckert number.
- (5)
- The values of skin friction coefficient and local Nusselt number increases with the increase of Pr. There is a decrease in local Nusselt number for large values of M and Ec (see Table 1).
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| a | positive constant |
| Bo | applied constant magnetic field |
| Be | Bejan number |
| c | stretching velocity rate |
| Cp | specific heat at constant pressure |
| Ec | Eckert number |
| g | acceleration due to gravity |
| Grx | local Grashof number |
| J | electric current density |
| k | thermal conductivity of the fluid |
| M | magnetic field parameter |
| Ns | entropy generation number |
| Pr | Prandtl number |
| Rex | local Reynolds number |
| Ṡgen''' | volumetric entropy generation rate |
| Ṡo''' | characteristic volumetric entropy generation rate |
| T | temperature of the fluid |
| Tw(x) | wall temperature |
| T∞ | ambient temperature |
| u | velocity component in x direction |
| uw(x) | velocity of the stretching surface |
| v | velocity component in y direction |
| x, y | Cartessian coordinates along the surface and normal to it respectively |
Greeks Symbols
| α | inclination of the stretching sheet with y-axis |
| α* | thermal diffusitivity |
| β | coefficient of thermal expansion |
| η | similarity variable |
| θ | dimensionless temperature |
| μ | dynamic viscosity |
| ν | kinematic viscosity |
| ρ | density of the fluid |
| σ | electric conductivity |
| λ | mixed convection parameter/buoyancy parameter |
| Ω | dimensionless temperature parameter |
References
- Sakiadis, B.C. Boundary-layer behaviour on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Salleh, M.Z.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. J. Taiwan Inst. Chem. E. 2010, 41, 651–655. [Google Scholar] [CrossRef]
- Hsiao, K.L. MHD mixed convection of viscoelastic fluid over a stretching sheet with ohmic dissipation. J. Mech. 2008, 24, 29–34. [Google Scholar] [CrossRef]
- Hsiao, K.L. MHD stagnation point viscoelastic fluid flow and heat transfer on a thermal forming stretching sheet with viscous dissipation. Can. J. Chem. Eng. 2011, 89, 1228–1235. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 2013, 62, 526–533. [Google Scholar] [CrossRef]
- Qasim, M.; Noreen, S. Heat transfer in the boundary layer flow of a Casson fluid over a permeable shrinking sheet with viscous dissipation. Eur. Phys. J. Plus 2014, 129, 1–7. [Google Scholar] [CrossRef]
- Hsiao, K.L. Heat and mass mixed convection for MHD viscoelastic fluid past a stretching sheet with ohmic dissipation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1803–1812. [Google Scholar] [CrossRef]
- Mehmood, R.; Nadeem, S.; Akbar, N.S. Oblique stagnation flow of Jeffery fluid over a stretching convective surface: Optimal solution. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 454–471. [Google Scholar] [CrossRef]
- Makinde, O.D.; Mabood, F.; Khan, W.A.; Tshehla, M.S. MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J. Mol. Liq. 2016, 219, 624–630. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Mohamed, M.K.A.; Salleh, M.Z.; Ishak, A.; Pop, I. Stagnation point flow and heat transfer over a stretching/shrinking sheet in a viscoelastic fluid with convective boundary condition and partial slip velocity. Eur. Phys. J. Plus 2015, 130, 1–9. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. J. Magn. Magn. Mater. 2016, 407, 235–240. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Lee, C. MHD boundary layer flow over an unsteady shrinking sheet: Analytical and numerical approach. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 1339–1346. [Google Scholar] [CrossRef]
- Qasim, M.; Hayat, T.; Hendi, A.A. Effects of slip conditions on stretching flow with ohmic dissipation and thermal radiation. Heat Tran. Asian Res. 2011, 40, 641–654. [Google Scholar] [CrossRef]
- Huang, J.S.; Tsai, R.; Haung, K.H.; Haung, C.H. Thermal-diffusion and diffusion-thermo effects on natural convection along an inclined stretching surface in a porous medium with chemical reaction. Chem. Eng. Commun. 2011, 198, 453–461. [Google Scholar] [CrossRef]
- Qasim, M.; Hayat, T.; Obaidat, S. Radiation effect on the mixed convection flow of a viscoelastic fluid along an inclined stretching sheet. Z. Naturforsch. A 2012, 67, 195–202. [Google Scholar] [CrossRef]
- Sravanthi, C.S. Homotopy analysis solution of MHD slip flow past an exponentially stretching inclined sheet with Soret-Dufour effects. J. Niger. Math. Soc. 2016, 35, 208–266. [Google Scholar] [CrossRef]
- Eldahab, E.M.A.; Aziz, M.A.E. Blowing/Suction effect on hydromagnetic heat transfer by mixed convection from an inclined continuously stretching surface with internal heat generation/absorption. Int. J. Therm. Sci. 2004, 43, 709–719. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Bejan, A.; Kestin, J. Entropy generation through heat and fluid flow. J. Appl. Mech. 1983, 50, 475. [Google Scholar] [CrossRef]
- Makinde, O.D. Entropy generation in a liquid film falling along an inclined porous heated plate. Mech. Res. Commun. 2006, 33, 692–698. [Google Scholar] [CrossRef]
- Arikodlu, A.; Ozkol, I.; Komurgoz, G. Effects of slip on entropy generation in a single rotating disk in MHD flow. Appl. Energy 2008, 85, 1225–1236. [Google Scholar] [CrossRef]
- Tamayol, A.; Hooman, K.; Bahrami, M. Thermal analysis of flow in a porous medium over a permeable stretching wall. Transp. Porous Med. 2010, 85, 661–676. [Google Scholar] [CrossRef]
- Reveillere, A.; Baytas, A.C. Minimum entropy generation for laminar boundary layer flow over a permeable plate. Int. J. Exergy 2010, 7, 164–177. [Google Scholar] [CrossRef]
- Makinde, O.D.; Eegunjobi, A.S.; Tshehla, M.S. Thermodynamics analysis of variable viscosity hydromagnetic Couette flow in a rotating system with Hall effects. Entropy 2015, 17, 7811–7826. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Entropy analysis of nanofluid flow over a convectively heated radially stretching disk embedded in a porous medium. J. Nanofluids 2016, 5, 48–58. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy effects in hydromagnetic free convection flow past a vertical plate embedded in a porous medium in the presence of thermal radiation. Eur. J. Phys. Plus 2013, 128, 1–15. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy analysis of magneto hydrodynamic flow and heat transfer due to a stretching cylinder. J. Taiwan Inst. Chem. Eng. 2014, 45, 780–786. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Analysis of entropy generation effects in flow and heat transfer of viscous fluid through a porous medium between two radially stretching surfaces. Int. J. Exergy 2015, 18, 501–520. [Google Scholar] [CrossRef]
- Makinde, O.D.; Olanrewaju, P.O. Buoyancy effects on thermal boundary layer over a vertical late with a convective surface boundary conditions. J. Fluids Eng. 2010, 132, 1–4. [Google Scholar] [CrossRef]
- Makinde, O.D. Similarity solution for natural convection from a moving vertical plate with internal heat generation and a convective boundary condition. Therm. Sci. 2011, 15, 137–143. [Google Scholar]
- Mushtaq, M.; Asghar, S.; Hossain, M.A. Mixed convection flow of second grade fluid along a vertical stretching flat surface with variable surface temperature. Heat Mass Transf. 2007, 43, 1049–1061. [Google Scholar] [CrossRef]
- Vyas, P.; Srivastava, N. On dissipative radiactive MHD boundary layer flow in a porous medium over a non-isothermal stretching sheet. J. Appl. Fluid Mech. 2012, 5, 23–31. [Google Scholar]
- Abel, M.S.; Begum, G. Heat transfer in MHD viscoelastic fluid flow on stretching sheet with heat source/sink, viscous dissipation, stress work, and radiation for the case of large Prandtl number. Chem. Eng. Commun. 2008, 195, 1503–1523. [Google Scholar] [CrossRef]
| λ | Pr = 0.7; Ec = 1.0; α = π/4; M = 1 | |
| 0.0 0.5 1.0 1.5 | 1.4142 1.2427 1.0886 0.9439 | 0.5546 0.6976 0.7931 0.8974 |
| M | Pr = 0.7; Ec = 1.0; α = π/4; λ = 0.5 | |
| 0.0 0.5 1.0 1.5 | 0.8155 0.9359 1.2427 1.6479 | 0.9293 0.8659 0.6976 0.4685 |
| Pr | M = 1.0; λ = 0.2; α = π/4; Ec = 1.0 | |
| 0.3 0.7 1.2 1.5 | 1.3284 1.3424 1.3516 1.3552 | 0.3897 0.6219 0.8106 0.8962 |
| Ec | M = 1.0; λ = 0.2; α = π/4; Pr = 1.2 | |
| 0.0 0.3 0.6 0.9 | 1.3603 1.3576 1.3551 1.3525 | 1.3873 1.2125 1.0393 0.8675 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afridi, M.I.; Qasim, M.; Khan, I.; Shafie, S.; Alshomrani, A.S. Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet. Entropy 2017, 19, 10. https://doi.org/10.3390/e19010010
Afridi MI, Qasim M, Khan I, Shafie S, Alshomrani AS. Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet. Entropy. 2017; 19(1):10. https://doi.org/10.3390/e19010010
Chicago/Turabian StyleAfridi, Muhammad Idrees, Muhammad Qasim, Ilyas Khan, Sharidan Shafie, and Ali Saleh Alshomrani. 2017. "Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet" Entropy 19, no. 1: 10. https://doi.org/10.3390/e19010010
APA StyleAfridi, M. I., Qasim, M., Khan, I., Shafie, S., & Alshomrani, A. S. (2017). Entropy Generation in Magnetohydrodynamic Mixed Convection Flow over an Inclined Stretching Sheet. Entropy, 19(1), 10. https://doi.org/10.3390/e19010010






