1. Introduction
Hundreds of thousands of humans have died in the two most recent giant tsunami tragedies. The Indian Ocean tsunami on 26 December 2004 was among the worst natural tragedies in human history, with human life losses exceeding 300,000 and destructive damage to buildings and infrastructure far beyond the 186 bridges damaged by the tsunami on Sumatra Island [
1]. The tragedy of the Great Eastern Japan Tsunami on 11 March 2011 recorded more than 15,883 deaths and more than 300 bridges experiencing significant destruction. Similar to a tsunami disaster, on 29 August 2005 in the United States, Hurricane Katrina caused substantial destruction on the Gulf Coast where more than 1800 people died, huge numbers of buildings were destroyed and 45 bridges suffered damage [
2].
Figure 1 illustrates two bridges affected by the Japan Tsunami. It can be concluded that the vital role of a bridge in a high tsunami hazard zone is a reminder to the international scientific community to evaluate, simulate and finally estimate in-depth the tsunami load induced on coastal bridges. A safe design structure for predicting the tsunami load influence on coastal structures requires careful consideration.
Figure 1.
(a) Damaged piers of the JR Rail Viaduct at the Tsuya River (photo: S. Dashti); (b) Damages to the deck and piers of Utatsu Bridge (Photo: Kenji Kosa).
Figure 1.
(a) Damaged piers of the JR Rail Viaduct at the Tsuya River (photo: S. Dashti); (b) Damages to the deck and piers of Utatsu Bridge (Photo: Kenji Kosa).
Researchers have conducted many valuable experimental studies of tsunami forces on bridges after the huge 2004 Indian Ocean tsunami disaster and 2011 Japan events. A preliminary laboratory examination evaluating the influence of tsunami wave forces on bridges was carried out by Kataoka
et al. [
3] and continued by other researchers [
4,
5,
6]. Hydraulic experiments were performed to assess tsunami wave loads on bridges and have shown that the impulsive load and uplift force are characteristic of the wave condition. Araki
et al. [
7] performed an experiment to evaluate the tsunami wave acting on a girder bridge beam. The result indicated that the bridge was influenced by a high amount of horizontal and vertical forces. It was also found that the horizontal force was considerably related to the tsunami height. Thusyanthan and Martinez [
8] stated that the highest value of impact pressure in case of a tsunami wave occurred at the bottom of the piers. Shoji
et al. [
9] conducted hydraulic tests to evaluate breaker bores on the valuation of the drag coefficient. They evaluated the effect of variations of the deck level on a variety of horizontal wave forces on a tsunami wave force. The results stated that the drag coefficient was 1.52 in the condition of surging breaker bores and 1.56 in the case of plunging bores. Lukkunaprasit and Lau [
10] and Lau [
11] evaluated tsunami loads due to tsunami bore in an inland bridge in two cases of a stand-alone pier and a complete bridge. They stated that the tsunami pressure in the case of a complete pier and deck was 50% higher than in the case of a stand-alone pier model. Hayatdavoodi
et al. [
12] evaluated the vertical and horizontal load on the bridge deck. The result showed that for shallow water, there was no effect on positive horizontal forces, but there were increases in the negative horizontal forces.
The results of the above studies could not be utilized to estimate the tsunami bore forces on bridges over water. In order to simplify the model fabrication, the piers of bridge models are assumed to be very thin in [
3,
4,
6]. However, in the research [
7,
9,
12], the effect of the tsunami on a complete pier and deck was neglected. This leads to reduced tsunami wave forces on the bridge models in hydraulic experiments. Lukkunaprasit and Lau [
10] studied the influence of tsunami bore on a bridge located in a dry bed but did not evaluate the tsunami bore force on coastal bridges over shallow water. Furthermore, all models except for Thusyanthan and Martinez [
8] utilized acrylic plates to construct the bridge models. Application of the acrylic plate resulted in decreased measured force by load cells due to reduction of the stiffness, weight of the model and increase in the flexibility of the models [
13]. Furthermore, air can be trapped which leads to exaggerated uplift and reduced drag forces. In order to overcome these problems and accurately estimate the bore force on coastal bridge, a more realistic bridge model was applied which utilizes actual materials for both piers and decks. For accurate evaluation, a six-axis load cell was employed in the experiment process.
Analysis of the tsunami bore forces on a coastal bridge require accurate on-line identification. In this article, we motivate and introduce an estimation model of tsunami bore forces including uplift force, drag force and overturning moment on a coastal bridge using a soft computing approach, namely Extreme Learning Machine (ELM). Currently, the application of modern computational approaches in determining the significant challenges and evaluating accurate values has drawn increased attention from scientists in various disciplines,
i.e., [
14,
15,
16]. Neural network (NN), as one of the efficient computational methods, has been developed recently in numerous engineering fields. This technique is able to determine challenging nonlinear issues which might be very difficult to eliminate by employing well-known parametric techniques.
Learning time requirement is a main shortcoming of NN techniques
. Consequently, an algorithm for a single layer feed forward NN, identified as Extreme Learning Machine (ELM), was presented by Huang
et al. [
17]. This algorithm is capable of solving problems caused by gradient descent-based algorithms like back propagation which are applied to artificial neural networks (ANNs). ELM methods are capable of reducing the essential time required for learning by a Neural Network. Certainly, it has been verified that by using the ELM, the training procedure becomes quick and it produces robust behavior [
17]. Consequently, numerous researches have been conducted associated with utilizing ELM algorithm efficiently for determining problems in various engineering fields [
18,
19,
20,
21,
22,
23,
24,
25,
26].
To summarize, ELM is not only an effective and strong algorithm with a faster learning rate in comparison with classic algorithms such as back-propagation (BP), but it also provides optimum performance. ELM attempts to obtain the lowest training error and also standard of weights. In this study, a predictive model of tsunami bore forces on a coastal bridge was developed using the ELM method. The results indicate that the proposed model can adequately predict the tsunami bore forces including drag force, uplift and overturning moment on a coastal bridge. ELM results were also compared with Genetic Programming (GP) and Artificial Neural Networks (ANNs) results. An attempt is made to establish a correlation between the wave heights, variety of girders in bridges and tsunami bore forces on a coastal bridge. The system should be able to forecast tsunami bore forces on coastal bridges in terms of wave heights.
2. Methodology
The experiments were performed in the Coastal & Offshore Laboratory of University Technology PETRONAS (UTP) and University of Malaya.
2.1. Experiments
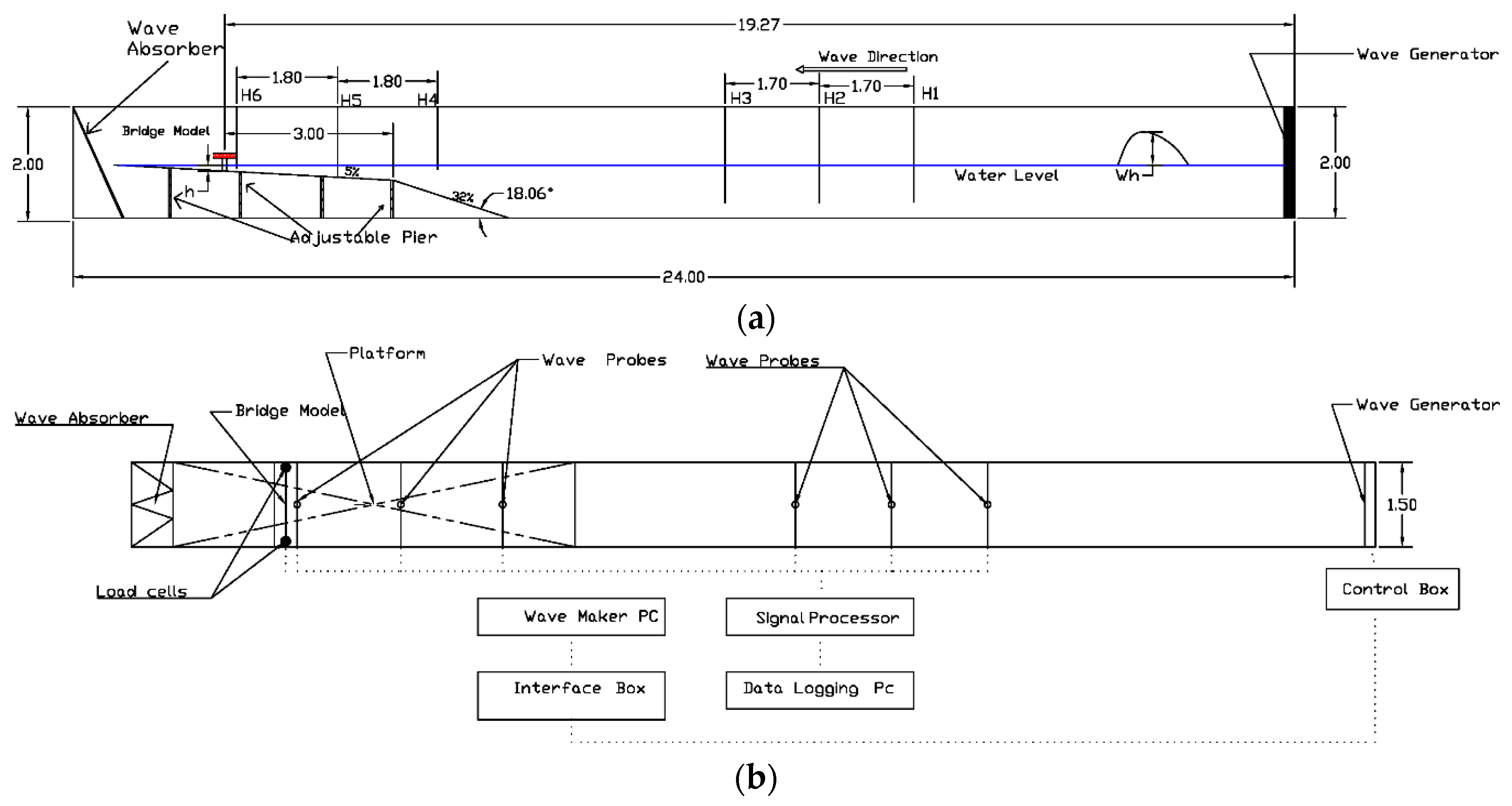
The experiments were carried out in a long wave flume with dimensions of 24 m length × 150 cm wide × 200 cm deep to evaluate and estimate time histories of tsunami bore forces on a bridge model with a variety of wave heights. As illustrated in
Figure 2 a piston-type wave generator (pneumatic type) driven by an electric motor controlled by a computer, was applied in this research. The computer automatically performs calculations and determines the necessary force to push the wave-making board by utilizing ocean and wave software supplied by Edinburgh Design Limited. To produce the desired solitary wave height in the wave flume, coded command signals should be employed with the wave computation software in a variety of water depths. For further interpretation of the raw data, the data acquired by WAVELAB (Version 5.0) were stored in the form of data files and analysed using MATLAB (Version 7.2) routines.
A solitary wave was created after the wave generator, as illustrated in
Figure 2. The solitary wave moved towards the bridge. On approaching the first slope of the platform, the solitary wave was transformed to an almost vertical wave and broke in the second slope in the still water level, in the form of a breaking wave. Then, the breaking wave changes to a bore in the shallow water. This turbulent bore moved forward and attacked the bridge. The bore then flowed over the platform and contacted the wave absorber at the end of the flume, as illustrated in
Figure 2.
Figure 2.
Wave flume and model installation in the flume.
Figure 2.
Wave flume and model installation in the flume.
2.2. Model
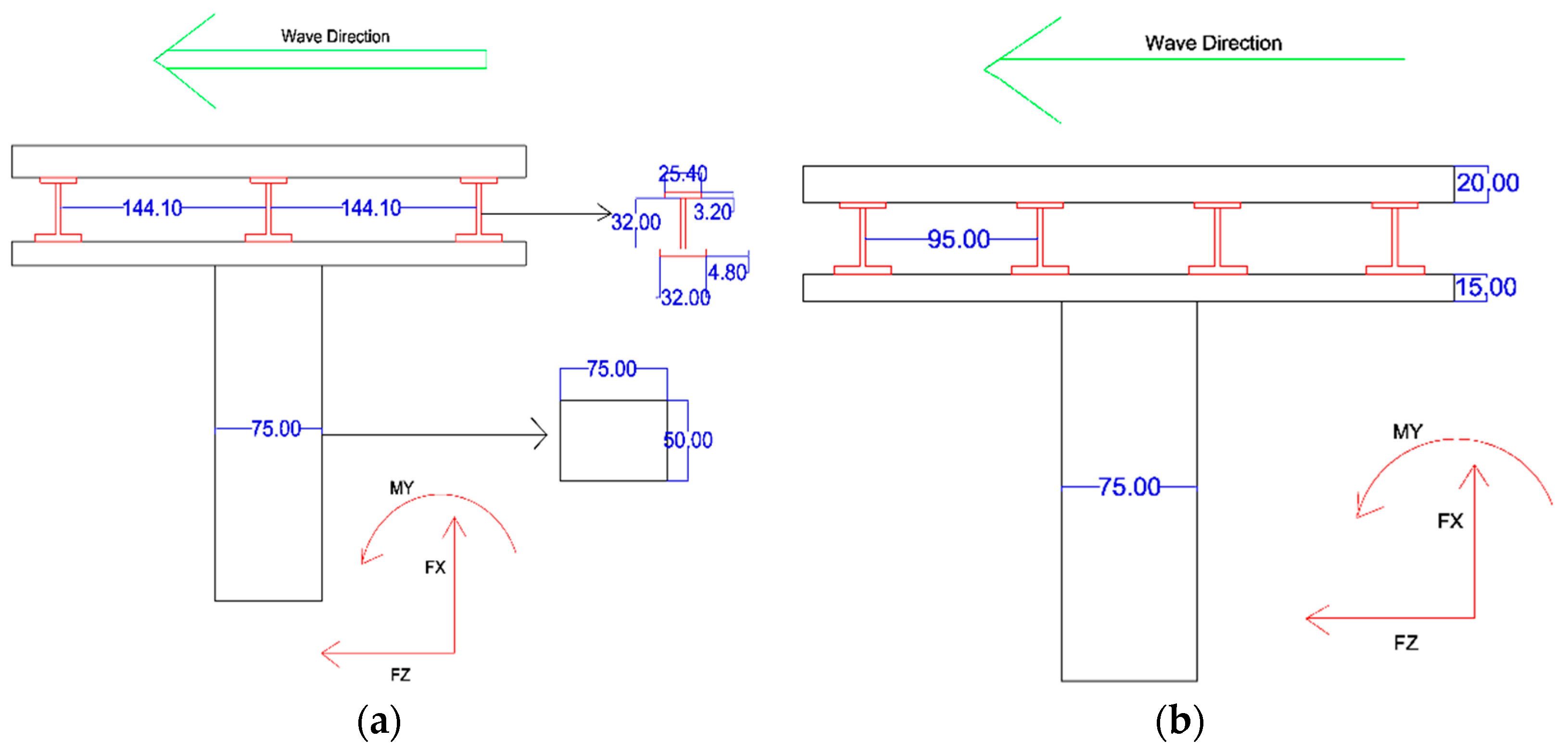
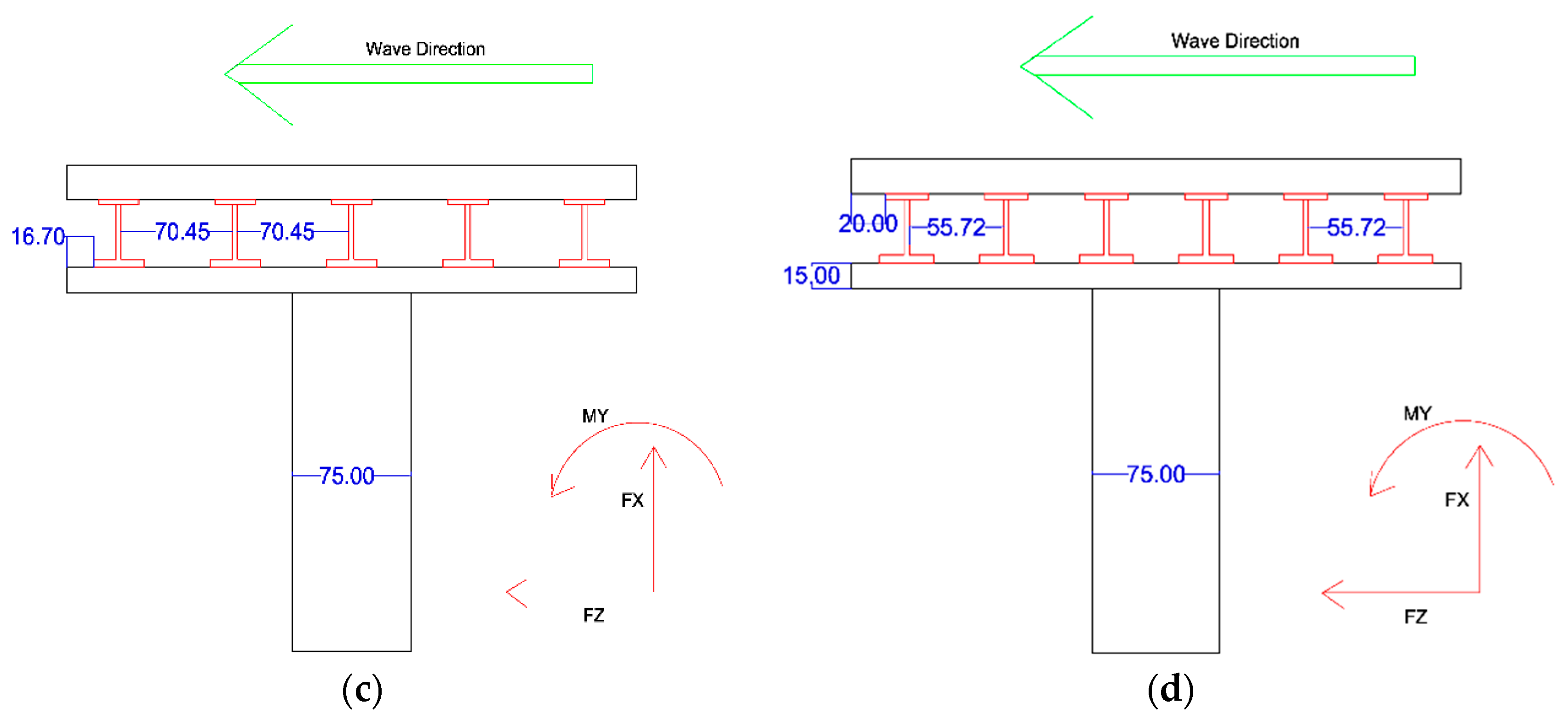
Four bridge models were applied in this research. The bridge model was a typical girder bridge which included a steel plate girder with a concrete deck. The dimensions of the model scaled to 1:40 are given in
Figure 3. In these models, three to six girder beams were used. The distance of the girder to the edge of the deck was kept constant for the variety of girder bridges. The distance between girders in three beams (Model A3), four beams (Model A4), five beams (Model A5) and six beams (Model A6) is 144.10 mm, 95.0 mm, 70.45 mm and 55.72 mm, respectively. All beams were fixed with two bolts 90 cm apart from each other and 20 cm from the edge. Two nodes in each side of the beam fixed the beam to the bolts.
Figure 3.
Bridge model dimension and the positive direction of drag force, uplift and overturning moment. (a) Model A3; (b) Model A4; (c) Model A5; (d) Model A6.
Figure 3.
Bridge model dimension and the positive direction of drag force, uplift and overturning moment. (a) Model A3; (b) Model A4; (c) Model A5; (d) Model A6.
2.3. Setup
In order to measure horizontal drag force, vertical uplift and overturning moment, six-axis load cells were connected to the base plate. The load cells are M3716A units (Sunrise, China) with 135 mm diameter. The capacities of the load cells were FX, FY = 400 N, FZ = 800 N, MX, MY = 40.00 Nm, MZ = 40.00 Nm.
Figure 3 illustrates the positive direction of drag force, uplift and overturning moment.
In this research the sampling rate was 1000 Hz. A side view and plan view of the experiment set up is shown in
Figure 4. Wave probes in the H1–H6 locations recorded the wave profile as shown in
Figure 4. All wave paddles, wave probes and load cells are connected to a data logger named Smart Dynamic Strain Recorder as illustrated in
Figure 4b. As illustrated in
Figure 4, the platform was designed to characterize the beach profile at the location of the bridge models. The first short steep slope rise of 32% represented the embankment on the proposed beach with a length of 2.2 m and the second slope raised gently by 5% represented the beach slope.
Figure 4.
Experimental set up in the flume (a) side view (b) plan view.
Figure 4.
Experimental set up in the flume (a) side view (b) plan view.
Three different water depths HW = 1.0 m, 0.95 m, 0.90 m, were applied in the flume. Ten solitary wave heights were utilized in this research to cover a variety of small to large tsunami wave heights, i.e., = 0.04, 0.8, 0.12, 0.16, 0.20, 0.24, 0.28, 0.32, 0.36, 0.40 m. In order to ensure repeatability and accuracy of the experiment, each hydraulic test was repeated three times and after eliminating the highest and lowest values, the average was recorded and presented in the Results section. The experiments errors were found to be less than 4.5%. The maximum values of vertical, horizontal forces and overturning moment were applied to the results.
2.4. Input and Output Variables
Table 1 and
Table 2 illustrate the input and output variables in terms of the definition and obtained values.
Table 1.
Input parameters of tsunami bore forces on a coastal bridge.
Table 1.
Input parameters of tsunami bore forces on a coastal bridge.
| Inputs | Parameter Description | Parameter Characterization |
|---|
| Input 1 | Wh | Wave height |
| Input 2 | T | Velocity |
Table 2.
Output parameters.
Table 2.
Output parameters.
| Output | Parameter Description | Parameter Characterization |
|---|
| Outputs | FX | Uplift |
| FZ | Drag force |
| MY | Overturning moment |
2.5. Extreme Learning Machine
Huang,
et al. [
17] introduced ELM method for Single Layer Feed-forward Neural Network (SLFN) design as a learning algorithm tool [
17,
27,
28]. The ELM algorithm has more effective general ability with faster learning speed. The proposed ELM in most cases has better generalization performance compared to gradient-based learning methods such as back propagation. In addition, ELM picks out the input weights randomly and determines the output weights of SLFN. This is another advantage of the method. ELM does not require excessive human involvement, and is utilized more efficiently than the classic algorithms. Like the unsupervised Artificial Neural Network (ANN), ELM is able to analyse all the network functions, which minimizes human involvement. This method presents an efficient algorithm with various important features such as convenience, prompt learning speed, effective performance, and capability to use most nonlinear stimulation and kernel functions [
29].
2.5.1. Single Hidden Layer Feed-Forward Neural Network
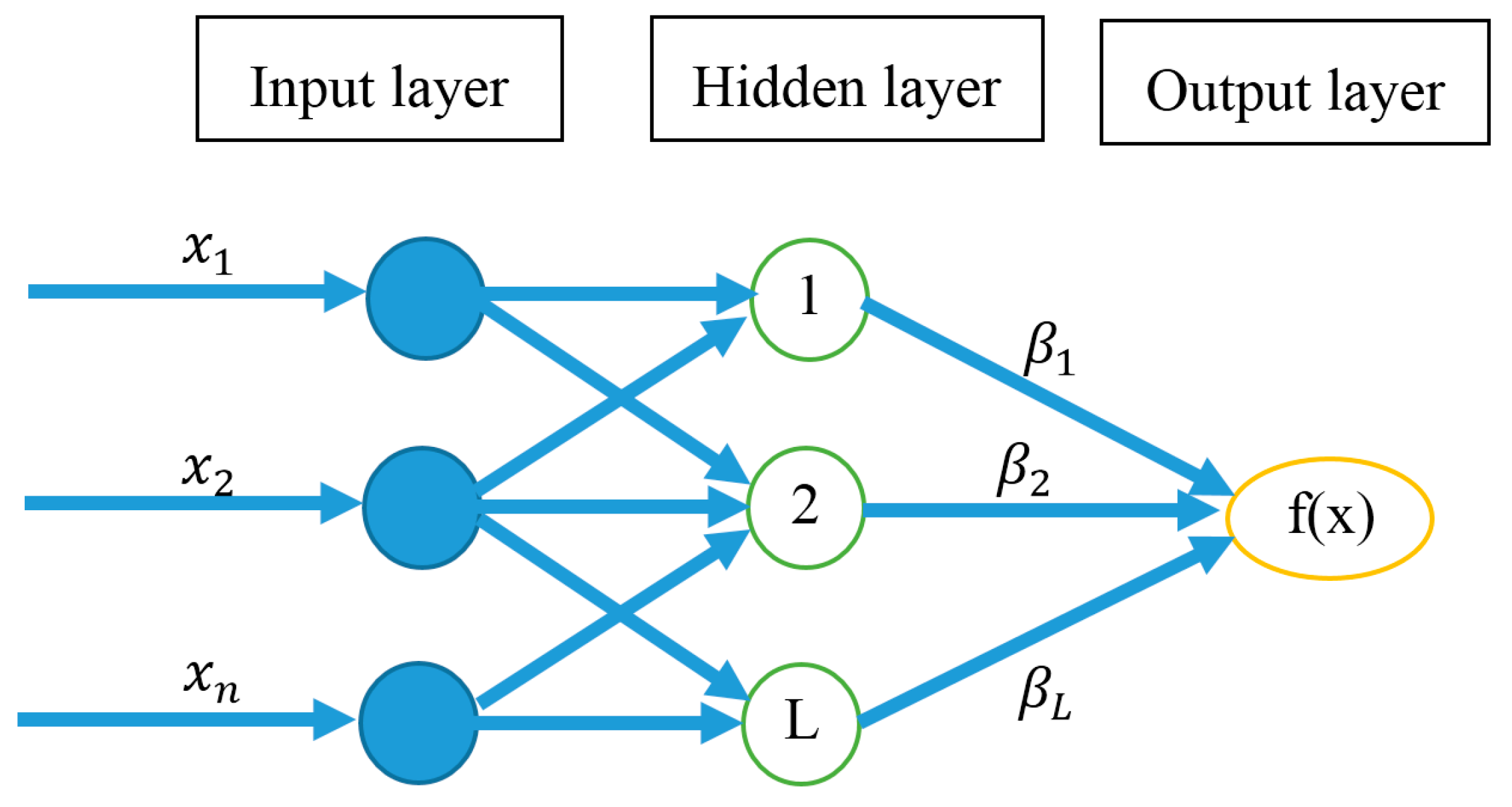
SLFN is a function with
L hidden nodes. It might be characterized by a mathematical equation of SLFN including both additive and radial basis function (RBF) hidden nodes in a unified way given as follows [
30,
31]:
In Equation (1)
ai and
bi represent the learning parameters of hidden nodes.
βi represents the weight connecting the
ith hidden node to the output node.
shows the output value of the
ith hidden node with respect to the input
x. The additive hidden node with the activation function of
(e.g., sigmoid and threshold),
is as per [
27]:
where
ai denotes the weight vector which connects the input layer to the
ith hidden node. In addition,
bi represented the bias of the
ith hidden node.
ai.
x represents the inner product of vector
ai and
x in
Rn. In addition,
might be obtained for RBF hidden node with the activation function
(e.g., Gaussian),
as per Huang
et al. [
27]:
In Equation (3), ai and bi represent the centre and impact factor of the ith RBF node, respectively.
R+ indicates the set of all positive real values. In this equation, the RBF network describes a particular case of SLFN with RBF nodes in its hidden layer. For
N arbitrary distinct samples
,
xi is
n × 1 input vector and
ti is
m × 1 target vector. In cases where an SLFN with L hidden nodes may estimate the value of N samples with zero error, then it signifies that there exist
βi,
ai and
bi such that [
27]:
Equation (4) can be written compactly as:
where:
with
:
In Equations (4)–(7), the
H represents the hidden layer output matrix of SLFN that includes the
ith column of
H, being the
ith hidden node’s output with respect to inputs
.
Figure 5 shows the general structure of SLFN ANN structure.
Figure 5.
The structure of SLFN.
Figure 5.
The structure of SLFN.
2.5.2. Concept of ELM
The ELM technique developed as a SLFN with
hidden neurons has the ability to discover and develop
L distinct samples with zero error [
20]. However, whenever the number of distinct samples (
N) is higher than the number of hidden neurons, ELM method can also randomly allocate variables to the hidden nodes and determine the output weights by pseudo-inverse of
H with only a small error ε > 0.
ai and
bi which are hidden node parameters of ELM, should not be tuned throughout learning and may conveniently be allocated with random values. Liang
et al. [
31] presented the same in the following theorems:
Theorem 1. In this theorem Liang et al. [
31]
presented an SLFN with L additive or RBF hidden nodes as well as an activation function g(x) that is extremely differentiable in every specific R provided. Consequently, for arbitrary L in different input vectors and , SLFN can randomly be produced by any continuous possibilities assigned. Furthermore, the hidden layer output matrix is invertible with probability one, the hidden layer output matrix H of the SLFN is invertible and , respectively. Theorem 2. In this theorem, Annema et al. [
28]
provide any small positive value ε > 0 and activation function that is extremely differentiable in every specification; there exists such that for N arbitrary distinct input vectors for any generated randomly according to any continuous possibility distribution provided as with probability one. The hidden node variables of ELM should not be tuned during training. Also, Equation (5) due to convenient allocation with arbitrary values, can be transferred to a linear device and the output weights could be determined using the following equation [
27]:
In Equation (8) the Moore-Penrose generalized inverse [
32] of the hidden layer output matrix
H presented by
could be estimated by numerous methods, including orthogonal projection, orthogonalization, iterative methods, Singular Value Decomposition (SVD)
etc. [
32]. The theory of orthogonal projection can be utilized only when
is non-singular and
.
There are restrictions in orthogonalization and iterative methods due to the utilization of searching and iterations. While ELM can to be employed in all cases, it can be employed to utilize SVD in calculating the Moore-Penrose generalized inverse of H. Hence, ELM is a batch learning method.
2.6. Artificial Neural Networks
One of the most desired neural network systems is the multilayer feed forward network including a back propagation learning algorithm. This method is extensively utilized in many disciplines such as engineering, science and computing.
The neural network generally includes three sections,
i.e., (i) an input section; (ii) an intermediate or hidden section; (iii) an output section. The input vectors consist of
and
, the outputs of
neurons in the hidden section are
, and the outputs of the output layer are
,
, where w
ij and y
j represent the weight and the threshold between the input layer and the hidden layer, respectively, w
jk and y
k assume the outputs of each neuron in a hidden layer and output layer, respectively, as indicated in Equations (9) and (10):
In Equations (9) and (10),
represents a transfer function, which is the rule for mapping the neuron’s summed input to its output, and utilizes an appropriate option in a device to present a non-linearity into the network design. Generally, the sigmoid function is one of most commonly used functions for monotonic improvement and ranges from zero to one. More details on ANNs can be found in work by several researchers [
33,
34,
35]. The parameters used for the ANN are summarized in
Table 3. MATLAB software was used for the ANN simulations.
Table 3.
User-defined parameters for ANN.
Table 3.
User-defined parameters for ANN.
| ANN Parameters |
|---|
| Learning Rate | Momentum | Hidden Node | Number of Iterations | Activation Function |
|---|
| 0.2 | 0.1 | 3, 6, 10 | 1000 | Continuous Log-Sigmoid Function |
2.7. Genetic Programming
Genetic programming (GP) is an evolutionary algorithm borrowed from the process of evolution occurring in Nature [
36] and according to Darwinian theories. It estimates, in symbolic structure, the equation that best expresses the relation of the output to the input variables.
The algorithm assumes an initial random population generated from equation or programs produced from the random combination of input variables, random numbers and functions, i.e., involving operators like multiplication, addition, subtraction, division, square root, log, etc.
This population of potential solutions is then exposed to an evolutionary procedure and the “fitness” (a measure of how well the problem is solved) of the developed programs is assessed. Then, an individual program that represents the higher matching of the data, is selected through the initial population. The individual programs which present better performance, are chosen to exchange part of their data to generate best programs via “crossover” as well as “mutation”. This has simulated the natural world’s reproduction process. However, crossover is exchanging the parts of the best programs with each other and mutation is the random selection of programs to produce a new program. This evolutionary method is continued for following generations and is influenced for obtaining symbolic expressions for describing the data. This leads to scientific interpretation to obtain knowledge about the method [
37,
38,
39].
Table 4 summarizes the parameters used per run of GP. MATLAB software was used for GP simulations.
Table 4.
The list of parameters employed in GP modelling.
Table 4.
The list of parameters employed in GP modelling.
| Parameter | Value |
|---|
| Population size | 512 |
| Function set | |
| Head size | 5–9 |
| Chromosomes | 20–30 |
| Linking functions | Addition, subtraction, arithmetic, Trigonometric, Multiplication |
| Number of genes | 2–3 |
| Mutation rate | 92 |
| One-point recombination rate | 0.2 |
| Two-point recombination rate | 0.2 |
| Homologue crossover rate | 99 |
| Crossover rate | 31 |
| Fitness function error type | RMSE |
| Inversion rate | 109 |
| Gene transposition rate | 0.1 |
| Gene recombination rate | 0.1 |
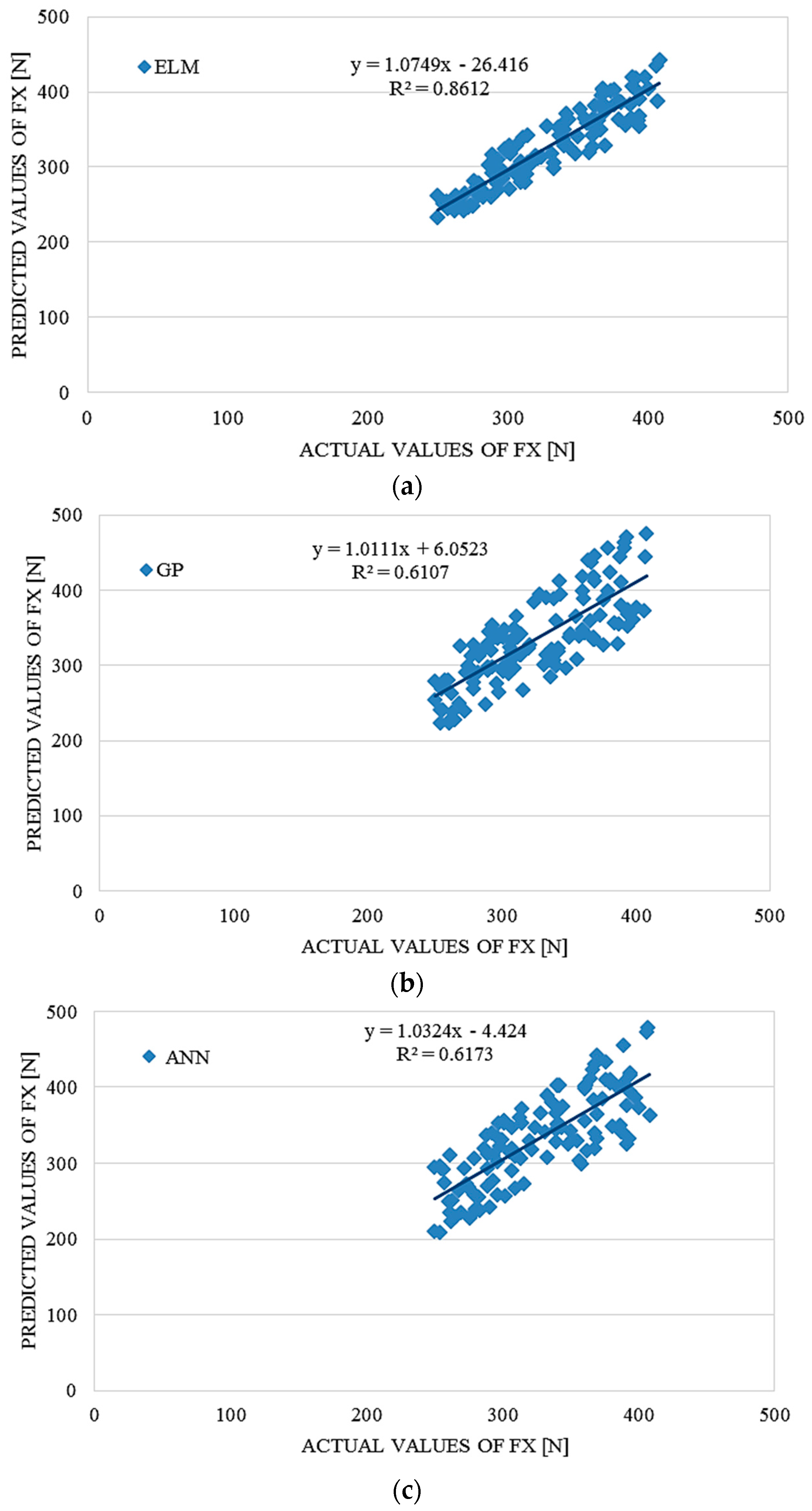
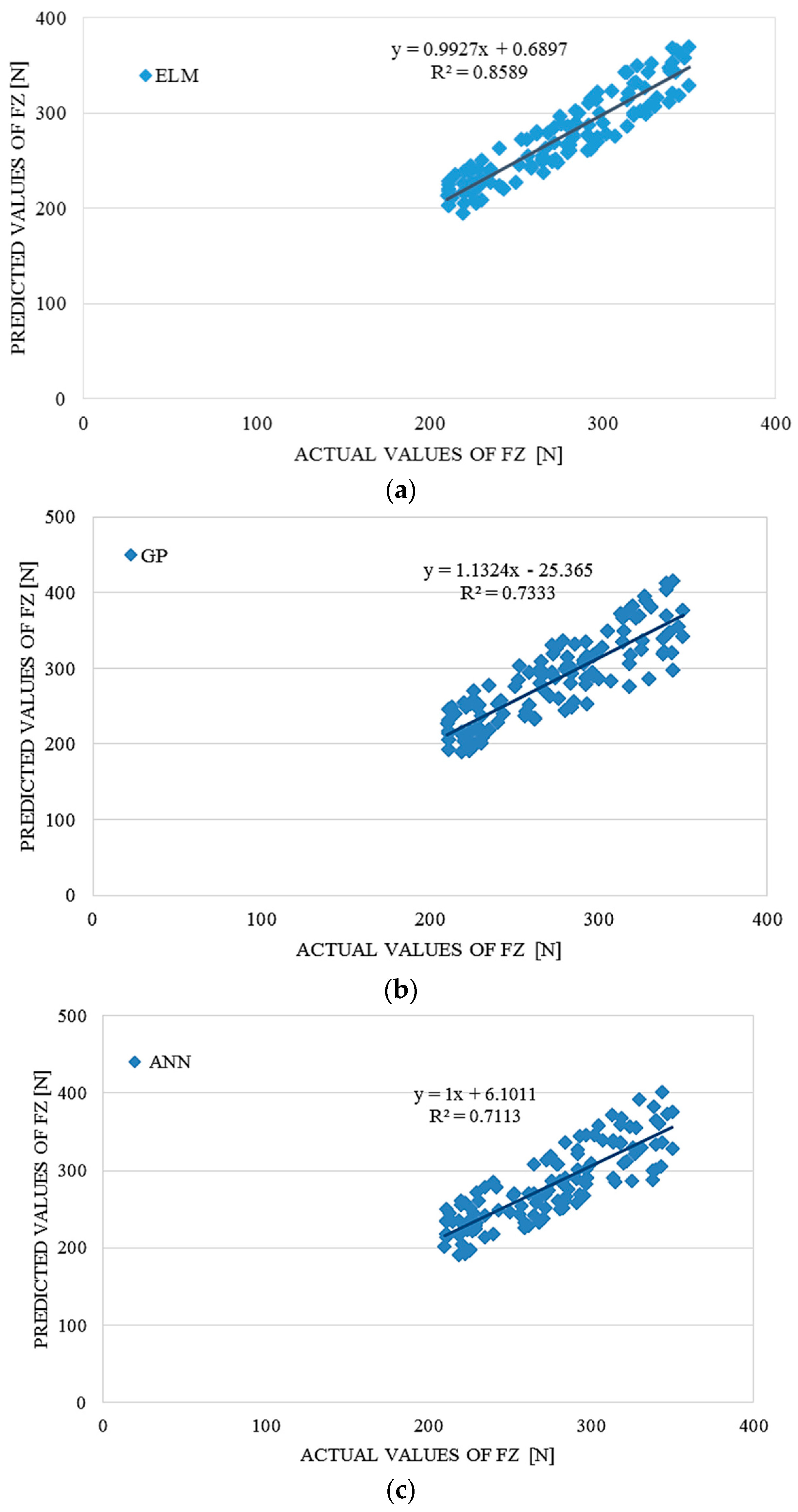
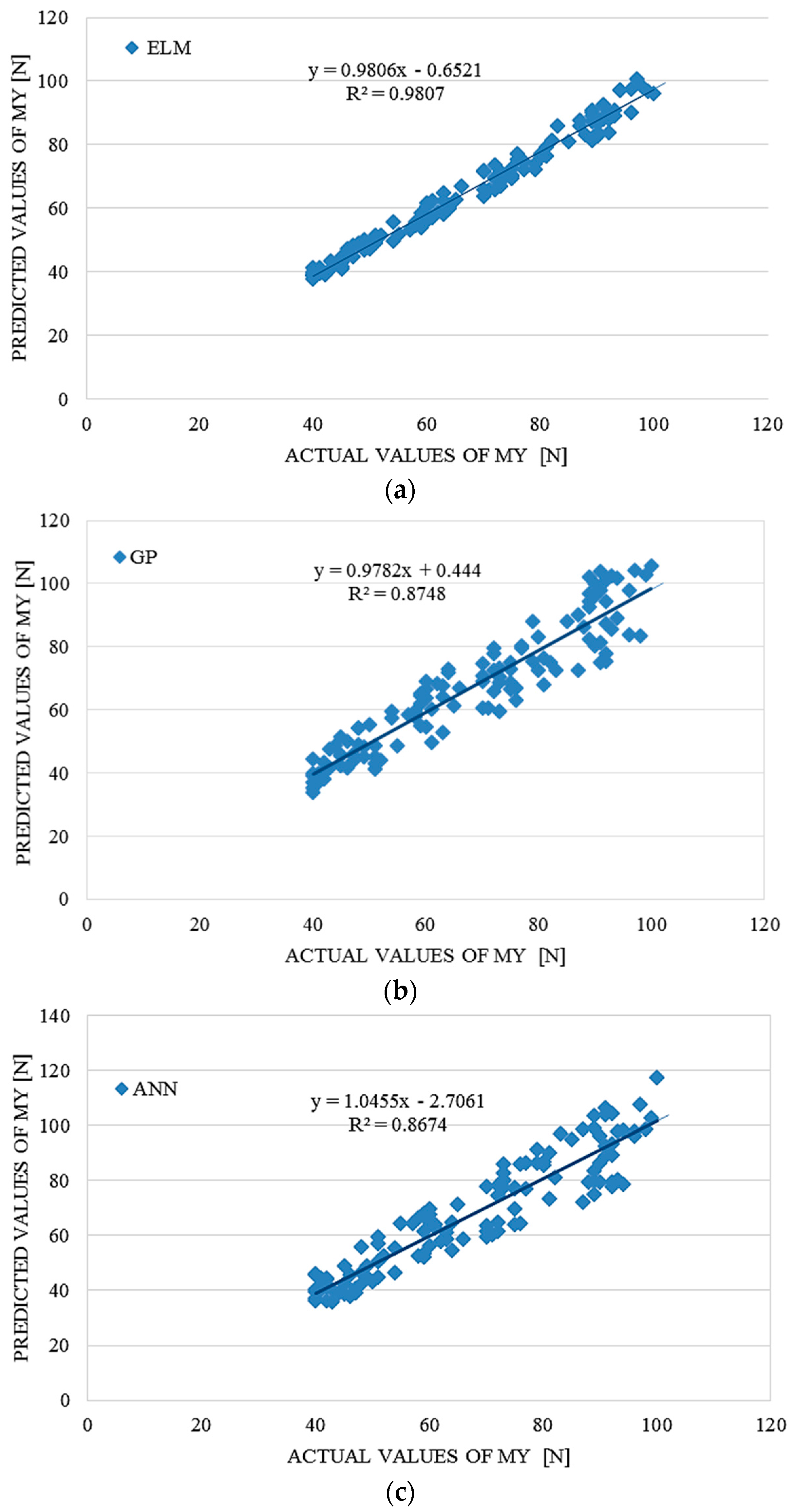
4. Performance Comparison of ELM, ANN and GP
To evaluate the accuracy and advantages of the proposed ELM approach, the ELM model’s prediction accuracy was compared with prediction accuracy of GP and ANN methods, which were used as a benchmark. In order to compare, conventional error statistical indicators, RMSE,
R2 and r, were applied.
Table 6 and
Table 7 summarize the prediction accuracy results for test data sets since training error is not a credible indicator for the prediction potential of the particular model. This results present average results after many repetitions and many iterations in order to fins optimal structures of the models. The average computation time for the ELM modelling was around 310 seconds using a PC with an Intel Core Duo CPU E7600 @3.06 GHz and 2 GB RAM. The average computation time for the ANN and GP modelling using the same PC with the same performances was 424 and 446 s, respectively. For the ELM modelling, MATLAB software was used.
The ELM model outperformed the GP and ANN models according to the results in
Table 6,
Table 7 and
Table 8, providing significantly better results than the benchmark models. On the basis of the RMSE analysis in comparison with ANN and GP, it could also be concluded that the proposed ELM outperformed the results obtained with benchmark models.
Table 6.
Comparative performance statistics of the ELM, ANN and GP tsunami bore force FX on a coastal bridge predictive model.
Table 6.
Comparative performance statistics of the ELM, ANN and GP tsunami bore force FX on a coastal bridge predictive model.
| ELM | ANN | GP |
|---|
| RMSE | R2 | r | RMSE | R2 | r | RMSE | R2 | r |
| 19.32297 | 0.8612 | 0.92799 | 36.39317 | 0.6173 | 0.78570 | 36.13951 | 0.6107 | 0.78150 |
Table 7.
Comparative performance statistics of the ELM, ANN and GP tsunami bore force FZ on a coastal bridge predictive model.
Table 7.
Comparative performance statistics of the ELM, ANN and GP tsunami bore force FZ on a coastal bridge predictive model.
| ELM | ANN | GP |
|---|
| RMSE | R2 | r | RMSE | R2 | r | RMSE | R2 | r |
| 17.00278 | 0.8589 | 0.92676 | 26.92342 | 0.7113 | 0.84336 | 28.85849 | 0.7333 | 0.85631 |
Table 8.
Comparative performance statistics of the ELM, ANN and GP tsunami bore moment MY on a coastal bridge predictive model.
Table 8.
Comparative performance statistics of the ELM, ANN and GP tsunami bore moment MY on a coastal bridge predictive model.
| ELM | ANN | GP |
|---|
| RMSE | R2 | r | RMSE | R2 | r | RMSE | R2 | r |
| 2.53381 | 0.9807 | 0.99030 | 7.52946 | 0.8674 | 0.93532 | 6.81423 | 0.8748 | 0.93132 |
5. Conclusions
This research used out a systematic experimental and numerical method to create a ELM predictive model of tsunami bore forces on a coastal bridge. The experimental validation was performed in a 24 m tsunami flume on 1/40 scale girder bridge with various numbers of girders and wave heights. The tsunami bore forces consisting of horizontal, uplift forces and overturning moment, were measured in various cases. A comparison of the ELM method with GP and ANN was conducted in order to evaluate the forecast accuracy and reliability. Accuracy results, measured in terms of RMSE, r and R2, indicate that the ELM predictions are superior to those of GP and ANN. Additionally, the results reveal the robustness of the method.
The produced ELM method provides numerous interesting and extraordinary capabilities which indicate the significant advantages of this method in comparison with conventional well-known gradient-based learning algorithms for feed-forward neural networks. Significantly higher accuracy and much faster learning speed could be achieved bu using ELM when compared with the classic feed-forward network learning algorithms, for instance the back-propagation (BP) algorithm. Furthermore, in contrast to traditional learning algorithms, the ELM algorithm is designed to produce the lowest training error and norm of weights.