An Informed Framework for Training Classifiers from Social Media †
Abstract
:1. Introduction
2. State of the Art
3. Proposed Framework
3.1. Class Dictionaries
3.2. Dictionary Filters
- Frequency filter: this strategy simply sorts the full class dictionary in descending order of frequency and then takes the first N tags, presumably indicative of widely shared visual semantics. Thus, concepts that are unrelated or occasionally related by context are ignored because they are lower in the ranking. For example, “Marie” might be used as a tag for an image of a dog, representing its owner, but its frequency in a large collection of images most likely will be low, as it is very situational. On the other hand, “Saint Bernard” might be higher in rank, as it is the name of a dog breed. The importance of tags by their frequencies is used in many applications [23,24,25].
- Keyword Position filter: similar to the previous filter, but starting from the keyword position class dictionary. The tags are sorted and the first N in the ranking are kept.
- Quality filter: here we exploit a semantic oracle developed in [26], which is essentially a list of 150 English terms considered by linguistic researchers to be “semantically rich and general”, covering a wide variety of descriptions for different entities. The quality filter takes the intersection between the full class dictionary and the oracle list, and keeps the first N tags when sorting by frequency.
- Noun filter: this filter intersects the full class dictionary with a set of nouns that are in the hyponym sets of the given keyword, or in its immediate hyperonym set (found by the help of WordNet). Again, the remaining tags are sorted and the first N in the ranking are kept.
Entropy-Based Selection
3.3. Query Expansion
4. Experiments
4.1. Comparison against the Semantic Trainer
4.2. Comparison against OPTIMOL
4.3. Entropy-Based Selection
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fei-Fei, L.; Fergus, R.; Perona, P. A Bayesian approach to unsupervised one-shot learning of object categories. In Proceedings of the 9th IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; pp. 1134–1141.
- Crowston, K. Amazon Mechanical Turk: A Research Tool for Organizations and Information Systems Scholars. In Shaping the Future of ICT Research. Methods and Approaches; Springer: Berlin/Heidelberg, Germany, 2012; pp. 210–221. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; pp. 248–255.
- Miller, G.A. WordNet: A lexical database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Flickr. Available online: http://www.flickr.com (accessed on 7 April 2016).
- Ames, M.; Naaman, M. Why we tag: Motivations for annotation in mobile and online media. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 30 April–3 May 2007; pp. 971–980.
- Petz, G.; Karpowicz, M.; Fürschuß, H.; Auinger, A.; Stříteský, V.; Holzinger, A. Computational approaches for mining user’s opinions on the Web 2.0. Inf. Process. Manag. 2014, 50, 899–908. [Google Scholar] [CrossRef]
- Kennedy, L.S.; Chang, S.F.; Kozintsev, I.V. To search or to label?: Predicting the performance of search-based automatic image classifiers. In Proceedings of the 8th ACM International Workshop on Multimedia Information Retrieval (MIR ’06), Santa Barbara, CA, USA, 23–27 October 2006; pp. 249–258.
- Mandala, R.; Tokunaga, T.; Tanaka, H. Combining multiple evidence from different types of thesaurus for query expansion. In Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Berkeley, CA, USA, 15–19 August 1999; pp. 191–197.
- Everingham, M.; van Gool, L.; Williams, C.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Visual Object Classes Challenge 2012. Available online: http://host.robots.ox.ac.uk/pascal/VOC/voc2012/index.html (accessed on 7 April 2016).
- Imagenet Large Scale Visual Recognition Challenge 2012. Available online: http://www.image-net.org/challenges/LSVRC/2012/index (accessed on 7 April 2016).
- Li, L.J.; Fei-Fei, L. Optimol: Automatic online picture collection via incremental model learning. Int. J. Comput. Vis. 2010, 88, 147–168. [Google Scholar] [CrossRef]
- Wang, G.; Hoiem, D.; Forsyth, D. Learning image similarity from Flickr groups using stochastic intersection kernel machines. In Proceedings of the 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 428–435.
- Fergus, R.; Fei-Fei, L.; Perona, P.; Zisserman, A. Learning Object Categories from Google’s Image Search. In Proceedings of the 10th International Conference on Computer Vision, Beijing, China, 17–21 October 2005; Volume 2, pp. 1816–1823.
- Chen, X.; Shrivastava, A.; Gupta, A. NEIL: Extracting Visual Knowledge from Web Data. In Proceedings of the 14th International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1409–1416.
- Divvala, S.K.; Farhadi, A.; Guestrin, C. Learning Everything about Anything: Webly-Supervised Visual Concept Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR ’14), Columbus, OH, USA, 23–28 June 2014; pp. 3270–3277.
- Li, L.J.; Wang, G.; Fei-Fei, L. OPTIMOL: Automatic Online Picture collecTion via Incremental Model Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR ’07), Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8.
- Cheng, D.S.; Setti, F.; Zeni, N.; Ferrario, R.; Cristani, M. Semantically-driven automatic creation of training sets for object recognition. Comput. Vis. Image Underst. 2015, 131, 56–71. [Google Scholar]
- WordNet. Available online: http://wordnet.princeton.edu (accessed on 7 April 2016).
- Sun, A.; Bhowmick, S.S. Image Tag Clarity: In Search of Visual-Representative Tags for Social Images. In Proceedings of the 1st SIGMM Workshop on Social Media (WSM ’09), Beijing, China, 19–24 October 2009; pp. 19–26.
- Spain, M.; Perona, P. Some Objects Are More Equal than Others: Measuring and Predicting Importance. In Proceedings of the 10th European Conference on Computer Vision: Part I (ECCV ’08), Marseille, France, 12–18 October 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 523–536. [Google Scholar]
- Weinberger, K.Q.; Slaney, M.; van Zwol, R. Resolving tag ambiguity. In Proceedings of the 16th ACM International Conference on Multimedia, ACM, MM ’08, Vancouver, BC, Canada, 26–31 October 2008; pp. 111–120.
- Shepitsen, A.; Gemmell, J.; Mobasher, B.; Burke, R. Personalized Recommendation in Social Tagging Systems Using Hierarchical Clustering. In Proceedings of the 2008 ACM Conference on Recommender Systems (RecSys ’08), Lausanne, Switzerland, 23–25 October 2008; pp. 259–266.
- Hassan-Montero, Y.; Herrero-Solana, V. Improving Tag-Clouds as Visual Information Retrieval Interfaces. In Proceedings of the International Conference on Multidisciplinary Information Sciences and Technologies (InSciT2006), Mérida, Spain, 25–28 October 2006.
- Ogden, C.K. Basic English: A General Introduction with Rules and Grammar; Kegan Paul: London, UK, 1932. [Google Scholar]
- Holzinger, A.; Hӧrtenhuber, M.; Mayer, C.; Bachler, M.; Wassertheurer, S.; Pinho, A.J.; Koslicki, D. On entropy-based data mining. In Interactive Knowledge Discovery and Data Mining in Biomedical Informatics; Holzinger, A., Jurisica, I., Eds.; Springer: Berlin/Heidelberg, 2014; pp. 209–226. [Google Scholar]
- Vedaldi, A.; Lenc, K. MatConvNet: Convolutional Neural Networks for MATLAB. In Proceedings of the 23rd ACM International Conference on Multimedia (MM ’15), Brisbane, Australia, 26–30 October 2015; pp. 689–692.
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates Inc.: New York, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Caltech 256. Available online: http://www.vision.caltech.edu/Image_Datasets/Caltech256/ (accessed on 7 April 2016).
- Opelt, A.; Pinz, A.; Fussenegger, M.; Auer, P. Generic object recognition with boosting. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 416–431. [Google Scholar] [CrossRef] [PubMed]
- Griffin, G.; Holub, A.; Perona, P. Caltech-256 Object Category Dataset. Available online: http://authors.library.caltech.edu/7694/ (accessed on 7 April 2016).
- Caltech 101. Available online: http://www.vision.caltech.edu/Image_Datasets/Caltech101/ (accessed on 7 April 2016).
- Vedaldi, A.; Fulkerson, B. Vlfeat: An Open and Portable Library of Computer Vision Algorithms. In Proceedings of the 18th ACM International Conference on Multimedia (MM ’10), Firenze, Italy, 25–29 October 2010; pp. 1469–1472.
- Fan, R.-E.; Chang, K.-W.; Hsieh, C.-J.; Wang, X.-R.; Lin, C.-J. LIBLINEAR: A library for large linear classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Digital Trends. Available online: http://www.digitaltrends.com/mobile/shazam-music-app-visual-recognition/ (accessed on 7 April 2016).

| Classes | Flickr | Semantic Trainer | Our Framework | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| basic | hypo | verb | vadj | fcom | ccom | freq-f | qual-f | keyw-f | noun-f | ||
| aeroplane | 97.7 | 97.3 | 95.2 | 97.4 | 97.1 | 97.9 | 97.3 | 97.3 | 96.4 | 97.3 | 93.6 |
| bicycle | 82.8 | 82.5 | 70.4 | 79.3 | 83.6 | 82.2 | 81.2 | 83.1 | 76.6 | 82.3 | 76.5 |
| bird | 90.7 | 90.4 | 91.5 | 89.9 | 90.2 | 90.1 | 91.7 | 90.7 | 92.7 | 89.3 | 92.0 |
| boat | 88.7 | 88.2 | 88.8 | 87.8 | 86.9 | 89.5 | 89.2 | 88.9 | 87.5 | 89.3 | 89.0 |
| bottle | 57.3 | 56.7 | 57.5 | 55.7 | 55.8 | 57.6 | 58.3 | 57.3 | 54.9 | 56.8 | 55.6 |
| bus | 93.8 | 93.7 | 87.3 | 94.3 | 93.0 | 94.1 | 93.0 | 93.4 | 91.6 | 93.1 | 92.8 |
| car | 72.6 | 75.6 | 69.8 | 71.9 | 75.9 | 71.6 | 74.7 | 73.2 | 74.6 | 73.9 | 73.2 |
| cat | 91.5 | 89.1 | 92.9 | 90.6 | 90.9 | 91.4 | 93.1 | 92.9 | 89.6 | 90.0 | 91.5 |
| chair | 70.3 | 69.9 | 73.3 | 71.1 | 72.3 | 67.8 | 74.3 | 68.9 | 66.5 | 71.0 | 59.5 |
| cow | 79.0 | 73.9 | 73.6 | 71.8 | 75.1 | 75.7 | 77.7 | 76.6 | 78.8 | 76.1 | 64.9 |
| dog | 88.9 | 87.3 | 89.5 | 87.3 | 87.1 | 86.1 | 89.7 | 88.8 | 88.7 | 86.6 | 87.5 |
| horse | 85.1 | 76.8 | 80.1 | 76.9 | 81.7 | 80.5 | 83.0 | 84.8 | 83.8 | 82.2 | 80.7 |
| motorbike | 89.1 | 89.4 | 4.7 | 88.9 | 91.0 | 90.7 | 91.3 | 89.1 | 89.8 | 85.5 | 79.2 |
| person | 60.4 | 61.5 | 72.8 | 60.6 | 58.1 | 63.9 | 68.4 | 57.8 | 71.8 | 66.8 | 58.1 |
| sheep | 84.9 | 84.0 | 85.6 | 82.9 | 85.2 | 84.9 | 87.2 | 84.9 | 86.3 | 86.2 | 79.5 |
| sofa | 58.0 | 59.6 | 45.7 | 52.7 | 58.7 | 58.2 | 59.0 | 10.6 | 62.7 | 49.8 | 39.1 |
| train | 92.8 | 92.4 | 90.6 | 93.1 | 92.2 | 93.6 | 93.2 | 89.1 | 92.7 | 91.8 | 91.0 |
| tv monitor | 25.0 | 74.1 | 55.4 | 26.2 | 45.0 | 46.8 | 53.1 | 73.4 | 77.1 | 31.5 | 69.3 |
| Mean AP | 78.3 | 80.15 | 73.6 | 76.6 | 78.9 | 79.1 | 80.9 | 77.8 | 81.3 | 77.8 | 76.3 |
| Train on: | Test on: | Mean | |||
|---|---|---|---|---|---|
| ImageNet | Graz | Caltech-256 | Pascal VOC | others | |
| Pascal VOC | 95.10 | 92.22 | 97.04 | 94.71 | 94.77 |
| Graz [31] | 92.10 | 99.46 | 94.32 | 88.06 | 93.48 |
| Caltech-256 [32] | 96.44 | 90.42 | 99.33 | 92.87 | 94.77 |
| ImageNet | 99.14 | 93.59 | 97.88 | 92.39 | 95.75 |
| ccom [19] | 97.61 | 97.76 | 96.07 | 88.01 | 94.86 |
| fcom [19] | 95.52 | 94.90 | 94.79 | 87.54 | 93.12 |
| freq-f | 95.72 | 95.72 | 95.03 | 88.22 | 93.68 |
| qual-f | 96.48 | 90.53 | 96.22 | 89.85 | 93.27 |
| keyw-f | 96.22 | 94.58 | 96.51 | 90.34 | 94.41 |
| noun-f | 97.21 | 94.50 | 98.00 | 91.28 | 95.25 |
| OPTIMOL | Our Framework | ||||
|---|---|---|---|---|---|
| freq-f | qual-f | keyw-f | noun-f | ||
| aeroplane | 76.00 | 84.07 | 69.10 | 79.21 | 79.87 |
| car | 94.50 | 95.20 | 94.98 | 95.11 | 94.84 |
| face | 82.90 | 83.44 | 83.32 | 78.40 | 90.70 |
| guitar | 60.40 | 97.14 | 96.99 | 98.09 | 97.03 |
| leopard | 89.00 | 92.24 | 95.49 | 91.80 | 92.21 |
| motorbike | 67.30 | 75.83 | 63.67 | 71.77 | 69.03 |
| watch | 53.60 | 94.66 | 95.98 | 90.45 | 89.58 |
| Mean AP | 74.81 | 88.94 | 85.65 | 86.40 | 87.61 |
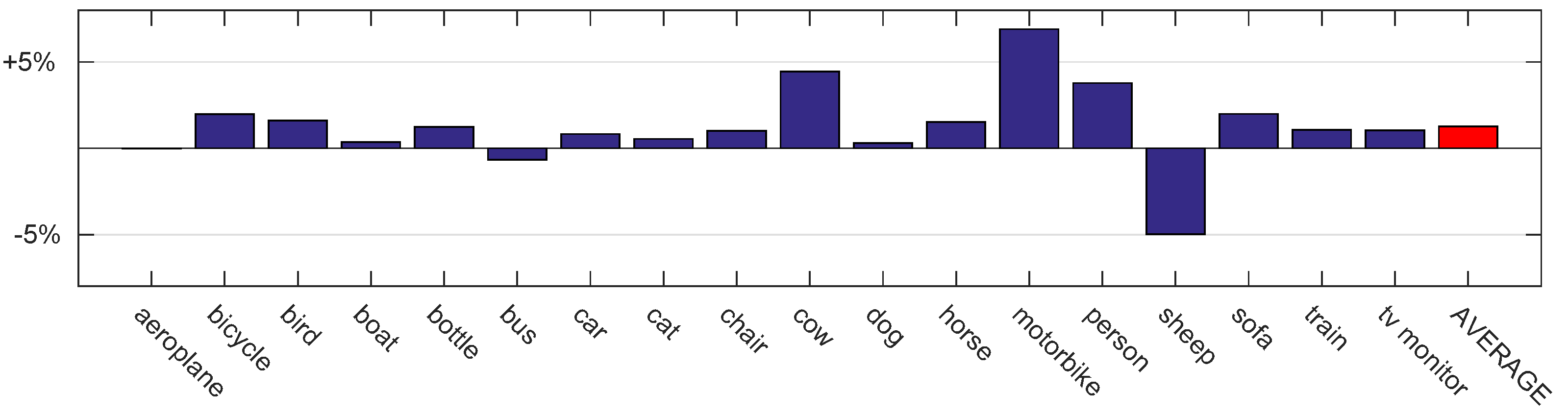
| Classes | Old Flickr | New Flickr | Baseline | freq-f | (Difference) | Entropy | (Difference) |
|---|---|---|---|---|---|---|---|
| aeroplane | 97.7 | 96.7 | 96.8 | 96.5 | () | 96.8 | (0) |
| bicycle | 82.8 | 79.4 | 79.8 | 79.9 | () | 81.7 | () |
| bird | 90.7 | 88.6 | 89.3 | 90.4 | () | 90.9 | () |
| boat | 88.7 | 84.3 | 84.8 | 85.4 | () | 85.2 | () |
| bottle | 57.3 | 58.9 | 57.6 | 59.0 | () | 58.8 | () |
| bus | 93.8 | 93.7 | 93.3 | 92.9 | () | 92.6 | () |
| car | 72.6 | 71.2 | 71.6 | 73.0 | () | 72.5 | () |
| cat | 91.5 | 92.9 | 94.2 | 94.0 | () | 94.7 | () |
| chair | 70.3 | 65.4 | 69.3 | 67.7 | () | 70.3 | () |
| cow | 79.0 | 65.8 | 66.0 | 70.0 | () | 70.4 | () |
| dog | 88.9 | 86.7 | 87.8 | 88.0 | () | 88.1 | () |
| horse | 85.1 | 80.9 | 82.5 | 84.9 | () | 84.0 | () |
| motorbike | 89.1 | 74.5 | 76.2 | 78.5 | () | 83.1 | () |
| person | 60.4 | 80.7 | 80.6 | 82.9 | () | 84.4 | () |
| sheep | 84.9 | 81.1 | 82.0 | 75.3 | () | 77.0 | () |
| sofa | 58.0 | 50.2 | 54.8 | 55.6 | () | 56.8 | () |
| train | 92.8 | 92.2 | 92.0 | 93.3 | () | 93.1 | () |
| tv monitor | 25.0 | 79.4 | 79.5 | 79.8 | () | 80.6 | () |
| Mean AP | 78.3 | 79.0 | 79.9 | 80.4 | () | 81.2 | () |
| Classes | Selected Tags | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| aeroplane | plane | airport | aviation | airplane | jet | flight | boeing | aircraft | raf | planespotting |
| 1.00 | 0.97 | 0.84 | 0.76 | 0.70 | 0.61 | 0.57 | 0.51 | 0.38 | 0.31 | |
| bicycle | bike | street | city | people | europe | monochrome | fahrrad | cycle | man | shadow |
| 1.00 | 0.90 | 0.57 | 0.55 | 0.47 | 0.37 | 0.35 | 0.31 | 0.29 | 0.26 | |
| bird | nature | wildlife | animal | birds | outdoor | vogel | water | oiseau | fauna | ngc |
| 1.00 | 0.84 | 0.75 | 0.67 | 0.55 | 0.47 | 0.45 | 0.40 | 0.32 | 0.25 | |
| boat | water | sea | landscape | sky | sunset | reflection | clouds | summer | ship | blue |
| 1.00 | 0.93 | 0.81 | 0.77 | 0.74 | 0.62 | 0.58 | 0.51 | 0.46 | 0.39 | |
| bottle | glass | green | wine | water | drink | beer | stilllife | blue | macro | red |
| 0.78 | 0.53 | 0.50 | 0.45 | 0.43 | 0.42 | 0.39 | 0.36 | 0.33 | 0.32 | |
| bus | london | street | city | transport | night | people | uk | road | travel | buses |
| 0.78 | 0.73 | 0.60 | 0.49 | 0.41 | 0.40 | 0.37 | 0.34 | 0.29 | 0.28 | |
| car | auto | vintage | street | cars | red | automobile | old | night | urban | classic |
| 0.73 | 0.67 | 0.64 | 0.58 | 0.50 | 0.47 | 0.43 | 0.41 | 0.37 | 0.35 | |
| cat | animal | pet | kitten | portrait | chat | kitty | cats | feline | eyes | nature |
| 0.97 | 0.68 | 0.66 | 0.60 | 0.55 | 0.46 | 0.41 | 0.36 | 0.33 | 0.27 | |
| chair | abandoned | window | table | urban | white | art | red | shadow | old | beach |
| 0.73 | 0.56 | 0.55 | 0.47 | 0.42 | 0.34 | 0.34 | 0.32 | 0.30 | 0.29 | |
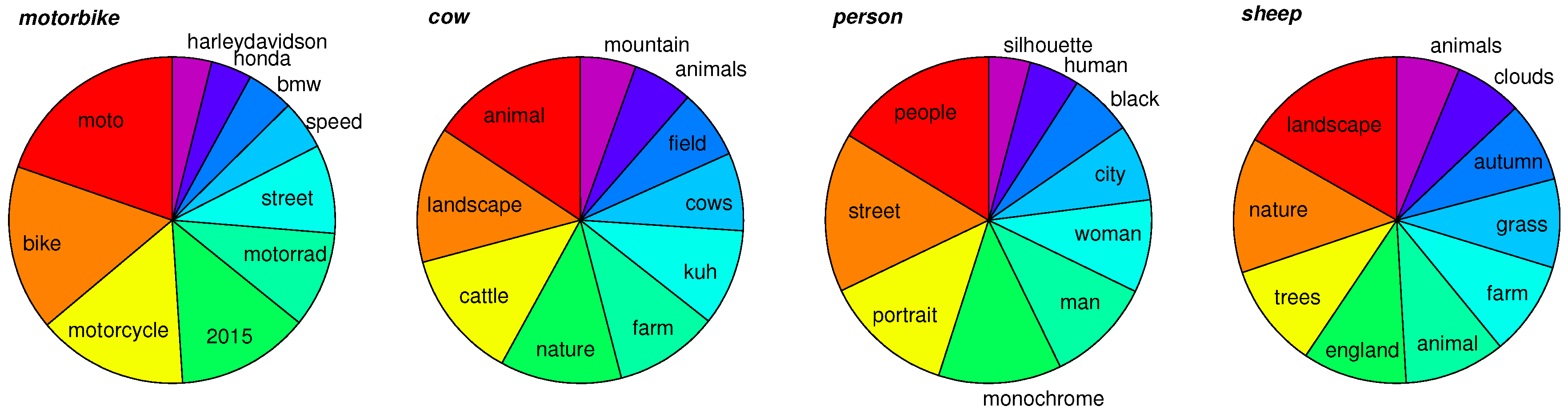
| cow | animal | landscape | cattle | nature | farm | kuh | cows | field | animals | mountain |
| 0.80 | 0.69 | 0.66 | 0.61 | 0.53 | 0.49 | 0.39 | 0.35 | 0.30 | 0.28 | |
| dog | animal | pet | portrait | white | nature | hund | street | beach | puppy | dogs |
| 0.87 | 0.71 | 0.59 | 0.46 | 0.44 | 0.38 | 0.38 | 0.35 | 0.34 | 0.30 | |
| horse | horses | animal | cheval | landscape | nature | white | equine | sky | sunset | outdoor |
| 0.93 | 0.66 | 0.57 | 0.47 | 0.44 | 0.35 | 0.32 | 0.30 | 0.28 | 0.27 | |
| motorbike | moto | bike | motorcycle | 2015 | motorrad | street | speed | bmw | honda | harleydavidson |
| 0.99 | 0.82 | 0.75 | 0.66 | 0.48 | 0.44 | 0.25 | 0.23 | 0.20 | 0.20 | |
| person | people | street | portrait | monochrome | man | woman | city | black | human | silhouette |
| 1.00 | 0.97 | 0.79 | 0.75 | 0.64 | 0.56 | 0.46 | 0.38 | 0.31 | 0.25 | |
| sheep | landscape | nature | trees | england | animal | farm | grass | autumn | clouds | animals |
| 0.85 | 0.68 | 0.52 | 0.52 | 0.50 | 0.47 | 0.44 | 0.40 | 0.34 | 0.32 | |
| sofa | couch | girl | abandoned | portrait | home | white | woman | bed | furniture | interior |
| 0.75 | 0.59 | 0.50 | 0.46 | 0.38 | 0.33 | 0.29 | 0.27 | 0.25 | 0.24 | |
| train | railway | station | railroad | city | rail | locomotive | travel | street | trains | monochrome |
| 0.85 | 0.80 | 0.63 | 0.59 | 0.49 | 0.42 | 0.38 | 0.36 | 0.33 | 0.30 | |
| tv monitor | television | video | screen | 3d | electronics | art | film | computer | germany | lcd |
| 0.89 | 0.79 | 0.55 | 0.48 | 0.40 | 0.34 | 0.29 | 0.27 | 0.24 | 0.21 | |
| Tag | Representative Images |
|---|---|
| motorbike |  |
| moto | |
| bike | |
| motorcycle | |
| 2015 | |
| motorrad | |
| street | |
| speed | |
| bmw | |
| honda | |
| harleydavidson | |
| sofa | |
| couch |  |
| girl | |
| abandoned | |
| portrait | |
| home | |
| white | |
| woman | |
| bed | |
| furniture | |
| interior |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, D.S.; Abdulhak, S.A. An Informed Framework for Training Classifiers from Social Media. Entropy 2016, 18, 130. https://doi.org/10.3390/e18040130
Cheng DS, Abdulhak SA. An Informed Framework for Training Classifiers from Social Media. Entropy. 2016; 18(4):130. https://doi.org/10.3390/e18040130
Chicago/Turabian StyleCheng, Dong Seon, and Sami Abduljalil Abdulhak. 2016. "An Informed Framework for Training Classifiers from Social Media" Entropy 18, no. 4: 130. https://doi.org/10.3390/e18040130
APA StyleCheng, D. S., & Abdulhak, S. A. (2016). An Informed Framework for Training Classifiers from Social Media. Entropy, 18(4), 130. https://doi.org/10.3390/e18040130






