A Novel Weak Fuzzy Solution for Fuzzy Linear System
Abstract
:1. Introduction and Motivation
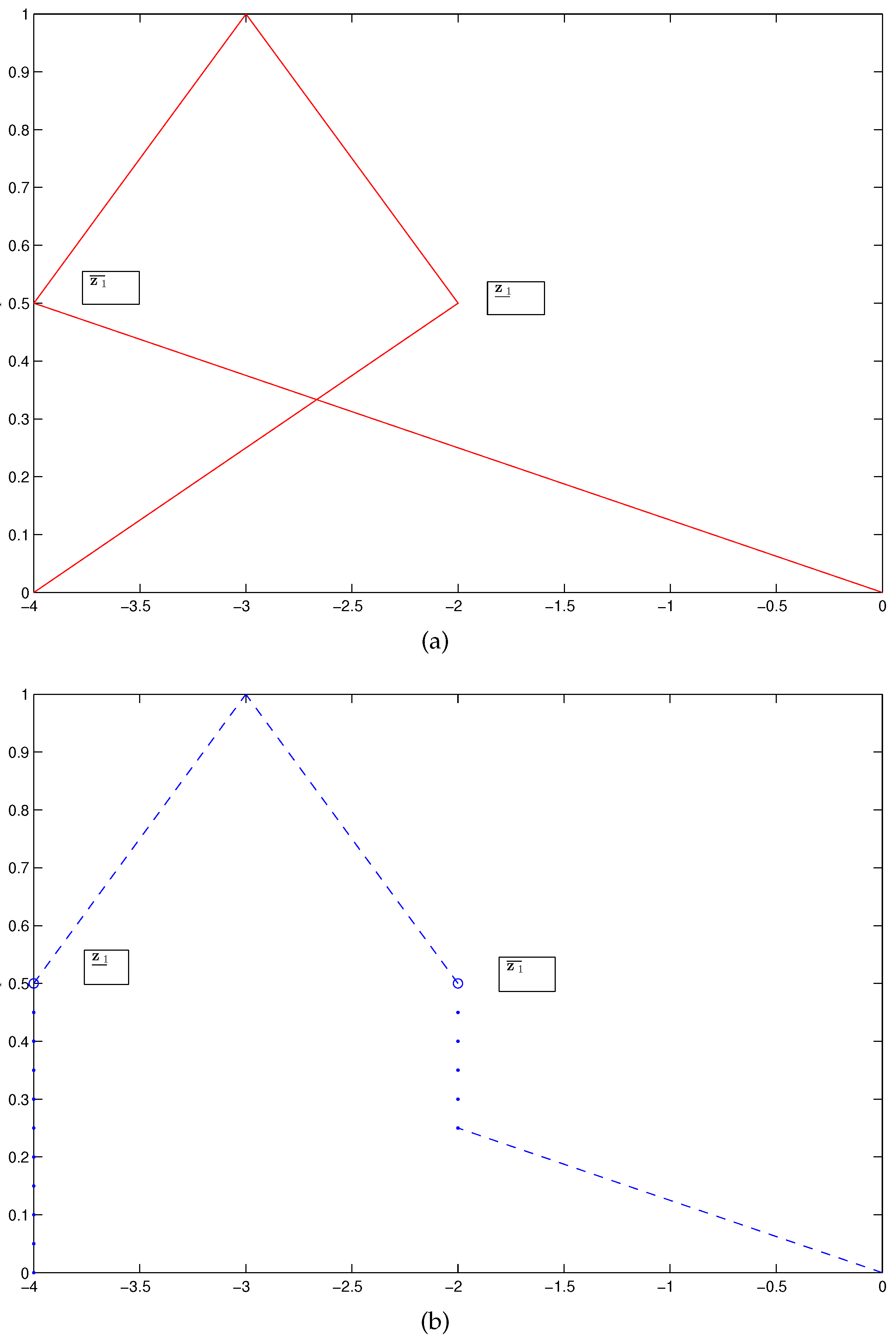
2. Fuzzy Linear Systems Revisit
- (a)
- is a bounded left-continuous non-decreasing function over ;
- (b)
- is a bounded right-continuous non-increasing function over ;
- (c)
- , .
- (a)
- (b)
3. A New Definition for the Weak Fuzzy Solution
4. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dimov, I.; Maire, S.; Sellier, J.M. A new Walk on Equations Monte Carlo method for solving systems of linear algebraic equations. Appl. Math. Model. 2015, 39, 4494–4510. [Google Scholar] [CrossRef]
- Fuyong, L. The solution of linear systems equations with circulant-like coefficient matrices. Appl. Math. Comput. 2013, 219, 8259–8268. [Google Scholar] [CrossRef]
- Mazandarani, M.; Najariyan, M. A note on “A class of linear differential dynamical systems with fuzzy initial condition”. Fuzzy Sets Syst. 2015, 265, 121–126. [Google Scholar] [CrossRef]
- Liang, X.S. Entropy evolution and uncertainty estimation with dynamical systems. Entropy 2014, 16, 3605–3634. [Google Scholar] [CrossRef]
- Chavanis, P.-H. Generalized Stochastic Fokker–Planck Equations. Entropy 2015, 17, 3205–3252. [Google Scholar] [CrossRef]
- Lodwick, W.A.; Dubois, D. Interval linear systems as a necessary step in fuzzy linear systems. Fuzzy Sets Syst. 2015, 281, 227–251. [Google Scholar] [CrossRef]
- Otadi, M.A.; Mosleh, M. Simulation and evaluation of dual fully fuzzy linear systems by fuzzy neural network. Appl. Math. Model. 2011, 35, 5026–5039. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Lotfi, F.H.; Kiasari, M.K.; Khezerloo, M. On the fuzzy solution of LR fuzzy linear systems. Appl. Math. Model. 2013, 37, 1170–1176. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Ghanbari, M. On the algebraic solution of fuzzy linear systems based on interval theory. Appl. Math. Model. 2012, 36, 5360–5379. [Google Scholar] [CrossRef]
- Behera, D.; Chakraverty, S. Solving fuzzy complex system of linear equations. Inf. Sci. 2014, 277, 154–162. [Google Scholar] [CrossRef]
- Amirfakhrian, M. Numerical solution of a fuzzy system of linear equations with polynomial parametric form. Int. J. Comput. Math. 2007, 84, 1089–1097. [Google Scholar] [CrossRef]
- Sun, X.-D.; Guo, S.-Z. Linear Formed General Fuzzy Linear Systems. Syst. Eng. Theory Pract. 2009, 29, 92–98. [Google Scholar] [CrossRef]
- Ghanbari, R. Solutions of fuzzy LR algebraic linear systems using linear programs. Appl. Math. Model. 2015, 39, 5164–5173. [Google Scholar] [CrossRef]
- Nuraei, R.; Allahviranloo, T.; Ghanbari, M. Finding an inner estimation of the solution set of a fuzzy linear system. Appl. Math. Model. 2013, 37, 5148–5161. [Google Scholar] [CrossRef]
- Muzzioli, S.; Reynaerts, H. Fuzzy linear systems of the form A1x + b1 = A2x + b2. Fuzzy Sets Syst. 2006, 157, 939–951. [Google Scholar] [CrossRef]
- Shary, S.P. New characterizations for the solution set to interval linear systems of equations. Appl. Math. Comput. 2015, 265, 570–573. [Google Scholar] [CrossRef]
- Friedman, M.; Ming, M.; Kandel, A. Fuzzy linear systems. Fuzzy Sets Syst. 1998, 96, 201–209. [Google Scholar] [CrossRef]
- Wu, C.-X.; Ma, M. Embedding problem of fuzzy number space: Part I. Fuzzy Sets Syst. 1991, 44, 33–38. [Google Scholar]
- Allahviranloo, T.; Ghanbari, M.; Hosseinzadeh, A.A.; Haghi, E.; Nuraei, R. A note on “Fuzzy linear systems”. Fuzzy Sets Syst. 2011, 177, 87–92. [Google Scholar] [CrossRef]
- Behera, D.; Chakraverty, S. Solving fuzzy complex system of linear equations. Inf. Sci. 2014, 277, 154–162. [Google Scholar] [CrossRef]
- Zheng, B.; Wang, K. General fuzzy linear systems. Appl. Math. Comput. 2006, 181, 1276–1286. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salahshour, S.; Ahmadian, A.; Ismail, F.; Baleanu, D. A Novel Weak Fuzzy Solution for Fuzzy Linear System. Entropy 2016, 18, 68. https://doi.org/10.3390/e18030068
Salahshour S, Ahmadian A, Ismail F, Baleanu D. A Novel Weak Fuzzy Solution for Fuzzy Linear System. Entropy. 2016; 18(3):68. https://doi.org/10.3390/e18030068
Chicago/Turabian StyleSalahshour, Soheil, Ali Ahmadian, Fudziah Ismail, and Dumitru Baleanu. 2016. "A Novel Weak Fuzzy Solution for Fuzzy Linear System" Entropy 18, no. 3: 68. https://doi.org/10.3390/e18030068
APA StyleSalahshour, S., Ahmadian, A., Ismail, F., & Baleanu, D. (2016). A Novel Weak Fuzzy Solution for Fuzzy Linear System. Entropy, 18(3), 68. https://doi.org/10.3390/e18030068







