Chaos on the Vallis Model for El Niño with Fractional Operators
Abstract
:1. Introduction
2. Analysis of Vallis Model with Local Derivative
2.1. Stability Analysis of Equilibrium Points
2.2. Existence of Exact Solution
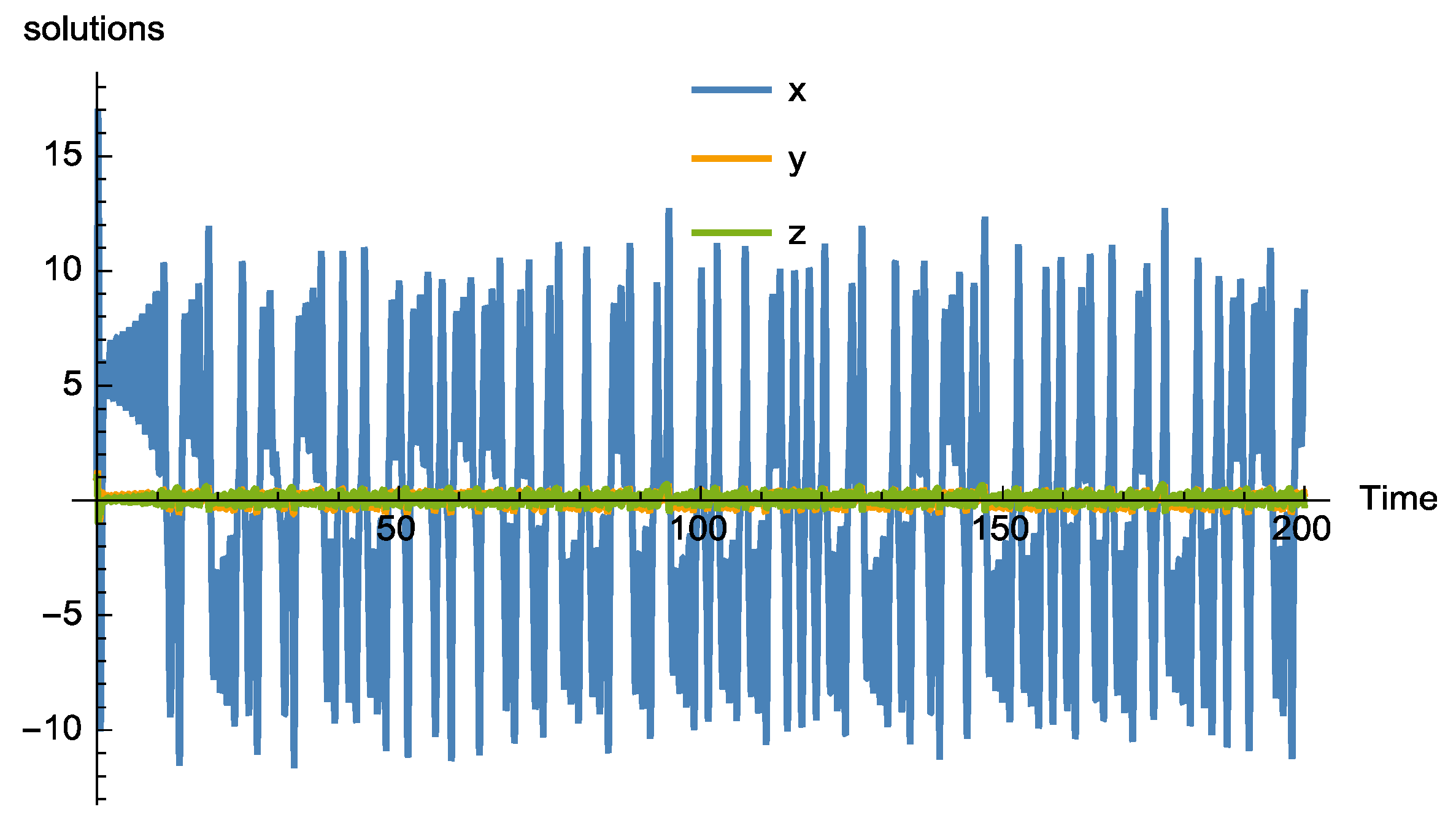
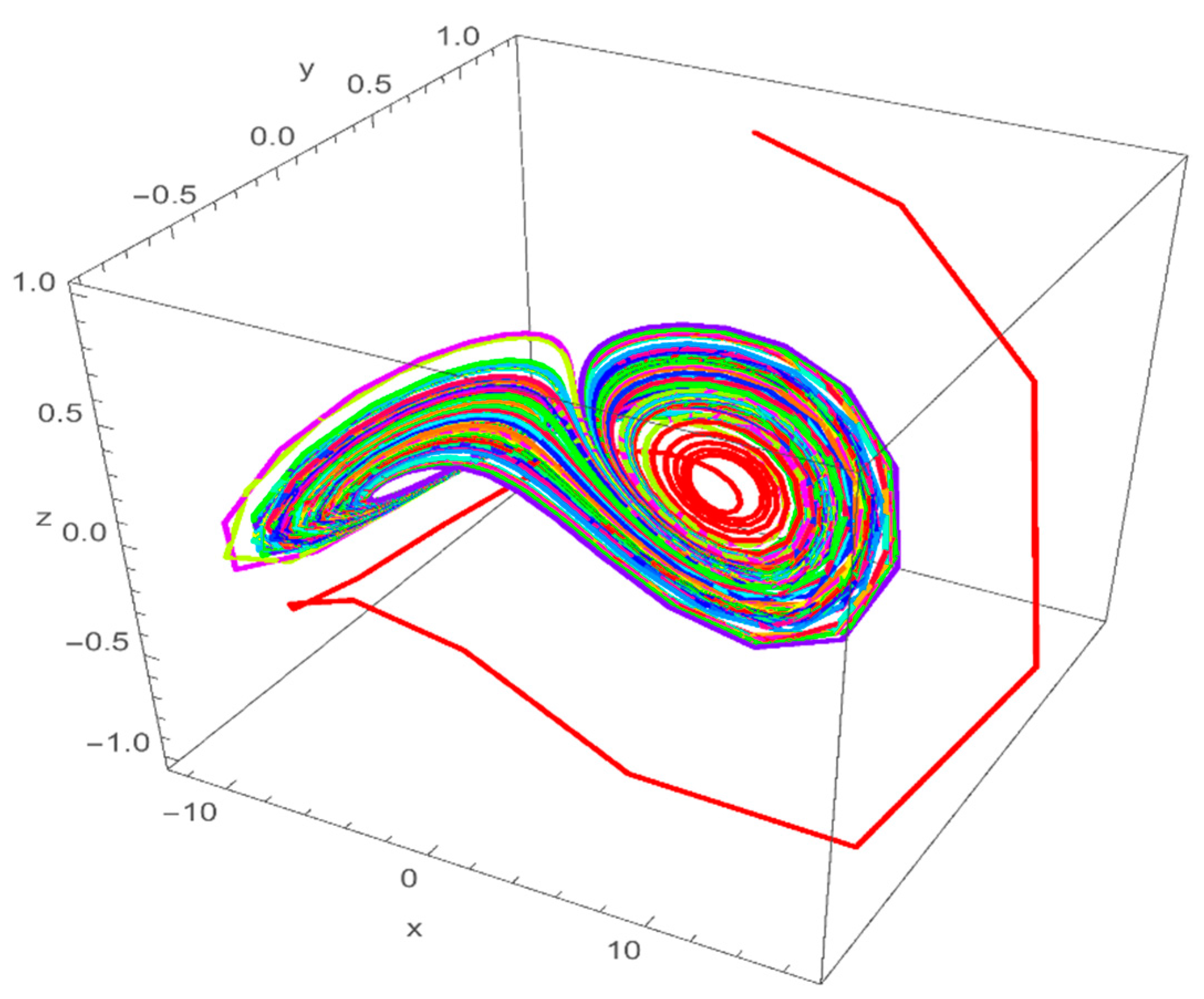
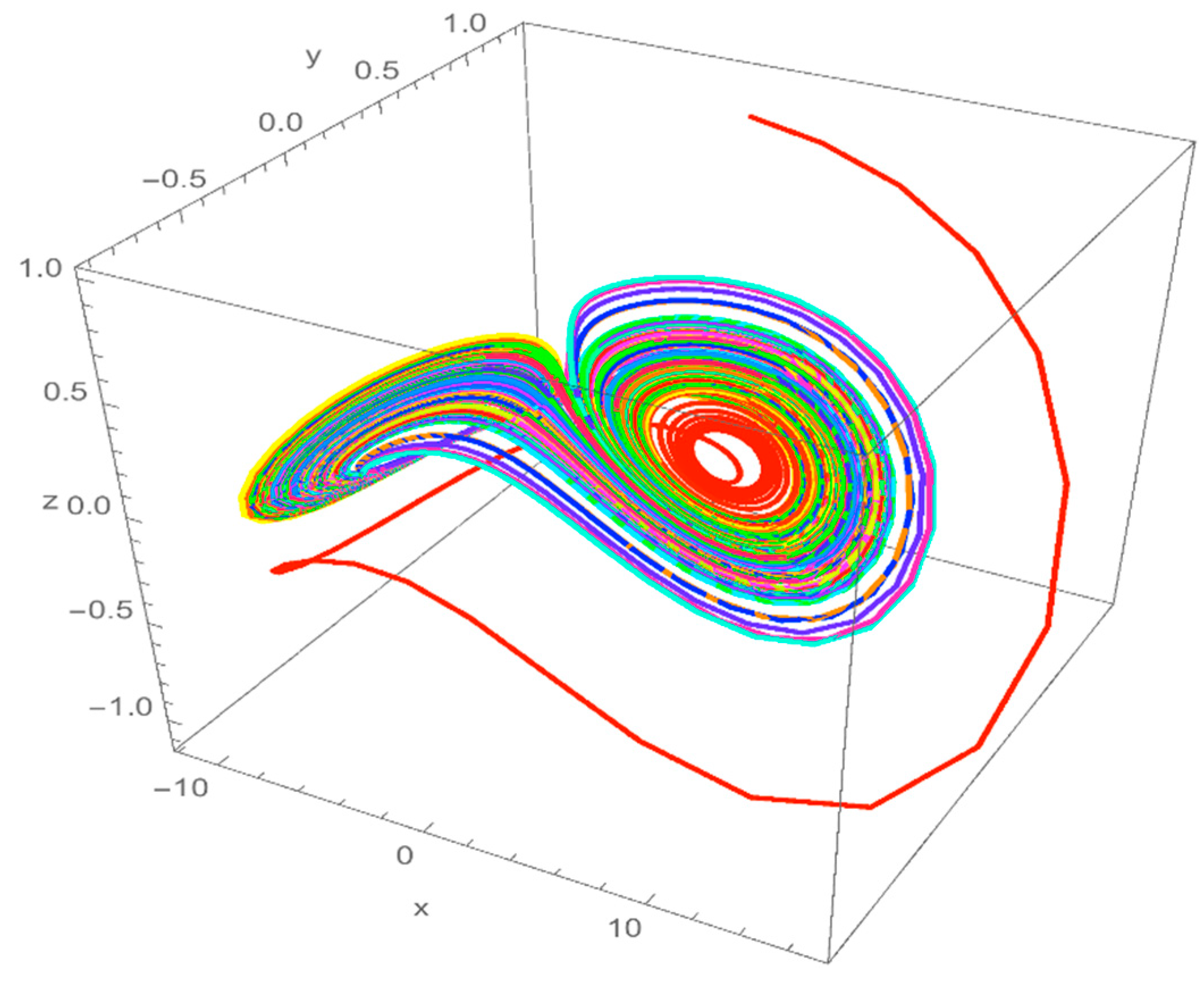
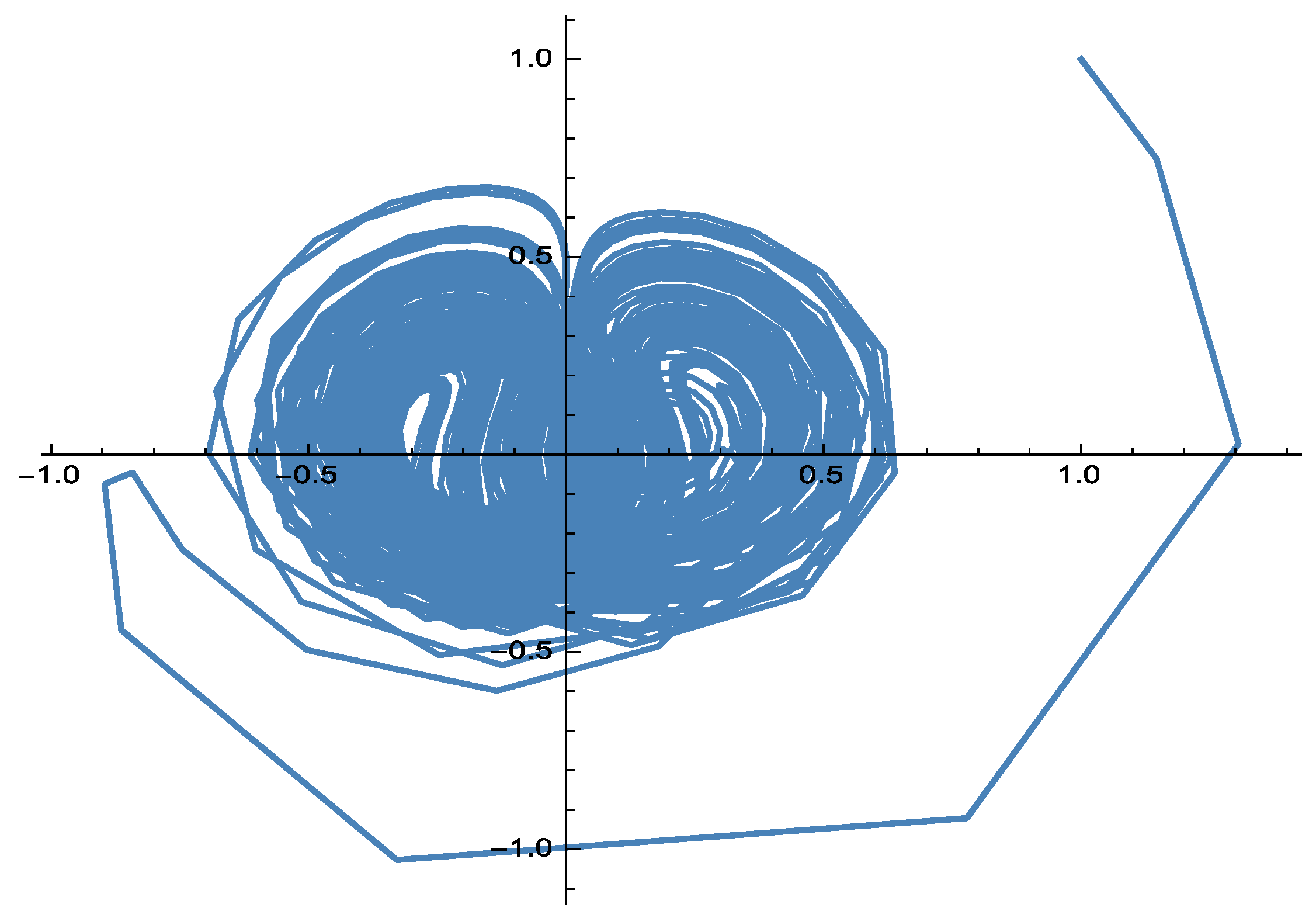
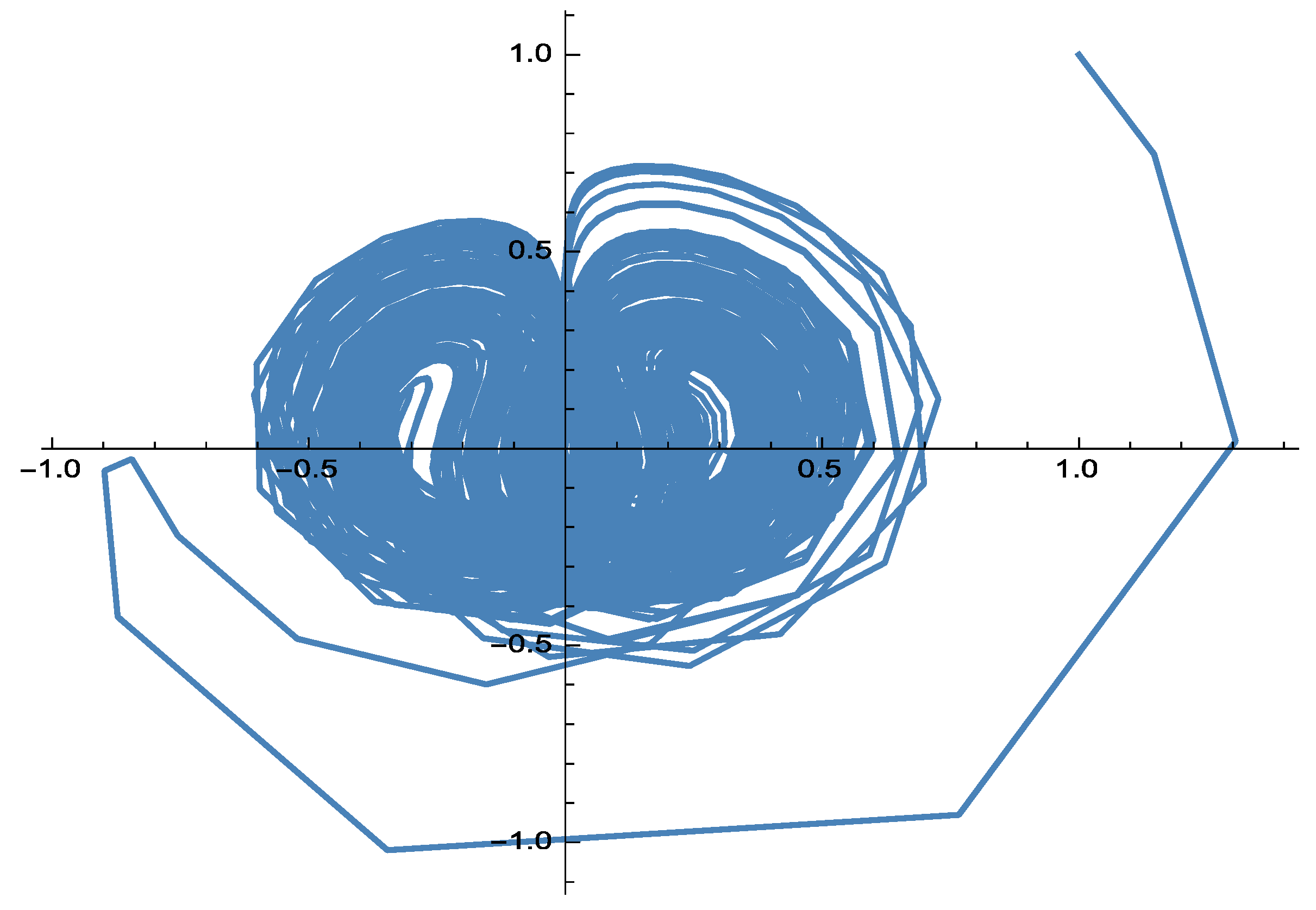
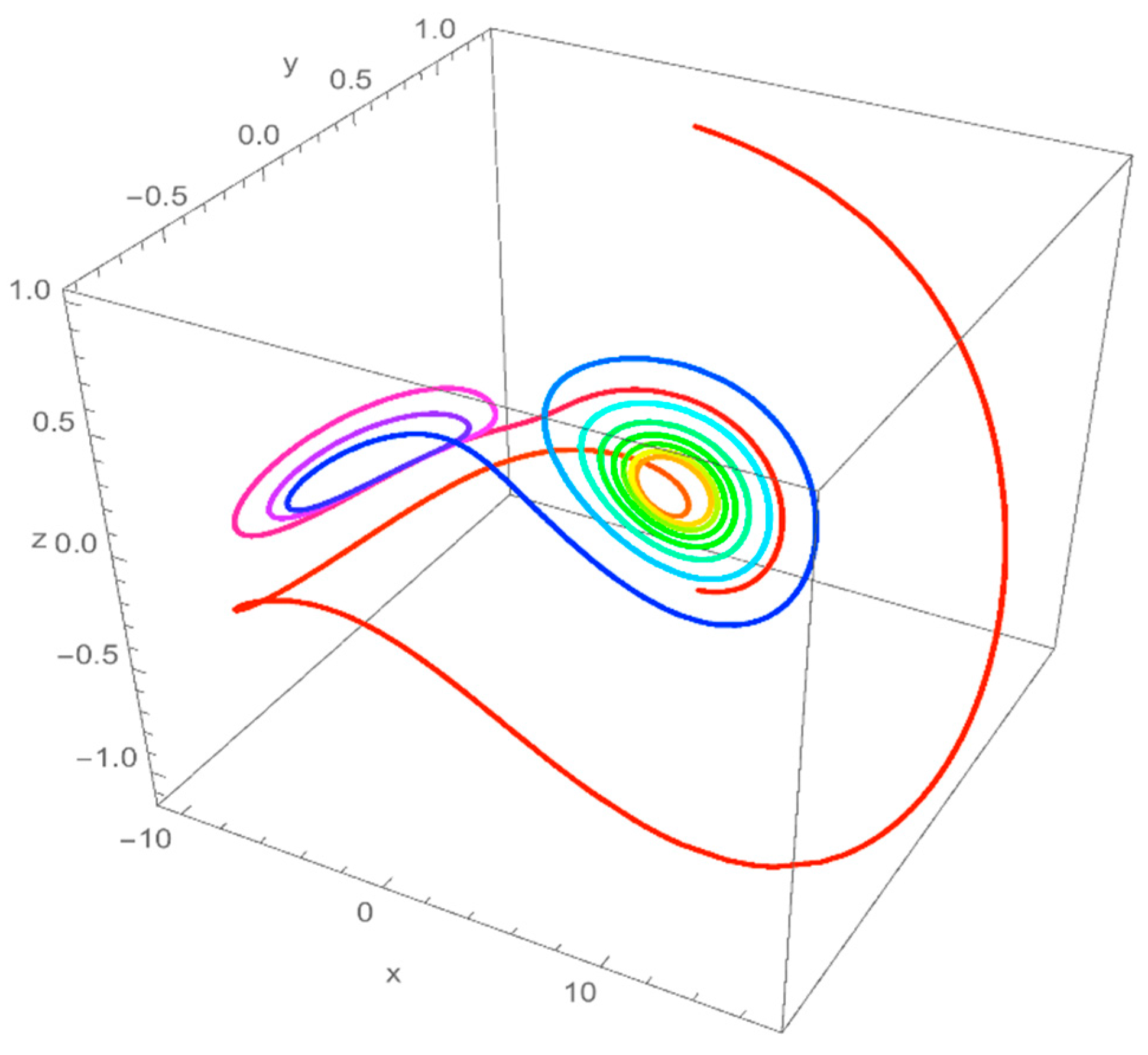
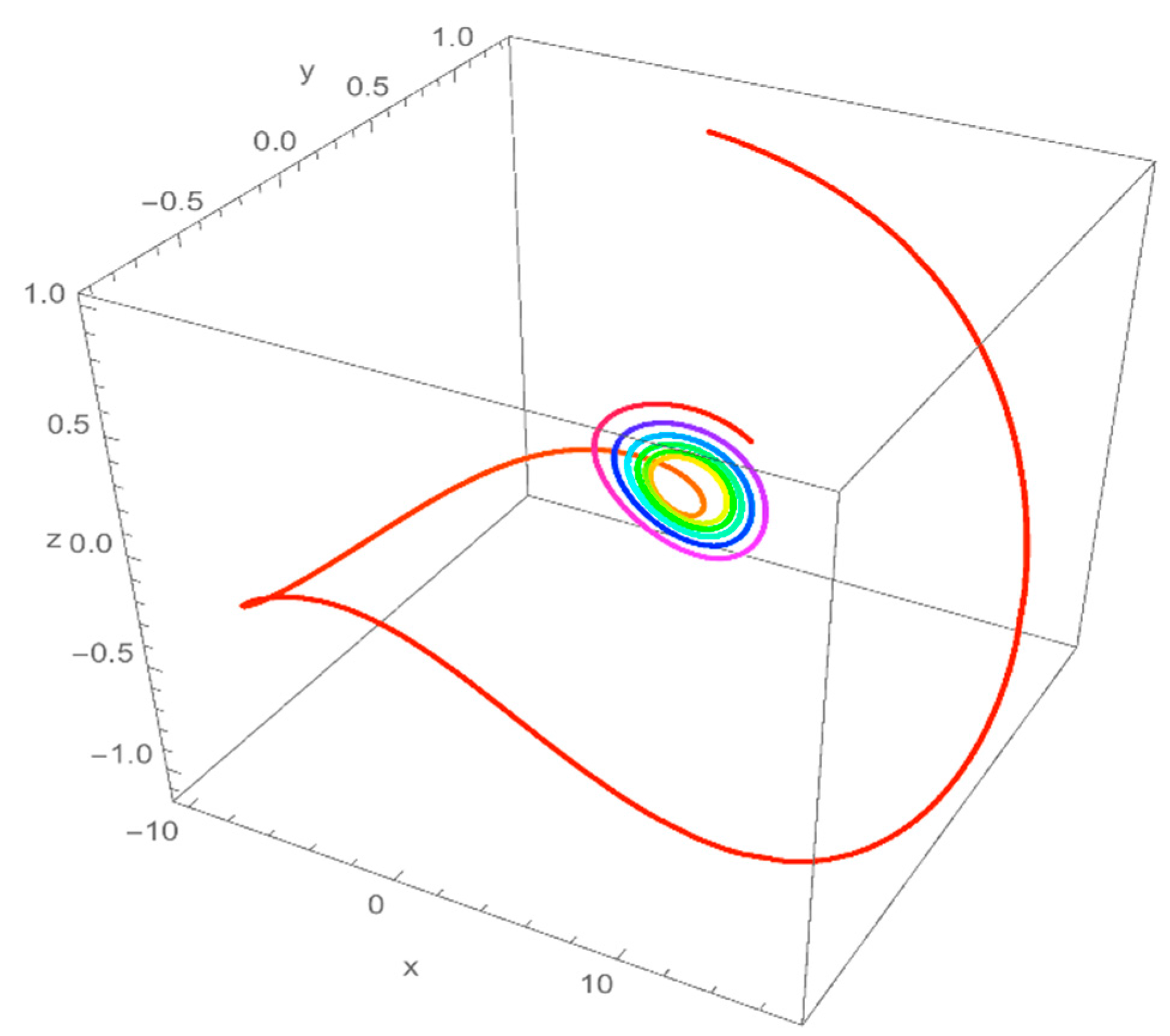
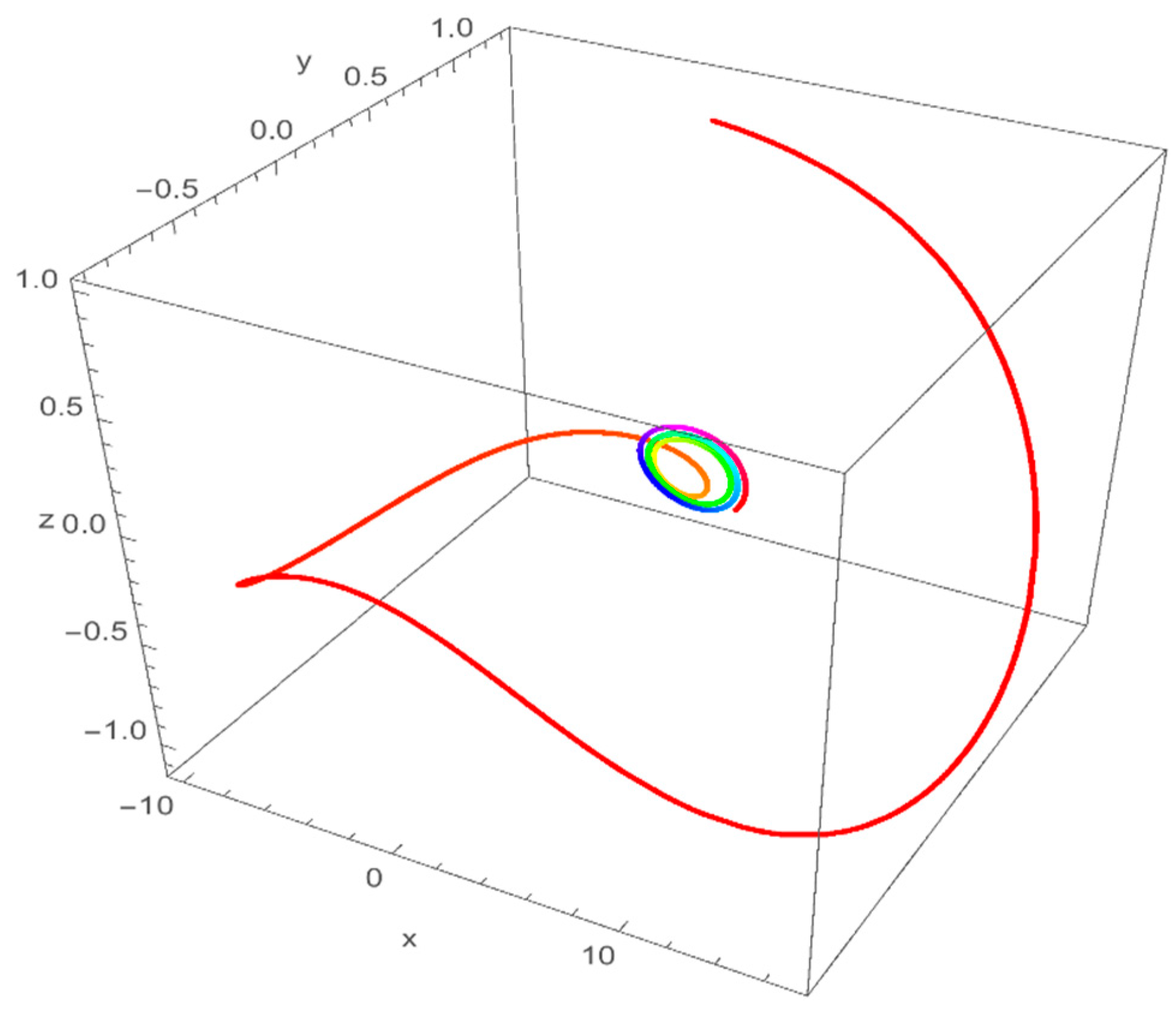
2.3. Numerical Simulations
| Algorithm 1. |
Input as preliminary input
|
| Step 1: Put and |
| Step 2: for i = 1 to n − 1 do step 3, step 4 and step 5
|
| Step 3: compute
|
| Step 4:
|
| Step 5: stop. |
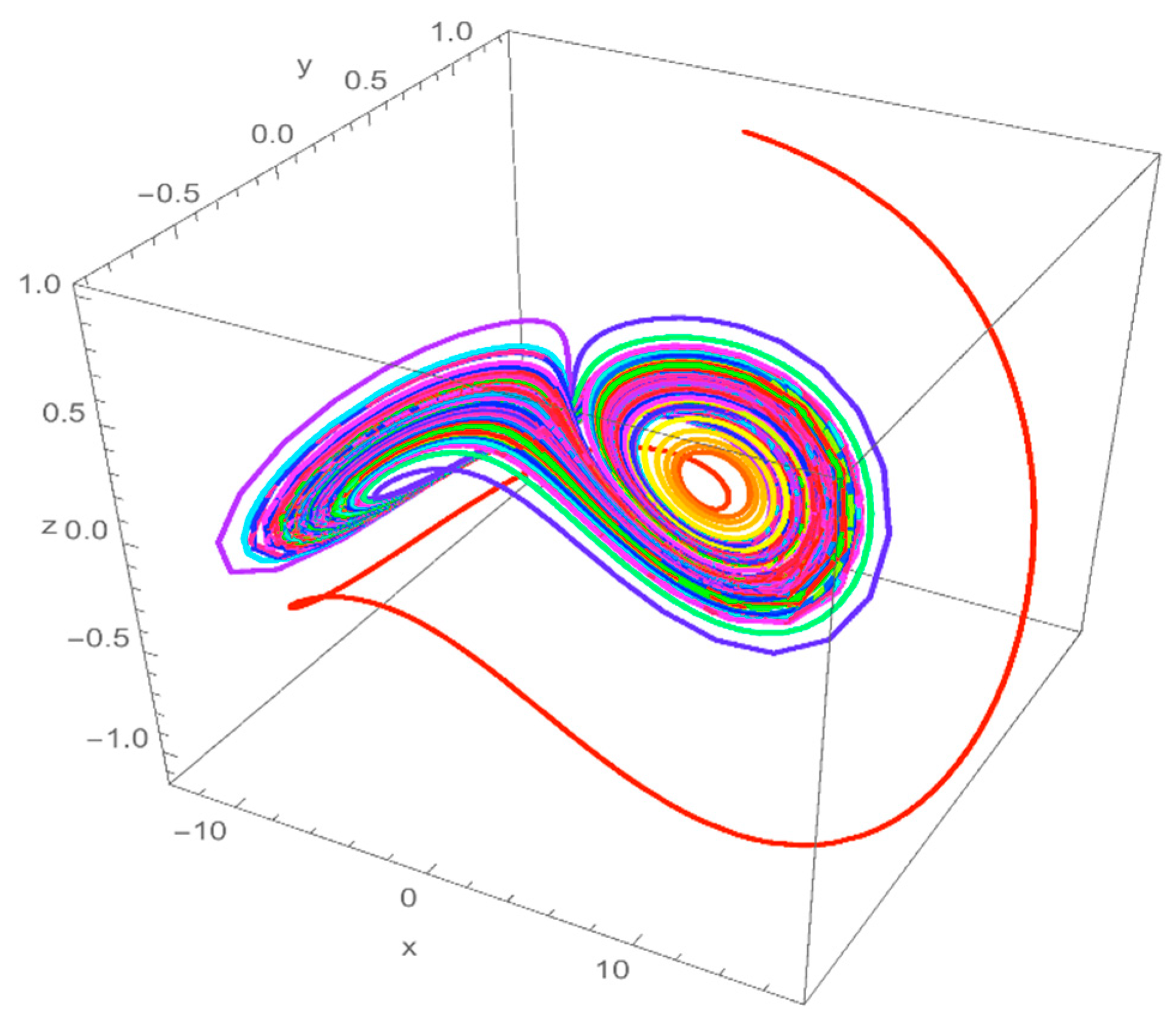
3. Analysis of Vallis Model with Caputo Derivative
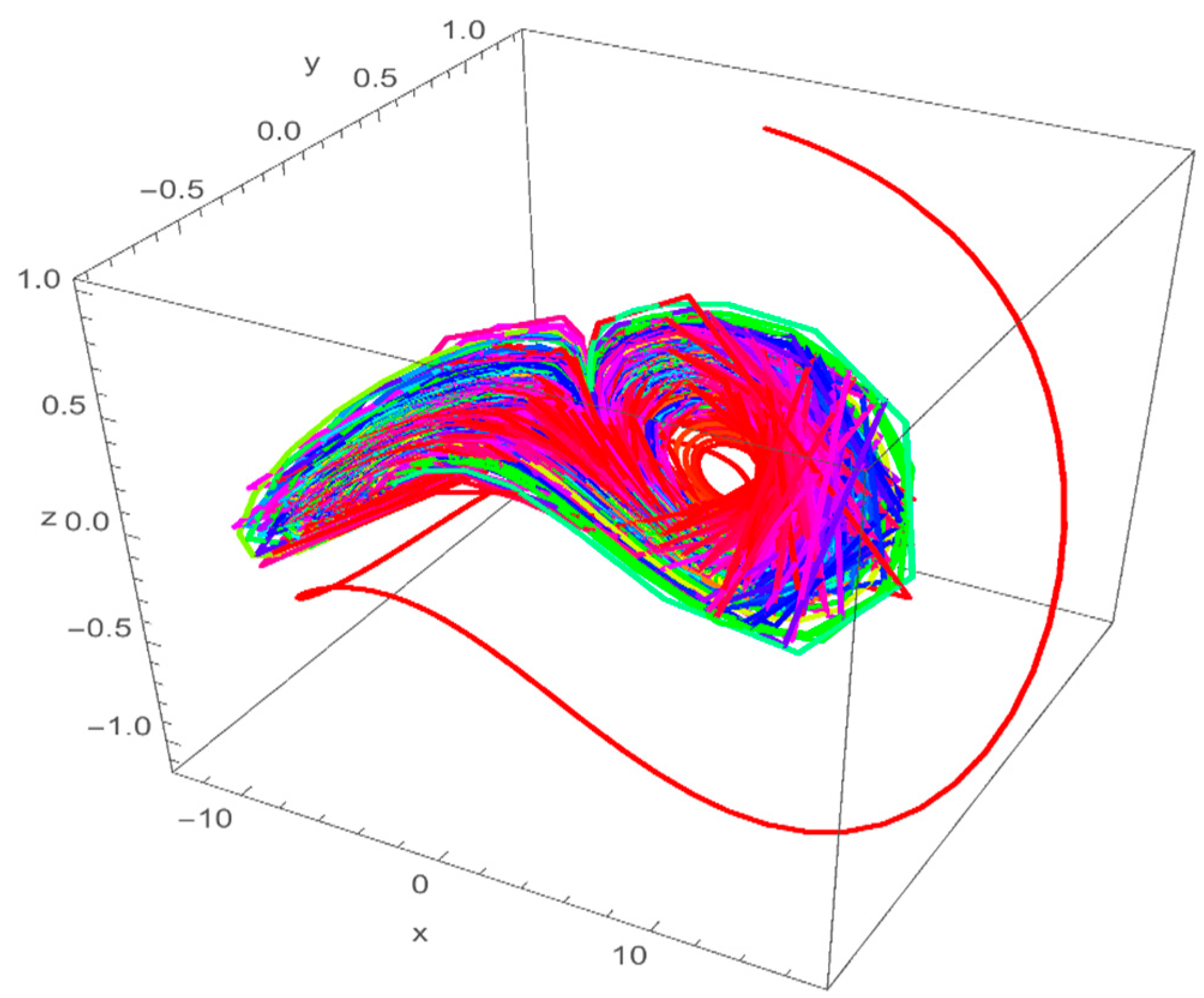
Stability Analysis of the Iteration Method
4. Analysis of the Vallis Model with Caputo–Fabrizio Derivative
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tenreiro Machado, J.A. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A. Entropy analysis of fractional derivatives and their approximation. J. Appl. Nonlinear Dyn. 2012, 1, 109–112. [Google Scholar] [CrossRef]
- Ibrahim, R.W. The fractional differential polynomial neural network for approximation of functions. Entropy 2013, 15, 4188–4198. [Google Scholar] [CrossRef]
- Mathai, A.M.; Haubold, H.J. On a generalized entropy measure leading to the pathway model with a preliminary application to solar neutrino data. Entropy 2013, 15, 4011–4025. [Google Scholar] [CrossRef]
- Jalab, H.A.; Ibrahim, R.W. Denoising algorithm based on generalized fractional integral operator with two parameters. Discret. Dyn. Nat. Soc. 2012, 2012, 529849. [Google Scholar] [CrossRef]
- Jalab, H.A.; Ibrahim, R.W. Texture enhancement based on the Savitzky-Golay fractional differential operator. Math. Probl. Eng. 2013, 2013, 149289. [Google Scholar] [CrossRef]
- Vallis, G.K. El Niño: A chaotic dynamical system? Science 1986, 232, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Letellier, C.; Dutertre, P.; Gouesbet, G. Characterization of the Lorenz system, taking into account the equivariance of the vector field. Phys. Rev. E 1994, 49. [Google Scholar] [CrossRef]
- Mischaikow, K.; Mrozek, M. Chaos in the Lorenz equations: A computer assisted proof. Part II: Details. Math. Comput. Am. Math. Soc. 1998, 67, 1023–1046. [Google Scholar] [CrossRef]
- Galias, Z.; Zgliczyński, P. Computer assisted proof of chaos in the Lorenz equations. Physica D 1998, 115, 165–188. [Google Scholar] [CrossRef]
- Magin, R.L.; Abdullah, O.; Baleanu, D.; Zhou, X.J. Anomalous diffusion expressed through fractional order differential operators in the Bloch–Torrey equation. J. Magn. Reson. 2008, 190, 255–270. [Google Scholar] [CrossRef] [PubMed]
- Cloot, A.; Botha, J.F. A generalised groundwater flow equation using the concept of non-integer order derivatives. Water SA 2006, 32, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-Fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, 22–30. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Jorge, L.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction-diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Atangana, A.; Nieto, J.J. Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Calderón-Ramón, C.; Cruz-Orduña, I.; Escobar-Jiménez, R.F.; Olivares-Peregrino, V.H. Modeling of a Mass-Spring-Damper System by Fractional Derivatives with and without a Singular Kernel. Entropy 2015, 17, 6289–6303. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Pene, M.K.; Mwambakana, J.N. Duplication in a model of rock fracture with fractional derivative without singular kernel. Open Math. 2015, 13. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; López-Lópezb, M.G.; Alvarado-Martínezb, V.M.; Reyes-Reyesb, J.; Adam-Medinab, M. Modeling diffusive transport with a fractional derivative without singular kernel. Physica A 2016, 447, 467–481. [Google Scholar] [CrossRef]
- Alsaedi, A.; Baleanu, D.; Etemad, S.; Rezapour, S. On coupled systems of time-fractional differential problems by using a new fractional derivative. J. Funct. Spaces 2016, 2016, 4626940. [Google Scholar] [CrossRef]
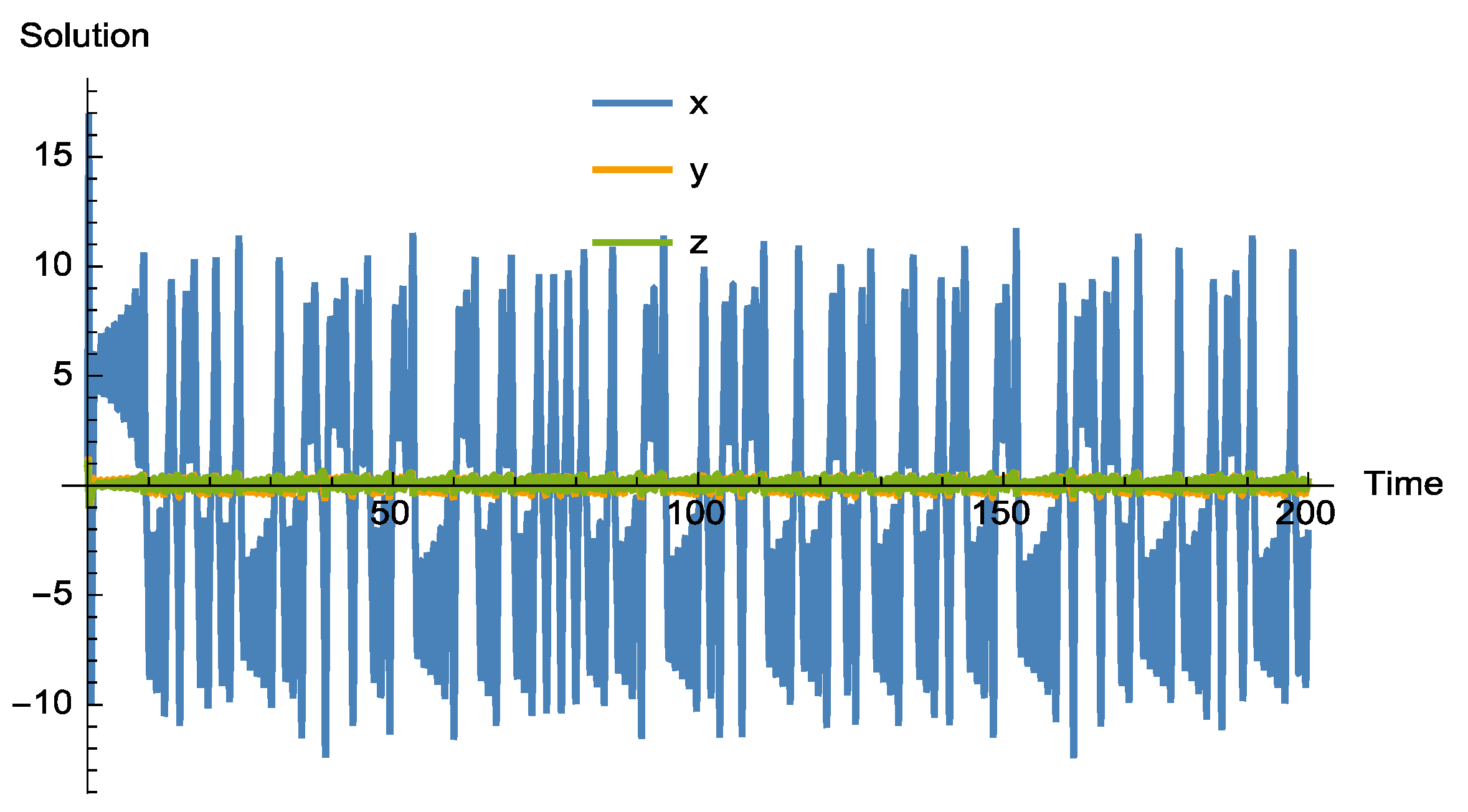

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkahtani, B.S.T.; Atangana, A. Chaos on the Vallis Model for El Niño with Fractional Operators. Entropy 2016, 18, 100. https://doi.org/10.3390/e18040100
Alkahtani BST, Atangana A. Chaos on the Vallis Model for El Niño with Fractional Operators. Entropy. 2016; 18(4):100. https://doi.org/10.3390/e18040100
Chicago/Turabian StyleAlkahtani, Badr Saad T., and Abdon Atangana. 2016. "Chaos on the Vallis Model for El Niño with Fractional Operators" Entropy 18, no. 4: 100. https://doi.org/10.3390/e18040100
APA StyleAlkahtani, B. S. T., & Atangana, A. (2016). Chaos on the Vallis Model for El Niño with Fractional Operators. Entropy, 18(4), 100. https://doi.org/10.3390/e18040100





