1. Introduction
We derive the extension to multivariate arrays of the thermodynamic-like approach that we have recently proposed for identifying pattern responses in cancerous cell lines and patient data. Our approach is based on information theory and surprisal analysis. It was earlier introduced to deal with physicochemical systems in disequilibrium [
1,
2,
3]. It is currently being applied to biophysicochemical systems [
4,
5,
6,
7,
8]. The essential difference with the methods already proposed [
9,
10,
11,
12,
13] is that we use the thermodynamic entropy instead of using entropy as a statistical measure of dispersion.
In this paper we discuss the approach to multilevel arrays and apply it to transcription level data. We treat each transcript as a molecule so we have the thermodynamics (of disequilibrium) in a multicomponent system. The thermodynamic-like approach allows for the defining of a base line level for the expression level of each transcript. We show by example that indeed transcripts from different patients and/or different cells do have the same base line level. It is with respect to this baseline that the changes induced by the different conditions are quantified. By using a thermodynamic entropy and surprisal analysis, we have previously shown that the base line can be determined from genomic data. In addition to the partition function of each transcript, the base line includes all the contributions to the entropy that are common to all the conditions: non ideality, environment effects, etc. We have recently argued that the reference base line corresponds to the essential cell machinery and is valid across cell types, patients, and organisms [
4]. Such a base line is also recovered in the multivariate case developed here.
One can use entropy in the information theoretic sense as a measure of dispersion from uniformity. Analyses of genetic networks from this point of view have received attention with special reference to the connectivity of the network [
10,
12,
14,
15,
16,
17,
18,
19,
20,
21]. It is the use of a thermodynamic-like expression for the entropy that places the present method apart. It is definitely not a minor correction because the base line distribution of expression levels of transcripts is a very non-uniform distribution that accounts for the great majority of an information theoretic entropy (>97%, [
4]). The change in expression level induced by the disease is small compared to the base line. In other words, even in diseased patients cells are inherently stable. It is possible to induce a change of the stable state (e.g., [
8]), but it is a change from one stable state to another.
Singular value decomposition (SVD) is used here as a mathematical tool to implement a fast and useful surprisal analysis of large data sets [
7]. The technical point is that it is the logarithm of the expression level that is being expanded. The invariant part of that expansion is the free energy (in units of the thermal energy) of the transcript and specifies the baseline value.
For 2D arrays, we previously reported on using SVD as a practical tool to implement surprisal analysis and determine the gene patterns in terms of which the data can be analyzed and compacted [
4,
5,
6,
7,
15,
22,
23,
24,
25]. In the multivariate case derived here, a High Order Singular Valued Decomposition (HOSVD) is used [
26]. Compared to other tensor decomposition methods based on the Tucker decomposition [
27,
28], HOSVD has the advantage of leading to orthogonal patterns which allows it to characterize the deviation of the observed expression level with respect to the base line in a unique way.
We turn next to the background for our work in terms of systems biology [
29]. High throughput genomic and proteomic data on various types of organisms are becoming routinely available. The purpose of measuring these massive data sets is to uncover trends and patterns in the genomic and proteomic responses to different conditions and perturbations, with the promise of a better understanding of diseases like cancer or for optimizing energy production biotechnologies based on unicellular organisms like yeast and algae. Typically, the number of conditions that can be engineered is much smaller than the number of gene transcripts that can be measured, where that number ranges in the tens of thousands depending on the organism. Similarly, the number of proteins that can nowadays be quantitatively measured is also quite large. Most of the methods of analysis deal with 2D rectangular arrays where all the conditions are treated on the same level. These can be different points in time [
8,
23,
24,
30], different nutrients conditions, or in the case of cancer, different cell types, oncogenes, and/or drug treatments. When all these different conditions are lumped into a 2D array, the correlation between different conditions is not easy to identify. In some cases, a multivariate analysis has been applied [
31,
32,
33].
Another case that calls for a multivariate analysis is that where the genomic response of cancer is analyzed for different patients and their different cell types. This is the case that we focus on. We show that identifying the gene response of the 3D tensor of data uncovers correlations between cell type and individual patients that are washed out if the 3D array is collapsed to a 2D one by averaging the gene response over patients and keeping the cell type as a relevant dimension, or averaging over cell type and keeping the different patients as the relevant axis.
The paper is organized as follows. We start by a brief outline of the 2D analysis in
Section 2. The extension to a 3D multivariate array is derived in
Section 3 where we show how the possible 2D results are limiting cases of the general case. The methodology is applied in
Section 4 to a 3D array: the gene response measured for different cell types and different patients in the case of prostate cancer. This example allows us to provide an operative definition of two opposite trends. One the one hand, a disease is defined as common features that affect patients in the same way, but on the other, the analysis of the gene response of individual patients shows that different patients have different disease gene patterns. Correlating cell types and patient responses using a multivariate analysis provides a step towards personalized diagnostics. This is a special advantage of the multivariate analysis.
2. Surprisal Analysis of 2D Arrays
In the bivariate case, the data are arranged as a rectangular matrix
X of dimension
I by
J where
I, the number of gene transcripts, is typically much larger than
J, the number of conditions for which the expression levels of the transcripts have been measured. Each column of
X is a distribution over the gene transcripts
i measured for the given condition
j. Each row is the distribution over the conditions
j measured for a given transcript
i. Each reading
Xij is the measured expression level of transcript
i under condition
j. In a typical experiment involving many cells,
Xij is an average value over the fluctuations that can occur from cell to cell because the individual cell is a finite system [
15].
Surprisal analysis seeks to characterize the level distribution
Xij as a distribution of maximal entropy subject to constraints. We assume that the same constraints operate for all the conditions but it can be that different constraints are more important for different conditions. The number of constraints,
C, is typically smaller than the number of conditions,
J, and therefore the constraints by themselves are not sufficient to determine a unique distribution. Among all the distributions that are consistent with the constraints, surprisal analysis determines that unique distribution whose entropy is maximal. When such a distribution exists it can be analytically constructed by the method of Lagrange undetermined multipliers [
4,
5,
22]. Surprisal analysis employs the following expression for the logarithm of the expression level of gene
i under condition
j:
where
is the base line level for transcript
i, that is the expression level of transcript
i at maximum entropy without any constraints imposed by the conditions:
The additional terms in Equation (1) reduce the value of the entropy from its thermodynamic maximum. is the Lagrange multiplier for the constraint α in condition j. For the condition j, each constraint α lowers the value of the entropy by an extent given by the Lagrange multiplier The Lagrange multiplier is common to all genes but does depend on the condition. By definition of a base line, in Equation (2) does not depend on the condition j. This invariance is not imposed in the numerical procedure described below and we show that up to numerical noise, the values of computed for each condition are indeed the same. The value of the constraint α for the transcript i is Giα. These values for the transcripts are common for all the different conditions.
A key property of Equation (1) that is retained also in the higher dimensional case is the separability. Each deviation term in Equation (1) is made up as a product of two factors, so that all the genes that contribute to pattern α are changing in the same way (i.e., coherently) as the condition is being changed. The “weight” of condition j is the same for all the genes that participate in pattern α.
The aim of surprisal analysis is to retain as few as possible terms in Equation (1), that is, to identify the minimum set of constraints
α that will give a good fit of
simultaneously for all conditions
j. The constraints can be given a biophysical interpretation in terms of the processes that restrain the value of the entropy of the distribution to reach its maximal value. Unlike in the univariate case typically encountered in physical chemistry where the form of the constraints can be known a priori on physicochemical grounds [
2], in the bivariate case, the constraints are typically not known. One efficient computational way to determine the constraints is to apply singular valued decomposition, SVD, of the logarithm of data, as follows. Construct the matrix
Y such that its elements are the logarithms of the expression levels
. The range of the indices
i and
j are quite different, 1 ≤
i ≤
I, 1 ≤
j ≤
J and so Y is a rectangular
I by
J matrix, where typically
I >>
J. Therefore
Y is a singular matrix but we can ‘diagonalize’ it in the manner of SVD as
where the columns of the matrices
G and
V are orthonormal. The matrix
G is an
I by
J rectangular matrix and its rank is therefore
J or lower. The matrix
Ω is a diagonal
J by
J matrix made up of the
J eigenvalues of
V (or of the non-zero eigenvalues of
G). If we want to express
Ω as a function of
Y, we get
which we can call “the most compact form” of the data.
The matrices
G and
V in Equation (3) are respectively the left and right eigenvectors of
Y. The number of non-zero eigenvalues of
Y is limited by its smallest dimension, which for us is the number of conditions
J. The left and right eigenvectors of
Y can be obtained as the normalized eigenvectors of the two covariance matrices that can be built from
Y: the “small”
J ×
J matrix
YTY and the “large”
I ×
I matrix
YYT. The matrix
Ω in Equation (3) is obtained from the eigenvalue equation
where
Ω2 is the diagonal matrix of the eigenvalues
and the vector
Vα the corresponding eigenvector. The maximum rank of
YTY is its dimension
J. The large
I by
I matrix
YYT is also maximum rank
J and has the same non-zero eigenvalues as
YTY. The eigenvectors
Gα correspond to the same eigenvalue as the eigenvector
Vα of the
YTY matrix. Knowing the eigenvalues
ωα and the normalized eigenvectors
Vα is sufficient to determine the vectors
Gα,
α = 0,…,
J−1, from the data:
The SV decomposition given in Equation (3) can be recast into the surprisal form of Equation (1)
where the Lagrange multiplier
is thereby expressed as
The Lagrange multiplier determines the importance of the constraint α for condition j. In Equation (8), this importance is shown to be a product of two terms. One factor, , is the overall importance of constraint α. The other is the (normalized) importance of this constraint for condition j. It is a normalized weight because the vector Vα is normalized.
For a 2D data array, the Lagrange multipliers can be written in a matrix form
For a 3D data array the Lagrange multipliers will form a 3D tensor.
From Equation (9) above, we see that the matrix Λ is a partial de-diagonalization of the diagonal most compact form of the data, Ω.
Using Equations (3) and (9), the surprisal given in Equation (1) can be written as matrix product
The SVD approach ensures that the constraints are linearly independent since they are orthogonal. Both the eigenvectors Gα and Vα are orthonormal. Therefore, also the rows of the matrix of the Lagrange multipliers Λ are orthogonal.
The 2D approach was successfully implemented on microarrays data of gene transcripts for patient data, for several cancer cell models, and for unicellular organisms [
4,
5,
6,
7,
15,
22,
23,
24,
25,
30,
34] subject to various conditions
j. In particular, the values of the Lagrange multipliers that define the base line,
, are found numerically to be independent of the condition index
j in agreement with Equation (2). From Equation (8), one can see that the only way to ensure that
does not depend on
j is that the eigenvector corresponding to the largest eigenvalue is uniform and from the condition that the eigenvectors are normalized the amplitudes in the vector have the value
. Note that the rows of the matrix
Y are not mean centered. When the rows of the matrix
Y are mean centered, the matrix
YTY becomes rank deficient and has one zero eigenvalue with the same corresponding uniform eigenvector. The remaining
J−1 eigenvalues are unchanged compared to the non-mean centered case. The 2D arrays analysis provides a clear meaning to the base line term of Equation (2). The analysis of the gene transcripts that dominate the
Gi0 constraint show that the pattern of the base line corresponds to the essential machinery of the cell [
4]. For
α > 0, the biological interpretation of the transcription patterns are defined by the analysis of the values of the Lagrange multipliers
on the different conditions
j. Each constra
Giα corresponds to a pattern in the gene expression associated with the phenotype
α. We will therefore use the terms transcription pattern and phenotype interchangeably where by phenotype we mean a biological process where all the participating genes act coherently (see Equation (1) or (7)). The analysis of the phenotypes
α > 0 and of the gene expression patterns was shown to characterize the progression of cancer in cell lines [
5,
24].
3. Generalization of the Surprisal Analysis for a Multivariate Array
The need for a generalization of surprisal analysis arises from the availability of gene transcript levels measured, for example, for individual patients and for different conditions or for different cell types. Keeping the different patients as a separate dimension in addition to cell type leads to data in the format of a 3D array. Another case where one can have more than 2D arrays of data is that where different cell types are submitted to different conditions [
31,
32,
33]. Of course, a 4D data or even higher is also possible.
To bring the 3D tensor into a surprisal form, we use HOSVD [
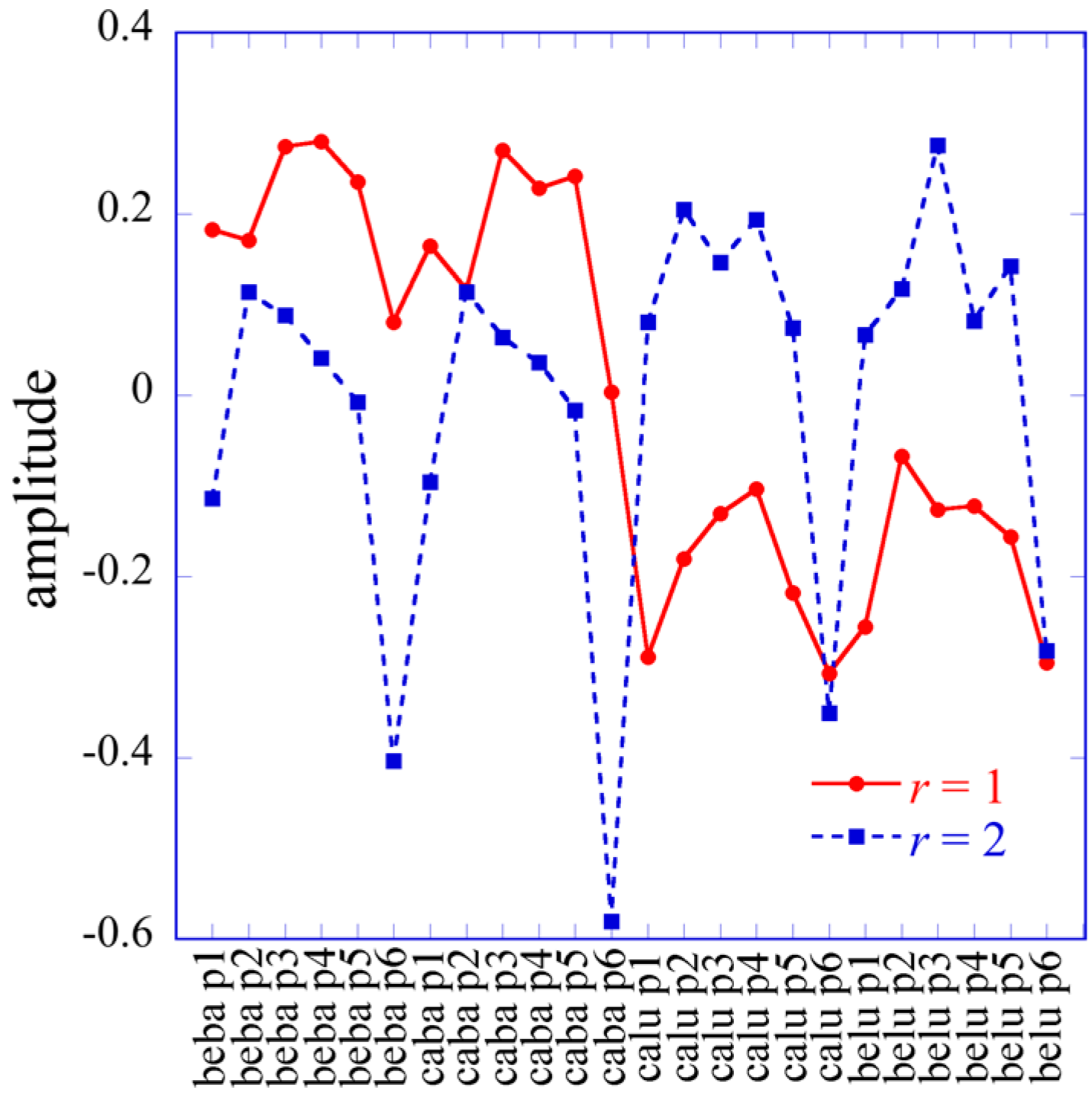
26]. This approach ensures that the constraints remain linearly independent and reverts to the 2D case discussed above as a limit. As an illustration of the formalism we will use data arrays where the gene expression level of different cell types is measured for several individual patients. The 3D analysis allows us to propose an interpretation of the notion of disease and of patient diversity.
We consider a 3D array, T, for which the three dimensions are the number of gene transcripts, I, the number of cell types, J, and the number of patients, K. The elements of the tensor are defined as where Xijk is the measured expression level for transcript i of cell type j of patient k. The number of transcripts, of the order of 20,000, is typically much larger than the numbers of cell types or the number of patients. We have therefore a rectangular 3D I × J × K tensor where I >> J ≈ K. This inequality, typical of gene expression data where the number I of transcripts is very large, plus the fact that we typically want the expression levels to remain an axis, dictates the compaction of the 3D data to a 2D form as discussed next.
3.1. Representing the Tensor Surprisal T in Matrix Form
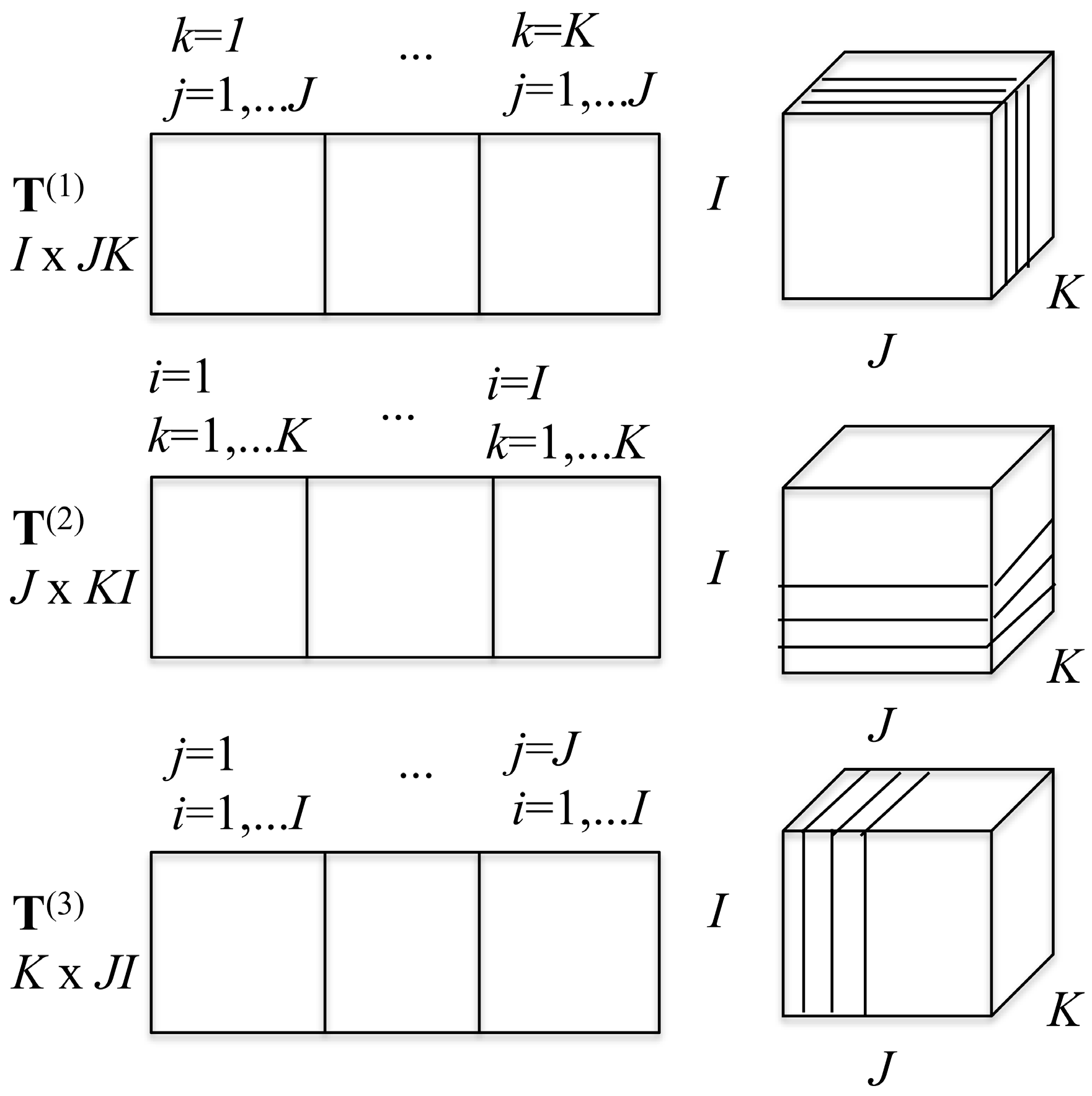
2D slices can be made from the 3D array in three ways. Keeping
i fixed, one has
I different
J ×
K matrices, keeping
j fixed, one has
JK ×
I matrices, and keeping
k fixed generates
KI ×
J matrices. These three possible decompositions of the 3D tensor are arranged as shown in
Scheme 1. From these three decompositions, one can build three matrices that possess the same information as the tensor itself, as is also shown in
Scheme 1. The matrix
T(1) is a 2D
I × (
J ×
K) matrix.
T(1) is made of
K side by side
I ×
J slices. The matrix
T(2) is of dimension
J × (
K ×
I) and is made of
I side by side (
J ×
K) matrices and the matrix
T(3) of dimension
K × (
I ×
J) that is made of
J side by side (
K ×
I) matrices. The three matrices
T(1),
T(2), and
T(3) are called the flattened matrices and correspond to the three ways to represent the tensor as a 2D matrix. These three flattened matrices are the basis for the high order SV decomposition of the tensor [
26]. Each of these flattened rectangular matrices can be decomposed using the 2D SVD procedure as explained in
Section 2 above. We get
The SV decomposition of each of the three flattened matrices
T(1),
T(2), and
T(3) is algebraically the same procedure as discussed in
Section 2 above for the 2D surprisal matrix. In particular, since the rows of the three matrices are not mean centered, for each of them, the normalized eigenvector of the small covariance matrix that corresponds to the largest eigenvalue has uniform amplitudes given by
where dim is the smallest dimension of each matrix.
The left-hand side matrices in Equations (11)–(13) provide a SV decomposition for the elements of the 3D tensor [
26]:
where the matrix
U is the
I ×
JK matrix of the left eigenvectors of
T(1),
V the
J ×
J matrix of the left eigenvectors of
T(2), and
W the
K ×
K matrix of the left eigenvectors of
T(3).
Ω is the core tensor. Its dimensions are
JK ×
J ×
K and correspond to the number of non-zero eigenvalues of the flattened matrices
T(1),
T(2), and
T(3), respectively. The elements of the core tensor can be computed from its
JK ×
JK flattened matrix
Ω(1) [
26] by
In Equation (15), the symbol ⊗ stands for the direct product of the
V and
W matrices (see Equations (12) and (13)), which leads to a square
JK × JK Ω(1) matrix. The matrices
U and
T(1) are defined in Equation (11) above. Equation (15) is the practical form that can be used to compute the core tensor as a flattened matrix. Formally, the core tensor
Ω is defined from the n mode multiplication [
26,
27] of the input tensor
T by the three matrices
U,
V, and
W:
where the symbol “×1” means to multiply the input tensor from the gene direction
I by the
I ×
KJ U matrix of the left eigenvectors of
T(1) (Equation (11)), “×2” means to multiply
T from the cell type direction
J by the matrix
V of the left eigenvectors of
T(2) (Equation (12)), and “×3”means to multiply
T from the patient direction
K by
W (Equation (13)). By doing so, one obtains the core tensor
Ω of dimensions
JK ×
J ×
K whose flattened expression is given by Equation (15).
The labels of matrix elements as used in Equation (14) are, of course, arbitrary. However, once we made a particular choice it carried through. Specifically, because we use the index i to label transcripts, the notation implies that r will index the transcription patterns where U is the left matrix of T(1) (Equation (11)). Similarly j is a cell type index so s will label cell type patterns where is an element of the left matrix of T(2) (Equation (12)) while r is a patient type index.
3.2. The Tensor Form of the Surprisal
Equation (14) generates a fully separable expression for the tensor form of the surprisal for a 3D data array
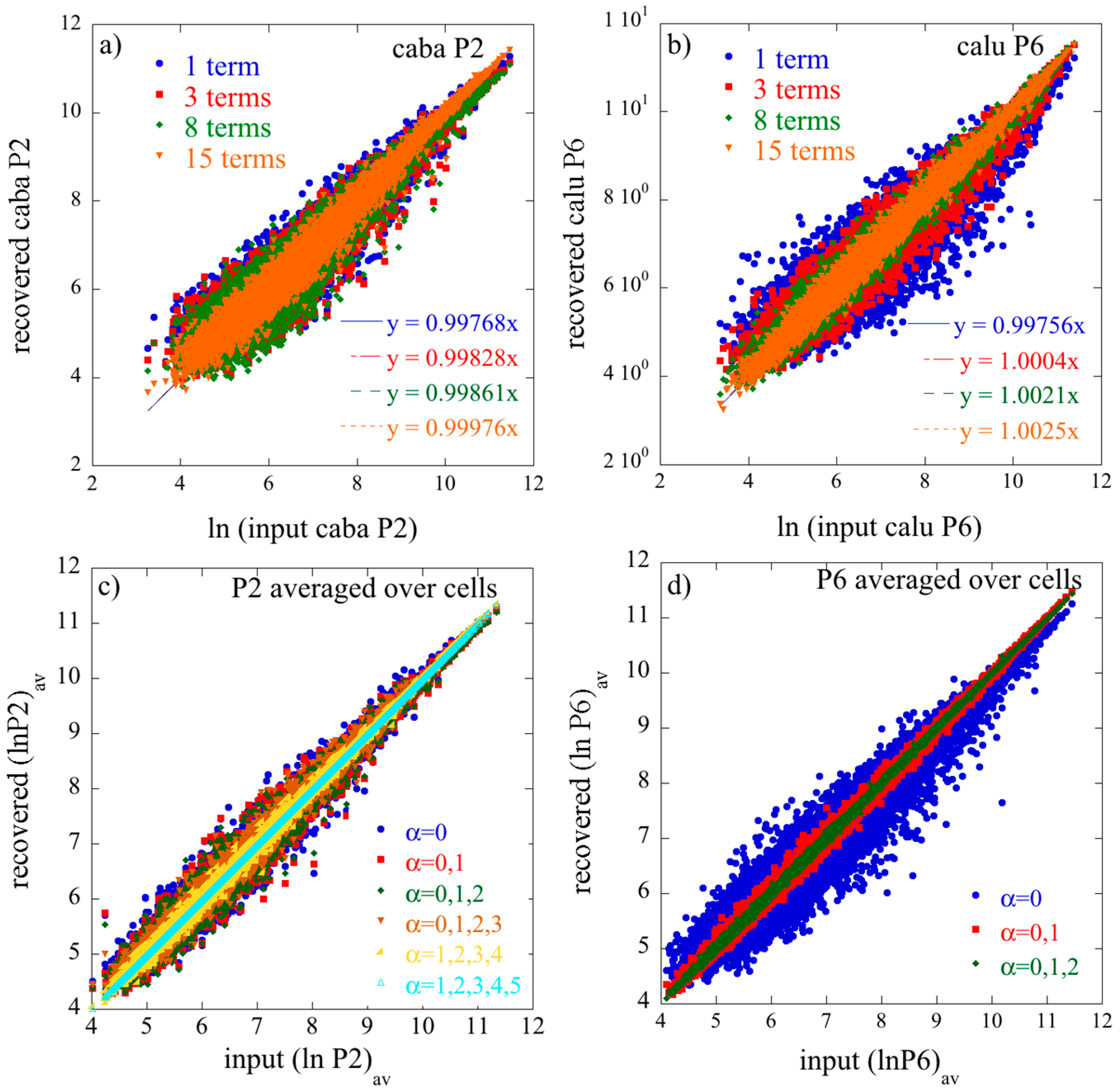
It takes JK × J × K terms to get an equality. The remarkable practical observation is that, in all the examples that we analyzed, very few terms need to be retained for this equation to provide an excellent approximation.
Equation (14) is analogous to Equation (3) of the 2D case. As in the 2D case it is possible to rewrite Equation (14) in a surprisal form. Here we discuss the surprisal of the expression level of the different transcripts, and since these are enumerated by the index
i we pull the vector
U up front in the summation. Rearrangement of the order of summations one has the 3D surprisal form as a summation over the different constraints labeled by
rThe Lagrange multiplier of the
r’th constraint,
, is thereby expressed as the term in the big bracket
In the 2D case the Lagrange multipliers for a given constraint (a given value of α) form a vector. The entries of this vector are labeled by the different conditions j. In the 3D case the Lagrange multipliers are matrices, one matrix for each value of the index r of the constraints. (We use a different letter for the index of the constraints in 2 and 3D so as to explicitly indicate the dimension). The elements of each matrix are labeled by j and k, the indices of the different cell types and the different patients.
The entire set of Lagrange multipliers that were a matrix in the 2D case (Equation (9)) are now a 3D tensor
Λ of dimension
JK ×
J ×
K,
whose flattened matrix form is given by
By analogy to the matrix product representation, Equation (10), of the 2D case, one can also rewrite the surprisal as given by Equation (17) as an n mode product of the tensor representing the Lagrange multipliers,
Λ, by a matrix representing the constraints,
U:
3.3. The Lagrange Multipliers
Numbering the eigenvalues by decreasing order, we can rewrite the surprisal form (17) as
where the first term is the base line for the 3D case, taking into account that
We stress that due to the condition on the dimensions of the tensor, I >> J ≈ K, the I components of the vector U0 are not uniform. They define the gene transcript pattern that corresponds to the base line. The vector U0 plays the role of the vector G0 in the 2D case.
The elements of the core tensor,
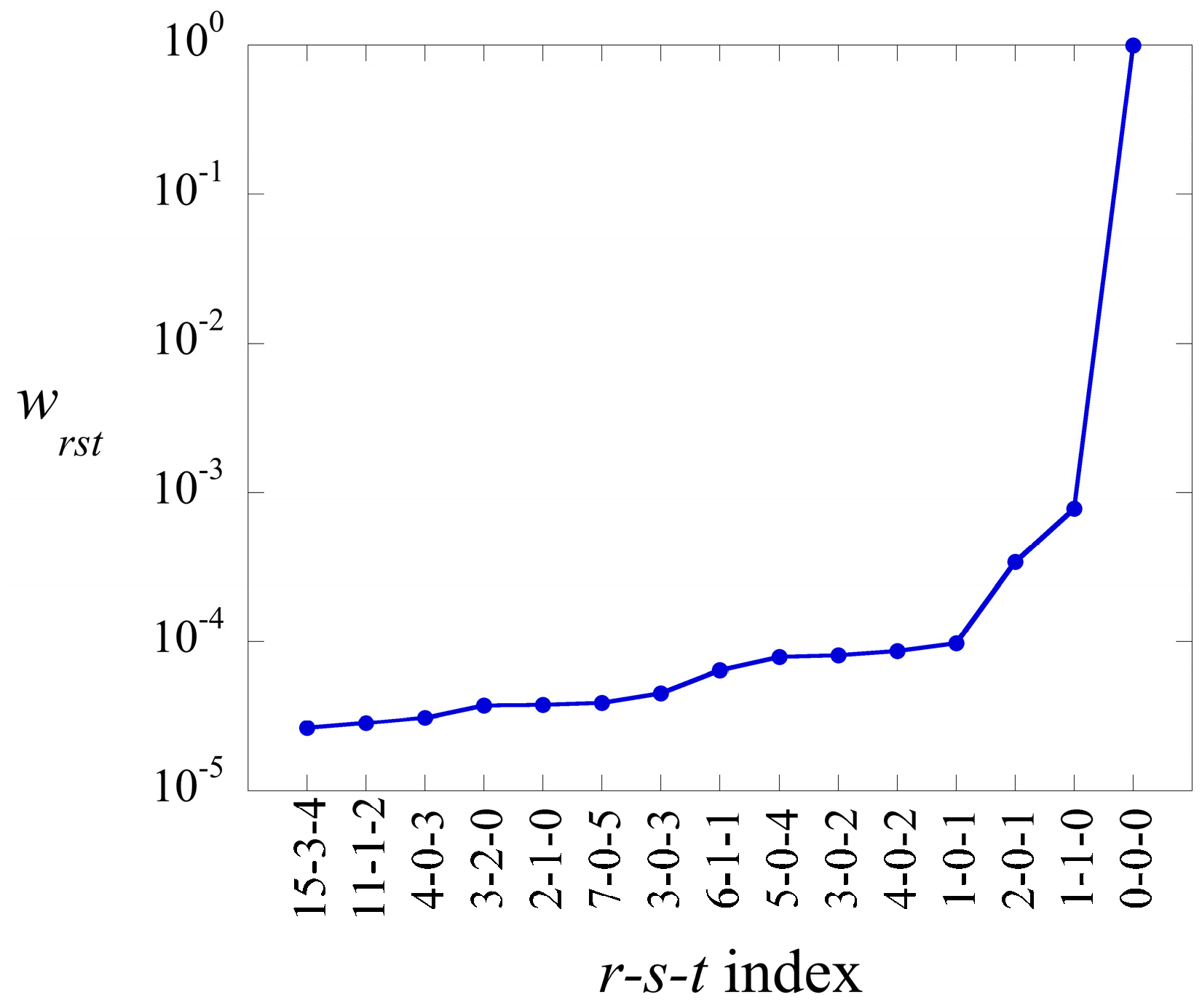
in Equation (17), can be ranked in decreasing order. Their weight is defined as
The term has always the highest weight. This is the term that defines the baseline. As we show in the illustrative example below, this term alone usually provides a semiquantitatively acceptable fit of the data. Often, fewer than a dozen terms suffice to recover most of the information contained in the data.
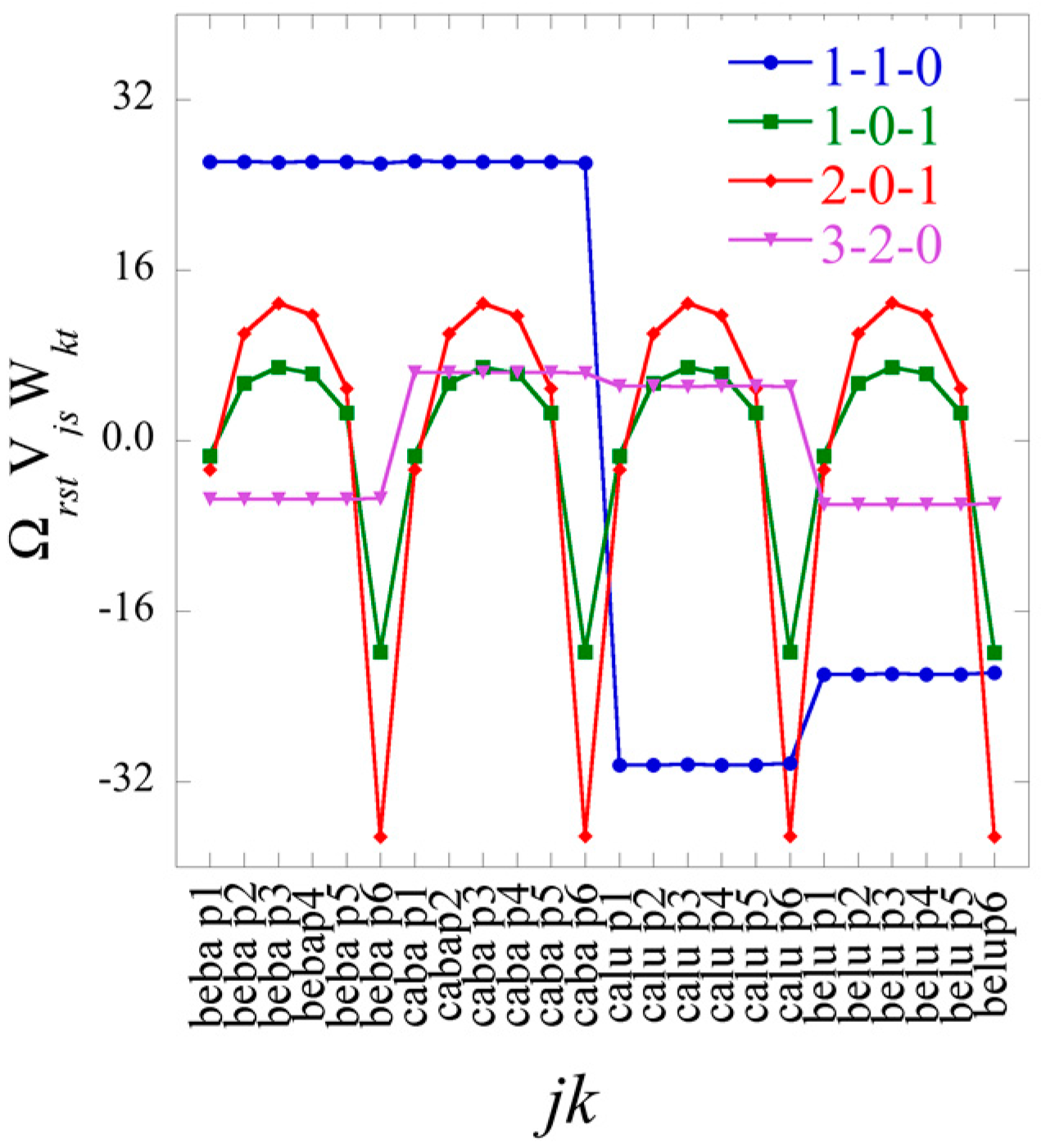
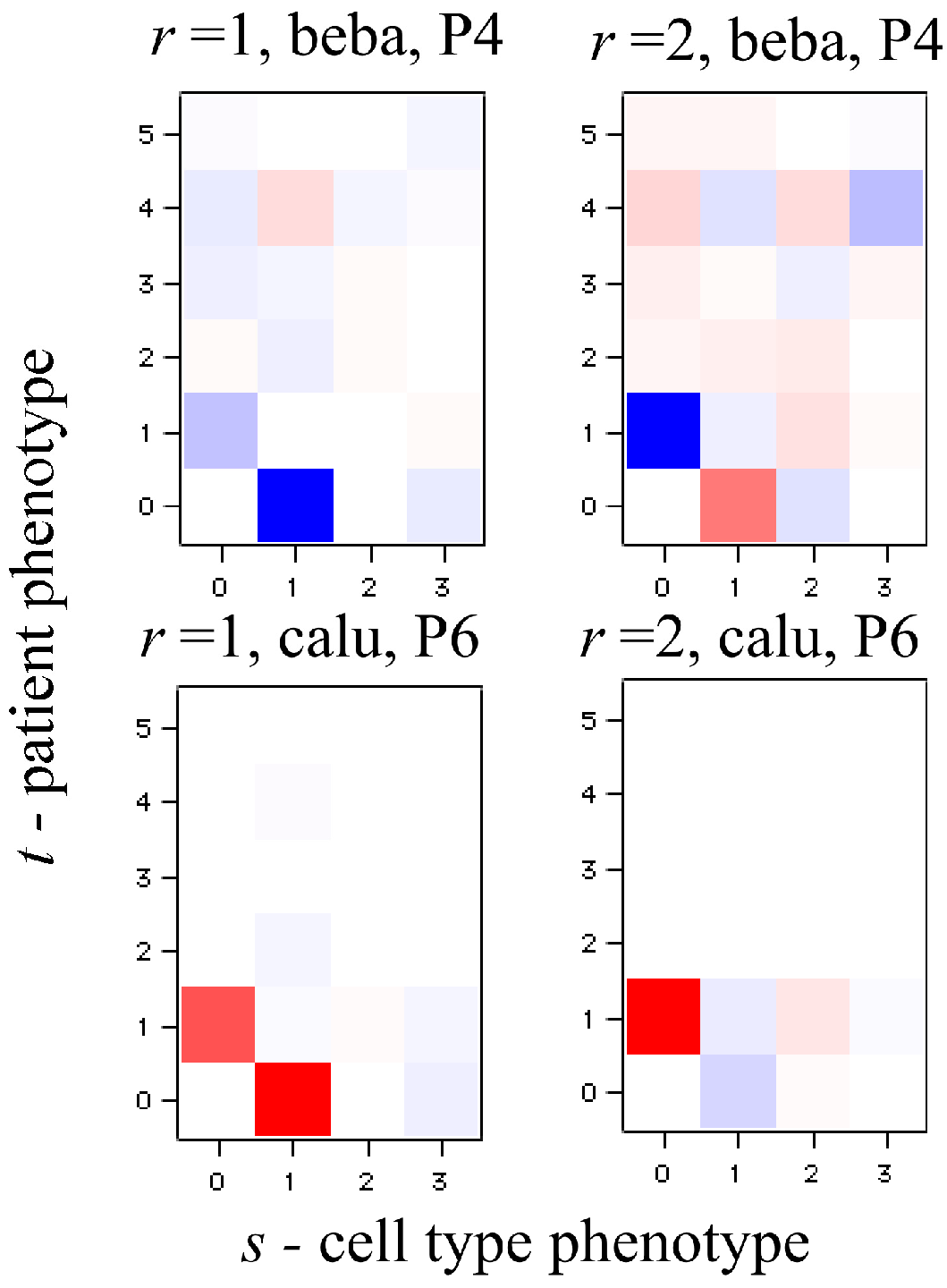
In Equation (21), each element of the tensor of the Lagrange multiplier
can be represented as a
J ×
K heat map. Among the
J ×
K terms in the sum typically very few ones of the highest weight dominate. We show an example of such heat maps of the elements of the tensor of the Lagrange multipliers in the analysis of the numerical example below. Here we draw attention to a 2D view that also leads to this form for the surprisal. In this 2D view we arrange the 3D data as a 2D array by giving each data column a double index
jk. On reflection this is exactly the matrix
T(1) of dimension
I ×
JK as discussed above. This matrix has
JK non-zero eigenvalues. Its SV decomposition is given by Equation (11), where
M is the matrix on the right:
From the surprisal form (21), we have the equality
3.4. 2D Limiting Forms of the Tensor Form of the Surprisal
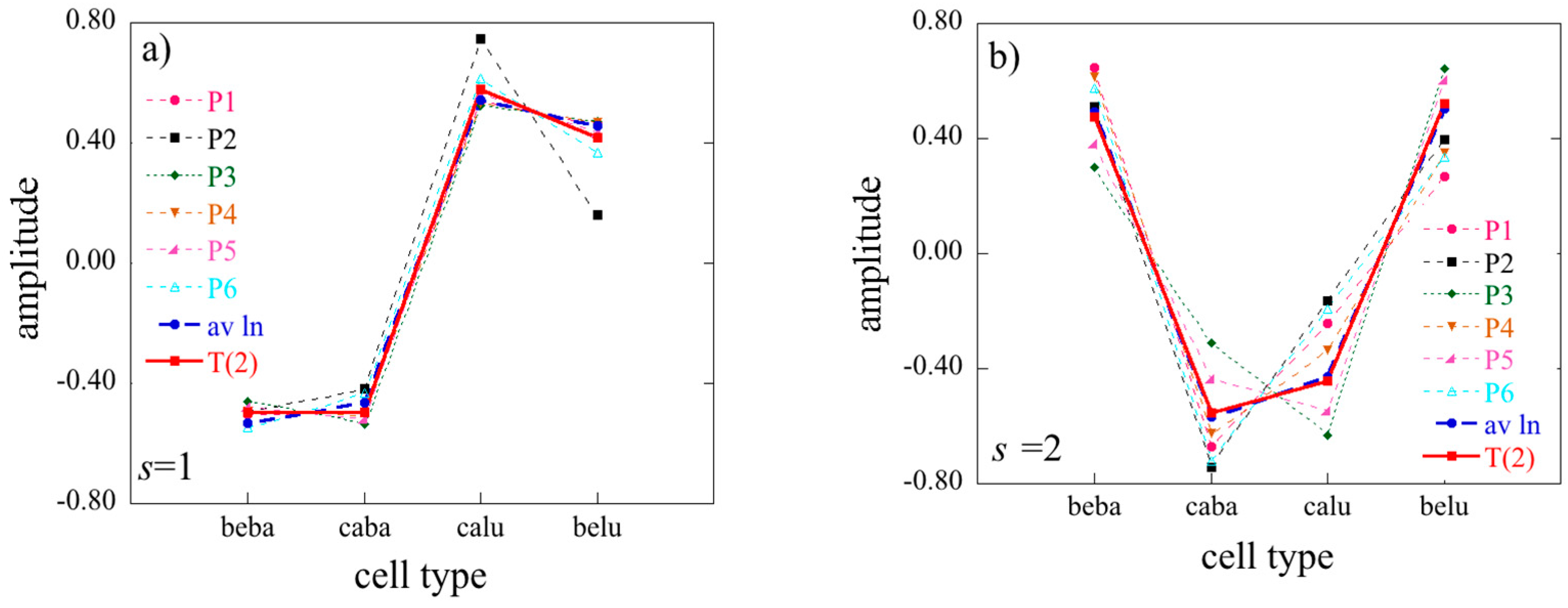
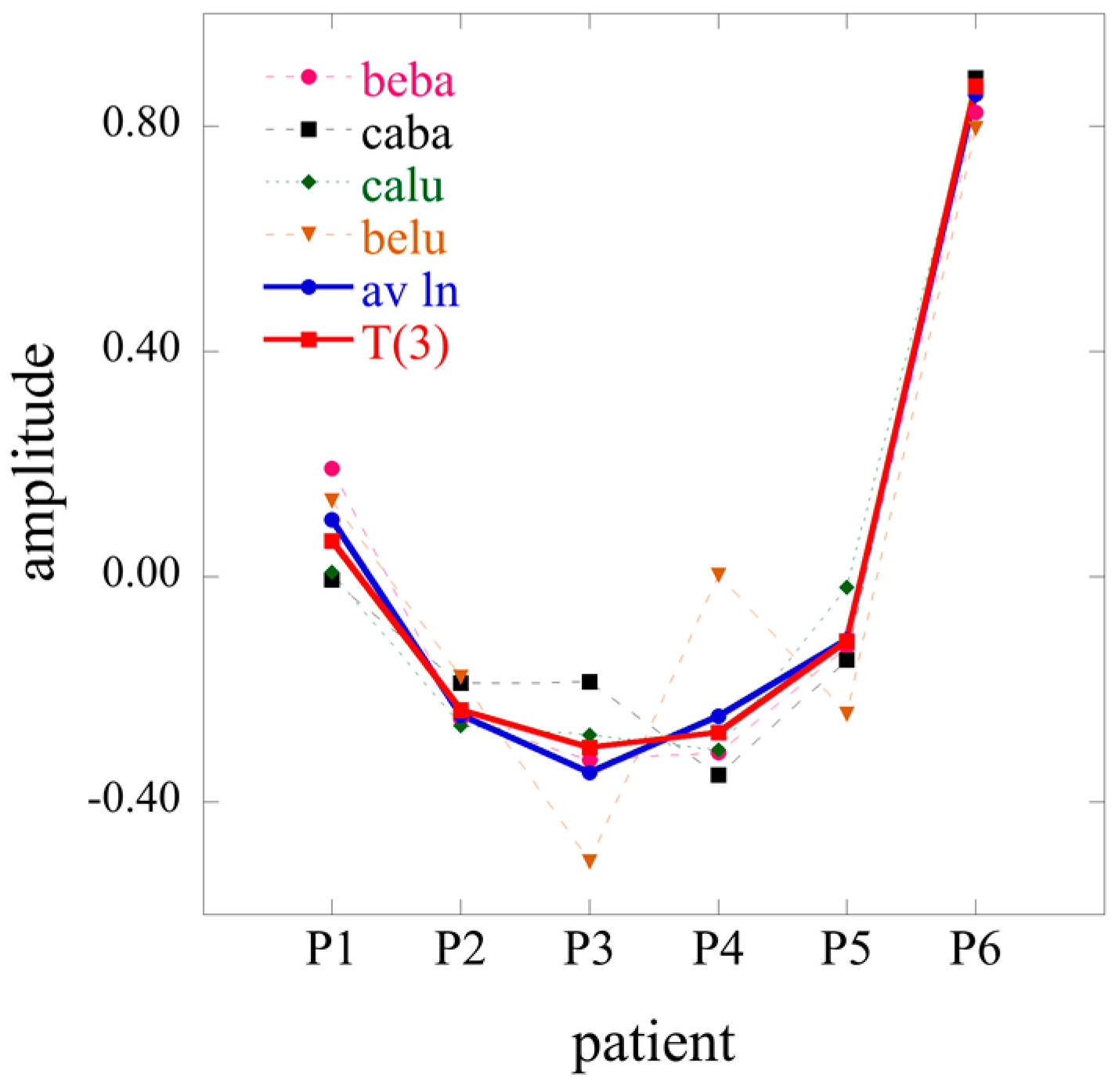
2D limits of the 3D surprisal enable us, for example, to analyze separately the correlations between cell types, irrespective of the patients or the correlations between patients irrespective of cell types. To do so one needs to average the data over patients or over cell type respectively. In the first case, one will get a 2D array of dimension
I ×
J, and in the second one, a 2D array of dimension
I ×
K. Using an overbar to designate an average we write when we average the surprisal
These two 2D matrices can be obtained by starting from the general surprisal form given by Equation (17) and, as we next show, retain only terms
t = 0 (average over patients) or only terms
s = 0 (average over cell type). From averaging over patients in the surprisal form of the tensor, Equation (27), takes the form:
where Equation (22) and the orthogonality between the eigenvectors of
T(3) have been taken into account. Similarly, when averaging over cell types, one obtains
The expressions of Equations (29) and (30) are not fully identical to what one would get by applying 2D SVD directly to averaged
I ×
J and
I ×
K data matrices where the difference is that the logarithm of the average is not the same as the average of the logarithm (see also
Section S1 of the
supplementary materials).
By performing a double average over both patients and cell types, the 1D limit is given by
The 2D and even more so the 1D limit show how information is lost upon averaging. When 3D data is available the Lagrange multiplier for constraint r is given by, cf. Equation (17)
When there is an averaging on either patient or cell type data
while in the 1D case when averaging is over both