Determining the Optimum Inner Diameter of Condenser Tubes Based on Thermodynamic Objective Functions and an Economic Analysis
Abstract
:1. Introduction
2. Description of Condensers under Consideration
3. Mathematical Models for Determining the Optimum Condenser Tube Diameter
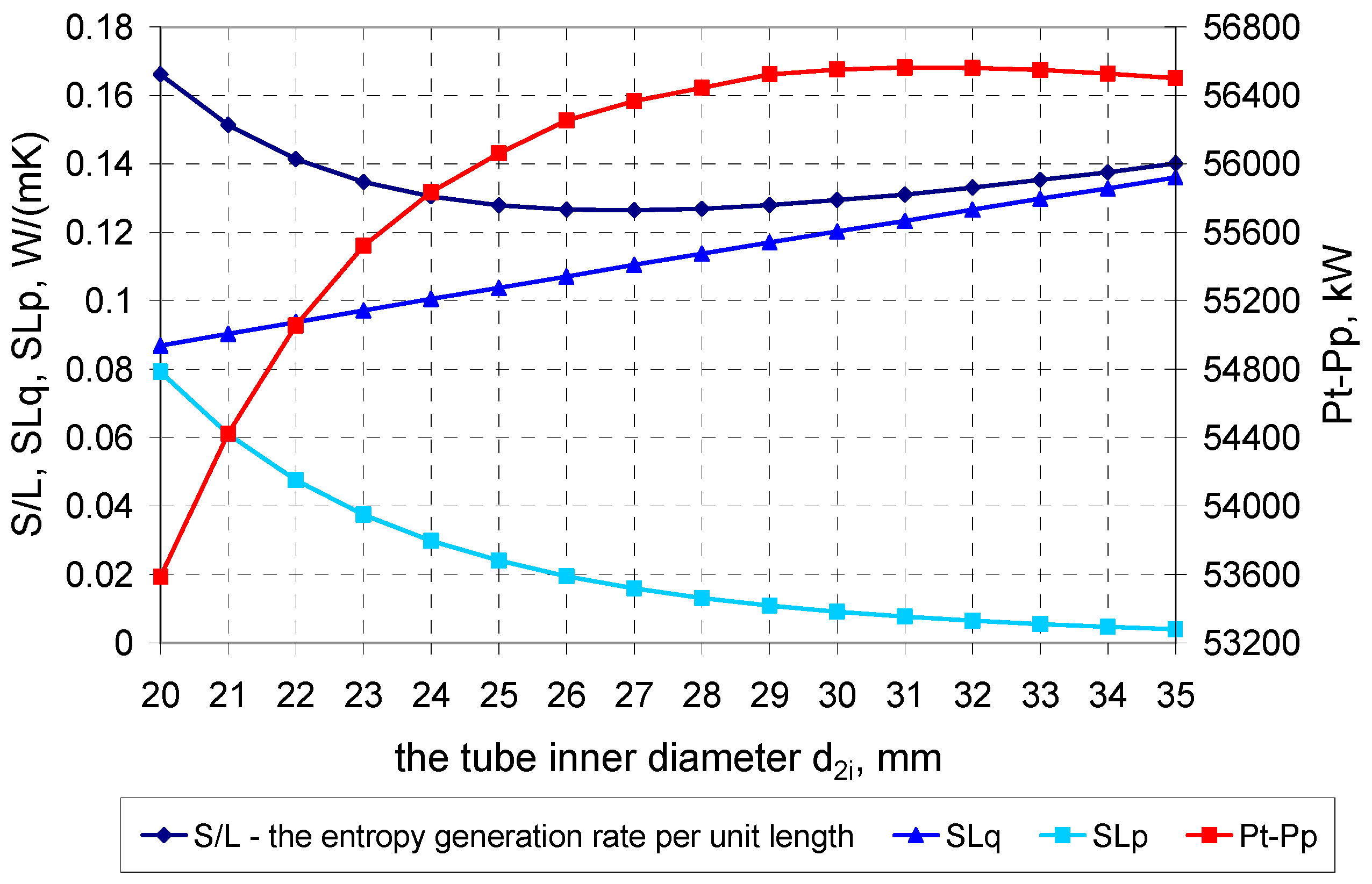
3.1. Minimization of the Entropy Generation Rate per Unit Length of a Condenser Tube: SL = f(d2i) → min
3.2. Minimization of the Total Entropy Generation Rate: = f(d2i) → min
3.3. Maximization of the Power Unit’s Output: P = f(p1(d2i)) → max
3.4. The Economic Method—Profit Maximization: Z = f(d2i) → max
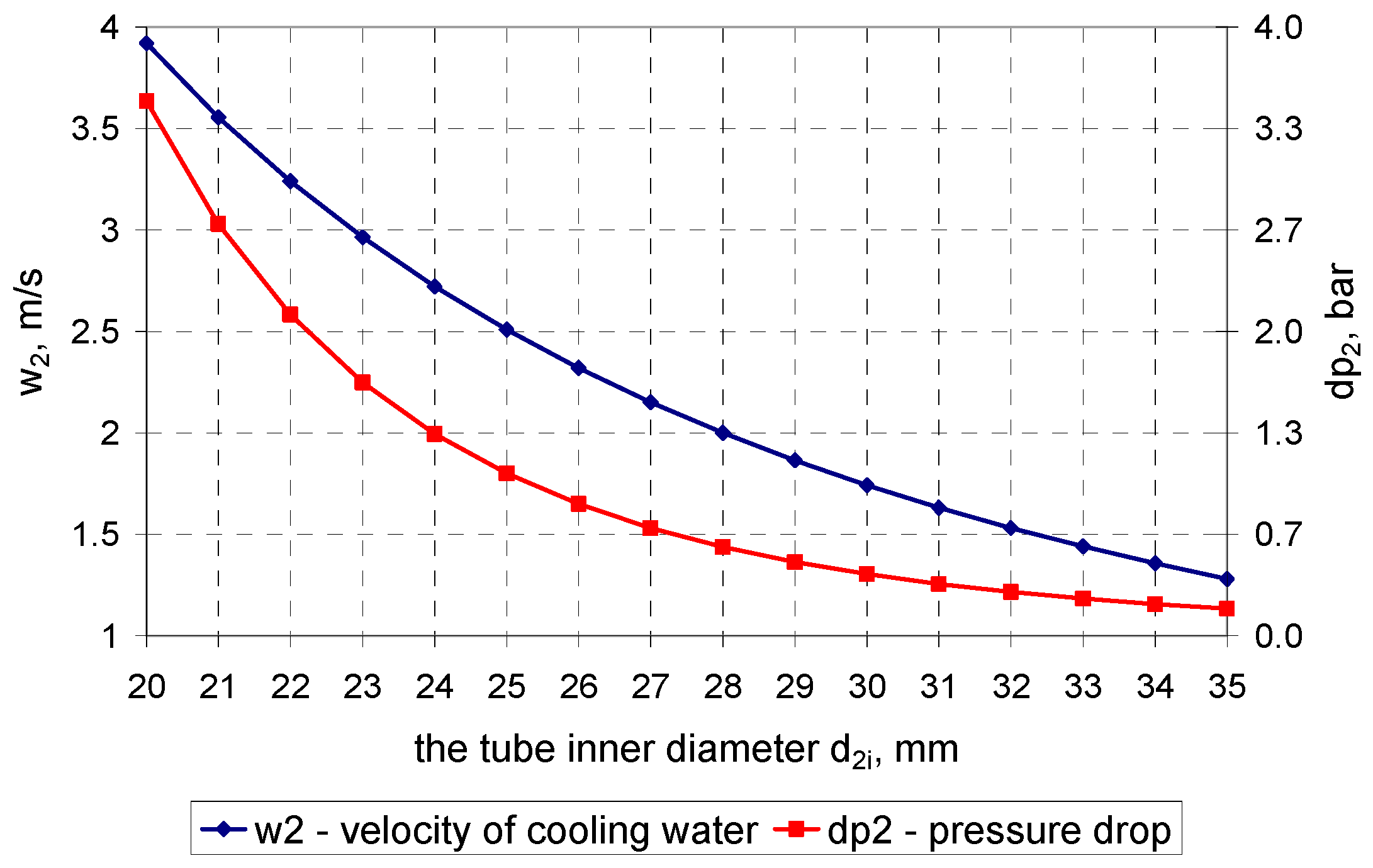
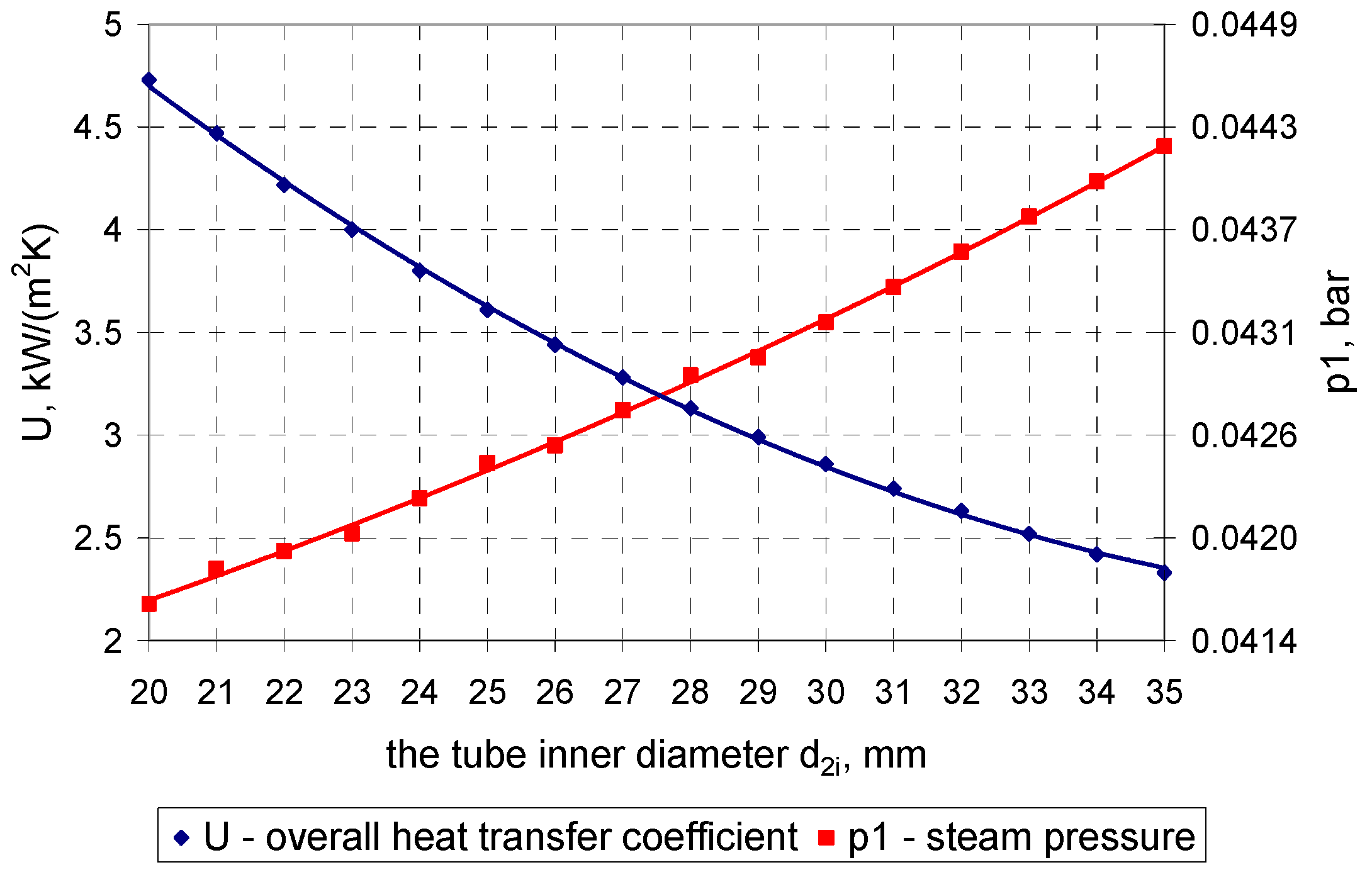
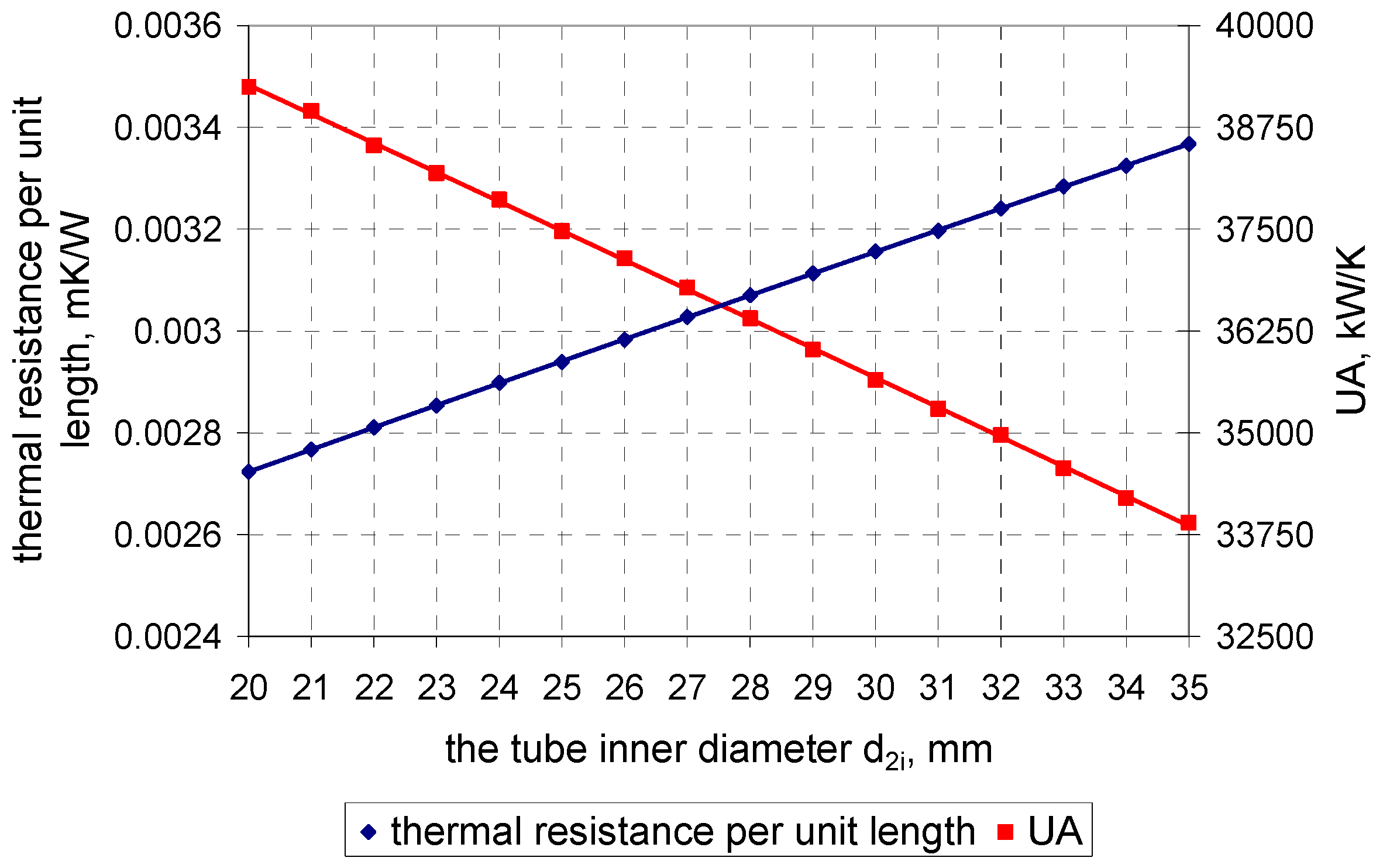
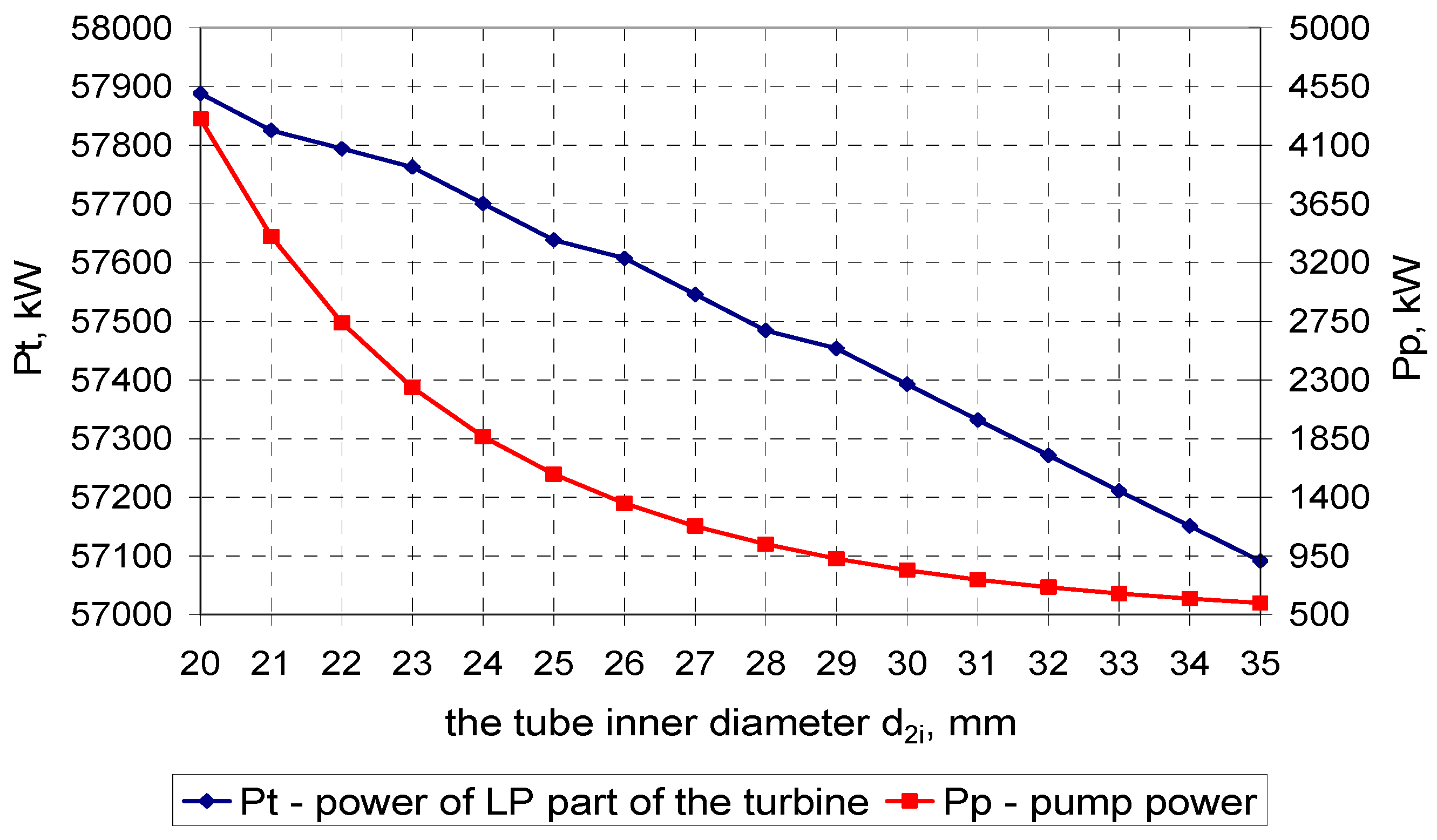
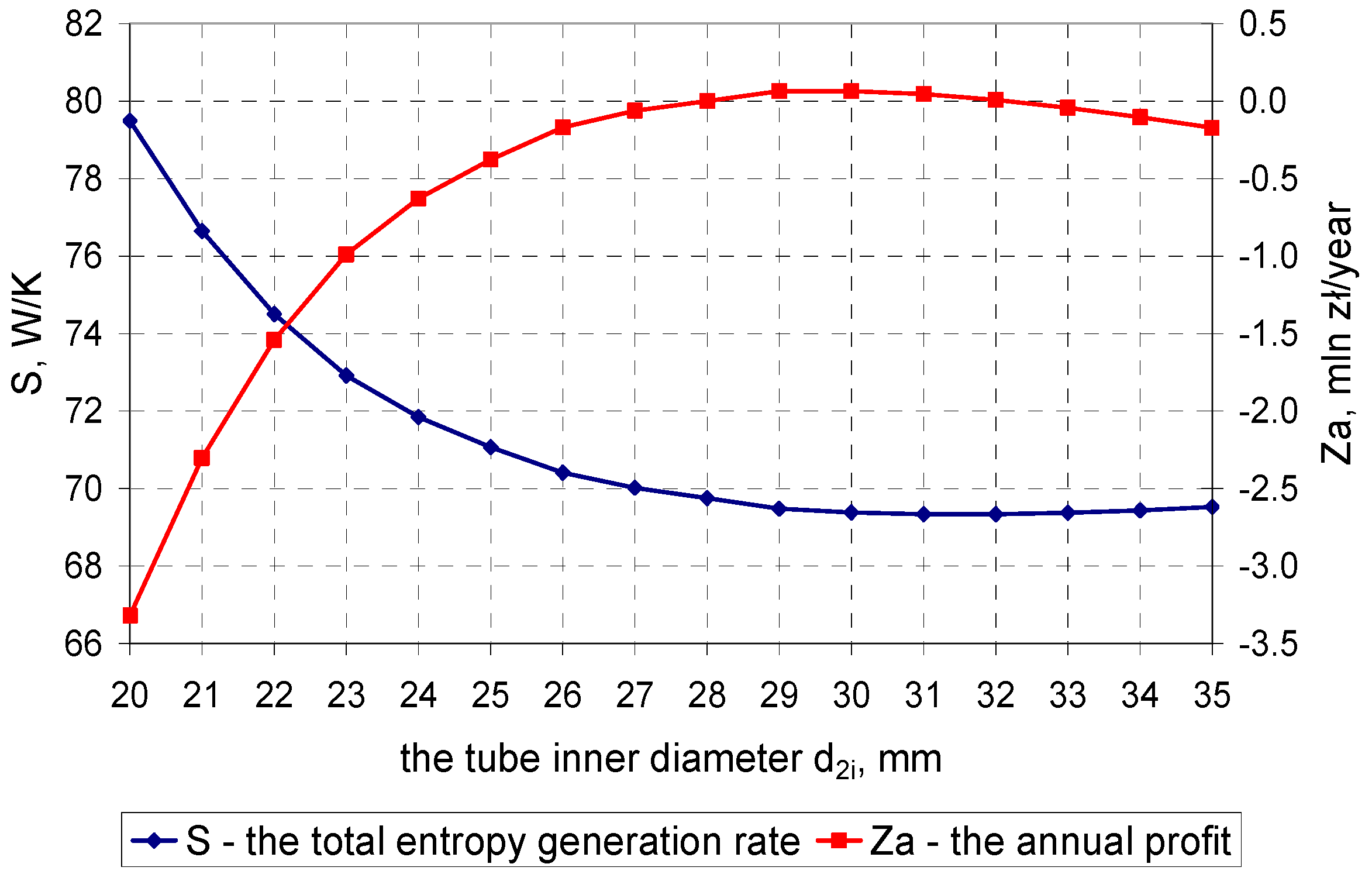
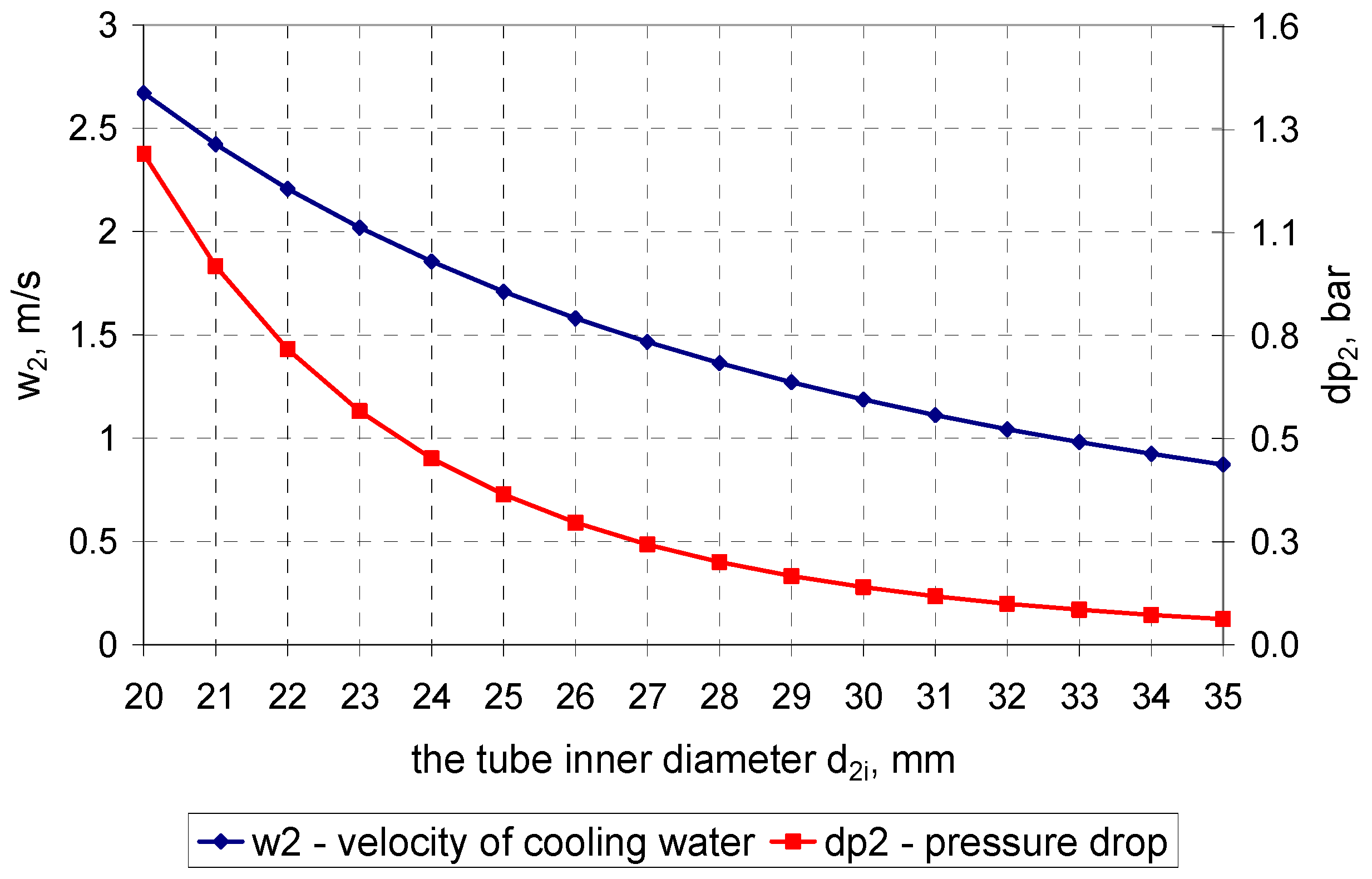
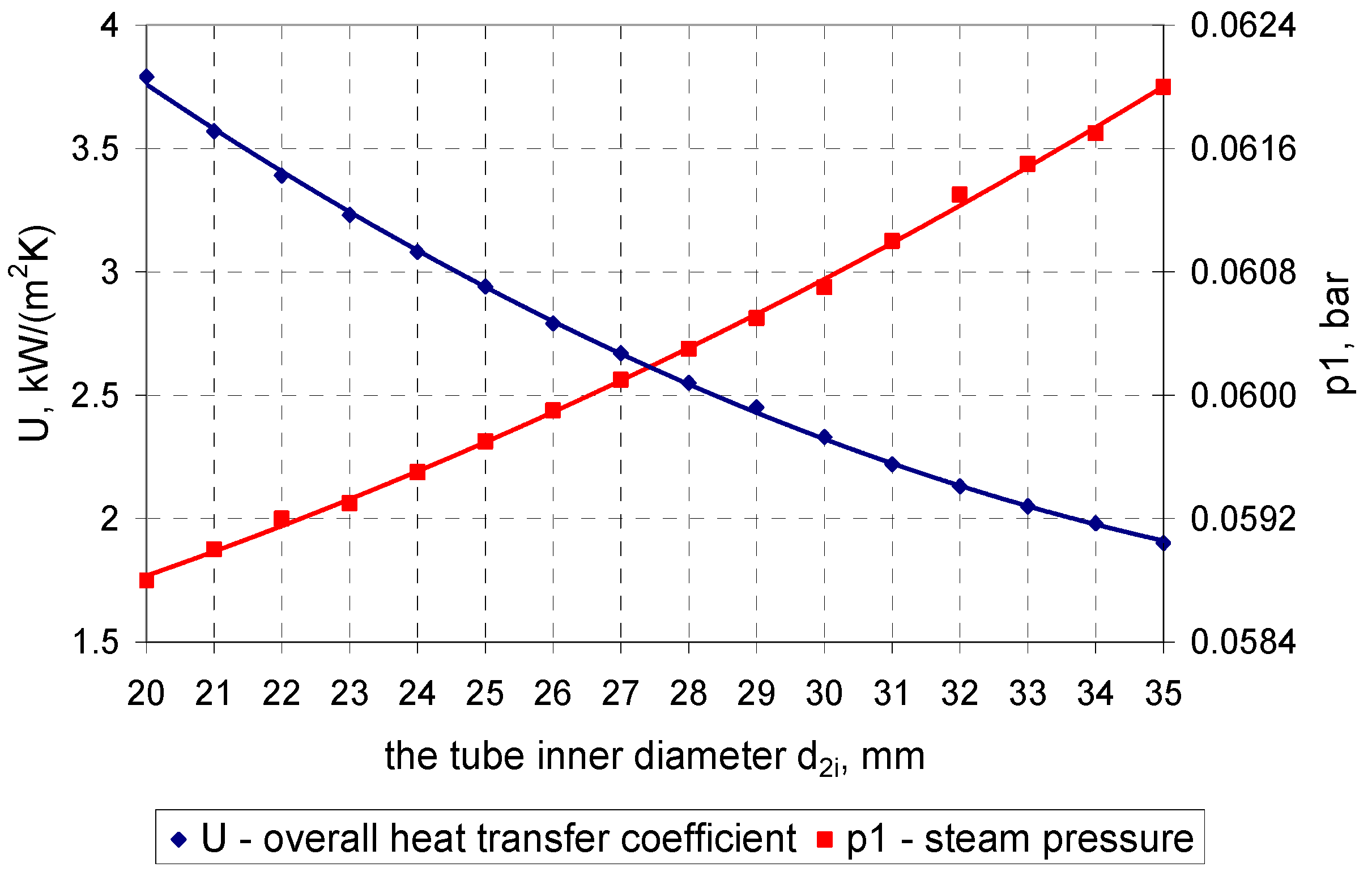
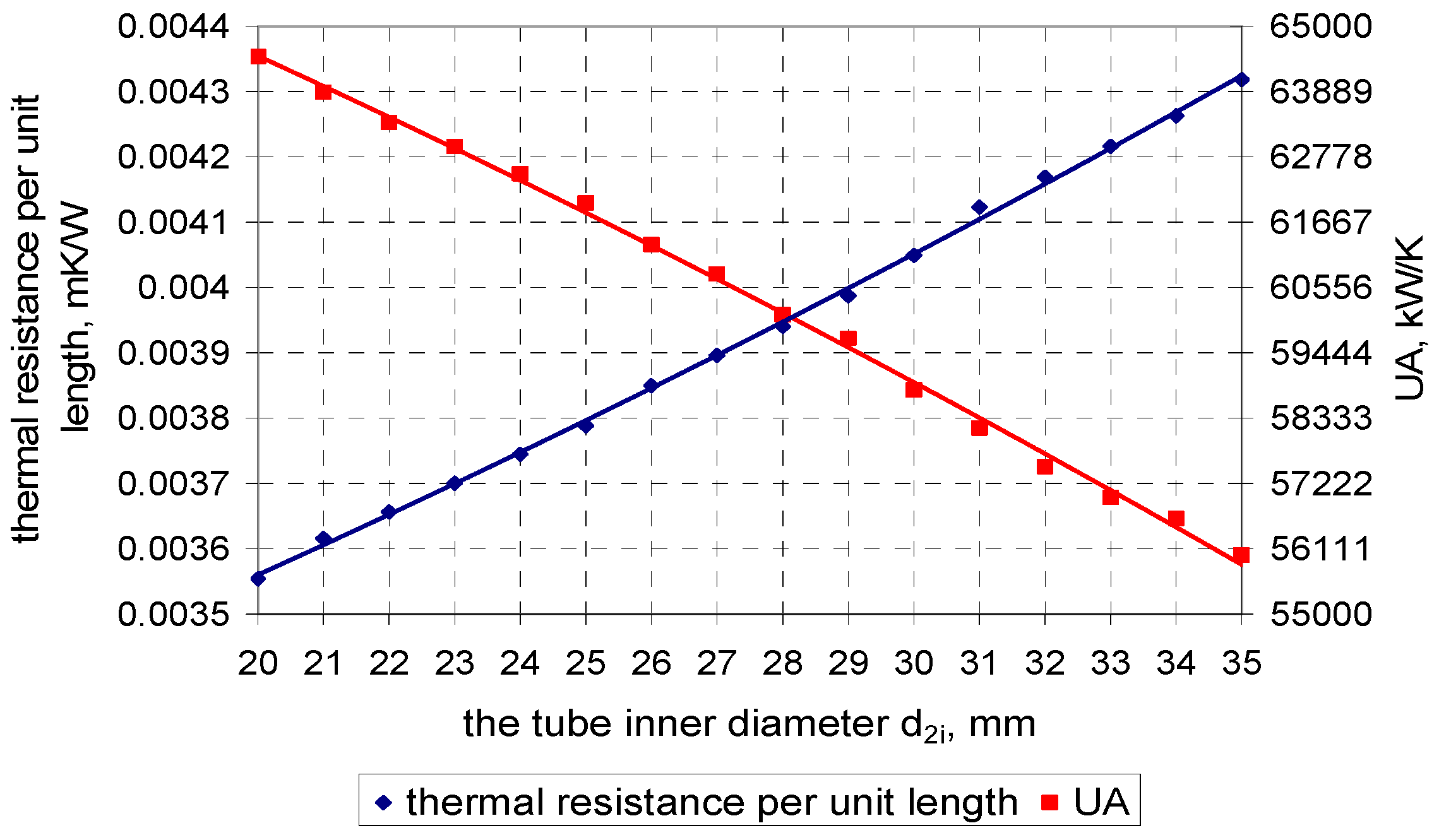
4. Calculation Results
4.1. Calculation Results for the Condenser in the 200-MW Power Unit
4.2. Calculation Results for the Condenser in the 500-MW Power Unit
5. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| A | heat transfer area, m2 |
| discount factor, - | |
| specific heat of water, J/(kg·K) | |
| electricity price, zł/MWh | |
| price of one square meter of the heat transfer area, zł/m2 | |
| coefficient of heat transfer intensity for steam and water mixture in a bank of tubes | |
| d | discount rate, - |
| tube inner diameter, m | |
| tube outer diameter, m | |
| f | surface area of steam flow across the section between tubes of a bank in the condenser within its outer circumference, m2 |
| fixed cost ratio, 1/year | |
| cross-section of the cooling water flow, m2 | |
| g | gravitational acceleration, m/s2 |
| h | specific enthalpy, J/kg |
| k | roughness, mm |
| tube length, m | |
| number of tubes, - | |
| N | years of power plant operation, year |
| Nu | Nusselt number, - |
| Nusselt number for steam condensing on a single tube, - | |
| rate of mass flow through one tube, kg/s | |
| steam mass flow rate to the condenser, kg/s | |
| mass flow rate of cooling water, kg/s | |
| steam mass flow rate at the inlet of the low-pressure part of the turbine, kg/s | |
| pressure, Pa (abs) | |
| pressure rise across the pump, Pa | |
| pump power, W | |
| power generated in the low-pressure part, W | |
| difference in power between the low-pressure part and the pump, W | |
| Pr | Prandtl number, - |
| flow rate of the heat transferred, kW | |
| heat flow rate per unit tube length, W/m | |
| phase transition heat of condensing steam, , kJ/kg | |
| thermal resistance per unit length, mK/W | |
| Re | Reynolds number, - |
| s | specific entropy, J/(kg·K) |
| S | circumference of steam inflow, measured across a section between tubes outside the bank, m |
| sum of entropy rates, W/K | |
| ratio of steam inflow in the area between tubes on the outer circumference of a bank, - | |
| SL | entropy generation rate per unit length of a condenser tube, W/(mK) |
| entropy generation rate due to the resistance of cooling-water flow, W/K | |
| entropy generation rate due to heat transfer to water, W/K | |
| entropy generation rate on the steam side, W/K | |
| entropy generation rate in the low-pressure part, W/K | |
| entropy generation rate in the pump, W/K | |
| entropy generation due to flow resistance of cooling water, W/(mK) | |
| entropy generation due to heat flow, W/(mK) | |
| cooling water temperature at the condenser inlet, K | |
| cooling water temperature at the condenser outlet, K | |
| average cooling water temperature, , K | |
| steam saturation temperature, K | |
| logarithmic temperature difference across the steam condenser, °C | |
| mean temperature difference between steam and the external surface of tubes, °C | |
| overall heat transfer coefficient, kW/(m2·K) | |
| velocity, m/s | |
| z | number of tube runs in a condenser, - |
| annual surplusprofit, zł/year | |
| profit over N years of operation, zł | |
| coefficient of heat transfer, kW/(m2·K) | |
| heat transfer coefficient for steam condensation on a single horizontal tube, kW/(m2·K) | |
| thickness of the fouling layer, m | |
| ratio of air content in the condenser to steam flow, - | |
| pump efficiency, - | |
| thermal conductivity of steam, kW/(mK) | |
| thermal conductivity of cooling water, kW/(mK) | |
| thermal conductivity of the fouling layer, kW/(mK) | |
| flow resistance coefficient, - | |
| thermal conductivity of condensate, kW/(mK) | |
| thermal conductivity of tube material, kW/(mK) | |
| kinematic viscosity of condensate, m2/s | |
| similarity number for a bank of tubes, - | |
| density, kg/m3 | |
| density of condensate, kg/m3 | |
| annual power plant operation time, h |
Subscripts
| 1 | relates to steam |
| 2 | relates to cooling water |
| ext | relates to parameters at the extraction in steam turbine |
| f | fouling |
| m | tube material |
| ti | relates to parameters at the inlet of the low-pressure part |
| to | relates to parameters at the outlet of the low-pressure part |
| pi | relates to parameters upstream the pump |
| po | relates to parameters downstream the pump |
| r | relates to reference (nominal) parameters |
References
- Nag, P.K. Power Plant Engineering; Tata McGraw-Hill Education: New York, NY, USA, 2002. [Google Scholar]
- Haseli, Y.; Dincer, I.; Naterer, G.F. Optimum temperatures in a shell and tube condenser with respect to exergy. Int. J. Heat Mass Transf. 2008, 51, 2462–2470. [Google Scholar] [CrossRef]
- Laskowski, R.; Smyk, A. Analysis of the working conditions of a steam condenser using measurements and an approximation model. Rynek Energii 2014, 1, 110–115. [Google Scholar]
- Laskowski, R.; Smyk, A.; Lewandowski, J.; Rusowicz, A. Cooperation of a Steam Condenser with a Low-pressure Part of a Steam Turbine in Off-Design Conditions. Am. J. Energy Res. 2015, 3, 13–18. [Google Scholar]
- Atria, S.I. The influence of condenser cooling water temperature on the thermal efficiency of a nuclear power plant. Ann. Nucl. Energy 2015, 80, 371–378. [Google Scholar]
- Anozie, A.N.; Odejobi, O.J. The search for optimum condenser cooling water flow rate in a thermal power plant. Appl. Therm. Eng. 2011, 31, 4083–4090. [Google Scholar] [CrossRef]
- Laskowski, R.; Smyk, A.; Lewandowski, J.; Rusowicz, A.; Grzebielec, A. Selecting the cooling water mass flow rate for a power plant under variable load with entropy generation rate minimization. Energy 2016, 107, 725–733. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite size devices and finite time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Laskowski, R.; Rusowicz, A.; Smyk, A. Verification of the condenser tubes diameter based on the minimization of entropy generation. Rynek Energii 2015, 1, 71–75. [Google Scholar]
- Laskowski, R.; Rusowicz, A.; Grzebielec, A. Estimation of a tube diameter in a ‘church window’ condenser based on entropy generation minimization. Arch. Thermodyn. 2015, 36, 49–59. [Google Scholar]
- Erdem, H.H.; Akkaya, A.V.; Cetin, B.; Dagdas, A.; Sevilgen, S.H.; Sahin, B.; Teke, I.; Gungor, C.; Atas, S. Comparative energetic and exergetic performance analyses for coal-fired thermal power plants in Turkey. Int. J. Therm. Sci. 2009, 48, 2179–2186. [Google Scholar] [CrossRef]
- Aljundi, I.H. Energy and exergy analysis of a steam power plant in Jordan. Appl. Therm. Eng. 2009, 29, 324–328. [Google Scholar] [CrossRef]
- Datta, A.; Sengupta, S.; Duttagupta, S. Exergy analysis of a coal-based 210 MW thermal power plant. Int. J. Energy Res. 2007, 31, 14–28. [Google Scholar]
- Wołowicz, M.; Milewski, J.; Badyda, K. Feedwater repowering of 800 MW supercritical steam power plant. J. Power Technol. 2012, 92, 127–134. [Google Scholar]
- Milewski, J.; Bujalski, W.; Wołowicz, M.; Futyma, K.; Kucowski, J. Off-design operation of an 900 MW-class power plant with utilization of low temperature heat of flue gases. J. Power Technol. 2015, 95, 221–227. [Google Scholar]
- Soltan, B.K.; Saffar-Avval, M.; Damangir, E. Minimizing capital and operating costs of shell and tube condensers using optimum baffle spacing. Appl. Therm. Eng. 2004, 24, 2801–2810. [Google Scholar] [CrossRef]
- Fertaka, S.; Thibault, J.; Gupta, Y. Design of shell-and-tube heat exchangers using multiobjective optimization. Int. J. Heat Mass Transf. 2013, 60, 343–354. [Google Scholar] [CrossRef]
- Allen, B.; Gosselin, L. Optimal geometry and flow arrangement for minimizing the cost of shell-and-tube condensers. Int. J. Energy Res. 2008, 32, 958–969. [Google Scholar] [CrossRef]
- Wildi-Tremblay, P.; Gosselin, L. Minimizing shell-and-tube heat exchanger cost with genetic algorithms and considering maintenance. Int. J. Energy Res. 2007, 31, 867–885. [Google Scholar] [CrossRef]
- Caputo, A.C.; Pelagagge, P.M.; Salini, P. Heat exchanger design based on economic optimization. Appl. Therm. Eng. 2008, 28, 1151–1159. [Google Scholar] [CrossRef]
- Azad, A.V.; Amidpour, M. Economic optimization of shell and tube heat exchanger based on constructal theory. Energy 2011, 36, 1087–1096. [Google Scholar] [CrossRef]
- Hajabdollahi, H.; Ahmadi, P.; Dincer, I. Thermoeconomic optimization of a shell and tube condenser using both genetic algorithm and particle swarm. Int. J. Refrig. 2011, 34, 1066–1076. [Google Scholar] [CrossRef]
- Sadeghzadeh, H.; Ehyaei, M.A.; Rosen, M.A. Techno-economic optimization of a shell and tube heat exchanger by genetic and particle swarm algorithms. Energy Convers. Manag. 2015, 93, 84–91. [Google Scholar] [CrossRef]
- Selbas, R.; Kızılkan, O.; Reppich, M. A new design approach for shell-and-tube heat exchangers using genetic algorithms from economic point of view. Chem. Eng. Process. 2006, 45, 268–275. [Google Scholar] [CrossRef]
- Patel, V.K.; Rao, R.V. Design optimization of shell-and-tube heat exchanger using particle swarm optimization technique. Appl. Therm. Eng. 2010, 30, 1417–1425. [Google Scholar] [CrossRef]
- Sahin, A.S.; Kilic, B.; Kilic, U. Design and economic optimization of shell and tube heat exchangers using Artificial Bee Colony (ABC) algorithm. Energy Convers. Manag. 2011, 52, 3356–3362. [Google Scholar] [CrossRef]
- Hadidi, A.; Hadidi, M.; Nazari, A. A new design approach for shell-and-tube heat exchangers using imperialist competitive algorithm (ICA) from economic point of view. Energy Convers. Manag. 2013, 67, 66–74. [Google Scholar] [CrossRef]
- Hadidi, A.; Nazari, A. Design and economic optimization of shell-and-tube heat exchangers using biogeography-based (BBO) algorithm. Appl. Therm. Eng. 2013, 51, 1263–1272. [Google Scholar] [CrossRef]
- Mohanty, D.K. Gravitational search algorithm for economic optimization design of a shell and tube heat exchanger. Appl. Therm. Eng. 2016, 107, 184–193. [Google Scholar] [CrossRef]
- Abed, A.M.; Abed, I.A.; Majdi, H.S.; Al-Shamani, A.N.; Sopian, K. A new optimization approach for shell and tube heat exchangers by using electromagnetism-like algorithm (EM). Heat Mass Transf. 2016, 52, 2621–2634. [Google Scholar] [CrossRef]
- Ozcelik, Y. Exergetic optimization of shell and tube heat exchangers using agenetic based algorithm. Appl. Therm. Eng. 2007, 27, 1849–1856. [Google Scholar] [CrossRef]
- Eryener, D. Thermoeconomic optimization of baffle spacing for shell and tube heat exchangers. Energy Convers. Manag. 2006, 47, 1478–1489. [Google Scholar] [CrossRef]
- Can, A.; Buyruk, E.; Eryener, D. Exergoeconomic analysis of condenser type heat exchangers. Exergy Int. J. 2002, 2, 113–118. [Google Scholar] [CrossRef]
- Sanaye, S.; Hajabdollahi, H. Multi-objective optimization of shell and tube heat exchangers. Appl. Therm. Eng. 2010, 30, 1937–1945. [Google Scholar] [CrossRef]
- Ponce-Ortega, J.M.; Serna-González, M.; Jiménez-Gutiérrez, A. Use of genetic algorithms for the optimal design of shell-and-tube heat exchangers. Appl. Therm. Eng. 2009, 29, 203–209. [Google Scholar] [CrossRef]
- Ayala, H.V.H.; Keller, P.; Morais, M.F.; Mariani, V.C.; Coelho, L.S.; Rao, R.V. Design of heat exchangers using a novel multiobjective free search differential evolution paradigm. Appl. Therm. Eng. 2016, 94, 170–177. [Google Scholar] [CrossRef]
- Muralikrishna, K.; Shenoy, U.V. Heat exchanger design targets for minimum area and cost. Chem. Eng. Res. Des. 2000, 78, 161–167. [Google Scholar] [CrossRef]
- Tol, H.I.; Svendsen, S. Improving the dimensioning of piping networks and network layouts in low-energy district heating systems connected to low energy buildings: A case study in Roskilde, Denmark. Energy 2012, 38, 276–290. [Google Scholar] [CrossRef]
- Nussbaumer, T.; Thalmann, S. Influence of system design on heat distribution costs in district heating. Energy 2016, 101, 496–505. [Google Scholar] [CrossRef]
- Smyk, A.; Pietrzyk, Z. Dobór średnicy rurociągów w sieci ciepłowniczej z uwzględnieniem optymalnych prędkości wody sieciowej. Rynek Energii 2011, 6, 98–105. (In Polish) [Google Scholar]
- Murat, J.; Smyk, A. Dobór średnicy rurociągów w układzie rozgałęźno-pierścieniowym dla przykładowych struktur sieci ciepłowniczej. Rynek Energii 2015, 9, 13–19. (In Polish) [Google Scholar]
- Salij, A.; Stępień, J.C. Performance of Turbine Condensers in Power Units of Thermal Systems; Kaprint: Warsaw, Poland, 2013. (In Polish) [Google Scholar]
- Rusowicz, A. Issues Concerning Mathematical Modelling of Power Condensers; Warsaw University of Technology: Warsaw, Poland, 2013. (In Polish) [Google Scholar]
- Cengel, Y.A. Heat Transfer; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Holman, J.P. Heat Transfer; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Grzebielec, A.; Rusowicz, A. Thermal Resistance of Steam Condensation in Horizontal Tube Bundles. J. Power Technol. 2011, 91, 41–48. [Google Scholar]
- Szkłowier, G.G.; Milman, O.O. Issledowanije I Rasczot Kondensacionnych Ustrojstw Parowych Turbin; Energoatomizdat: Moskwa, Russia, 1985. (In Russian) [Google Scholar]
- Smyk, A. The Influence of Thermodynamic Parameters of a Heat Cogeneration System of the Nuclear Heat Power Plant on Fuel Saving in Energy System. Ph.D. Thesis, Warsaw University of Technology, Warsaw, Poland, 1999. [Google Scholar]
- Chmielniak, T.; Trela, M. Diagnostics of New-Generation Thermal Power Plants; Wydawnictwo IMP PAN: Gdańsk, Poland, 2008. [Google Scholar]
- Saari, J.; Kaikko, J.; Vakkilainen, E.; Savolainen, S. Comparison of power plant steam condenser heat transfer models for on-line condition monitoring. Appl. Therm. Eng. 2014, 62, 37–47. [Google Scholar] [CrossRef]
- Brodowicz, K.; Czaplicki, A. Condensing Vapour Flow Resistance Throught Tubes Bundle in the Presence of Condensate on Tubes. In Proceedings of the 8th International Heat Transfer Conference, San Francisco, CA, USA, 17–22 August 1986; Volume 4, pp. 1689–1694.
- Carlucci, L. Computations of flow and heat transfer in power plant condenser. In Proceedings of the 8th International Heat Transfer Conference, San Francisco, CA, USA, 17–22 August 1986; Volume 5, pp. 2541–2546.
- Fujii, T.; Honda, H.; Oda, K. Condensation of Steam on Horizontal Tube—the Influence of Oncoming Velocity and Thermal Conduction at the Tube Wall. In Proceedings of the 18th National Heat Transfer Conference, San Diego, CA, USA, 6–8 August 1979; pp. 35–43.
- Fujii, T.; Uehara, H.; Hirata, K.; Oda, K. Heat transfer and flow resistance in condensation of low pressure steam flowing through tube banks. Int. J. Heat Mass Transf. 1972, 15, 247–259. [Google Scholar] [CrossRef]
- Malin, M.R. Modelling flow in an experimental marine condenser. Int. Commun. Heat Transf. 1997, 24, 597–608. [Google Scholar] [CrossRef]
- Roy, R.P.; Ratisher, M.; Gokhale, V.K. A Computational Model of a Power Plant Steam Condenser. J. Energy Resour. Technol. 2001, 123, 81–91. [Google Scholar] [CrossRef]
- Zeng, H.; Meng, J.; Li, Z. Numerical study of a power plant condenser tube arrangement. Appl. Therm. Eng. 2012, 40, 294–303. [Google Scholar] [CrossRef]
- Zhang, C. Numerical Modeling Using a Quasi-Three-Dimensional Procedure for Large Power Plant Condenser. J. Heat Transf. 1994, 116, 180–188. [Google Scholar] [CrossRef]
- Zhang, C.; Bokil, A. A quasi-three-dimensional approach to simulate the two-phase fluid flow and heat transfer in condensers. Int. J. Heat Mass Transf. 1997, 40, 3537–3546. [Google Scholar] [CrossRef]
- Zhang, C.; Sousa, A.C.M.; Venart, J.E.S. Numerical Simulation of Different Types of Steam Surface Condensers, Journal of Energy Resources Technology. Trans. ASME 1991, 113, 63–70. [Google Scholar]
- Zhou, L.X.; Li, F.Y.; Li, W.H. Quasi-three-dimensional numerical study of shell side of condenser. Proc. CSEE 2008, 28, 25–30. [Google Scholar]
- Nedelkovski, I.; Vilos, I.; Geramitoioski, T. Finite element solution of Navier-Stokes equations for steam flow and heat transfer. Trans. Eng. Comput. Technol. 2005, 5, 171–175. [Google Scholar]
- Prieto, M.M.; Suarez, I.M.; Montanes, E. Analisys of the thermal performance of a church window steam condenser for different operational conditions using three models. Appl. Therm. Eng. 2003, 23, 163–178. [Google Scholar] [CrossRef]
- Bekdemir, S.; Ozturk, R.; Yumurtac, Z. Condenser Optimization in Steam Power Plant. J. Therm. Sci. 2003, 12, 176–179. [Google Scholar] [CrossRef]
- Ozdamar, G.; Ozturk, R. Optimization of a condenser in a thermal power plant. In Proceedings of the 9th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Valletta, Malta, 16–18 July 2012.
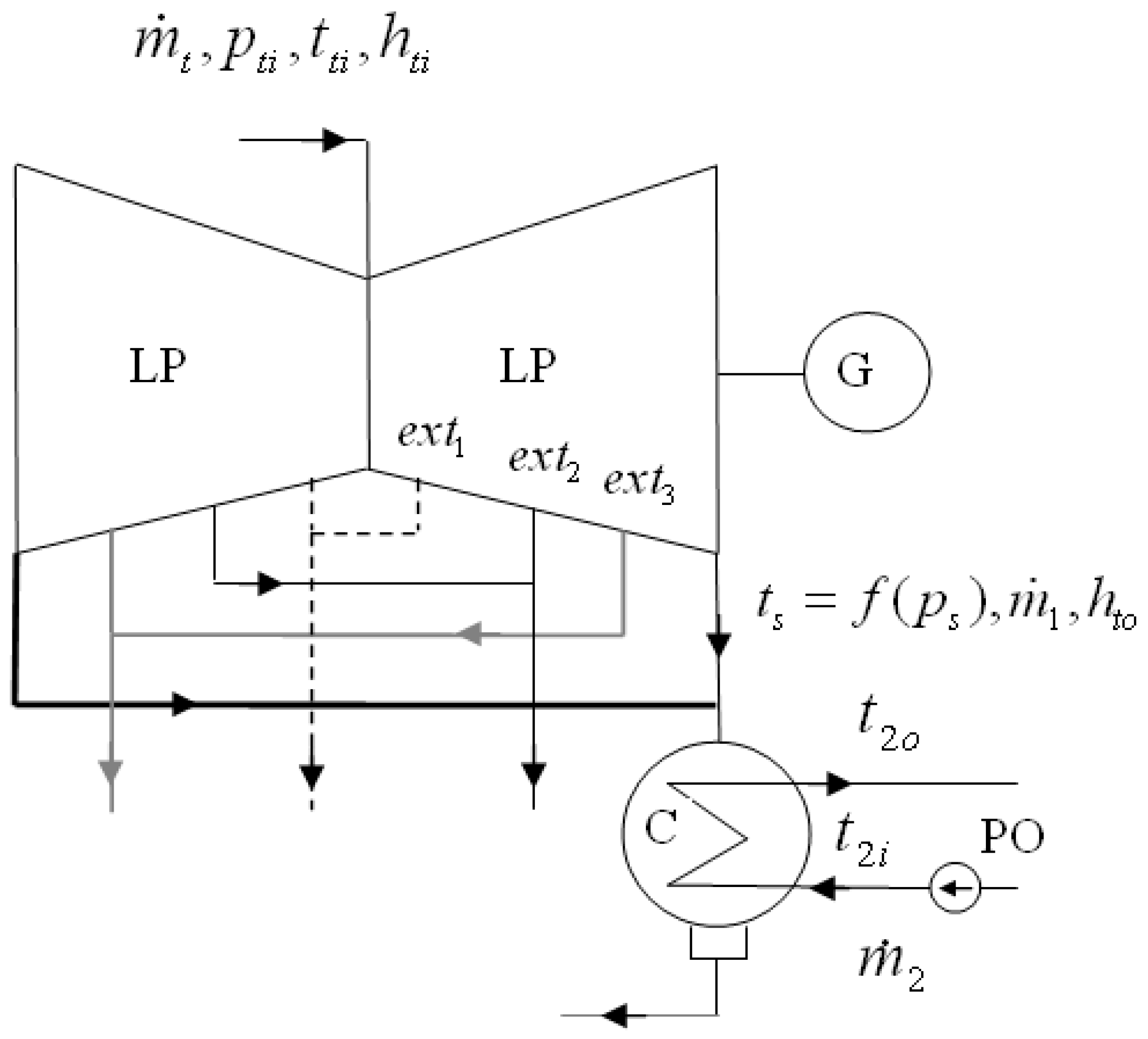
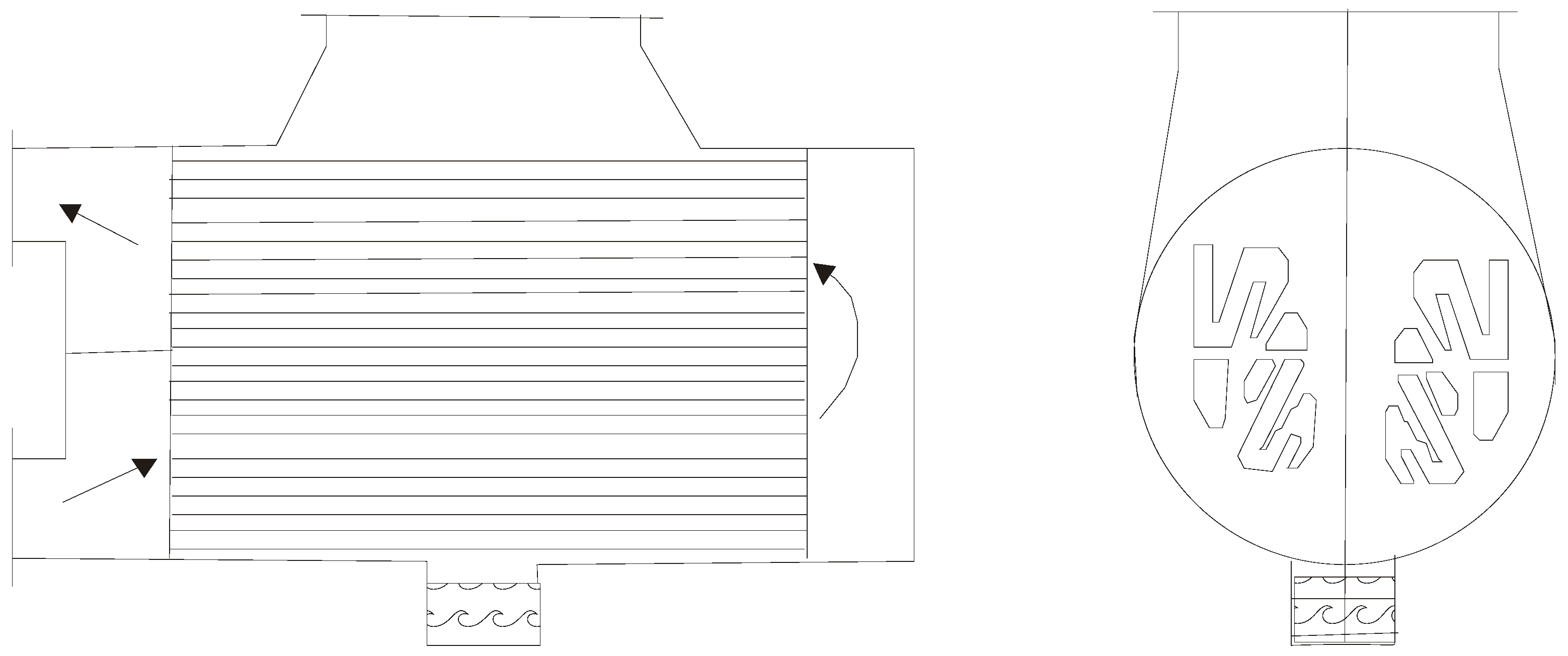
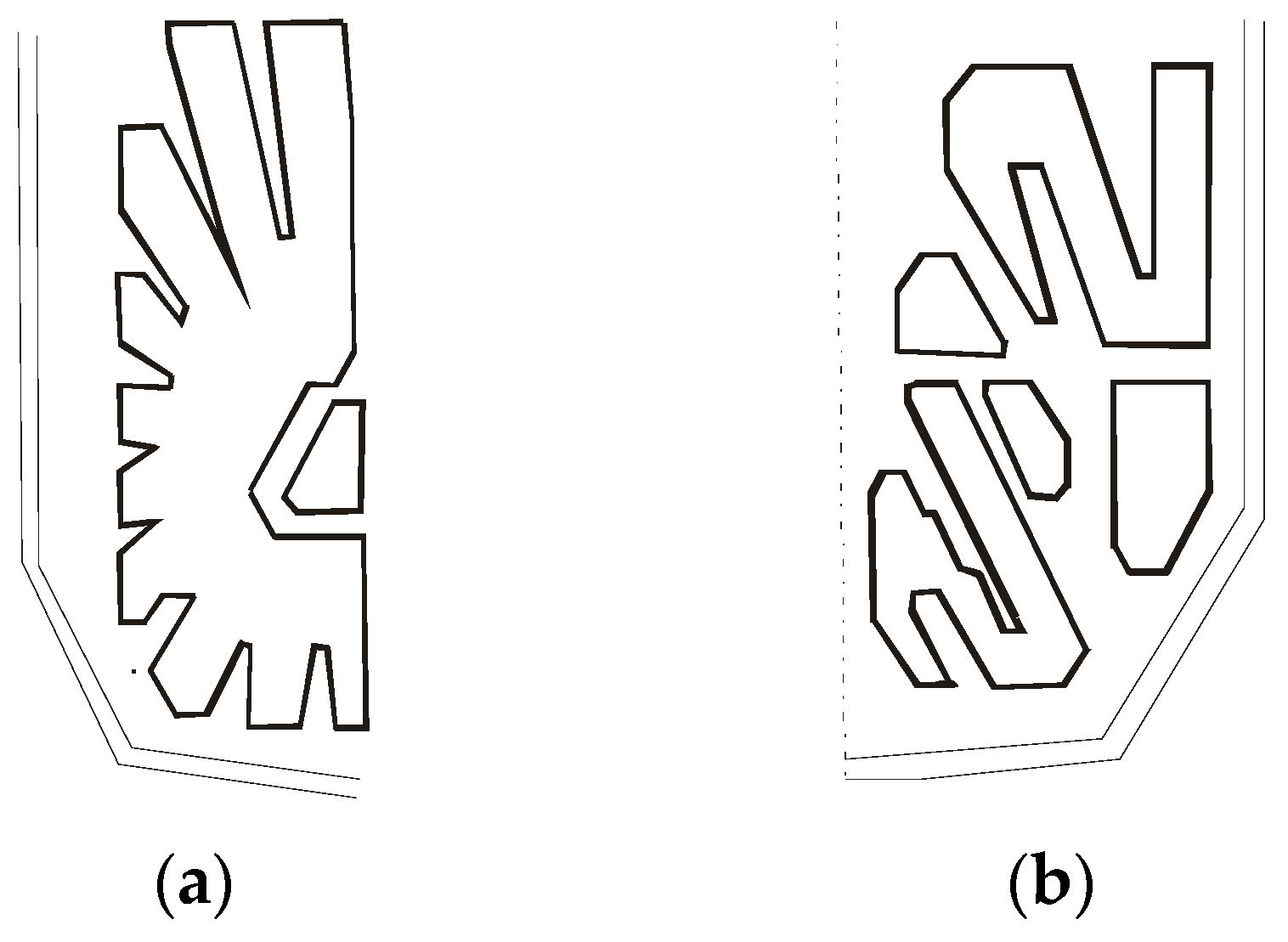
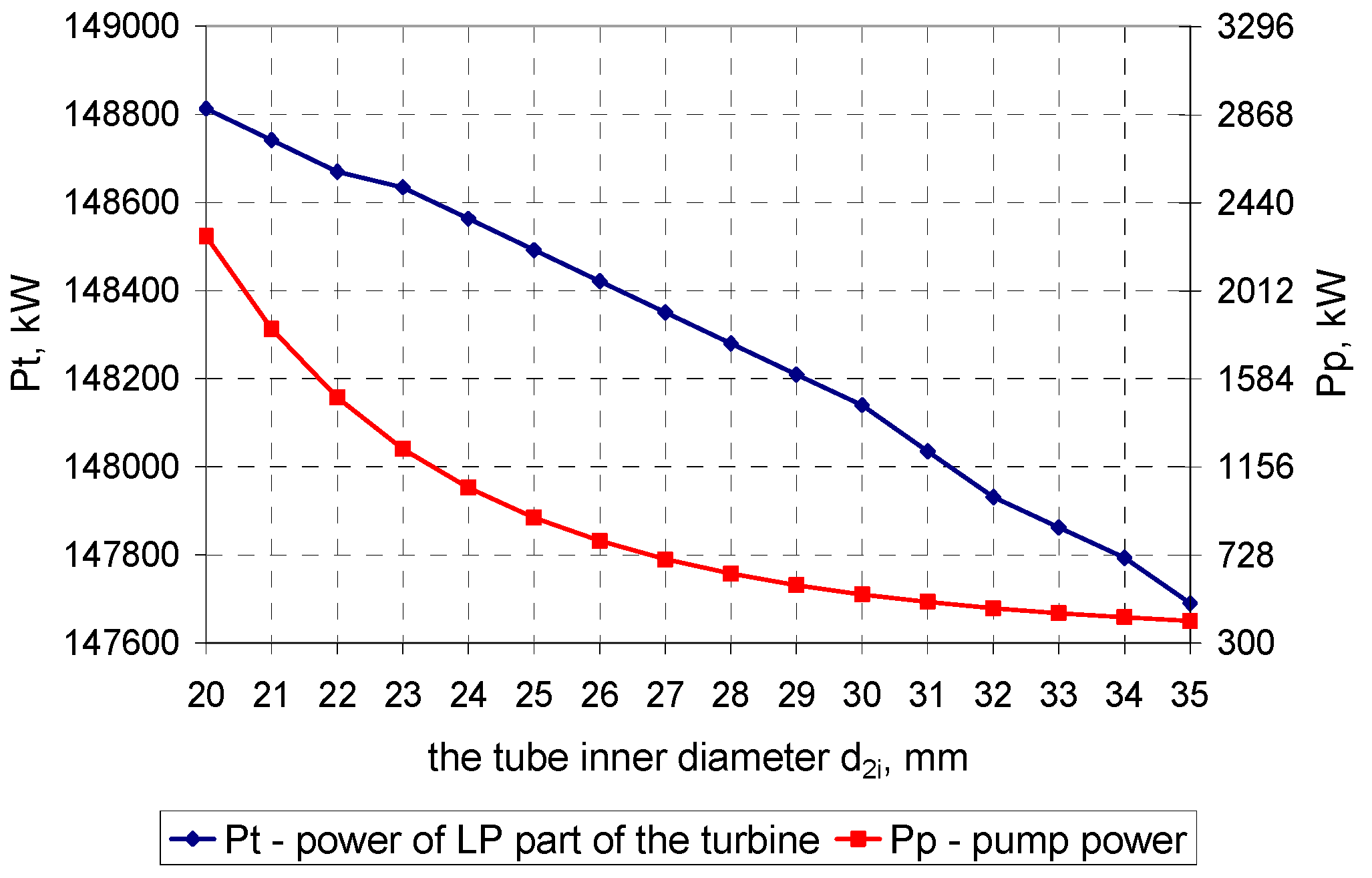
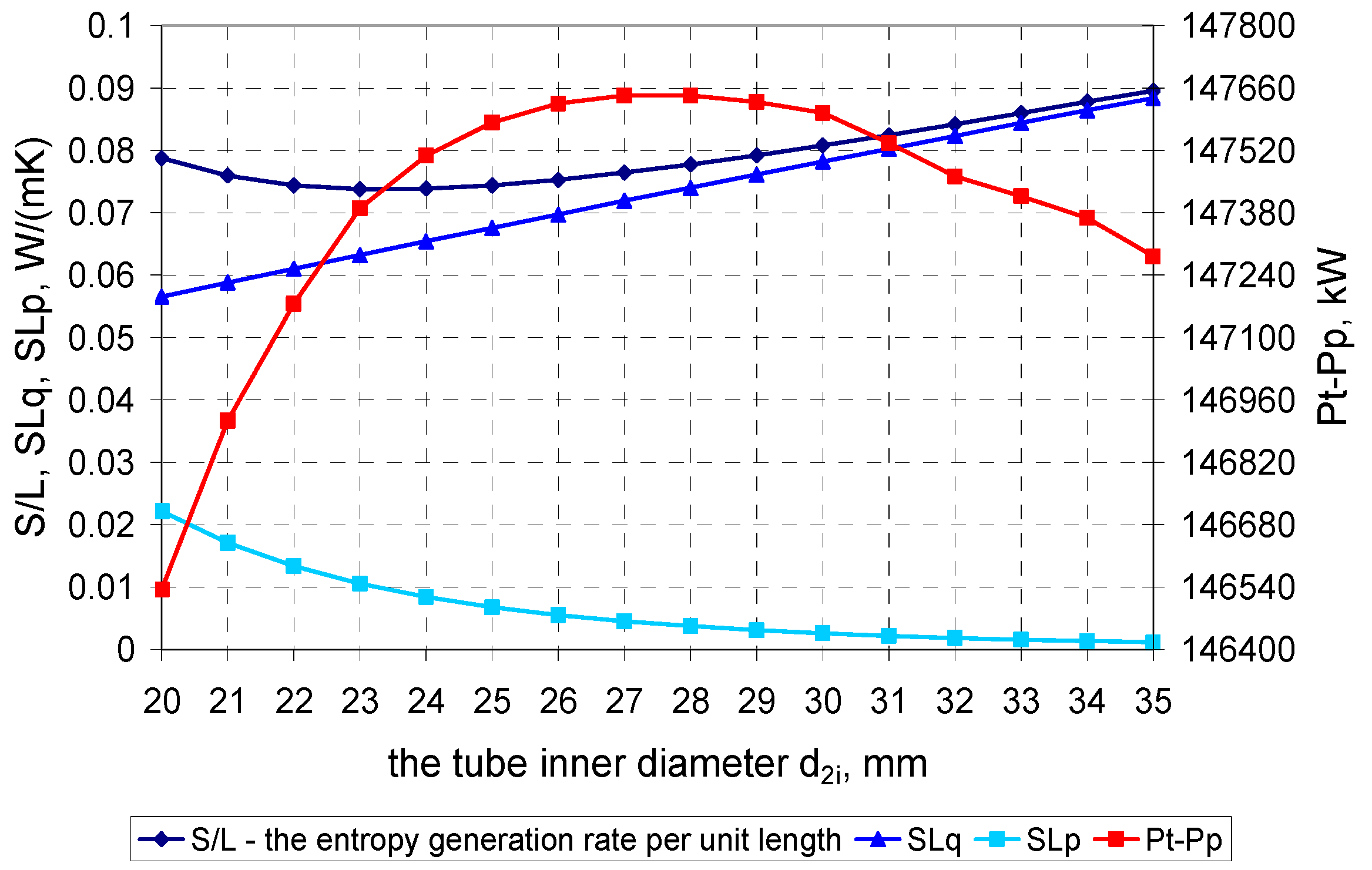
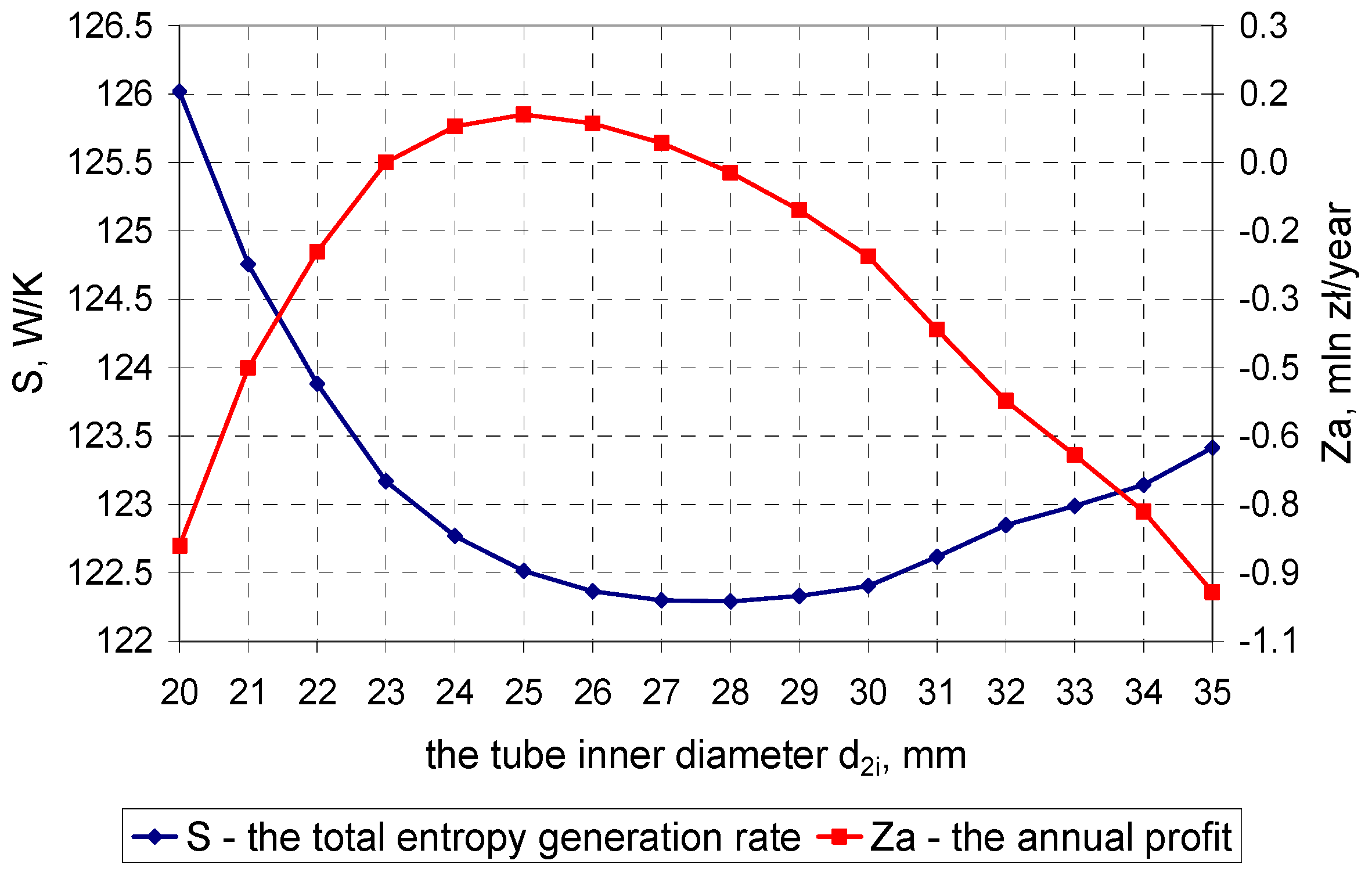
| Item | Symbol | Unit | Value |
|---|---|---|---|
| Heat transfer area | A | m2 | 2 × 5710 = 11,420 |
| Number of tubes | n | - | 2 × 6878 = 13,756 |
| Cooling-water mass flow rate | kg/s | 2 × 4000 = 8000 | |
| Inlet/outlet cooling water temperature, norm. | t2i/t2o | °C | 17/25.7 |
| Rated condensed-steam mass flow rate | kg/s | 129 | |
| Tube outer diameter | d2o | mm | 30 |
| Tube inner diameter | d2i | mm | 28 |
| Tube length | L | mm | 9000 |
| Mean water pressure | p2 | bar (abs) | 3 |
| Number of passes | - | - | 2 |
| Item | Symbol | Unit | Value |
|---|---|---|---|
| Heat transfer area | A | m2 | 2 × 9500 = 19,000 |
| Number of tubes | n | - | 2 × 16,000 = 32,000 |
| Cooling-water mass flow rate | kg/s | 2 × 6700 = 13,400 | |
| Inlet/outlet cooling water temperature, norm. | t2i/t2o | oC | 24/32 |
| Rated condensed-steam mass flow rate | kg/s | 207.5 | |
| Tube outer diameter | d2o | mm | 24 |
| Tube inner diameter | d2i | mm | 22.6 |
| Tube length | L | mm | 8000 |
| Mean water pressure | p2 | bar (abs) | 3 |
| Number of passes | - | - | 2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laskowski, R.; Smyk, A.; Rusowicz, A.; Grzebielec, A. Determining the Optimum Inner Diameter of Condenser Tubes Based on Thermodynamic Objective Functions and an Economic Analysis. Entropy 2016, 18, 444. https://doi.org/10.3390/e18120444
Laskowski R, Smyk A, Rusowicz A, Grzebielec A. Determining the Optimum Inner Diameter of Condenser Tubes Based on Thermodynamic Objective Functions and an Economic Analysis. Entropy. 2016; 18(12):444. https://doi.org/10.3390/e18120444
Chicago/Turabian StyleLaskowski, Rafał, Adam Smyk, Artur Rusowicz, and Andrzej Grzebielec. 2016. "Determining the Optimum Inner Diameter of Condenser Tubes Based on Thermodynamic Objective Functions and an Economic Analysis" Entropy 18, no. 12: 444. https://doi.org/10.3390/e18120444
APA StyleLaskowski, R., Smyk, A., Rusowicz, A., & Grzebielec, A. (2016). Determining the Optimum Inner Diameter of Condenser Tubes Based on Thermodynamic Objective Functions and an Economic Analysis. Entropy, 18(12), 444. https://doi.org/10.3390/e18120444






