Multivariable Fuzzy Measure Entropy Analysis for Heart Rate Variability and Heart Sound Amplitude Variability
Abstract
:1. Introduction
2. Multivariate Entropy Measures
2.1. Multivariate Sample Entropy (mvSE)
- (1)
- For a p-variate time series , , where is the number of samples in each variate, firstly normalize each time series for , and then form the composite delay vector using a composite delay factor based on the multivariate embedded reconstruction:where is the embedding vector, is the time lag vector, and is the dimension composite delay vector with , and with .
- (2)
- Define the distance between any two composite delay vectors and as the maximum norm, that is,
- (3)
- For a given vector and a threshold , count the number of instances where , , and then calculate the frequency of occurrence, , and define a global quantity .
- (4)
- Extend the dimensionality of the multivariate delay vector in Equation (1) from to . This can be performed in different ways, as the system can evolve to any space with (). Thus, a total of vectors are obtained. The k-th vector is:
- (5)
- For a given , count the number of instances , where , , and then calculate the frequency of occurrence, , and define .
- (6)
- Finally, mvSE is defined by
2.2. Multivariate Fuzzy Measure Entropy (mvFME)
- (1)
- For a -variate time series , , where is the number of samples in each variate, firstly normalize each time series for , and then form the local composite delay vector and global composite delay vector using a composite delay factor based on the multivariate embedded reconstruction:where the local composite delay vector represents consecutive values ; however, removing the local baseline of , the global composite delay vector represents consecutive values but removing global mean value of , is the embedding vector, is the time lag vector, , and .
- (2)
- Define the distance between any two local composite delay vectors and , and the distance between any two global composite delay vectors and , as the maximum norm, that is,
- (3)
- Given the parameters’ local vector similarity weight , local tolerance threshold , global vector similarity weight and global tolerance threshold , calculate the similarity degree between the local composite delay vectors and by the fuzzy function , as well as calculate the similarity degree between the global composite delay vectors and by the fuzzy function :Define the function and as:
- (4)
- Extend the dimensionality of the multivariate delay vectors in Equations (5) and (6) from to . This can be performed in different ways, as the system can evolve to any space with (). Thus, a total of vectors and a total of vectors are obtained. The kth vectors and are respectively:where and have the same meanings as Equations (5) and (6).
- (5)
- Similarly, define the function for the local composite delay vectors and and the function for the global composite delay vectors and as:
- (6)
- Then, the local multivariate fuzzy entropy (mvFEL) and global multivariate fuzzy entropy (mvFEG) are defined by:
- (7)
- Finally, mvFME is defined byIn this study, we used the following parameter setting as suggested in our previous studies [22,35]: the local similarity weight nL = 2 and global vector similarity weight nG = 2, and the local tolerance threshold rL was set equal to the global threshold rG, i.e., rL = rG = r. Thus, Equation (19) becomes:For both mvSE and mvFME, the entropy results were only based on the four parameters: embedding dimension vector , time lag vector , tolerance threshold and time series length . In addition, if we set , the multivariate entropy method becomes the univariate analysis. Thus, mvSE is the same as the traditional SampEn method and mvFME is the same as the traditional FuzzyMEn method.
3. Experiment Design
3.1. Simulation Signals
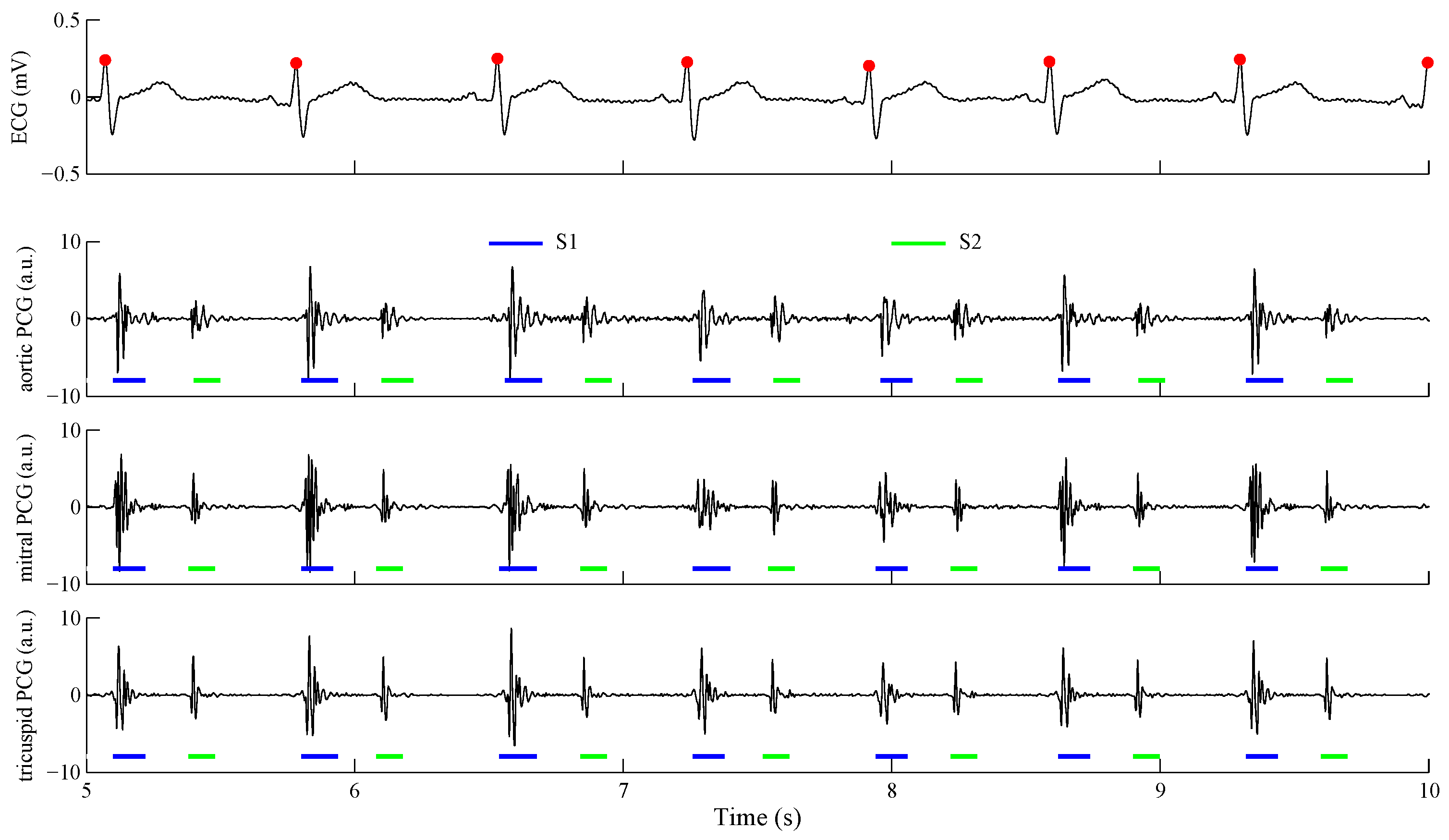
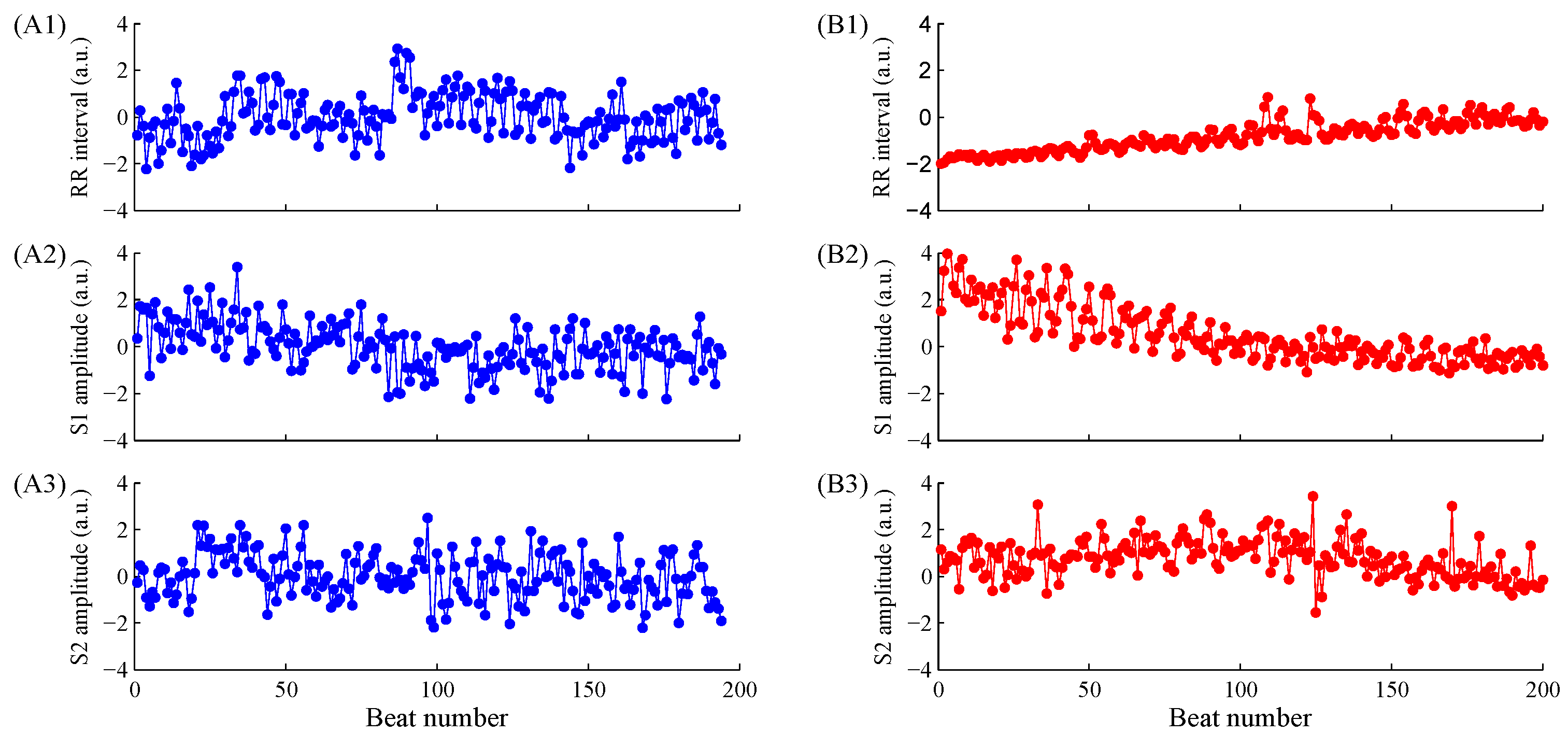
3.2. Cardiovascular Signals
3.3. Statistical Analysis
4. Results
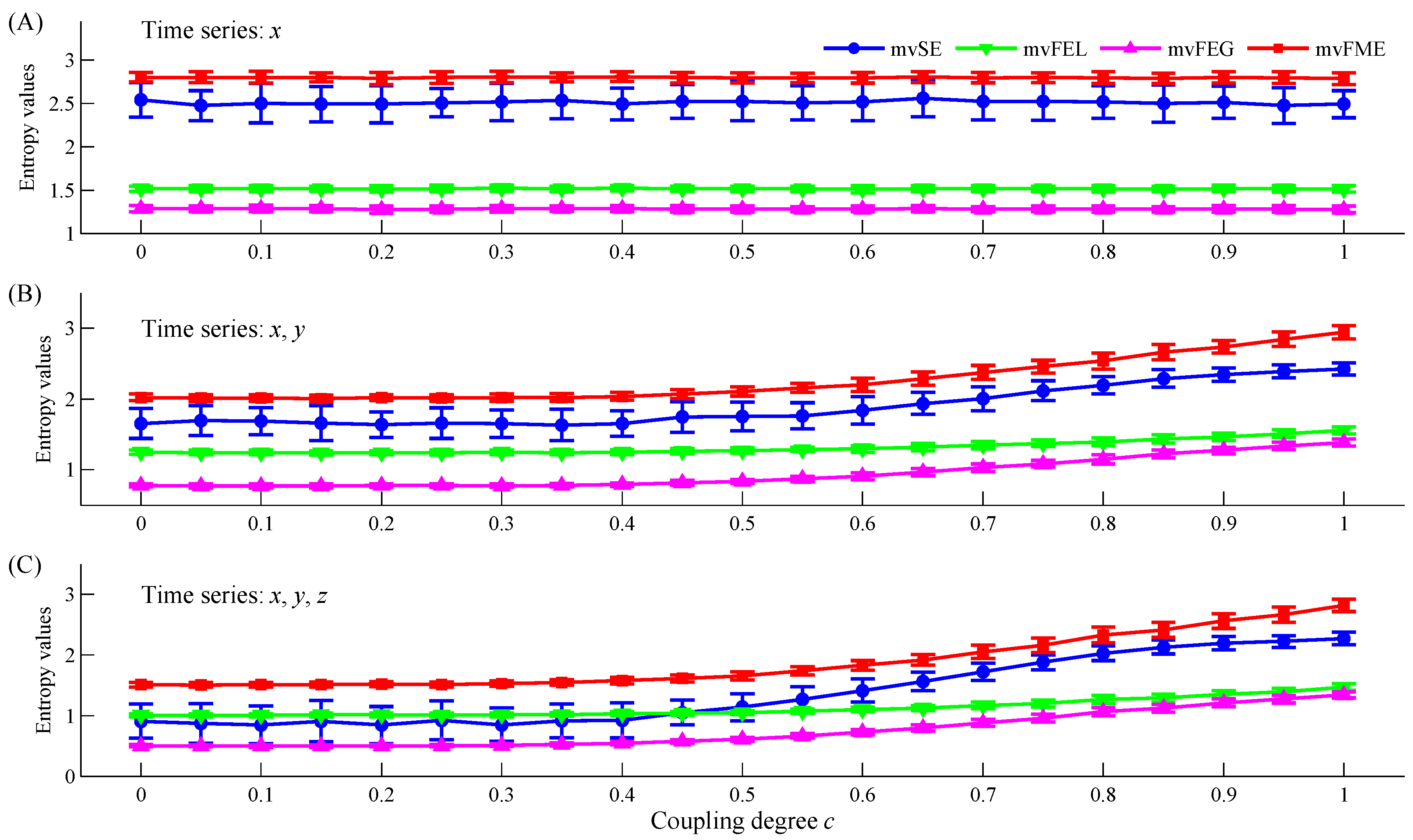
4.1. Results on Simulation Signals
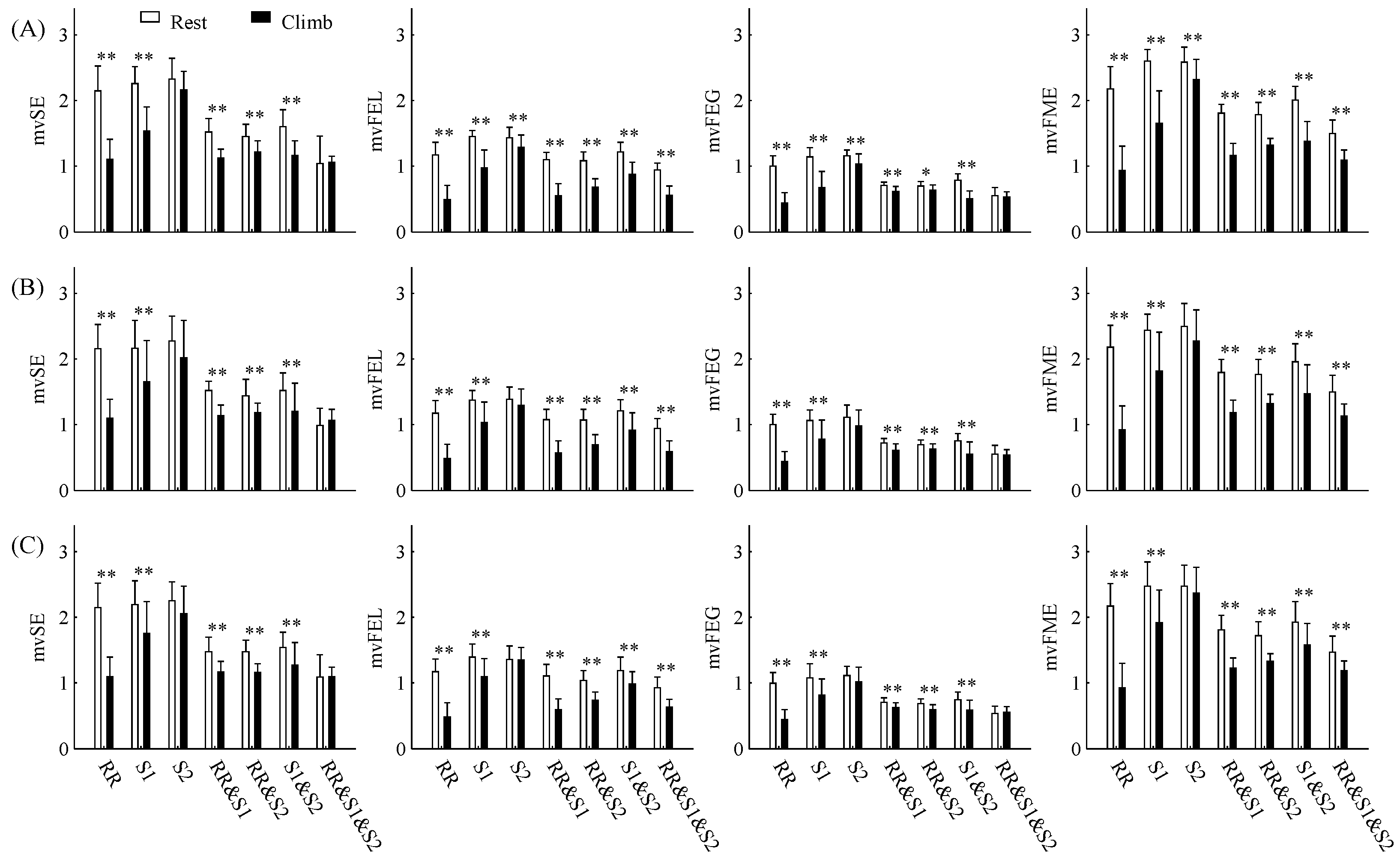
4.2. Results on Cardiovascular Signals
5. Discussions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xiao, X.S.; Mullen, T.J.; Mukkamala, R. System identification: A multi-signal approach for probing neural cardiovascular regulation. Physiol. Meas. 2005, 26, R41–R71. [Google Scholar] [CrossRef] [PubMed]
- Bravi, A.; Longtin, A.; Seely, A.J. Review and classification of variability analysis techniques with clinical applications. Biomed. Eng. Online 2011, 10. [Google Scholar] [CrossRef] [PubMed]
- Nozawa, M.; Yana, K.; Kaeriyama, K.; Mizuta, H.; Ono, T. Spontaneous variability analysis for characterizing cardiovascular responses to water ingestion. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 1816–1819.
- Seely, A.; Macklem, P. Complex systems and the technology of variability analysis. Crit. Care 2004, 8, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Glass, L. Synchronization and rhythmic processes in physiology. Nature 2001, 410, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A.; Baumert, M.; Mahé, G.; Abraham, P. Multiscale compression entropy of microvascular blood flow signals: Comparison of results from laser speckle contrastand laser doppler flowmetry data in healthy subjects. Entropy 2014, 16, 5777–5795. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Rehman, N.; Looney, D.; Mandic, D.P.; Kidmose, P.; Rutkowski, T.M. Multivariate entropy analysis with data-driven scales. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, 25–30 March 2012; pp. 3901–3904.
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. Heart Circ. Physiol. 1994, 266, H1643–H1656. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.Y.; Liu, C.C.; Shao, P.; Li, L.P.; Sun, X.; Wang, X.P.; Liu, F. Comparison of different threshold values r for approximate entropy: Application to investigate the heart rate variability between heart failure and healthy control groups. Physiol. Meas. 2011, 32, 167–180. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Phys. D Nonlinear Phenom. 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Gao, Z.K.; Fang, P.C.; Ding, M.S.; Jin, N.D. Multivariate weighted complex network analysis for characterizing nonlinear dynamic behavior in two-phase flow. Exp. Therm. Fluid Sci. 2015, 60, 157–164. [Google Scholar] [CrossRef]
- Labate, D.; La Foresta, F.; Morabito, G.; Palamara, I.; Morabito, F.C. Entropic measures of eeg complexity in alzheimer’s disease through a multivariate multiscale approach. IEEE Sens. J. 2013, 13, 3284–3292. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Refined composite multivariate generalized multiscale fuzzy entropy: A tool for complexity analysis of multichannel signals. Physica A 2017, 465, 261–276. [Google Scholar] [CrossRef]
- Chen, W.T.; Wang, Z.Z.; Xie, H.B.; Yu, W.X. Characterization of surface emg signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhuang, J.; Yu, W.X.; Wang, Z.Z. Measuring complexity using fuzzyen, apen, and sampen. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Liu, C.Y.; Li, L.P.; Ji, L.Z.; Yu, S.Y.; Liu, C.C. Multiscale multivariate fuzzy entropy analysis. Acta Phys. Sin. 2013, 62. [Google Scholar] [CrossRef]
- Liu, C.Y.; Zhang, C.Q.; Zhang, L.; Zhao, L.N.; Liu, C.C.; Wang, H.J. Measuring synchronization in coupled simulation and coupled cardiovascular time series: A comparison of different cross entropy measures. Biomed. Signal Process. Control 2015, 21, 49–57. [Google Scholar] [CrossRef]
- Liu, C.Y.; Li, K.; Zhao, L.N.; Liu, F.; Zheng, D.C.; Liu, C.C.; Liu, S.T. Analysis of heart rate variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.Y.; Zhao, L.N. Using fuzzy measure entropy to improve the stability of traditional entropy measures. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; pp. 681–684.
- Liu, C.Y.; Liu, C.C.; Li, L.P.; Zhang, Q.G.; Li, B. Systolic and diastolic time interval variability analysis and their relations with heart rate variability. In Proceedings of the 3rd International Conference on Bioinformatics and Biomedical Engineering, Beijing, China, 11–13 June 2009; pp. 1–4.
- Ji, L.Z.; Li, P.; Liu, C.Y.; Wang, X.P.; Yang, J.; Liu, C.C. Measuring electromechanical coupling in patients with coronary artery disease and healthy subjects. Entropy 2016, 18, 153. [Google Scholar] [CrossRef]
- Aletti, F.; Bassani, T.; Lucini, D.; Pagani, M.; Baselli, G. Multivariate decomposition of arterial blood pressure variability for the assessment of arterial control of circulation. IEEE Trans. Biomed. Eng. 2009, 56, 1781–1790. [Google Scholar] [CrossRef] [PubMed]
- Javed, F.; Middleton, P.M.; Malouf, P.; Chan, G.S.; Savkin, A.V.; Lovell, N.H.; Steel, E.; Mackie, J. Frequency spectrum analysis of finger photoplethysmographic waveform variability during haemodialysis. Physiol. Meas. 2010, 31, 1203–1216. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.Y.; Zheng, D.C.; Zhao, L.N.; Li, P.; Liu, C.C.; Murray, A. Analysis of cardiovascular time series using multivariate sample entropy: A comparison between normal and congestive heart failure subjects. In Proceedings of the Computing in Cardiology, Cambridge, MA, USA, 7–10 September 2014; pp. 237–240.
- Kofman, S.; Bickel, A.; Eitan, A.; Weiss, A.; Gavriely, N.; Intrator, N. Discovery of multiple level heart-sound morphological variability resulting from changes in physiological states. Biomed. Signal Process. Control 2012, 7, 315–324. [Google Scholar] [CrossRef]
- Clifford, G.D.; Liu, C.Y.; Springer, D.; Moody, B.; Li, Q.; Juan, R.A.; Millet, J.; Silva, I.; Johnson, A.; Mark, R.G. Classification of normal/abnormal heart sound recordings: The physionet/computing in cardiology challenge 2016. In Proceedings of the Computing in Cardiology 2016, Vancouver, BC, Canada, 11–14 September 2016; pp. 609–612.
- Liu, C.Y.; Springer, D.B.; Li, Q.; Moody, B.; Juan, R.A.; Chorro, F.J.; Castells, F.; Riog, J.M.; Silva, I.; Johnson, A.E.W.; et al. An open access database for the evaluation of heart sound algorithms. Physiol. Meas. 2016, 37, 2181–2213. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.Z.; Cai, S.X.; Liu, G.C. Studying the significance of cardiac contractility variability. IEEE Eng. Med. Biol. Mag. 2002, 19, 102–105. [Google Scholar] [CrossRef]
- Wu, W.Z.; Guo, X.M.; Xie, M.L.; Xiao, Z.F.; Yang, Y.; Xiao, S.Z. Research on first heart sound and second heart sound amplitude variability and reversal phenomenon—A new finding in athletic heart study. J. Med. Biol. Eng. 2009, 29, 202–205. [Google Scholar]
- Zhao, L.N.; Wei, S.S.; Zhang, C.Q.; Zhang, Y.T.; Jiang, X.E.; Liu, F.; Liu, C.Y. Determination of sample entropy and fuzzy measure entropy parameters for distinguishing congestive heart failure from normal sinus rhythm subjects. Entropy 2015, 19, 6270–6288. [Google Scholar] [CrossRef]
- Ansari-Asl, K.; Senhadji, L.; Bellanger, J.-J.; Wendling, F. Quantitative evaluation of linear and nonlinear methods characterizing interdependencies between brain signals. Phys. Rev. E 2006, 74. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Li, T.; Qiu, T.S.; Park, Y. Segmentation of heart sounds based on dynamic clustering. Biomed. Signal Process. Control 2012, 7, 509–516. [Google Scholar] [CrossRef]
- Tang, H.; Li, T.; Qiu, T.S. Noise and disturbance reduction for heart sounds in the cycle frequency domain based on non-linear time scaling. IEEE Trans. Biomed. Eng. 2010, 57, 325–333. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.Y.; Li, L.P.; Zhao, L.N.; Zheng, D.C.; Li, P.; Liu, C.C. A combination method of improved impulse rejection filter and template matching for identification of anomalous intervals in electrocardiographic RR sequences. J. Med. Biol. Eng. 2012, 32, 245–250. [Google Scholar] [CrossRef]
- Springer, D.B.; Tarassenko, L.; Clifford, G.D. Logistic regression-hsmm-based heart sound segmentation. IEEE Trans. Biomed. Eng. 2016, 63, 822–832. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.B.; Luisada, A.A.; Miletich, D.J.; Albrecht, R.F. Phonocardiography as a monitor of cardiac performance during anesthesia. Anesth. Analg. 1989, 68, 385–387. [Google Scholar] [CrossRef] [PubMed]
- Durand, L.G.; Langlois, Y.E.; Lanthier, T.; Chiarella, R.; Coppens, P.; Carioto, S.; Bertrand-Bradley, S. Spectral analysis and acoustic transmission of mitral and aortic valve closure sounds in dogs. Part 4: Effect of modulating cardiac inotropy. Med. Biol. Eng. Comput. 1990, 28, 439–445. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.Z.; Wang, Z.G.; Hu, D.Y. Studying cardiac contractility change trend to evaluate cardiac reserve. IEEE Eng. Med. Biol. Mag. 2002, 21, 74–76. [Google Scholar] [CrossRef] [PubMed]
- Perloff, J.K. The physiologic mechanisms of cardiac and vascular physical signs. J. Am. Coll. Cardiol. 1983, 1, 184–198. [Google Scholar] [CrossRef]
- Liu, C.Y.; Zheng, D.C.; Li, P.; Zhao, L.N.; Liu, C.C.; Murray, A. Is cross-sample entropy a valid measure of synchronization between sequences of RR interval and pulse transit time? In Proceedings of the Computing in Cardiology Conference, Zaragoza, Spain, 22–25 September 2013; pp. 939–942.
- Li, P.; Liu, C.Y.; Wang, X.P.; Li, B.; Che, W.B.; Liu, C.C. Cross-sample entropy and cross-fuzzy entropy for testing pattern synchrony: How results vary with different threshold value r. In World Congress on Medical Physics and Biomedical Engineering, Beijing, China, 26–31 May 2012; Long, M., Ed.; Springer: Beijing, China, 2013; pp. 485–488. [Google Scholar]
- Xie, H.B.; Zheng, Y.P.; Guo, J.Y.; Chen, X. Cross-fuzzy entropy: A new method to test pattern synchrony of bivariate time series. Inf. Sci. 2010, 180, 1715–1724. [Google Scholar] [CrossRef]
- Xie, H.B.; Guo, J.Y.; Zheng, Y.P. A comparative study of pattern synchronization detection between neural signals using different cross-entropy measures. Biol. Cybern. 2010, 102, 123–135. [Google Scholar] [CrossRef] [PubMed]
| Variable | Value |
|---|---|
| Age (year) | 24.2 ± 1.9 |
| Height (cm) | 174 ± 4 |
| Weight (kg) | 64 ± 7 |
| Heart rate (beats/min) | 69 ± 9 |
| Systolic blood pressure (mmHg) | 121 ± 9 |
| Diastolic blood pressure (mmHg) | 65 ± 7 |
| Gaussian Time Series | Time (s) | |||
|---|---|---|---|---|
| mvSE | mvFEL | mvFEG | mvFME | |
| Univariate analysis | 6.58 | 16.67 | 16.61 | 33.28 |
| Bivariate analysis | 19.42 | 51.20 | 51.03 | 102.23 |
| Trivariate analysis | 44.01 | 108.84 | 108.47 | 217.31 |
| Signals | Time Series | mvSE | mvFME | ||||
|---|---|---|---|---|---|---|---|
| Rest | Climb | p-Value | Rest | Climb | p-Value | ||
| ECG + aortic PCG | RR | 2.15 ± 0.38 | 1.11 ± 0.30 | 6 × 10−9 | 2.17 ± 0.34 | 0.93 ± 0.37 | 3 × 10−10 |
| S1 | 2.26 ± 0.26 | 1.53 ± 0.37 | 6 × 10−7 | 2.60 ± 0.18 | 1.65 ± 0.50 | 3 × 10−7 | |
| S2 | 2.33 ± 0.32 | 2.16 ± 0.29 | 0.1 | 2.59 ± 0.23 | 2.32 ± 0.31 | 3 × 10−3 | |
| RR & S1 | 1.52 ± 0.20 | 1.13 ± 0.13 | 2 × 10−6 | 1.81 ± 0.13 | 1.16 ± 0.19 | 9 × 10−11 | |
| RR & S2 | 1.46 ± 0.19 | 1.22 ± 0.19 | 9 × 10−4 | 1.78 ± 0.19 | 1.32 ± 0.11 | 1 × 10−8 | |
| S1 & S2 | 1.60 ± 0.25 | 1.16 ± 0.22 | 6 × 10−6 | 2.00 ± 0.21 | 1.38 ± 0.30 | 2 × 10−9 | |
| RR & S1 & S2 | 1.04 ± 0.42 | 1.06 ± 0.09 | 0.8 | 1.50 ± 0.21 | 1.09 ± 0.16 | 1 × 10−8 | |
| ECG + mitral PCG | RR | 2.15 ± 0.38 | 1.11 ± 0.30 | 6 × 10−9 | 2.17 ± 0.34 | 0.93 ± 0.37 | 3 × 10−10 |
| S1 | 2.16 ± 0.42 | 1.66 ± 0.62 | 5 × 10−3 | 2.43 ± 0.25 | 1.81 ± 0.59 | 2 × 10−4 | |
| S2 | 2.27 ± 0.38 | 2.01 ± 0.57 | 0.1 | 2.50 ± 0.34 | 2.27 ± 0.48 | 0.1 | |
| RR & S1 | 1.52 ± 0.14 | 1.14 ± 0.16 | 2 × 10−8 | 1.80 ± 0.20 | 1.18 ± 0.20 | 3 × 10−11 | |
| RR & S2 | 1.44 ± 0.25 | 1.18 ± 0.15 | 5 × 10−4 | 1.76 ± 0.23 | 1.32 ± 0.14 | 3 × 10−6 | |
| S1 & S2 | 1.52 ± 0.26 | 1.20 ± 0.43 | 9 × 10−3 | 1.96 ± 0.27 | 1.46 ± 0.44 | 3 × 10−4 | |
| RR & S1 & S2 | 0.98 ± 0.27 | 1.06 ± 0.17 | 0.3 | 1.50 ± 0.25 | 1.12 ± 0.19 | 2 × 10−5 | |
| ECG + tricuspid PCG | RR | 2.15 ± 0.38 | 1.11 ± 0.30 | 6 × 10−9 | 2.17 ± 0.34 | 0.93 ± 0.37 | 3 × 10−10 |
| S1 | 2.19 ± 0.37 | 1.75 ± 0.48 | 7 × 10−3 | 2.47 ± 0.37 | 1.92 ± 0.49 | 2 × 10−3 | |
| S2 | 2.25 ± 0.29 | 2.05 ± 0.42 | 0.1 | 2.47 ± 0.32 | 2.37 ± 0.39 | 0.3 | |
| RR & S1 | 1.47 ± 0.23 | 1.17 ± 0.16 | 2 × 10−6 | 1.81 ± 0.22 | 1.22 ± 0.16 | 2 × 10−9 | |
| RR & S2 | 1.47 ± 0.18 | 1.16 ± 0.13 | 1 × 10−6 | 1.72 ± 0.21 | 1.33 ± 0.12 | 3 × 10−8 | |
| S1 & S2 | 1.54 ± 0.23 | 1.27 ± 0.34 | 9.9 × 10−3 | 1.93 ± 0.31 | 1.58 ± 0.33 | 2 × 10−3 | |
| RR & S1 & S2 | 1.09 ± 0.34 | 1.10 ± 0.14 | 0.97 | 1.47 ± 0.24 | 1.18 ± 0.15 | 1 × 10−4 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Wei, S.; Tang, H.; Liu, C. Multivariable Fuzzy Measure Entropy Analysis for Heart Rate Variability and Heart Sound Amplitude Variability. Entropy 2016, 18, 430. https://doi.org/10.3390/e18120430
Zhao L, Wei S, Tang H, Liu C. Multivariable Fuzzy Measure Entropy Analysis for Heart Rate Variability and Heart Sound Amplitude Variability. Entropy. 2016; 18(12):430. https://doi.org/10.3390/e18120430
Chicago/Turabian StyleZhao, Lina, Shoushui Wei, Hong Tang, and Chengyu Liu. 2016. "Multivariable Fuzzy Measure Entropy Analysis for Heart Rate Variability and Heart Sound Amplitude Variability" Entropy 18, no. 12: 430. https://doi.org/10.3390/e18120430
APA StyleZhao, L., Wei, S., Tang, H., & Liu, C. (2016). Multivariable Fuzzy Measure Entropy Analysis for Heart Rate Variability and Heart Sound Amplitude Variability. Entropy, 18(12), 430. https://doi.org/10.3390/e18120430







