Numerical Study of Entropy Generation in Mixed MHD Convection in a Square Lid-Driven Cavity Filled with Darcy–Brinkman–Forchheimer Porous Medium

Abstract

This investigation deals with the numerical simulation of entropy generation at mixed convection flow in a lid-driven saturated porous cavity submitted to a magnetic field. The magnetic field is applied in the direction that is normal to the cavity cross section. The governing equations, written in the Darcy–Brinkman–Forchheimer formulation, are solved using a numerical code based on the Control Volume Finite Element Method. The flow structure and heat transfer are presented in the form of streamlines, isotherms and average Nusselt number. The entropy generation was studied for various values of Darcy number (10⁻³ ≤ Da ≤ 1) and for a range of Hartmann number (0 ≤ Ha ≤ 10²). It was found that entropy generation is affected by the variations of the considered dimensionless physical parameters. Moreover, the form drag related to the Forchheimer effect remains significant until a critical Hartmann number value.

1. Introduction

The mixed magneto-convection in a lid-driven porous cavity has received extensive attention due to itswide variety of uses in engineering applications, such as the cooling of electronic devices, solar collectors, energy storage, crystal growth, food processing and nuclear reactors. Some text booksthat presented a numerical study on convective flow in porous media areby Nield and Bejan [1], Ingham and Pop [2], Vafai [3], and Bejan et al. [4]. Chamkha [5] presented a numerical work on hydromagnetic convection flow in a lid-driven cavity in the presence of a magnetic field. He found that the flow behavior and the heat transfer characteristics inside the cavity are strongly affected by the presence of the magnetic field.Khanafer and Vafai [6] numerically studied the double mixed convection in a saturated porous lid-driven enclosure filled with a non-Darcian fluid. The influence of the Lewis, Reynolds and Darcy numbers on the heat and mass transfer processes was analyzed. Results revealed that the flow characteristics and the heat transfer are strongly dependent on the Richardson number. Cheng [7] numerically investigated mixed convection in a lid-driven square cavity with the aim to characterizing the heat transfer behavior and to validate the Nusselt number correlations reported in the literature. Mixed convection in a lid-driven porous cavity in the presence of a magnetic field was studied numerically by Muthtamilselvan et al. [8]. It was found that the heat transfer strongly depends on the magnetic field strength and the Darcy number. Rahman et al. [9] numerically investigated the Magneto-hydrodynamics mixed convection in a lid-driven square cavity. They showed that the Reynolds number has a significant effect on the streamlines and isotherms for different convective regimes. Mansour et al. [10] analyzed the numerical simulation of mixed convection flow in a square lid-driven cavity partially heated from below using Cu-water, Ag-water, Al₂O₃-water and TiO₂-water nanofluid. They showed that the increase in the solid volume fraction leads to a decrease in the activity of the fluid motion and the fluid temperature. Hydrodynamic mixed convection in a lid-driven cavity heated from the top with a wavy bottom surface was numerically studied by Saha et al. [11], using the Galerkin finite element method. They observed that the variation in the Reynolds number affects the flow and thermal current activities. Mamourian et al. [12] presented the optimum conditions of the mixed convection heat transfer in a wavy surface square cavity filled with Cu-water nanofluid by utilizing the Taguchi method. They observed that the entropy generation and the mean Nusselt number decrease with the increase of the wavelength of the wavy surface for a given Richardson number. Akbar et al. [13] studied the effect of the entropy and the magnetic field in an endoscope filled with Cu-water. They found that the increase of the Brinkman and the Hartmann numbers tends to increase the temperature. Also, the increase of the Brinkman number induced the increase of the entropy generation. Ellahi et al. [14] investigated the shape effect of the nanoparticles suspended in HFE-7100 over a wedge in the mixed convection. They showed that the entropy generation approaches zero near to the free stream region. Akbar et al. [15] presented the effect of the entropy and the magnetic field on the peristaltic flow of the copper water fluid in an asymmetric horizontal channel. They showed that the entropy generation number increases with the Brinkman number. In the middle of the channel, the flow velocity decreases when the magnetic Reynolds number increases.

The main objective of the present investigation is to examine the effect of a magnetic field on heat transfer and entropy generation in a lid-driven saturated porous cavity, under the Brinkman–Forchheimer extended Darcy formulation. The governing equations of the considered problem are solved using the Control Volume Finite Elements method. The influence of the Hartman, Rayleigh, Reynolds numbers and the Forchheimer parameter, on thermodynamic irreversibility, was studied.

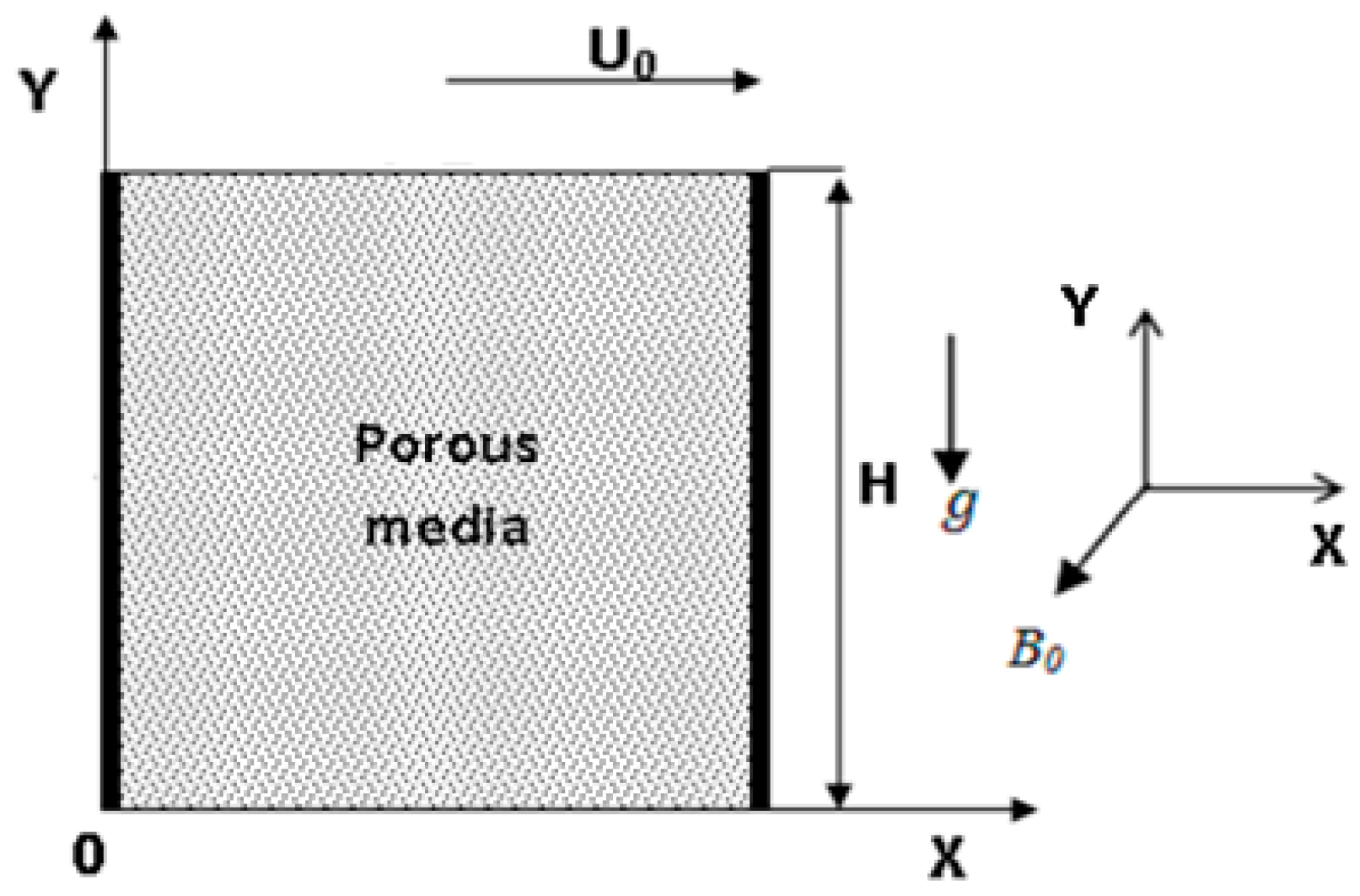
2. Mathematical Formulation

Consider a steady-state two-dimensional laminar flow in a lid-driven saturated porous cavity filled with a Newtonian, incompressible and electrically conducting fluid. The square cavity with porosity (ɛ) has a height (H) as shown in Figure 1. The top wall is moving from left to right at a constant speed U₀ and is maintained at a constant temperature ${\mathsf{\theta }}_{\mathrm{c}}$, whereas the bottom wall is maintained at a constant temperature ${\mathsf{\theta }}_{\mathrm{h}}$ (${\mathsf{\theta }}_{\mathrm{c}}$ < ${\mathsf{\theta }}_{\mathrm{h}}$). All other remaining walls are adiabatic and insulated. A uniform magnetic field of strength (B₀) is applied in the direction normal to the cavity cross section. The physical properties of the fluid are considered to be constant, except the density variation which is applied in the Boussinesq approximation for the buoyancy term $(\mathsf{\rho }={\mathsf{\rho }}_0[1-{\mathsf{\beta }}_{\mathsf{\theta }}(\mathsf{\theta }-{\mathsf{\theta }}_0)])$. ${\mathsf{\rho }}_0$ is the fluid density at temperature ${\mathsf{\theta }}_0$ and ${\mathsf{\beta }}_{\mathsf{\theta }}$ is the thermal expansion coefficient.

Using the Darcy–Brinkman–Forchheimer model with the above assumptions, the governing equations of continuity, momentum and energy conservations can be written in dimensionless form as (Nield and Bejan [1]):

Continuity equation:

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0$$

(1)

X-Momentum Equation:

$$\frac{\partial U}{\partial \tau }+div{J}_U=-\mathsf{\epsilon }\frac{\partial P}{\partial X}-\frac{\mathsf{\epsilon }}{\mathrm{ReDa}}U-\frac{{\mathsf{\epsilon }\mathrm{F}}_{\mathsf{\epsilon }}}{\sqrt{\mathrm{Da}}}\sqrt{U^2+V^2}U-\frac{{\mathsf{\epsilon }\mathrm{Ha}}^2}{\mathrm{Re}}U$$

(2)

Y-Momentum Equation:

$$\frac{\partial V}{\partial \tau }+div{J}_V=-\mathsf{\epsilon }\frac{\partial P}{\partial Y}-\frac{\mathsf{\epsilon }}{\mathrm{ReDa}}V-\frac{{\mathsf{\epsilon }\mathrm{F}}_{\mathsf{\epsilon }}}{\sqrt{\mathrm{Da}}}\sqrt{U^2+V^2}V-\frac{{\mathsf{\epsilon }\mathrm{Ha}}^2}{\mathrm{Re}}V-{\mathsf{\epsilon }\mathrm{R}}_{\mathrm{i}}T$$

(3)

Energy Equation:

$$\frac{\partial T}{\partial \tau }+div{J}_T=0$$

(4)

With:

$$\begin{gathered} J_U=\frac{1}{\mathsf{\epsilon }}\left(\mathit{U}·\mathbf{\nabla }\right)U-\frac{1}{\mathrm{Re}}gradU \\ {J}_V=\frac{1}{\mathsf{\epsilon }}\left(\mathit{U}·\mathbf{\nabla }\right)V-\frac{1}{\mathrm{Re}}gradV \\ {J}_T=\frac{1}{\mathsf{\epsilon }}\left(\mathit{U}·\mathbf{\nabla }\right)T-\frac{1}{\mathrm{Pe}}gradT \end{gathered}$$

(5)

The reference length, velocity, temperature, pressure and time for scaling are the height H of the cavity, the Lid velocity U₀, the temperature difference $\left(\mathsf{\theta }-{\mathsf{\theta }}_0\right)$ between the two horizontal walls of the cavity, ${\mathsf{\rho }}_0{\mathrm{U}}_0^2$ and $\mathrm{H}/{\mathrm{U}}_0$, respectively. Thus $\mathrm{Ra}={\mathrm{g}\mathsf{\beta }}_{\mathsf{\theta }}\left({\mathsf{\theta }}_{\mathrm{h}}-{\mathsf{\theta }}_{\mathrm{c}}\right){\mathrm{L}}^3/\left(\mathsf{\nu }\mathsf{\alpha }\right)$ is the Rayleigh number, $\mathrm{Re}={\mathrm{U}}_0\mathrm{H}/\mathsf{\nu }$ is the Reynolds number, $\mathrm{Da}=\mathrm{K}/{\mathrm{H}}^2$ is the Darcy number, $\mathrm{Ha}={\mathrm{B}}_0\mathrm{H}\sqrt{{\mathsf{\sigma }}_0/\mathsf{\mu }}$ is the Hartman number, $\mathrm{Ri}=\mathrm{Ra}/\left(\mathrm{PeRe}\right)$ is the Richardson number, $\mathrm{Pe}=\mathrm{RePr}$ is the Peclet number and $\mathrm{Pr}=\mathsf{\nu }/\mathsf{\alpha }$ is the Prandtl number. g is the gravity constant.

The initial and boundary conditions, expressed in dimensionless form are:

Initial conditions:

U (X, Y) = V (X, Y) = P = 0; T (X, Y) = 1 − Y

(6a)

Boundary conditions

At the vertical walls

$$U(0,Y)=V(0,Y)=0;\frac{\partial T}{\partial X}=0$$

(6b)

$$U(1,Y)=V(1,Y)=0;\frac{\partial T}{\partial Y}=0$$

(6c)

At the horizontal active walls

U (X, 0) = 0; V (X, 0) = 0; T (X, 0) = 1

(6d)

U (X, 1) = 1; V (X, 1) = 0; T (X, 1) = 0

(6e)

The heat transfer along the heated wall is given by the average Nusselt number, defined as follows:

$$\mathrm{Nu}={{\displaystyle \int }}_0^1-\left(\frac{\partial T}{\partial Y}\right)dX$$

(7)

3. Second Law Formulation

The local entropy generation in a porous medium denoted (S_l) can be calculated by following the equation of (Woods [16]):

$$S_l=\left[{\left(\frac{\partial T}{\partial X}\right)}^2+{\left(\frac{\partial T}{\partial Y}\right)}^2\right]+\frac{{\mathrm{Br}}^{*}}{\mathrm{Da}}\left[U^2+V^2\right]+{\mathrm{Br}}^{*}\left[{\left(\frac{\partial U}{\partial X}\right)}^2+{\left(\frac{\partial V}{\partial Y}\right)}^2+{\left(\frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}\right)}^2\right]+{\mathrm{Br}}^{*}{\mathrm{Ha}}^2\left[U^2+V^2\right]$$

(8)

The first term of the right hand side of Equation (8) is the heat transfer irreversibility, the second represents the Darcy viscous irreversibility, the third is related to the clear fluid viscous irreversibility and the fourth is relative to the magnetic effect. The dimensionless total entropy generation (S) is obtained by a numerical integration of the dimensionless local entropy generation over the entire volume of the cavity, Ω. It is given by:

$$S={{\displaystyle \int }}_{\mathsf{\Omega }}{S}_{l}d\mathsf{\Omega }$$

(9)

4. Numerical Method

Equations (1)–(4) were solved by the SIMPLE algorithm of Patankar [17] and the SIMPLEC approximation of Van Doormal and Raithby [16]. The used numerical code, described and validated in detail in Abbassi et al. [18], employs the Control Volume Finite Element Method (CVFEM) of Patankar [17] and Saabas and Baliga [19]). Note that the SIMPLE algorithm was developed at Imperial College-London by Pantakar and Spalding [20].

The convergence criterion is given by (χ represents U, V or T):

$$\max \left|\frac{{\chi }^{t+\Delta t}-{\chi }^t}{{\chi }^{t+\Delta t}}\right|\le {10}^{-5}$$

(10)

The local entropy generation is calculated after calculating the temperature and velocity components in each control volume in the mesh. Results shown in the following section have been calculated by taking into account the initial and the boundary conditions (6) given above. In order to validate the accuracy of the proposed computational model, results of the present work are compared to those provided from Muthtamilselvan et al. [8] and Jue [21] for Rayleigh numbers equal to 10³, 10⁴ and 10⁵. As can be seen in

Table 1. Validation of the numerical results.

Ra	103	104	105
Present study	1.099	2.295	4.664
Davis (1983)	1.118	2.243	4.519
Nithyadevi et al. (2009)	1.123	2.304	4.899

and

Table 2. Validation of the numerical results.

Ra	ε	Present Results	Muthtamilselvan et al. (2009)	June (2001)
105	0.4	2.9482	2.9004	2.9435
	0.6	3.1310	3.0893	3.0877

, a good agreement was obtained.

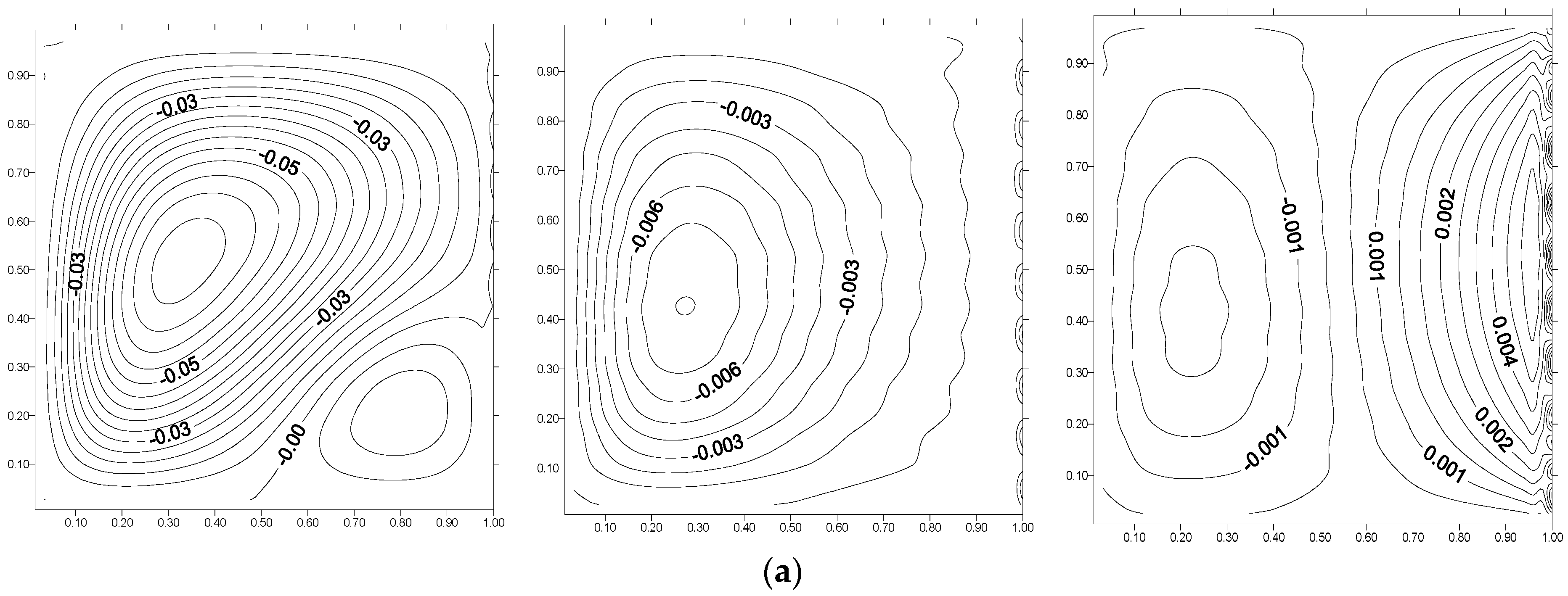
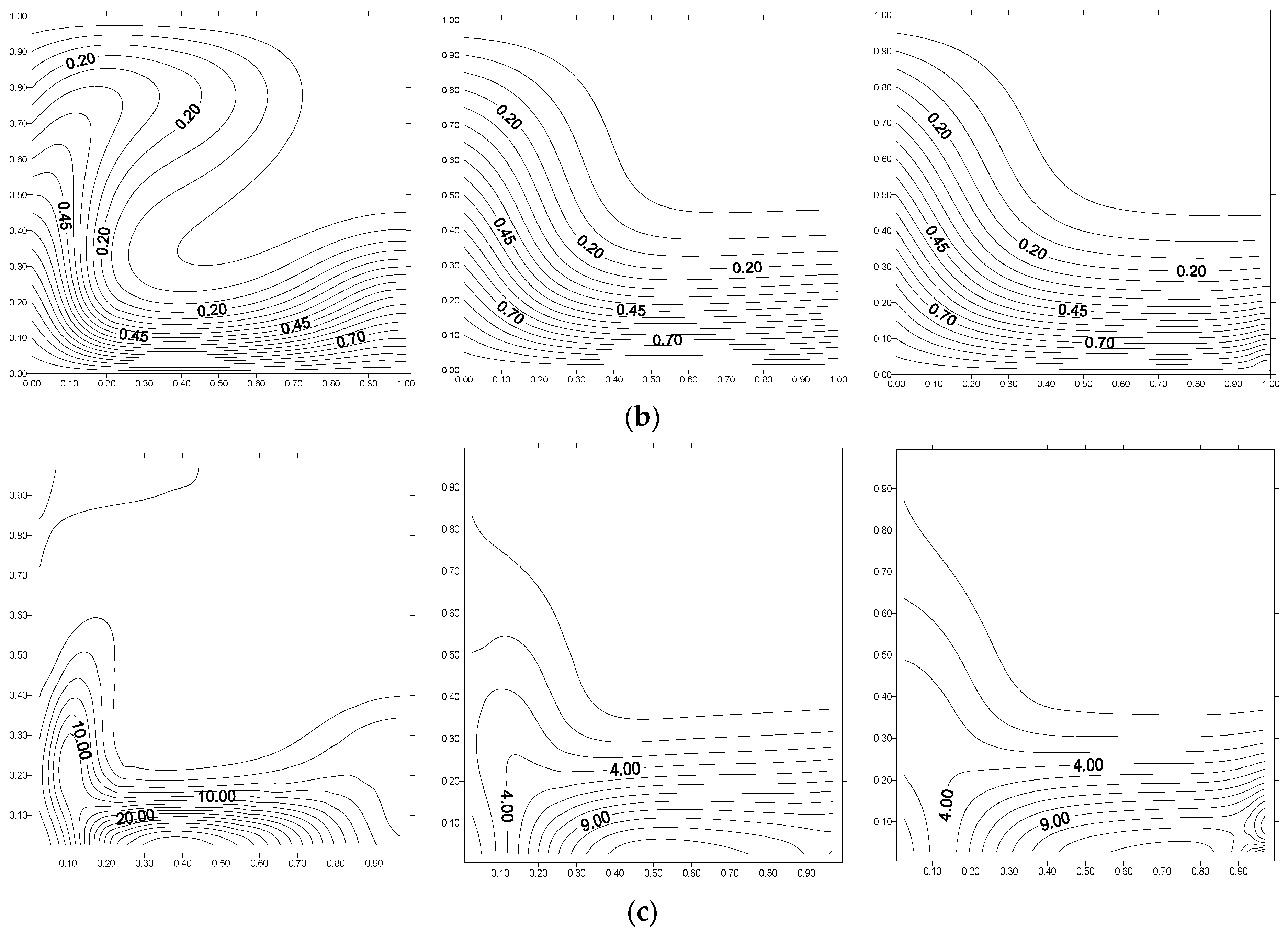
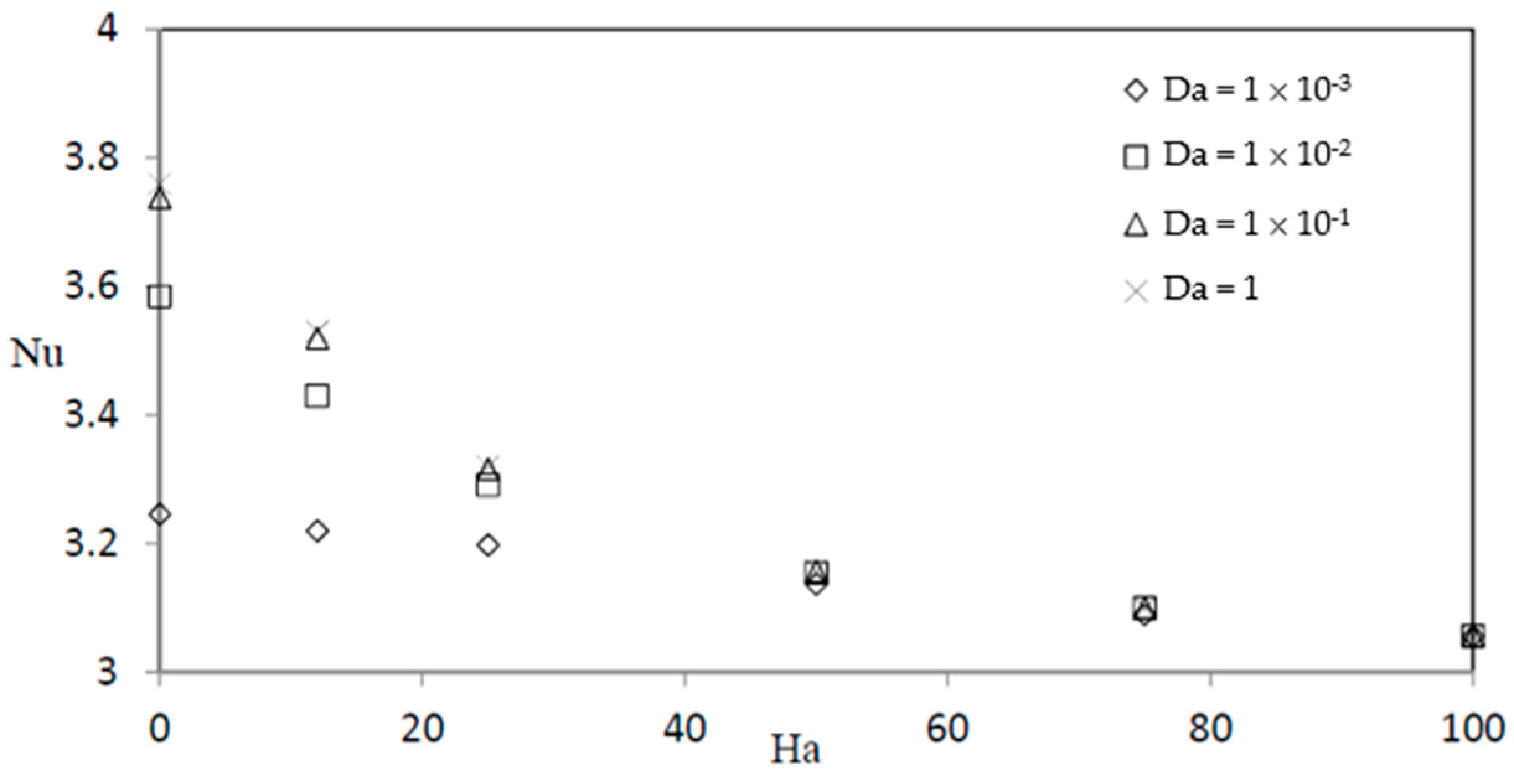
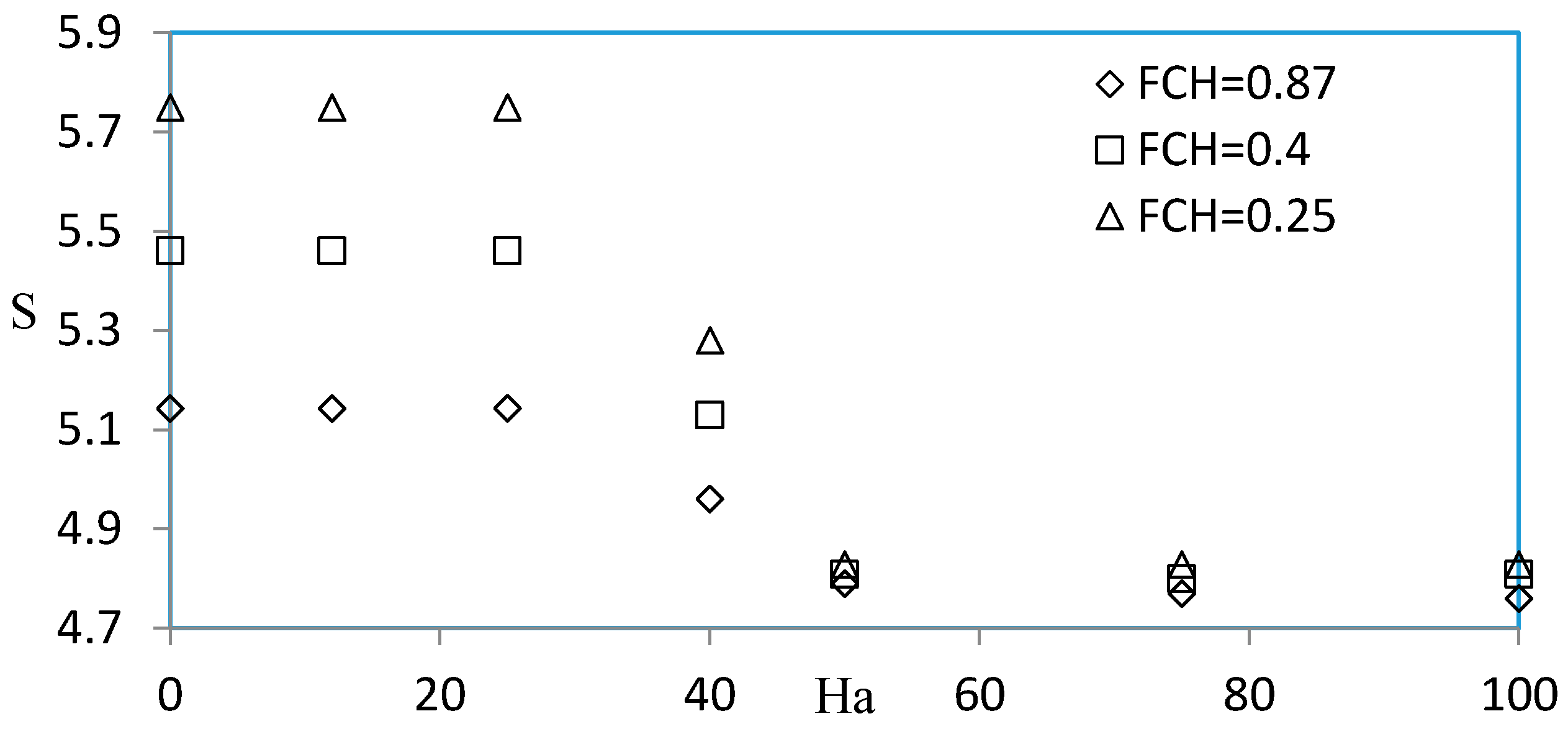
5. Results and Discussion

This section illustrates the influence of the Darcy number (Da), Hartmann number (Ha), Reynolds number (Re), Rayleigh number (Ra) and the Forchheimer parameter (Fε), on the irreversibility, heat transfer and flow structure of a Darcy–Brinkman–Forchheimer fluid flow (Pr = 7) in a lid-driven porous cavity. The dimensionless numbers listed above were ranging from 10⁻³ to 1, from 0 to 100, from 10 to 50, from 10⁴ to 10⁵ and from 0.25 to 0.87 respectively. The porosity (ɛ) of the media is fixed at 0.5. The modified Brinkman number is fixed at 5 × 10⁻⁷.

The streamlines, isotherms and isentropic lines at steady state are shown in Figure 2 for different Hartmann numbers (Ha = 0, 50 and 100). As can be seen in Figure 2a, the flow is characterized by the predominance of one cell at low (Ha). As Ha increases (Ha > 50), the flow structure changes and takes the shape of two cells. This change in the flow structure is accompanied by a decrease in the flow velocity, which is the result of the decelerator effect of the Lorentz force via the magnetic field. As seen in Figure 2b, isotherms are strongly deformed near the top wall at zero Hartmann number. This is due to the inertial force resulting from the driven wall. As (Ha) increases, the deformation of the isotherms gradually decreases and becomes practically absent in the right side of the cavity. As seen in Figure 2c, the upper half of the cavity is not engendered in entropy generation. Isentropic lines are tightened close to the hot wall, where the thermal gradients are important.

Figure 3 and Figure 4 show the effect of both (Da) and (Ha), on the average Nusselt number (Nu) and the total entropy generation (S) respectively. Results show that (Nu) and (S) decrease with the decrease of (Da). In fact, when decreasing (Da) from unity, the permeability of the porous medium decreases and therefore the convection reduces. This reduction leads to a decrease in the thermal and velocity gradients, which induces a decrease in both (Nu) and (S). At fixed (Da), Figure 3 and Figure 4 show a decrease of (Nu) and (S) when (Ha) increases. This is due to the retarding effect of the Lorentz force on the flow. The influence of the Reynolds number on the Nusselt number and the entropy generation is depicted in Figure 5 and Figure 6. At a fixed Hartman number, Figure 5 shows that (Nu) increases with the increase of (Re). This could be the result of an increase in the form drag related to the Forchheimer effect in the porous medium. Note that the increase of the Nusselt number and the entropy generation is less important as (Ha) is important. In this case, for important (Ha), the Lorentz force becomes significant enough to be able to reduce the form drag effect. Similar observations to those of Figure 4 can be conducted for Figure 6, related to the variation of the entropy generation versus the Reynolds number. It is important to notice that the irreversibility in the lid-driven cavity is principally caused by the heat transfer, since the chosen value of the modified Brinkman number is small.

Figure 7 illustrates the evolution of the total entropy generation with the Hartman number for Ra = 10⁴ and 10⁵. As shown in Figure 7, at a fixed Hartmann number, the entropy generation generally increases as the Rayleigh number increases. This is due to the improvement of the convection in the porous cavity which will, in turn, increase the thermal and the velocity gradients and consequently the entropy generation.

Figure 8 illustrates the Forchheimer parameter effect on the entropy generation when (Ha) progresses from 0 to 100. Since the modified Brickman number value is very small, there is virtually no intrinsic effect of (Ha) via the magnetic and the Darcy viscous irreversibility terms on the total entropy generation (Equation (10)). Consequently, the effect of (Ha) on the total entropy generation is principally extrinsic through the momentum balance equation. Figure 8 shows that for (Ha) ranging from 0 to 25, the total entropy generation takes a constant value depending on the Forchheimer parameter. When (Ha) increases from 25 to 50, the total entropy generation decreases and converges towards the same constant value close to 4.8 for all selected Forchheimer parameters. For (Ha) exceeding 50, no significant effect of the Forchheimer parameter is observed and the entropy generation remains almost constant. These observations show the existence of three flow regimes. The first is the Forchheimer regime which persists until a critical Hartmann number Ha_c = 25, for which the form drag linked to the non-linear velocity term is important. The second is similar to the Darcy regime for (Ha) greater than 50. In this case, the fluid undergoes a deceleration due to the dominant effect of the Lorentz force and consequently the form drag becomes insignificant. The third regime, for (Ha) between 25 and 50, is transitional from the first where the form drag is dominant to the second where the Lorentz force is dominant.

6. Conclusions

Entropy generation and heat transfer in MHD mixed convection in a porous lid-driven cavity submitted to a vertical temperature gradient were studied. The Navier–Stokes and energy equations written in the Darcy–Brinkman–Forchheimer formulation were solved by using CVFEM numerical code. The effect of the Darcy, Rayleigh, Reynolds, Hartmann numbers and the Forchheimer parameter on heat transfer and entropy generation were investigated. Main conclusions are:

(1)

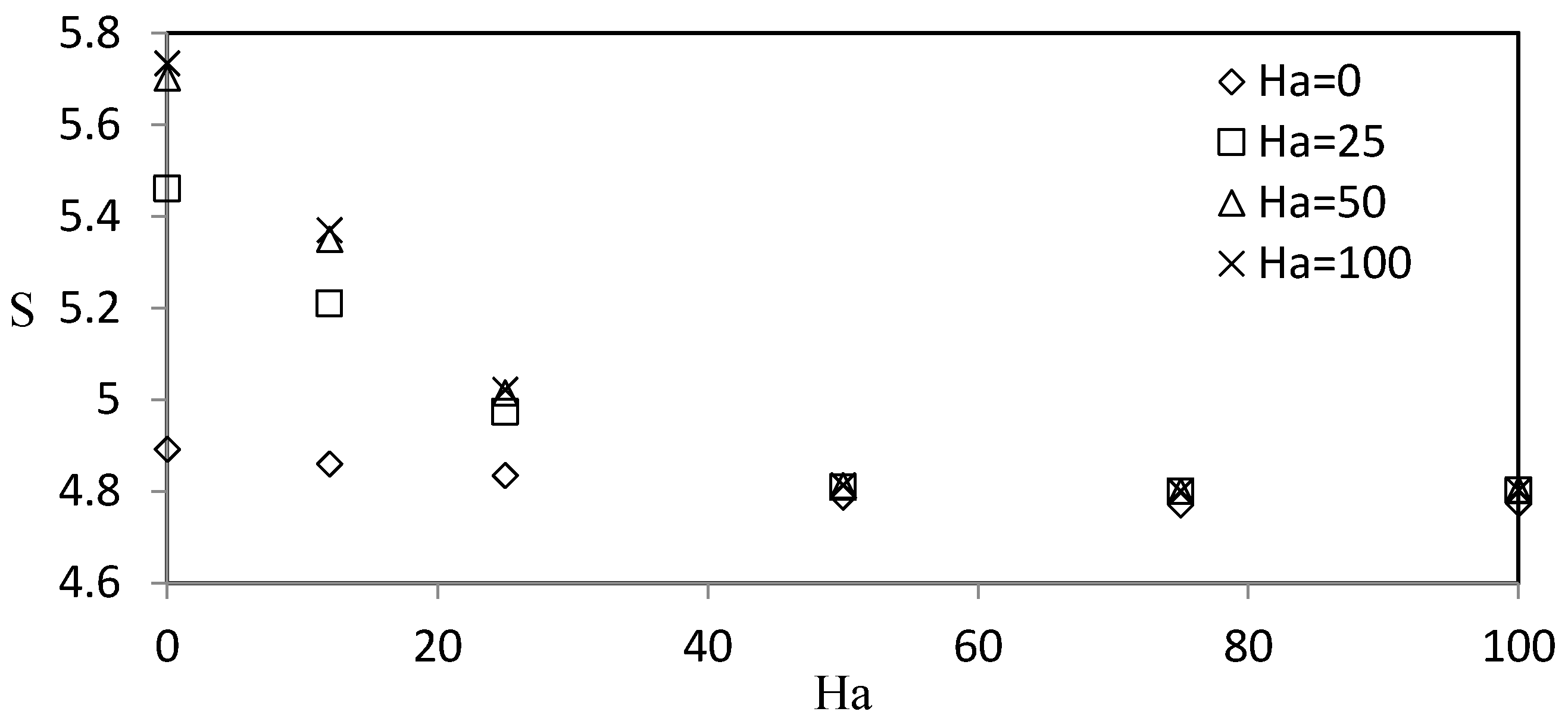
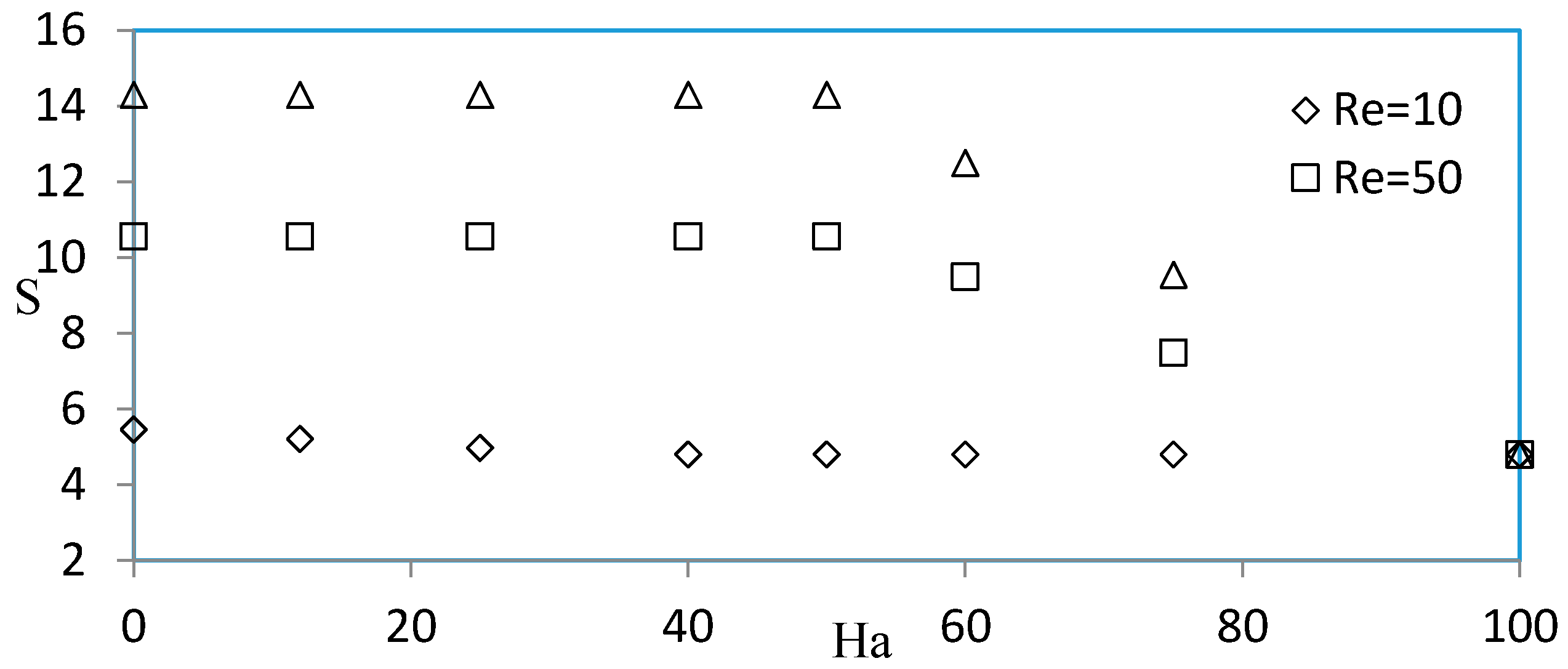
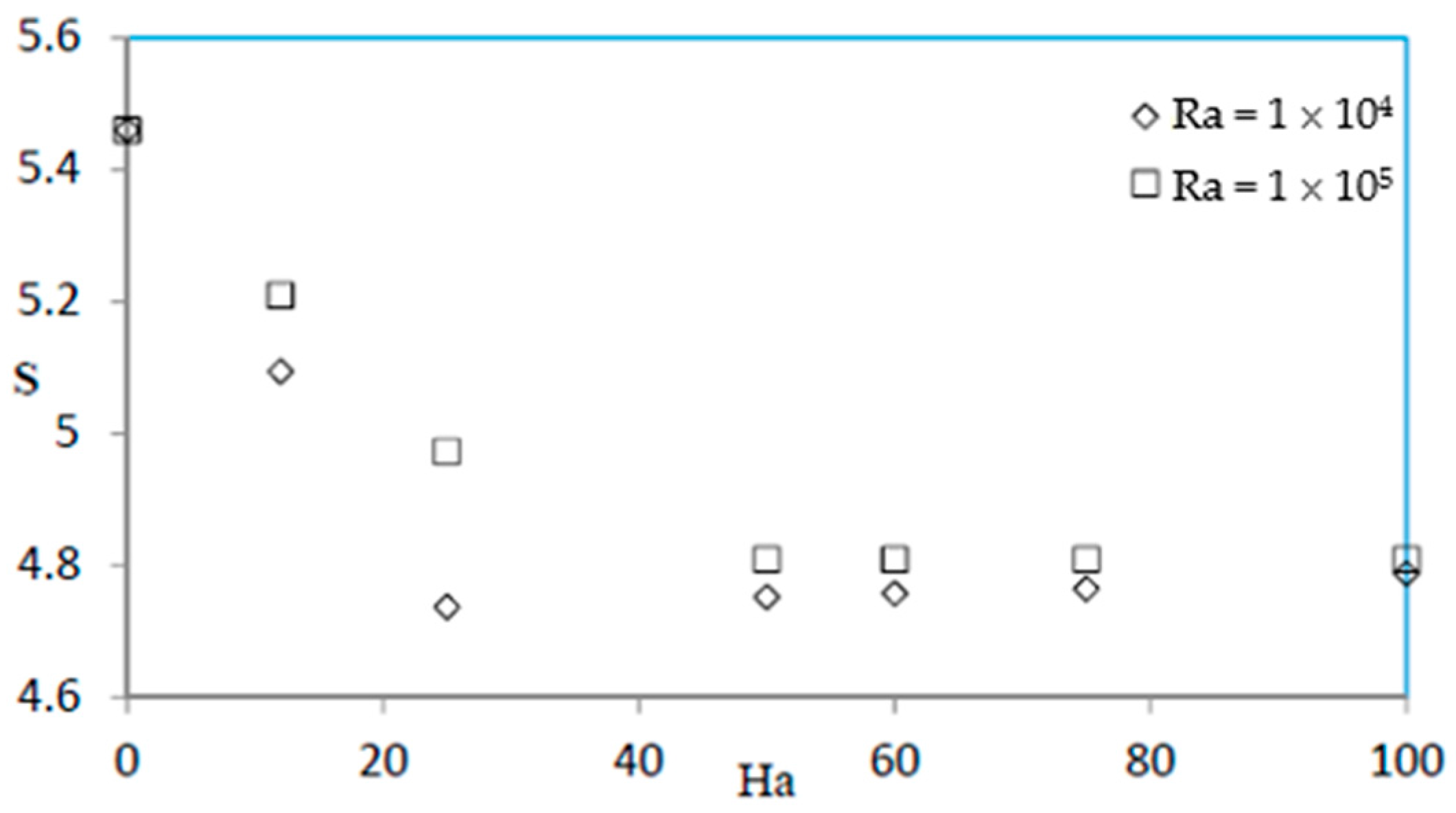
The entropy generation rate decreases with the decrease of Darcy number and the increase of Hartmann number.

(2)

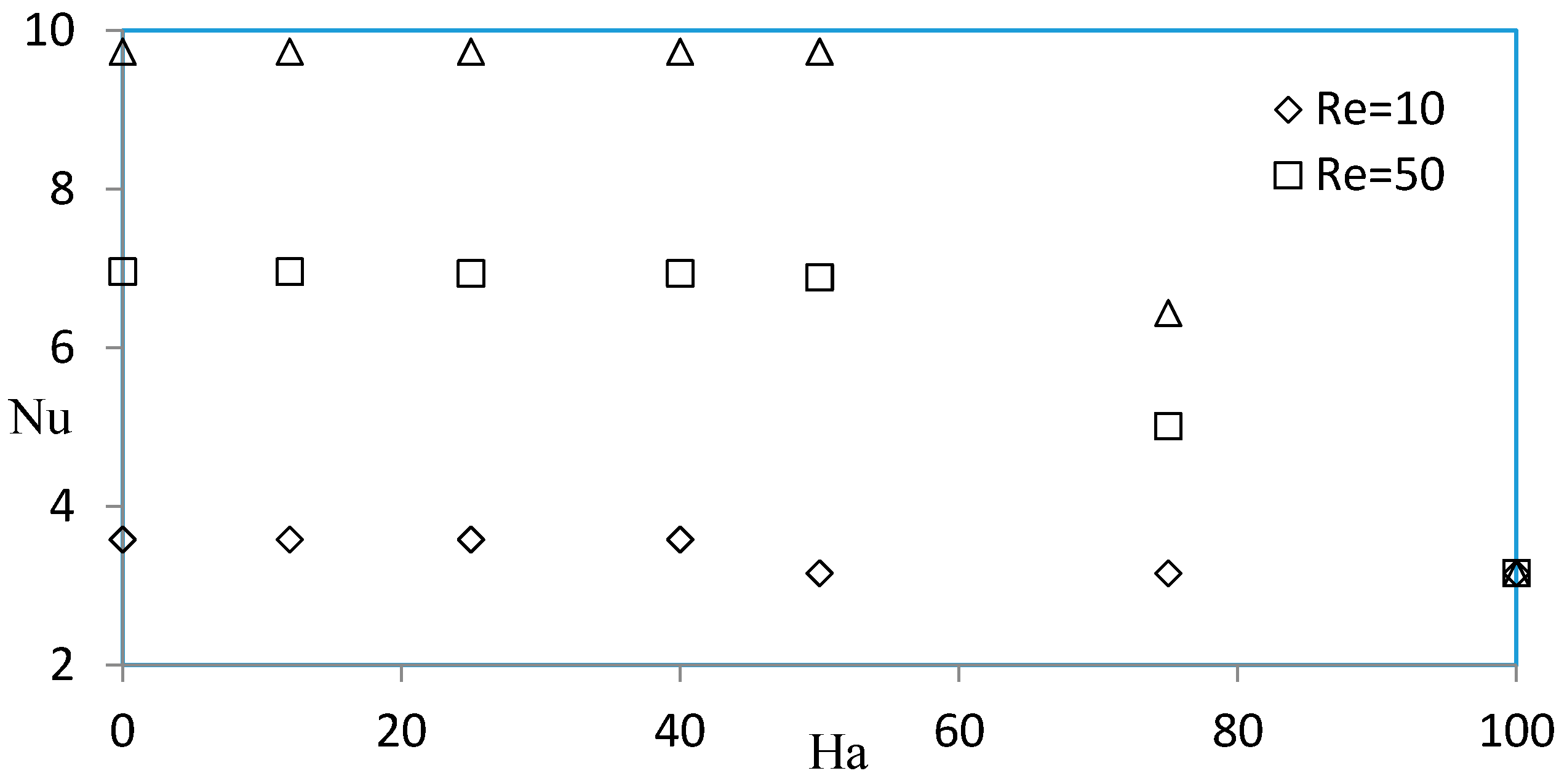
The flow structure strongly depends on the Hartmann number.

(3)

At a fixed Hartmann number, the entropy generation increases with the increase of the Reynolds number.

(4)

At a fixed and relatively high Reynolds number, the entropy generation remains constant for a Hartmann number smaller than 50.

(5)

The Forchheimer effect is significant for a Hartmann number between 0 and 25 and negligible for a Hartmann number greater than 50.