Recognition of Abnormal Uptake through 123I-mIBG Scintigraphy Entropy for Paediatric Neuroblastoma Identification
Abstract
:1. Introduction
2. Related Work
3. Materials and Methods
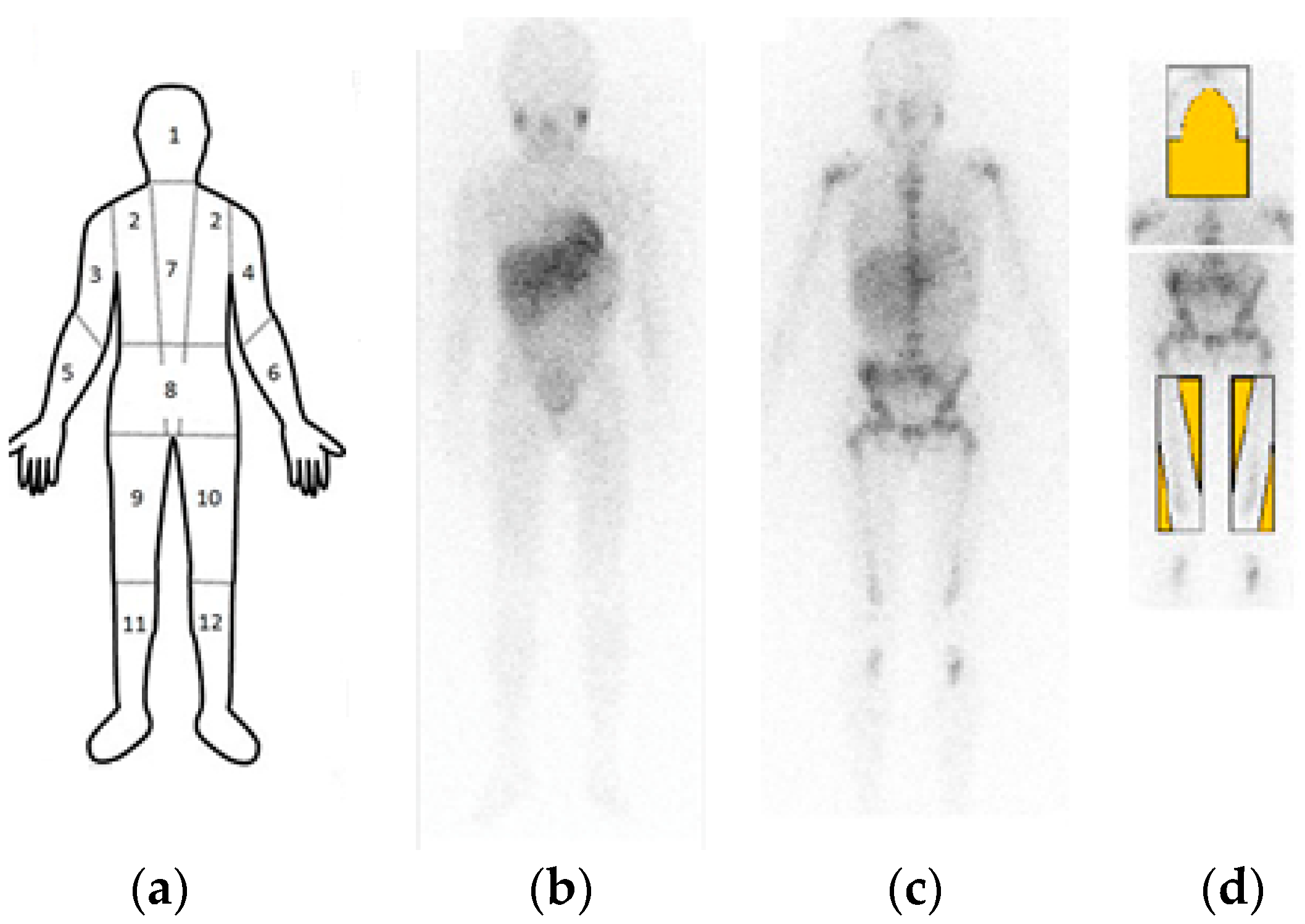
3.1. Data Acquisition and Analysis
3.2. Pre-Processing
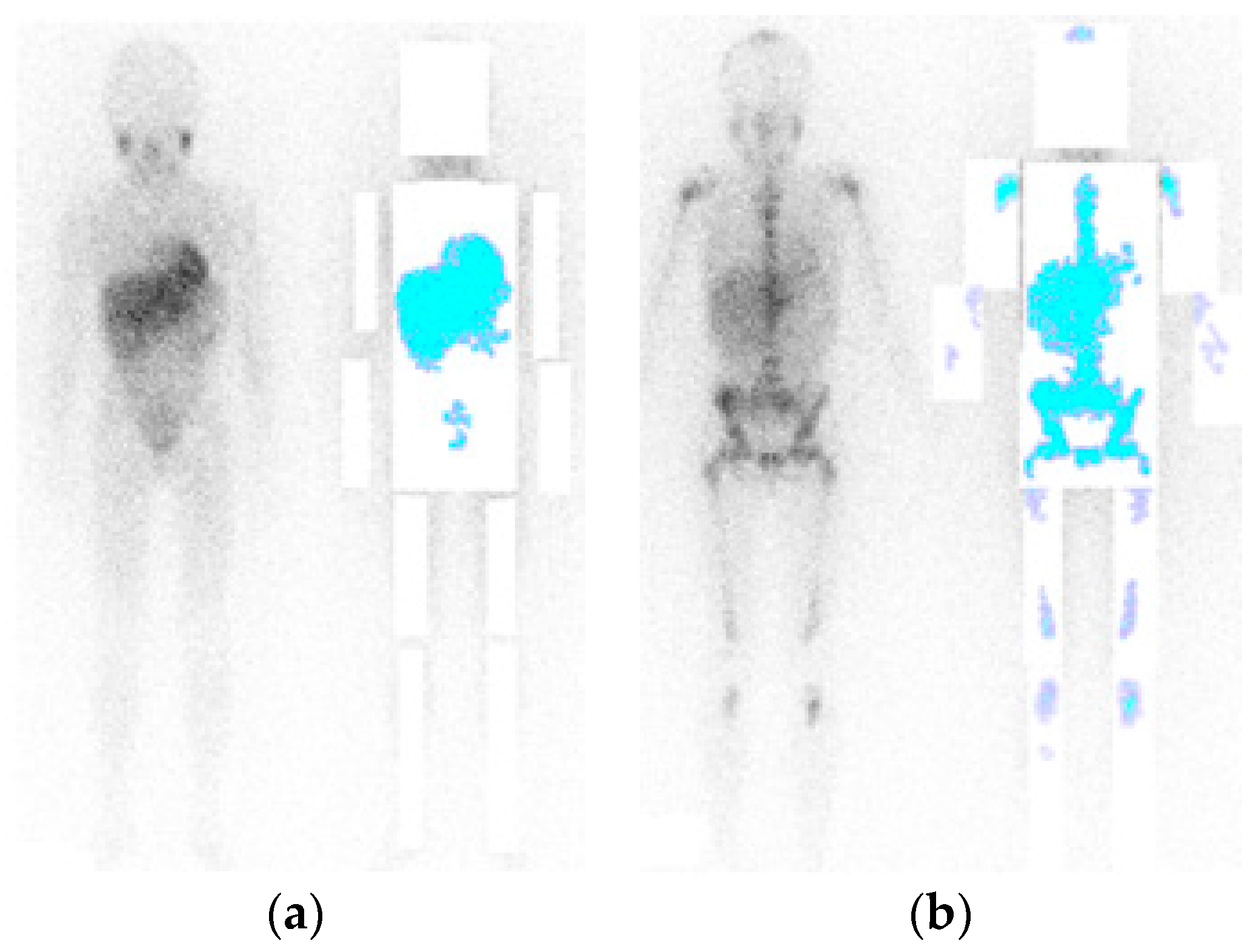
3.3. Peaks Detection
3.4. Region Growth and Classification
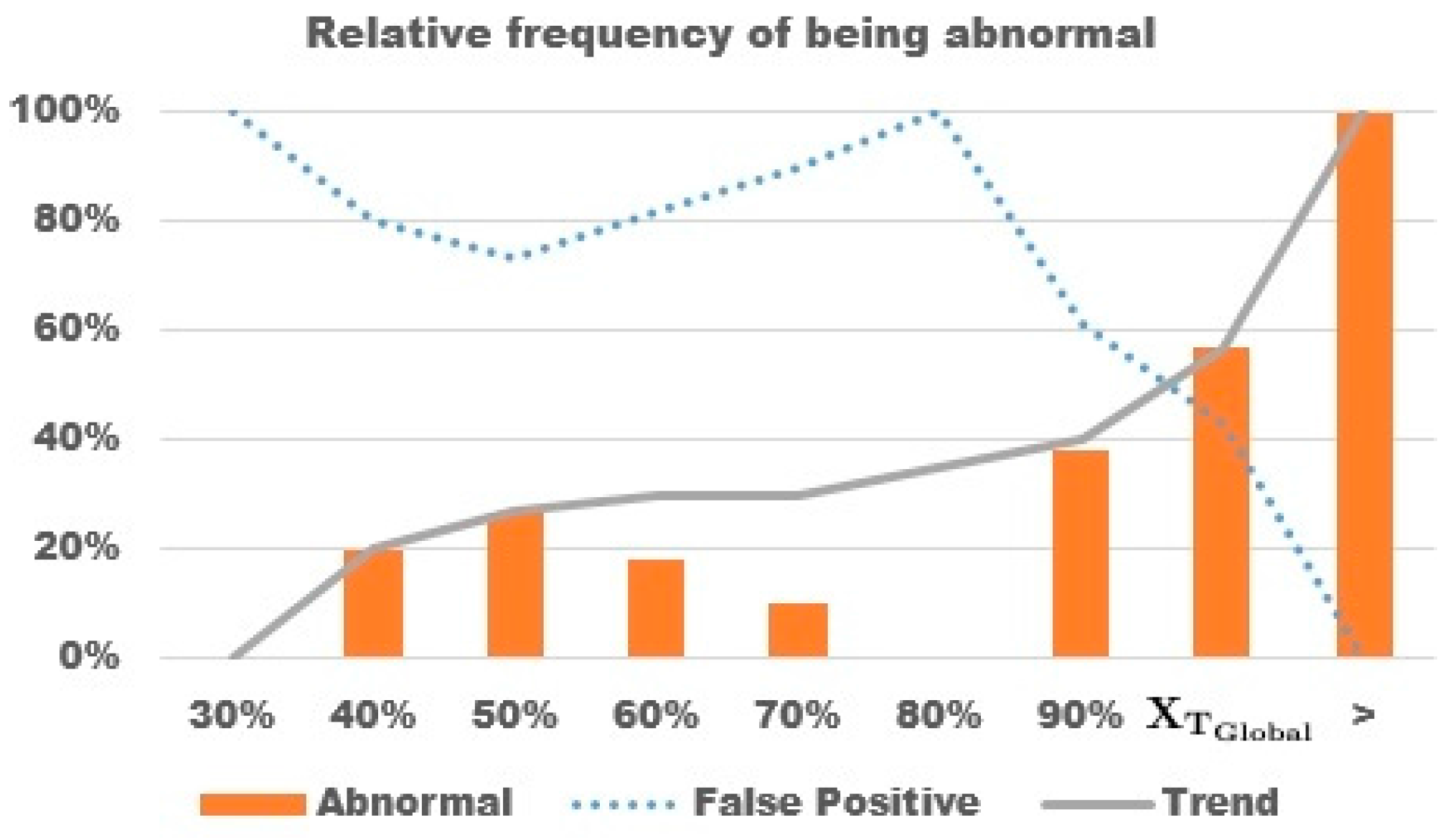
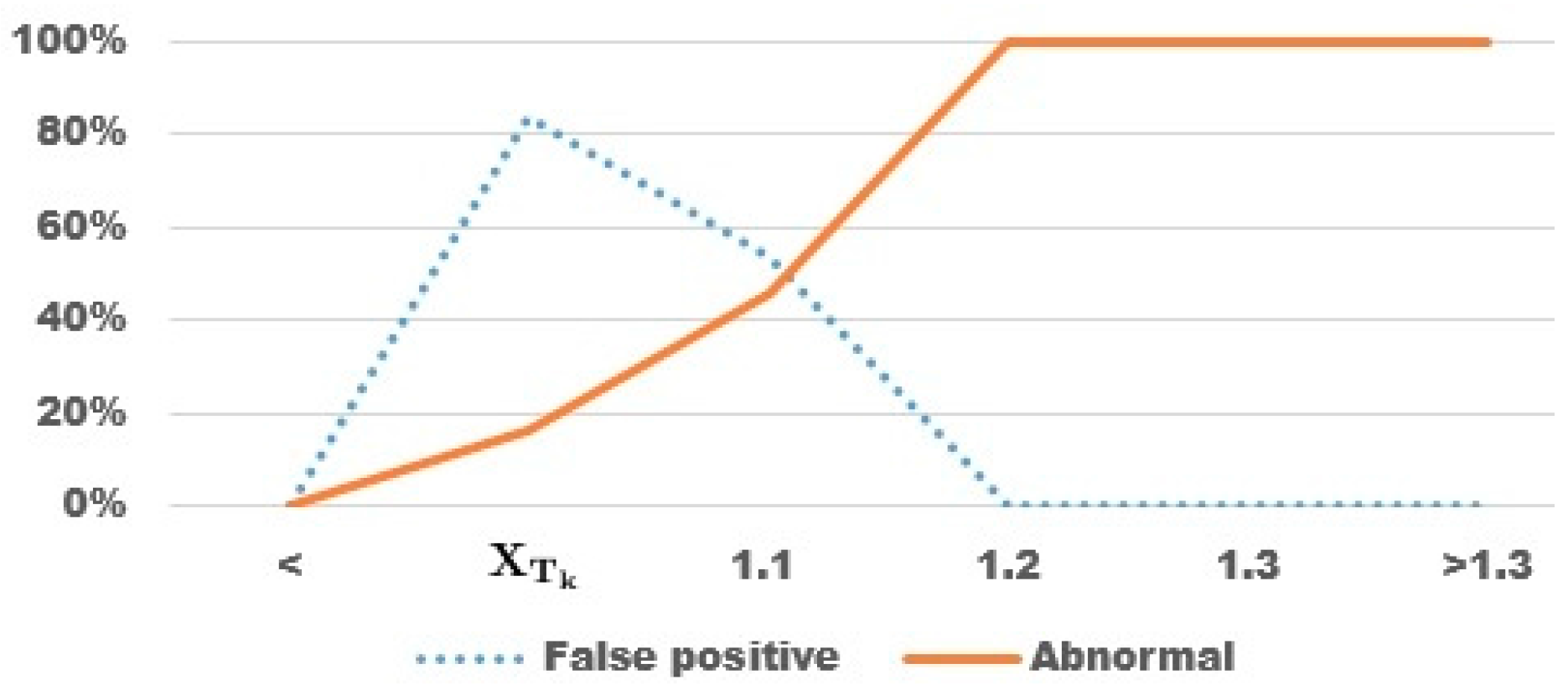
4. Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Charron, M. Contemporary approach to diagnosis and treatment of neuroblastoma. Q. J. Nucl. Med. Mol. Imaging 2013, 57, 40–52. [Google Scholar] [PubMed]
- Olivier, P.; Colarinha, P.; Fettich, J.; Fischer, S.; Frokier, J.; Giammarile, F.; Gordon, I.; Hahn, K.; Kabasakal, L.; Mann, M.; et al. Guidelines for radioiodinated mIBG scintigraphy in children. Eur. J. Nucl. Med. Mol. Imaging 2003, 30, B45–B50. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.S. The Adaptive Wiener Filter. In Two-Dimensional Signal and Image Processing, 1st ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1990; pp. 536–540. [Google Scholar]
- Krom, A.; Wickham, F.; Hall, M. Evaluation of image enhancement software as a method of performing half-count bone scans. Nucl. Med. Commun. 2013, 34, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Hannequin, P.; Mas, J. Statistical and heuristic image noise extraction (SHINE): A new method for processing Poisson noise in scintigraphic images. Phys. Med. Biol. 2002, 47, 4329–4344. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Díaz, R.; Balaguer, J.; Sánchez-Ruiz, L.; Bello, P.; Castel, V.; Perís-Fajarnés, G. On analytical methods in neuroblastoma detection. Abstr. Appl. Anal. 2013, 2013, 341346. [Google Scholar] [CrossRef]
- Martínez-Díaz, R.; Balaguer, J.; Sánchez Ruiz, L.; Bello, P.; Castel, V.; Rivas, A.; Cañete, A.; Falgas, M.; Luis Loaiza, J.; Perís-Fajarnés, G. Quantitative approach to assist neuroblastoma assesment by measuring I-123 mIBG uptake in scintigraphic images. Image Anal. Stereol. 2015, 34, 135–144. [Google Scholar]
- Hasegawa, B.; Tang, H.; Da Silva, A.J.; Wong, K.; Iwata, K.; Wu, M. Dual-modality imaging. Nucl. Instrum. Methods Phys. Res. 2001, 471, 140–144. [Google Scholar] [CrossRef]
- Brisse, H.; McCarville, M.; Granata, C.; Krug, K.; Wootton-Gorges, S.; Kanegawa, K.; Giammarile, F.; Schmidt, M.; Shulkin, B.; Matthay, K.; et al. Guidelines for imaging and staging of neuroblastic tumors: Consensus report from the international neuroblastoma risk group project. Radiology 2011, 261, 243–257. [Google Scholar] [CrossRef] [PubMed]
- Rufini, V.; Giordano, A.; Di Giuda, D.; Petrone, A.; Deb, G.; De Sio, L.; Donfrancesco, A.; Troncone, L. 123I-mIBG scintigraphy in neuroblastoma: A comparison between planar and SPECT imaging. Q. J. Nucl. Med. 1995, 39, 25–28. [Google Scholar] [PubMed]
- Gelfand, M.; Elgazzar, A.; Kriss, V.; Masters, P.; Golsch, G. Iodine-123-mIBG SPECT versus planar imaging in children with neural crest tumors. J. Nucl. Med. 1994, 35, 1753–1757. [Google Scholar] [PubMed]
- Keidar, Z.; Israel, O.; Krausz, Y. SPECT/CT in tumor imaging: Technical aspects and clinical applications. Semin. Nucl. Med. 2003, 33, 205–218. [Google Scholar] [CrossRef] [PubMed]
- Matthay, K.; Shulkin, B.; Ladenstein, R.; Michon, J.; Giammarile, F.; Lewington, V.; Pearson, A.; Cohn, S. Criteria for evaluation of disease extent by 123I-metaiodobenzylguanidine scans in neuroblastoma: A report for the International Neuroblastoma Risk Group (INRG) Task Force. Br. J. Cancer 2010, 102, 1319–1326. [Google Scholar] [CrossRef] [PubMed]
- Ady, N.; Zucker, J.; Asselain, B.; Edeline, V.; Bonnin, F.; Michon, J.; Gongora, R.; Manil, L. A new 123I-mIBG whole body scan scoring method—Application to the prediction of the response of metastases to induction chemotherapy in stage IV neuroblastoma. Eur. J. Cancer 1995, 31, 256–261. [Google Scholar] [CrossRef]
- Suc, A.; Lumbroso, J.; Rubie, H.; Hattchouel, J.; Boneu, A.; Rodary, C.; Robert, A.; Hartmann, O. Metastatic neuroblastoma in children older than one year: Prognostic significance of the initial metaiodobenzylguanidine scan and proposal for a scoring system. Cancer 1996, 77, 805–811. [Google Scholar] [CrossRef]
- Perel, Y.; Conway, J.; Kletzel, M.; Goldman, J.; Weiss, S.; Feyler, A.; Cohn, S. Clinical impact and prognostic value of metaiodobenzylguanidine imaging in children with metastatic neuroblastoma. J. Pediatr. Hematol. Oncol. 1999, 21, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Matthay, K.; Edeline, V.; Lumbroso, J.; Tanguy, M.; Asselain, B.; Zucker, J.; Valteau-Couanet, D.; Hartmann, O.; Michon, J. Correlation of early metastatic response by 123I-metaiodobenzylguanidine scintigraphy with overall response and event-free survival in stage IV neuroblastoma. J. Clin. Oncol. 2003, 21, 2486–2491. [Google Scholar] [CrossRef] [PubMed]
- Katzenstein, H.; Cohn, S.; Shore, R.; Bardo, D.; Haut, P.; Olszewski, M.; Schmoldt, J.; Liu, D.; Rademaker, A.; Kletzel, M. Scintigraphic response by 123I-metaiodobenzylguanidine scan correlates with event-free survival in high-risk neuroblastoma. J. Clin. Oncol. 2004, 22, 3909–3915. [Google Scholar] [CrossRef] [PubMed]
- Messina, J.; Cheng, S.; Franc, B.; Charron, M.; Shulkin, B.; To, B.; Maris, J.; Yanik, G.; Hawkins, R.; Matthay, K. Evaluation of semiquantitative scoring system for metaiodobenzylguanidine (mIBG) scans in patients with relapsed neuroblastoma. Pediatr. Blood Cancer 2006, 47, 865–874. [Google Scholar] [CrossRef] [PubMed]
- Yanik, G.; Parisi, M.; Shulking, B.; Naranjo, A.; Kreissman, S.; London, W.; Villablanca, J.; Maris, J.; Park, J.; Cohn, S.; et al. Semiquantitative mIBG scoring as a prognostic indicator in patients with stage 4 neuroblastoma: A report from the children’s oncology group. J. Nucl. Med. 2013, 54, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Decarolis, B.; Scheneider, C.; Hero, B.; Simon, T.; Volland, R.; Roels, F.; Dietlein, M.; Berthold, F.; Schmidt, M. Iodine-123 metaiodobenzylguanidine scintigraphy scoring allows prediction of outcome in patients with stage 4 neuroblastoma: Results of the cologne interscore comparison study. J. Clin. Oncol. 2013, 31, 944–951. [Google Scholar] [CrossRef] [PubMed]
- Lewington, V.; Sever, Z.; Lynch, T.; Giammarile, F.; McEwan, A.; Shulkin, B.; Staudenherz, A.; Ladenstein, R. Development of a new, semiquantitative I-123 mIBG reporting method in high risk neuroblastoma. Eur. J. Nucl. Med. Mol. Imaging 2009, 50, 1379–1379. [Google Scholar]
- Lewington, V.; Poetschger, U.; Boubaker, A.; Bar-Sever, Z.; Drake, B.; Staudenherz, A.; Castellani, M.R.; Lambert, B.; Grange, K.; Brock, P.; et al. The prognostic value of semi-quantitative 123I-mIBG scintigraphy at diagnosis in high-risk neuroblastoma: Validation of the SIOPEN score method. J. Clin. Oncol. 2011, 29, 9511. [Google Scholar]
- Yin, T.; Chiu, N. A computer-aided diagnosis for locating abnormalities in bone scintigraphy by a fuzzy system with a three-step minimization approach. IEEE Trans. Med. Imaging 2004, 23, 639–654. [Google Scholar] [CrossRef]
- Jia-Yann, H.; Pan-Fu, K.; Yung-Sheng, C. A set of image processing algorithms for computer-aided diagnosis in nuclear medicine whole body bone scan images. IEEE Trans. Nucl. Sci. 2007, 54, 514–522. [Google Scholar]
- Sajn, L.; Kononenko, I.; Milcinski, M. Computerized segmentation and diagnostics of whole-body bone scintigrams. Comput. Med. Imaging Graph. 2007, 31, 531–541. [Google Scholar] [CrossRef] [PubMed]
- Sajn, L.; Kukar, M.; Kononenko, I.; Milcinski, M. Computerized segmentation of whole-body bone scintigrams and its use in automated diagnostics. Comput. Meth. Programs Biomed. 2005, 80, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Jeong, C.; Kim, K.; Kim, T.; Kim, S. Comparison of image enhancement methods for the effective diagnosis in successive whole-body bone scans. J. Digit. Imaging 2011, 24, 424–436. [Google Scholar] [CrossRef] [PubMed]
- Wesolowski, C.; Yahil, A.; Puetter, R.; Babyn, P.; Gilday, D.; Khan, M. Improved lesion detection from spatially adaptive, minimally complex, Pixon reconstruction of planar scintigraphic images. Comput. Med. Imaging Graph. 2005, 29, 65–81. [Google Scholar] [CrossRef] [PubMed]
- Bombardieri, E.; Giammarile, F.; Aktolun, C.; Baum, R.; Delaloye, A.; Maoli, L.; Moncayo, R.; Mortelmans, L.; Pepe, G.; Reske, S.; et al. 131I/123I-metaiodobenzylguanidine (mIBG) scintigraphy procedures guidelines for tumour imaging. Eur. J. Nucl. Med. Mol. Imaging 2010, 37, 2436–2446. [Google Scholar] [CrossRef] [PubMed]
- King, M.; Doherty, P.; Schwinger, R.; Penney, B. A Wiener Filter for nuclear medicine images. Med. Phys. 1983, 10, 876–880. [Google Scholar] [CrossRef] [PubMed]
- King, M.; Schwinger, R.; Doherty, P.; Penney, B. Two-dimensional filtering of SPECT images using the Metz and Wiener filters. J. Nucl. Med. 1984, 25, 1234–1240. [Google Scholar]
- Vieira, M.; Bakic, P.; Maidment, A.; Schiabel, H.; Mascarenhas, N. Filtering of poisson noise in digital mammography using local statistics and adaptive wiener filter. In Breast Imaging; Maidment, A.D.A., Bakic, P.R., Gavenonis, S., Eds.; Springer Berlin Heidelberg: Philadelphia, PA, USA, 2012; pp. 268–275. [Google Scholar]
| %False Positive | %False Negative | |
|---|---|---|
| I1 | 0.0% | 25.0% |
| IT | 4.2% | 0.0% |
| I3 | 0.0% | 50.0% |
| I4 | 0.0% | 36.4% |
| I5 | 0.0% | 100.0% |
| I6 | 0.0% | 75.0% |
| I9 | 0.0% | 54.6% |
| I10 | 0.0% | 58.3% |
| I11 | 0.0% | 83.3% |
| I12 | 0.0% | 83.3% |
| Totals: | 2.8% | 29.6% |
| Results with global threshold | ||
| %False Positive | %False Negative | |
|---|---|---|
| I1 | 11.1% | 0.0% |
| IT | 4.2% | 0.0% |
| I3 | 10.0% | 0.0% |
| I4 | 21.4% | 0.0% |
| I5 | 62.5% | 0.0% |
| I6 | 63.6% | 0.0% |
| I9 | 0.0% | 18.2% |
| I10 | 9.1% | 16.7% |
| I11 | 14.3% | 0.0% |
| I12 | 0.0% | 14.3% |
| Totals: | 16.0% | 3.3% |
| Results with local threshold | ||
| do | |
| if () then else if () then else end if end if | |
| Done | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Díaz, M.; Martínez-Díaz, R.; Sánchez-Ruiz, L.M.; Peris-Fajarnés, G. Recognition of Abnormal Uptake through 123I-mIBG Scintigraphy Entropy for Paediatric Neuroblastoma Identification. Entropy 2016, 18, 349. https://doi.org/10.3390/e18100349
Martínez-Díaz M, Martínez-Díaz R, Sánchez-Ruiz LM, Peris-Fajarnés G. Recognition of Abnormal Uptake through 123I-mIBG Scintigraphy Entropy for Paediatric Neuroblastoma Identification. Entropy. 2016; 18(10):349. https://doi.org/10.3390/e18100349
Chicago/Turabian StyleMartínez-Díaz, Milagros, Rafael Martínez-Díaz, Luis M. Sánchez-Ruiz, and Guillermo Peris-Fajarnés. 2016. "Recognition of Abnormal Uptake through 123I-mIBG Scintigraphy Entropy for Paediatric Neuroblastoma Identification" Entropy 18, no. 10: 349. https://doi.org/10.3390/e18100349
APA StyleMartínez-Díaz, M., Martínez-Díaz, R., Sánchez-Ruiz, L. M., & Peris-Fajarnés, G. (2016). Recognition of Abnormal Uptake through 123I-mIBG Scintigraphy Entropy for Paediatric Neuroblastoma Identification. Entropy, 18(10), 349. https://doi.org/10.3390/e18100349








