Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Wavelet Time-Frequency Entropy and One-Class Support Vector Machine
Abstract
:1. Introduction
2. S-Transform
3. Feature Extraction from STMM Based on Wavelet Time-Frequency Entropy
3.1. Wavelet Time-Frequency Entropy
3.2. Feature Vector Extraction
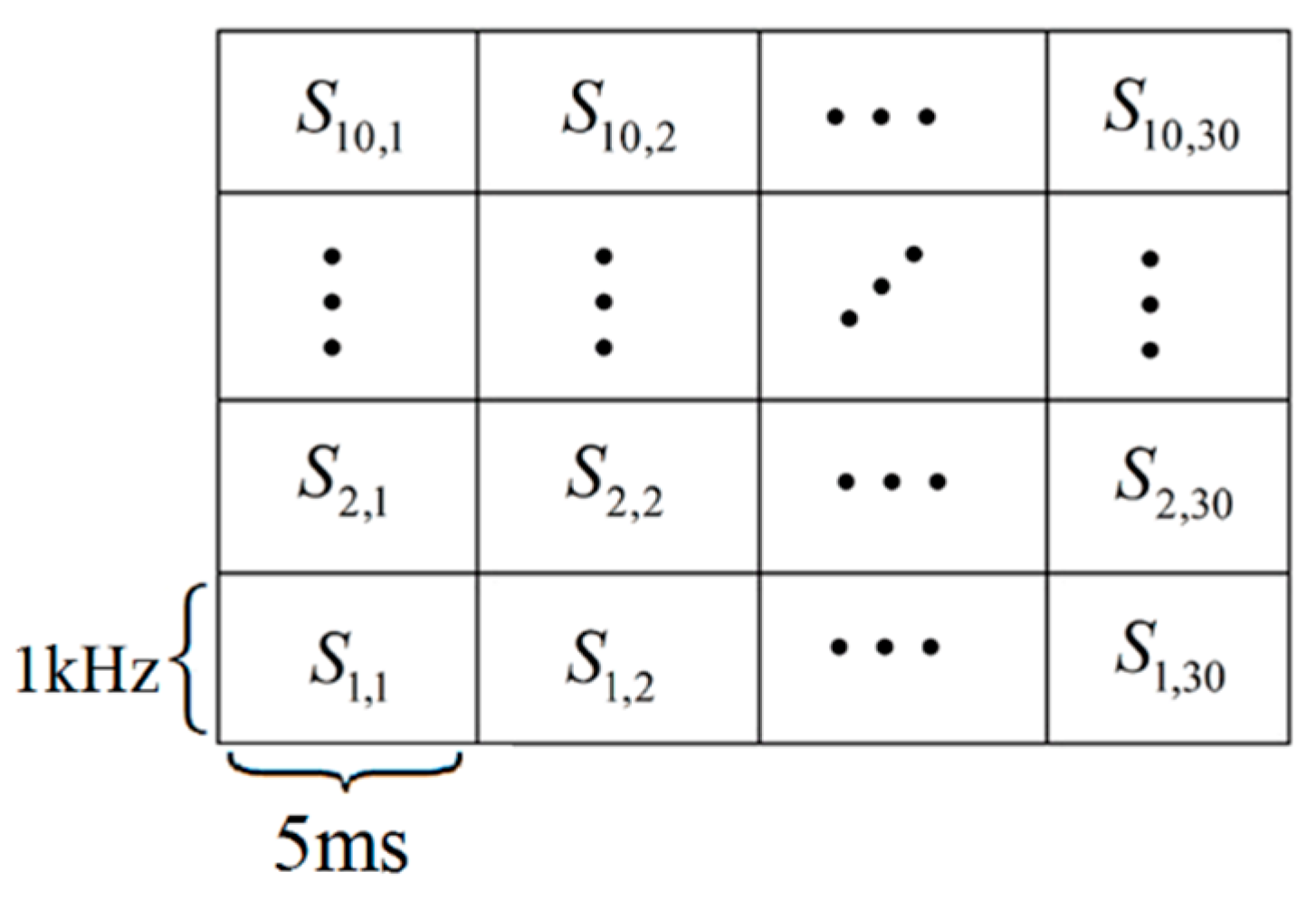
4. Condition and Fault Classifier Based on OCSVM and SVM
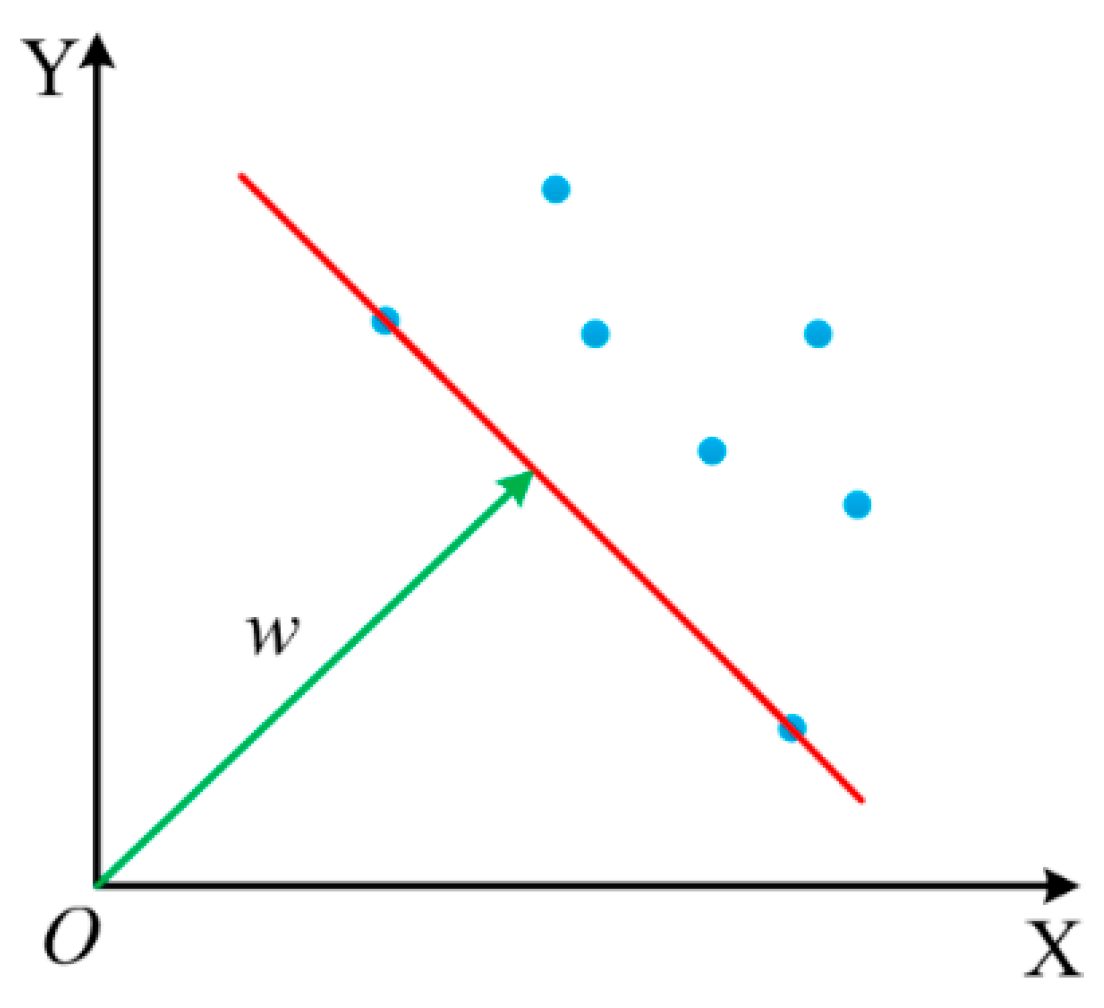
4.1. One-Class Support Vector Machine
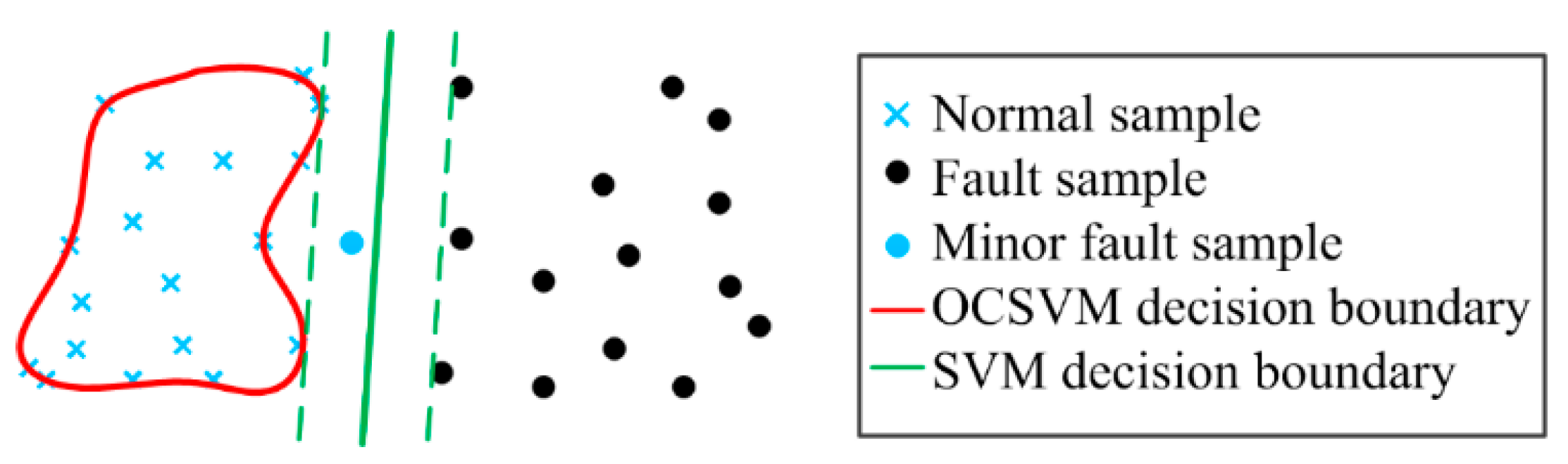
4.2. Advantages of OCSVM for Condition Diagnosis
4.3. An Improved PSO-Based OCSVM
- (1)
- Adjustment of the inertia weight
- (2)
- Adjustment of the acceleration coefficients and
4.4. Fault Diagnostic Process
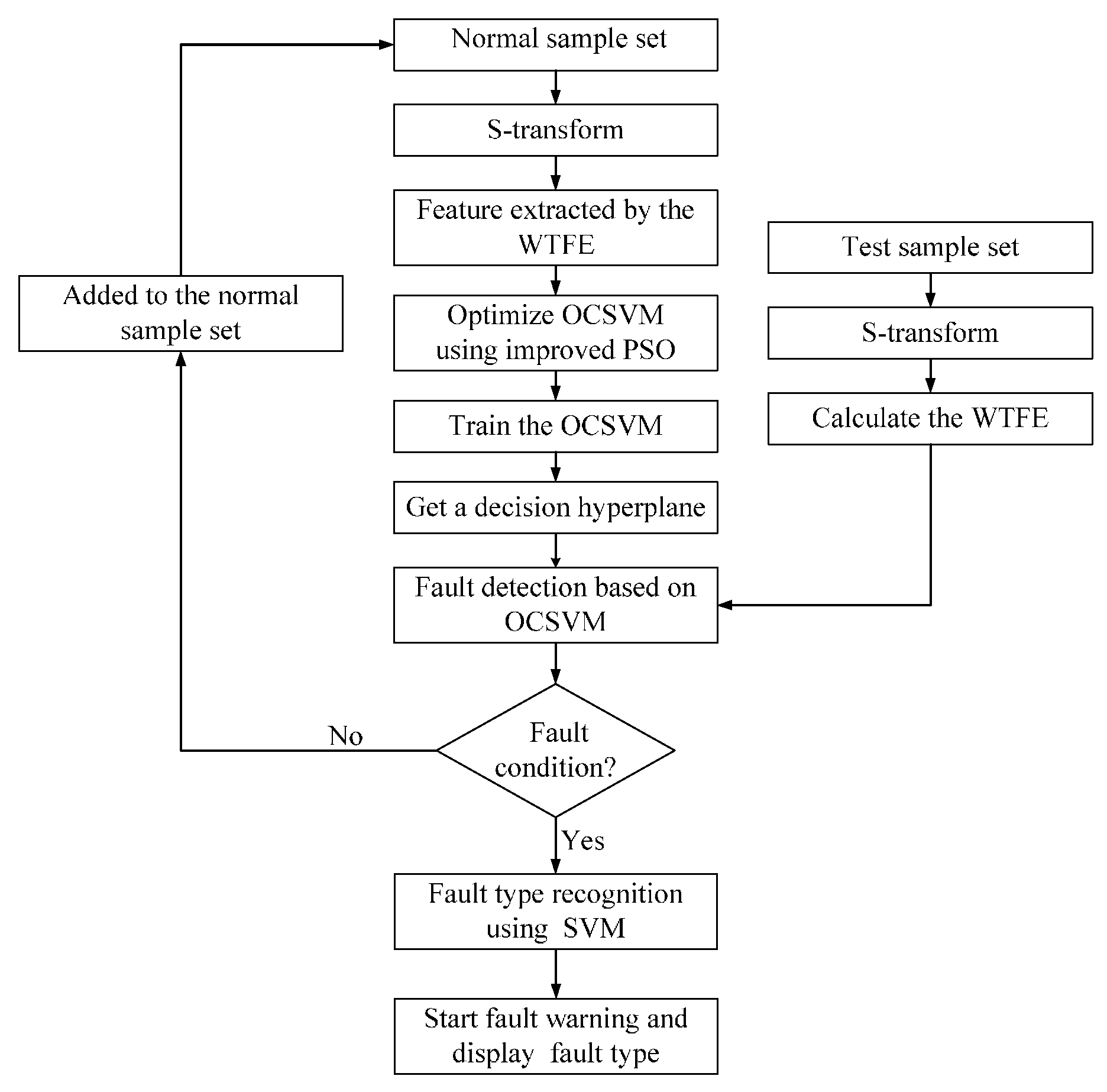
5. Experimental Results and Analysis
5.1. Data Collection and Processing
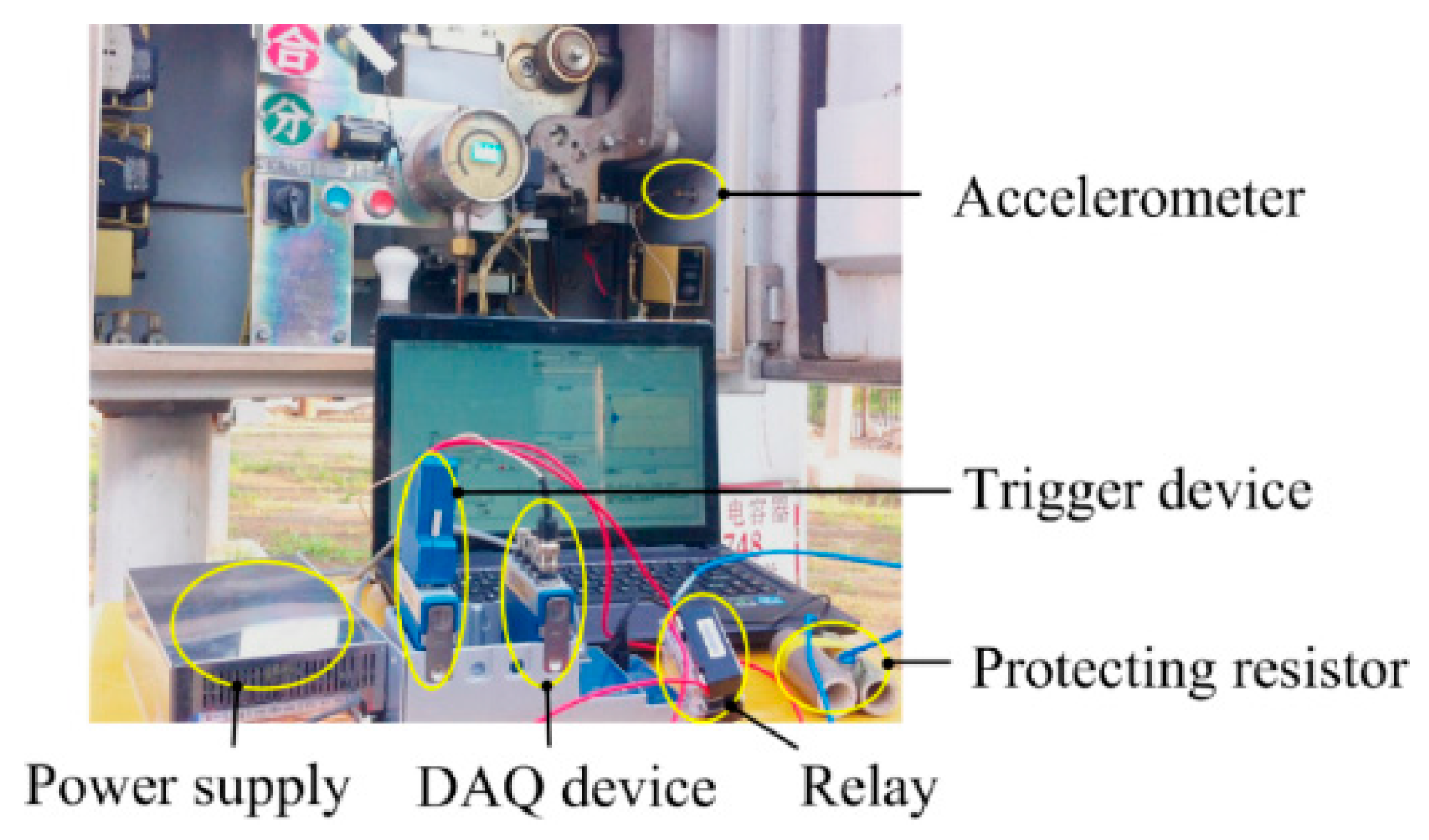

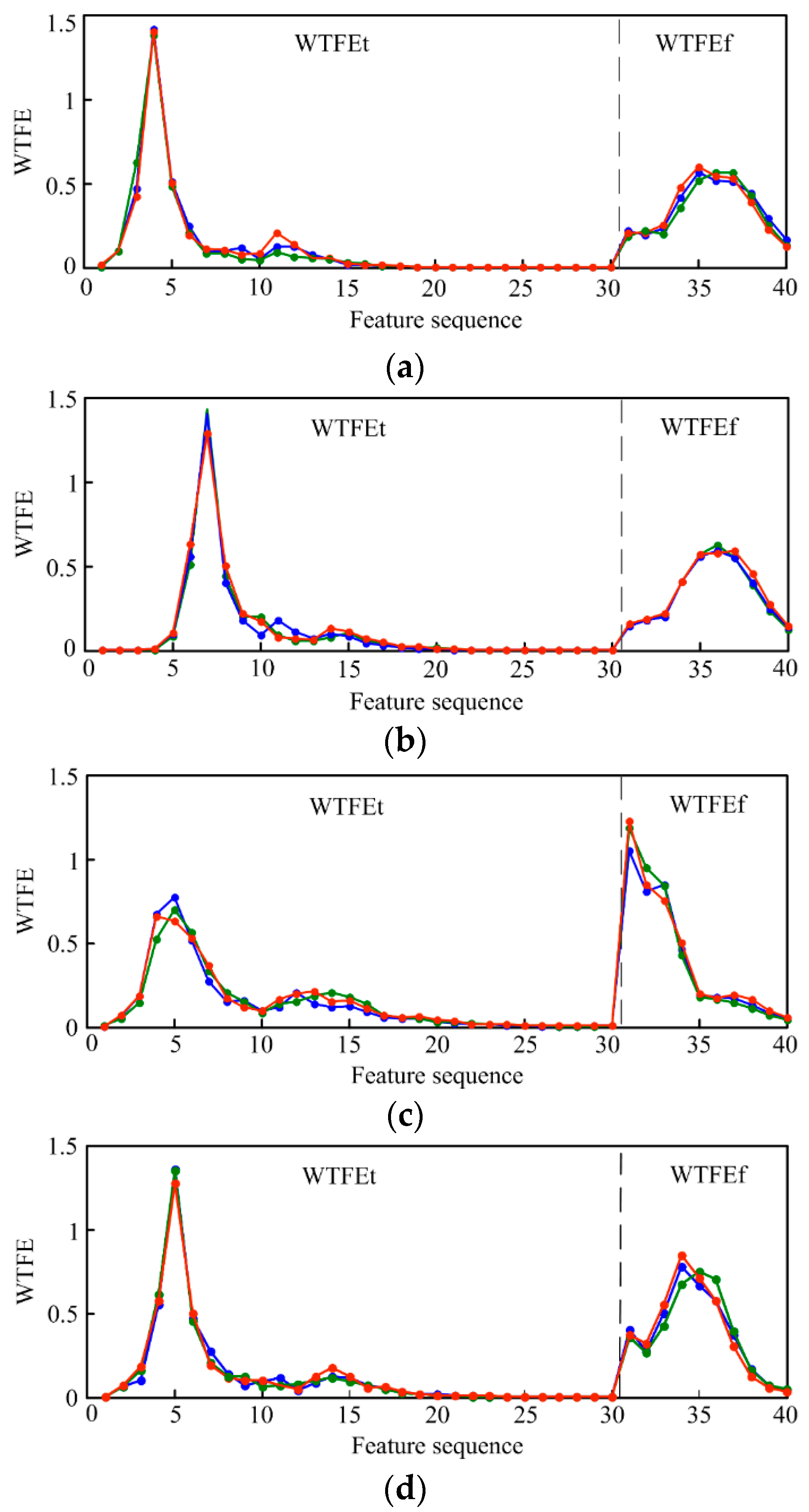
5.2. Feature Extraction and Analysis
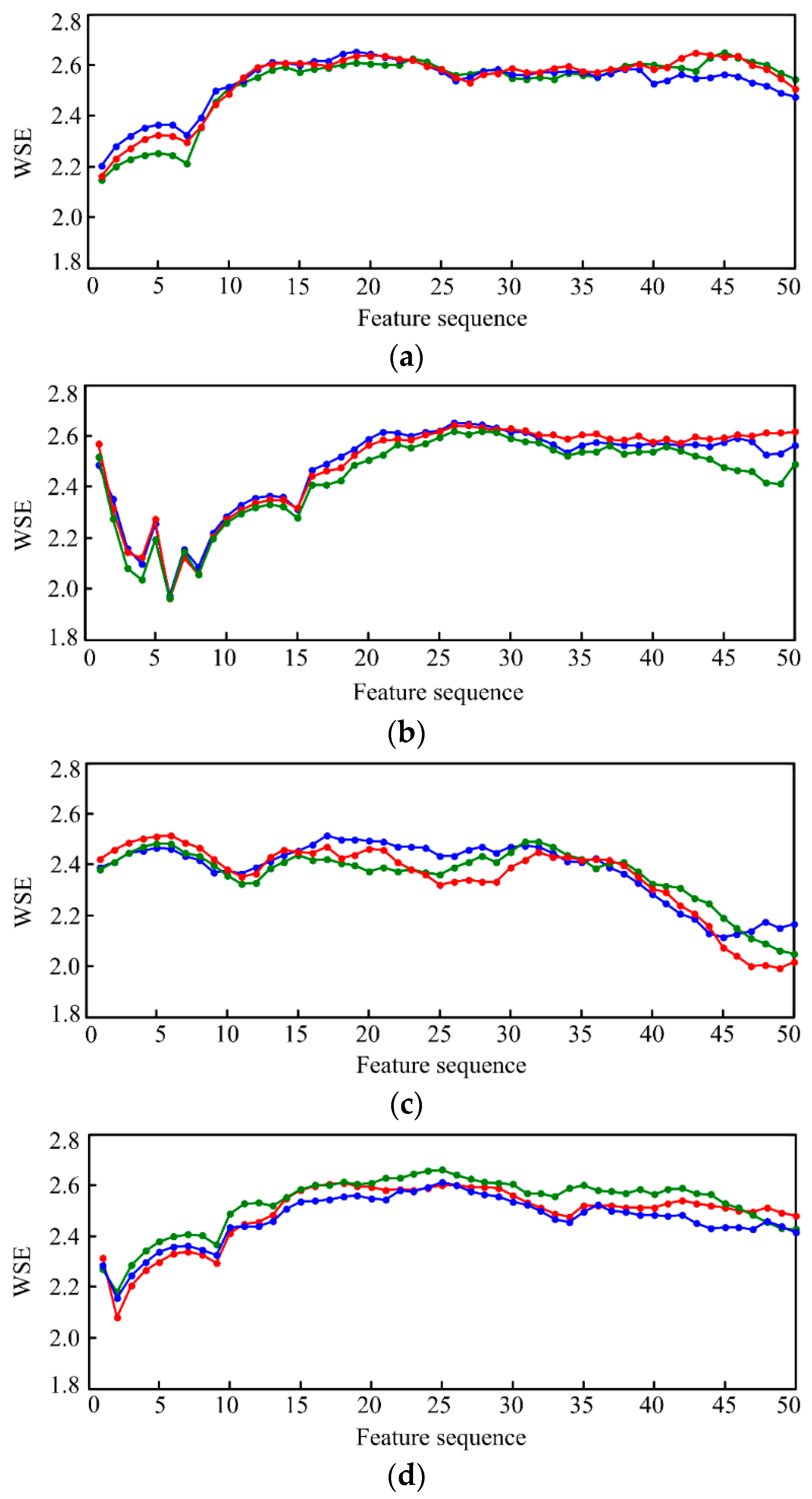
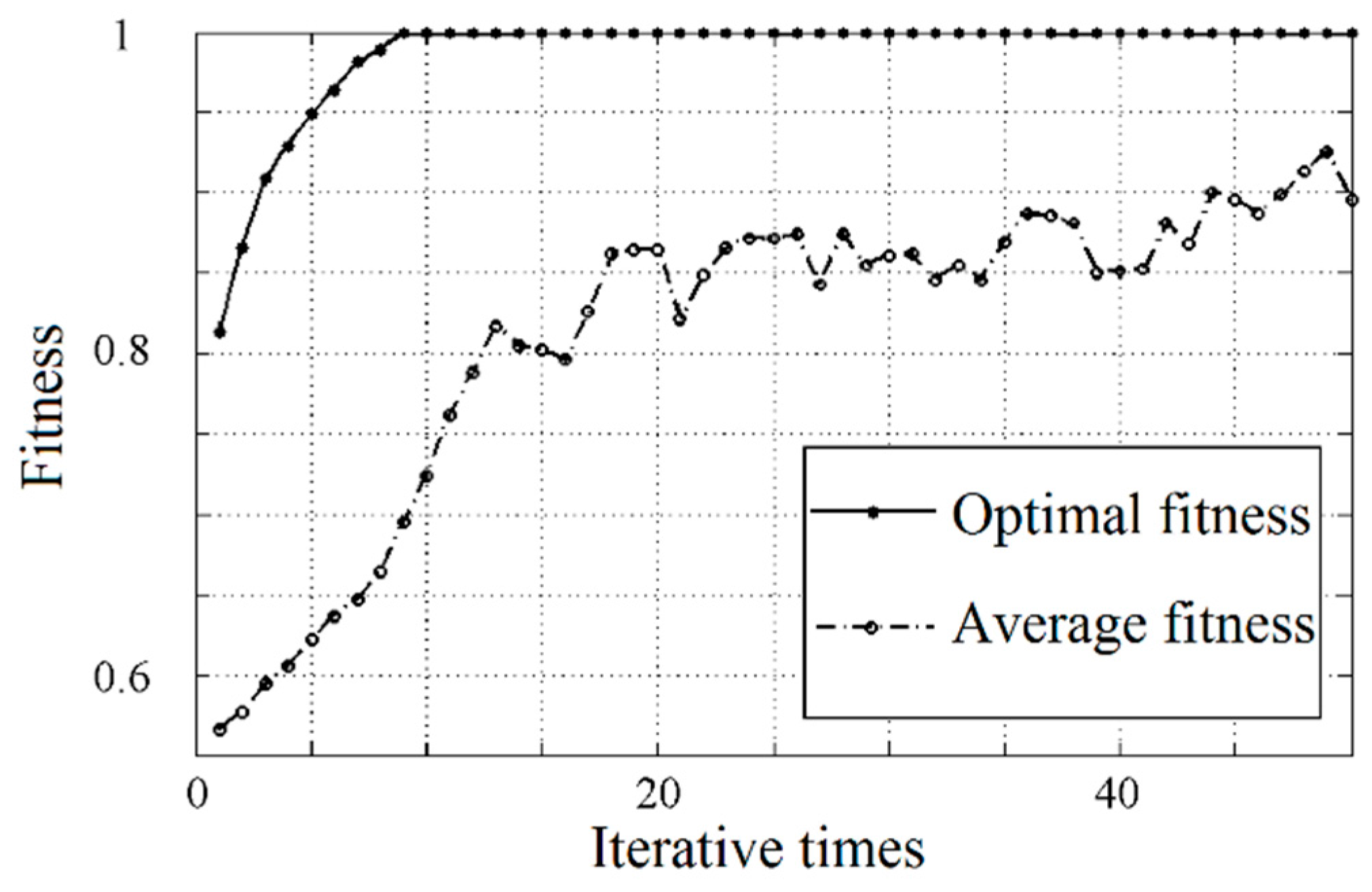
5.3. Classification Using OCSVM-SVM
| Test Sample | Diagnosis Results | STA | CA | |||
|---|---|---|---|---|---|---|
| Normal State | Fault Type I | Fault Type II | Fault Type III | |||
| Normal state | 18 | 0 | 0 | 2 | 90% | 90% |
| Fault type I | 0 | 20 | 0 | 0 | 100% | 100% |
| Fault type II | 0 | 0 | 20 | 0 | 100% | 100% |
| Fault type III | 0 | 0 | 0 | 20 | 100% | 100% |
| Test Sample | Diagnosis Results | STA | CA | |||
|---|---|---|---|---|---|---|
| Normal State | Fault Type I | Fault Type II | Fault Type III | |||
| Normal state | 14 | 0 | 1 | 5 | 70% | 70% |
| Fault type I | 0 | 20 | 0 | 0 | 100% | 100% |
| Fault type II | 0 | 0 | 18 | 2 | 100% | 90% |
| Fault type III | 2 | 0 | 1 | 17 | 90% | 85% |
| Classifier | Test Sample | Diagnosis Results | STA | CA | |||
|---|---|---|---|---|---|---|---|
| Normal State | Fault Type I | Fault Type II | Fault Type III | ||||
| SVM | Normal state | 17 | 0 | 0 | 3 | 85% | 85% |
| Fault type I | 0 | 20 | 0 | 0 | 100% | 100% | |
| Fault type II | 0 | 0 | 20 | 0 | 100% | 100% | |
| Fault type III | 2 | 0 | 0 | 18 | 90% | 90% | |
| ELM | Normal state | 18 | 0 | 0 | 2 | 90% | 90% |
| Fault type I | 0 | 20 | 0 | 0 | 100% | 100% | |
| Fault type II | 0 | 0 | 0 | 20 | 100% | 100% | |
| Fault type III | 3 | 0 | 0 | 17 | 85% | 85% | |
| Classifier | Test Sample | Diagnosis Results | STA | CA | ||
|---|---|---|---|---|---|---|
| Normal State | Fault Type I | Fault Type II | ||||
| OCSVM-SVM | Fault type III | 0 | 14 | 6 | 100% | 0 |
| SVM | Fault type III | 20 | 0 | 0 | 0 | 0 |
| ELM | Fault type III | 20 | 0 | 0 | 0 | 0 |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Runde, M.; Aurud, T.; Lundgaard, L.E.; Ottesen, G.E.; Faugstad, K. Acoustic diagnosis of high voltage circuit-breakers. IEEE Trans. Power Deliv. 1992, 7, 1306–1315. [Google Scholar] [CrossRef]
- Demjanenko, V.; Valtin, R.A.; Soumekh, M.; Haidu, H.; Antur, A.; Hess, D.P.; Soom, A.; Wright, S.E.; Tangri, M.K.; Park, S.Y. A noninvasive diagnostic instrument for power circuit breakers. IEEE Trans. Power Deliv. 1992, 7, 656–663. [Google Scholar] [CrossRef]
- Polycarpou, A.A.; Soom, A.; Swarnakar, V.; Valtin, R.A.; Acharya, R.S.; Demjanenko, V.; Soumekh, M.; Benenson, D.M.; Porter, J.W. Event timing and shape analysis of vibration bursts from power circuit breakers. IEEE Trans. Power Deliv. 1995, 11, 848–857. [Google Scholar] [CrossRef]
- Runde, M.; Ottesen, G.E.; Skyberg, B.; Ohlen, M. Vibration analysis for diagnostic testing of circuit-breakers. IEEE Trans. Power Deliv. 1996, 11, 1816–1823. [Google Scholar] [CrossRef]
- CIGRE Working Group. Final Report of the Second International Enquiry on High Voltage Circuit Breaker Failures and Defects in Service; CIGRE Report No. 83; CIGRE: Paris, France, 1994. [Google Scholar]
- Gao, Z.W.; Cecati, S.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques-Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Meng, Y.P.; Jia, S.L.; Shi, Z.Q.; Rong, M.Z. The detection of the closing moments of a vacuum circuit breaker by vibration analysis. IEEE Trans. Power Deliv. 2006, 21, 652–658. [Google Scholar] [CrossRef]
- Landry, M.; Leonard, F.; Landry, C.; Beauchemin, R. An improved vibration analysis algorithm as a diagnostic tool for detecting mechanical anomalies on power circuit breakers. IEEE Trans. Power Deliv. 2008, 23, 1986–1994. [Google Scholar] [CrossRef]
- Lee, D.S.; Lithgow, B.J.; Morrison, R.E. New fault diagnosis of circuit breakers. IEEE Trans. Power Deliv. 2003, 18, 454–459. [Google Scholar] [CrossRef]
- Huang, J.; Hu, X.G.; Yang, F. Support vector machine with genetic algorithm for machinery fault diagnosis of high voltage circuit breaker. Measurement 2011, 44, 1018–1027. [Google Scholar] [CrossRef]
- Huang, J.; Hu, X.G.; Geng, X. An intelligent fault diagnosis method of high voltage circuit breaker based on improved EMD energy entropy and multi-class support vector machine. Electr. Power Syst. Res. 2011, 81, 400–407. [Google Scholar] [CrossRef]
- Høidalen, H.K.; Runde, M. Continuous monitoring of circuit-breakers using vibration analysis. IEEE Trans. Power Deliv. 2005, 20, 2458–2465. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- He, Z.Y.; Chen, X.Q.; Luo, G.M. Wavelet entropy measure definition and its application for transmission line fault detection and identification. In Proceedings of the International Conference on Power System Technology, Chongqing, China, 22–26 October 2006.
- Chen, J.K.; Li, G.Q. Tsallis wavelet entropy and its application in power signal analysis. Entropy 2014, 16, 3009–3025. [Google Scholar] [CrossRef]
- He, Z.Y.; Gao, S.B.; Chen, X.Q.; Zhang, J.; Bo, Z.Q.; Qian, Q.Q. Study of a new method for power system transients classification based on wavelet entropy and neural network. Int. J. Electr. Power Energy Syst. 2011, 33, 402–410. [Google Scholar]
- Kumar, Y.; Dewal, M.L.; Anand, R.S. Epileptic seizure detection using DWT based fuzzy approximate entropy and support vector machine. Neurocomputing 2014, 133, 271–279. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. An integrated index for the identification of focal electroencephalogram signals using discrete wavelet transform and entropy measures. Entropy 2015, 17, 5218–5240. [Google Scholar] [CrossRef]
- Boškoski, P.; Juričić, Đ. Fault detection of mechanical drives under variable operating conditions based on wavelet packet Rényi entropy signatures. Mech. Syst. Signal Process. 2012, 31, 369–381. [Google Scholar] [CrossRef]
- Dubey, R.; Samantaray, S.R. Wavelet singular entropy-based symmetrical fault-detection and out-of-step protection during power swing. IET Gener. Transm. Distrib. 2013, 7, 1123–1134. [Google Scholar] [CrossRef]
- Wong, P.K.; Yang, Z.X.; Vong, C.M.; Zhong, J.H. Real-time fault diagnosis for gas turbine generator systems using extreme learning machine. Neurocomputing 2014, 128, 249–257. [Google Scholar] [CrossRef]
- Yang, Z.X.; Wong, P.K.; Vong, C.M.; Zhong, J.H.; Liang, J.J. Simultaneous-fault diagnosis of gas turbine generator systems using a pairwise-coupled probabilistic classifier. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, S.; Shah, S.L. Fault detection and diagnosis in process data using one-class support vector machines. J. Process Control 2009, 19, 1627–1639. [Google Scholar] [CrossRef]
- Shin, H.J.; Eom, D.H.; Kim, S.S. One-class support vector machines—An application in machine fault detection and classification. Comput. Ind. Eng. 2005, 48, 395–408. [Google Scholar] [CrossRef]
- Xiao, Y.C.; Wang, H.G.; Xu, W.L. Parameter selection of Gaussian kernel for one-class SVM. IEEE Trans. Cybern. 2015, 45, 927–939. [Google Scholar] [PubMed]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Piscataway, NJ, USA, 27 November–1 December 1995; pp. 1942–1948.
- Mishra, S.; Bhende, C.N.; Panigrahi, K.B. Detection and classification of power quality disturbances using S-transform and probabilistic neural network. IEEE Trans. Power Deliv. 2008, 23, 280–287. [Google Scholar] [CrossRef]
- Olsson, A.E. Particle Swarm Optimization: Theory, Techniques and Applications; Nova Science Publishers: Hauppauge, NY, USA, 2011. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, N.; Chen, H.; Zhang, S.; Cai, G.; Li, W.; Xu, D.; Fang, L. Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Wavelet Time-Frequency Entropy and One-Class Support Vector Machine. Entropy 2016, 18, 7. https://doi.org/10.3390/e18010007
Huang N, Chen H, Zhang S, Cai G, Li W, Xu D, Fang L. Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Wavelet Time-Frequency Entropy and One-Class Support Vector Machine. Entropy. 2016; 18(1):7. https://doi.org/10.3390/e18010007
Chicago/Turabian StyleHuang, Nantian, Huaijin Chen, Shuxin Zhang, Guowei Cai, Weiguo Li, Dianguo Xu, and Lihua Fang. 2016. "Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Wavelet Time-Frequency Entropy and One-Class Support Vector Machine" Entropy 18, no. 1: 7. https://doi.org/10.3390/e18010007
APA StyleHuang, N., Chen, H., Zhang, S., Cai, G., Li, W., Xu, D., & Fang, L. (2016). Mechanical Fault Diagnosis of High Voltage Circuit Breakers Based on Wavelet Time-Frequency Entropy and One-Class Support Vector Machine. Entropy, 18(1), 7. https://doi.org/10.3390/e18010007







