Abstract
Aim: To detect pathological brain conditions early is a core procedure for patients so as to have enough time for treatment. Traditional manual detection is either cumbersome, or expensive, or time-consuming. We aim to offer a system that can automatically identify pathological brain images in this paper. Method: We propose a novel image feature, viz., Fractional Fourier Entropy (FRFE), which is based on the combination of Fractional Fourier Transform (FRFT) and Shannon entropy. Afterwards, the Welch’s t-test (WTT) and Mahalanobis distance (MD) were harnessed to select distinguishing features. Finally, we introduced an advanced classifier: twin support vector machine (TSVM). Results: A 10 × K-fold stratified cross validation test showed that this proposed “FRFE + WTT + TSVM” yielded an accuracy of 100.00%, 100.00%, and 99.57% on datasets that contained 66, 160, and 255 brain images, respectively. Conclusions: The proposed “FRFE + WTT + TSVM” method is superior to 20 state-of-the-art methods.
1. Background
Pathological brain detection (PBD) is of essential importance. It can help physicians make decisions, and to avoid wrong judgements on subjects’ condition. Magnetic resonance imaging (MRI) features high-resolution on soft tissues in the subjects’ brains, generating a mass dataset [1]. At present, there are numerous works on the use of brain magnetic resonance (MR) images for solving PBD problems [2,3].
Due to the enormous volume of the imaging dataset from the human brain, traditional manual techniques are either tedious, or time-consuming, or costly. Therefore, it is necessary to develop a novel computer-aided diagnosis (CAD) system [4] to help patients have enough time to receive treatment.
In the last decade, many methods from different countries were presented with the same goal of detecting pathological brains [5,6,7,8] (more references will be introduced in Section 2). Most of them have two stages: (1) Feature extraction, to extract efficient features that can distinguish pathological brain from healthy brains; feature reduction can be skipped if the size of features dataset is reasonable; and (2) Classification, to construct a classifier using the extracted (and reduced) features.
For the first stage of feature extraction, the latest solutions transform the brain image by discrete wavelet transform (DWT) [9], which is proven to be superior to the traditional Fourier transform. Nevertheless, DWT comes across a problem of choosing the best decomposition level and the optimal wavelet function.
For the final stage of classification, recent approaches like to use feed-forward neural network (FNN) or support vector machine (SVM), which are becoming popular in the fields of classification and detection [10]. However, SVM has the limitation that its hyperplanes should be parallel. This parallelism restrains the classification perform.
To solve the above two problems, we propose two improvements: on the one hand, we propose a novel image feature—Fractional Fourier Entropy (FRFE)—which is based on two steps: (1) the use of a Fraction Fourier Transform (FRFT) to replace the traditional Fourier transform; and (2) Shannon entropy to extract features from the FRFT spectrums.
On the other hand, we suggest removing the hyperplane parallelism restraint [11]. We introduce for this purpose two non-parallel SVMs, the generalized eigenvalue proximal SVM (GEPSVM) and twin support vector machine (TSVM).
In the remainder of this paper Section 2 offers the state-of-the-art. Then, Section 3 describes the materials used. Section 4 presents the extracted features and how to select important features. Section 5 offers the mechanisms of the standard support vector machine and non-parallel support vector machine. Section 6 covers the experimental design. Section 7 provides the results. Discussions are presented in Section 8. Finally Section 9 is devoted to our conclusions.
2. State-of-the-Art
Recent PBD methods are of two types. One treats a 3D dataset as a whole, and the other selects the most important slice from the 3D data. The former needs to scan the whole brain, which is expensive and time-consuming. The latter only needs to scan the focus related slice, which is cheap and rapid. In this study, we focus on the latter.
Chaplot et al. [12] were the first to apply “DWT” to PBD problems. Their classifiers are SVM and self-organizing map (SOM). El-Dahshan et al. [13] employed a 3-level discrete wavelet transform. Dong et al. [14] proposed the use of a novel scaled conjugate gradient (SCG) approach for PBD. Zhang and Wu [15] proposed to employ kernel support vector machine (KSVM). Saritha et al. [16] combined wavelet transform with Shannon entropy, and they named the novel feature wavelet-entropy (WE). They harnessed spider-web plots (SWPs) with the aim of decreasing the number of WEs. They employed the probabilistic NN (PNN) for classification. Zhang et al. [17,18] found spider-web plots had no effect on PBD. Das et al. [19] suggested using a Ripplet transform (RT) in PBD. Their classifier is a least squares support vector machine (LS-SVM). Zhang et al. [20] employed particle swarm optimization (PSO) to find the optimal parameters in a kernel support vector machine. El-Dahshan et al. [21] proposed the use of a feedback pulse-coupled neural network to segment brain images. Following Saritha’s work, Zhou et al. [22] employed WE, and Naive Bayes classifier (NBC) as the classifier. Zhang et al. [23] employed a discrete wavelet packet transform (DWPT) to replace DWT, and employed Tsallis entropy (TE) to replace Shannon entropy (SE). Yang et al. [24] employed wavelet-energy as the features. Damodharan and Raghavan [25] used tissue segmentation to detect neoplasms in brains. Guang-Shuai et al. [26] employed both wavelet-energy and SVM. The overall accuracy was less than 83%. Wang et al. [27] employed genetic algorithm (GA) to solve the task of PBD. Nazir et al. [28] proposed performing image denoising first. Their overall accuracy was higher than 91%. Harikumar and Kumar [29] used ANN with optimal performance achieved by use of a db4 wavelet and radial basis function (RBF) kernel. Wang et al. [30] suggested the use of a stationary wavelet transform (SWT). Zhang et al. [31] offered a new Hybridization of Biogeography-based optimization (BBO) and the Particle swarm optimization (PSO) method. Hence, they termed it HBP for short. Farzan et al. [32] used the longitudinal percentage of brain volume changes (PBVC) in a two-year follow up and its intermediate counterparts in early 6-month and late 18-month tests as features. Their experimental results showed SVM with RBF performed the best with an accuracy of 91.7%, higher than K-means at 83.3%, fuzzy c-means (FCM) at 83.3%, and linear SVM at 90%. Zhang et al. [33] used two types of features: one is Hu moment invariants (HMI); the other is wavelet entropy. Munteanu et al. [34] employed Proton Magnetic Resonance Spectroscopy (MRS) data, in order to identify mild cognitive impairment (MCI) and Alzheimer’s disease (AD) in healthy controls. Savio and Grana [35] employed Regional Homogeneity to build a CAD for detecting schizophrenia based on resting-state function magnetic resonance imaging (fMRI). Zhang et al. [36] proposed employing a three dimensional discrete wavelet transform to extract features from structural MRI, with the aim of detecting Alzheimer’s disease and mild cognitive impairment.
The contribution of this paper is to use fractional Fourier entropy and non-parallel SVMs, with the aim of developing a novel PBD system which has superior classification performance than the above approaches.
3. Materials
At present, there are three benchmark datasets of different sizes, viz., D66, D160, and D255. They were all used for our tests. All datasets contain T2-weighted MR brain images, which were acquired along the axial axis with sizes of 256 × 256. The readers can download them from the Medical School of Harvard University website. The first two datasets consisted of examples from seven types of diseases (meningioma, AD, AD plus visual agnosia, Huntington’s disease, sarcoma, Pick’s disease, and glioma) along with normal brain images. The last dataset D255 contains all seven types of diseases as mentioned before, and four new diseases (multiple sclerosis, cerebral toxoplasmosis, chronic subdural hematoma, and herpes encephalitis). Figure 1 shows samples of the brain images.
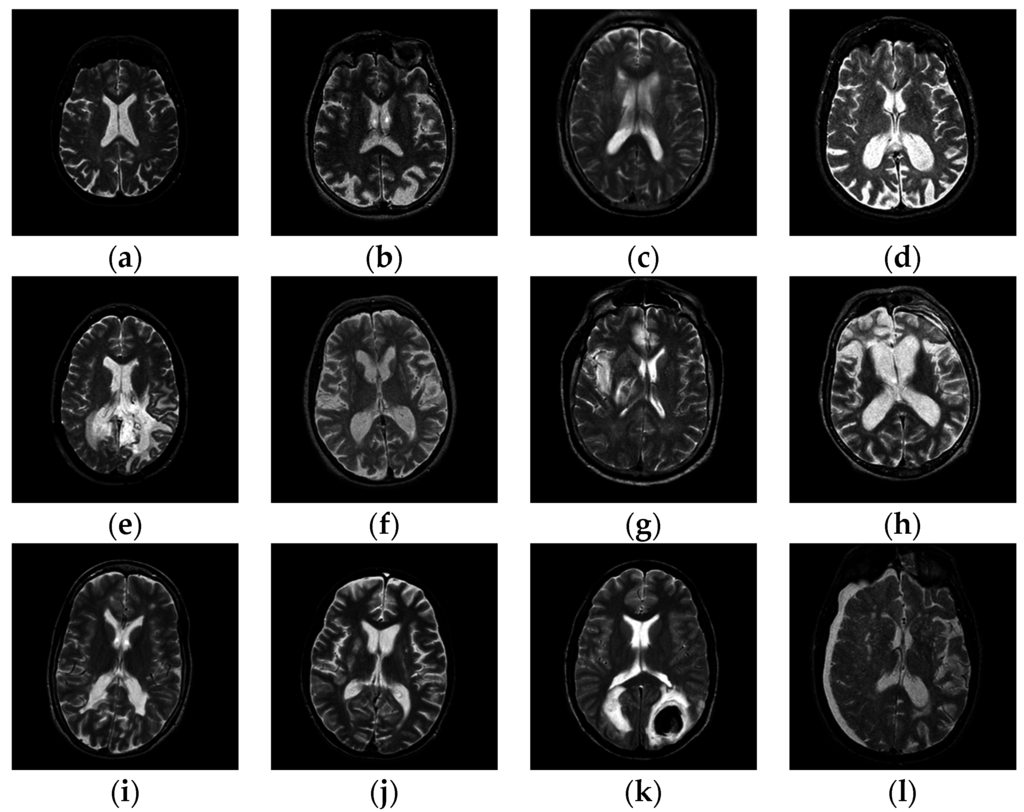
Figure 1.
Samples of pathological brain images: (a) healthy brain; (b) AD with visual agnosia; (c) Meningioma; (d) AD; (e) Glioma; (f) Huntington’s disease; (g) Herpes encephalitis; (h) Pick’s disease; (i) Multiple sclerosis; (j) Cerebral toxoplasmosis; (k) Sarcoma; (l) Subdural hematoma.
The cost of predicting pathological images as normal is severe, as the treatmen s of patients may be deferred. On the other hand, the cost of misclassification of normal as abnormal is not serious, since other diagnosis means can remedy the error.
This cost-sensitivity (CS) problem can be solved by changing the class distribution at the beginning stage, since the original data is accessible. That means, we intentionally pick more abnormal brains than normal brains in the dataset, with the aim of making the classifier biased to pathological brains, with the aim of addressing the CS problem.
4. Feature Extraction and Selection
The difference between Fourier transform (FT) [37] and its variant “fractional FT (FRFT) [38]”, is that FRFT can analyze nonstationary signals, which FT cannot. Besides, FRFT transforms a particular signal into a unified time-frequency domain.
4.1. Basic Concept
The α-angle fractional Fourier transform (FRFT) of a particular signal x(t) was denoted by Xα:
where α is real-valued, t the time, u the frequency, and K the transform kernel as:
here j denotes the imaginary unit. To solve the problem that cot and csc will diverge when the values of α are assigned with multiples of π, we take the limit and obtain the following equation [39]:
here δ represents the Diract delta function, and m an arbitrary integer. Sometimes scholars used angular frequency ω, so:
where:
In this study, 2D-FRFT was performed on 2D brain images. Due to the linearity of FRFT [40], 2D-FRFT can be implemented by first applying 1D-FRFT to rows and then to columns. Besides, for 2D-FRFT, there are two angles: named α and β. At the condition of α = β = 0, the FRFT degrades to an identity operator. At the condition of α = β = 1, the FRFT becomes the conventional FT.
4.2. Fractional Fourier Domain
An example of FRFT on a one-dimensional signal tri(t) was implemented, in order to illustrate how the angle α influences the fractional Fourier domain (see Figure 2). Note that the frequency spectrum of tri(t) is the square of the sinc function, that is sinc2(u). We can observe that the FRFT output is in an intermediate domain between time and frequency, viz., a unified time-frequency domain.
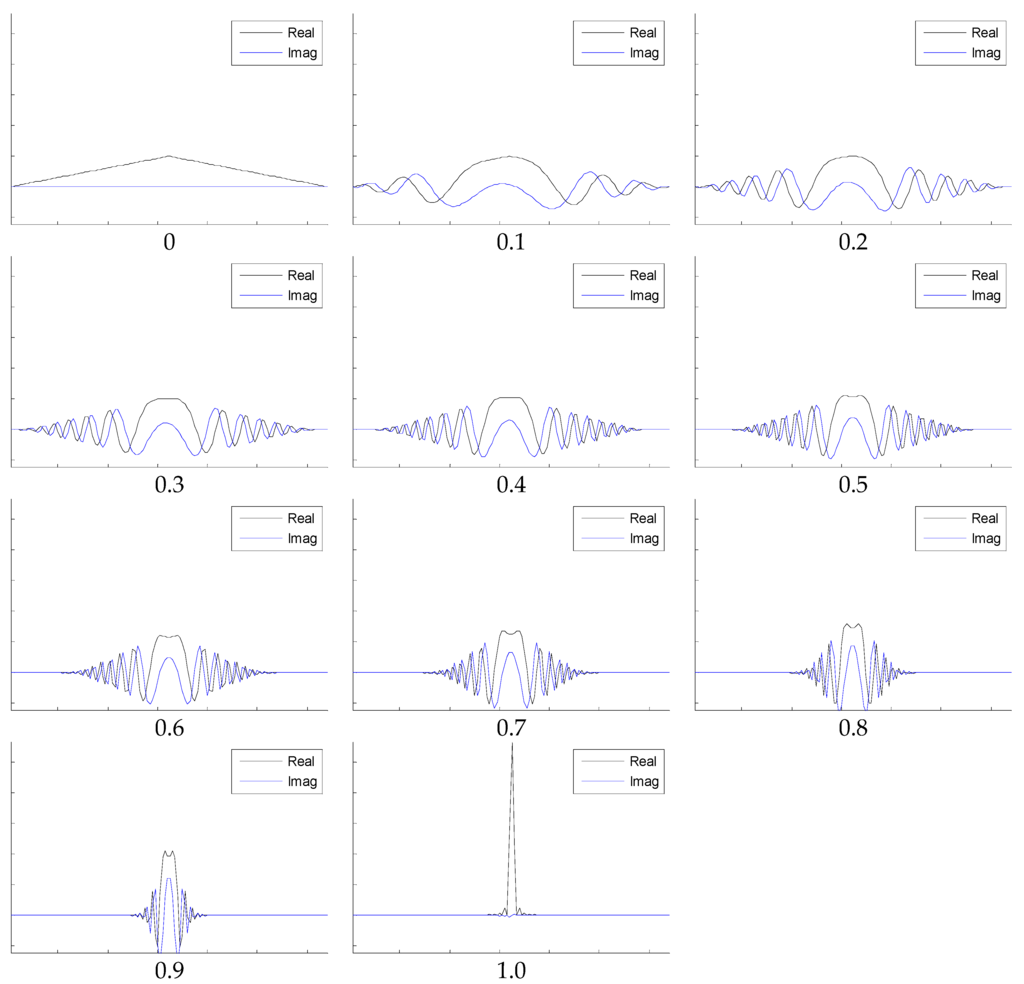
Figure 2.
Illustration of how FRFT changes with α, whose value varies from zero to one (the real and imaginary parts are shown in black and blue lines, respectively).
4.3. Weighted-Type FRFT
Weighted-type fractional Fourier transform (WFRFT) belongs to the simplest implementation method of FRFT. It replaced the continuous variables t by its discrete version n, and replaced the variable u by the discrete one k. The form of WFRFT is listed below [41,42]:
Then, the WFRFT of signal x can be defined as:
We can observe by Equation (6) that WFRFT can be treated as a linear weighted combination of DFT matrix, Inverse DFT (IDFT) matrix, time inverse matrix, and identity matrix [43].
4.4. Shannon Entropy
In information theory the Shannon entropy is the expected information content (IC) received in a message. Entropy is a measure of the unpredictability of IC [44]. Suppose X is a discrete random variable, whose values may fall within the set of (x1, x2, …, xn) with a probability mass function P(X), we have entropy H defined in the form of:
where E represents the expected value operator and q the logarithm base. Equation (9) can be generalized to a finite sample with explicit form of:
The units of entropy H are bits when q = 2, nats when q = e, and Hartleys when q = 10. Sometimes P(xi) is equal to zero, then, we force the 0loga0=0.
4.5. Fractional Fourier Entropy
To the best of the author’s knowledge we are the first to propose the concept of “FRFE”, i.e., by implementing the entropy operator H on the spectra obtained by the Fractional Fourier Transform X:
After WFRFT was performed on the brain images (no matter whether pathological or healthy), we obtained in total 25 unified time-frequency spectra with different combinations of αx and αy. The entropy over all spectra of 25 domains are extracted and aligned into a set of vectors:
Here X(α, β) represents a FRFT performed with α-angle along the x-axis and β-angle along the y-axis. I is the brain image. In this study, both angles were set to change within the range from 0.6 to 1 with equal increases of 0.1. The range of [0, 0.5] was not considered since FRFT with angles near 0 will yield an identity operation.
4.6. Feature Selection
We employ the two-sample location test, with the aim of selecting the most important FRFEs from the 25 ones. Student’s t-test is the most popular method that assumes “equal means” and “equal variances” of the two data sets [45]. This “equal variances” does not make sense and can be discarded; while the “equal means” is necessary. Therefore, we used Welch’s t-test (WTT) that is an adaption of the Student’s t-test. WTT only checks whether the two populations have equal means [46]. WTT is widely used in various applications to select important features [47,48,49]. The WTT is computed by:
where μ denotes the sample mean and σ2 denotes the variance of a particular feature, n the sample size, w the WTT score. The null hypothesis in this work is that the FRFE values of both pathological and healthy brains have the same means (equal variances are not of concern). The alternative hypothesis is that they have unequal means. WTT was performed at the confidence interval of 95%. Then, the selected FRFEs are used as input features for following classification.
Mahalanobis distance (MD) [50] is another popular feature selection method. MD measures the distance between various datasets of two different classes. Its definition is written as:
where m represents the MD score, ∑ is defined as:
where Cp and Cq represents the covariance matrixes of the characteristic vectors in class p and class q, respectively.
In this work, we treat the WTT score w and MD score m as a measure of the distinguishability of individual features of two classes. The higher the score is, the more distinguishable the feature is.
5. Classification
5.1. Support Vector Machine (SVM)
Suppose there is an N-sample training set with a p-dimension size. Suppose xn denotes a p-dimensional data point, and yi denotes the corresponding class, with a value of either −1 or +1, denoting the sample target is either class 1 or class 2. Our aim is to build a hyperplane, which separates the first class from the second class is the desired SVM. Usually the hyperplane is (p−1)-dimensional.
With the help of simple mathematical knowledge, a hyperplane can be written as , where w and b denotes the weights and biases. Hence, SVM can be written as:
Positive slack vector ξ = (ξ1, …, ξi, …, ξN) are introduced to measure the misclassification degree of sample xi. Then, the optimal hyperplane corresponding to the SVM is yielded by solving:
here c represents is the error penalty and o is a vector of ones of N-dimension. Scholars have tend to drop this parallelism and proposed a different non-parallel support vector machine (NPSVM).
5.2. NPSVM I—Generalized Eigenvalue Proximal SVM
Mangasarian and Wild [51] proposed a GEPSVM, which yielded better performance than standard support vector machines [52,53]. Samples from class 1 are denoted as X1 and samples from class 2 are denoted as X2, GEPSVM builds the two nonparallel planes by:
Take the first plane as the example (the second plane can be obtained in a similar way), we deduce from Equation (18):
here o represents a vector of ones of any dimension. Simplifying Equation (19) gives:
Tikhonov regularization term is included to decrease the norm of z:
here t represents a nonnegative Tikhonov factor. Equation (22) can be solved by the “Rayleigh Quotient (RQ)” approach.
5.3. NPSVM II—Twin Support Vector Machine
Jayadeva et al. [54] were the first to propose the TSVM. Reports have shown that TSVM is better than both SVM and GEPSVM [55,56,57]. Another advantage of TSVM is that its convergence rate is four times faster than conventional SVM [54]. The TSVM is constructed by solving the two QP tasks:
here oi (i = 1,2) are the same as in Equation (19), and ci (i = 1,2) are positive parameters. The constraint requires the hyperplane to be at a distance of more than one from points of the other class. The first and second terms in the equations above represent the sum of squared distances from the hyperplane to one class, and the sum of error variables, respectively.
6. Experimental Design
6.1. K-Fold Stratified Cross Validation
Obeying common convention, and considering the advantages of stratified cross validation (SCV), 6- and 5-fold SCV were employed for D66 and the other two datasets, respectively. Table 1 lists the SCV settings of the three datasets. Note that true class here represents the abnormal brains, and false class the normal brains.

Table 1.
SCV setting of all datasets (P = Pathological, H = Healthy).
| Data | Training | Validation | Total | Fold No. | |||
|---|---|---|---|---|---|---|---|
| P | H | P | H | P | H | ||
| D66 | 40 | 15 | 8 | 3 | 48 | 18 | 6 |
| D160 | 112 | 16 | 28 | 4 | 140 | 20 | 5 |
| D255 | 176 | 28 | 44 | 7 | 220 | 35 | 5 |
Note that D160 and D255 are divided into five folds, while D66 is divided into six folds. This is because of stratification. The D66 dataset contains 48 pathological brains and 18 healthy brains, so a 6-fold partition can guarantee each fold includes eight pathological brains and three healthy brains. If we divide D66 into five folds, then the stratification cannot be guaranteed.
6.2. Implementation
The proposed PBD system contains three successful components: FRFE, WTT, and SVM (or GEPSVM or TSVM). Figure 3 shows the diagram and Table 2 presents the pseudocode, where offline learning is to train the classifier, and online prediction is used to predict new brain images.
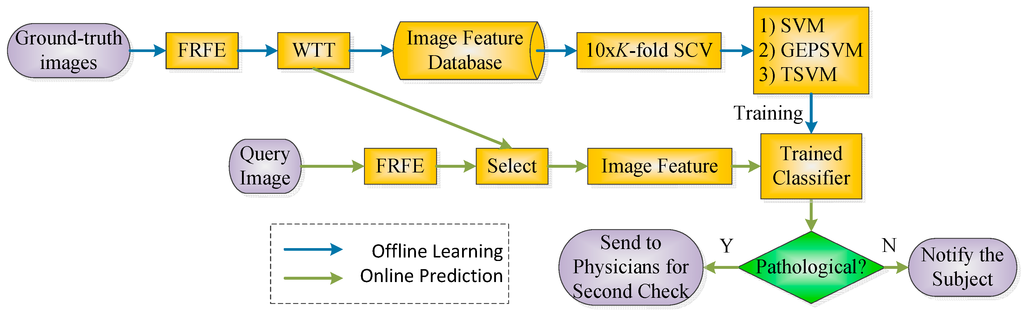
Figure 3.
Diagram of our method.

Table 2.
Pseudocode of our method.
| Offline learning | |
| Step I | Feature Extraction: Fractional Fourier Entropy (FRFE) were performed on all ground-truth images: Twenty-five different WFRFT were carried out with α and β from the set of [0.6, 0.7, 0.8, 0.9, 1.0], respectively. Entropy was extracted based on the 25 fractional Fourier spectrums. |
| Step II | Feature Selection: Welch’s t-test (WTT) was employed to select the most important FRFEs among the 25 ones the 95% confidence interval. |
| Step III | Classifier Training: Those chosen FRFEs with their class labels, were fed into train SVM and two NPSVMs. |
| Step IV | Classifier Evaluation: Evaluate the classification performance based on a 10 times K-fold SCV, and report which classifiers performs best. |
| Online prediction | |
| Step I | Feature Extraction: A new query image is decomposed with 25 FRFE results extracted |
| Step II | Feature Selection: Select the most important FRFEs from the 25 ones. |
| Step III | Query Image Prediction: Input the selected FRFEs of the query image to the reported best classifier, so as to obtain whether the query brain is pathological or healthy. |
7. Results and Discussion
The programs were developed by in house on the basis of the signal processing toolbox of 64 bit Matlab 2014a (The Mathworks ©, Natick, MA, USA). The simulation experiments were implemented on a P4 IBM computer equipped with a 3.2 GHz processor, 8 GB RAM, and the Windows 7 operating system.
7.1. WFRFT Result
Figure 4 illustrates the 25 WFRFT decomposition results for a healthy brain,. Both α and β fall within the set of [0.6, 0.7, 0.8, 0.9, 1.0]. The spectra are log-enhanced and mixed with pseudo-color for a clearer view.

Figure 4.
WFRFT of a normal brain.
7.2. FRFE Results
In the second experiment, we calculate the FRFE of each ground truth image. The mean and standard deviation (SD) of pathological and healthy brains are listed below in Table 3. In each cell, the numbers above represents the mean and SD of FRFEs of pathological brain, the numbers below the ones of healthy brain.

Table 3.
Mean and SD of Two Different Brains.
| β = 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| α =0.6 | 6.14 ± 0.15 | 5.96 ± 0.14 | 5.79 ±0.15 | 5.69 ± 0.16 | 5.65 ± 0.18 |
| 6.07 ± 0.43 | 5.92 ± 0.41 | 5.74 ± 0.36 | 5.57 ± 0.28 | 5.50 ± 0.28 | |
| 0.7 | 5.99 ± 0.14 | 5.85 ± 0.14 | 5.73 ± 0.15 | 5.67 ± 0.16 | 5.64 ± 0.18 |
| 5.94 ± 0.41 | 5.81 ± 0.38 | 5.66 ± 0.31 | 5.53 ± 0.27 | 5.48 ± 0.26 | |
| 0.8 | 5.88 ± 0.14 | 5.78 ± 0.15 | 5.70 ± 0.16 | 5.66 ± 0.17 | 5.63 ± 0.18 |
| 5.79 ± 0.36 | 5.68 ± 0.31 | 5.58 ± 0.27 | 5.50 ± 0.24 | 5.46 ± 0.25 | |
| 0.9 | 5.82 ± 0.15 | 5.76 ± 0.16 | 5.70 ± 0.16 | 5.66 ± 0.17 | 5.63 ± 0.18 |
| 5.68 ± 0.32 | 5.61 ± 0.30 | 5.54 ± 0.26 | 5.48 ± 0.25 | 5.45 ± 0.24 | |
| 1.0 | 5.75 ± 0.16 | 5.71 ± 0.16 | 5.68 ± 0.17 | 5.65 ± 0.17 | 5.59 ± 0.18 |
| 5.58 ± 0.30 | 5.53 ± 0.27 | 5.49 ± 0.25 | 5.45 ± 0.24 | 5.41 ± 0.24 |
7.3. Feature Selection
Then, using either WTT or MD, we finally obtain the same results, i.e., we select 12 distinguishable features as shown in Table 4, where S represents the corresponding feature is selected and X represents unselected. Remember that the values of both α and β are within the range of [0,1] because of their periodical and symmetric property.

Table 4.
Twelve Selected Features (S = Selected, X = Unselected).
| β | ||||||
| 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
| α | 0.6 | X | X | X | X | S |
| 0.7 | X | X | X | X | S | |
| 0.8 | X | X | X | S | S | |
| 0.9 | X | X | S | S | S | |
| 1.0 | S | S | S | S | S | |
7.4. Feature Comparison
To demonstrate the performance of the FRFE, we compared it with the “wavelet entropy” and “wavelet energy”. Reference [22] used seven wavelet entropy as features, and used NBC for detection. Reference [26] used seven wavelet energy as features, and used SVM for detection. In that paper, it is proven that seven features can obtain the highest accuracy, and adding more features will not improve the classification performance.
For a fair comparison, we also combined FRFE with NBC and SVM, respectively. Those two methods are termed as “FRFE + WTT + NBC” and “FRFE + WTT + SVM”. We run K-fold SCV 10 times on the three datasets. The comparison results are listed in Table 5 and Table 6.

Table 5.
FRFE Compared to Wavelet Entropy based on 10 × K-fold SCV (# stands for number).
| Method | Feature # | Accuracy | ||
|---|---|---|---|---|
| D66 | D160 | D255 | ||
| “Wavelet Entropy + NBC” [22] | 7 | 92.58 | 91.87 | 90.51 |
| FRFE + WTT + NBC (Proposed) | 12 | 97.12 | 95.94 | 95.69 |

Table 6.
FRFE compared to Wavelet Energy based on 10 × K-fold SCV (# stands for number).
| Method | Feature # | Accuracy | ||
|---|---|---|---|---|
| D66 | D160 | D255 | ||
| “Wavelet Energy + SVM” [26] | 7 | 82.58 | 80.13 | 77.76 |
| FRFE + WTT + SVM (Proposed) | 12 | 100 | 99.69 | 98.98 |
7.5. SVM versus Non-Parallel SVMs
To compare the performance among standard SVM and two NPSVMs, we used 12 selected FRFE features. Again, K-fold SCV was run 10 times over three datasets. We recorded the accuracy of each K-fold SCV, and averaged the results of 10 runs. The results of FRFE + WTT + SVM, FRFE + WTT + GEPSVM, FRFE + WTT + TSVM, are listed in Table 7. In following experiments, TSVM is the default classifier.

Table 7.
Average Accuracy Comparison based 10 × K-fold SCV.
| Method | Classifier | D66 | D160 | D255 |
|---|---|---|---|---|
| FRFE + WTT + SVM | SVM | 100 | 99.69 | 98.98 |
| FRFE + WTT + GEPSVM | GEPSVM | 100 | 100 | 99.18 |
| FRFE + WTT + TSVM | TSVM | 100 | 100 | 99.57 |
7.6. Best Proposed Approach
We analyzed the results obtained. Taking the best of our proposed approaches, FRFE + WTT + TSVM, as instance, its first run of 5-fold SCV is listed in Table 8, and its total 10 runs accuracy results are listed in Table 9. The evaluation (sensitivity, specificity and precision) is listed in Table 10.

Table 8.
First run of a 5-fold SCV by FRFE + WTT + TSVM.
| CM on Validation Set | Correct Cases | Accuracy | |
|---|---|---|---|
| Fold 1 | 51 | 100.00 | |
| Fold 2 | 51 | 100.00 | |
| Fold 3 | 50 | 98.04 | |
| Fold 4 | 51 | 100.00 | |
| Fold 5 | 51 | 100.00 | |
| Sum | 254 | 99.61% |

Table 9.
Accuracy Results of each run.
| Run | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 | Sum |
|---|---|---|---|---|---|---|
| Run 1 | 51 (100.00%) | 51 (100.00%) | 50 (98.04%) | 51 (100.00%) | 51 (100.00%) | 254 (99.61%) |
| Run 2 | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 50(98.04%) | 51 (100.00%) | 254 (99.61%) |
| Run 3 | 50 (98.04%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 254 (99.61%) |
| Run 4 | 50 (98.04%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 254 (99.61%) |
| Run 5 | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 50 (98.04%) | 254 (99.61%) |
| Run 6 | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 50 (98.04%) | 254 (99.61%) |
| Run 7 | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 50 (98.04%) | 51 (100.00%) | 254 (99.61%) |
| Run 8 | 51 (100.00%) | 51 (100.00%) | 50 (98.04%) | 50 (98.04%) | 51 (100.00%) | 253 (99.22%) |
| Run 9 | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 50 (98.04%) | 51 (100.00%) | 254 (99.61%) |
| Run 10 | 50 (98.04%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 51 (100.00%) | 254 (99.61%) |
| Sum | 2539 (99.57%) |

Table 10.
Evaluation of FRFE + WTT + TSVM.
| Method | Accuracy | Sensitivity | Specificity | Precision |
|---|---|---|---|---|
| FRFE + WTT + TSVM | 99.57% | 99.59% | 99.43% | 99.91% |
7.7. Comparison with State-of-the-Art
To further validate the efficiency of our “FRFE + WTT + TSVM”, we compared it with 20 existing algorithms, such as DWT+SOM [12], DWT+SVM [12], DWT + SVM + RBF [12], DWT + PCA + KNN [13], DWT + PCA + ANN [13], DWT + PCA + SCG-FNN [14], DWT + PCA + SVM [15], DWT + PCA + SVM + HPOL [15], DWT + PCA + SVM + IPOL [15], DWT + PCA + SVM + RBF [15], WE + SWP + PNN [16], RT + PCA + LS-SVM [19], PCNN + DWT + PCA + BPNN [21], DWPT + TE + GEPSVM [23], DWPT + SE + GEPSVM [23], SWT + PCA + ABC-SPSO-FNN [30], SWT + PCA + IABAP-FNN [30], SWT + PCA + HPA-FNN [30], WE + HMI + GEPSVM [33], and WE + HMI + GEPSVM + RBF [33]. The meaning of these abbreviations can be found in the Nomenclature section below.
8. Discussion
Figure 4 indicates that if both angles increase to one, the FRFT degrades to a standard FT. Contrarily, if both angles reduce to zero, the FRFT degrades to identity operator, which does not contain any frequency spectral information.
Table 4 shows the final selected twelve features are FRFE with parameters (α, β) are assigned with twelve different values of (0.6, 1.0), (0.7, 1.0), (0.8, 0.9), (0.8, 1.0), (0.9, 0.8), (0.9, 0.9), (0.9, 1.0), (1.0, 0.6), (1.0, 0.7), (1.0, 0.8), (1.0, 0.9), and (1.0, 1.0). Note that (α, β) = (1.0, 1.0) represents the standard Fourier Transform (SFT). Those selected features are all closer to the SFT point than those unselected features. It indicates that the SFT and those FRFT near to SFT are more efficient features than others. Note that ONLY (α, β) = (1.0, 1.0) corresponds the SFT. For example, the (0.6, 1.0) means a FRFT with angle of 0.6 along x-axis and a SFT along y-axis, so (0.6, 1.0) should be considered a 2D-FRFT other than SFT.
The proposed FRFE measures the information contents in the fractional Fourier domain (FRFD), which is extended from the standard Fourier domain. From another point of view, FRFE is a measure of diversity or unpredictability. A limitation is that FRFE value is not absolute. It depends on the model over FRFD.
Table 5 shows that for NBC, the wavelet entropy obtained accuracies of 92.58%, 91.87%, and 90.51 on D66, D160, and D255, respectively, while the FRFE + WTT + NBC obtained accuracies of 97.12%, 95.94%, and 95.69%, which are higher than the accuracies obtained by wavelet entropy. Therefore, we can conclude the FRFE performed better than wavelet entropy. Table 6 shows the wavelet energy with SVM achieves accuracies of 82.58%, 80.13%, and 77.76% over three datasets, nevertheless, the FRFE + WTT + SVM yields accuracies of 100.00%, 99.69%, and 98.98% over three datasets. It suggests us FRFE is significantly better than wavelet energy. Comparing the “FRFE + WTT + SVM” in Table 6 with “FRFE + WTT + NBC” in Table 5, another finding is SVM is superior to NBC. The reason is SVM works well for large dimensional problems with relative few instances due to its regularization form [58].
Results in Table 7 indicate that GEPSVM is superior to standard SVM. Both obtain perfect detection for D66. For D160, the accuracy of GEPSVM is higher than that of SVM by 0.31%. For D255, the accuracy of GEPSVM is higher than that of SVM by 0.20%. Meanwhile, TSVM is superior to GEPSVM. The accuracy of TSVM is 0.39% higher than that of GEPSVM for D255.
The parallel hyperplane setting restrains standard SVM to generate complicated and flexible hyperplanes. NPSVMs discard this setting, so their performances are much better than SVM. TSVM has a resemblance to GEPSVM in spirit, since both drop parallelism. Their difference is that TSVM uses simpler formulation than GEPSVM, and the former can be solved by merely two QP problems. Our results align with the finding in Kumar and Gopal [59], which says “generalization performance of TSVM is better than GEPSVM and conventional SVM”. Nevertheless, Ding et al. [60] claimed that TSVM has a lower generalization ability, so it is too early to make a decision about the classification performance of TSVM before more rigorous tests are implemented.
In total, our proposed FRFE + WTT + TSVM predicts 2539 success cases and 13 fail cases in 10 × 5-fold SCV for D255. Remember D255 contains 220 pathological brains and 35 healthy brains, so in total 2200 pathological and 350 healthy instances after 10 repetitions. For 2200 pathological instances, our method predicts 2191 cases successfully, and misclassifies nine pathological instances as healthy. For 350 healthy instances, our method predicts 348 instances successfully, and misclassifies two healthy instances as pathological. Therefore, the sensitivity of our method is 99.59%, specificity is 99.43%, and precision is 99.91% (See Table 10).
Table 11 lists the comparison results. The first column lists the abbreviated name of the different algorithms. The second column lists the feature number used in each method. The third column lists the number of runs. Here all new algorithms were run 10 times, except some old algorithms which ran five times that were reported in literature [19]. The last three columns list the classification accuracy over D66, D160, and D255, respectively.

Table 11.
Comparison with other Methods based on 10 × K-fold SCV (# stands for number).
| Existing Algorithms | Feature # | Run # | Accuracy | ||
|---|---|---|---|---|---|
| D66 | D160 | D255 | |||
| DWT+SOM [12] | 4761 | 5 | 94.00 | 93.17 | 91.65 |
| DWT+SVM [12] | 4761 | 5 | 96.15 | 95.38 | 94.05 |
| DWT + SVM + RBF [12] | 4761 | 5 | 98.00 | 97.33 | 96.18 |
| DWT + PCA + ANN [13] | 7 | 5 | 97.00 | 96.98 | 95.29 |
| DWT + PCA + KNN [13] | 7 | 5 | 98.00 | 97.54 | 96.79 |
| DWT + PCA + SCG-FNN [14] | 19 | 5 | 100.00 | 99.27 | 98.82 |
| DWT + PCA + SVM [15] | 19 | 5 | 96.01 | 95.00 | 94.29 |
| DWT + PCA + SVM + HPOL [15] | 19 | 5 | 98.34 | 96.88 | 95.61 |
| DWT + PCA + SVM + IPOL [15] | 19 | 5 | 100.00 | 98.12 | 97.73 |
| DWT + PCA + SVM + RBF [15] | 19 | 5 | 100.00 | 99.38 | 98.82 |
| WE + SWP + PNN [16] | 3 | 10 | 100.00 | 99.94 | 98.86 |
| RT + PCA + LS-SVM [19] | 9 | 5 | 100.00 | 100.00 | 99.39 |
| PCNN + DWT + PCA + BPNN [21] | 7 | 10 | 100.00 | 98.88 | 98.24 |
| DWPT + SE + GEPSVM [23] | 16 | 10 | 99.85 | 99.62 | 98.78 |
| DWPT + TE + GEPSVM [23] | 16 | 10 | 100.00 | 100.00 | 99.33 |
| SWT + PCA + IABAP-FNN [30] | 7 | 10 | 100.00 | 99.44 | 99.18 |
| SWT + PCA + ABC-SPSO-FNN [30] | 7 | 10 | 100.00 | 99.75 | 99.02 |
| SWT + PCA + HPA-FNN [30] | 7 | 10 | 100.00 | 100.00 | 99.45 |
| WE + HMI + GEPSVM [33] | 14 | 10 | 100.00 | 99.56 | 98.63 |
| WE + HMI + GEPSVM + RBF [33] | 14 | 10 | 100.00 | 100.00 | 99.45 |
| FRFE + WTT + TSVM (Proposed) | 12 | 10 | 100 | 100.00 | 99.57 |
Table 11 shows that D66 contains too few instances so that many algorithms achieve accuracy of 100%. For the D160, four algorithms achieve perfect classification. They are RT + PCA + LS-SVM [19], DWPT + TE + GEPSVM [23], SWT + PCA + HPA-FNN [30], WE + HMI + GEPSVM + RBF [33], and the proposed method of “FRFE + WTT + TSVM”. D255 is the most difficult one and no one yields a perfect classification. Among all algorithms, the proposed “FRFE + WTT + TSVM” yields the highest accuracy of 99.57%.
Comparing to “SWT + PCA + HPA-FNN [30]” with accuracy of 99.45% over D255, our method increases this about 0.12%. Although the improvement is slight, it is obtained by 10 repetitions of 5-fold stratified cross validation, which means the improvement is robust and reliable. SWT + PCA + HPA-FNN [30] used seven features and proved seven features is the best feature combination, and introducing new features will not improve their accuracy. It does not cost too much time for our method to use 14 features (double of that of SWT + PCA), since 14 features are not a burden to classifiers in current computers.
Our contributions are: (i) we are the first to propose a novel image feature called “Fractional Fourier Entropy (FRFE)”; (ii) WTT is employed to select important FRFEs; (iii) the proposed system “FRFE + WTT + TSVM” is superior to 20 state-of-the-art methods w.r.t. pathological brain detection.
9. Conclusions and Future Research
In this paper, we proposed a novel image feature—Fractional Fourier Entropy (FRFE)—and then use Welch’s t-test (WTT) to select important FRFEs for developing a PBD system. We finally tested four classifiers (NBC, SVM, GEPSVM, and TSVM). The simulation results showed that the proposed “FRFE + WTT + TSVM” yield better results than both other three proposed methods (FRFE + WTT + NBC, FRFE + WTT + SVM, and FRFE + WTT + GEPSVM) and 20 state-of-the-art approaches. Our PBD system may be further applied to brains with more complicated pathological conditions.
In the future research may be performed on the following points: (1) to develop evaluation methods to measure the influence from different values of α and β; (2) trying to consider the use of the least-squares technique to further improve the performance of SVM and NPSVMs; (3) application the FRFE to other pattern recognition problems, such as fruit classification [61] and tea classification [62]; (4) testing kernel methods [63]; (4) mutual entropy [64] will be introduced to test its performance in feature selection; (5) our method may be applied to X-ray [65], AD images [66], and CT images; (6) support vector data description (SVDD) [67] is commonly used for detecting novel data or outliers, so we will get more medical image data, and test SVDD; (7) swarm intelligence approaches [68] may be applied to help train classifiers.
Acknowledgments
This paper was supported by NSFC (51407095, 61503188), Natural Science Foundation of Jiangsu Province (BK20150982, BK20150983), Jiangsu Key Laboratory of 3D Printing Equipment and Manufacturing (BM2013006), Key Supporting Science and Technology Program (Industry) of Jiangsu Province (BE2012201, BE2013012-2, BE2014009-3), Program of Natural Science Research of Jiangsu Higher Education Institutions (13KJB460011, 14KJB480004, 14KJB520021, 15KJB470010), Special Funds for Scientific and Technological Achievement Transformation Project in Jiangsu Province (BA2013058), Nanjing Normal University Research Foundation for Talented Scholars (2013119XGQ0061, 2014119XGQ0080), Open Fund of Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology (15-140-30-008K).
Author Contributions
Shuihua Wang and Yudong Zhang conceived this study; Yudong Zhang and Xiaojun Yang designed this model; Ping Sun, Zhengchao Dong, and Aijun Liu acquired the data; Yudong Zhang and Ti-Fei Yuan processed the data; Shuihua Wang, Yudong Zhang, and Ti-Fei Yuan analyzed the results; Yudong Zhang and Aijun Liu developed the program; Shuihua Wang, Yudong Zhang, and Xiaojun Yang wrote the draft; Zhengchao Dong and Aijun Liu gave critical revision. All authors have read and approved the final manuscript.
Conflict of interest
We have no conflicts of interest to disclose with regard to the subject matter of this paper.
Nomenclature
| Abbreviation | Definition |
| (A)(BP)(F)(PC)NN | (Artificial) (Back-propagation) (Feed-forward) (Pulse-coupled) neural network |
| (D)(S)W(P)T | (Discrete) (Stationary) wavelet (packet) transform |
| (H)(I)POL | (Homogeneous) (Inhomogeneous) Polynomial |
| (I)(D)(S)FT | (Inverse) (Discrete) (Standard) Fourier Transform |
| (k)(F)(LS)(GEP)(NP)SVM | (kernel) (Fuzzy) (Lease-Square) (Generalized eigenvalue proximal) (Non-Parallel) Support vector machine |
| (S)(C)ABC(-SPSO) | (Scaled) (Chaotic) Artificial bee colony (-Standard PSO) |
| (W)(P)(S)(T)E | (Wavelet) (Packet) (Shannon) (Tsallis) entropy |
| CAD | Computer-aided diagnosis |
| CM | Confusion matrix |
| FRF(T)(E)(D) | Fractional Fourier (Transform) (Entropy) (Domain) |
| HPA | Hybridization of PSO and ABC |
| IABAP | Integrated algorithm based on ABC and PSO |
| IC | Information Content |
| KNN | K-nearest neighbors |
| MD | Mahalanobis distance |
| MR(I) | Magnetic resonance (imaging) |
| NBC | Naive Bayesian Classifier |
| PCA | Principal Component Analysis |
| PNN | Probabilistic neural network |
| PSO | Particle Swarm Optimization |
| QP | Quadratic programming |
| RBF | Radial Basis Function |
| RQ | Rayleigh Quotient |
| RT | Ripplet transform |
| SCV | Stratified cross validation |
| SD | Standard deviation |
| SOM | Self-organizing map |
References
- Zhang, Y.; Dong, Z.; Phillips, P.; Wang, S.; Ji, G.; Yang, J. Exponential Wavelet Iterative Shrinkage Thresholding Algorithm for compressed sensing magnetic resonance imaging. Inf. Sci. 2015, 322, 115–132. [Google Scholar] [CrossRef]
- Goh, S.; Dong, Z.; Zhang, Y.; DiMauro, S.; Peterson, B.S. Mitochondrial dysfunction as a neurobiological subtype of autism spectrum disorder: Evidence from brain imaging. JAMA Psychiatry 2014, 71, 665–671. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, S.; Ji, G.; Dong, Z. Exponential wavelet iterative shrinkage thresholding algorithm with random shift for compressed sensing magnetic resonance imaging. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 116–117. [Google Scholar] [CrossRef]
- Thorsen, F.; Fite, B.; Mahakian, L.M.; Seo, J.W.; Qin, S.; Harrison, V.; Johnson, S.; Ingham, E.; Caskey, C.; Sundstrøm, T.; et al. Multimodal imaging enables early detection and characterization of changes in tumor permeability of brain metastases. J. Controll. Release 2013, 172, 812–822. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, S.; Wu, L. A Novel Method for Magnetic Resonance Brain Image Classification based on Adaptive Chaotic PSO. Prog. Electromagn. Res. 2010, 109, 325–343. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Dong, Z. Classification of Alzheimer Disease Based on Structural Magnetic Resonance Imaging by Kernel Support Vector Machine Decision Tree. Prog. Electromagn. Res. 2014, 144, 171–184. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Liu, A.; Wang, S.; Ji, G.; Zhang, Z.; Yang, J. Magnetic Resonance Brain Image Classification via Stationary Wavelet Transform and Generalized Eigenvalue Proximal Support Vector Machine. J. Med. Imaging Health Inf. 2015, 5, 1395–1403. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Wang, S. Magnetic Resonance Brain Image Classification by an Improved Artificial Bee Colony Algorithm. Prog. Electromagn. Res. 2011, 116, 65–79. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S. Detection of Alzheimer’s disease by displacement field and machine learning. PeerJ 2015, 3. [Google Scholar] [CrossRef] [PubMed]
- Birlutiu, A.; d’Alche-Buc, F.; Heskes, T. A Bayesian Framework for Combining Protein and Network Topology Information for Predicting Protein-Protein Interactions. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 12, 538–550. [Google Scholar] [CrossRef] [PubMed]
- Mehrkanoon, S.; Huang, X.; Suykens, J.A.K. Non-parallel support vector classifiers with different loss functions. Neurocomputing 2014, 143, 294–301. [Google Scholar] [CrossRef]
- Chaplot, S.; Patnaik, L.M.; Jagannathan, N.R. Classification of magnetic resonance brain images using wavelets as input to support vector machine and neural network. Biomed. Signal Process. Control 2006, 1, 86–92. [Google Scholar] [CrossRef]
- El-Dahshan, E.-S.A.; Hosny, T.; Salem, A.-B.M. Hybrid intelligent techniques for MRI brain images classification. Digit. Signal Process. 2010, 20, 433–441. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Wu, L.; Wang, S. A hybrid method for MRI brain image classification. Expert Syst. Appl. 2011, 38, 10049–10053. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. An MR Brain Images Classifier via Principal Component Analysis and Kernel Support Vector Machine. Prog. Electromagn. Res. 2012, 130, 369–388. [Google Scholar] [CrossRef]
- Saritha, M.; Joseph, K.P.; Mathew, A.T. Classification of MRI brain images using combined wavelet entropy based spider web plots and probabilistic neural network. Pattern Recognit. Lett. 2013, 34, 2151–2156. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Ji, G.; Wang, S. Effect of spider-web-plot in MR brain image classification. Pattern Recognit. Lett. 2015, 62, 14–16. [Google Scholar] [CrossRef]
- Zhang, Y.-D.; Wang, S.-H.; Yang, X.-J.; Dong, Z.-C.; Liu, G.; Phillips, P.; Yuan, T.-F. Pathological brain detection in MRI scanning by wavelet packet Tsallis entropy and fuzzy support vector machine. SpringerPlus 2015, 4. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Chowdhury, M.; Kundu, M.K. Brain MR Image Classification Using Multiscale Geometric Analysis of Ripplet. Prog. Electromagn. Res. 2013, 137. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G.; Dong, Z. An MR Brain Images Classifier System via Particle Swarm Optimization and Kernel Support Vector Machine. Sci. World J. 2013, 2013, 130134. [Google Scholar] [CrossRef] [PubMed]
- El-Dahshan, E.-S.A.; Mohsen, H.M.; Revett, K.; Salem, A.-B.M. Computer-aided diagnosis of human brain tumor through MRI: A survey and a new algorithm. Expert Syst. Appl. 2014, 41, 5526–5545. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, S.; Xu, W.; Ji, G.; Phillips, P.; Sun, P.; Zhang, Y. Detection of Pathological Brain in MRI Scanning Based on Wavelet-Entropy and Naive Bayes Classifier. In Bioinformatics and Biomedical Engineering; Springer: Berlin/Heidelberg, Germany, 2015; pp. 201–209. [Google Scholar]
- Zhang, Y.; Dong, Z.; Wang, S.; Ji, G.; Yang, J. Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM). Entropy 2015, 17, 1795–1813. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, Y.; Yang, J.; Ji, G.; Dong, Z.; Wang, S.; Feng, C.; Wang, Q. Automated classification of brain images using wavelet-energy and biogeography-based optimization. Multimedia Tools Appl. 2015. [Google Scholar] [CrossRef]
- Damodharan, S.; Raghavan, D. Combining Tissue Segmentation and Neural Network for Brain Tumor Detection. Int. Arab J. Inf. Technol. 2015, 12, 42–52. [Google Scholar]
- Zhang, G-S.; Wang, Q.; Feng, C.; Lee, E.; Ji, G.; Wang, S.; Zhang, Y.; Yan, J. Automated Classification of Brain MR Images Using Wavelet-Energy and Support Vector Machines. In Proceedings of the 2015 International Conference on Mechatronics, Electronic, Industrial and Control Engineering (MEIC 2015), Shenyang, China, 1–3 April 2015; pp. 683–686.
- Wang, S.; Ji, G.; Phillips, P.; Dong, Z.; Zhang, Y. Application of genetic algorithm and kernel support vector machine to pathological brain detection in MRI Scanning. In Proceedings of the 2nd National Conference on Information Technology and Computer Science (CITCS 2015), Shanghai, China, 21–22 March 2015.
- Nazir, M.; Wahid, F.; Khan, S.A. A simple and intelligent approach for brain MRI classification. J. Intell. Fuzzy Syst. 2015, 28, 1127–1135. [Google Scholar]
- Harikumar, R.; Kumar, B.V. Performance Analysis of Neural Networks for Classification of Medical Images with Wavelets as a Feature Extractor. Int. J. Imaging Syst. Technol. 2015, 25, 33–40. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Dong, Z.; Du, S.; Ji, G.; Yan, J.; Yang, J.; Wang, Q.; Feng, C.; Phillips, P. Feed-forward neural network optimized by hybridization of PSO and ABC for abnormal brain detection. Int. J. Imaging Syst. Technol. 2015, 25, 153–164. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Dong, Z.; Phillips, P.; Ji, G.; Yang, J. Pathological brain detection in magnetic resonance imaging scanning by wavelet entropy and hybridization of biogeography-based optimization and particle swarm optimization. Prog. Electromagn. Res. 2015, 152, 41–58. [Google Scholar] [CrossRef]
- Farzan, A.; Mashohor, S.; Ramli, A.R.; Mahmud, R. Boosting diagnosis accuracy of Alzheimer’s disease using high dimensional recognition of longitudinal brain atrophy patterns. Behav. Brain Res. 2015, 290, 124–130. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, S.; Sun, P.; Phillips, P. Pathological brain detection based on wavelet entropy and Hu moment invariants. Bio-Med. Mater. Eng. 2015, 26, S1283–S1290. [Google Scholar] [CrossRef] [PubMed]
- Munteanu, C.R.; Fernandez-Lozano, C.; Abad, V.M.; Fernández, S.P.; Álvarez-Linera, J.; Hernández-Tamames, J.A.; Pazos, A. Classification of mild cognitive impairment and Alzheimer’s Disease with machine-learning techniques using 1H Magnetic Resonance Spectroscopy data. Expert Syst. Appl. 2015, 42, 6205–6214. [Google Scholar] [CrossRef]
- Savio, A.; Graña, M. Local activity features for computer aided diagnosis of schizophrenia on resting-state fMRI. Neurocomputing 2015, 164, 154–161. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Phillips, P.; Dong, Z.; Ji, G.; Yang, J. Detection of Alzheimer's disease and mild cognitive impairment based on structural volumetric MR images using 3D-DWT and WTA-KSVM trained by PSOTVAC. Biomed. Signal Process. Control 2015, 21, 58–73. [Google Scholar] [CrossRef]
- Ajmera, P.K.; Holambe, R.S. Fractional Fourier transform based features for speaker recognition using support vector machine. Comput. Electr. Eng. 2013, 39, 550–557. [Google Scholar] [CrossRef]
- Cattani, C. Harmonic wavelet approximation of random, fractal and high frequency signals. Telecommun. Syst. 2010, 43, 207–217. [Google Scholar] [CrossRef]
- Atangana, A.; Jafari, H.; Belhaouari, S.B.; Bayram, M. Partial Fractional Equations and Their Applications. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Cagatay, N.D.; Datcu, M. FrFT-Based Scene Classification of Phase-Gradient InSAR Images and Effective Baseline Dependence. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1131–1135. [Google Scholar] [CrossRef]
- Shih, C.-C. Fractionalization of Fourier transform. Opt. Commun. 1995, 118, 495–498. [Google Scholar] [CrossRef]
- Santhanam, B.; McClellan, J.H. The discrete rotational Fourier transform. IEEE Trans. Signal Process. 1996, 44, 994–998. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Arikan, O.; Kutay, M.A.; Bozdagt, G. Digital computation of the fractional Fourier transform. IEEE Trans. Signal Process. 1996, 44, 2141–2150. [Google Scholar] [CrossRef]
- Cattani, C. Fractional Calculus and Shannon Wavelet. Math. Probl. Eng. 2012, 2012, 502812. [Google Scholar] [CrossRef]
- Heskes, T.; Eisinga, R.; Breitling, R. A fast algorithm for determining bounds and accurate approximate p-values of the rank product statistic for replicate experiments. BMC Bioinform. 2014, 15. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.; Phillips, P.; Wang, S.; Ji, G.; Yang, J.; Yuan, T.-F. Detection of subjects and brain regions related to Alzheimer’s disease using 3D MRI scans based on eigenbrain and machine learning. Front. Comput. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Modesitt, S.C.; Hallowell, P.T.; Slack-Davis, J.K.; Michalek, R.D.; Atkins, K.A.; Kelley, S.L.; Arapovic, S.; Shupnik, M.A.; Hoehn, K. Women at extreme risk for obesity-related carcinogenesis: Baseline endometrial pathology and impact of bariatric surgery on weight, metabolic profiles and quality of life. Gynecol. Oncol. 2015, 138, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.H.; Park, H.J.; Jung, Y.W.; Shim, S.H.; Sung, S.R.; Park, J.E.; Cha, D.H.; Ahn, E.H. Comparative Transcriptome Analysis of Cell-Free Fetal RNA from Amniotic Fluid and RNA from Amniocytes in Uncomplicated Pregnancies. PLoS ONE 2015, 10, e0132955. [Google Scholar] [CrossRef] [PubMed]
- Maswadeh, W.M.; Snyder, A.P. Variable ranking based on the estimated degree of separation for two distributions of data by the length of the receiver operating characteristic curve. Anal. Chimica Acta 2015, 876, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-D.; Wu, C.-W.; Wu, T.-Y.; Wang, C.-C. Multi-Scale Analysis Based Ball Bearing Defect Diagnostics Using Mahalanobis Distance and Support Vector Machine. Entropy 2013, 15, 416–433. [Google Scholar] [CrossRef]
- Mangasarian, O.L.; Wild, E.W. Multisurface proximal support vector machine classification via generalized eigenvalues. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Khemchandani, R.; Karpatne, A.; Chandra, S. Generalized eigenvalue proximal support vector regressor. Expert Syst. Appl. 2011, 38, 13136–13142. [Google Scholar] [CrossRef]
- Shao, Y.-H.; Deng, N.-Y.; Chen, W.-J.; Wang, Z. Improved Generalized Eigenvalue Proximal Support Vector Machine. IEEE Signal Process. Lett. 2013, 20, 213–216. [Google Scholar] [CrossRef]
- Khemchandani, R.; Chandra, S. Twin support vector machines for pattern classification. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 905–910. [Google Scholar]
- Nasiri, J.A.; Charkari, N.M.; Mozafari, K. Energy-based model of least squares twin Support Vector Machines for human action recognition. Signal Process. 2014, 104, 248–257. [Google Scholar] [CrossRef]
- Xu, Z.; Qi, Z.; Zhang, J. Learning with positive and unlabeled examples using biased twin support vector machine. Neural Comput. Appl. 2014, 25, 1303–1311. [Google Scholar] [CrossRef]
- Shao, Y.-H.; Chen, W.-J.; Zhang, J.-J.; Wang, Z.; Deng, N.-Y. An efficient weighted Lagrangian twin support vector machine for imbalanced data classification. Pattern Recognit. 2014, 47, 3158–3167. [Google Scholar] [CrossRef]
- Kašćelan, L.; Kašćelan, V.; Jovanović, M. Hybrid support vector machine rule extraction method for discovering the preferences of stock market investors: Evidence from Montenegro. Intell. Autom. Soft Comput. 2015, 21, 503–522. [Google Scholar] [CrossRef]
- Kumar, M.A.; Gopal, M. Least squares twin support vector machines for pattern classification. Expert Syst. Appl. 2009, 36, 7535–7543. [Google Scholar] [CrossRef]
- Ding, S.; Yu, J.; Qi, B.; Huang, H. An overview on twin support vector machines. Artif. Intell. Rev. 2014, 42, 245–252. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Ji, G.; Yang, J.; Wu, J.; Wei, L. Fruit Classification by Wavelet-Entropy and Feedforward Neural Network Trained by Fitness-Scaled Chaotic ABC and Biogeography-Based Optimization. Entropy 2015, 17, 5711–5728. [Google Scholar] [CrossRef]
- Wang, S.; Yang, X.; Zhang, Y.; Phillips, P.; Yang, J.; Yuan, T.-F. Identification of Green, Oolong and Black Teas in China via Wavelet Packet Entropy and Fuzzy Support Vector Machine. Entropy 2015, 17, 6663–6682. [Google Scholar] [CrossRef]
- Alama, J.; Heskes, T.; Kühlwein, D.; Tsivtsivadze, E.; Urban, J. Premise Selection for Mathematics by Corpus Analysis and Kernel Methods. J. Autom. Reason. 2014, 52, 191–213. [Google Scholar] [CrossRef]
- Fang, L.; Zhao, H.; Wang, P.; Yu, M.; Yan, J.; Cheng, W.; Chen, P. Feature selection method based on mutual information and class separability for dimension reduction in multidimensional time series for clinical data. Biomed. Signal Process. Control 2015, 21, 82–89. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, D.; Nie, C.; Luo, L.; Chen, W.; Yin, X.; Lin, Y. Bayesian statistical reconstruction for low-dose X-ray computed tomography using an adaptive-weighting nonlocal prior. Comput. Med. Imaging Graph. 2009, 33, 495–500. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liu, G.; Yuan, T.F. Detection of Alzheimer’s disease by three-dimensional displacement field estimation in structural magnetic resonance imaging. J. Alzheimer Disease. 2016, 50, 1–23. [Google Scholar]
- Kim, S.; Choi, Y.; Lee, M. Deep learning with support vector data description. Neurocomputing 2015, 165, 111–117. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 501, 931256. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).